Применение графического метода и симплекс-метода для решения задач линейного программирования
Содержание
Введение
Задание
1. Графический метод
решения задачи линейного программирования
2. Решение задачи
линейного программирования симплекс-методом
3. Решение задачи
двойственной к исходной
4. Решение транспортной
задачи
Выводы
Введение
Исследование операций - это математическая дисциплина, занимающаяся
разработкой и применением методов нахождения наилучших решений в различных
областях человеческой деятельности.
Под операциями обычно понимают целенаправленные управляемые процессы.
Природа их может быть различной - это могут быть военные действия,
производственные процессы, коммерческие мероприятия, административные решения,
и т.д. Что интересно - операции эти (совершенно несхожие по своей природе)
могут быть описаны одними и теми же математическими моделями, более того,
анализ этих моделей позволяет лучше понять суть того или иного явления и даже
предсказать его дальнейшее развитие. Мир, как оказалось, устроен необычайно
компактно (в информационном смысле), поскольку одна и та же информационная схема
реализуется в самых разных физических (и не только физических) проявлениях. В
кибернетике это называется термином "изоморфизм моделей".
Если бы не изоморфизм моделей, для каждой конкретной ситуации пришлось бы
отыскивать собственный, уникальный метод решения, и исследование операций как
научное направление не сформировалось бы. К счастью, дело обстоит иначе.
Благодаря наличию общих закономерностей в развитии самых разных систем возможно
исследование их математическими методами. Исследование операций как математический
инструментарий, поддерживающий процесс принятия решений в самых разных областях
человеческой деятельности, как совокупность средств, позволяющих обеспечить
лицо, принимающее решение, необходимой количественной информацией, полученной
научными методами, сформировалось на стыке математики и разнообразных
социально-экономических дисциплин. Свой вклад в его становление внесли
представители самых различных областей науки.
Одним из разделов исследования операций является линейное
программирование. Можно сказать, что линейное программирование применимо для
построения математических моделей тех процессов, в основу которых может быть
положена гипотеза линейного представления реального мира: экономических задач,
задач управления и планирования, оптимального размещения оборудования и пр.
Задачами линейного программирования называются задачи, в которых линейны
как целевая функция, так и ограничения в виде равенств и неравенств. Кратко
задачу линейного программирования можно сформулировать следующим образом: найти
вектор значений переменных, доставляющих экстремум линейной целевой функции при
m ограничениях в виде линейных равенств или неравенств.
Итак, линейное программирование - это наука о методах исследования и
отыскания наибольших и наименьших значений линейной функции, на неизвестные
которой наложены линейные ограничения. Таким образом, задачи линейного
программирования относятся к задачам на условный экстремум функции.
Рассмотрим вкратце два метода решения задач линейного программирования:
графический и симплекс-метод; также рассмотрим транспортную задачу, которая
тоже является задачей линейного программирования и может быть решена
симплекс-методом, но поскольку она имеет своеобразную матрицу ограничений, то
для нее разработаны специальные методы решения.
Графический метод довольно прост и нагляден для решения задач линейного
программирования с двумя переменными. Он основан на геометрическом
представлении допустимых решений и целевой функции задачи.
Каждое из неравенств задачи линейного программирования определяет на
координатной плоскости некоторую полуплоскость, а система неравенств в целом -
пересечение соответствующих плоскостей. Множество точек пересечения данных
полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда
представляет собой выпуклую фигуру.
Вектор C = (c1, c2) с координатами из коэффициентов
целевой функции при x1 и x2 перпендикулярен к каждой из линий уровня. Направление
вектора C совпадает с направлением возрастания
целевой функции, что является важным моментом для решения задачи. Направление
убывания целевой функции противоположно направлению вектора C.
Суть графического метода заключается в следующем. По направлению (против
направления) вектора C в
ОДР производится поиск оптимальной точки x* = (x1*, x2*). Оптимальной считается точка, через которую проходит линия
уровня Lmax (Lmin), соответствующая наибольшему
(наименьшему) значению функции L(x). Оптимальное решение всегда
находится на границе ОДР, например, в последней вершине многоугольника ОДР,
через которую пройдет целевая прямая, или на всей его стороне.
Симплекс-метод - алгоритм решения оптимизационной задачи линейного
программирования путём перебора вершин выпуклого многогранника в многомерном
пространстве.
Суть симплекс-метода состоит в следующем:
. Находят какое-либо допустимое базисное решение. Его можно найти, приняв
какие-либо m-n переменные за свободные, приравняв их к нулю и решив
получившуюся систему уравнений. Если при этом некоторые из базисных переменных
окажутся отрицательными, то нужно выбрать другие свободные переменные, т.е.
перейти к новому базису.
. Проверяют, не достигнут ли уже максимум целевой функции при найденном
допустимом базисном решении.
. Если оптимальное решение не найдено, то ищут новое допустимое базисное
решение, но не любое, а такое, которое увеличивает значение целевой функции.
Проверку того, достигнут ли при найденном допустимом решении максимум
целевой функции, можно сделать путем поиска нового базисного решения. Для
перехода к новому базисному решению одну из свободных переменных следует
сделать базисной, при этом она будет отличаться от нуля, т.е. возрастет.
Следовательно, если какая-либо из свободных переменных входит в выражение для
целевой функции со знаком плюс и при ее увеличении целевая функция
увеличивается, то максимум целевой функции не достигнут, и данную переменную
следует превратить в базисную, сделав ее отличной от нуля. Однако при
возрастании свободной переменной некоторые из базисных переменных будут
уменьшаться. Поскольку отрицательные значения переменных недопустимы, то в
качестве новой свободной переменной следует принять ту из базисных переменных,
которая раньше других обращается в нуль.
Транспортная
задача является задачей линейного программирования. Для ее решения применяют
также симплекс-метод, но в силу специфики задачи здесь можно обойтись без
симплекс-таблиц. Решение можно получить путем некоторых преобразований таблицы
перевозок. Эти преобразования соответствуют переходу от одного плана перевозок
к другому. Но, как и в общем случае, оптимальное решение ищется среди базисных
решений. Следовательно, мы будем иметь дело только с базисными (или опорными)
планами. Так как в данном случае ранг системы ограничений-уравнений равен 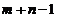 то среди всех
то среди всех  неизвестных
неизвестных
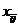 выделяется
выделяется 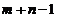 базисных
неизвестных, а остальные
базисных
неизвестных, а остальные  ·
· неизвестных являются свободными. В базисном решении
свободные неизвестные равны нулю. Обычно эти нули в таблицу не вписывают,
оставляя соответствующие клетки пустыми. Таким образом, в таблице перевозок,
представляющей опорный план, мы имеем
неизвестных являются свободными. В базисном решении
свободные неизвестные равны нулю. Обычно эти нули в таблицу не вписывают,
оставляя соответствующие клетки пустыми. Таким образом, в таблице перевозок,
представляющей опорный план, мы имеем 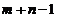 заполненных
и
заполненных
и  ·
· пустых клеток.
пустых клеток.
симплекс графический программирование
Задание
1. Решить задачу линейного программирования графическим
методом.
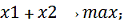
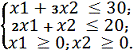
2. Решить задачу линейного программирования симплекс-методом,
сформулировать и решить двойственную к исходной задаче.
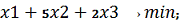

3. Имеются три пункта поставки однородного груза - А1;
А2; А3 и пять пунктов потребления этого груза - В1;
В2; В3; В4; В5. В пунктах А1;
А2; А3 находится 200; 450; 250 единиц груза
соответственно, который надо доставить в пункты В1; В2; В3;
В4; В5 в количестве 100; 125; 325; 250; 100
соответственно. Расстояние между пунктами задано в километрах следующей матрицей:
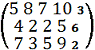
Требуется найти оптимальный план закрепления потребителей за
поставщиками однородного груза при условии минимизации общего пробега
автомобилей. Рассмотреть два метода получения начального плана.
1. Графический метод решения задачи линейного
программирования
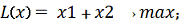
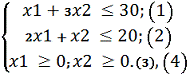
Построим прямые ограничений, для чего вычислим координаты
точек пересечения этих прямых с осями координат. Из условий ограничения получим
область допустимых значений G
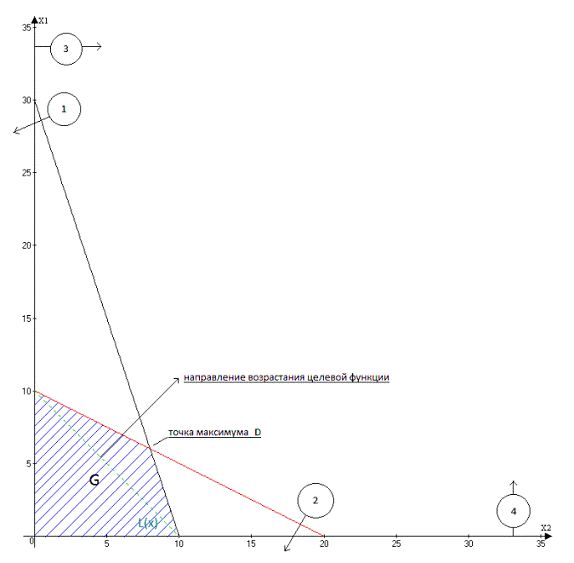
Рисунок 1. Графический метод решения задачи линейного программирования.
Направление возрастания целевой функции указано на рисунке 1.
Соответственно, точкой максимума является точка D. Найдем ее координаты исходя из того, что она является
точкой пересечения графиков (1) и (2). Для этого решим систему уравнений:
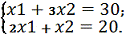
Решением
этой системы уравнений будут координаты точки D: x1 =
6, x2 = 8. Подставляя эти значения в целевую функцию,
получим окончательный ответ: 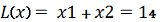
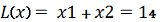 .
.
.
Решение задачи линейного программирования симплекс-методом
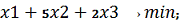

Запишем задачу в канонической форме как того требует симплекс-метод, для
этого введем две переменные y4 и y5, получим:
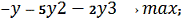
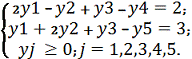
В получившейся системе отсутствуют базисные переменные, поэтому в первое
и второе уравнения добавляем искусственные переменные y6 и y7. Чтобы можно было применить
симплекс-метод система уравнений-ограничений должна быть системой с базисом,
т.е. в каждом уравнении должна быть переменная с коэффициентом 1, которая
входит только в одно уравнение системы, в нашем случае это y6 и y7. Получаем, так называемую, М-задачу:
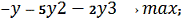
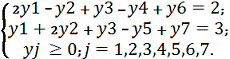 = (0, 0, 0, 0, 0, 2, 3)T
= (0, 0, 0, 0, 0, 2, 3)T
Данная система является системой с базисом, следовательно, для решения
можно применить симплекс-метод. Запишем начальную симплекс-таблицу:
|
БП
|
y1
|
y2
|
y3
|
y4
|
y5
|
y6
|
y7
|
Решение
|
Отношение
|
|
f
|
1
|
5
|
2
|
0
|
0
|
0
|
0
|
0
|
-
|
|
y6
|
2
|
-1
|
1
|
-1
|
0
|
1
|
0
|
2
|
2/2 = 1
|
|
y7
|
1
|
2
|
1
|
0
|
-1
|
0
|
1
|
3
|
3/1 = 3
|
|
φ
|
-3
|
-1
|
-2
|
1
|
1
|
-1
|
-1
|
-
|
-
|
В данную таблицу добавлена строка «φ». Она получается суммированием
соответствующих коэффициентов строк с искусственными переменными (y6 и y7) с обратным знаком. Она будет
присутствовать в таблице до тех пор, пока хотя бы одна из искусственных
переменных есть в базисе. По наибольшему по модулю отрицательному коэффициенту
строки «φ»
определяется разрешающий
столбец, пока она есть в таблице. Когда строка «φ» выйдет из таблицы (в базисе нет
искусственных переменных), разрешающий столбец будет определяться по строке f. В данной таблице разрешающий
столбец y1, он выбран по наибольшей по модулю отрицательной
оценке (-3). Разрешающая строка y6 выбрана по наименьшему отношению
столбца "Решение" к соответствующим положительным элементам
разрешающего столбца. Это значит, что на следующей итерации симплекс-метода
переменная y1 из свободной перейдет в базисную, а переменная y6 из базисной - в свободную. Запишем следующую
симплекс-таблицу:
|
БП
|
y1
|
y2
|
y3
|
y4
|
y5
|
y6
|
y7
|
Решение
|
Отношение
|
|
f
|
0
|
11/2
|
3/2
|
1/2
|
0
|
-1/2
|
0
|
-1
|
-2/11
|
|
y1
|
1
|
-1/2
|
1/2
|
-1/2
|
0
|
1/2
|
0
|
1
|
-
|
|
y7
|
0
|
5/2
|
1/2
|
1/2
|
-1
|
-1/2
|
1
|
2
|
4/5
|
|
φ
|
0
|
-5/2
|
-1/2
|
-1/2
|
1
|
1/2
|
-1
|
-
|
-
|
На следующей итерации строка «φ» выходит из таблицы, так как в
базисе не остается искусственных переменных:
|
БП
|
y1
|
y2
|
y3
|
y4
|
y5
|
y6
|
y7
|
Решение
|
Отношение
|
|
f
|
0
|
0
|
2/5
|
-3/5
|
11/5
|
3/5
|
-11/5
|
-27/5
|
9
|
|
y1
|
1
|
0
|
3/5
|
-2/5
|
-1/5
|
2/5
|
1/5
|
7/5
|
-
|
|
y2
|
0
|
1
|
1/5
|
1/5
|
-2/5
|
-1/5
|
2/5
|
4/5
|
4
|
|
БП
|
y1
|
y2
|
y3
|
y4
|
y5
|
y6
|
y7
|
Решение
|
Отношение
|
|
f
|
0
|
3
|
1
|
0
|
8/5
|
0
|
-1
|
-3
|
|
|
y1
|
1
|
2
|
1
|
0
|
-1
|
0
|
1
|
3
|
|
|
y4
|
0
|
5
|
1
|
1
|
-2
|
-1
|
2
|
4
|
|
В строке f все
коэффициенты неотрицательны кроме коэффициента при искусственной переменной y7, который не влияет на оптимальность, когда
искусственные переменные вышли из базиса. Следовательно, симплекс-методом
получено оптимальное решение: Y =
(3, 0, 0, 4, 0, 0, 0)T,
X = (3, 0, 0), f = 3 + 5*0 + 2*0 = 3.
. Решение задачи двойственной к исходной
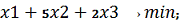

Приведем систему неравенств и целевую функцию к следующему виду:
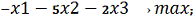

Составим следующие векторы и матрицу коэффициентов:
c = (-1, -5, -2) -коэффициенты целевой функции;
b = (-2, -3) - свободные коэффициенты;
A = 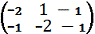
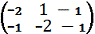 - коэффициенты
из приведенной системы неравенств.
- коэффициенты
из приведенной системы неравенств.
Сформулируем
двойственную к исходной задачу на основе полученных коэффициентов. Свободные
коэффициенты станут коэффициентами новой целевой функции, коэффициенты целевой
функции станут новыми свободными коэффициентами, а коэффициенты системы
неравенств образуют новую систему неравенств следующего вида:
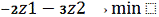
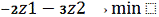 ;
;
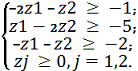
Запишем задачу в канонической форме для возможности применить
симплекс-метод, для этого введем три переменные w3, w4, w5:
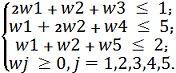 = (0, 0, 1, 2, 5)T
= (0, 0, 1, 2, 5)T
Данная система является системой с базисом, следовательно, для решения
можно применить симплекс-метод. Запишем начальную симплекс-таблицу:
|
БП
|
w1
|
w2
|
w3
|
w4
|
w5
|
Решение
|
Отношение
|
|
f
|
-2
|
-3
|
0
|
0
|
0
|
0
|
-
|
|
w3
|
2
|
1
|
1
|
0
|
0
|
1
|
1/1 = 1
|
|
w4
|
-1
|
2
|
0
|
1
|
0
|
5
|
5/2 = 2.5
|
|
w5
|
1
|
1
|
0
|
0
|
1
|
2
|
2/1 = 2
|
|
БПw1w2w3w4w5РешениеОтношение
|
|
|
|
|
|
|
|
|
f
|
4
|
0
|
3
|
0
|
0
|
3
|
|
|
w2
|
2
|
1
|
1
|
0
|
0
|
1
|
|
|
w4
|
-5
|
0
|
-2
|
1
|
0
|
3
|
|
|
w5
|
-3
|
0
|
-2
|
0
|
1
|
0
|
|
В строке f все
коэффициенты неотрицательны, следовательно, симплекс-методом получено
оптимальное решение: W =
(0, 1, 0, 3, 0)T, Z = (0, 1), f = 3.
. Решение транспортной задачи
Метод северо-западного угла:
Составим опорный план в соответствие с условием задачи:
|
МП/СП
|
100
|
125
|
325
|
250
|
100
|
|
|
200
|
5 100
|
8 100
|
7
|
10
|
3
|
5
|
|
450
|
4
|
2 25 -
|
2 325
|
5 100 +
|
6
|
-1
|
|
250
|
7
|
3 +
|
5
|
9 150 -
|
2 100
|
3
|
|
0
|
3
|
3
|
6
|
-1
|
|
Рисунок 1. Итерация №1
Проверка на сбалансированность: ∑МП = 900, ∑СП
= 900 → они равны, следовательно, транспортная задача является закрытой.
Проверка на вырожденность: N = n + m - 1; N - количество
базисных клеток = 7, n - количество строк = 3, m - количество столбцов = 5; 7 = 3 + 5 - 1 = 7 →
транспортная задача является невырожденной.
Начальные затраты: Рнач = 500 + 800 + 50 + 650 + 500 + 1350 +
200 = 4050.
Проведем поэтапное улучшение опорного плана с помощью метода потенциалов.
Добавим к опорному плану дополнительные строку и столбец (см. рисунок 1).
Примем значение одной из получившихся дополнительных ячеек за 0. Рассчитаем по
формуле: «значение издержки» = «значение в ячейке дополнительной строки» +
«значение ячейки дополнительного столбца» остальные значения дополнительных
ячеек. После этого, составим вспомогательную матрицу, значения в которой
рассчитываются по следующей формуле: «значение в матрице» = «значение издержки»
- («значение в ячейке дополнительной строки» + «значение ячейки дополнительного
столбца»).
0 -1 -1 -1
0 0 0 8
-3 -1 0 0
В данной вспомогательной матрице присутствуют отрицательные числа. Так
как каждое число в матрице показывает на сколько изменятся общие транспортные
затраты при загрузке данной клетки единицей груза, то данный план можно
улучшить переместив в соответствующую клетку некоторое количество продукции
(если число отрицательное, затраты уменьшаются). Из всех отрицательных значений
выбираем наибольшее по модулю, так как ее воздействие на общие затраты является
максимальным. Отметим знаком «+» в транспортной таблице ячейку соответствующую
положению максимального по модулю отрицательного числа в вспомогательной
матрице. Кроме нее мы пометим знаками «-» и «+» другие занятые числами ячейки
таким образом, что в каждой строке и каждом столбце транспортной таблицы число
знаков «+» будет равно числу знаков «-». Это всегда можно сделать единственным
образом, причем в каждой строке и каждом столбце содержится по одному «+» и
«-». То есть помеченные знаками клетки должны образовывать цикл (см. рисунок
1). Затем мы определим минимум из всех элементов, помеченных знаком «-», и
выберем одну ячейку, где этот минимум достигается. В нашем случае таковой
является ячейка, содержащая 25 единиц груза. Следовательно, данная ячейка при
пересчете должна стать свободной.
|
МП/СП
|
100
|
125
|
325
|
250
|
100
|
|
|
200
|
5 100
|
8 100 -
|
7
|
10
|
5
|
|
450
|
4
|
2
|
2 325
|
5 125
|
6
|
-4
|
|
250
|
7
|
3 25 +
|
5
|
9 125
|
2 100 -
|
0
|
|
0
|
3
|
6
|
9
|
2
|
|
Р1 = 500 + 800 + 75 + 650 + 625 + 1125 + 200 =
3975. 4
минимальное количество груза в ячейке: 100
0 0 -4 -4 -
8 3 0 0 8
0 -1 0 0
|
МП/СП
|
100
|
125
|
325
|
250
|
100
|
|
|
200
|
5 100
|
8
|
7
|
10
|
3 100
|
5
|
|
450
|
4
|
2
|
2 325 -
|
5 125 +
|
6
|
0
|
|
250
|
7
|
3 125
|
5 +
|
9 125 -
|
2 0
|
4
|
|
0
|
-1
|
2
|
5
|
-2
|
|
Р2 = 500 + 0 + 375 + 650 + 625 + 1125 + 300 =
3575.
минимальное количество груза в ячейке: 125
0 4 0 0 0
4 3 0 0 8
3 0 -1 0 0
|
МП/СП
|
100
|
125
|
325
|
250
|
100
|
|
|
200
|
5 100
|
8
|
7
|
10
|
3 100
|
5
|
|
450
|
4
|
2
|
2 200
|
5 250
|
6
|
1
|
|
250
|
7
|
3 125
|
5 125
|
9
|
2 0
|
4
|
|
0
|
-1
|
1
|
4
|
-2
|
|
Ропт = 500 + 300 + 400 + 1250 + 375 + 625 = 3450.
4 1 1 0
2 0 0 1
0 0 1 0
В данной матрице не содержится отрицательных значений, следовательно,
план улучшить нельзя, а значит достигнуто оптимальное решение.
Метод минимального элемента:
Составим опорный план в соответствие с условием задачи:
|
МП/СП
|
100
|
125
|
325
|
250
|
100
|
|
|
200
|
5 100
|
8
|
7
|
10 100
|
3
|
5
|
|
450
|
4
|
2 125 -
|
2 325
|
5 +
|
6
|
6
|
|
250
|
7
|
3 0 +
|
5
|
9 150 -
|
2 100
|
4
|
|
0
|
-4
|
-4
|
5
|
-2
|
|
Проверка
на вырожденность: N = n + m - 1; N - количество базисных клеток = 6, n - количество
строк = 3, m - количество столбцов = 5; 6 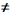
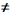 3 + 5 - 1
= 7 → вводим фиктивную поставку.
3 + 5 - 1
= 7 → вводим фиктивную поставку.
Начальные
затраты: Рнач = 500 + 1000 + 250 + 650 + 1350 + 200 = 3950. минимальное
количество груза в ячейке: 125
0
7 6 0 0
0
0 -6 2
3 0 5 0 0
|
МП/СП
|
100
|
125
|
325
|
250
|
100
|
|
|
200
|
5 100
|
8
|
7
|
10 100
|
3
|
5
|
|
450
|
4
|
2
|
2 325 -
|
5 125 +
|
6
|
0
|
|
250
|
7
|
3 125
|
5 +
|
9 25 -
|
2 100
|
4
|
|
0
|
-1
|
2
|
5
|
-2
|
|
Р1 = 500 + 1000 + 650 + 625 + 375 + 225 + 200 = 3575.
минимальное количество груза в ячейке: 25
4 0 0 0
3 0 0 8
0 -1 0 0
|
МП/СП
|
100
|
125
|
325
|
250
|
100
|
|
|
200
|
5 100
|
8
|
7
|
10 100 -
|
3 +
|
5
|
|
450
|
4
|
2
|
2 300 -
|
5 150 +
|
6
|
0
|
|
250
|
7
|
3 125
|
5 25 +
|
9
|
2 100 -
|
3
|
|
0
|
0
|
2
|
5
|
-1
|
|
Р2 = 500 + 1000 + 600 + 750 + 375 + 125 + 200 = 3550.
минимальное количество груза в ячейке: 100
3 0 0 -1
2 0 0 7
0 0 1 0
|
МП/СП
|
100
|
125
|
325
|
250
|
100
|
|
|
200
|
5 100
|
8
|
7
|
10
|
3 100
|
5
|
|
450
|
4
|
2
|
2 200
|
5 250 +
|
6
|
1
|
|
250
|
7
|
3 125
|
5 125
|
9
|
2 0
|
4
|
|
0
|
-1
|
1
|
4
|
-2
|
|
Р3 = 500 + 300 + 400 + 1250 + 375 + 625 = 3450.
4 1 1 0
3 2 0 0 7
3 0 0 1 0
В данной матрице не содержится отрицательных значений, следовательно,
план улучшить нельзя, а значит достигнуто оптимальное решение.
Выводы
В данной курсовой работе решены три задачи линейного программирования.
Первая задача решена графическим методом. Метод достаточно прост, но позволяет
решать задачи, содержащие не более трех переменных. Уже при трех переменных
возникают значительные трудности в решении. Вторая задача решена
симплекс-методом. Решение производится путём перебора вершин выпуклого
многогранника в многомерном пространстве. Также сформулирована и решена
двойственная к ней задача. Третья - транспортная - задача решена двумя
методами, которые различаются только в способе получения опорного плана. Оба
способа дали одинаковый результат по количеству итераций. Отличие заключается в
том, что при втором методе получается лучше оптимизированный опорный план.