Статистический анализ рождаемости
Оглавление
Введение
1. Ряды динамики
1.1
Анализ интенсивности изменения во времени
.2
Выявление тенденции развития ряда динамики
.3
Выявление тенденции развития в рядах динамики с использованием Microsoft Excel
1.4
Отбор функции в качестве тренда
1.5
Расчет показателей колеблемости
1.6
Прогнозирование
2.
Корреляционно-регрессионный анализ
Заключение
Библиографический
список
Введение
Являясь обязательной частью подготовки бакалавров экономики,
учебная практика предназначена для общей ориентации студентов в реальных
условиях будущей деятельности по выбранной специальности на предприятиях,
учреждениях и организациях и получения первичных профессиональных умений и
навыков.
Основными целями учебной практики «Информационные системы в
экономике» являются:
· закрепление, расширение и углубление
теоретических знаний, полученных в Университете;
· выработка умений применять полученные
практические навыки при решении конкретных экономических вопросов.
Задачами учебной практики «Информационные системы в
экономике» являются:
· получение представлений об использовании
компьютерных методов поиска, сбора, хранения и обработки экономической
информации;
· формирование умений и навыков выполнения
экономического анализа и экономических расчетов;
· организация систематической
самостоятельной работы с учебной, научной, специальной, нормативно-методической
литературой, способствующей формированию творческого подхода к решению проблем
профессиональной деятельности.
Учебная практика бакалавра в соответствии с ООП базируется на
основе полученных ранее знаний обучающихся по таким предметам как
«Информатика», «Статистика», «Микроэкономика», «Макроэкономика», «Теория
экономических информационных систем», «Математические основы финансового
менеджмента» и т.д.
1. Ряды динамики
1.1 Анализ интенсивности изменения во времени
статистический анализ рождаемость
Анализ скорости и интенсивности развития явления во времени
осуществляется с помощью статистических показателей, которые получаются в
результате сравнения уровней между собой. К таким показателям относятся:
абсолютный прирост, темп роста, темп прироста и абсолютное значение одного
процента прироста (таблица 1.1). При этом принято сравниваемый уровень называть
отчетным, а уровень с которым производят сравнение - базисным.
Для исследования интенсивности изменения явления во времени
рассчитываются показатели ряда динамики численность родившихся в России за
1997-2011год.
Таблица 1.1 Исходные данные для исследования интенсивности
явления во времени
|
Годы
|
Численность
родившихся в РФ на 1000 человек
|
Абсолютный
прирост, кг
|
Темп роста,%
|
Темп прироста,%
|
Абсолютное
содержание 1% прироста, чел
|
|
|
Δбаз
|
Δцеп
|
ТР баз
|
Тр цеп
|
Тпр баз
|
Тпр цеп
|
|
|
1997
|
8,6
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
1998
|
8,8
|
0,2
|
0,2
|
102,3
|
102,3
|
2,3
|
2,3
|
0,088
|
|
1999
|
8,3
|
-0,3
|
-0,5
|
96,5
|
94,3
|
-3,5
|
-5,7
|
0,083
|
|
2000
|
8,7
|
0,1
|
0,4
|
101,2
|
104,8
|
1,2
|
4,8
|
0,087
|
|
2001
|
9
|
0,4
|
0,3
|
104,7
|
103,4
|
4,7
|
3,4
|
0,09
|
|
2002
|
9,6
|
1,0
|
0,6
|
111,6
|
106,7
|
11,6
|
6,7
|
0,096
|
|
2003
|
10,2
|
1,6
|
0,6
|
118,6
|
106,3
|
18,6
|
6,3
|
0,102
|
|
2004
|
10,4
|
1,8
|
0,2
|
120,9
|
102,0
|
20,9
|
2,0
|
0,104
|
|
2005
|
10,2
|
1,6
|
-0,2
|
118,6
|
98,1
|
18,6
|
-1,9
|
0,102
|
|
2006
|
10,4
|
1,8
|
0,2
|
120,9
|
102,0
|
20,9
|
2,0
|
0,104
|
|
2007
|
11,3
|
2,7
|
0,9
|
131,4
|
108,7
|
31,4
|
8,7
|
0,113
|
|
2008
|
12,1
|
3,5
|
0,8
|
140,7
|
107,1
|
40,7
|
7,1
|
0,121
|
|
2009
|
12,4
|
3,8
|
0,3
|
144,2
|
102,5
|
44,2
|
2,5
|
0,124
|
|
2010
|
12,5
|
3,9
|
0,1
|
145,3
|
100,8
|
45,3
|
0,8
|
0,125
|
|
2011
|
12,6
|
4,0
|
0,1
|
146,5
|
100,8
|
46,5
|
0,8
|
0,126
|
|
В среднем
|
10,34
|
0,29
|
0,29
|
102,8
|
102,8
|
2,8
|
2,8
|
X
|
1. Средний абсолютный прирост:
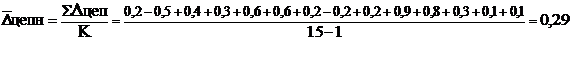
К=n-1, где К - количество цепных абсолютных приростов,- количество
уровней ряда.
2. Средний коэффициент роста:
=
;
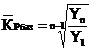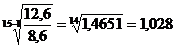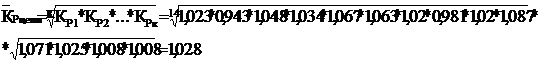
К=n-1,
где К - количество цепных коэффициентов роста
3. Средний темп роста:
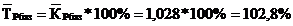
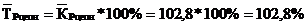
4. Средний темп прироста:
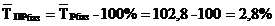
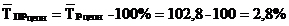
5. Средний уровень ряда динамики:
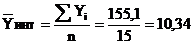
1.2 Выявление тенденции развития ряда динамики
Одним из методов выравнивания является механическое
выравнивание отдельных членов ряда динамики с использованием фактических
значений соседних уровней. Механическое выравнивание проводится методом
укрупнения интервалов и методом скользящей средней.
Проведем выравнивание ряда динамики методом укрупнения
периодов по данным численности родившихся за 1997-2011 гг. Результаты расчетов
изложим в таблице 1.2.
Таблица 1.2 Выравнивание ряда динамики методом укрупнения
периодов
|
Годы
|
Численность
родившихся в РФ на 1000 человек
|
По 3х летиям
|
|
|
Периоды
|
Сумма
|
Среднее
|
|
|
|
|
|
|
1997
|
8,6
|
|
|
|
|
1998
|
8,8
|
1997-1999
|
25,7
|
8,6
|
|
1999
|
8,3
|
|
|
|
|
2000
|
8,7
|
|
|
|
|
2001
|
9
|
2000-2002
|
27,3
|
9,1
|
|
2002
|
9,6
|
|
|
|
|
2003
|
10,2
|
|
|
|
|
2004
|
10,4
|
2003-2005
|
30,8
|
10,3
|
|
2005
|
10,2
|
|
|
|
|
2006
|
10,4
|
|
|
|
|
2007
|
11,3
|
2006-2008
|
33,8
|
11,3
|
|
2008
|
12,1
|
|
|
|
|
2009
|
12,4
|
|
|
|
|
2010
|
12,5
|
2009-2011
|
37,5
|
12,5
|
|
2011
|
12,6
|
|
|
|
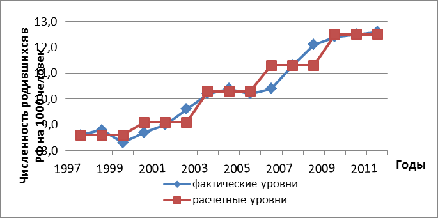
Рисунок 1.1 Выравнивание ряда динамики методом укрупнения
периодов
С помощью метода укрупнения интервалов основанного на
укрупнении периодов времени, к которым относятся уровни ряда, в рядах динамики
выявлена тенденция увеличения числа рождаемости.
Проведем выравнивание ряда динамики методом скользящей
средней по данным численности родившихся за 1997-2011 гг. Результаты расчетов
изложим в таблице 1.3.
Таблица 1.3 Выравнивание ряда динамики методом скользящей
средней
|
Годы
|
Численность
родившихся в РФ на 1000 человек
|
По 3х летиям
|
|
|
Периоды
|
Сумма
|
Среднее
|
|
1997
|
8,6
|
-
|
-
|
-
|
|
1998
|
8,6
|
1997-1999
|
25,5
|
8,5
|
|
1999
|
8,3
|
1998-2000
|
25,6
|
8,5
|
|
2000
|
8,7
|
1999-2001
|
26,0
|
8,7
|
|
2001
|
9
|
2000-2002
|
27,3
|
9,1
|
|
2002
|
9,6
|
2001-2003
|
28,8
|
9,6
|
|
2003
|
10,2
|
2002-2004
|
30,2
|
10,1
|
|
2004
|
10,4
|
2003-2005
|
30,8
|
10,3
|
|
2005
|
10,2
|
2004-2006
|
31
|
10,3
|
|
2006
|
10,4
|
2005-2007
|
31,9
|
10,6
|
|
2007
|
11,3
|
2006-2008
|
33,8
|
11,3
|
|
2008
|
2007-2009
|
35,8
|
11,9
|
|
2009
|
12,4
|
2008-2010
|
37
|
12,3
|
|
2010
|
12,5
|
2009-2011
|
37,5
|
12,5
|
|
2011
|
12,6
|
-
|
-
|
-
|
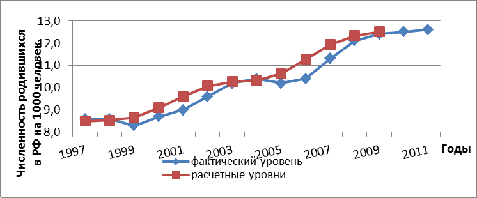
Рисунок 1.2 Выравнивание ряда динамики методом скользящей средней
Методом скользящей средней выявлена тенденция увеличения числа
рождаемости, за исключением 2005 года, в котором произошло незначительное
уменьшение числа рождаемости.
Таблица 1.4 Выравнивание ряда динамики по среднему абсолютному
приросту и среднему коэффициенту роста
|
Годы
|
Численность
родившихся в РФ на 1000 человек, Yt
|
Порядковый
номер года,t
|
Yt=8,6+0,29*(t-1)
|
Yt=8,6*1,028(t-1)
|
|
1997
|
8,6
|
1
|
8,6
|
8,6
|
|
1998
|
8,8
|
2
|
8,9
|
8,8
|
|
1999
|
8,3
|
3
|
9,2
|
9,1
|
|
2000
|
8,7
|
4
|
9,5
|
9,3
|
|
2001
|
9
|
5
|
9,8
|
9,6
|
|
2002
|
9,6
|
6
|
10,1
|
9,9
|
|
2003
|
10,2
|
7
|
10,3
|
10,1
|
|
2004
|
10,4
|
8
|
10,6
|
10,4
|
|
2005
|
10,2
|
9
|
10,9
|
10,7
|
|
2006
|
10,4
|
10
|
11,2
|
11,0
|
|
2007
|
11,3
|
11
|
11,5
|
11,3
|
|
2008
|
12,1
|
12
|
11,8
|
11,7
|
|
2009
|
12,4
|
13
|
12,1
|
12,0
|
|
2010
|
12,5
|
14
|
12,4
|
12,3
|
|
2011
|
12,6
|
15
|
12,66
|
12,66
|
Рисунок 1.3 Выравнивание ряда динамики по среднему
абсолютному приросту и среднему коэффициенту роста
Таблица 1.4 и рисунок 1.3 показывают, что методом
выравнивания ряда динамики по среднему абсолютному приросту с 1997 по 2011 годы
выявлена тенденция увеличения числа рождаемости.
Методом выравнивания ряда динамики по среднему коэффициенту
роста за исследуемый период выявлена тенденция увеличения числа рождаемости
ежегодно в среднем в 1,028 раза или на 2,8%.
Таблица 1.5 Выравнивание ряда динамики аналитическим методом
по уравнению прямой
|
Годы
|
Численность
родившихся в РФ на 1000 чел.,Yt
|
Отклонение от
центрального года, t
|
t2
|
y*t
|
Yt=10,33+0,33*t
|
|
1997
|
8,6
|
-7
|
49
|
-60,2
|
8,0
|
|
1998
|
8,8
|
-6
|
36
|
-52,8
|
8,4
|
|
1999
|
8,3
|
-5
|
25
|
-41,5
|
8,7
|
|
2000
|
8,7
|
-4
|
16
|
-34,8
|
9,0
|
|
2001
|
9
|
-3
|
9
|
-27
|
9,3
|
|
2002
|
9,6
|
-2
|
4
|
-19,2
|
9,7
|
|
2003
|
10,2
|
-1
|
1
|
-10,2
|
10,0
|
|
2004
|
10,4
|
0
|
0
|
0
|
10,3
|
|
2005
|
10,2
|
1
|
1
|
10,2
|
10,7
|
|
2006
|
10,4
|
2
|
4
|
20,8
|
11,0
|
|
2007
|
11,3
|
3
|
9
|
33,9
|
11,3
|
|
2008
|
12,1
|
4
|
16
|
48,4
|
11,7
|
|
2009
|
12,4
|
5
|
25
|
62
|
12,0
|
|
2010
|
12,5
|
6
|
36
|
75
|
12,3
|
|
2011
|
12,6
|
7
|
49
|
88,2
|
12,6
|
|
Итого
|
155,1
|
0
|
280
|
92,8
|
155,0
|
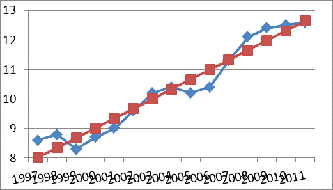
Рисунок 1.4 Выравнивание ряда динамики аналитическим методом по
уравнению прямой
Аналитическим методом по уравнению прямой выявлена тенденция
роста числа рождаемости в среднем ежегодно на 0,33 чел..
.3 Выявление тенденции развития в рядах динамики с
использованием Microsoft Excel
Аналитическое выравнивание основано на том, что уровни ряда
динамики выражаются в виде функции времени. Функцию выбирают таким образом,
чтобы она давала содержательное объяснение изучаемого процесса.
Таблица 1.6 Выравнивание ряда динамики аналитическим методом
по линейной функции
|
Годы
|
Численность
родившихся в РФ на 1000 чел.
|
Порядковый
номер года, t
|
Линейная
функция
|
|
|
|
Yt
|
Yi-Yt
|
(Yi-Yt)2
|
|
1997
|
8,6
|
1
|
7,7
|
0,9
|
0,83
|
|
1998
|
8,8
|
2
|
8,0
|
0,8
|
0,61
|
|
1999
|
8,3
|
3
|
8,4
|
-0,1
|
0,00
|
|
2000
|
8,7
|
4
|
8,7
|
0,0
|
0,00
|
|
2001
|
9
|
5
|
9,0
|
0,0
|
0,00
|
|
2002
|
9,6
|
6
|
9,3
|
0,3
|
0,06
|
|
2003
|
10,2
|
7
|
9,7
|
0,5
|
0,27
|
|
2004
|
10,4
|
8
|
10,0
|
0,4
|
0,15
|
|
2005
|
10,2
|
9
|
10,3
|
-0,1
|
0,02
|
|
2006
|
10,4
|
10
|
10,7
|
-0,3
|
0,07
|
|
2007
|
11,3
|
11
|
11,0
|
0,3
|
0,09
|
|
2008
|
12,1
|
12
|
11,3
|
0,8
|
0,59
|
|
2009
|
12,4
|
13
|
11,7
|
0,7
|
0,54
|
|
2010
|
12,5
|
14
|
12,0
|
0,5
|
0,25
|
|
2011
|
12,6
|
15
|
12,3
|
0,3
|
0,07
|
|
2012
|
x
|
16
|
12,7
|
x
|
x
|
|
2013
|
x
|
17
|
13,0
|
x
|
x
|
|
Итого
|
155,1
|
x
|
x
|
x
|
3,6
|
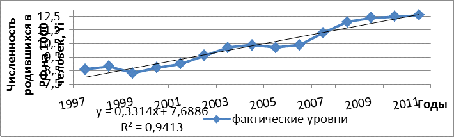
Рисунок 1.5 Выравнивание ряда динамики аналитическим методом по
линейной функции
По уравнению линейного тренда имеем, что средний фактический и
выравненный уровень рождаемости, отнесенный к середине периода, равен 11,7%, а
среднегодовое уменьшение составляет 0,3% в год (среднее изменение за единицу
времени). По таблице 1.6 видно, что наибольшее увеличение рождаемости было в
20011гг.
Линейный тренд хорошо отражает тенденцию изменений уровня инфляции
при действии множество факторов, изменяющихся различным образом по разным
закономерностям.
Проведем выравнивание ряда динамики аналитическим методом по
логарифмической функции по данным числа рождаемости за 1997-2011 гг. Результаты
расчетов изложим в таблице 1.7.
Таблица 1.7 Выравнивание ряда динамики аналитическим методом по
логарифмической функции
|
Годы
|
Численность
родившихся в РФ на 1000 человек, Yt
|
Порядковый
номер года, t
|
Логарифмическая
функция
|
|
|
|
Yt
|
Yi-Yt
|
(Yi -
Yt)2
|
|
1997
|
8,6
|
1
|
7,2
|
1,4
|
1,9
|
|
1998
|
2
|
8,4
|
0,4
|
0,2
|
|
1999
|
8,3
|
3
|
9,1
|
-0,8
|
0,6
|
|
2000
|
8,7
|
4
|
9,5
|
-0,8
|
0,7
|
|
2001
|
9
|
5
|
9,9
|
-0,9
|
0,8
|
|
2002
|
9,6
|
6
|
10,2
|
-0,6
|
0,4
|
|
2003
|
10,2
|
7
|
10,5
|
-0,3
|
0,1
|
|
2004
|
10,4
|
8
|
10,7
|
-0,3
|
0,1
|
|
2005
|
10,2
|
9
|
10,9
|
-0,7
|
0,5
|
|
2006
|
10,4
|
10
|
11,1
|
-0,7
|
0,5
|
|
2007
|
11,3
|
11
|
11,2
|
0,1
|
0,0
|
|
2008
|
12,1
|
12
|
11,4
|
0,7
|
0,5
|
|
2009
|
12,4
|
13
|
11,5
|
0,9
|
0,8
|
|
2010
|
12,5
|
14
|
11,7
|
0,8
|
0,7
|
|
2011
|
12,6
|
15
|
11,8
|
0,8
|
0,7
|
|
2012
|
x
|
16
|
11,9
|
x
|
x
|
|
2013
|
x
|
17
|
12,0
|
x
|
x
|
|
Итого
|
155,1
|
x
|
x
|
0,0
|
8,5
|
Выравнивание ряда динамики аналитическим методом по
логарифмической функции выявлена тенденция уменьшения числа рождаемости.
Рисунок 1.6 Выравнивание ряда динамики аналитическим методом по
логарифмической функции
Проведем выравнивание ряда динамики по полиномиальной функции
по данным численности рождаемости за 1997-2011 гг. Результаты расчетов изложим
в таблице 1.8.
Таблица 1.8 Выравнивание ряда динамики аналитическим методом
по полиномиальной функции
|
Годы
|
Численность
родившихся в РФ на 1000 человек.,Yi
|
Порядковый
номер года, t
|
Полиноминальная
функция
|
|
|
|
Yt
|
Yi -
Yt
|
(Yi -
Yt)2
|
|
1997
|
8,6
|
1
|
8,3
|
0,3
|
0,1
|
|
1998
|
8,8
|
2
|
8,5
|
0,3
|
0,1
|
|
1999
|
8,3
|
3
|
8,8
|
-0,5
|
0,2
|
|
2000
|
8,7
|
4
|
9,0
|
-0,3
|
0,1
|
|
2001
|
9
|
5
|
9,2
|
-0,2
|
0,1
|
|
2002
|
9,6
|
6
|
9,5
|
0,1
|
0,0
|
|
2003
|
10,2
|
7
|
9,8
|
0,4
|
0,1
|
|
2004
|
10,4
|
8
|
10,1
|
0,3
|
0,1
|
|
2005
|
10,2
|
9
|
10,5
|
-0,3
|
0,1
|
|
2006
|
10,4
|
10
|
10,8
|
-0,4
|
0,2
|
|
2007
|
11,3
|
11
|
11,2
|
0,1
|
0,0
|
|
2008
|
12,1
|
12
|
11,6
|
0,5
|
0,2
|
|
2009
|
12,4
|
13
|
12,1
|
0,3
|
0,1
|
|
2010
|
12,5
|
14
|
12,5
|
0,0
|
0,0
|
|
2011
|
12,6
|
15
|
13,0
|
-0,4
|
0,1
|
|
2012
|
x
|
16
|
13,5
|
x
|
x
|
|
2013
|
x
|
17
|
14,0
|
x
|
x
|
|
Итого
|
155,1
|
x
|
x
|
0,0
|
1,5
|
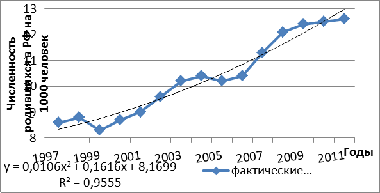
Рисунок 1.7 Выравнивание ряда динамики аналитическим методом по
полиномиальной функции
Выравнивание ряда динамики аналитическим методом по
полиномиальной функции выявлена тенденция уменьшения численности рождаемости.
По уравнению полиномиального тренда имеем, что абсолютный прирост рождаемости
замедляется в среднем на 2*0,0106% в год за год. Сам же абсолютный прирост уже
не является константой полиномиального тренда, а является средней величиной за
период. В год, принятый за начало отсчета, т.е. 1997 г., тренд проходит через
точку с ординатой 8,1699%.
Проведем выравнивание ряда динамики аналитическим методом по
степенной функции по данным уровни инфляции за 1997-2011 гг. Результаты
расчетов изложим в таблице 1.9.
Таблица 1.9 Выравнивание ряда динамики аналитическим методом
по степенной функции
|
Годы
|
Численность
родившихся в РФ на 1000 чел., Yi
|
Порядковый
номер года,t
|
Степенная
функция
|
|
|
|
Yt
|
Yi -
Yt
|
(Yi -
Yt)2
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1997
|
8,6
|
1
|
7,5
|
1,1
|
1,1
|
|
1998
|
8,8
|
2
|
8,4
|
0,4
|
0,1
|
|
1999
|
8,3
|
3
|
9,0
|
-0,7
|
0,5
|
|
2000
|
8,7
|
4
|
9,5
|
-0,8
|
0,6
|
|
2001
|
9
|
5
|
9,8
|
-0,8
|
0,7
|
|
2002
|
9,6
|
6
|
10,1
|
-0,5
|
0,3
|
|
2003
|
10,2
|
7
|
10,4
|
-0,2
|
0,0
|
|
Продолжение
таблицы 1.9
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
2004
|
10,4
|
8
|
10,6
|
-0,2
|
0,0
|
|
2005
|
10,2
|
9
|
10,8
|
-0,6
|
0,4
|
|
2006
|
10,4
|
10
|
11,0
|
-0,6
|
0,4
|
|
2007
|
11,3
|
11
|
11,2
|
0,1
|
0,0
|
|
2008
|
12,1
|
12
|
11,3
|
0,8
|
0,6
|
|
2009
|
12,4
|
13
|
11,5
|
0,9
|
0,8
|
|
2010
|
12,5
|
14
|
11,6
|
0,9
|
0,7
|
|
2011
|
12,6
|
15
|
11,8
|
0,8
|
0,7
|
|
2012
|
x
|
16
|
11,9
|
x
|
x
|
|
2013
|
x
|
17
|
12,0
|
x
|
x
|
|
Итого
|
155,1
|
x
|
0,4
|
7,0
|
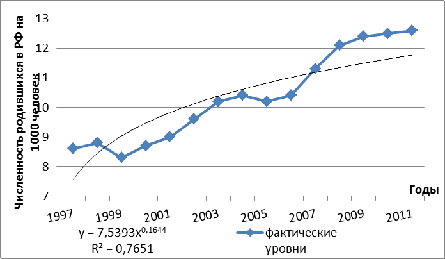
Рисунок 1.8 Выравнивание ряда динамики аналитическим методом по
степенной функции
Выравнивание ряда динамики аналитическим методом по степенной
функции выявлена тенденция незначительного изменения численности рождаемости.
Степенная форма - гибкая, пригодная для отображения изменений с разной мерой
пропорциональности изменений во времени.
Проведем выравнивание ряда динамики аналитическим методом по
экспоненциальной функции по данным численности рождаемости за 1997-2011 гг.
Результаты расчетов изложим в таблице 1.10.
Таблица 1.10 Выравнивание ряда динамики аналитическим методом по
экспоненциальной функции
|
Годы
|
Численность
родившихся в РФ на 1000 чел., Yi
|
Порядковый
номер года, t
|
Экспонциальная
функция
|
|
|
|
Yt
|
Yi -
Yt
|
(Yi -
Yt)2
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1997
|
8,6
|
1
|
8,2
|
0,4
|
0,2
|
|
1998
|
8,8
|
2
|
8,5
|
0,3
|
0,1
|
|
1999
|
8,3
|
3
|
8,7
|
-0,4
|
0,2
|
|
2000
|
8,7
|
4
|
9,0
|
-0,3
|
0,1
|
|
2001
|
9
|
5
|
9,3
|
-0,3
|
0,1
|
|
2002
|
9,6
|
6
|
9,6
|
0,0
|
0,0
|
|
2003
|
10,2
|
7
|
9,9
|
0,3
|
0,1
|
|
2004
|
10,4
|
8
|
10,2
|
0,2
|
0,0
|
|
2005
|
10,2
|
9
|
10,6
|
-0,4
|
0,1
|
|
2006
|
10,4
|
10
|
10,9
|
-0,5
|
0,3
|
|
2007
|
11,3
|
11
|
11,3
|
0,0
|
0,0
|
|
2008
|
12,1
|
12
|
11,6
|
0,5
|
0,2
|
|
2009
|
12,4
|
13
|
12,0
|
0,4
|
0,1
|
|
2010
|
12,5
|
14
|
12,4
|
0,1
|
0,0
|
|
2011
|
12,6
|
15
|
12,8
|
-0,2
|
0,0
|
|
2012
|
x
|
16
|
13,2
|
x
|
x
|
|
2013
|
x
|
17
|
13,7
|
x
|
x
|
|
Итого
|
155,1
|
x
|
181,9
|
0,0
|
182,0
|
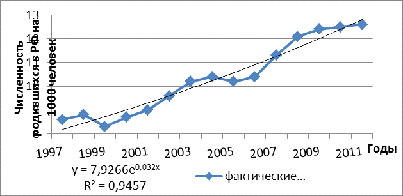
Рисунок 1.9 Выравнивание ряда динамики аналитическим методом по
экспоненциальной функции
Выравнивание ряда динамики аналитическим методом по
экспоненциальной функции выявлена тенденция незначительного изменения численности
рождаемости. По экспоненциальному тренду имеем, что среднегодовой темп роста
численности рождаемости составил 3,2%. В точке, принятой за начало отчета,
тренд проходит точку с ординатой 7,93%. При росте по экспоненте абсолютный
прирост пропорционален достигнутому уровню.
.4 Отбор функции в качестве тренда
Произведём отбор функции в качестве тренда используя F - критерий
Фишера при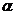 
=0.05.
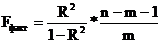
1) Линейная функция:
=
>
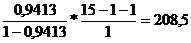
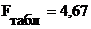
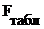, таким образом линейная функция считается
статистически значимой и существенной.
2) Логарифмическая функция:
= 
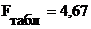
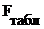>, таким образом логарифмическая функция
считается статистически значимой и существенной.
3) Полиномиальная функция:
= 
;
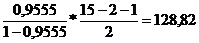
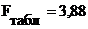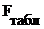>, таким образом полиномиальная функция
функция считается статистически значимой и существенной.
4) Степенная функция:
= 
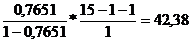
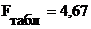
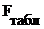>, таким образом, степенная функция
считается статистически значимой и существенной.
5) Экспоненциальная функция:
=
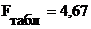
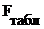>, таким образом, экспоненциальная функция
считается статистически значимой и существенной.
Так как по F-критерию Фишера все пять функций подходят для
отображения тенденции, то отберем наиболее адекватную функцию по наименьшему
среднему квадратическому отклонению остаточному.
Отбор наиболее адекватной функции проведем с помощью
среднеквадратического отклонения:
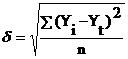
1. Линейная функция:
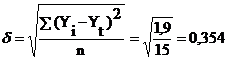
2. Логарифмическая функция:
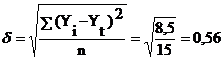
3. Полиномиальная функция:
4. Степенная функция:
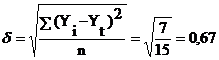
5. Экспоненциальная функция:
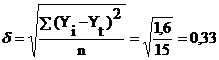
Наиболее адекватной функцией будет - полиномиальная функция,
так как у нее среднеквадратическое отклонение наименьшее.
= 0,0106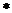
t2 +0,1616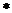t + 8,1699
1.5 Расчет показателей колеблемости
По отобранной функции в качестве тренда определим показатели
колеблемости и сделаем вывод о возможности прогнозирования.
. Размах колеблемости:
-
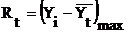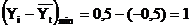
. Среднее абсолютное отклонение:
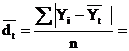
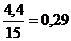
. Дисперсия колеблемости
=
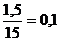
4. Среднеквадратическое отклонение тренда
. Относительный размах колеблемости
. Относительное линейное отклонение
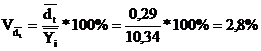
. Коэффициент колеблемости
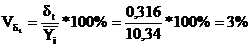
.Коэффициент устойчивости уровня ряда динамики
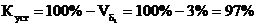
Так как коэффициент устойчивости больше 50%, то уровни ряда
динамики устойчивы и данное уравнение тренда подходит для расчета прогноза на
перспективу.
1.6 Прогнозирование
Выполним интервальный прогноз на 2 года:
,
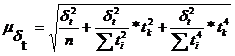где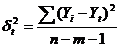 
=
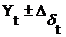- интервальный прогноз,
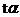- табличное значение Стьюдента,
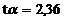при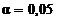 
,
Интервальный прогноз на 2012 год:
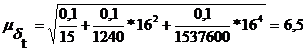
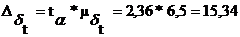
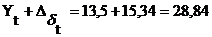чел.
чел.
Интервальный прогноз на 2013 год:
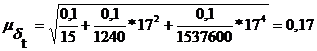
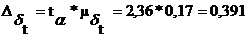
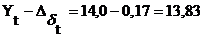чел.
чел.
Таким образом, если выявленная тенденция по полиномиальной функции
сохранится, то в следующие два года с вероятностью 97% можно ожидать увеличение
числа рождаемости, причем в 2009 году число рождаемости будет составлять от
-1,84 до 28,84 чел, а в 2013 году - от 13,83 до 14,17 чел.
2. Корреляционно-регрессионный анализ
Создадим таблицу исходных данных (таблица 1.1). Построим
корреляционную модель связи численности рождаемости с включением трех факторов
- прибывших, выбывших и естественного прироста.
Таблица 2.1 Исходные данные для корреляционно-регрессионного
анализа
|
Годы
|
Численность
родившихся в РФ на 1000 человек, Yi
|
Прибыло в РФ на
10 тыс. чел
|
Выбыло из РФ на
10 тыс. чел
|
Естественный
прирост
|
|
|
|
|
|
|
Y
|
X1
|
X2
|
X3
|
|
1997
|
8,6
|
272,5
|
269,8
|
-5,2
|
|
1998
|
8,8
|
258,2
|
256
|
-4,8
|
|
1999
|
8,3
|
247,7
|
245,7
|
-6,4
|
|
2000
|
8,7
|
230,3
|
277,5
|
-6,6
|
|
2001
|
9
|
214
|
213,1
|
-6,6
|
|
2002
|
9,6
|
201,7
|
200,8
|
-6,5
|
|
2003
|
10,2
|
203,9
|
203
|
-6,2
|
|
2004
|
10,4
|
199,8
|
199,6
|
-5,6
|
|
2005
|
10,2
|
191,1
|
191,1
|
-5,9
|
|
2006
|
10,4
|
193,5
|
193,5
|
-4,8
|
|
2007
|
11,3
|
199,8
|
199,8
|
-3,3
|
|
2008
|
12,1
|
193,4
|
193,4
|
-2,5
|
|
2009
|
12,4
|
170,7
|
170
|
-1,8
|
|
2010
|
12,5
|
191
|
191,4
|
-1,7
|
|
2011
|
12,6
|
238,8
|
216,4
|
-1
|
Выполним корреляционно-регрессионного анализа с
использованием EXCEL. Для удобства анализа разобьем результаты статистической
обработки на отдельные фрагменты.
Таблица 2.2 Корреляционная матрица
|
|
Y
|
X1
|
X2
|
X3
|
|
Y
|
1
|
|
|
|
|
X1
|
-0,621748468
|
1
|
|
|
|
X2
|
-0,729345641
|
0,900314482
|
1
|
|
|
X3
|
0,885690072
|
-0,258400506
|
-0,4177716
|
1
|
Корреляционная матрица (таблица 1.2) содержит частные
коэффициенты корреляции. Коэффициенты второго столбца матрицы характеризуют
степень тесноты связи между результативным (У) и факторными признаками (Х1, Х2,
Х3). Например, связь между численностью родившимися и прибывшими (rУХ1
= -0,621) обратная, средняя; связь между родившимися и выбывшими (rУХ2
= -0,729) обратная, сильная; связь между родившимися и естественным припостом
(rУХ3 = 0,659) прямая, сильная. Коэффициенты корреляции между
факторами свидетельствуют об отсутствии мультиколлинеарности.
Таблица 2.3 Регрессионная статистика
|
Множественный R
|
0,976827325
|
|
R-квадрат
|
0,954191622
|
|
Нормированный
R-квадрат
|
0,941698428
|
|
Стандартная
ошибка
|
0,368884627
|
|
Наблюдения
|
15
|
Множественный коэффициент корреляции R = 0,977 показывает,
что теснота связи между численностью родившихся и признаками, включенными в
модель, сильная. Множественный коэффициент детерминации (R-квадрат) D = 0,954,
т.е. 95,4% говорит о том, что y зависит от выбранных факторов на 95,4%, на
остальные 4,6% зависит от других факторов, которые не учтены в данной модели.
Таблица 2.4 Дисперсионный анализ
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
3
|
31,17916545
|
10,39305515
|
76,3769159
|
1,19448E-07
|
|
Остаток
|
11
|
0,136075868
|
|
|
|
Итого
|
14
|
32,676
|
|
|
|
Проверим значимость коэффициента множественной корреляции,
для этого воспользуемся F-критерием, для чего сравним фактическое значение F с
табличным значением Fтабл. При вероятности ошибки α = 0,05 и степенях свободы v1=k-1=3-1=2, v2=n-k=15-3=12, где k -
число факторов в модели, n - число наблюдений, Fтабл = 3,29. Так как
Fфакт = 76,37 > Fтабл = 3,29, то коэффициент
корреляции значим, следовательно, построенная модель в целом адекватна.
Таблица 2.5 Коэффициенты регрессии
|
|
Y-пересечение
|
Переменная X 1
|
Переменная X 2
|
Переменная X 3
|
|
1
|
2
|
3
|
4
|
5
|
|
Коэффициенты
|
17,79739348
|
-0,014607566
|
-0,00802266
|
0,568670758
|
|
Стандартная
ошибка
|
0,73262348
|
0,008165609
|
0,007857387
|
0,056909457
|
|
t-статистика
|
24,29268782
|
-1,788913243
|
-1,021033992
|
9,992552912
|
|
P-Значение
|
6,57796E-11
|
0,101168728
|
0,329169337
|
7,44823E-07
|
|
Нижние 95%
|
16,18490007
|
-0,032579949
|
-0,025316653
|
0,443413888
|
|
Верхние 95%
|
19,40988689
|
0,003364818
|
0,009271333
|
0,693927628
|
|
Нижние 95,0%
|
16,18490007
|
-0,032579949
|
-0,025316653
|
0,443413888
|
|
Верхние 95,0%
|
19,40988689
|
0,003364818
|
0,009271333
|
0,693927628
|
Используя таблицу 2.5 составим уравнение регрессии:
У = 17,79 - 0,014Х1 - 0,008Х2 - 0,57Х3.
Интерпретация полученных параметров следующая:
а0= 17,79 - свободный член уравнения регрессии,
содержательной интерпретации не подлежит;
а1 = -0,014 - коэффициент чистой регрессии при первом факторе
свидетельствует о том, что увеличении рождаемости, уменьшается количество
прибывшего населения на 0,14%, при условии, что другие факторы остаются
постоянными;
а2 = -0,008 - коэффициент чистой регрессии при втором факторе
свидетельствует о том, что при увеличении рождаемости, количество выбывшего
населения уменьшился на 0,008%;
а3 = 0,57 - коэффициент чистой регрессии при третьем факторе
свидетельствует о том, что при увеличении числа рождаемости, естественный
прирост увеличился на 0,57%.
Проверку значимости коэффициентов регрессии осуществим с
помощью t-критерия Стьюдента; для этого сравним фактические значения t-критерия
с табличным значением t-критерия. При вероятности ошибки α = 0,05 и степени свободы v= n-k-1=15-3-1 =11, где k - число факторов
в модели, n - число наблюдений, tтабл = 2,201. Получим:факт = -1,78 < tтабл
= 2,201,факт = -1,02 < tтабл = 2,201,факт = 9,99 > tтабл = 2,201,
Значит, статистически значимыми является третий фактор. В
этом случае модель пригодна для принятия решений, но не для прогнозов.
Заключение
С помощью учебной практики мы закрепили, расширили и углубили
теоретические знания, полученных в Университете; выработали умения применять
полученные практические навыки при решении конкретных экономических вопросов;
приобрели практические навыки самостоятельной работы.
Научились проводить расчеты по выравниваниям, делать
корреляционно-регрессионный анализ и делать экономические выводы по ним.
В данной практической работе я выявила основную тенденцию
развития динамики исследуемого явления с использованием пакетов прикладных
программ «EXCEL», «STRAZ» и выполнила прогноз на перспективу;
Я изучила методику выполнения корреляционно-регрессионного
анализа, по фактическим данным выполнила корреляционно-регрессионный анализ,
проанализировала полученные результаты.
Я рассчитала показатели изменения уровней ряда динамики;
выполнила выравнивание ряда динамики исследуемого явления с помощью методов
механического выравнивания и плавного уровня; провела аналитическое выравнивание
ряда динамики с использованием пакетов прикладных программ «EXCEL», «STRAZ»;
отобрала функцию в качестве тренда; на основе отобранной функции в качестве
тренда, рассчитала показатели колеблемости и сделала прогноз с расчетом
точечных прогнозов и доверительных интервалов прогнозной оценки.
Библиографический список
1.
Елисеева, И.И. М.М. Общая теория статистики: учебник/ И.И. Елисеева, М.М.
Юзбашев. - 4-е изд., перераб. и доп. - М.: Финансы и статистика, 2008. - 480 с.
.
Ефимова, М.Р. Общая теория статистики: учебник / Ефимова М.Р. - М.: ИНФРА-М,
2011. - 414 с.
.
Башина, О.Э. Общая теория статистики: Статистическая методология в изучении
коммерческой деятельности: учебник / О.Э. Башина, В.Т. Бабурин, А.А. Спирин. -
М.: Финансы и статистика, 2011. - 440 с.
.
Шмойлова, Р.А. Теория статистики: учебник / Р.А. Шмойлова, Е.Б. Шувалова, Н.Ю.
Глубокова. - М.: Финансы и статистика, 2011. - 560 с.
.
Рафикова, Н.Т. Основы статистики: учеб. пособие / Н.Т. Рафикова. - М.: Финансы
и статистика, 2007. - 352 с.
.
Рождаемость, смертность и естественный прирост России. [Электронный ресурс]
Режим доступа: http://www.gks.ru/free_doc/new_ site/population/demo/demo21.xls
- 23.05.2012
.Миграция
населения в России [Электронный ресурс] Режим доступа:
http://www.gks.ru/free_doc/new_site/population/demo/migr1.xls -24.05.2012