Решение систем уравнений различными способами
Задание 1. Метод Гаусса
a. В электронных таблицах MS Excel составить такую систему
пяти линейных уравнений с пятью неизвестными, чтобы коэффициенты системы и
свободные члены были целые числа от 0 до 10, полученные с помощью
функции-генератора случайных чисел.
b. Решить полученную систему уравнений методом
исключений Гаусса с выбором главного элемента.
Решение
Составили систему пяти линейных уравнений с пятью
неизвестными
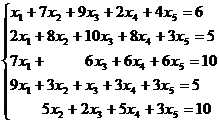
Запишем расширенную прямоугольную матрицу
коэффициентов системы
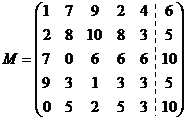
Алгоритм метода главных элементов состоит
в следующем:
Среди элементов матрицы aij, j = 1, n выбираем
наибольший по модулю а23 = 10.
Матрицу М преобразуем: из каждой i-ой неглавной строки
вычтем почленно главную строку, умноженную на mt. В результате получится
матрица, у которой все элементы главного столбца, за исключением самого
главного элемента равны нулю.
m1 = 0,9; m3 = 0,6; m4 = 0,1; m5 = 0,2.

Получим новую матрицу M1 с
меньшим на единицу числом строк и столбцов, отбрасывая из полученной матрицы М
главную строку и столбец.
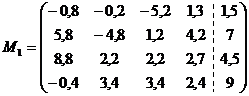
Наибольший по модулю элемент а31
= 8,8.
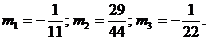

Получим новую матрицу M2 с
меньшим на единицу числом строк и столбцов, отбрасывая из полученной матрицы М1
главную строку и столбец.
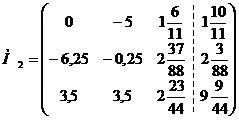
Наибольший по модулю элемент а21 = -6,25. 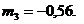
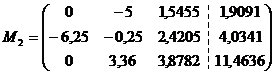
Получим новую матрицу M3 с
меньшим на единицу числом строк и столбцов, отбрасывая из полученной матрицы М2
главную строку и столбец.

Наибольший по модулю элемент а11 = -5. 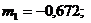
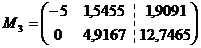
Объединим все главные строки, начиная с
последней строки.
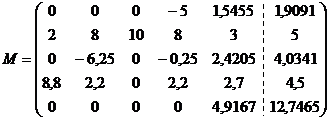
Полученная матрица, эквивалентная исходной.

,4167х5 = 12,7465 х5
= 2,5925;
х4 = 1,9091 - 1,5455х5
х4 = 0,4195;
,25х2 = 4,0341 + 0,25х4
- 2,4205 х5 х2 = 0,3418;
,8х1 = 4,5 - 2,2х2 -
2,2х4 - 2,7х5 х1 = -0,4744;
х3 = 5 - 2х1 - 8х2
- 8х4 - 3х5 х3 = -0,7919;
Ответ: х1 = -0,4744; х2
= 0,3418; х3 = -0,7919; х4 = 0,4195; х5 =
2,5925.
Задание 2. Интерполяционный многочлен Ньютона
a. В электронных таблицах MS Excel задать таблично функцию
в точках 0, 1, 2, …, 10 так, чтобы ее значения были целые числа от 0 до 10,
полученные с помощью функции-генератора случайных чисел.
b. Для полученной функции построить интерполяционный
многочлен Ньютона.. Вычислить значения полученного интерполяционного
многочлена в точках
, 1, 2, …, 10.
Решение
Пусть для функции y = f (x) заданы значения yi =
f(xi) для равностоящих значений независимых переменных:
n = x0 +nh, где h - шаг интерполяции.
Необходимо найти полином Pn (x) степени не выше n,
принимающий в точках (узлах) xi значения:
n (xi) = yi, i=0,…, n. (1)
Интерполирующий полином ищется в виде:
Рn(X) = a0 + a1(X - X0)
+ a2(X - X0) (X - X1) + … + an(X - X0)… (X - Xn-1) (2)
Задача построения многочлена сводится к определению
коэффициентов аi из условий:
Pn(x0)=y0,
Pn(x1)=y1,
. .
Pn(xn)=yn.
Найдем коэффициент а1.
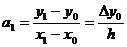
Для определения а2, составим конечную разность
второго порядка.
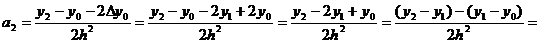
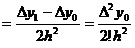
Аналогично можно найти другие коэффициенты. Общая формула
имеет вид:
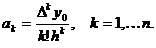
Подставляя эти выражения в формулу (2), получаем:
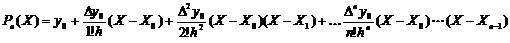 (3)
(3)
где xi, yi - узлы интерполяции;-
текущая переменная;- разность между двумя узлами интерполяции h - величина
постоянная, т.е. узлы интерполяции равноотстоят друг от друга.
Этот многочлен называют интерполяционным полиномом Ньютона.
С помощью функции-генератора случайных чисел задаем таблицу
значений функцию в точках 0, 1, 2, …, 10.
|
X
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Y
|
4
|
9
|
2
|
7
|
9
|
6
|
3
|
4
|
8
|
5
|
4
|
Составим таблицу конечных разностей функции.
|
х
|
у
|
Dу
|
D2у
|
D3у
|
D4у
|
D5у
|
D6у
|
D7у
|
D8у
|
D9у
|
D10у
|
|
0
|
4
|
5
|
-12
|
24
|
-39
|
52
|
-58
|
56
|
-50
|
40
|
6
|
|
1
|
9
|
-7
|
12
|
-15
|
13
|
-6
|
-2
|
6
|
-10
|
46
|
|
|
2
|
2
|
5
|
-3
|
-2
|
7
|
-8
|
4
|
-4
|
36
|
|
|
|
3
|
7
|
2
|
-5
|
5
|
-1
|
-4
|
0
|
32
|
|
|
|
|
4
|
9
|
-3
|
0
|
4
|
-5
|
-4
|
32
|
|
|
|
|
|
5
|
6
|
-3
|
4
|
-1
|
-9
|
28
|
|
|
|
|
|
|
6
|
3
|
1
|
3
|
-10
|
19
|
|
|
|
|
|
|
|
7
|
4
|
4
|
-7
|
9
|
|
|
|
|
|
|
|
|
8
|
8
|
-3
|
2
|
|
|
|
|
|
|
|
|
|
9
|
5
|
-1
|
|
|
|
|
|
|
|
|
|
|
10
|
4
|
|
|
|
|
|
|
|
|
|
|
Воспользуемся формулой (3)
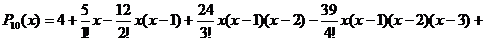
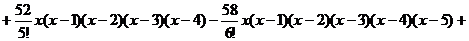
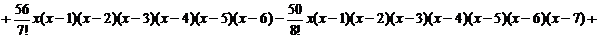


После выполнения преобразований получим интерполяционный
многочлен вида:
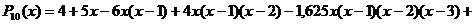
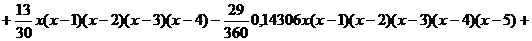
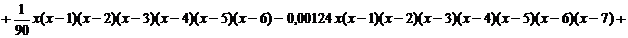
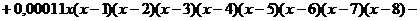
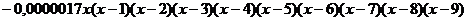
Вычислим значения полученного интерполяционного многочлена.
Р10(0) = 4 Р10(6) = 2,9994
Р10(1) = 9 Р10(7) = 3,9964
Р10(2) = 2 Р10(8) = 7,9875
Р10(3) = 7 Р10(9) = 4,8935
Р10(4) = 9 Р10(10) = 4,4251
Р10(5) = 6
Задание 3. Численное интегрирование
Функция 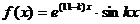 определена на отрезке [-1; 5] (k - номер варианта).
определена на отрезке [-1; 5] (k - номер варианта).
· используя метод интегрирования по частям, вычислить интеграл 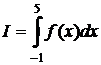 ;
;
· используя метод прямоугольников вычислить этот же интеграл с
точностью 0,1;
· используя метод трапеций вычислить этот же интеграл с точностью
0,1.
Решение
Используя метод интегрирования по частям, вычислим интеграл
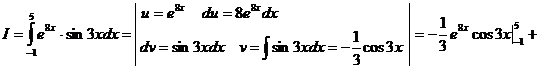

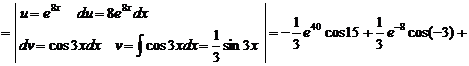

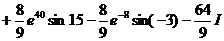
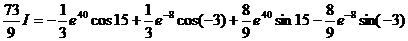
I » 2,412×1016
Для расчетов составим расчетную таблицу.
По формуле прямоугольников
Пусть f(х) = 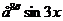 , тогда разобьем отрезок интегрирования на 20 частей, с шагом h=
, тогда разобьем отрезок интегрирования на 20 частей, с шагом h=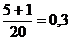 и составим таблицу, в которой найдены
середины отрезков
и составим таблицу, в которой найдены
середины отрезков 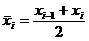 , i = 1, 2, …, 10 и значение функции в этих точках
, i = 1, 2, …, 10 и значение функции в этих точках 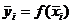 .
.
|
№
|
xi
|
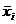 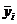 уi уi
|
|
|
|
1.
|
-1
|
-0,85
|
-0,0006
|
-0,00005
|
|
2.
|
-0,7
|
-0,55
|
-0,0122
|
-0,0032
|
|
3.
|
-0,4
|
-0,25
|
-0,0922
|
-0,0380
|
|
4.
|
-0,1
|
0,05
|
0,2229
|
-0,1328
|
|
5.
|
0,2
|
0,35
|
14,2645
|
2,7967
|
|
6.
|
0,5
|
0,65
|
168,3946
|
54,4614
|
|
7.
|
0,8
|
0,95
|
574,4374
|
406,5242
|
|
8.
|
1,1
|
1,25
|
-12589,4758
|
-1046,5234
|
|
9.
|
1,4
|
1,55
|
-2,42E+05
|
-6,37E+04
|
|
10.
|
1,7
|
1,85
|
-1,79E+06
|
-7,46E+05
|
|
11.
|
2
|
2,15
|
4,90E+06
|
-2,48E+06
|
|
12.
|
2,3
|
2,45
|
2,85E+08
|
5,67E+07
|
|
13.
|
2,6
|
2,75
|
3,31E+09
|
1,08E+09
|
|
14.
|
2,9
|
3,05
|
1,07E+10
|
7,89E+09
|
|
15.
|
3,2
|
3,35
|
-2,55E+11
|
-2,29E+10
|
|
16.
|
3,5
|
3,65
|
-4,80E+12
|
-1,27E+12
|
|
17.
|
3,8
|
3,95
|
-3,48E+13
|
-1,47E+13
|
|
18.
|
4,1
|
4,25
|
1,07E+14
|
-4,63E+13
|
|
19.
|
4,4
|
4,55
|
5,68E+15
|
1,15E+15
|
|
20.
|
4,7
|
4,85
|
6,49E+16
|
2,13E+16
|
|
21.
|
5
|
|
7,07E+16
|
|
По формуле средних прямоугольников получим:
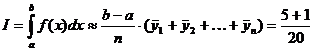 ×(-0,0006 - 0,0122+ … +1,15E+15 + 2,13E+16= 0,3×(7,07E+16) » 2,121×1016
×(-0,0006 - 0,0122+ … +1,15E+15 + 2,13E+16= 0,3×(7,07E+16) » 2,121×1016
По формуле трапеции получим:
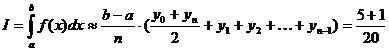 ×(
×(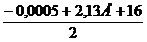 -0,0032 - 0,038+ … +1,15E+15 + 2,13E+16 =
0,3×(9,90E+16) » 2,969×1016
-0,0032 - 0,038+ … +1,15E+15 + 2,13E+16 =
0,3×(9,90E+16) » 2,969×1016
Ответ: интеграл равен:
,412×1016
- по методу интегрирования по частям;
,121×1016
- по методу прямоугольников;
,969×1016
- по методу трапеций.
Задание 4. Решение нелинейных уравнений
Функция 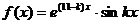 определена на отрезке [-1; 5] (k - номер варианта).
определена на отрезке [-1; 5] (k - номер варианта).
Найти один корень уравнения:

· методом дихотомии;
· методом касательных.
Решение
f(х) = 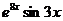 ,
,
Для нахождения минимума и максимума функции необходимо вычислить
1-ую производную функции.

Так как в задании требуется найти только одни корень, то можно
уменьшить заданный интервал до интервала, в котором будет находиться минимум и
максимум функции.
Построим график первой производной на интервале [-1; 1] (рис. 1).
На интервале [-0,5; 0] производная меняет знак с «-» на «+»,
значит на этом интервале расположена точка минимума.
На интервале [0,5; 1] производная меняет знак с «+» на «-», значит
на этом интервале расположена точка максимума.
Приравняем f ¢(x) нулю и
вычислим корень уравнения. Так как е8х > 0, то для нахождения
точки экстремума надо решить уравнение 8sin3x + cos3x = 0.
Обозначим F(x) = 8sin3x + cos3x и решим уравнение методом дихотомии.
Метод дихотомии заключается в следующем.
. Задать интервал [а, b], на котором корень
уравнения существует. Функция на границах данного интервала должна иметь разные
знаки, т.е. F(a) F(b)<0.
2. Найти середину интервала по формуле 
. Выбрать из полученных двух половин: [а, Х] и [Х, b] интервала [а, b] ту, на
которой находится корень по условию F(a) F(X)<0.
Если данное условие выполняется, то корень находится на [а, Х],
правую границу интервала [а, b] перенесем в
середину интервала: b=Х. Перейти в п. 2.
Иначе: корень - на интервале [Х, b]; тогда левую границу
интервала [а, b]
перенесем в середину интервала: а=Х. Перейти в п. 2.
Зададим точность вычисления е = 0,1.
Рассмотрим интервал [-0,5; 0].
Вычислим значение функции на границах интервала.
F(a) = F (-0,5) = 8sin (-1,5) + 3cos (-1,5) =
-7,77(b) = F(0) = 8sin(0) + 3cos(0) = 3
Функция на границах интервала имеет разные знаки, значит,
решение лежит в указанном интервале.
Определяем середину отрезка 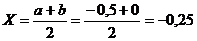 и вычисляем значение функции в этой точке F(Х) = F (-0,25) = 8sin (-0,75) + 3cos (-0,25) = -3,26 Функция на границах интервалов [a, c] и [c, b] имеет разные
знаки, значит, в каждом из этих интервалов есть корень.
и вычисляем значение функции в этой точке F(Х) = F (-0,25) = 8sin (-0,75) + 3cos (-0,25) = -3,26 Функция на границах интервалов [a, c] и [c, b] имеет разные
знаки, значит, в каждом из этих интервалов есть корень.
| F (-0,25)| > 0,1.
Точность не достигнута.
F(а) × F(Х) = -7,77×(-3,26)
> 0.
Следовательно, корень находится на промежутке [X, b]. Отсюда a = -0,25.
Итерация 2.
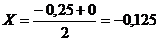
F (-0,125) = -0,14 | F (-0,125)| >
0,1.
Точность не достигнута.
F(а) × F(Х) = -3,26×(-0,14)
> 0.
Следовательно, корень находится на промежутке [X, b]. Отсюда a = -0,125.
Итерация 3.

F (-0,0625) = 1,46 | F (-0,0625)| >
0,1.
Точность не достигнута.
F(a) × F(Х) = -0,14×1,46 < 0.
Следовательно, корень находится на промежутке [а, X]. Отсюда b = -0,0625.
Итерация 4.
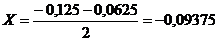
F (-0,09375) = 0,66 | F (-0,09375)| > 0,1.
Точность не достигнута.
F(a) × F(Х) = -0,14×0,66 < 0.
Следовательно, корень находится на промежутке [а, X]. Отсюда b = -0,09375.
Итерация 5.
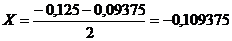
F (-0,109375) = 0,26 | F (-0,109375)| > 0,1.
Точность не достигнута.
F(a) × F(Х) = -1,4×0,26 < 0.
Следовательно, корень находится на промежутке [а, X]. Отсюда b = -0,09375.
Итерация 6.
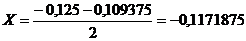
F (-0,1171875) = 0,06 | F (-0,1171875)| < 0,1.
Точность достигнута.
Корень уравнения Х = -0,1171875.
fmin (-0,1171875) = -0,135
Ответ: x = -0,1171875; fmin (-0,1171875) = -0,135
Точку максимум определяем на интервале [0,5; 1].
Вычислим значение функции на границах интервала.
F(a) = F (0,5) = 8sin (1,5) + 3cos (1,5) =
8,19(b) = F(1) = 8sin(3) + 3cos(3) = -1,84
Итерация 1.
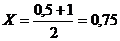
F (0,75) = 4,34 | F (0,75)| >
0,1.
Точность не достигнута.
F(a) × F(Х) = 8,19×4,34 > 0.
Следовательно, корень находится на промежутке [X, b]. Отсюда a = 0,75.
Итерация 2.

F (0,875) = 1,34 | F (0,875)| >
0,1.
Точность не достигнута.
F(a) × F(Х) = 4,34×1,34 > 0.
Следовательно, корень находится на промежутке [X, b]. Отсюда a = 2,75.
Итерация 3.
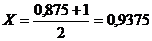
F (0,9375) = -0,25 | F (0,9375)| >
0,1.
Точность не достигнута.
F(a) × F(Х) = 1,34×(-0,25) < 0.
Следовательно, корень находится на промежутке [а, X]. Отсюда b = 0,9375.
Итерация 4.
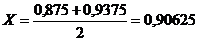
F (0, 90625) = 0, 55 | F (2, 9375)| > 0, 1.
Точность не достигнута.
F(a) × F(Х) = 1,34×0,55 > 0.
Следовательно, корень находится на промежутке [X, b]. Отсюда a = 0,90625.
Итерация 5.
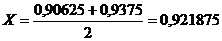
F (0,92875) = 0,15 | F(092875)| >
0,1.
Точность не достигнута.
F(a) × F(Х) = 0,55×0,15 > 0.
Следовательно, корень находится на промежутке [X, b]. Отсюда a = 0,921875.
Итерация 6.

F (0,9296875) = -0,05 | F (0,9296875)| < 0,1.
Точность достигнута.
Корень уравнения Х = 0,9296875.
Вычисли 2-ую производную f ¢¢= 20cos (3,03125) + 99sin (3,03125) = -8,98 < 0, значит это точка максимума.
fmах (0,9296875) = 586,447
Ответ: x = 0,9296875; fmах
(0,9296875) = 586,447
Найти один корень уравнения:

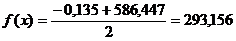
Для нахождения экстремума методом касательных надо решить
уравнение 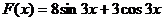
F ¢(x) = 24cos3x - 9sin3x
Если х0 - начальное приближение корня уравнения
f(x) = 0, то последовательные приближения находят по формуле:
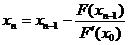
Минимум лежит в пределах [-0,5; 0].
Итерация 1.
Вычисляем значения функций в точке х0 = 0.
F(х0) = 8sin(0) + 3cos(0) = 3
F '(х0) = 24
 х1= 0 - 0,333 = -0,333
х1= 0 - 0,333 = -0,333
Итерация 2.
Вычисляем значения функций в точке х1= -0.125.
F(х1) = -0,1387
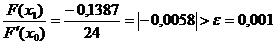 х2= -0,125 + 0,0058 = -0,1192
х2= -0,125 + 0,0058 = -0,1192
Итерация 3.
Вычисляем значения функций в точке х2= -0,1192.
F(х2) = 0,0094
F ' (-0,1192) = 25,6320
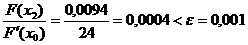
Точность достигнута.
fmin (-0,1192) = -0,135
Максимум лежит в пределах [0,5; 1].
Итерация 1.
Вычисляем значения функций в точке х0 = 1.
F(х0) = 1,8410
F '(х0) = 25,0299
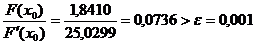 х1= 1 - 0,0736 = 0,9264
х1= 1 - 0,0736 = 0,9264
Итерация 2.
Вычисляем значения функций в точке х1= 0,9264.
F(х1) = 0,0297
 х2= 0,9264 + 0,0012 = 0,9276
х2= 0,9264 + 0,0012 = 0,9276
Итерация 3.
Вычисляем значения функций в точке х2= 0,9276.
F(х2) = -0,0007
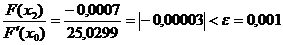
Точность достигнута.
fmах (0,9276) = 586,540
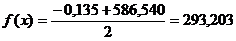
Ответ: 293,156 по методу дихотомии;
,203 по методу касательных
Задание 5. Метод Рунге - Кутта четвертого порядка
гаусс интерполяционный многочлен нелинейный
Методом Рунге - Кутта найти решение на отрезке [a, b]
дифференциального уравнений вида 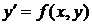 при заданных начальных условиях с указанным шагом h
при заданных начальных условиях с указанным шагом h
Решение
Метод Рунге - Кутта описывается системой следующих
соотношений:
yi+1 = yi + Dyi или yi+1 = yi + 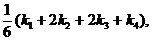
где k1 = h×f(xi, yi)
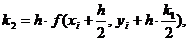


Из начальных условий имеем х0 = 0, у0 = 1, h = 0,01. Найдем первое приближение
у1= у0 + Dу0, где 
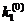 = 0,1×
= 0,1×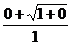 = 0,1
= 0,1
 = 0,1×
= 0,1×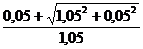 = 0,10488
= 0,10488
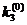 = 0,1×
= 0,1×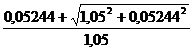 = 0,10512
= 0,10512
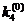 = 0,1×
= 0,1×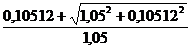 = 0,11001
= 0,11001
Следовательно, 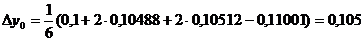
и у1= 0 + 0,105 = 0,105.
Дальнейшее решение уравнения представлено в таблице.
|
|
Х
|
y
|
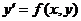 kDy kDy
|
|
|
|
0
|
0
|
1
|
0
|
1
|
0,1
|
0,1
|
|
1
|
1,05
|
0,05
|
1,048752
|
0,10488
|
0,20975
|
|
2
|
1,05
|
0,05244
|
1,051187
|
0,10512
|
0,21024
|
|
3
|
1,1
|
0,10512
|
1,100118
|
0,11001
|
0,11001
|
|
|
|
|
|
|
0,10500
|
|
1
|
0
|
1,1
|
0,10500
|
1,1
|
0,11000
|
0,11000
|
|
1
|
1,15
|
0,16000
|
1,148763
|
0,11488
|
0,22975
|
|
2
|
1,15
|
0,16244
|
1,151177
|
0,11512
|
0,23024
|
|
3
|
1,2
|
0,22012
|
1,200116
|
0,12001
|
0,12001
|
|
|
|
|
|
|
0,11500
|
|
2
|
0
|
1,2
|
0,22000
|
1,2
|
0,12000
|
0,12000
|
|
1
|
1,25
|
0,28000
|
1,248781
|
0,12488
|
0,24976
|
|
2
|
1,25
|
0,28244
|
1,25116
|
0,12512
|
0,25023
|
|
3
|
1,3
|
0,34512
|
1,300112
|
0,13001
|
0,13001
|
|
|
|
|
|
|
0,12500
|
|
3
|
0
|
1,3
|
0,34500
|
1,3
|
0,13000
|
0,13000
|
|
1
|
1,35
|
0,41000
|
1,348804
|
0,13488
|
0,26976
|
|
2
|
1,35
|
0,41244
|
1,351139
|
0,13511
|
0,27023
|
|
3
|
1,4
|
0,48011
|
1,400107
|
0,14001
|
0,14001
|
|
|
|
|
|
|
0,13500
|
|
4
|
0
|
1,4
|
0,48000
|
1,4
|
0,14000
|
0,14000
|
|
1
|
1,45
|
0,55000
|
1,448832
|
0,14488
|
0,28977
|
|
2
|
1,45
|
0,55244
|
1,451114
|
0,14511
|
0,29022
|
|
3
|
1,5
|
0,62511
|
1,500102
|
0,15001
|
0,15001
|
|
|
|
|
|
|
0,14500
|
|
5
|
0
|
1,5
|
0,62500
|
1,5
|
0,15000
|
0,15000
|
|
1
|
1,55
|
0,70000
|
1,548861
|
0,15489
|
0,30977
|
|
2
|
1,55
|
0,70244
|
1,551087
|
0,15511
|
0,31022
|
|
3
|
1,6
|
0,78011
|
1,600097
|
0,16001
|
0,16001
|
|
|
|
|
|
|
0,15500
|
|
6
|
0
|
1,6
|
0,78000
|
1,599999
|
0,16000
|
0,16000
|
|
1
|
1,65
|
0,86000
|
1,648892
|
0,16489
|
0,32978
|
|
2
|
1,65
|
0,86244
|
1,651059
|
0,16511
|
0,33021
|
|
3
|
1,7
|
0,94511
|
1,700092
|
0,17001
|
0,17001
|
|
|
|
|
|
|
0,16500
|
|
7
|
0
|
1,7
|
0,94500
|
1,699999
|
0,17000
|
0,17000
|
|
1
|
1,75
|
1,03000
|
1,748923
|
0,17489
|
0,34978
|
|
2
|
1,75
|
1,03245
|
1,75103
|
0,17510
|
0,35021
|
|
3
|
1,8
|
1,12010
|
1,800087
|
0,18001
|
0,18001
|
|
|
|
|
|
|
0,17500
|
0
|
1,8
|
1,12000
|
1,799999
|
0,18000
|
0,18000
|
|
1
|
1,85
|
1,21000
|
1,848954
|
0,18490
|
0,36979
|
|
2
|
1,85
|
1,21245
|
1,851001
|
0,18510
|
0,37020
|
|
3
|
1,9
|
1,30510
|
1,900082
|
0,19001
|
0,19001
|
|
|
|
|
|
|
0,18500
|
|
9
|
0
|
1,9
|
1,30500
|
1,899999
|
0,19000
|
0,19000
|
|
1
|
1,95
|
1,40000
|
1,948984
|
0,19490
|
0,38980
|
|
2
|
1,95
|
1,40245
|
1,950973
|
0,19510
|
0,39019
|
|
3
|
2
|
1,50010
|
2,000077
|
0,20001
|
0,20001
|
|
10
|
|
|
|
|
0,19500
|
|
|
2
|
1,50000
|
|
|
|
Таким образом, окончательно имеем у ¢(2) = 1,5.
Литература
гаусс
интерполяционный многочлен нелинейный
1. Поршнев С.В. Вычислительная математика. - СПб.: Питер, 2004. -
320 с.: ил.
2. Бахвалов Н.С. Численные методы. - М.: Бином, 2004. - 631
с.
. Лапчик М.П. Численные методы. - М.: Академия, 2005
. Высшая математика для экономистов / Под ред. Н.М.
Кремера. - М.: ЮНИТИ - ДАНА, 2007