Нейронные сети
Содержание
Определение
нейронных сетей
Биологический
нейрон
Искусственные
нейронные сети
Применение
нейронных сетей
Обучение
нейронных сетей
Модели
нейронных сетей
Персептрон
Сеть
Кохонена
Определение нейронных сетей
Нейронная сеть - это система, которая принимает
решения при множестве заданных условий (на входе много разных условий, по
которым выдается решение на выходе).
Биологический нейрон
Нейрон является нервной клеткой биологической
системы. Он состоит из тела и отростков, соединяющих его с внешним миром рис.
1.1.

Отростки, по которым нейрон получает
возбуждение, называются дендритами. Отросток, по которому нейрон передает
возбуждение, называется аксоном, причем аксон у каждого нейрона один. Место
соединения аксона нейрона - источника возбуждения с дендритом называется
синапсом. Основная функция нейрона заключается в передаче возбуждения с
дендритов на аксон. Но сигналы, поступающие с различных дендритов, могут
оказывать различное влияние на сигнал в аксоне. Нейрон выдаст сигнал, если
суммарное возбуждение превысит некоторое пороговое значение, которое в общем
случае изменяется в некоторых пределах. В противном случае на аксон сигнал
выдан не будет: нейрон не ответит на возбуждение. У этой основной схемы много
усложнений и исключений, тем не менее, большинство искусственных нейронных
сетей моделируют лишь эти простые свойства.
Искусственные нейронные сети.

Искусственный нейрон имитирует в
первом приближении свойства биологического нейрона. На вход искусственного
нейрона поступает некоторое множество сигналов, каждый из которых является
выходом другого нейрона. Каждый вход умножается на соответствующий вес,
аналогичный синаптической силе, и все произведения суммируются, определяя
уровень активации нейрона. На рисунке можно увидеть множество входных сигналов,
обозначенных x1, x2,:, xn, поступает на искусственный нейрон. Эти входные
сигналы, в совокупности, обозначаемые вектором X, соответствуют сигналам,
приходящим в синапсы биологического нейрона. Каждый сигнал умножается на
соответствующий вес w1, w2,..., wn, и поступает на суммирующий блок. Каждый вес
соответствует "силе" одной биологической синаптической связи.
Суммирующий блок, соответствующий телу биологического элемента, складывает
взвешенные входы алгебраически, создавая выход, который мы будем называть NET.
В векторных обозначениях это может быть компактно записано следующим образом:
NET = XW.

Хотя один нейрон и способен
выполнять простейшие процедуры распознавания, сила нейронных вычислений
проистекает от соединений нейронов в сетях. Простейшая сеть состоит из группы
нейронов, образующих слой, как показано на рис.1.3. Отметим, что вершины-круги
слева служат лишь для распределения входных сигналов. Они не выполняют каких-
либо вычислений, и поэтому не будут считаться слоем. По этой причине они
обозначены кругами, чтобы отличать их от вычисляющих нейронов, обозначенных
квадратами. Каждый элемент из множества входов Х отдельным весом соединен с
каждым искусственным нейроном. Вычисление выходного вектора N, компонентами
которого являются выходы OUT нейронов, сводится к матричному умножению N = XW,
где N и Х - векторы-строки.
Более крупные и сложные нейронные
сети обладают, как правило, и большими вычислительными возможностями. Хотя
созданы сети всех конфигураций, какие только можно себе представить, послойная
организация нейронов копирует слоистые структуры определенных отделов мозга.
Многослойные сети могут образовываться каскадами слоев. Выход одного слоя
является входом для последующего слоя. Подобная сеть показана на рис 1.4 и
снова изображена со всеми соединениями.
Применение нейронных сетей
Нейрокомпьютеры (компьютеры на
основе нейронных сетей) обладают целым рядом свойств, привлекательных с точки
зрения их практического использования:
Сверхвысокое быстродействие за счет
использования массового параллелизма обработки информации.
Толерантность (терпимость) к
ошибкам: работоспособность сохраняется при повреждении значительного числа
нейронов.
Способность к обучению;
программирование вычислительной системы заменяется обучением.
Способность к распознаванию образов
в условиях сильных помех и искажений.
Однако, первые 2 свойства имеют
место только при аппаратной реализации нейронных сетей. Аппаратно реализованные
нейронные сети обеспечивают решение сложных задач за времена порядка времен
срабатывания цепочек электронных и/или оптических элементов. Решение слабо
зависит от неисправности отдельного нейрона. Это делает их привлекательными для
использования в составе бортовых вычислительных систем.
В настоящее время нейронные сети
применяются для решения многих неформализуемых или трудно формализуемых задач:
распознавания и синтеза речи;
распознавания аэрокосмических
изображений;
прогнозирования котировки ценных
бумаг и курса валют;
предупреждения мошенничества с
кредитными карточками;
оценки стоимости недвижимости;
оценки финансового состояния
предприятий и риска невозврата кредитов;
обработки радиолокационных сигналов;
контроля движения на скоростных
автомагистралях и железных дорогах;
диагностики в медицине;
добычи знаний из больших объемов
данных в бизнесе, финансах и научных исследованиях.
Нейронные сети можно использовать
при следующих условиях:
Если при решении задачи можно
выделить множество входных факторов (сигналов, признаков, данных и т.п.) и множество
выходных факторов.
Если изменения входных факторов
приводит к изменению выходных.
В то же время применение нейронных
сетей при решении некоторых задач может оказаться эффективнее использования
разума человека. Это объясняется тем, что человеческий разум ориентирован на
решение задач в трехмерном пространстве. Многомерные задачи для него
характеризуются значительно большей трудоемкостью. Искусственным нейронным
сетям не свойственно такое ограничение. Им все равно решать трехмерную или
10-мерную задачу.
При применении нейронных сетей
необходимо решить следующие задачи:
Постановка задачи, пригодной для
решения с помощью нейронной сети.
Выбор модели ИНС.
Подготовка исходных данных для
обучения ИНС.
Обучение ИНС.
Собственно решение задачи с помощью
обученной ИНС
Кроме того, иногда нужен еще один
этап - интерпретация решения, полученного нейронной сетью.
Наиболее трудоемкими процессами при
использовании нейронных сетей являются подготовка исходных данных для обучения
и обучение нейронной сети.
Обучение нейронных сетей
По организации обучения разделяют
обучение нейронных сетей с учителем (supervised neural networks) и без учителя
(nonsupervised). При обучении с учителем предполагается, что есть внешняя
среда, которая предоставляет обучающие примеры (значения входов и
соответствующие им значения выходов) на этапе обучения или оценивает
правильность функционирования нейронной сети и в соответствии со своими
критериями меняет состояние нейронной сети или поощряет (наказывает) нейронную
сеть, запуская тем самым механизм изменения ее состояния. Под состоянием
нейронной сети, которое может изменяться, обычно понимается:
веса синапсов нейронов (карта весов
- map) (коннекционистский подход);
веса синапсов и пороги нейронов
(обычно в этом случае порог является более легко изменяемым параметром, чем
веса синапсов);
установление новых связей между
нейронами (свойство биологических нейронов устанавливать новые связи и
ликвидировать старые называется пластичностью).
По способу обучения разделяют
обучение по входам и по выходам. При обучении по входам обучающий пример
представляет собой только вектор входных сигналов, а при обучении по выходам в
него входит и вектор выходных сигналов, соответствующий входному вектору.
По способу предъявления примеров
различают предъявление одиночных примеров и "страницы" примеров. В
первом случае изменение состояния нейронной сети (обучение) происходит после
предъявления каждого примера. Во втором - после предъявления
"страницы" (множества) примеров на основе анализа сразу их всех.
По особенностям модели нейрона
различают нейроны с разными нелинейными функциями:
пороговой;
рациональной сигмоидой;
гиперболическим тангенсом.
Перечисленные функции относятся к
однопараметрическим. Также используются многопараметрические передаточные
функции.
Модели нейронных сетей
Персептроны
Многослойная сеть с обратным распространением
ошибки
Модель Хопфилда
Машина Больцмана
Сеть Кохонена (карты Кохонена)
Модель Хэмминга
Модель ART (Сеть Гросберга)
Двунаправленная ассоциативная память (ДАП)
Когнитрон и неокогнитрон.
Персептрон
Первое систематическое изучение искусственных
нейронных сетей было предпринято Маккалокком и Питтсом в 1943 г. Простая
нейронная модель, показанная на рисунке 2.1, использовалась в большей части их
работы.
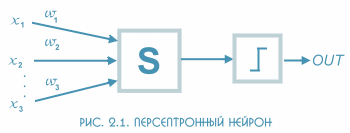
нейронная
сеть персептрон кохонен
Элемент S умножает каждый вход х на
вес w и суммирует взвешенные входы. Если эта сумма больше заданного порогового
значения, выход равен единице, в противном случае - нулю. Эти системы получили
название персептронов. Они состоят из одного слоя искусственных нейронов,
соединенных с помощью весовых коэффициентов с множеством входов. Персептрон
обучают, подавая множество образов по одному на его вход, и подстраивая веса до
тех пор, пока для всех образов не будет достигнут требуемый выход.
Целью обучения является такая
подстройка весов НС, чтобы приложение некоторого множества векторов входов
приводило к требуему множеству векторов выходов. При обучении предполагается,
что у каждого входного вектора есть парный ему выходной. Сеть обучается на
многих парах, называемых обучающими парами. Множество обучающих пар называется
тренировочным набором.
Сеть Кохонена
Входные сигналы - вектора действительных чисел -
последовательно предъявляются сети. Желаемые выходные сигналы не определяются.
После того, как было предъявлено достаточное число входных векторов,
синаптические веса сети определяют кластеры. Кроме того, веса организуются так,
что топологически близкие узлы чувствительны к похожим внешним воздействиям
(входным сигналам).