|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
|
|
|
|
95
|
160
|
135
|
110
|
|
|
1
|
105
|
17 95
|
12 10
|
17 2
|
21 1
|
U1 = 0
|
|
2
|
70
|
6 -10
|
11 70
|
20 6
|
28 9
|
U2 = -1
|
|
3
|
240
|
+ 10 -14
|
- 19 80
|
22 135
|
27 25
|
U3 = 7
|
|
4
|
85
|
18 14
|
14 15
|
23 21
|
7 85
|
U4 = -13
|
|
Vj
|
V1 = 17
|
V2 = 12
|
V3 = 15
|
V4 = 20
|
№1
|
Здесь в верхнем правом углу клеток записана стоимость
перевозки.
Заполнять таблицу первоначального опорного плана
начинаем с клетки а1b1
- это северо-западный угол.
Закрываем потребности b1
поставкой из а1 и этот столбец исключаем из дальнейшего
рассмотрения. Остаток груза из а1 отправляем потребителю b2
и строку а1 исключаем из дальнейшего рассмотрения. Затем весь груз
из а2 отправляем в b2,
исключая строку а2 и частью груза из а3 закрываем
потребность b2,
исключая столбец b2.
Далее закрываем потребность b3
поставкой из а3, а остаток груза из а3 отправляем
потребителю b4.
Груз из а4 отправляем потребителю b4.
Опорный план составлен.
Стоимость перевозок по этому плану:
Z1 =
95·17 + 10∙12 + 70∙11 + 80∙19 + 135∙22 + 25·27 +
85·7 = 8265 д.е.
Число заполненных клеток должно быть m
+ n -1 = 4 + 4 - 1 =
7, что так и есть, т.е. план не вырожден.
Проверяем оптимальность плана методом
потенциалов, присвоив первой строке нулевой потенциал U1
= 0. Потенциалы других строк и столбцов определяем по формулам:
Ui
= Cij - Vj;
Vj = Cij
-
Ui;
V1 = C11 - U1
= 17 - 0 = 17; V2 = C12 - U1 = 12 - 0 = 12; U2
= C22 - V2 = 11 - 12 = -1;3 = C32 -
V2 = 19 - 12 = 7; V3 = C33 - U3 =
22 - 7 = 15; V4 = C34 - U3 = 27 - 7 = 20.4
= C44
- V4
= 7 - 20 = -13;
Определяем характеристики клеток, оставшихся
свободными по формуле:
Eij
= Cij - (Vj
+ Ui) (вписаны в левый
нижний угол)
Е13 = С13 - (V3
+ U1)
= 17 - (15 + 0) = 2; Е14 = С14 - (V4
+ U1)
= 21 - (20 + 0) = 1;
Е21 = С21 - (V1
+ U2)
= 6 - (17 - 1) = -10; Е23 = С23 - (V3
+ U2)
= 20 - (15 - 1) = 6;
Е24 = С24 - (V4
+ U2)
= 28 - (20 - 1) = 9; Е31 = С31 - (V1
+ U3)
= 10 - (17 + 7) = -14;
Е41 = С41 - (V1
+ U4)
= 18 - (17 - 13) = 14; Е42 = С42 - (V2
+ U4)
= 14 - (12 - 13) = 15;
Е43 = С43 - (V3
+ U4)
= 23 - (15 - 13) = 21;
Среди характеристик свободных клеток есть две
отрицательные (Е21 = -10 и Е31 = -14), значит полученный
план не оптимален.
Строим для клетки а3b1
с
отрицательной характеристикой (-14), цикл (показан пунктиром) и перемещаем по
нему наименьшую из перевозок (80), находящихся в углах цикла, смежных с этой
клеткой. Получаем новый план (табл. №2).
Таблица 2
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
|
|
|
|
95
|
160
|
135
|
110
|
|
|
1
|
105
|
17 15
|
12 90
|
17 12
|
21 13
|
U1 = 0
|
|
2
|
70
|
6 10
|
11 70
|
20 8
|
28 5
|
U2 = -1
|
|
3
|
240
|
10 80
|
19 14
|
22 135
|
27 25
|
U3 = -7
|
|
4
|
85
|
18 8
|
14 29
|
23 21
|
7 85
|
U4 = -27
|
|
Vj
|
V1 = 17
|
V2 = 12
|
V3 = 29
|
V4 = 34
|
№2
|
Цена этого плана:
2 =
15·17 + 90∙12 + 70∙11 + 80∙10 + 135∙22 + 25·27 +
85·7 = 7145 д.е.
что меньше первого плана на 1120 ден. ед.
Проверка методом потенциалов показывает, что
этот план не оптимален, т.к. среди характеристик свободных клеток есть
отрицательные.
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
|
|
|
|
95
|
160
|
135
|
110
|
|
|
1
|
105
|
17 13
|
12 90
|
17 1
|
21 15
|
U1 = 0
|
|
2
|
70
|
6 3
|
11 70
|
20 5
|
28 8
|
U2 = -1
|
|
3
|
240
|
10 95
|
19 1
|
22 135
|
27 10
|
U3 = 6
|
|
4
|
85
|
18 8
|
14 16
|
23 21
|
7 85
|
U4 = -14
|
|
Vj
|
V1 = 4
|
V2 = 12
|
V3 = 16
|
V4 = 21
|
№3
|
Далее без комментариев повторяем итерацию с
перемещением перевозки по циклу в клетку a1b4
с отрицательной характеристикой (-13). Получаем третий план (табл. №3).
Его цена:
Z3 =
90∙12 + 15·21 + 70∙11 + 95∙10 + 135∙22 + 10·27
+ 85·7 = 6950 д.е.
что меньше второго плана на 195 ден. ед.
Этот план оптимальный, т.к. все характеристики
свободных клеток положительны.
Zопт = Zmin
= Z3
= 6950 ден. ед.
Построение оптимального плана
методом минимального элемента.
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
|
|
|
|
95
|
160
|
135
|
110
|
|
|
1
|
105
|
17 14
|
12 105
|
17 2
|
21 1
|
U1 = 0
|
|
2
|
70
|
6 70
|
11 -4
|
20 2
|
28 5
|
U2 = 3
|
|
3
|
240
|
10 25
|
19 55
|
22 135
|
27 25
|
U3 = 7
|
|
4
|
85
|
18 29
|
14 16
|
23 22
|
7 85
|
U4 = -14
|
|
Vj
|
V1 = 3
|
V2 = 12
|
V3 = 15
|
V4 = 20
|
№1
|
Минимальная стоимость перевозок (6) в клетке а2b1
- отправляем весь груз из а2 потребителю b1
и строку а2 исключаем из дальнейшего рассмотрения.
Следующий минимум (7) в клетке а4b4
- отправляем весь груз из а4 потребителю b4
и строку а4 исключаем из дальнейшего рассмотрения.
Следующий минимум (10) в клетке а3b1
- закрываем потребность b1
поставкой из а3 и столбец b1
исключаем из дальнейшего рассмотрения.
Следующий минимум (12) в клетке а1b2
- весь груз из а1 отправляем в b2
и строку а1 исключаем из дальнейшего рассмотрения.
Следующий минимум (19) в клетке а3b2
- закрываем потребность b2
поставкой из а3 и столбец b2
исключаем из дальнейшего рассмотрения.
Поставкой остатка груза из а3
закрываем потребности b3
и b4.
Опорный план составлен.
Стоимость перевозок по этому плану:
Z1 =
105·12 + 70∙6 + 25∙10 + 55∙19 + 135∙22 + 25·27 +
85·7 = 7215 д.е.
Проверяем оптимальность плана методом
потенциалов, присвоив первой строке нулевой потенциал U1
= 0. Потенциалы других строк и столбцов определяем по формулам:
Ui
= Cij - Vj;
Vj = Cij
-
Ui;
Определяем характеристики клеток, оставшихся
свободными по формуле:
Eij
= Cij - (Vj
+ Ui) (вписаны в левый
нижний угол).
Среди характеристик свободных клеток есть одна
отрицательная (Е22 = -4), значит полученный план не оптимален.
Строим для клетки а2b
,
цикл (показан пунктиром) и перемещаем по нему наименьшую из перевозок (55),
находящихся в углах цикла, смежных с этой клеткой. Получаем новый план (табл.
№2).
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
|
|
|
|
95
|
160
|
135
|
110
|
|
|
1
|
105
|
17 10
|
12 105
|
17 -2
|
21 -3
|
U1 = 0
|
|
2
|
70
|
6 15
|
11 55
|
20 2
|
28 5
|
U2 = -1
|
|
3
|
240
|
10 80
|
19 4
|
22 135
|
27 25
|
U3 = 3
|
|
4
|
85
|
18 28
|
14 19
|
23 21
|
7 85
|
U4 = -17
|
|
Vj
|
V1 = 7
|
V2 = 12
|
V3 = 19
|
V4 = 24
|
№2
|
Очевидно, что полученный план не является
оптимальным, т.к. среди характеристик свободных клеток есть отрицательные.
Далее без комментариев повторяем итерацию с
перемещением перевозки (15) по циклу в клетку a1b4
с отрицательной характеристикой (-3). Получаем третий план (табл. №3).
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
|
|
|
|
95
|
160
|
135
|
110
|
|
|
1
|
105
|
17 13
|
12 90
|
17 1
|
21 15
|
U1 = 0
|
|
2
|
70
|
6 3
|
11 70
|
20 5
|
28 8
|
U2 = -1
|
|
3
|
240
|
10 95
|
19 1
|
22 135
|
27 10
|
U3 = 6
|
|
4
|
85
|
18 8
|
14 16
|
23 21
|
7 85
|
U4 = -14
|
|
Vj
|
V1 = 4
|
V2 = 12
|
V3 = 16
|
V4 = 21
|
№3
|
Этот план оптимальный, т.к. все характеристики
свободных клеток положительны. План повторяет план, ране полученный методом
северо-западного угла.
Zопт = Zmin
= 6950 ден. ед.
Построение оптимального плана
методом Фогеля.
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
|
|
|
|
|
|
|
|
95
|
160
|
135
|
110
|
105
|
17
|
12 90
|
17
|
21 15
|
5
|
5
|
5
|
5
|
5
|
|
2
|
70
|
6
|
11 70
|
20
|
28
|
5
|
5
|
9
|
|
|
|
3
|
240
|
10 95
|
19
|
22 135
|
27 10
|
9
|
9
|
3
|
3
|
3
|
|
4
|
85
|
18
|
14
|
23
|
7 85
|
7
|
|
|
|
|
|
|
4
|
1
|
3
|
14
|
|
|
|
|
|
|
|
4
|
1
|
3
|
6
|
|
|
|
|
|
|
|
|
1
|
3
|
6
|
|
|
|
|
|
|
|
|
2
|
5
|
6
|
|
|
|
|
|
|
|
|
2
|
5
|
|
|
|
|
|
|
При определении опорного плана методом
аппроксимации Фогеля на каждой итерации по всем столбцам и по всем строкам
находим разность между двумя записанными в них минимальными затратами. Эти
разности записаны в специально отведенных для этого строках и столбцах для
каждого шага. Среди указанных разностей выбрана максимальная. В строке (или в
столбце), которой данная разность соответствует, определён минимальный тариф и
клетка, в которой он записан, заполнена на данной итерации (выделено жирным
шрифтом).
Например, на первом шаге в первой строке
минимальные затраты 17 и 12, разность - 5, во 2-ой строке 11 и 6, разность 5, в
3-ей 19 и 10, разность 9, в 4-ой 14 и 7, разность 7.
В 1-ом столбце минимальные затраты 10 и 6,
разность 4, во 2-ом 12 и 11, разность 1, в 3-ем 20 и 17, разность 3, в 4-ом 21
и 7, разность 14.
Наибольшая из этих разностей - 14 соответствует
4-му столбцу. В этом столбце минимум затрат - 7 в строке 4. Заполняем клетку а4b4
объёмом поставок 85 единиц, который может быть поставлен от четвёртого
поставщика и строку 4 из дальнейшего рассмотрения исключаем. По аналогии
заполнены остальные клетки таблицы и получен опорный план.
Цена этого плана:
Z1 =
90∙12 + 15·21 + 70∙11 + 95∙10 + 135∙22 + 10·27
+ 85·7 = 6950 д.е.
Этот полученный план является оптимальным, т.к.
такой же план получен при использовании методов северо-западного угла и
минимального элемента.
Задача 7.2
Решить транспортную задачу.
Первичный опорный план необходимо найти тремя способами: методом
северо-западного угла, методом минимальной стоимости, методом Фогеля. Для
каждого найденного опорного плана, произвести перепланировку поставок с помощью
метода потенциалов.

Решение:
Общий
объём запасов:
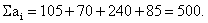
Общая потребность:
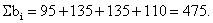
Т.к. 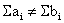 , то это транспортная задача
открытого типа.
, то это транспортная задача
открытого типа.
Для приведения её к закрытому типу
вводим фиктивного потребителя с нулевой стоимостью перевозок, имеющего
потребность:
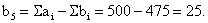
Построение оптимального плана
методом северо-западного угла.
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
|
1
|
105
|
17 95
|
12 10
|
17 2
|
21 1
|
0
-13
|
U1 = 0
|
|
2
|
70
|
6 -10
|
11 70
|
20 6
|
28 9
|
0
-12
|
U2 = -1
|
|
3
|
240
|
10 -14
|
19 55
|
22 135
|
27 50
|
0
-20
|
U3 = 7
|
|
4
|
85
|
18 14
|
14 15
|
23 21
|
7 60
|
0
25
|
U4 = -13
|
|
Vj
|
V1 = 17
|
V2 = 12
|
V3 = 15
|
V4 = 20
|
V5
= 13
|
№1
|
Порядок составления опорного плана этим методом
описан в задаче 7.1.
Стоимость перевозок по этому плану:
Z1 =
95·17 + 10∙12 + 70∙11 + 55∙19 + 135∙22 + 50·27 +
60·7 = 8290 д.е.
Число заполненных клеток должно быть m
+ n -1 = 4 + 5 - 1 =
8, что имеет место в действительности, т.е. план не вырожден.
Проверяем оптимальность плана методом
потенциалов, присвоив первой строке нулевой потенциал U1
= 0. Потенциалы других строк и столбцов определяем по формулам:
Ui
= Cij - Vj;
Vj = Cij
-
Ui;
Определяем характеристики клеток, оставшихся
свободными по формуле:
Eij
= Cij - (Vj
+ Ui) (вписаны в правый
нижний угол).
Среди характеристик свободных клеток есть
отрицательные, значит полученный план не оптимален.
Строим для клетки а3b1
с
отрицательной характеристикой (-14), цикл (показан пунктиром) и перемещаем по
нему наименьшую из перевозок (55), находящихся в углах цикла, смежных с этой
клеткой. Получаем новый план (табл. №2) с ценой z2
= 7520.
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
|
1
|
105
|
17 40
|
12 65
|
17 -12
|
21 -13
|
0
-27
|
U1 = 0
|
|
2
|
70
|
6 10
|
11 70
|
20 8
|
28 5
|
0
-26
|
U2 = -1
|
|
3
|
240
|
10 55
|
19 14
|
22 135
|
27 50
|
0
20
|
U3 = -7
|
|
4
|
85
|
18 28
|
14 29
|
23 21
|
7 60
|
0
25
|
U4 = -27
|
|
Vj
|
V1 = 17
|
V2 = 12
|
V3 = 29
|
V4 = 34
|
V5
= 27
|
№2
|
Среди характеристик свободных клеток есть
отрицательные значит полученный план не оптимален.
Строим для клетки а1b4
с
отрицательной характеристикой (-13), цикл (показан пунктиром) и перемещаем по
нему наименьшую из перевозок (40), находящихся в углах цикла, смежных с этой
клеткой.
Получаем новый план (табл. №3) с ценой z3
= 7000.
Таблица 3
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
|
1
|
105
|
17 13
|
12 65
|
17 1
|
21 40
|
0
14
|
U1 = 0
|
|
2
|
70
|
6 3
|
11 70
|
20 5
|
28 8
|
0
-13
|
U2 = -1
|
|
3
|
240
|
10 95
|
19 1
|
22 135
|
27 10
|
0
20
|
U3 = 6
|
|
4
|
85
|
18 28
|
14 16
|
23 21
|
7 60
|
0
25
|
U4 = -14
|
|
Vj
|
V1 = 4
|
V2 = 12
|
V3 = 16
|
V4 = 21
|
V5
= 14
|
№3
|
Проверка методом потенциалов показывает, что
этот план тоже не оптимален, т.к. среди характеристик свободных клеток есть отрицательные.
Cтроим цикл для
клетки а3b5
с
характеристикой (-20).
Получаем четвёртый план (табл. №4) c
ценой z4
= 6800.
Проверка методом потенциалов показывает, что
этот план тоже не оптимален, т.к. среди характеристик свободных клеток есть
отрицательные. Cтроим цикл
для клетки а2b1
с
характеристикой (-17).
Перемещаем по этому циклу наименьшую перевозку
(15), отмеченную знаком "минус".
Таблица 4
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
|
1
|
105
|
17 7
|
12 65
|
17 19
|
21 40
|
0
14
|
U1 = 0
|
|
2
|
70
|
6 17
|
11 70
|
20 15
|
28 8
|
0
13
|
U2 = -1
|
|
3
|
240
|
10 95
|
19 21
|
22 135
|
27 20
|
0
10
|
U3 = -14
|
|
4
|
85
|
18 28
|
14 16
|
23 3
|
7 70
|
0
15
|
U4 = -14
|
|
Vj
|
V1 = 24
|
V2 = 12
|
V3 = 36
|
V4 = 21
|
V5
= 14
|
№4
|
Получаем пятый план (табл. №5) с ценой z5
= 6545.
опорный план стоимость поставка
Таблица 5
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
1 105 17

|
1012
8017 221 250 3U1 = 0
|
|
|
|
|
|
|
|
2
|
70
|
6 15
|
11 55
|
20 2
|
28 8
|
0
4
|
U2 = -1
|
|
3
|
240
|
10 80
|
19 4
|
22 135
|
27 3
|
0
25
|
U3 = 3
|
|
4
|
85
|
18 25
|
14 16
|
23 18
|
7 85
|
0
|
U4 = -14
|
|
Vj
|
V1 = 7
|
V2 = 12
|
V3 = 19
|
V5
= -3
|
№5
|
Ещё одна итерация по клетке а1b3
с перемещением 15 единиц груза и получаем оптимальный план с положительными
характеристиками всех свободных клеток (табл.№6):
Таблица 6
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
1 105 17 
|
1212
6517 1521 250 5U1 = 0
|
|
|
|
|
|
|
|
2
|
70
|
6 2
|
11 70
|
20 4
|
28 8
|
0
6
|
U2 = -1
|
|
3
|
240
|
10 95
|
19 2
|
22 120
|
27 1
|
0
25
|
U3 = 5
|
|
4
|
85
|
18 27
|
14 16
|
23 20
|
7 85
|
0
19
|
U4 = -14
|
|
Vj
|
V1 = 5
|
V2 = 12
|
V3 = 17
|
V4 = 21
|
V5
= -5
|
№6
|
Цена этого плана:
6 =
65·12 + 15∙17 + 25·21 + 70∙11 + 95·10
+ 120·22 + 85·7 = 6515 ден.ед.
Zопт = Zmin
= Z6
= 6515 ден. ед.
Т.о. у поставщика а3 не будет
запрошено 25 единиц груза, т.к. этой частью своего груза он прикрепился к
фиктивному потребителю.
Построение оптимального плана
методом минимального элемента.
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
|
1
|
105
|
17 14
|
12 105
|
17 2
|
21 1
|
0
7
|
U1 = 0
|
|
2
|
70
|
6 70
|
11 4
|
20 2
|
28 5
|
0
4
|
U2 = 3
|
|
3
|
240
|
10 25
|
19 30
|
22 135
|
27 25
|
0
25
|
U3 = 7
|
|
4
|
85
|
18 28
|
14 15
|
23 21
|
7 85
|
0
20
|
U4 = -13
|
|
Vj
|
V1 = 3
|
V2 = 12
|
V3 = 15
|
V4 = 20
|
V5
= -7
|
№1
|
Построение опорного плана эти методом описано в
задаче 7.1.
Стоимость перевозок по этому плану Z1
=
6740 д.е.
Проверяем оптимальность плана методом
потенциалов, присвоив первой строке нулевой потенциал U1
= 0. Потенциалы других строк и столбцов определяем по формулам:
Ui
= Cij - Vj;
Vj = Cij
-
Ui;
Определяем характеристики клеток, оставшихся
свободными по формуле:
Eij
= Cij - (Vj
+ Ui) (вписаны в правый
нижний угол).
Среди характеристик свободных клеток есть
отрицательные, значит полученный план не оптимален. По аналогии производим
итерации по перемещению груза в клетки с отрицательными характеристиками.
Второй план (табл. №2) с ценой Z2
=
6620 д.е.
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
|
1
|
105
|
17 10
|
12 105
|
17 -2
|
21 -3
|
0
3
|
U1 = 0
|
|
2
|
70
|
6 40
|
11 30
|
20 2
|
28 5
|
0
4
|
U2 = -1
|
|
3
|
240
|
10 55
|
19 4
|
22 135
|
27 25
|
0
25
|
U3 = 3
|
|
4
|
85
|
18 28
|
14 19
|
23 21
|
7 85
|
0
20
|
U4 = -17
|
|
Vj
|
V1 = 7
|
V2 = 12
|
V3 = 19
|
V4 = 24
|
V5
= -3
|
№2
|
Третий план (табл. №3) с ценой Z3
=
6540 д.е
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
|
1
|
105
|
17 12
|
12 65
|
17 40
|
21 1
|
0
5
|
U1 = 0
|
|
2
|
70
|
6
|
11 70
|
20 4
|
28 7
|
0
6
|
U2 = -1
|
|
3
|
240
|
10 95
|
19 2
|
22 95
|
27 25
|
0
25
|
U3 = 5
|
|
4
|
85
|
18 28
|
14 17
|
23 21
|
7 85
|
0
20
|
U4 = -15
|
|
Vj
|
V1 = 5
|
V2 = 12
|
V3 = 17
|
V4 = 22
|
V5
= -5
|
№3
|
Четвёртый план (табл. №4) с ценой Z4
=
6515 д.е
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
|
1
|
105
|
17 12
|
12 65
|
17 15
|
21 25
|
0
5
|
U1 = 0
|
|
2
|
70
|
6 2
|
11 70
|
20 4
|
28 8
|
0
6
|
U2 = -1
|
|
3
|
240
|
10 95
|
19 2
|
22 120
|
27 1
|
0
25
|
U3 = 5
|
|
4
|
85
|
18 27
|
14 16
|
23 20
|
7 85
|
0
19
|
U4 = -14
|
|
Vj
|
V1 = 5
|
V2 = 12
|
V3 = 17
|
V4 = 21
|
V5
= -5
|
№4
|
На четвёртой итерации получен оптимальный план,
т.к. все характеристики свободных клеток положительны. Этот план совпадает с
планом, полученным методом северо-западного угла.
Zопт = Zmin
= Z4
= 6515 ден. ед.
Построение оптимального плана
методом Фогеля.
Построение опорного плана эти методом описано в
задаче 7.1.
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
|
|
|
|
|
|
1
|
105
|
17
|
12 55
|
17
|
21 25
|
0
25
|
12
|
12
|
5
|
5
|
5
|
5
|
|
2
|
70
|
6
|
11 70
|
20
|
28
|
0
|
6
|
6
|
5
|
9
|
|
|
|
3
|
240
|
10 95
|
19 10
|
22 135
|
27
|
0
|
10
|
10
|
9
|
3
|
3
|
3
|
|
4
|
85
|
18
|
14
|
23
|
7 85
|
0
|
7
|
|
|
|
|
|
|
|
|
4
|
1
|
3
|
14
|
0
|
|
|
|
|
|
|
|
|
|
4
|
1
|
3
|
6
|
0
|
1
|
3
|
6
|
|
|
|
|
|
|
|
|
|
|
|
1
|
3
|
6
|
|
|
|
|
|
|
|
|
|
|
|
1
|
5
|
6
|
|
|
|
|
|
|
|
|
|
|
|
1
|
5
|
|
|
|
|
|
|
|
|
Т.о. получен опорный план с ценой: Z1
= 6660 ден. ед.
Проверяем оптимальность плана методом
потенциалов, присвоив первой строке нулевой потенциал U1
= 0. Потенциалы других строк и столбцов определяем по формулам:
Ui
= Cij - Vj;
Vj = Cij
-
Ui;
Определяем характеристики клеток, оставшихся
свободными по формуле:
Eij
= Cij - (Vj
+ Ui) (вписаны в правый
нижний угол).
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
|
1
|
105
|
17 14
|
12 55
|
17 2
|
21 25
|
0
25
|
U1 = 0
|
|
2
|
70
|
6 4
|
11 70
|
20 6
|
28 8
|
0
1
|
U2 = -1
|
|
3
|
240
|
10 95
|
19 10
|
22 135
|
27 -1
|
0
-7
|
U3 = 7
|
|
4
|
85
|
18 27
|
14 16
|
23 20
|
7 85
|
0
14
|
U4 = -14
|
|
Vj
|
V1 = 3
|
V2 = 12
|
V3 = 15
|
V4 = 21
|
V5
= 0
|
№1
|
Среди характеристик свободных клеток есть
отрицательные, значит полученный план не оптимален. По аналогии производим
итерации по перемещению груза в клетки с отрицательными характеристиками.
Второй план (табл. №2) с ценой Z2
=
6590 д.е.
Таблица
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
|
1
|
105
|
17 7
|
12 65
|
17 5
|
21 25
|
0
15
|
U1 = 0
|
|
2
|
70
|
6 3
|
11 70
|
20 1
|
28 8
|
0
1
|
U2 = -1
|
|
3
|
240
|
10 95
|
19 21
|
22 135
|
27 6
|
0
10
|
U3 = 0
|
|
4
|
85
|
18 22
|
14 16
|
23 15
|
7 85
|
0
14
|
U4 = -14
|
|
Vj
|
V1 = 10
|
V2 = 12
|
V3 = 22
|
V4 = 21
|
V5
= 0
|
№2
|
Третий план (табл. №3) с ценой Z2
=
6590 д.е.
|
Номер
поставщика
|
Мощность
поставщика
|
Потребители
и их спрос
|
Ui
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
95
|
135
|
135
|
110
|
25
|
|
|
1
|
105
|
17 12
|
12 65
|
17 15
|
21 25
|
0
5
|
U1 = 0
|
|
2
|
70
|
6 3
|
11 70
|
20 4
|
28 8
|
0
6
|
U2 = -1
|
|
3
|
240
|
10 95
|
19 21
|
22 120
|
27 1
|
0
25
|
U3 = 5
|
|
4
|
85
|
18 27
|
14 16
|
23 20
|
7 85
|
0
19
|
U4 = -14
|
|
Vj
|
V1 = 5
|
V2 = 12
|
V3 = 17
|
V4 = 21
|
V5
= -5
|
№3
|
Очевидно, что полученный план является
оптимальным, т.к. он не отличается от предыдущих оптимальных планов решения.
Такой же план получен после итераций при использовании метода северо-западного
угла и минимального элемента.
Zопт = Zmin
= Z3
= 6515 ден. ед.
Заключение
Проделав данную работу, мы нашли оптимальное
решение поставленных задач. Опыт, полученный при работе над данной курсовой,
несомненно, пригодится в моей будущей деятельности, так как эта работа научила
определять тип транспортной задачи, решать транспортные задачи открытого и
закрытого типа, используя три основных метода решения транспортных задач, а так
же оптимизировать полученные опорные планы при помощи метода потенциалов.
Цель данной работы - построение оптимального
плана перевозок груза с минимальной стоимостью, была достигнута.
Список
литературы
1. Дойхен
Л.А. Математическое моделирование. - Хабаровск, 2002
. Коровина
А.П. Экономико-математическое моделирование. - М.: ИНФРА-М, 2007.
. Стодоля
И.Н. Экономическое моделирование. - М.: Альма, 2005.
. Якушев
Р.Н. Математическое моделирование в экономике. - М.: Экономист, 2006.