Расходные характеристики труб, гидравлический расчет каналов
Задача 18 вар 9
Определить
отметку воды в баке 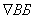 водонапорной башни и построить пьезометрическую линию
по магистрали 1 - 2 - 3 - 4 при q’ = 0,5 л/с. Произвести расчёт ответвлений.
водонапорной башни и построить пьезометрическую линию
по магистрали 1 - 2 - 3 - 4 при q’ = 0,5 л/с. Произвести расчёт ответвлений.
l1 - 2 = 462 м, l2 -
3 = 352 м, l3 - 4 = 528 м, l2 - 5 = 198 м, l3 -
6 = 264 м, q4=10,45 л/с, q5=3,3 л/с, q6=19,8
л/с, 
Решение:
Расчётный расход участка сети равняется сумме расходов, забираемых из
сети ниже по течению. Расчёт начинаем с конца магистрали
4-3 = q4 =10,45 л/с;
Q3-2 =
q4+ q6=10,45+19,8=30,25 л/с;
Q2-1 =
Q3-2 +q5+ l2-5 ∙q’=30,25+3,3+198∙0,5=132,55 л/с;
По расходам на участках из [2] таблица VIII определяем диаметры труб.
Скорость воды на участке определяем по формуле
 .
.
По
[2] таблица VI определяем поправки Θ2 в зависимости от скорости v.
По
[2] таблица V определяем значения расходных характеристик К для
нормальных труб (величину 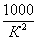 ).
).
Потери
напора Н определяем по формуле:
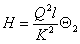 .
.
Расчёт
сводим в таблицу 1.
Отметка
пьезометрической линии в точке 4:

Таблица
1.
|
Точки
|
Участки магистрали
|
l, км
|
Q, л/с
|
d, мм
|
ω,
дм2
|
v, м/с
|
Θ2
|
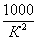 Н, мОтметки пьезометрической линии, м Н, мОтметки пьезометрической линии, м
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
295,6
|
|
4 - 3
|
0,528
|
10,45
|
125
|
1,23
|
0,85
|
1,06
|
0,10543
|
6,44
|
|
|
3
|
|
|
|
|
|
|
|
|
|
302,04
|
|
3 - 2
|
0,325
|
30,25
|
200
|
3,14
|
0,96
|
1,03
|
0,00861
|
2,64
|
|
|
2
|
|
|
|
|
|
|
|
|
|
304,68
|
|
2 - 1
|
0,462
|
132,55
|
400
|
12,57
|
1,05
|
1,03
|
0,218∙10-3
|
1,82
|
|
|
1
|
|
|
|
|
|
|
|
|
|
306,50
|
Отметка
воды в баке: 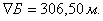
Производим
расчёт ответвлений 2 - 5 и 3 - 6.
Отметка
трубы в точке 5: 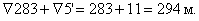
Отметка
трубы в точке 6: 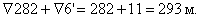
Расчётный
расход для ветви 2 - 5: Q2-5 = q5+ 0,5∙l2-5 ∙q’=3,3+0,5∙198∙0,5=52,8
л/с;
По
гидравлическому уклону ветви 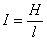 и
заданному расчётному расходу Q вычисляем расходную характеристику
и
заданному расчётному расходу Q вычисляем расходную характеристику 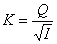 и, пользуясь [2] таблица V, определяем
диаметр d, соответствующий ближайшему большему значению К.
и, пользуясь [2] таблица V, определяем
диаметр d, соответствующий ближайшему большему значению К.
Расчёт
сводим в таблицу 2.
|
Ветви
|
l, м
|
Q, л/с
|
Отметки пьезометрической
линии, м
|
Н, м
|
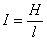 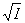 К, л/сd,
ммω,
дм2v, м/с К, л/сd,
ммω,
дм2v, м/с
|
|
|
|
|
|
|
|
|
начала
|
конца
|
|
|
|
|
|
|
|
|
3 - 6
|
264
|
19,8
|
302,04
|
293
|
9,04
|
0,0342
|
0,185
|
107,0
|
150
|
1,77
|
1,11
|
|
2 - 5
|
198
|
52,8
|
304,68
|
294
|
10,68
|
0,0539
|
0,232
|
227,6
|
200
|
3,14
|
1,68
|
Задача 22. вар.9
Определить глубину трапецеидального канала, который пропускает расход Q = 1,0 м3/с, ширина по дну b = 0,6 м. Уклон дна канала i =
0,0004 проверить из условия неразмыва русла канала. Грунт - гравий, условия
содержания канала - затянут илистой плёнкой.
Решение.
По [2], табл.2 (категория IX)
принимаем коэффициент шероховатости русла n=0,018.
По [2], табл. IX принимаем
коэффициент откоса для гравелистых грунтов m=1,5.
Подбором
по уравнению 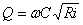 , задаваясь рядом значений h, определяем
глубину канала.
, задаваясь рядом значений h, определяем
глубину канала.
Данные
заносим в таблицу 1.
Таблица
1.
|
h, м
|
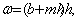 м2 м2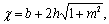 м м м м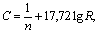 м0,5/с м0,5/с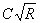 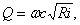 м3/с м3/с
|
|
|
|
|
|
|
0,80
|
1,440
|
3,484
|
0,413
|
48,755
|
31,34
|
0,903
|
|
0,82
|
1,501
|
3,557
|
0,422
|
48,915
|
31,77
|
0,954
|
|
0,84
|
1,562
|
3,629
|
0,431
|
49,071
|
32,20
|
1,006
|
|
0,86
|
1,625
|
3,701
|
0,439
|
49,224
|
32,62
|
1,060
|
0,675
|
2,403
|
0,281
|
45,785
|
24,27
|
1,036
|
Принимаем h = 0,84 м.
Проверяем правильность расчёта по способу Н. Н. Агроскина.
Для m =
1,5: m0 = 2,106, (4m0)-1 = 0,119.
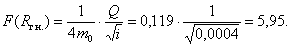
По
[2], табл. X принимаем Rг.н. = 0,43 м. Тогда
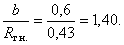
По
[2], табл. XI принимаем

Тогда
глубина воды в канале:
 .
.
Проверим
уклон дна канала из условия неразмыва русла.
По
[1], табл. 6 - 1, стр.256 для гравелистых грунтов максимально допустимая
скорость 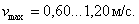 Скорость течения воды в данном канале
Скорость течения воды в данном канале

Следовательно,
при данном уклоне i = 0,0004 русло канала не будет размываться.
Задача 26. Вариант 9
Проектируется двухступенчатый перепад на сбросном канале для пропуска
расхода Q=4,6 м3/с. Высота перепада Р=4,6 м с вертикальными стенками падения.
Входная часть выполнена в виде водослива с широким порогом (Р0=0). Канал
трапецеидального сечения с коэффициентом откоса m=1,5 имеет ширину bk=4,8 м и
глубину h0 = 1,6 м при равномерном движении. Бытовая глубина в НБ hб=h0.
Рассчитать:
a) перепад и входную часть, исходя из условия сохранения в канале
скорости v0 , т.е. в канале перед перепадом не должно
быть ни подпора, ни спада.
b) глубину и длину водобойного колодца за перепадом исходя из
условия сопряжения с отводящим каналом в форме надвинутого прыжка.
c) начертить план сооружения и разрез по оси с указанием всех
размеров, определенных расчетом.
Решение:
1. Расчет
входной части перепада.
Площадь живого сечения канала:
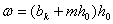 =
=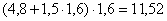 (м2).
(м2).
Скорость
подхода к водосливу
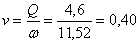 (м/с).
(м/с).
Расход через неподтопленный водослив с широким порогом определяется
формулой:
 ,
,
где полный напор на входе перепада
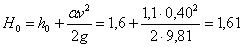 (м).
(м).
Коэффициент расхода при наличии бокового сжатия в случае неплавного
входа:
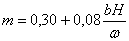 ,
,
b- ширина
входной части перепада.
Задаваясь различными значениями b, подберем расход Q,
соответствующий заданному Q=4,6 м3/с. Результаты подбора отразим в таблице 1.
Таблица 1
|
b, м
|
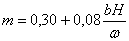  , м3/с , м3/с
|
|
|
2,00
|
0,322
|
5,831
|
|
1,80
|
0,320
|
5,212
|
|
1,60
|
0,318
|
4,601
|
|
1,40
|
0,316
|
3,998
|
Принимаем
ширину входной части перепада  (м).
(м).
Длина водослива с широким порогом:
 , или
, или 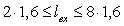 м,
м, 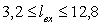 м.
м.
Принимаем
 (м).
(м).
2. Расчет ступеней перепада.
При двух ступенях высота каждой из них будет:
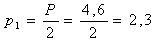 м.
м.
Расчет
первой ступени.
Определим высоту водобойной стенки и длину ступени.
Удельная энергия струи, падающей на первую ступень:
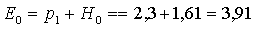 (м).
(м).
В
месте падения струи на ступень перепада сжатая глубина  определяется из уравнения:
определяется из уравнения:
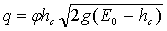
 ,
,
где
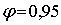 - коэффициент скорости для перепада,
- коэффициент скорости для перепада,
 м2/с -
удельный расход на перепаде.
м2/с -
удельный расход на перепаде.
Данное
уравнение решим подбором, составив таблицу 2.
Таблица
2.
|
|
|
|
|
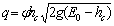 2,7792,8542,9292,907 2,7792,8542,9292,907
|
|
|
|
|
Принимаем 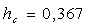 (м).
(м).
Тогда
вторая сопряженная глубина:

Спроектируем
водобойную стенку на выходе первой ступени. Напор над стенкой (считаем стенку
незатопленной, коэффициент расхода прямоугольной стенки 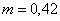 ):
):
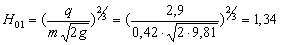 м.
м.
Скорость подхода потока к стенке:
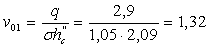 м/с.
м/с.
Здесь
 - коэффициент запаса.
- коэффициент запаса.
Геометрический
напор над стенкой:
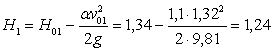 м.
м.
Высота
водобойной стенки:
 м.
м.
Принимаем
 м.
м.
Определяем
длину водобоя ступени (длину ступени без учета толщины стенки).
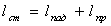 ,
,
труба канал поток уклон перепад
где
длина падения струи:
 м,
м,
длина
прыжка:
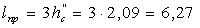 м.
м.
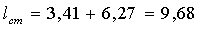 (м).
(м).
Принимаем
 (м).
(м).
Расчет второй ступени (проводится аналогично вышеизложенному).
Удельная энергия струи, падающей на вторую ступень:
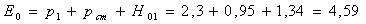 м.
м.
Таблица
3.
|
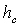 0,3200,3300,335 0,3200,3300,335
|
|
|
|
|
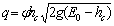 2,7832,8662,908 2,7832,8662,908
|
|
|
|
Принимаем 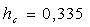 м.
м.
Вторая
сопряженная глубина:
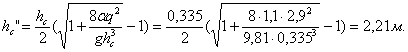
Так
как 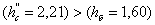 , то сопряжение произойдет с отогнанным прыжком. Чтобы
создать надвинутый прыжок, проектируем водобойный колодец.
, то сопряжение произойдет с отогнанным прыжком. Чтобы
создать надвинутый прыжок, проектируем водобойный колодец.
3. Расчет
водобойного колодца.
Глубина колодца в первом приближении:
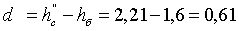 м.
м.
При наличии колодца удельная энергия увеличится и будет равна:
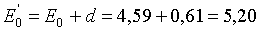 м.
м.
Определяем
глубины 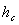 и
и  способом,
примененным в п.2 для значения
способом,
примененным в п.2 для значения 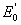 .
.
Таблица
4.
|
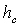 0,3000,3100,312 0,3000,3100,312
|
|
|
|
|
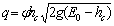 2,7942,8852,903 2,7942,8852,903
|
|
|
|
Принимаем 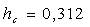 м.
м.
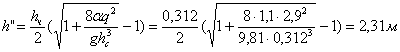
Глубина
колодца во втором приближении:
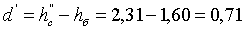 м.
м.
Полученная
глубина отличается от первоначальной на:
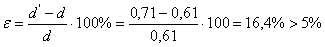 (допустимой
погрешности).
(допустимой
погрешности).
Следующее
приближение:
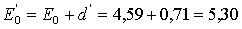 (м).
(м).
Таблица
5.
|
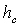 0,3000,310 0,3000,310
|
|
|
|
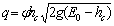 2,8232,914 2,8232,914
|
|
|
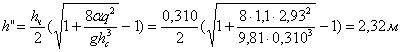
Глубина
колодца во втором приближении:
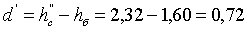 м
м
Погрешность
 .
.
Принимаем
глубину водобойного колодца 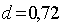 м.
м.
Длина колодца:
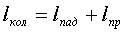
Длина падения струи:
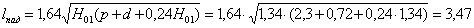 м.
м.
Длина
подпертого прыжка в колодце
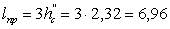 м.
м.
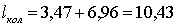 м.
м.
Принимаем
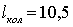 м.
м.
Для определения укрепления перепада определим максимальную скорость струи
(скорость в сжатом сечении):
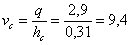 м/с.
м/с.
Этим
скоростям соответствует бетонный перепад (допустимые скорости течения до 10
м/с). Дополнительного усиления конструкции не требуется.
Окончательно имеем:
ширина
входной части  (м),
(м),
высота
ступени:  (м),
(м),
высота
водобойной стенки: 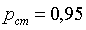 (м),
(м),
длина
первой ступени: 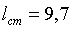 (м),
(м),
длина
водобойного колодца: 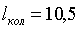 (м),
(м),
глубина
колодца: 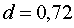 (м).
(м).
Задача
30. Вариант 9
По
лотку прямоугольного сечения шириной 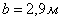 пропускают
расход
пропускают
расход 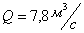 . Часть лотка необходимо запроектировать в виде
бетонного быстротока
. Часть лотка необходимо запроектировать в виде
бетонного быстротока 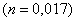 при отметках верхнего бьефа
при отметках верхнего бьефа 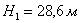 и нижнего
и нижнего  . В лотке
перед быстротоком должна быть обеспечена глубина
. В лотке
перед быстротоком должна быть обеспечена глубина 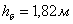 . Ширина
быстротока на всем протяжении одинаковая и равна ширине лотка. Входная часть
выполнена водосливом с широким порогом (уклон быстротока определить из условия
допустимой скорости на водоскате
. Ширина
быстротока на всем протяжении одинаковая и равна ширине лотка. Входная часть
выполнена водосливом с широким порогом (уклон быстротока определить из условия
допустимой скорости на водоскате 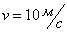 ).
).
Выполняя расчет, необходимо определить:
· уклон, с которым необходимо выполнить водоскат и его длину;
· рассчитать кривую свободной поверхности на водоскате;
· рассчитать сопряжение с НБ;
· вычертить профиль сооружения.
Решение:
Скорость в лотке
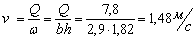 ,
,
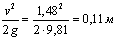 .
.
Удельный расход
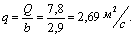
. Расчет
входной части.
Входную
часть рассчитываем как водослив с широким порогом, прямоугольного сечения, без
бокового сжатия, предварительно полагая 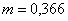 ([2],
табл.8-5), для низкого порога при
([2],
табл.8-5), для низкого порога при 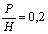 ).
).
Напор перед водосливом

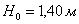 .
.
Без учета скорости подхода
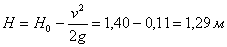 .
.
Для
сохранения глубины перед быстротоком  принимаем
высоту входного порога водослива
принимаем
высоту входного порога водослива
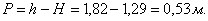
Так
как 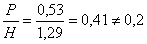 , то уточним глубины:
, то уточним глубины:
примем
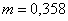 для
для 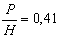 , тогда
, тогда
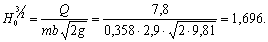
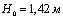


Принимаем
высоту порога входной части 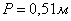 .
.
Длина
входной части лотка:  .
.
2. Расчет
водоската.
Уклон
быстротока определим, исходя из допустимой скорости на водоскате 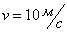 .
.
Следовательно, минимальная площадь живого сечения на водоскате
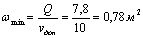 и
глубина
и
глубина 
Коэффициент
Шези будем определять по формуле Маннинга: 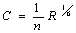
Таблица 1.
Тогда максимально допустимый уклон определится из формулы:
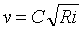 .
.
Уклон
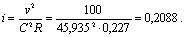
Длина
водоската, исходя из разности отметок Н1 и Н2 и при  :
:
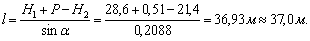
Критическая глубина на водоскате:
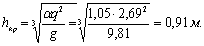
Так
как  , то на водоскате будет формироваться кривая спада
бурного потока.
, то на водоскате будет формироваться кривая спада
бурного потока.
Рассчитаем кривую свободной поверхности по способу Бахметьева.
Гидравлический показатель русла по формуле Р.Р.Чугаева ([1], стр. 298,
формула 7-127):
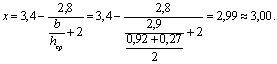
Из уравнения
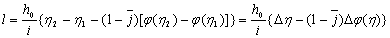 ,
,
Где
 ,
, 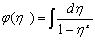
определим
длину участков кривой свободной поверхности на водоскате между глубинами от 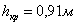 до
до  . Расчет
сводим в таблицу 2.
. Расчет
сводим в таблицу 2.
Таблица
2
|
h, м
|
 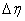  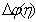 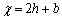  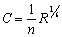   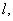 м (по
формуле)Сумма [11] с накопле- нием, м м (по
формуле)Сумма [11] с накопле- нием, м
|
|
|
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
10
|
11
|
12
|
|
0,92
|
3,41
|
|
0,044
|
|
4,74
|
0,56
|
53,451
|
39,064
|
|
|
|
|
0,80
|
2,96
|
-0,44
|
0,058
|
0,014
|
4,50
|
0,52
|
52,674
|
39,960
|
-38,5121
|
0,1225
|
0,12
|
|
0,70
|
2,59
|
-0,37
|
0,076
|
0,018
|
4,30
|
0,47
|
51,907
|
40,609
|
-39,2848
|
0,44
|
0,56
|
|
0,60
|
2,22
|
-0,37
|
0,106
|
0,030
|
4,10
|
0,42
|
50,993
|
41,104
|
-39,8569
|
1,07
|
1,63
|
|
0,50
|
1,85
|
-0,37
|
0,156
|
0,050
|
3,90
|
0,37
|
49,881
|
41,348
|
-40,2262
|
2,12
|
3,75
|
|
0,40
|
1,48
|
-0,37
|
0,263
|
0,107
|
3,70
|
0,31
|
48,483
|
41,175
|
-40,2615
|
5,09
|
8,84
|
1,30
|
-0,19
|
0,373
|
0,110
|
3,60
|
0,28
|
47,633
|
40,848
|
-40,0115
|
5,45
|
14,29
|
|
0,28
|
1,06
|
-0,24
|
0,838
|
0,465
|
3,47
|
0,24
|
46,313
|
40,061
|
-39,4546
|
23,41
|
37,20
|
Длина
кривой спада (см. графу 12 таблицы 2)  - длине
лотка.
- длине
лотка.
3. Расчет
выходной части.
Глубина
в конце водоската 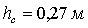 .
.
Сопряженная
с  глубина
глубина

Так
как 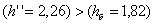 (глубина в отводящем канале), то сопряжение
произойдет с отогнанным прыжком.
(глубина в отводящем канале), то сопряжение
произойдет с отогнанным прыжком.
Чтобы
создать надвинутый прыжок, проектируем водобойную стенку.
Полагаем,
что водобойная стенка образует подтопленный водослив (высоту стенки
предполагаем меньше 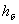 и в НБ имеет место спокойный режим движения воды).
и в НБ имеет место спокойный режим движения воды).
Скорость подхода потока к стенке:
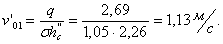 .
.
Здесь
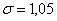 - коэффициент запаса.
- коэффициент запаса.
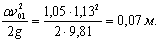
Высоту
водобойной стенки 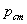 для подтопленных водосливов определим по методике,
изложенной в [1] стр.416-417 методом последовательных приближений:
для подтопленных водосливов определим по методике,
изложенной в [1] стр.416-417 методом последовательных приближений:
Задаемся
некоторым значением 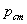 и вычисляем величины:
и вычисляем величины:
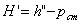 ,
,
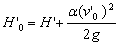 ,
,
коэффициент
подтопления примем 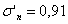 ,
,
Тогда удельный расход
 ,
,
где
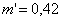 для водобойной стенки. Вычисления сводим в таблицу 3.
для водобойной стенки. Вычисления сводим в таблицу 3.
Таблица 3.
|
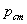 
|
|
|
0,93
|
2,799
|
|
0,96
|
2,710
|
|
0,97
|
2,680
|
|
0,98
|
2,651
|
Удельному
расходу q = 2,69 м2/c соответствует высота стенки 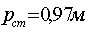 .
.
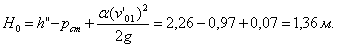
Выясним сопряжение потока за стенкой:

Сжатая
глубина hc определится из уравнения
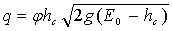 ,
,
где
 для стенки,
для стенки, 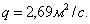 Составим
таблицу 4.
Составим
таблицу 4.
Таблица
4.
|
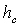 0,460,470,48 0,460,470,48
|
|
|
|
|
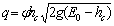 2,6292,6792,728 2,6292,6792,728
|
|
|
|
Принимаем 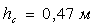 ,тогда
,тогда
 - уровня
воды в НБ.
- уровня
воды в НБ.
Следовательно,
после стенки прыжок надвинут и дальнейшего гашения потока не требуется.
Расстояние
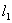 от конца водоската до стенки примем равным длине
подпертого прыжка:
от конца водоската до стенки примем равным длине
подпертого прыжка:
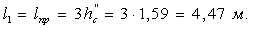
Литература
1. Р.Р.Чугаев. «Гидравлика». Ленинград,
Энергоиздат. 1982.
2. А.В.Андреевская и др. «Задачник по
гидравлике». М. 1970.