|
МОД с контурной продувкой
|
СОД и ВОД с прямоточной
продувкой
|
|
 , МПаPa= (0,85
÷ 1,05) Рk , МПаPa= (0,85
÷ 1,05) Рk
|
|
Коэффициент остаточных газов
Количество остаточных газов, оставшихся в цилиндре после окончания
процесса выталкивания отработавших газов, характеризуется коэффициентом
остаточных газов γr.
Коэффициент остаточных газов представляет собой отношение количества
остаточных газов Mr (в
молях) к количеству свежего заряда L (в молях)
 . (3.3)
. (3.3)
Необходимо
стремиться к получению минимальных значений γr, так как
с увеличением количества остаточных газов уменьшается коэффициент наполнения ηн.
На
величину ηн
оказывает влияние:
2)
давление Pr и температура Tr
остаточных газов.
Коэффициент
остаточных газов возрастает с увеличением Vc,
т.е. с уменьшением ε
и с увеличением давления остаточных газов
Pr.
При
увеличении противодавления на выпуске Pг увеличивается потерянная часть хода поршня на
расширение остаточных газов (смещение точки r0), что приводит к уменьшению ηн.
При
повышении температуры остаточных газов Tr
уменьшается их плотность, а следовательно и их количество. Сама же величина Tr зависит от ε,
нагрузки и частоты вращения двигателя.
Очевидно, что с увеличением ε увеличивается
и степень последующего расширения δ, следовательно уменьшается Tr.
В
противоположность этому с увеличением нагрузки и оборотов увеличивается степень
нагрева деталей в рабочем цилиндре, что приводит к повышению Tr.
Благоприятное
влияние на уменьшение γr
оказывает продувка камеры сжатия, т.е. перекрытие клапанов.
В
2-т двигателях величина γr
зависит в основном от системы продувки и качества осуществления продувки
цилиндра и степени быстроходности двигателя.
Значения
параметра γr
для выполненных конструкций ДВС находятся в следующих пределах:
-т
двигатели с наддувом γr = 0,04 ÷ 0,06;
4-т
двигатели без наддува γr = 0,06 ÷ 0,08;
2-т
двигатели с прямоточной продувкой γr = 0,10 ÷ 0,15;
2-т
двигатели с контурной продувкой γr = 0,15 ÷ 0,20.
Температура
остаточных газов находится в пределах
Tr = 600 ÷ 900 К.
Температура
рабочей смеси
Температуру
рабочей смеси Tа можно
определить из уравнения баланса теплоты за период процесса наполнения
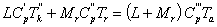 . (3.4)
. (3.4)
Допустим
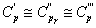 из-за малости Mr.
из-за малости Mr.
Тогда
уравнение (3.4) приобретёт следующий вид
 . (3.5)
. (3.5)
Выразим
из (3.5) Tа
 . (3.6)
. (3.6)
Разделим
в уравнении (3.6) числитель и знаменатель на L
 . (3.7)
. (3.7)
и,
зная, что  получим выражение для определения Tа
получим выражение для определения Tа
 . (3.8)
. (3.8)
Величина
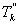 определяется по формуле
определяется по формуле
 , (3.9)
, (3.9)
где
ΔTa = 10 ÷ 20° - для четырёхтактных ДВС;
ΔTa = 5 ÷ 10° - для двухтактных ДВС.
Коэффициент наполнения
Выражение для определения коэффициента наполнения ηн получим при следующих допущениях:
) Процесс наполнения рабочего цилиндра заканчивается в точке а
индикаторной диаграммы.
) Кинетическая энергия газов в цилиндре после наполнения равна нулю.
) Абсолютная работа, совершаемая газами за ход наполнения равна нулю.
) Теплоёмкость свежего заряда и остаточных газов одинакова (при
температурах наполнения).
Из уравнения материального баланса газа найдём количество рабочей смеси в
конце процесса наполнения (точка а)
Ma = L + Mr = L(1 + γr), (3.10)
где L - количество свежего воздуха;
Mr - количество остаточных газов.
Заменив Ma и L из характеристического уравнения PV = MRT
 ,
,  (3.11)
(3.11)
и
подставив V0 = ηнVh получим
 . (3.12)
. (3.12)
Откуда
 . (3.13)
. (3.13)
Введя
вместо Va =
ε∙Vc и Vh = Vc (ε -1) найдём выражение для коэффициента наполнения
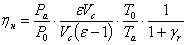 , (3.14)
, (3.14)
 . (3.15)
. (3.15)
Для
ДВС с наддувом вместо Р0 и Т0 подставим значения Pk и Tk
 . (3.16)
. (3.16)
Для
двухтактного ДВС вместо геометрической степени сжатия ε стоит действительная степень сжатия εд и тогда
коэффициент
наполнения отнесённый к полезной части хода поршня
 ;
;
коэффициент
наполнения отнесённый ко всему ходу поршня
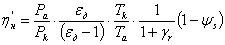 .
.
Лекция 4. 3.2. Процесс сжатия
Процесс сжатия воздуха в цилиндре осуществляется после закрытия всех
газораспределительных органов при движении поршня от НМТ к ВМТ. Существенных
различий процесса сжатия двухтактного и четырёхтактного дизелей не существует.
Основное назначение процесса сжатия - повышение давления и температуры
заряда для обеспечения надёжного самовоспламенения впрыскиваемого топлива.
Сжатие представляет собой сложный процесс зависящий от ряда следующих
факторов:
переменного теплообмена между зарядом и стенками, изменяющегося как по
величине, так и по знаку;
непрерывного уменьшения поверхности охлаждения по мере приближения поршня
к ВМТ;
частичной утечки заряда через неплотности поршневых колец;
впрыска и испарения части топлива до окончания процесса сжатия.

Рис. 3.4 - Диаграмма линии сжатия
В начале хода сжатия температура заряда обычно ниже средней температуры
стенок рабочего цилиндра, что вызывает подогрев заряда. На этом участке кривая
сжатия действительного процесса идёт круче адиабаты, поскольку происходит
отдача теплоты от стенок заряду воздуха (n1 > k1).
По мере сжатия заряда и повышения его температуры передача теплоты от
стенок к заряду уменьшается и наступает момент (точка 1), когда температура
заряда становится равной средней температуре стенок и имеет место мгновенный
адиабатный процесс (n1 = k1).
При дальнейшем сжатии заряда температура последнего становится выше
средней температуры стенок цилиндра, вследствие чего уже происходит отдача
теплоты от заряда к стенкам. Кривая действительного процесса становится более
пологой нежели адиабата (n1 < k1).
Величина n1 по мере приближения поршня к ВМТ
непрерывно уменьшается. В результате давление конца сжатия (точка С)
действительного процесса обычно меньше давления адиабатного сжатия.
Характер действительного процесса теплообмена при сжатии представлен на
энтропийной диаграмме из которой видно, что АВ - приток, ВС - отдача теплоты
стенкам рабочего цилиндра.
При расчёте рабочего процесса полагают, что процесс сжатия протекает по
политропе с постоянным показателем n1, величина
которого обеспечивает получение такой же работы сжатия на линии АС как и при
переменном показателе реального процесса.
Давление в конце сжатия определяется из уравнения политропы на линии
сжатия АС:
 . (3.17)
. (3.17)
Откуда
 . (3.18)
. (3.18)
Температура
конца сжатия определится из уравнения состояния заряда для точек А и С
PaVa = GaRTa =
L(1+γr)RTa, (3.19)cVc
= GcRTc = L(1+γr)RTc. (3.20)
Делим
уравнение (4.4) на уравнение (4.3)
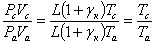 .
.
Откуда
 . (3.30)
. (3.30)
Если
отсутствуют надёжные данные по оценке n1, то её значение определяется исходя из равенства
работ в адиабатном процессе с переменной теплоёмкостью и в действительном
процессе с постоянным значением политропы сжатия n1.
Для
одного моля газа
 , (3.40)
, (3.40)
где
Uc - внутренняя энергия одного моля заряда в конце
сжатия;
Uа - внутренняя энергия одного моля заряда в начале
сжатия;
Тc
- температура заряда в конце сжатия;
Та
- температура заряда в начале сжатия;
В
левой части этого уравнения записана разность внутренних энергий одного моля
заряда в конце и в начале сжатия, равная работе сжатия для адиабатного
процесса, а в правой части - работа сжатия одного моля газа с постоянным
значением показателя n1.
Значения
внутренних энергий можно выразить через произведение средних мольных изохорных
теплоёмкостей на температуру
Uc = (av +bTc)Tc,
(3.41)a = (av +bTa)Ta. (3.42)
Подставим
(4.7) и (4.8) в уравнение (4.6)
 (3.43)
(3.43)
 ,
,
 ,
,
 .
.
Сокращая
на (Тс - Та) получим
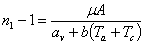 . (3.44)
. (3.44)
Заменив
μA =
8,315 кДж/(кмоль∙К) и  окончательно
получим
окончательно
получим
 . (3.45)
. (3.45)
Поскольку
в левой и правой части этого уравнения находится неизвестная величина n1, то оно решается методом итераций.
Выбор
степени сжатия ε
У
судовых дизелей величина степени сжатия ε зависит от типа двигателя, его быстроходности, способа
смесеобразования, наддува, конструктивных особенностей, условий эксплуатации.
Значения ε
у выполненных конструкций составляют:
МОД
ε
= 11 ÷ 13;
Длинноходовые
и супердлинноходовые МОД ε
= 14 ÷ 20;
СОД
ε
= 13 ÷ 14;
ВОД
ε
= 15 ÷ 16;
ВОД
с разделёнными камерами сгорания ε = 16 ÷ 18.
Нижний
предел ε
выбирают исходя из условия обеспечения
надёжного самовоспламенения топлива, что достигается при
Tc min > Tв
+ ΔТ ≈ 550 + (150 ÷ 250) =
700 ÷ 800 K,
где
Tв -
средняя температура самовоспламенения топлива;
ΔТ - дополнительная разность для надёжного воспламенения.
Величина
Tв зависит
от давления
Рс
= 0,29 МПа Тв = 673 К
Рс
= 0,88 МПа Тв = 535 К
Рс
= 1,47 МПа Тв = 483 К
Рс
= 2,94 МПа Тв = 473 К
Особенно
обостряется проблема надёжного самовоспламенения при пуске дизеля. При пуске n1 = 1,2 ÷
1,25.
Для
обеспечения хороших пусковых качеств применяют поршни автоматически
регулирующие степень сжатия (ПАРСС), у которых величина ε варьируется в пределах 8÷12 в зависимости от нагрузки на дизель. Причём высшие
значения имеют место при пуске и малых нагрузках дизеля.
3.3
Процесс сгорания
Фазы
протекания процесса
Процесс
сгорания топлива в цилиндре дизеля условно подразделяется на четыре фазы исходя
из характера изменения давления и температуры.
Фаза
1. Эта фаза соответствует периоду от начала поступления топлива в цилиндр
(точка В) до момента отрыва линии давления р = f(φ) от
политропы сжатия (точка С) которая условно принимается за начало воспламенения.
Эта
фаза называется период задержки воспламенения φi (τi). За эту
фазу происходят процессы физико-химической подготовки топлива к
самовоспламенению (предпламенные реакции). Однако какого-либо повышения
давления над политропой сжатия не наблюдается так как 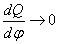 .
.
Продолжительность
фазы 1
 , с от 1∙10-3
до 5∙10-3 с. (3.46)
, с от 1∙10-3
до 5∙10-3 с. (3.46)
В
период задержки воспламенения в цилиндр впрыскивается от 30 до 60% цикловой
подачи топлива, которое испаряется и образует начальные очаги воспламенения.
Продолжительность
фазы 1 оказывает влияние на характер всего последующего процесса сгорания.
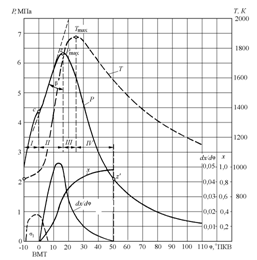
Рис.
3.5 - Фазы протекания процесса воспламенения и сгорания топлива в дизеле
Фаза
2. Эта фаза идёт от точки С до точки достижения Pz в
цилиндре и соответствует периоду воспламенения и сгорания топлива. Она
сопровождается интенсивным выделением теплоты  и резким
нарастанием давления при продолжающемся впрыске топлива и увеличении его
концентрации в рабочей смеси (период быстрого сгорания).
и резким
нарастанием давления при продолжающемся впрыске топлива и увеличении его
концентрации в рабочей смеси (период быстрого сгорания).
Фаза
2 характеризуется взрывообразным воспламенением и сгоранием топлива, впрыснутого
в цилиндр за фазу 1, а также частично поступившего за фазу 2.
Основным
показателем интенсивности процесса сгорания в течение фазы 2 являются:
средняя
скорость нарастания давления в цилиндре  ;
;
максимальная
скорость нарастания давления в цилиндре  .
.
Для
выполненных конструкций дизелей значения  МПа/°ПКВ.
МПа/°ПКВ.
Основным
фактором оказывающим влияние на  является
продолжительность фазы 1, от которой зависит количество топлива, поданного в
цилиндр за период φi.
Чем большее количество топлива охватывается одновременно пламенем по всему
объёму камеры сгорания, тем резче происходит нарастание давления при сгорании.
Среди других факторов оказывающих влияние на характер протекания фазы 2 следует
отметить скорость впрыска топлива, особенности процесса смесеобразования,
вихревое движение заряда воздуха.
является
продолжительность фазы 1, от которой зависит количество топлива, поданного в
цилиндр за период φi.
Чем большее количество топлива охватывается одновременно пламенем по всему
объёму камеры сгорания, тем резче происходит нарастание давления при сгорании.
Среди других факторов оказывающих влияние на характер протекания фазы 2 следует
отметить скорость впрыска топлива, особенности процесса смесеобразования,
вихревое движение заряда воздуха.
Фаза
3. Эта фаза соответствует периоду от момента достижения Pz в цилиндре до момента достижения Тmax в
цилиндре. Она характеризуется наиболее интенсивным протеканием сгорания по
всему объёму камеры сгорания при наибольшей скорости выделения теплоты
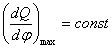 .
.
В
течение фазы 3 обычно заканчивается поступление топлива в цилиндр и сгорание
топлива, поступившего за время фазы 2 и частично поданного за фазу 3. Задержка
воспламенения топлива значительно сокращается благодаря высоким давлению и
температуре в камере сгорания.
Высокая
интенсивность сгорания топлива в фазе 3 достигается за счёт протекания
процессов при положении поршня около ВМТ, т.е. при наибольших давлении и
температуре, хорошо организованного смесеобразования, обеспечения для данного
дизеля необходимой величины коэффициента избытка воздуха для сгорания α, относительно небольших потерь теплоты в воду,
охлаждающую камеру сгорания.
Фаза
4. Эта фаза соответствует завершению замедленного сгорания топлива не успевшего
сгореть за фазу 3. То есть происходит догорание топлива на линии расширения при
непрерывно понижающихся давлении и температуре. За конец фазы 4 обычно условно
принимается момент выгорания 98 % поданного в цилиндр топлива.
Лекция 5. 3.3.2. Термохимия процесса сгорания
Основным процессом, происходящим в цилиндре дизеля, является горение
распыленного жидкого топлива.
Элементарный состав топлива можно записать
С + Н + О + S = 1,
где С - массовая доля в топливе углерода;
H -
массовая доля в топливе водорода;
О - массовая доля в топливе кислорода;
S -
массовая доля в топливе серы.
Процесс горения топлива состоит в окислении его составных частей с
выделением теплоты.
Определим теоретически необходимое количество воздуха для сгорания 1 кг
топлива.
Если исходить из стехиометрических соотношений и игнорировать тепловой
эффект реакции, то в результате полного сгорания получим
С + О2 = СО2
12 кг (углерода) + 32 кг (кислорода) = 44 кг (углекислого газа)
кг (углерода) + 1 кг/моль (кислорода) = 1 кг/моль (углекислого газа)
кг (углерода) + 1/12 кг/моль (кислорода) = 1/12 кг/моль (углекислого
газа)
С кг (углерода) + С/12 кг/моль (кислорода) = С/12 кг/моль (углекислого
газа)
Таким образом, для сгорания С кг (углерода) требуется С/12 кг/моль
(кислорода)
Н2 + О2 = 2 Н2 О
кг (водорода) + 32 кг (кислорода) = 36 кг (водяных паров)
кг (водорода) + 1 кг/моль (кислорода) = 2 кг/моль (водяных паров)
кг (водорода) + 1/4 кг/моль (кислорода) = 1/2 кг/моль (водяных паров)
H кг
(водорода) + H/4 кг/моль (кислорода) = H/2 кг/моль (водяных паров)
Таким образом, для сгорания H кг (водорода) требуется Н/4 кг/моль
(кислорода)
Аналогично можно получить, что для сгорания S кг серы требуется S/32 кг/молей кислорода.
Учитывая, что, кроме того, в самом топливе содержится кислород, найдем
теоретически необходимое количество воздуха для сжигания 1 кг топлива
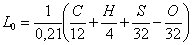 , (3.47)
, (3.47)
где
0,21 - объемное, мольное содержание кислорода в воздухе.
То
же количество воздуха, выраженное в кг на 1 кг топлива
L’ = μ L0 = 28,27 L0 ,
μ - молекулярная масса воздуха.
Для дизельного топлива среднего состава (С = 0,87; Н = 0,126; О = 0,004)
получим L0 = 0,495 кг/моль/кг и L’ = 14,35 кг/кг.
В двигателях с самовоспламенением для обеспечения качественного сгорания
топлива процесс осуществляется с некоторым избытком воздуха.
Отношение действительного количества введенного в цилиндр воздуха L к теоретически необходимому L0 называется коэффициентом избытка воздуха α
 , (3.48)
, (3.48)
 . (3.49)
. (3.49)
Значения
α на номинальном режиме
МОД
α
= 1,8 ÷ 2,2;
СОД
α
= 1,6 ÷ 2,0;
ВОД
α
= 1,5 ÷ 1,8.
Теплоемкость
воздуха и продуктов сгорания
Теплоемкость газов в цилиндре двигателя изменяется в процессе сгорания
вместе с изменением температуры и состава смеси. Так как это обстоятельство
оказывает заметное влияние на мощность и экономичность двигателя, то расчет
рабочего цикла и анализ процессов в нем необходимо вести с учетом зависимости
теплоемкости от температуры и состава смеси в цилиндре.
В отличие от истинной теплоемкости, которая представляет предел отношения
приращения количества тепла к соответствующему приращению температуры в данной
точке процесса, в теплохимических расчетах удобнее пользоваться понятием средней
теплоемкости в определенном интервале температур.
Под средней теплоемкостью в интервале от 0о до данной Т
температуры подразумевается такая условная одинаковая в данном интервале
теплоемкость, произведение которой на приращение температуры дает такое же количество
тепла, какое получается в результате интегрирования по переменному значению
истинной теплоемкости.
В расчета оперируют средней мольной изохорной теплоемкостью СV и средней мольной изобарной
теплоемкостью CP:
CP - СV = 8,315
кДж/(кмоль∙оК)
Применяемые на судах сорта жидких топлив имеют примерно одинаковый
состав. При сгорании таких топлив с теоретически необходимым количеством
воздуха (α = 1) получаются так называемые "чистые" продукты
сгорания, состав которых, а следовательно теплоемкость, мало отличаются друг от
друга для различных сортов топлив. Поэтому значения теплоемкости
"чистых" продуктов сгорания для топлива среднего состава можно
определить заранее и затем рассматривать при любом другом α > 1 как смесь только двух
составляющих: воздуха и "чистых" продуктов сгорания.
В точных расчетах можно пользоваться табличными значениями средней
теплоемкости, рекомендованные ВТИ на базе отбора и обработки спектроскопических
данных.
При расчетах с меньшей точностью можно упростить расчет. Для этого истинный
закон изменения средней теплоемкости заменяют приближенной зависимостью вида
С = а + b T. (3.50)
Тогда для сухого воздуха имеем, Кдж/(кмоль оК)
СV = 19,26 + 0,0025 T, (3.51)
СP = 27,575 + 0,0025 T, (3.52)
Наибольшая погрешность при этом составляет 0,7 %.
Тогда для "чистых" продуктов сгорания (α = 1) жидкого топлива среднего
состава имеем, Кдж/(кмоль оК)
СV = 20,47 + 0,0036 T, (3.53)
СP = 28,785 + 0,0036 T, (3.54)
Наибольшая погрешность при этом составляет 0,9 %.
В цилиндре двигателя в результате сгорания топлива при α > 1 образуется газовая смесь,
которую можно рассматривать как смесь "чистых" продуктов сгорания и
чистого воздуха.
Определим теплоемкость смеси для произвольного момента времени сгорания,
когда доля сгоревшего топлива равна Х
Так как количество остаточных газов в цилиндре невелико, можно принять,
что они состоят из Mr /α "чистых" продуктов
сгорания и Mr (1 - 1/α) свежего воздуха. Тогда в
произвольны момент сгорания общее количество "чистых" продуктов
сгорания на 1 кг сжигаемого топлива будет равно
 . (3.55)
. (3.55)
Для
топлива принятого среднего состава
 . (3.56)
. (3.56)
Следовательно
количество "чистых" продуктов сгорания в рассматриваемый момент
времени равно L0 (1,064 X + γr ), а количество
свежего воздуха в тот же момент времени
 . (3.57)
. (3.57)
Таким
образом, средняя мольная изохорная теплоемкость смеси воздуха и продуктов
сгорания согласно правилу смешения газов будет равна
 . (3.58)
. (3.58)
Для
процесса сжатия Х = 0
 . (3.59)
. (3.59)
В
конце видимого сгорания (точка Z)
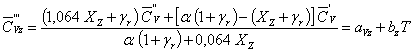 . (3.60)
. (3.60)
В
конце процесса горения (точка b, Х = 1)
 . (3.61)
. (3.61)
Средняя
мольная изобарная теплоемкость
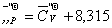 . (3.62)
. (3.62)
Средняя
мольная изохорная теплоемкость для смеси продуктов сгорания при заданном
составе топлива
 , (3.63)
, (3.63)
где
K = 1+ ΔM/L0
Изменение объема при сгорании
Если весовое количество продуктов сгорания остается равным сумме весов
воздуха и топлива до сгорания, то объемное количество рабочей смеси до сгорания
и после равны. Приращение объема продуктов сгорания ΔМ происходит вследствие увеличения
суммарного количества молекул в результате химических реакций распада молекул
топлива и образования новых молекул (продуктов сгорания).
 . (3.64)
. (3.64)
Критерием оценки приращения количества К-молей при сгорании является
теоретический (химический) коэффициент молекулярного изменения.
Расчетный, действительный коэффициент молекулярного изменения учитывает
помимо воздуха и продуктов сгорания также остаточные газы:
 , (3.65)
, (3.65)
β = 1,03 - 1,04
Текущее
значение
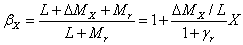 . (3.66)
. (3.66)
Подставив
ΔМ/L = β0 - 1
найдем
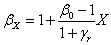 . (3.67)
. (3.67)
Коэффициенты
выделения и использования теплоты
При термодинамическом рассмотрении процесса сгорания со смешанным
подводом теплоты кривую изменения давления р = f(V) условно
заменяют изохорой СY и изобарой YZ.
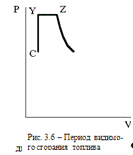
Участок процесса сгорания от точки C (условное начало сгорания) до точки Z (условный конец сгорания) называется периодом видимого
сгорания CYZ топлива.
Теплота, выделяющаяся при сгорании, используется для повышения внутренней
энергии рабочего тела, а также для совершения работы. Сгорание топлива
сопровождается неизбежными потерями теплоты на неполноту сгорания (QH.C.) , диссоциацию продуктов сгорания (QДИС.), отдачу части выделенной теплоты
охлаждаемым стенкам (QW.).
Неполнота сгорания обусловлена следующими факторами:
1) часть поданного топлива не успевает
сгореть на участке CУZ ;
2) газы содержат некоторое количество
продуктов неполного сгорания топлива.
В обоих случаях на кривой расширения наблюдается догорание топлива,
следовательно, величина неполноты сгорания до точки Z не предопределяет общую неполноту сгорания за весь цикл.
Диссоциация продуктов сгорания, т.е. расщепление молекул некоторых
соединений, сопровождается поглощением теплоты и понижением температуры конца
сгорания. Наблюдается только при высокой температуре.
Показателем количества теплоты, выделяющейся при сгорании топлива,
является коэффициент выделения теплоты:
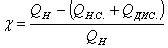 . (3.69)
. (3.69)
Величина QДИС. менее 2 %.
За время процесса сгорание-расширение происходит потеря теплоты в
охлаждающую воду QW.
Долю теплоты, которую можно использовать для повышения внутренней энергии
рабочего тела и совершения механической работы, оценивают коэффициентом
использования теплоты:
 . (3.70)
. (3.70)
Этот коэффициент учитывает все потери теплоты за процесс сгорание-расширение.
Коэффициент использования теплоты на протяжении хода поршня является
величиной переменной.
Опытные значения
МОД, СОД ξZ = 0,75 - 0,85 ξB = 0,86-0,92
ВОД ξZ = 0,70 - 0,80 ξB = 0,85-0,90
Наибольшие значения ξB MAX = 0,88-0,95
Связь между
параметрами линии сжатия и расширения
Эта связь устанавливается на основе характеристического уравнения при
условии пренебрежения утечками.
Количество газа на линии сжатия
L(1 + γr). (3.71)
Количество газа в произвольной точке при сгорании или расширении
L(1 + γr) βХ.. (3.72)
Характеристическое уравнение для любой точки и начальной точки а
запишется:
P V = L(1+ γr) R T βХ; (3.73)
PaVa= L(1+ γr) R TaβХ. (3.74)
Разделив первое уравнение на второе, получим
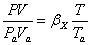 . (3.75)
. (3.75)
Заменив
Va =Vc ε и обозначив V/Vc =εx
- текущая степень сжатия получим
 (3.76)
(3.76)
 . (3.77)
. (3.77)
Для
точки Z получим βХ = βZ εХ =VZ /VC = ρ
 . (3.79)
. (3.79)
Или
заменив через параметры точки С
 . (3.80)
. (3.80)
 или
или  . (3.81)
. (3.81)
Лекция 6. 3.3.7. Уравнение сгорания для цикла со смешанным подводом
теплоты
Применительно к циклу со смешанным теплоты в соответствии с первым
законом термодинамики теплота, образующаяся при сгорании 1 кг топлива,
расходуется на повышение внутренней энергии рабочего тела (участок CYZ), а
также на совершение работы расширения при p = const.
Если предположить, что процесс сгорания протекает сперва при V = const, а
затем при p = const и затем заканчивается в т. Z, и пренебречь незначительной
разницей между тепловыми эффектами реакций сгорания при температурах Tc
и Т0, а также теплоемкостями остаточных газов и продуктов сгорания,
то уравнение баланса теплоты для процесса сгорания, протекающего на участке CYZ
примет вид:
 (3.90)
(3.90)
 , (3.91)
, (3.91)
где
QWZ- потеря теплоты в охлаждаемые стенки,c и Uz
- внутренняя энергия соответственно воздуха и продуктов сгорания в т. С и Z.-
работа расширения газов на участке YZ.
Подставим
в уравнение параметры рабочего процесса

 (3.94)
(3.94)

Подставим
уравнение (3.95) в уравнение (3.93) получим
 . (3.96)
. (3.96)
Разделим
на L и заменяя  и
и  найдем
найдем
 . (3.97)
. (3.97)
Окончательно
уравнение сгорания примет вид
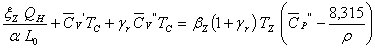 , (3.98)
, (3.98)
или,
что тоже самое
 . (3.99)
. (3.99)
Оценка
параметров сгорания
При
расчетах 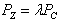 , а если
, а если 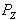 задано,
то
задано,
то  .
.
Ориентировочные
значения при номинальной мощности
МОД
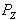 = 6...9, МПа
= 6...9, МПа  =
1700...1800 K, l = 1,2...1,35
=
1700...1800 K, l = 1,2...1,35
СОД
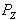 = 8...14, МПа
= 8...14, МПа  =
1800...1900 K, l = 1,4...1,5
=
1800...1900 K, l = 1,4...1,5
ВОД
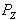 = 10...15, МПа
= 10...15, МПа  =
1900...2000 K, l = 1,2...1,4
=
1900...2000 K, l = 1,2...1,4
Параметр
r изменяется от 1,2 до 1,6.
.4
Процесс расширения
Основной
полезный ход поршня происходит при расширении продуктов сгорания. Процесс
расширения включает в себя:
изменение
давления и температуры;
непрерывный
теплообмен между газами и охлаждающими стенками;
догорание
топлива;
утечку
газов через неплотности поршневых колец.
В
первой фазе расширения происходит догорание топлива, не успевшего сгореть в
период видимого сгорания. При снижении температуры в цилиндре дизеля кроме
теплоты догорания топлива выделяется еще некоторое количество теплоты
вследствие восстановления продуктов диссоциации, в это время показатель
политропы расширения n1 = 1,1...1,2.
Во
второй фазе расширения происходит интенсивная отдача теплоты в охлаждающую воду
и n2 = 1,4...1,5.
Аналогично
процессу сжатия процесс расширения условно считают политропным со средним
постоянным значением показателя политропы n2.
Влияние
на n2 различных факторов.
.
С увеличением частоты вращения n2 снижается, так как уменьшается
время на теплоотдачу в стенки, кроме того с ростом оборотов интенсифицируется
догорание топлива.
.
С повышением нагрузки Pe (при n = const) показатель политропы n2
возрастает, так как увеличивается количество продуктов сгорания, их температура
и, следовательно, теплоотдача в стенки.
.
С ростом рабочего объема цилиндра Vh уменьшается отношение площади
поверхности охлаждения к рабочему объему (Fохл/Vh), а
следовательно снижается теплоотдача и и уменьшается n2.
.
С падением скорости сгорания количество догорающего топлива увеличивается, что
приводит к снижению n2.
Для
определения n2 расчетным путем пользуются уравнением баланса теплоты
на линии расширения
 , (3.100)
, (3.100)
где
 - потери теплоты в охлаждающую воду на участке ZB;
- потери теплоты в охлаждающую воду на участке ZB;
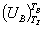 -
изменение внутренней энергии продуктов сгорания в диапазоне изменения
температуры от TZ до TB;ZB - работа
политропного расширения на участке ZB;
-
изменение внутренней энергии продуктов сгорания в диапазоне изменения
температуры от TZ до TB;ZB - работа
политропного расширения на участке ZB;
 -
количество теплоты, подведенное к рабочему телу в процессе расширения.
-
количество теплоты, подведенное к рабочему телу в процессе расширения.
Можно
записать
 . (3.101)
. (3.101)
Работа
расширения для политропного процесса запишется как
 , (3.102)
, (3.102)
где
 и
и 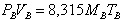 .
.
Тогда
после преобразований получим уравнения, решая которое определим n2:
 . (3.103)
. (3.103)
Это
уравнение решается методом последовательных приближений совместно с уравнением
 . (3.104)
. (3.104)
Параметры
процесса расширения
Давление
продуктов сгорания в конце процесса расширения
 . (3.105)
. (3.105)
Температура
газов в конце процесса расширения
 . (3.106)
. (3.106)
МОД
и СОД PB = 0,25...0,4 МПа TB = 900...1000 K
ВОД
PB = 0,4...0,6 МПа TB = 1000...1200 K
При
форсировании двигателя, если TB > 1200 K, следует предусматривать
меры по увеличению срока службы клапанов.
МОД
и СОД с охлаждаемыми поршнями n2 =1,2...1,3.
ВОД
с неохлаждаемыми поршнями n2 =1,15...1,25.
Лекция 7. 3.5. Процесс выпуска
Протекание процесса продувки и выпуска 2-тактных дизелей
Исходя их характера изменения давления в цилиндре дизеля, процесс выпуска
подразделяется на три фазы.
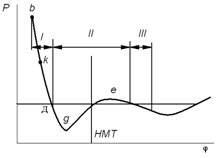
Рис. 3.8 - Изменение давления в цилиндре в период выпуска у двухтактного
ДВС
Фаза 1 - свободный выпуск, соответствует истечению газов, происходящего в
результате перепада давлений между цилиндром и выпускным коллектором.
Начинается с момента открытия выпускных окон (точка b) и заканчивается обычно при открытых
на некоторую величину продувочных окнах (точка d), т. е. до момента начала удаления продуктов сгорания под
выталкивающим воздействием продувочного воздуха.
Процесс истечения в фазе 1 подразделяется на два периода: надкритический
(от b до k Pг/Рд ≤ βкр); скорость истечения постоянна и
равна местной скорости звука) и подкритический. В точке k критическое отношение давление
 . (3.108)
. (3.108)
В
подкритическом периоде расход газа уменьшается с падением скорости истечения до
0 при Рг/Рц = 1 .
В
точке д - открытие продувочных окон.
Угол
φbд - предварение выпуска.
Фаза
2 - принужденный выпуск (dgef ) делится на два периода. За время первого периода
наблюдается интенсивное нарастание давления (ge). В течение
второго периода (ef) амплитуда давления снижается и характер процесса
приближается к установившемуся.
Фаза
3. За время фазы 3 в зависимости от системы продувки происходит либо потеря
заряда либо дозарядка.
Параметры
процесса продувки
Коэффициент
избытка продувочного воздуха
Коэффициент
продувки
 . (3.110)
. (3.110)
Процесс
выпуска отработавших газов у 4-тактных дизелей
Выпуск
продуктов сгорания отработавших газов у 4-тактных дизелей осуществляется в
течение ч-го такта. Для эффективной очистки цилиндра следует выбрать
оптимальные фазы газораспределения. Весь процесс выпуска подразделяется на три
фазы.
За
время первой фазы, начинающейся с момента открытия выпускного клапана и
примерно до НМТ происходит свободный выпуск за счёт перепада давления между рабочим
цилиндром и выпускным коллектором.
Вторая
фаза выпуска состоит в выталкивании продуктов сгорания поршнем при движении
поршня от НМТ к ВМТ (4-й такт).
Третья
фаза - это удаление продуктов сгорания из цилиндра за счёт отсасывающего
действия потока выпускных газов движущихся по выпускному трубопроводу с большой
скоростью.
Процесс
выпуска сопровождается газодинамическими потерями давления
 , (3.111)
, (3.111)
где
 - потери давления в выпускном клапане, газоотводном
канале и крышке;
- потери давления в выпускном клапане, газоотводном
канале и крышке;
 - потери
давления в выпускном коллекторе и выпускном тракте;
- потери
давления в выпускном коллекторе и выпускном тракте;
 - потери
давления в специальных устройствах впускного тракта, например, глушителе,
турбокомпрессоре, утилизационном котле.
- потери
давления в специальных устройствах впускного тракта, например, глушителе,
турбокомпрессоре, утилизационном котле.
 = 0,01÷0,04 МПа.
= 0,01÷0,04 МПа.
Системы
продувки и выпуска 2-тактных дизелей
В
зависимости от характера направления потоков продувочного воздуха системы
продувки делятся на контурные и прямоточные.
В
контурных системах выпускные и продувочные окна расположены в нижней части
цилиндра. Поэтому при движении продувочного воздуха от НМТ к ВМТ сначала
продувается одна сторона цилиндра, а затем (при обратном движении воздуха) -
противоположная.
В
прямоточных системах выпускные и впускные органы расположены по концам
цилиндра. Потоки продувочного воздуха перемещаются только в одном направлении
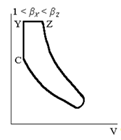
от НМТ к ВМТ. Поэтому общая длина пути потоков воздуха (при газообмене) в
прямоточных системах примерно в два раза короче, чем в контурных.
По
взаимному расположению окон в цилиндре контурные системы делятся на поперечные
и петлевые.
Поперченная
контурная система с эксцентричным расположением продувочных окон
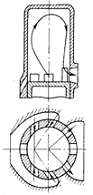
Рис.
3.9 - Схема поперченной контурной системы газообмена
Такая
система обеспечивает образование потоков воздуха продувающих последовательно
стороны цилиндра, примыкающих соответственно к продувочным и выпускным окнам.
Продувочные
окна расположены на одной стороне цилиндра, занимая 60 % окружности, а
выпускные - напротив.
Так
как выпускные окна выше, то они открываются первыми и вначале происходит
свободный выпуск под действием перепада давления в цилиндре и выпускном
коллекторе (ΔР = Рц - Рг). Затем открываются
продувочные окна и находящийся в ресивере воздух начинает поступать в цилиндр.
В
начале фазы продувки благодаря эксцентричному расположению продувочных окон и
их наклону к вертикальной оси потоки воздуха направляются вверх к крышке
цилиндра, прижимаясь к стенке прилегающей к продувочным окнам. У крышки потоки
воздуха меняют своё направление и движутся вниз к выпускным окнам, описывая
цилиндр по контуру. По мере опускания поршня к НМТ потоки воздуха отклоняются
от стенки и направляются к противоположной стороне не достигая верха. Сзади
этого основного потока образуется вихревой поток, возникновение которого
приводит к увеличению перемешивания воздуха с продуктами сгорания и ухудшению
качества очистки и рост значения коэффициента остаточных газов γr.
Недостатки
этой системы газообмена - потеря заряда при положении поршня в НМТ, так как
выпускные окна закрываются после продувочных, возможно, так называемое,
"короткое замыкание" потока воздуха, когда он идёт не по контуру, а
напрямую поперек цилиндров в выпускные окна, что возможно при малых давлениях
продувки, например, на долевых режимах.
Рассмотренная
система продувки применяется на дизелях завода "Русский дизель". Это
дизели 4ДР30/50, 6ДР30/50, 8ДР43/61.
Усовершенствованная
поперченная контурная система с эксцентричным расположением продувочных окон
В
этой системе кроме основных продувочных окон предусмотрены дополнительные
продувочные окна под выпускными. Они увеличивают общее проходное сечение
продувочных окон и одновременно прижимают основные потоки продувочного воздуха
к продувочной стороне цилиндра.
Существенный
недостаток этой системы - большая потеря заряда. Доля хода поршня, потерянная
на продувку достигает 22%. Для уменьшения потери заряда применяют вращающиеся
заслонки. Однако в эксплуатации эти заслонки часто выходят из строя, так как
работают в потоке горячих выпускных газов с большим содержанием углистых
частиц.

Рис.
3.10 - Схема усовершенствованной поперченной контурной системы газообмена
Рассмотренная
система продувки применяется на дизеля фирмы "Зульцер". Это дизели
типа RD (5RD68, 6RD76) с импульсной системой наддува. При последующем
форсировании дизелей отказались от применения вращающихся заслонок с целью
повышения надёжности и перешли на систему наддува с постоянным давлением перед
турбиной (изобарная система). Это дизели RND105 и др.
Поперченная
контурная система с центральным расположением продувочных и выпускных окон и
дозарядкой
В
этой системе продувочные окна расположены выше впускных и поэтому они перекрыты
автоматическими клапанами. Клапаны пластинчатого типа.
Потоки
воздуха направляются вверх к крышке цилиндра, прижимаясь к стенке прилегающей к
продувочным окнам. У крышки потоки воздуха меняют своё направление и движутся
вниз к выпускным окнам, описывая цилиндр по контуру. Пока давление в цилиндре
выше давления продувочного воздуха в коллекторе (Рц > Pk) клапаны прижаты и происходит свободный выпуск при открытии выпускных
окон.
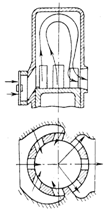
Рис.
3.11 - Схема поперченной контурной системы газообмена с центральным
расположением продувочных и выпускных окон
Поступление
продувочного происходит тогда когда давление в цилиндре меньше давления
продувочного воздуха (Рц < Pk) и
благодаря этому клапаны открыты.
Достоинства
данной системы: нет потери заряда, более того есть даже дозарядка цилиндра.
Недостатки:
при эксплуатации имеют место поломки пластин клапанов, что чревато попаданием
их обломков в цилиндр, наблюдается отложение смол и асфальтенов на пластинах,
что приводит к уменьшению проходных сечений. Поэтому необходимо часто их мыть и
менять.
Такую
систему применяют на двигателях фирмы "Фиат".
Контурная
петлевая система с односторонним лучеобразным расположением продувочных и
выпускных окон
Наклон
продувочных окон в сочетании с вогнутой формой днища поршня способствует
направлению потоков воздуха в сторону днища с последующим движением вверх вдоль
противоположной к окнам стороны цилиндра. У крышки воздух снова меняет своё
направление и спускаясь выходит через выпускные окна.

Рис.
3.12 - Схема контурная петлевая система с односторонним лучеобразным
расположением продувочных и выпускных окон
Таким
образом, продувочный воздух, двигаясь по контуру, описывает петлю. При этом на
большей фазы "продувка-принуждённый выпуск" происходит вытеснение
газов воздухом с незначительным перемешиванием. Лишь в конце этого периода
происходит полное перемешивание.
Такая
система применяется на двигателях фирмы МАН. Для устранения потерь заряда на
первых моделях применяли вращающиеся заслонки от которых в последующем отказались
из-за низкой их надёжности в эксплуатации.
Из
всех известных систем по качеству газообмена это наихудшая система продувки.
Однако её достоинством является компоновочные преимущества. При использовании
такой системы выпускной и продувочный ресивер расположены с одной стороны друг
над другом. Тем самым экономится габарит по ширине дизеля и облегчается
компоновка турбокомпрессора, поскольку выпускной и продувочный тракт
расположены рядом.
Прямоточно-клапанная
система продувки
При
прямоточно-клапанной продувке в крышке цилиндра размещаются выпускные клапаны
(один, два или четыре). Воздух движется в одном направлении от продувочных окон
к крышке цилиндра вытесняя остаточные газы.

Рис.
3.13 - Схема прямоточно-клапанной системы продувки
Благодаря
послойному замещению газов продувочным воздухом достигается хорошая очистка
цилиндра. Выпуск газов через клапаны даёт возможность подбирать оптимальные
фазы газораспределения и тем самым обеспечивать осуществление дозарядки цилиндра.
Продувочные
окна имеют большие проходные сечения, равномерное распределение воздуха.
Вихревое движение воздуха сохраняется до конца такта сжатия, благодаря чему
улучшается смесеобразование.
Привод
клапанов осуществляется от распредвала. У некоторых дизелей, например, первых
моделей фирмы "Гетавёркен" кулачки насажены на щёках коленвала.
Впоследствии они отказались от такого решения и тоже используют распредвал. В
современных дизелях чаще всего используется гидропривод.
Данная
система продувки применяется в малооборотных , среднеоборотных и
высокооборотных дизелях фирм "B&W", БМЗ,
"Сторк", "Гетавёркен" и др.
Прямоточно-щелевая
система продувки

Рис.
3.14 - Схема прямоточно-щелевой системы продувки
Данная
система применяется на дизелях с противоположно-движущимися поршнями. Обычно
продувочные окна располагаются вверху цилиндра, а выпускные - внизу. Поток
продувочного воздуха движется только в одном направлении. При тангенциальном
наклон в плане продувочных окон обеспечивается вихревое движение заряда до
окончания процесса сжатия.
Данная
система продувки применяется в дизелях фирм "Доксфорд", "Русский
дизель" - дизели типа 58, 61, завод транспортного машиностроения им.
Малышева (г. Харьков) - дизели типа Д100.
Лекция 8. 4. Интегральные показатели рабочего цикла дизеля
.1 Индикаторные показатели работы дизеля
Общие показатели рабочего цикла делятся на индикаторные (внутренние) и
эффективные (внешние). Первые характеризуют степень совершенства цикла с учётом
только потерь теплоты; вторые, кроме потерь теплоты, учитывают также
механические потери при передаче энергии расширения газов на коленчатый вал
дизеля.
. Среднее индикаторное давление (Pi , МПа) представляет собой условное,
постоянное давление, при действии которого на поршень за время одного хода
поршня совершается работа, равная индикаторной работе газов за цикл.
Геометрический смысл среднего индикаторного давления в том, что это величина
постоянного давления условной прямоугольной диаграммы, равной по длине и равновеликой
по площади индикаторной диаграмме.

Рис. 4.1 - Индикаторная диаграмма работы замкнутого цикла
Если работу за цикл Li отнести к единице рабочего объёма цилиндра, то получим среднее
индикаторное давление, МПа
 . (4.1)
. (4.1)
То
есть среднее индикаторное давление представляет собой работу, приходящуюся на
единицу рабочего объёма цилиндра.
Li -
индикаторная работа расчётного цикла, КДж;
Vh -
рабочий объём цилиндра, м3.
Полезная
индикаторная работа цикла определяется как разность работ сжатия и расширения

Рис.
4.2 - Расчётная индикаторная диаграмма
Li = LYZ + LZB + LAC
LYZ =PZ (VZ - VY)
LZB
=(PZ VZ - PB VB)/(n2 - 1)
LAC =(PC VC - PA
VA)/(n1 - 1)
Li =PZ (VZ - VY)
+ (PZ VZ - PB VB)/(n2 -
1) - (PC VC - PA VA)/(n1
- 1)h = VC (ε - 1)
Подставляя полученные значения в формулу (14.1), получим
Рi =[PZ (VZ - VY) + (PZ VZ - PB VB)/(n2 - 1) - (PC VC - PA VA)/(n1 - 1)]/[VC (ε - 1)]
Заменим ряд выражений уже известными
PZ = λ PC;  ;
;  ;
;  ;
;  ; ε = ρ δ
; ε = ρ δ
и
вынося за скобки PС найдём
среднее индикаторное давление расчётного цикла
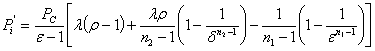 (4.2)
(4.2)
Среднее
индикаторное давление действительного цикла меньше расчётного из-за скруглений
индикаторной диаграммы на участках cyz ab, а
также вследствие отклонений действительных процессов сжатия и расширения от
политропных. В связи с этим

где
ζ - коэффициент полноты индикаторной диаграммы.
Для
2-тактных ДВС ζ = 0,96 ÷ 1,0
Для
4-тактных ДВС ζ = 0,95 ÷ 0,97
В
двухтактных двигателях среднее индикаторное давление определённое по формуле
(14.2) относится к полезному ходу поршня (в расчётах оперируют с действительной
степенью сжатия); Поэтому для полного хода поршня
 .
.
На
практике Pi определяют путём интегрирования экспериментальной
диаграммы
Значения
Pi для
современных дизелей
-тактные
без наддува Pi = 0,6 ÷
0,9 МПа;
-тактные
с наддувом Pi = 0,9 ÷
2,5 МПа;
-тактные
без наддува Pi = 0,6 ÷
0,8 МПа;
-тактные
с наддувом Pi = 0,8 ÷
1,8 МПа.
.
Индикаторная мощность (Ni, кВт)
Индикаторная
мощность - это мощность, соответствующая индикаторной работе за цикл.
Индикаторная
работа за цикл, кДж
Li = VhPi,
где
Vh -
рабочий объём цилиндра, м3;
Pi -
среднее индикаторное давление, кПа.
Рабочий
объём цилиндра, м3
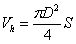 ,
,
где
D - диаметр цилиндра, м;
S - ход поршня,
м.
С
учётом этого
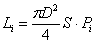 .
.
Индикаторная
мощность цилиндра, кВт
 ,
,
где
n - частота вращения двигателя, мин-1;
z - коэффициент
тактности, z = 1 для двухтактных ДВС, z = 0,5 для
четырёхтактных ДВС.
Для
многоцилиндрового двигателя
 ,
,
где
i - число рабочих цилиндров.
Для
двигателя выполненной конструкции можно записать
 ,
,
 .
.
Т.е.
для существующего двигателя индикаторная мощность изменяется с изменением
частоты вращения и среднего индикаторного давления.
.
Индикаторный КПД
(ηi).
При
рассмотрении термодинамического цикла учитываешься только один вид потерь -
неизбежная отдача теплоты холодному телу в соответствии со вторым законом
термодинамики.
В
действительном цикле отводу теплоты к холодному телу соответствует потеря
теплоты с выпускными газами. Кроме этой потери в действительном цикле имеются
потери теплоты от неполноты сгорания топлива и в результате теплообмен рабочего
тела со стенками камеры сгорания. Все тепловые потери в действительном цикле
учитываются индикаторным КПД, который является критерием совершенства
использования теплоты, подведённой к рабочему телу с топливом.
Индикаторный
КПД представляет собой отношение количества теплоты, преобразованной в
индикаторную работу в цилиндре двигателя к количеству теплоты, подведённой для
совершения этой работы
 .
.
Количество
теплоты подведённой с топливом за час, кДж
Qпод = Вч∙Qн,
где
Вч - часовой расход топлива, кг/ч;
Qн - низшая теплота сгорания топлива, кДж/кг.
Количество
теплоты, соответствующее индикаторной работе за час, кДж/ч
Li =
3600∙Ni,
где
3600 кДж/(кВт∙ч) - термический эквивалент работы одного кВт∙ч.
Тогда
 ,
,
где
 - удельный индикаторный расход топлива, кг/(кВт∙ч).
- удельный индикаторный расход топлива, кг/(кВт∙ч).
Индикаторный
КПД дизелей составляет:
двухтактных
……………………….0,43 - 0,60;
четырёхтактных
……………..…….0,45 - 0,66.
Удельный
индикаторный расход топлива, г/(кВт∙ч):
Двухтактных
…………………….. 140 - 200;
Четырехтактных
………………… 130 - 190.
Значение
индикаторного КПД зависит от целого ряда факторов. Наибольшее влияние оказывают
следующие: степень сжатия ε, конструкция
камеры сгорания, коэффициент избытка воздуха α, угол опережения подачи топлива θ, частота вращения n.
.
При увеличении степени сжатия индикаторный КПД ηi
увеличивается так же как и термический КПД ηt.
.
Значительное влияние на ηi
оказывает способ смесеобразования, а также конструкция камеры сгорания. У
дизелей с неразделёнными камерами сгорания ηi как
правило выше. Это связано с потерями теплоты поскольку в этом случае отношение
площади стенок к объёму камеры сгорания (Fкс/Vкс)
меньше.
.
Зависимость индикаторного КПД от величины коэффициента избытка воздуха
апроксимируется формулой Толстова ηi = η0i∙α1/α, где η0i
- значение индикаторного КПД при α =1.
4.
Зависимость ηi
от отклонения от оптимального угла опережения впрыска топлива при котором
достигается ηimax.
При
отклонении от оптимального угла опережения впрыска топлива в сторону увеличения
ηi
уменьшается из-за увеличения отрицательной работы процесса сжатия (слишком
ранее воспламенение топлива до ВМТ). При этом повышаются значения Pz и λ.
При
чрезмерном уменьшении θ
увеличивается период догорания топлива на
линии расширения и растут потери теплоты с выпускными газами, что также приводи
к понижению ηi.
Оптимальное
значение θ
подбирается опытным путём, при этом
следует кроме ηi
также учитывать значения Pz, λ и dP/dφ.
.
При повышении частоты вращения ηi понижается вследствие
увеличения продолжительности периода догорания топлива и возрастания потерь
теплоты с выпускными газами.
.2
Эффективные показатели работы дизеля
Механические
потери
Передача
энергии на коленчатый вал сопровождается механическими потерями. Выразим эти
потери (аналогично среднему индикаторному давления Pi)
через среднее условное давление механических потерь (Pмех), отнесённое к единице площади поршня, получим
Pмех.= Pтр.+ Pнас + Pвсп.+ Pвент.,
где
Pтр. -
потери на трение между деталями двигателя. Они зависят от величины Pz, удельных давлений, относительной скорости перемещения деталей,
свойств материалов, качества изготовления и монтажа дизеля, качества смазочного
масла.
При
повышении n работа трения возрастает из-за увеличения окружных
скоростей шеек коленчатого вала и сил инерции, вызывающих рост удельных
давлений на подшипники.
Среди
составляющих потерь не трение подавляющая часть приходится на поршневую группу
и трение в подшипниках деталей движения:
55 ÷ 65 % - доля потерь на терние поршня и поршневых колец;
45 ÷ 35 % - доля потерь на терние в подшипниках движения.
Pнас. - насосные потери (имют место только у четырёхтакных
ДВС. Это потери на хода всасывания и выталкивания). Обычно они составляют (1,5 ÷ 3,0) % от величины Pi.
Pвент. - вентиляционные потери на трение между движущимися
деталями и воздухом. Для судовых дизелей ими обычно пренебрегают в виду
малости. Для лёгких высокооборотных авиационных и автомобильных двигателей
рекомендуют учитывать.
Pвсп. - потери на привод вспомогательных механизмов
навешенных на двигатель. Величина Pвсп. составляет (1,5 ÷ 3,0) % от величины Pi.
У
двухтактных дизелей без наддува добавляются потери на привод надувочного
агрегата (1,5 ÷
3,0 % от величины Pi.).
При
использовании подпоршневых полостей в надувочной ступени потери мощности
составляют 3,0 % от Ni.
Показатели
Среднее
эффективное давление Pе,
учитывающее кроме тепловых все механические потери определится по формуле
Pe = Pi - Pмех.
Среднее
эффективное давление - это условное постоянное давление действующее на поршень
за рабочий ход и совершающее работу, эквивалентную полезной эффективной работе
на выходном фланце двигателя.
Другим
словами - среднее эффективное давление представляет собой удельную эффективную
работу двигателя.
Механический
КПД
Механический
КПД представляет собой отношение Pe/Pi, т.е.
 .
.
Механический
КПД оценивает все механические потери в двигателе, а, следовательно,
совершенство его конструкции в целом.
Механический
КПД может быть выражен через мощность
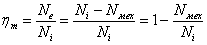 .
.
Мощность
механических потерь Nмех может
быть приближённо определена как индикаторная работа мощность холостого хода при
той же частоте вращения.
Эффективная
мощность, кВт
Ne = Ni ηm.
Удельный
эффективный расход топлива, кг/(кВт∙ч)
 .
.
Эффективный
КПД
ηe
= ηi ηm.
.3
Тепловой баланс судового дизеля
Внешним
тепловым балансом называется распределение теплоты, выделяющейся при сгорании
топлива в дизеле на отдельные составляющие, включая как полезно использованную
теплоту, так и потери теплоты. Внешний тепловой баланс определяется, как
правило, экспериментальным путём.
Внешний
тепловой баланс оценивает характер и величину потерь теплоты в дизеле на
эксплуатационных режимах и даёт возможность:
оценить
теплонапряжённость наиболее нагретых узлов и детадей;
установить
целесообразность использования теряемой теплоты в целях повышения КПД судовой
дизельной установки.
Уравнение
теплового баланса в удельных единицах, кДж/(кВт∙ч)
qт = qe +
qохл + qг
+ qост,
где
qт -
теплота сгоревшего топлива;
qе - теплота, эквивалентная эффективной работе;
qохл - теплота, отводимая в охлаждающую среду;
qг - теплота, отводимая с выпускными газами;
qост - остаточный член баланса (невязка) включает в себя
неучтённые потери, в том числе лучеиспускание в окружающую среду и неточности
измерений.
Располагаемая
теплота определяется по низшей теплоте сгорания Qн и удельному эффективному расходу топлива ge:
qт = ge∙Qн.
Теплота,
превращённая в полезную работу может быть определена из теплового эквивалента
работы, совершаемого двигателем мощностью один кВт в течение одного часа
 .
.
Теплота,
отводимая в охлаждающую среду
 ,
,
где
qв -
теплота, отводимая в охлаждающую воду;
qм - теплота, отводимая в смазочное масло;
Gохл - расход охлаждающей жидкости, кг/ч;
t2 - t1 -
разность температур на выходе и входе охлаждающей жидкости, К (°С);
С
- теплоёмкость охлаждающей жидкости, кДж/(кг∙К).
Теплота
отводимая в охлаждающую среду состоит из теплоты, отданной рабочим телом и
теплоты эквивалентной работе трения двигателя.
Теплота,
отводимая с выпускными газами, определяется как разность энтальпий выпускных
газов и поступающего в цилиндр свежего воздуха
qг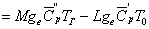
где
Т0 и Тг - температура газов за выпускным коллектором и
свежего заряда, поступающего в цилиндр.
Принимая
 и M = L получаем
и M = L получаем
qг .
.
Остаточный
член теплового баланса qост включает
в себя потери теплоты от неполноты сгорания, потери теплоты эквивалентные
потерям на трение и не перешедшим в охлаждающую среду и кинетической энергии
газов (если она не используется)., лучеиспускание от дизеля в окружающую среду,
сумму ошибок о неточностей измерения и неучтённые потери теплоты.
Примерные
статьи теплового баланса, %
|
Дизели
|
qe
|
qохл
|
qг
|
qн.с
|
qост
|
|
Без наддува
|
29÷42
|
20÷35
|
25÷40
|
0÷5
|
2÷7
|
|
С умеренным наддувом
|
35÷45
|
10÷25
|
25÷45
|
0÷5
|
2÷6
|
|
С высоким наддувом
|
40÷48
|
10÷18
|
20÷40
|
0÷5
|
2÷5
|
Как видно из таблицы при увеличении степени наддува происходит
значительное уменьшение qохл и немного qг.
При повышении температуры охлаждающей воды происходит уменьшение qохл и потерь на трение.
У
дизелей с небольшим диаметром цилиндра отношение площади поверхности камеры
сгорания к её объёму ( ) имеют наибольшие значения и поэтому qохл достигает 35 %.
) имеют наибольшие значения и поэтому qохл достигает 35 %.
Лекция 9. 5 способы совершенствования рабочего цикла ДВС
.1 Повышение удельной мощности судовых дизелей
Агрегатную эффективную мощность судовых дизелей можно повысить за счёт
конструктивных мероприятий и улучшения параметров рабочего процесса. Это видно
из выражения для мощности дизеля
 .
.
Конструктивные
мероприятия (увеличение D, S, n, i) в значительной мере уже исчерпаны и кроме того ведут
к увеличению габаритов и массы цилиндропоршневой группы.
Наиболее
целесообразным и эффективным способом увеличения удель-ной мощности судовых
дизелей является повышение Ре за счёт увеличения плотности вводимого
в цилиндр воздуха - наддув. Применение наддува позволяет в несколько раз (до 4
- 5) увеличить удельную мощность двигателей без изменения их основных размеров
за счёт соответствующего повышения давления наддува Рk
и охлаждения надувочного воздуха.
Критерием
относительного увеличения мощности при наддуве служит степень наддува -
отношение средних эффективных давлений двигателя с наддувом и без наддува
 .
.
К
основным способам увеличения массового заряда воздуха относятся:
повышение
плотности за счёт возрастания давления (наддув);
повышение
плотности за счёт снижения его температуры (охлаждение);
повышение
коэффициента наполнения за счёт продувки камеры сгорания и дозарядки рабочего
цилиндра.
Существуют
три категории наддува:
-
умеренная у 4-тактных Ре = 0,7÷1,2; у 2-тактных Ре =
0,6÷0,8;
-
повышенная у 4-тактных Ре =1,21÷2,0; у 2-тактных Ре =
0,81÷1,2;
-
высокая у 4-тактных Ре = 2,01÷3,0; у 2-тактных Ре =
1,21÷1,6.
Преимущества
дизеля с наддувом по сравнению с дизелем без наддува при заданной мощности
1. Меньшие габариты двигателя, так как меньше число цилиндров.
2. Меньшая масса двигателя и, соответственно, меньшая удельная
масса (масса на единицу мощности).
. Более высокий КПД двигателя при турбонаддуве.
. Меньшая стоимость на единицу мощности.
. Используются холодильники меньших размеров, поскольку при
одинаковой мощности необходимо отводить тепла меньше, чем у двигателей без
наддува.
. При газотурбинном наддуве газовая турбина сама заметно снижает
шум выхлопа.
. Меньшее падение мощности при понижении плотности окружающего
воздуха.
. Лучшее качество отработавших газов при одинаковом способе
организации рабочего процесса.
Недостатки двигателей с наддувом
1. Более высокие механические и тепловые нагрузки деталей, чем у
двигателей без наддува.
2. Худшая приёмистость при газотурбинном наддуве.
. При определённых условиях менее благоприятное протекание кривой
крутящего момента при газотурбинном наддуве, особенно при высоких степенях
наддува.
Основными способами осуществления наддува являются:
механический;
инерционный;
газотурбинный;
комбинированный.
При механическом наддуве надувочный агрегат ротативного или центробежного
типа приводится в действие через передачу от коленчатого вала. Как
самостоятельная эта система наддува не рентабельна.
Например при Pk = 0,16÷0,17 МПа затраты мощности на привод
надувочного агрегата составляют 10 % от индикаторной мощности дизеля.
Инерционный наддув применяются на маломощных дизелях, и требует
усложнения систем впускного тракта и газораспределения.
Классификация систем наддува
а) По виду привода нагнетателя:
1. От постороннего источника (электродвигатель).
2. От самого двигателя (мощность отбирается от коленвала).
. От турбины приводимой выпускными газами (турбонаддув).
б) По конструкции нагнетателя
. С объёмным нагнетателем (поршневой, роторный типа РУТ, винтовой
компрессор и др.).
. С лопаточным нагнетателем (радиальный, осевой, полуосевой).
в) По типу связи между надувочным агрегатом и двигателем
. Нагнетатель соединён с коленчатым валом, осуществляется отбор мощности
от коленвала - механический наддув.
. Нагнетатель соединён с турбиной. Надувочный агрегат свободный, т.е. не
имеет механической связи с двигателем - свободный турбонаддув.
. Нагнетатель, турбина и коленвал двигателя механически связаны.
Производится либо отбор мощности от коленвала, либо отдача мощности от
коленвалу - комбинированный ДВС (КДВС).
Впервые в мире запатентовал наддув Готлиб Даймлер в 1885 г. Рудольф
Дизель применил наддув и охлаждение в 1896 г.
.2 Системы наддува
1. Система ГТН со свободным турбокомпрессором
Выхлопные газы и выпускного коллектора направляются к турбине и приводят
её во вращение. Турбина находится на одном валу с компрессором и вращает его.
Компрессор засасывает воздух, сжимает его и подаёт под давлением сначала в
воздухоохладитель, где происходит его охлаждение, благодаря чему повышается его
плотность, и затем - в наддувочный ресивер откуда сжатый и охлаждённый воздух
поступает в цилиндры двигателя.

При этой системе наддува мощность турбины на всех режимах равна мощности
компрессора Nт = Nк.
Основные преимущества:
простота конструкции;
небольшой габарит газотурбокомпрессора;
автоматическая связь между нагрузкой двигателя и частотой вращения
турбины.
Недостатки:
ухудшение пусковых качеств;
ухудшение приёмистости.
2. Комбинированная последовательная система наддува
Двухступенчатое сжатие воздуха осуществляется сначала в турбокомпрессоре
(первая ступень), затем - в приводном нагнетателе (вторая ступень). В качестве
второй ступени часто используют подпоршневые полости двухтактных МОД (дизели
типа RD и RND фирмы "Зульцер").
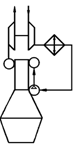
Достоинства:
обеспечивается возможность получения высоких степей наддува;
обеспечивается хорошая приемистость в эксплуатации.
. Комбинированная параллельная система наддува
Эта система применяется, когда турбокомпрессор не может обеспечить
необходимое количество воздуха для рабочего процесса дизеля.
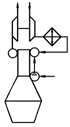
Воздух подаётся в общий ресивер дизеля как из турбокомпрессора, так и
приводного нагнетателя. При этом недостающая производительность турбокомпрессора
восполняется добавочным нагнетателем.
Недостаток: трудно подобрать оптимальные размеры нерегулируемого
нагнетателя, которые удовлетворяли бы всем условиям эксплуатации как на полном
ходу судна, так и на долевых режимах.
Чтобы устранить это недостаток применяют систему с автономным приводом
добавочного нагнетателя.

. Комбинированная система с двухступенчатым наддувом
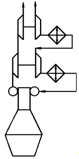
Применяется при высокой степени наддува с целью повышения показателей
экономичности за счёт эффективного использования энергии выпускных газов и
более высоких КПД турбин. Первая ступень - ступень низкого давления, как правило,
выполняется изобарной, вторая ступень - ступень высокого давления, как правило,
выполняется импульсной. Тем самым реализуются преимущества импульсной и
изобарной систем наддува при соответствующих давлениях выпускных газов.
Данная система наддува внедрена на дизелях фирм "Пилстик",
"Мицубиси".
. Комбинированная система с турбокомпрессором, имеющим механическую связь
с коленвалом дизеля
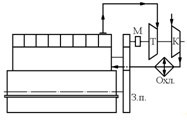
При балансе мощностей турбины и компрессора механический привод
разгружается и КПД дизеля растёт.
При дисбалансе, когда Nк >Nт, что наблюдается при пониженных частотах вращения коленвала
и нагрузках недостающая мощность отбирается от двигателя за счёт включения в
работу обгонной муфты (М).
Преимущества:
обеспечивает хорошие пусковые качества дизеля;
обеспечивает хорошую приёмистость дизеля.
Недостатки:
усложнение конструкции дизеля из-за наличия зубчатой передачи.
.3 Охлаждение надувочного воздуха в дизелях
Охлаждение надувочного воздуха в дизелях применяется для повышения мощности
и понижения теплонапряжённости деталей ЦПГ двигателя.
Охлаждение надувочного воздуха позволяет увеличить его плотность и
следовательно, массу заряда цилиндра двигателя, а это в свою очередь позволяет
сжечь большее количество топлива и выполнить основную задачу наддува - повысить
мощность двигателя.
Положительные качества охлаждения:
. Масса воздуха повышается на 2 - 3 % при снижении температуры воздуха на
каждые 10°.
. Начальная температура воздуха Та снижается, в связи с чем
снижается и средняя температура за цикл. Это позволяет улучшить условия работы
деталей ЦПГ благодаря понижению температуры поршня, цилиндровой втулки, крышки
цилиндров и органов газообмена.
. Вследствие роста давления конца сжатия Рс можно понизить
степень сжатия ε без ухудшения процесса сгорания и увеличения периода
задержки самовоспламенения τi.
Способы охлаждения надувочного воздуха
. Посредством теплообмена в холодильниках поверхностного
(рекуперативного) типа, когда по одну сторону теплообменной поверхности
циркулирует охлаждаемый воздух а по другую - забортная вода.
. За счёт изменения внутренней энергии сжатого воздуха в расширительных
турбинах или цилиндрах дизеля при соответствующем изменении фаз
газораспределения.
. За счёт испарения в надувочном воздухе впрыснутой в распыленном
состоянии жидкости, например, воды, аммиака и т.п. (испарительной охлаждение).
. Путём комбинации вышеперечисленных способов (смешанное охлаждение).
Первый способ относится к внешнему охлаждению, т.е. передача теплоты от
одного источника к другому происходит через разделяющую их поверхность.
Охлаждение вторым и третьим способами связано с протеканием определённых
термодинамических процессов в заряде воздуха. (Эти способы относятся к
внутреннему охлаждению).
Следует отметить, что охлаждение вторым способом самостоятельного
значения не имеет и возможно лишь при дополнительном использовании
холодильников поверхностного типа.
Охлаждение надувочного воздуха в поверхностных водовоздушных
холодильниках.
Это наиболее распространённый способ охлаждения, который применяется в
судовых ДВС. Его отличительные особенности:
простота;
надёжность в работе;
возможность уменьшения температуры в одной секции на 60°;
потери давления в одной секции составляют 0,0015÷0,005
МПа.
В судовых ДВС применяют трубчатые или пластинчатые воздухоохладители. В трубчатых воздухоохладителях вода протекает по трубкам
изготовленным из мельхиора или титана, которые со стороны воздуха имеют
оребрение.
Недостатки:
наименьшая температура надувочного воздуха на выходе из воздухоохладителя
зависит от температуры забортной воды
Тk = Тз.в
+ (7÷12);
- при охлаждении влажного воздуха до температуры, которая ниже точки
росы, происходит конденсация паров воды в охладителе. В двигателях имеющих
невозвратные пластинчатые клапаны в надувочном ресивере, влага отрицательно
влияет на работу надёжность работы этих клапанов и деталей ЦПГ. В связи с эти
температуру воздуха на выходе из холодильника рекомендуется поддерживать на 8÷19°
выше точки росы.
Выделение влаги наиболее вероятно при низкой температуре забортной воды,
высокой относительной влажности воздуха и на долевых нагрузках дизеля. По этой
причине спускной краник на воздушном ресивере на долевых режимах рекомендуется
держать открытым.
Турбодетандерное охлаждение надувочного воздуха
Такое охлаждение позволяет понизить температуру надувочного воздуха ниже
границы, определённой температурой окружающей среды. Этот способ применялся
фирмой "Купер-Бессемер".

Рис. 5.1 - Схема турбодетандерного охлаждения
Воздух сжимается в компрессоре К, после промежуточного охлаждения в
воздухоохладителе ВО1, сжимается далее в компрессоре Ктд
турбодетандера.
Так как температура на входе в компрессор (т. 3) и на входе в турбину Ттд
турбодетандера (т. 5) различаются немного, благодаря охлаждению в
воздухоохладителе ВО2, то баланс мощностей в турбодетандере устанавливается
тогда, когда степень расширения в турбине турбодетандера будет значительно
выше, чем степень повышения давления в компрессоре.
Если общий КПД турбодетандера равен 50%, то степень расширения в турбине
должна быть вдвое больше, чем степень повышения давления в компрессоре. Отсюда
следует, что давление за компрессором (т. 2) должно быть значительно выше
давления на входе в цилиндр (т. 6). Это более высокое давление за компрессором
К может быть достигнуто при большом теплоперепаде, срабатываемом турбиной Т.
Способ охлаждения Миллера
Этот способ применяется на дизелях фирм "Нордберг",
"Мицубиси".
Этот способ отличается от обычного способа наддува наличием изменяющейся
фазы закрытия впускного клапана до НМТ. При увеличении нагрузки, т.е. при
увеличении степени наддува, угол опережения впускного клапана до НМТ
увеличивается, вследствие чего цилиндр лишь частично заполняется свежим
зарядом. Перед ходом сжатия, т.е. ещё во время хода впуска заряд в цилиндре
расширяется (при движении поршня до НМТ) и при этом охлаждается. Сжатие
начинается при более низкой температуре, чем при поступлении в цилиндр полного
заряда.
Смысл применения способа Миллера можно объяснить перераспределением
сжатия между компрессором и цилиндром двигателя.

Рис. 5.2 - Индикаторные диаграммы при обычном способе наддува (а) и
способе Миллера (б)
При обычном наддуве (т. 2) состояние воздуха на выходе из компрессора
совпадает с состоянием, соответствующем началу сжатия (т. 1ц ). В случае
применения способа Миллера точка 2 лежит уже на линии сжатия.
Так как при одинаковой температуре охлаждающей среды в охладителе
температуру Твп на входе в цилиндр можно поддерживать за счёт
охлаждения надувочного воздуха примерно постоянной независимо от степени
повышения давления в компрессоре, то температура в точке 1ц, соответствующая
началу процесса сжатия при использовании способа Миллера получается ниже, чем
при обычном охлаждении.
Величину давления наддува можно подобрать такой, чтобы давление в точке
1ц было равно давлению в этой же точке как и при обычном наддуве.
Лекция 10.
6. Характеристики
судовых дизелей
Характеристики представляют собой функциональные зависимости, обычно
выраженные в графической форме, между параметрами двигателя, характеризующими
его работу на различных режимах (мощностные и экономические показатели,
параметры тепловой и механической напряжённости)
Следует различать характеристики собственно двигателя и характеристики
двигателя и потребителя мощности.
К характеристикам двигателя относятся внешние, ограничительные,
нагрузочные и универсальные характеристики, к совместной характеристике
двигателя и потребителя мощности относится винтовая характеристика.
Помимо этого в процессе доводки двигателя на стенде завода-изготовителя
снимают регулировочные характеристики, которые представляют зависимость
показателей работы дизеля от угла опережения впрыска топлива, фаз
газораспределения, давления наддува, давления распыливания топлива, давления
затяжки иглы форсунки и др. Регулировочные характеристики не являются
эксплуатационными. Ими пользуются в заводских, лабораторных условиях для
отыскания рациональных путей улучшения показателей работы двигателей.
Все характеристики делятся на скоростные и нагрузочные. К скоростным
относят характеристики при построении которых за независимую переменную
принимают частоту вращения коленчатого (гребного) вала; при рассмотрении
нагрузочных характеристик за независимую переменную принимают показатели
нагрузки - Ne, Mкр, Ре.
.1 Внешняя характеристика
Под внешней характеристикой подразумевают зависимость показателей работы
двигателя от частоты вращения при закреплённом положении органа управления
подачей топлива
В общем случае этот орган может быть закреплён в разных положениях,
поэтому вводится понятие об эксплуатационной внешней характеристике,
характеристиках частичных мощностей, полной, номинальной, максимальной
мощностей.
Характеристику максимальной мощности иногда называют абсолютной внешней
характеристикой.

Рис. 6.1 - Внешние характеристики дизеля: 1 - максимальной мощности
(абсолютная внешняя характеристика); а - номинальной мощности; б -
эксплуатационной мощности; в - частичной мощности
Эксплуатационная внешняя характеристика или просто внешняя характеристика
снимается при ограниченной подаче топлива, обеспечивающей бездымный выпуск
отработавших газов. Площадь расположенная под внешней характеристикой
представляет собой область всех возможных в условиях эксплуатации режимов
работы двигателя.
Внешние характеристики обычно снимают на стенде при определённых
условиях, указанных в технических документах, т.е. при вполне определённых
давлении и температуре окружающей среды, определённом разрежении на всасывании
и противодавлении на выхлопе определённом температурном режиме охлаждения.
При работе дизеля на режиме внешней характеристики при снижении оборотов
наблюдается ухудшение индикаторных показателей и возрастание механической и
тепловой напряжённости.
В ряде случаев при работе по внешней характеристике температура выпускных
газов и максимальное давление сгорания не превышают предельных значений. Вместе
с тем работа по внешней характеристике на пониженной частоте вращения не
допускается вследствие резкого ухудшения рабочего процесса и связанного с эти
усиления нагаро - и смолообразовании, нарушающего нормальную смазку, теплоотвод
и подвижность поршневых колец, т.е. вредно отражается на ресурсе двигателя.
Кратковременный выход нагрузок до значений внешней характеристики при
реверсе, разгоне, циркуляции не отражается существенно на надёжности и ресурсе
дизеля, поэтому его можно считать вполне допустимым.
.2 Ограничительная характеристика
Как указывалось ранее площадь под внешней характеристикой представляет
область возможных режимов работы двигателя. Однако координаты внешней
характеристики не определяют допустимую нагрузку двигателя в условиях
эксплуатации, поскольку работа на по этой характеристике сопряжена с
возрастанием механической и тепловой напряжённости. К тому же следует иметь
виду, что реальные условия использования двигателя могут значительно отличаться
от тех, при которых проводилось снятие внешней характеристики, что в свою
очередь вызывает необходимость уменьшения нагрузки. Исходя из этого и было
введено понятие об ограничительной характеристике.
Ограничительной характеристикой называется зависимость между частотой
вращения и максимально допустимой мощностью двигателя при условии обеспечения
полной надёжности его работы.
В связи с рассмотрением ограничительной характеристики необходимо
рассмотреть факторы, ограничивающие допустимую нагрузку на двигатели. Их можно
разбить на три группы:
. Характеризующие механическую нагрузку на детали двигателя;
. Характеризующие тепловую нагрузку;
. Характеризующие качество протекания рабочего процесса.
К
первой группе следует отнести Pz, 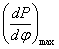 ,
,  , Мкр. Из приведённых параметров только
крутящий момент достаточно полно характеризует нагрузку, прежде всего, на
коленчатый вал - наиболее дорогостоящую деталь двигателя.
, Мкр. Из приведённых параметров только
крутящий момент достаточно полно характеризует нагрузку, прежде всего, на
коленчатый вал - наиболее дорогостоящую деталь двигателя.
Важно
иметь ввиду, что судовых условиях можно определять или косвенным путём
оценивать величину крутящего момента на валу. В ряде случаев при постоянстве
крутящего момента обеспечивается примерное постоянство температуры выпускных
газов. В связи с вышесказанным заводы обычно в качестве ограничительной
характеристики принимают Ne = f(n) при Мкр = const, которая в
координатах Ne - n представляет собой прямую линию. Что тоже немаловажно.
Тепловая
напряжённость деталей двигателя зависит от величины теплового потока,
проходящего через эту деталь.
Тепловое
состояние двигателя в целом обычно оценивают по температуре донышка поршня,
поэтому она является надёжным критерием теплового состояния двигателя. Однако в
условиях эксплуатации не представляется возможным контролировать температуру
поршня. В реальных условиях тепловое состояние двигателя оценивают по косвенным
показателям, например, температуре выпускных газов. Однако это недостаточно
надёжный критерий тепловой напряжённости двухтактных дизелей и четырёхтактных
дизелей с перекрытием клапанов (там, где имеет место продувка камеры сгорания).
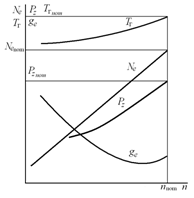
Рис.
6.2 - Ограничительная характеристика Мкр = const
Экспериментальные
исследования показали, что тепловое состояние ЦПГ достаточно точно определяется
величиной теплоотвода в охлаждающую воду, поэтому можно пользоваться
ограничительной характеристикой Qw = const.
Тепловое
состояние поршня зависит и от величины коэффициента избытка воздуха. Для
обеспечения наиболее экономичного режима работы двигателя необходимо добиваться
поддержания на высоком уровне индикаторных показателей - gi, ηi.
Последние зависят, главным образом от величины коэффициента избытка воздуха α. В этой связи целесообразно принимать α за критерий допустимой нагрузки и пользоваться
ограничительной характеристикой α = const. Такая
ограничительная характеристика применяется для быстроходных дизелей ПО
"Звезда".
.3
Винтовая характеристика
Главные
судовые двигатели обычно нагружаются гребным винтом. Поэтому для любого режима
плавания мощность, развиваемая двигателем будет определяться мощностью,
потребляемой гребным винтом.
Винтовой
характеристикой называется зависимости параметров работы двигателя нагружаемого
гребным винтом от частоты вращения.
Отсюда
следует, что винтовая характеристика является совместной характеристикой
двигателя и потребителя мощности - гребного винта.
При
использовании винта фиксированного шага (ВФШ) изменение мощности двигателя от
оборотов представляется в виде параболической зависимости Ne = Cnm.
Для
судов с круглыми обводами (водоизмещающие суда) m = 2,7 ÷ 3,2; для полуглиссирующих судов в период глиссирования m = 1,8 ÷ 2,2; для глиссирующих m = 1,6 ÷ 1,8.
Вид
винтовой характеристики зависит от конструкции гребного винта, обводов корпуса
судна, гидравлических условий работы гребного винта (состояние моря, осадка,
глубина под килем, направление потока воды, обтекающего гребной винт) и других
факторов. Поэтому в эксплуатации гребной винт создаёт поле характеристик,
ограничиваемое следующими винтовыми характеристиками:
1) при работе на швартовах (а также момент снятия с мели);
2) с оголёнными гребными винтами.
Первая соответствует наибольшей мощности, потребляемой гребным винтом,
вторая сбросу нагрузки.
При определении номинальной частоты вращения и номинальной мощности при
непосредственной связи с гребным валом, совмещают внешнюю, ограничительную
характеристики с нормальной винтовой. Нормальная винтовая характеристика
снимется при прямом свободном ходе судна, на спокойной воде, чистом корпусе и
нормальной осадке судна при работе всех гребных валов судна.
Обычно винтовую характеристику представляют в виде кубической параболы Ne = Cn3. Коэффициент "С" определяется по данным для номинального
режима. Для данного судна при неизменных гидродинамических условиях работы
гребного винта коэффициент "С" сохраняется постоянным. В этом случае
внешняя, ограничительная и винтовая характеристики пересекаются в одной при
номинальной частоте вращения. При изменении гидравлических условий работы
гребного винта значение коэффициента "С" будет меняться. В связи с
этим изменится мощность, поглощаемая гребным винтом при данной частоте вращения
гребного вала.
Обычно на практике чаще всего происходит увеличение коэффициента
"С", так называемое "утяжеление" винтовых характеристик. В
этом случае возникнут ограничения по частоте вращения, поскольку максимально
допустимую мощность двигатель будет развивать при пониженной частоте вращения. Предельным
случаем "утяжёления" винтовой характеристики Является швартовная
характеристика, когда судно стоит на месте а гребной вал вращается, создавая
упор.
Однако, на практике возможны и другие случаи, когда судно идёт в
балласте, попутном ветре, по течению, попутной волне. Тогда будет происходить
"облегчение" винтовой характеристики и она будет располагаться ниже
нормальной винтовой характеристики. Предельным случаем "облегчения"
винтовой характеристики является работа двигателя с оголённым гребным винтом
(при сильном дифференте на нос).
Характер изменения параметров при работе дизеля 6ЧНСП 18/22 по винтовой
характеристике приведён на рисунке 6.4.

Рис. 6.3 - Винтовая характеристика дизеля 6ЧНСП 18/22
6.4 Нагрузочная характеристика
Нагрузочная характеристика показывает зависимость параметров,
характеризующих работу двигателя, от нагрузки при постоянной частоте вращения. Характер изменения параметров при работе двигателя ДН 23/30
по нагрузочной характеристике приведён на рисунке 6.4.
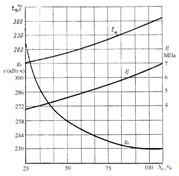
Рис. 6.4 - Нагрузочная характеристика дизеля ДН 23/20
.5 Универсальная характеристика
Универсальная характеристика - это семейство кривых постоянных значений
удельного эффективного расхода топлива, температуры выпускных газов,
построенных в координатах Ne - n, Рe - n.
Эта характеристика нужна для оценки технико-экономических показателей
дизеля при работе на переменных режимах в различных эксплуатационных условиях.
Они выражают связь трёх исследуемых параметров. Для построения универсальных
характеристик нужно иметь серию нагрузочных характеристик.
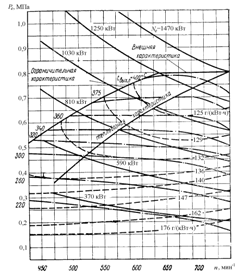
Рис. 6.5 - Универсальная характеристика дизеля 14Д40 (10ДН20,7/2х25,4)
Универсальные характеристики дают возможность выбирать для дизеля наиболее
экономичные режимы с учётом требований эксплуатации.
Лекция 11.
7. Кинематика
кривошипно-шатунного механизма
.1 Определения и обозначения
Кривошипно-шатунный механизм (КШМ) служит для преобразования
поступательного движения поршня во вращательное движение коленчатого вала.
При рассмотрении кинематики КШМ предполагается, что угловая скорость
вращения коленчатого вала постоянна. В действительности из-за неравномерности
крутящего момента двигателя угловая скорость вала переменна, но изменяется в
незначительных пределах.
Различают три основных вида КШМ:
центральный (нормальный) КШМ, в котором ось цилиндра пересекает ось
вращения коленвала (рис. 7.1, а);
смещённый (дезаксиальный) КШМ, в котором ось цилиндра не проходит через
ось коленвала, при этом смещение оси цилиндра "С", которое называется
дезаксаж, обычно не превышает 10 % хода поршня (рис. 7.1, б);
КШМ с прицепным шатуном, у которого два шатуна передают усилия на одну и
ту же шатунную шейку коленвала (рис. 7.1, в). Шатун соединённый с шейкой
называется главным, шатун шарнирно соединённый с нижней головкой - главного
шатуна - прицепным. Поршень, сочлёнённый с главным шатуном, называется главным
поршнем, а сочленённый с прицепным шатуном - боковым. В общем случае с главным
шатуном могут соединяться два прицепных шатуна (W - образный двигатель) или более двух (звёздообразный
двигатель).

Рис. 7.1 - Виды КШМ
L -
длина шатуна; l- длина прицепного шатуна;
R -
радиус кривошипа; r - радиус
прицепа;
α - угол поворота кривошиап от ВМТ;
Smax - ход поршня;
S -
перемещение поршня от ВМТ, соответствующее повороту кривошипа на угол α;
β - угол отклонения оси шатуна от оси
цилиндра;
βl - угол отклонения оси прицепного
шатуна от оси цилиндра;
ω - угловая скорость вращения коленвала;
γ - угол развала цилиндров.
Угол β считается положительным при отклонении оси шатуна от
оси цилиндра в сторону вращения коленвала. В
судовых ДВС наиболее распространённым является центральный КШМ. Смещённый КШМ
применяется главным образом в автомобильных и поршневых авиационных ДВС для
снижения нормальной силы поршня на втулку цилиндра.
Отношение
 - называется постоянной КШМ.
- называется постоянной КШМ.
Для
современных ДВС значения λ
имеют следующие значения:
ВОД
тронковые λ
= 0,25 ÷ 0,30;
СОД
тронковые λ
= 0,20 ÷ 0,25;
МОД
крейцкопфные λ
= 0,24 ÷ 0,28;
7.2
Перемещение поршня
Рассмотрим
центральный КШМ при некотором положении поворота колена на угол α (рис. 7.1, а).
Максимальное
перемещение поршня Smax = 2R. Текущее перемещение поршня S в функции от α определится следующим образом:
 ,
,
или,
вынеся R за скобки получим
 (7.1)
(7.1)
Угол
β находим по теореме синусов из треугольника 
 . (7.2)
. (7.2)
Откуда
sinβ = λ∙sinα. Поскольку в формуле для определения перемещения
поршня S стоит cosβ, т,о используя известную зависимость sin2β + cos2β = 1, получим
 . (7.3)
. (7.3)
Используя
формулу бинома Ньютона, это выражение можно записать в виде сходящегося ряда
 . (7.4)
. (7.4)
При
λ
= 0, 20 ÷ 0,30 практически
достаточно сохранить два первых члена сходящегося ряда, т.е.
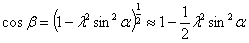 . (7.5)
. (7.5)
Тогда
формулу (7.1) можно записать в следующем виде
 . (7.6)
. (7.6)
Зная,
что sin2α = 1 - cos2α = 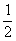 (1- cos2α) подставим это выражение в формулу (7.6) получим
(1- cos2α) подставим это выражение в формулу (7.6) получим
 , (7.7)
, (7.7)
Перемещение
поршня, отнесённое к радиусу кривошипа называют безразмерным  .
.
Формула
безразмерного перемещения поршня 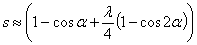 приближённо
представляет перемещение поршня как сумму двух гармонических перемещений
первого и второго порядка
приближённо
представляет перемещение поршня как сумму двух гармонических перемещений
первого и второго порядка
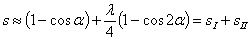 . (7.8)
. (7.8)
7.3
Определение угла поворота кривошипа по заданному перемещению поршня
Эта
задача наиболее часто возникает в двухтактных ДВС при определении угла поворота
коленвала в момент выпускных и продувочных открытия окнах по известной их
относительной высоте ψ.
Для
этого воспользуемся формулой
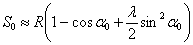 . (7.9)
. (7.9)
Зная,
что  имеем S0 = h = ψ2R.
имеем S0 = h = ψ2R.
Решаем
уравнение (7.9) относительно α0
 ; (7.10)
; (7.10)
 ;
;
 . (7.11)
. (7.11)
.4
Скорость поршня
Выражение
для скорости поршня найдём дифференцируя по времени зависимость, для
перемещения поршня и делая замену переменных дифференцирования
 , (7.12)
, (7.12)
где
 - угловая скорость коленвала, с-1.
- угловая скорость коленвала, с-1.
Для
нахождения точного выражения скорости поршня дифференцируем уравнение (7.1) по
времени
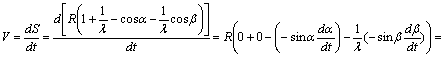
 (7.13)
(7.13)
Для
определения  продифференцируем полученное ранее выражение sinβ = λ∙sinα
продифференцируем полученное ранее выражение sinβ = λ∙sinα
 .
.
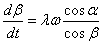 .
.
Подставим
полученное выражение для  в формулу 7.13 и зная, что
в формулу 7.13 и зная, что  , получим
, получим
 ,
,
 . (7.14)
. (7.14)
Безразмерная
скорость определяется следующим образом
 . (7.15)
. (7.15)
Приближённое
выражение для скорости поршня выводится путём дифференцирования выражения (7.7)
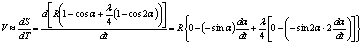
 . (7.16)
. (7.16)
Из
этой формулы видно, что при λ ≠ 0 скорость
поршня находится как сумма двух гармонических составляющих первого и второго
порядков.
.5
Ускорение поршня
Ускорение
поршня находится путём дифференцирования скорости по времени
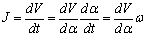 . (7.17)
. (7.17)
Для
точного выражения ускорения имеем
 . (7.18)
. (7.18)
Подставим
ране полученные выражения  ,
, 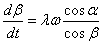 в
уравнение (7.18) и используя формулы тригонометрических соотношений, выполним
следующие преобразования
в
уравнение (7.18) и используя формулы тригонометрических соотношений, выполним
следующие преобразования

Окончательно
 . (7.19)
. (7.19)
Безразмерное
ускорение поршня
 .
.
Следовательно
 .
.
Приближённое
выражение для ускорения получается путём дифференцирования приближённого
выражения для скорости (формула 7.16)

 . (7.20)
. (7.20)
Для
безразмерного ускорения
 . (7.21)
. (7.21)
То
есть это сумма гармоник первого и второго порядка.
Значения
углов поворота кривошипа α
при которых ускорение поршня j
получается экстремальным находят приравняв к нулю производную по α от правой части уравнения (7.20)
 .
.
Откуда
sinα + 2∙λ∙2∙sinα∙cosα = sinα (1+4∙λ∙cosα) = 0.
Следовательно
экстремумы будут при α = 0, α = 180 и α = arccos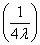 .
.
Подставим
эти значения α в уравнение (7.21) найдём следующие значения
1. В положении ВМТ α = 0, j = 1 + λ, JВМТ = Rω(1+
λ).
2. В положении НМТ α = 180, j = - (1 - λ) , JВМТ = -Rω(1
- λ).
3.
Третье экстремальное значение возможно при 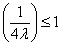 , т.е.
при λ
≥ 0,25.
, т.е.
при λ
≥ 0,25.
Лекция 12.
8. Динамика
кривошипно-шатунного механизма
КШМ во время работы двигателя подвергается воздействию следующих сил: от
давления газов на поршень, инерции движущихся масс механизма, тяжести отдельных
деталей, трения в звеньях механизма и сопротивления приемника энергии.
Расчётное определение сил трения весьма сложно и при расчёте сил
нагружающих КШМ обычно не учитывается.
В ВОД и СОД обычно пренебрегают силами тяжести деталей ввиду их незначительной
величины по сравнению другими силами.
Таким образом основными силами действующими в КШМ являются силы от
давления газов и силы инерции движущихся масс. Силы от давления газов зависят
от характера протекания рабочего цикла, силы инерции определяются величиной
масс движущихся деталей, размером хода поршня и частотой вращения.
Нахождение этих сил необходимо для расчёта деталей двигателя на
прочность, выявления нагрузок на подшипники, определения степени
неравномерности вращения коленвала, расчёт коленвала на крутильные колебания.
.1 Приведение масс деталей и звеньев КШМ
Действительные массы движущихся звеньев КШМ для упрощения расчётов
заменяют приведёнными массами, сосредоточенными в характерных точках КШМ и
динамически или, в крайнем случае, статически эквивалентными реальным
распределённым массам.
За характерные точки КШМ принимают центры поршневого пальца, шатунной
шейки, точку на оси коленвала. В крейцкопфных дизелях вместо центра поршневого
пальца за характерную точку принимают центр поперечины крейцкопфа.
К поступательно-движущимся массам (ПДМ) Ms в тронковых дизелях относят массу
поршня с кольцами, поршневого пальца, поршневых колец и часть массы шатуна. В
крейцкопфных двигателях в приведённую массу входит масса поршня с кольцами,
штока, крейцкопфа и часть массы шатуна.
Приведённая ПДМ MS считается сосредоточенной либо в центре поршневого пальца (тронковые
ДВС), либо в центре поперечины крейцкопфа (крейцкопфные двигатели).
Неуравновешенная вращающаяся масса (НВМ) MR складывается из оставшейся части
массы шатуна и части массы кривошипа, приведённой к оси шатунной шейки.
Распределённую массу кривошипа условно заменяют двумя массами. Одной
массой, расположенной в центре шатунной шейки, другой - находящейся на оси
коленвала.
Уравновешенная вращающаяся масс кривошипа не вызывает сил инерции, так
как центр её масс находится на оси вращения коленвала. Однако момент инерции
этой массы входит как составляющая часть в приведённый момент инерции всего
КШМ.
При наличии противовеса его распределённая масса заменяется приведённой
сосредоточенной массой, расположенной на расстоянии радиуса кривошипа R от оси вращения коленвала.
Замена распределённых масс шатуна, колена (кривошипа) и противовеса
сосредоточенными массами называется приведением масс.
Приведением масс шатуна
Динамическая модель шатуна представляет собой отрезок прямой (невесомый
жёсткий стержень), имеющий длину, равную длине шатуна L с двумя массами, сосредоточенными по концам. На оси
поршневого пальца располагается масса поступательно-движущейся части шатуна MшS, на оси шатунной шейки - масса вращающейся части
шатуна MшR.

Рис. 8.1 - Шатун и его динамическая модель
Mш - фактическая масса шатуна; ц.м. -
центр масс шатуна; L - длина шатуна; LS и LR - расстояния от концов шатуна до его
центра масс; MшS - масса поступательно-движущейся части шатуна; MшR - масса вращающейся части шатуна
Для полной динамической эквивалентности реального шатуна и его
динамической модели должны выполняться три условия
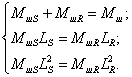 (8.1)
(8.1)
Для
удовлетворения всех трёх условий следовало бы составить динамическую модель
шатуна с тремя массами.
Для
упрощения расчётов сохраняют двухмассовую модель, ограничиваясь условиями
только статической эквивалентности
 (8.2)
(8.2)
В
этом случае
 ,
,  . (8.3)
. (8.3)
Как
видно из полученных формул (8.3) для расчёта MшS
и MшR необходимо знать LS и LR, т.е. расположение центра масс шатуна. Эти величины
можно определить расчётным (графо-аналитическим) методом или экспериментально
(методом качания или взвешивания). Можно воспользоваться эмпирической формулой
проф. В.П.Терских
 ,
,
где
n - частота вращения двигателя, мин-1.
Также
ориентировочно можно принимать
MшS ≈ 0,4∙Mш; MшR ≈ 0,6∙Mш.
Приведение
масс кривошипа
Динамическую
модель кривошипа можно представить в виде радиуса (невесомый жёсткий стержень)
с двумя массами по концам Мк и Мк0.
Условие
статической эквивалентности
 (8.4)
(8.4)
где
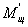 - масса щеки;
- масса щеки;  - часть массы щеки, приведённая к оси шатунной шейки;
- часть массы щеки, приведённая к оси шатунной шейки; 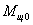 - часть массы щеки, приведённая к оси колевала; с - расстояние
от центра масс щеки до оси вращения коленвала; R - радиус кривошипа. Из формул (8.4) получаем
- часть массы щеки, приведённая к оси колевала; с - расстояние
от центра масс щеки до оси вращения коленвала; R - радиус кривошипа. Из формул (8.4) получаем
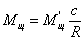 ; (8.5)
; (8.5)
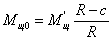 . (8.6)
. (8.6)
В
результате приведённые массы кривошипа примут вид
 ;
;  , (8.7)
, (8.7)
где
 - масса шатунной шейки;
- масса шатунной шейки;
 - масса
рамовой шейки.
- масса
рамовой шейки.

Рис.
8.2 - Кривошип и его динамическая модель
Приведение
масс противовеса
Динамическая
модель противовеса аналогична модели кривошипа.

Рис.8.3
- Противовес и его динамическая модель
Приведённая
неуравновешенная масса противовеса
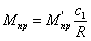 , (8.8)
, (8.8)
где - фактическая масса противовеса;
- фактическая масса противовеса;
c1 - расстояние от центра масс противовеса до оси
вращения коленвала;
R - радиус
кривошипа.
Приведённая
масса противовеса  считается расположенной в точке на расстоянии R в
сторону центра масс относительно оси коленвала.
считается расположенной в точке на расстоянии R в
сторону центра масс относительно оси коленвала.
Динамическая
модель КШМ
Динамическую
модель КШМ в целом составляют на основе моделей его звеньев, при этом массы
сосредоточенные в одноимённых точках суммируют.
.
Приведённая поступательно-движущаяся масса, сосредоточенная в центре поршневого
пальца или поперечины крейцкопфа
MS = MП + МШТ + МКР + МШS, (8.9)
где
MП - масса
комплекта поршня;
МШТ
- масса штока;
МКР
- масса крейцкопфа;
МШS
- ПДМ части шатуна.
2. Приведённая неуравновешенная вращающаяся масса, сосредоточенная в
центре шатунной шейки
MR = МК + МШR, (8.10)
где MК - неуравновешенная вращающаяся часть массы колена;
МШR
- НВМ части шатуна;
Обычно для удобства расчётов абсолютные массы заменяют относительными
 ;
; 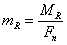 , (8.11)
, (8.11)
где
Fп -
площадь поршня.
Дело
в том, что силы инерции суммируются с давлением газов и в случае использования
масс в относительной форме получается одинаковая размерность. Кроме того, для
однотипных дизелей значения mS и mR изменяются в узких пределах и их значения приводятся
в специальной технической литературе.
В
случае необходимости учёта сил тяжести деталей, они определяются по формулам
gR = mRg;
gS = mSg,
где
g - ускорение свободного падения, g =
9,81 м/с2.
Лекция 13.
8.2. Силы инерции одного
цилиндра
При движении КШМ возникают силы инерции от поступательно-движущихся и
вращающихся масс КШМ.
Силы инерции ПДМ (отнесённые к FП)
судовой двигатель термодинамический поршневый
qS = -mSJ. (8.12)
Знак "-" потому что направление сил инерции обычно обратно
направлено вектору ускорения.
Зная,
что  , получим
, получим
 . (8.13)
. (8.13)
В
ВМТ (α
= 0)  .
.
В
НМТ (α
= 180)  .
.
Обозначим
амплитуды сил инерции первого и второго порядков
PI = - mSRω2 и PII = - mSλ Rω2
Получим
qS = PIcosα+ PIIcos2α, (8.14)
где
PIcosα - сила инерции первого порядка ПДМ;
PIIcos2α - сила инерции второго порядка ПДМ.
Сила
инерции qS приложена к поршневому пальцу и направлена по оси
рабочего цилиндра, её величина и знак зависят от α.
Силу
инерции первого порядка ПДМ PIcosα можно представить как проекцию на ось цилиндра
некоторого вектора  , направленного по кривошипу от центра коленвала и
действующего так, будто он представляет собой центробежную силу инерции массы mS, расположенной в центре шатунной шейки.
, направленного по кривошипу от центра коленвала и
действующего так, будто он представляет собой центробежную силу инерции массы mS, расположенной в центре шатунной шейки.

Рис.
8.4 - Векторное изображение сил инерции ПДМ первого порядка
Проекция
вектора  на горизонтальную ось представляет фиктивную величину
PIsinα, так как в действительности такой величины не
существует. В соответствии с этим и сам вектор
на горизонтальную ось представляет фиктивную величину
PIsinα, так как в действительности такой величины не
существует. В соответствии с этим и сам вектор  , имеющий
сходство с центробежной силой также не существует и поэтому носит название
фиктивной силы инерции первого порядка.
, имеющий
сходство с центробежной силой также не существует и поэтому носит название
фиктивной силы инерции первого порядка.
Введение
в рассмотрение фиктивных сил инерции, имеющих только одну реальную вертикальную
проекцию, является условным приемом, позволяющим упростить расчёты ПДМ.
Вектор
фиктивной силы инерции первого порядка можно представить как сумму двух
составляющих: действительной силы PIcosα, направленной по оси цилиндра и фиктивной силы PIsinα, направленной перпендикулярно к ней.
Силу
инерции второго порядка PIIcos2α можно аналогично представить как проекцию на ось цилиндра вектора PII фиктивной силы инерции ПДМ второго порядка,
составляющего с осью цилиндра угол 2α и вращающегося с угловой скоростью 2ω.

Рис.
8.5 - Векторное изображение сил инерции ПДМ второго порядка
Фиктивную
силу инерции второго порядка ПДМ можно также представить как сумму двух
составляющих из которых одна - действительная PIIcos2α, направленная по оси цилиндра, а вторая фиктивная PIIsin2α, направленная перпендикулярно к первой.
Силы
инерции НВМ (отнесённые к FП)
 . (8.15)
. (8.15)
Сила
qR приложен к оси шатунной шейки и направлена вдоль
кривошипа в сторону от оси коленвала. Вектор силы инерции 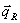 вращается вместе с коленвалом в ту же сторону и с той
же частотой вращения.
вращается вместе с коленвалом в ту же сторону и с той
же частотой вращения.
Если
переместить 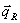 так, чтобы начало совпало с осью коленвала, то его
можно разложить на две составляющие
так, чтобы начало совпало с осью коленвала, то его
можно разложить на две составляющие
вертикальную
 ;
;
горизонтальную
 .
.

Рис.
8.6 - Силы инерции неуравновешенных вращающихся масс
Суммарные
силы инерции
Суммарная
сила инерции ПДМ и НВМ в вертикальной плоскости
 . (8.16)
. (8.16)
Если
рассматривать отдельно силы инерции первого и второго порядков, то в
вертикальной плоскости суммарная сила инерции первого порядка
 . (8.17)
. (8.17)
Сила
инерции второго порядка в вертикальной плоскости
 . (8.18)
. (8.18)
Вертикальная
составляющая сил инерции первого порядка стремится приподнять или прижать
двигатель к фундаменту один раз за оборот, а сила инерции второго порядка - два
раза за оборот.
Сила
инерции первого порядка в горизонтальной плоскости  стремится смещать двигатель справа налево и обратно
один раз в течение одного оборота.
стремится смещать двигатель справа налево и обратно
один раз в течение одного оборота.
Совместное
действие силы от давления газов на поршень и сил инерции КШМ
Возникающее
во время работы двигателя давление газов действует как на поршень, так и на
крышку цилиндра. Закон изменения P = f(α) определяется по развёрнутой индикаторной диаграмме, полученной
экспериментальными или расчётным путём.
)
Считая, что на обратную сторону поршня действует атмосферное давление, найдём
избыточное давление газов на поршень
Pг = P - P0, (8.19)
где
Р - текущее абсолютное давление газов в цилиндре, взятое из индикаторной
диаграммы;
Р0
- давление окружающей среды.

Рис.8.7
- Силы, действующие в КШМ: а - без учёта сил инерции; б - с учётом сил инерции
)
С учётом сил инерции вертикальная сила, действующая на центр поршневого пальца
определится как движущая сила
Pд = Рг + qs.
(8.20)
3)
Разложим движущую силу на две составляющие - нормальную силу Pн и силу действующую по шатуну Pш:
Pн = Рдtgβ; (8.21)
 . (8.22)
. (8.22)
Нормальная
сила Pн
прижимает поршень к втулке цилиндра или ползун крейцкопфа к его направляющей.
Сила,
действующая по шатуну Pш сжимает
или растягивает шатун. Она действует по оси шатуна.
)
Перенесём силу Pш по линии
действия в центр шатунной шейки и разложим на две составляющие - тангенциальную
силу t, направленную касательно к окружности описываемую
радиусом R
 (8.23)
(8.23)
и
радиальную силу z, направленную по радиусу кривошипа
 . (8.24)
. (8.24)
К
центру шатунной шейки кроме силы Pш будет
приложена сила инерции qR.
Тогда
суммарная радиальная сила
 . (8.25)
. (8.25)
Перенесём
радиальную силу z по линии её действия в центр рамовой шейки и приложи
в этой же точке две взаимно уравновешивающиеся силы 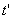 и
и 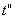 ,
параллельные и равные тангенциальной силе t. Пара сил t и
,
параллельные и равные тангенциальной силе t. Пара сил t и 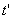 приводит во вращение коленчатый вал. Момент этой пары
сил называется крутящим моментом. Абсолютное значение крутящего момента
приводит во вращение коленчатый вал. Момент этой пары
сил называется крутящим моментом. Абсолютное значение крутящего момента
Mкр = tFпR. (8.26)
Сумма
сил 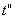 и z, приложенных к оси коленвала даёт результирующую силу
и z, приложенных к оси коленвала даёт результирующую силу
 , нагружающую рамовые подшипники коленвала. Разложим
силу
, нагружающую рамовые подшипники коленвала. Разложим
силу  на две составляющие - вертикальную
на две составляющие - вертикальную 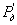 и горизонтальную
и горизонтальную  .
Вертикальная сила совместно с силой давления газов на крышку цилиндра
растягивает детали остова и на фундамент не передаётся. Противоположно
направленные силы
.
Вертикальная сила совместно с силой давления газов на крышку цилиндра
растягивает детали остова и на фундамент не передаётся. Противоположно
направленные силы  и
и  образуют
пару сил с плечом H. Эта пара сил стремится повернуть остов вокруг
горизонтальной оси. Момент данной пары сил называется опрокидывающим или
обратным крутящим моментом Mопр.
образуют
пару сил с плечом H. Эта пара сил стремится повернуть остов вокруг
горизонтальной оси. Момент данной пары сил называется опрокидывающим или
обратным крутящим моментом Mопр.
Опрокидывающий
момент передаётся через остов двигателя на опоры фундаментной рамы, на корпус
судового фундамента. Следовательно, Mопр должен быть уравновешен внешним моментом реакций rф судового фундамента.
Порядок
определения сил, действующих в КШМ
Расчёт
этих сил ведётся в табличной форме. Шаг расчёта следует выбирать с
использованием следующих формул:
 - для
двухтактных;
- для
двухтактных; 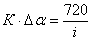 - для четырёхтактных,
- для четырёхтактных,
где K - целое число: i - число цилиндров.
|
α°
|
Рд
|
tgβ
|
Pн = Pдtgβ
|
cosβ
|
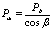   
|
|
|
|
|
0 5 10
|
|
|
|
|
|
|
|
|
Движущая сила, отнесённая к площади поршня
Pд = Рг + qs + gs +Pтр. (8.20)
Силой трения Pтр пренебрегаем.
Если gs ≤ 1,5 % Pz, то также пренебрегаем.
Значения Pг определяем, используя давление
индикаторной диаграммы Р.
Pг
= Р - Р0.
(8.21)
Силу инерции определяем аналитически
 . (8.22)
. (8.22)
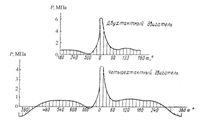
Кривая
движущих сил Pд является
исходной для построения диаграмм сил Pн = f(α), Pш = f(α), t = f(α), z = f(α).
Для
проверки правильности построения тангенциальной диаграммы следует определить
среднюю по углу поворота кривошипа тангенциальную сил tср.
Из
диаграммы тангенциальной силы видно, что tср определится как отношение площади между линией t = f(α) и осью абсцисс к длине диаграммы.
Площадь
определяется планиметром либо путём интегрирования по методу трапеций
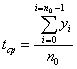 ,
,
где
n0 - число
участков, на которые разбивается искомая площадь;
yi -
ординаты кривой на границах участков;
Определив
tcp в см, используя масштаб по оси ординат перевести её в
МПа.
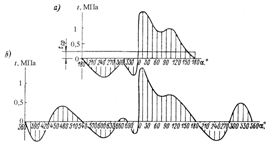
Рис.
8.9 - Диаграммы тангенциальных сил одного цилиндра: а - двухтактного двигателя;
б - четырёхтактного двигателя
Индикаторную
работу за цикл можно выразить через среднее индикаторное давление Pi и среднее значение тангенциальной силы tcp
следующим образом
Pi Fп2Rz = tcp FпR2π,
где
коэффициент тактности z = 1 для двухтактных ДВС и z = 0,5 для
четырёхтактных ДВС.
Тогда
для
двухтактных ДВС
 ;
;
-
для четырёхтактных ДВС
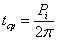 .
.
Допустимое
расхождение не должно превышать 5%.
Лекция 14.
8.3. Определение
набегающих тангенциальных сил на шейках коленвала многоцилиндрового двигателя
Определим законы изменения крутящих моментов на коленчатом валу многоцилиндрового
двигателя
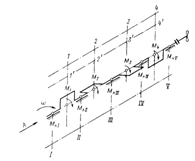
Рис.
8.10 - Схема коленчатого вала двухтактного четырёхцилиндрового двигателя: 1, 2,
3, 4 - номера цилиндров;  - номера шатунных шеек; I, II, II,I V - номера рамовых шеек; M1, М2, М3, М4 -
крутящие моменты, передаваемые на коленвал от соответствующих цилиндров; MШ1, МШ2, МШ3, МШ4 -
крутящие моменты, скручивающие шатунные шейки; МPI, МPII, МPIII, МPIV, МPV,- моменты, скручивающие соответствующие рамовые
шейки.
- номера шатунных шеек; I, II, II,I V - номера рамовых шеек; M1, М2, М3, М4 -
крутящие моменты, передаваемые на коленвал от соответствующих цилиндров; MШ1, МШ2, МШ3, МШ4 -
крутящие моменты, скручивающие шатунные шейки; МPI, МPII, МPIII, МPIV, МPV,- моменты, скручивающие соответствующие рамовые
шейки.
Моменты,
скручивающие рамовые шейки называются набегающими крутящими моментами на
рамовых шейках. Очевидно, что набегающий крутящий момент на последней рамовой
шейке представляет собой суммарный крутящий момент всего двигателя.
Следует
отличать MШ1 от M1, MШ2 от M2, MШ3 от M3, MШ4 от M4. Действительно, при положении кривошипа четвёртого
цилиндра в НМТ M4 = 0, а
четвёртая шатунная шейка скручивается почти полным крутящим моментом двигателя
и, следовательно, МШ4 ≠ 0.
Крутящие
моменты MШ1, МШ2,
МШ3, МШ4 называют набегающими крутящими моментами на
шатунных шейках коленвала.
При
исследовании динамики двигателя первое колен всегда располагают в положении
ВМТ.
Схема
коленвала задаётся диаграммой заклинки кривошипов, которая по существу
представляет вид по стрелке А. Применяется, как правило, равномерная заклинка.

Рис.
8.11 - Схема диаграммы заклинки коленвала. Последовательность вспышек 1-3-4-2
-
для двухтактных ДВС 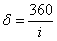 ;
;
для
четырёхтактных ДВС  .
.
Для
двухтактных ДВС последовательность вспышек (порядок работы цилиндров) полностью
определяется диаграммой заклинки кривошипов и направлением вращения. Для
рассматриваемого двигателя этот порядок 1-2-4-3.
Зная
порядок работы цилиндров и подсчитав δ нетрудно представить диаграмму заклинки.
Определим
скручивающие моменты на рамовых и шатунных шейках коленвала.
На
рис. 8.10 рамовая шейка I является свободной, и если пренебречь моментом сил
трения, то
МPI
= 0.
Производим
суммирование моментов, начиная со свободного конца коленвала
МPI = 0; МPII =
М1; МPIII,= М1 + М2;
МPIV = М1 + М2 + М3;
МPV = М1 + М2 + М3 +
М4.
Эти
уравнения можно записать в другой форме
МPI = 0; МPII =
МPI + М1;
МPIII,= МPII +
М2; МPIV = МPIII
+ М3; МPV = МV
+ М4.
В
общем виде
МP(i+1),= МPi + Мi.
Крутящий
момент от данного КШМ
Мi=
tiFпR.
Следовательно,
значение тангенциальной силы
 .
.
Введём
понятие условных тангенциальных сил на рамовых и шатунных шейках коленвала
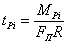 ;
;
 .
.
Тогда
tP(i+1)= tPi + ti; 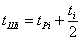 .
.
Если
имеется диаграмма тангенциальных сил одного цилиндра, то определение ординаты в
любом цилиндре начинается с угла
для
двухтактных ДВС ξ
= 360 -γз;
для
четырехтактных ДВС ξ
= 720 -γз.
Рассмотрим
порядок определения набегающих тангенциальных сил на рамовых и шатунных шейках.
Имеем
шестицилиндровый четырёхтактный ДВС с порядком вспышек 1-3-5-2-4-6. Угол
заклинки  °. Определяем начальные фазы цилиндров ξ1 = -360°; ξ2 = -360 + 360 = 0°; ξ3 = -360 + 120 = -240°; ξ4 = -360 + 480 = 120°; ξ5 = -360 + 240 = -120°; ξ6 = -360 +
600 = 240°.
°. Определяем начальные фазы цилиндров ξ1 = -360°; ξ2 = -360 + 360 = 0°; ξ3 = -360 + 120 = -240°; ξ4 = -360 + 480 = 120°; ξ5 = -360 + 240 = -120°; ξ6 = -360 +
600 = 240°.
Исходным
материалом служит диаграмм тангенциальной силы первого КШМ. Расчёт ведём в
табличной форме.
Таблица 8.1 - Расчёт тангенциальных сил на рамовых шейках
|
φ
|
tр2 = t1
|
t2 ξ = 0
|
tр3 = tр2+t2
|
t3 ξ = -240
|
tр4 = tр3+t3
|
t4 ξ = 120
|
tр5= tр4+t4
|
t5 ξ = -120
|
tр6= tр5+t5
|
t6 ξ = 240
|
tр7= tр6+t6
|
|
˚ ПКВ
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
|
-360 -330 -300 -270 -240
-210 -180 -150 -120 -90 -60 -30 0 30 60 90 120 150 180 210 240 270 300 330
|
0,0000 -0,5467 -0,1816
0,4969 0,6415 0,3551 0,0000 -0,3618 -0,7089 -0,7872 -0,7233 -1,6603 0,0000
5,3779 2,9277 1,9755 1,3199 0,6199 0,0000 -0,3573 -0,6459 -0,5029 0,1757
0,5430
|
0,0000 5,3779 2,9277 1,9755
1,3199 0,6199 -0,0000 -0,3573 -0,6459 -0,5029 0,1757 0,5430 0,0000
-0,5467 -0,1816 0,4969 0,6415 0,3551 0,0000 -0,3618 -0,7089 -0,7872 -0,7233
-1,6603
|
0,0000 4,8312 2,7460 2,4724
1,9613 0,9750 0,0000 -0,7991 -1,3547 -1,2901 -0,5476 -1,1172 0,0000 4,8312
2,7460 2,4724 1,9613 0,9750 0,0000 -0,7191 -1,3547 -1,2901 -0,5476 -1.1172
|
0,6415 0,3551 0,0000 -0,3618 -0,7089 -0,7872 -0,7233
-1,6603 0,0000 5,3779 2,9277 1,9755 1,3199 0,6199 0,0000 -0,3573
-0,6459 -0,5029 0,1757 0,5430 0,0000 -0,5467 -0,1816 0,4969
|
0,6415 5,1863 2,7460
2,1106 1,2524 0,1878 -0,7233
-2,4594 -1,3547 4,0878 2,3801
0,8583 1,3199 5,4511 2,7460 2,1151 1,3154 0,4721 0,1757 -0,1761 -1,3547
-1,8368 -0,7292 -0,6203
|
1,3199 0,6199 0,0000
-0,3573 -0,6459 -0,5029 0,1757 0,5430 0,0000 -0,5467 -0,1816 0,4969 0,6415
0,3551 0,0000 -0,3618 -0,7089 -0,7872 -0,7233 -1,6603 0,0000 5,3779 2,9277
1,9755
|
1,9614 5,8062 2,7460 1,7533
0,6065 -0,3151 -0,5476 -1,9164 -1,3547 3,5411 2,1985 1,3502 1,9614 5,8062
2,7460 1,7533 0,6065 -0,3151 -0,5476 -1,8364 -1,3547 3,5411 2,1985 1,3552
|
-0,7089 -0,7872 -0,7233
-1,6603 0,0000 5,3779 2,9277 1,9755 1,3199 0,6199 0,0000 -0,3573 -0,6459
-0,5029 0,1757 0,5430 0,0000 -0,5467 -0,1816 0,4969 0,6415 0,3551 0,0000
-0,3618
|
1,2525 5,0190 2,0227 0,0930
0,6065 5,0628 2,3801 0,0591 -0,0348 4,1610 2,1985 0,9929 1,3155 5,3033 2,9217
2,2963 0,6065 -0,8618 -0,7192 -1,3395 -0,7132 3,8962 2,1985 0,9934
|
-0,6459 -0,5029 0,1757
0,5430 0,0000 -0,5467 -0,1816 0,4969 0,6415 0,3551 0,0000 -0,3618 -0,7089
-0,7872 -0,7233 -1,6603 0,0000 5,3779 2,9277 1,9755 1,3199 0,6199 0,0000
-0,3573
|
0,6066 4,5161 2,1984 0,6361
0,6065 4,5161 2,1984 0,6361 0,6065 4,5161 2,1984 0,6361 0,6065 4,5161 2,1984
0,6361 0,6065 4,5161 2,1984 0,6361 0,6065 4,5161 2,1984 0,6361
|
Таблица служат исходным материалом при расчёте на прочность рамовых шеек
коленчатого вала многоцилиндрового двигателя
Таблица 8.2 - Расчёт тангенциальных сил на шатунных шейках
|
φ
|
tш1
|
tр2
|
t2 ξ = 0
|
tш2
|
t3 ξ = -240
|
tш3
|
t4 ξ = 120
|
tш4
|
t5 ξ = -120
|
tш5
|
t5 ξ = 240
|
tш6
|
|
˚ ПКВ
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
МПа
|
|
-360 -330 -300 -270 -240
-210 -180 -150 -120 -90 -60 -30 0 30 60 90 120 150 180 210 240 270 300 330
|
0,0000 -0,2734 -0,0908
0,2485 0,3207 0,1775 0,0000 -0,1809 -0,3544 -0,3936 -0,3616 -0,8301 0,0000
2,6890 1,4638 0,9878 0,6599 0,3099 0,0000 -0,1787 -0,3229 -0,2514 0,0879
0,2715
|
0,0000 -0,5467 -0,1816
0,4969 0,6415 0,3551 0,0000 -0,3618 -0,7089 -0,7872 -0,7233 -1,6603 0,0000
5,3779 2,9277 1,9755 1,3199 0,6199 0,0000 -0,3573 -0,6459 -0,5029 0,1757
0,5430
|
0,0000 2,6890 1,4638 0,9878
0,6599 0,3099 0,0000 -0,1787 -0,3229 -0,2514 0,0879 0,2715 0,0000 -0,2734
-0,0908 0,2485 0,3207 0,1775 0,0000 -0,1809 -0,3544 -0,3936 -0,3616 -0,8301
|
0,0000 2,1422 1,2822 1,4847
1,3014 0,6650 0,0000 -0,5404 -1,0318 -1,0386 -0,6354 -1,3888 0,0000 5,1046
2,8368 2,2240 1,6406 0,7974 0,0000 -0,5382 -1,0003 -0,8965 -0,1859 -0,2871
|
0,3207 0,1775 0,0000
-0,1809 -0,3544 -0,3936 -0,3616 -0,8301 0,0000 2,6890 1,4638 0,9878 0,6599
0,3099 0,0000 -0,1787 -0,3229 -0,2514 0,0879 0,2715 0,0000 -0,2734 -0,0908
0,2485
|
0,3207 2,3197 1,2822 1,3038
0,9470 0,2714 0,3616 -1,3705 -1,0318 1,6504 0,8284 -0,4010 0,6599 5,4145
2,8368 2,0453 1,3177 0,5460 0,0879 -0,2667 -1,0003 -1,1699 -0,2767 -0,0386
|
0,6599 0,3099 0,0000
-0,1787 -0,3229 -0,2514 0,0879 0,2715 0,0000 -0,2734 -0,0908 0,2485 0,3207
0,1775 0,0000 -0,1809 -0,3544 -0,3936 -0,3616 -0,8301 0,0000 2,6890 1,4638
0,9878
|
0,9806 2,6296 1,2822 1,1251
0,6241 0,0200 0,4495 -1,0990 -1,0318 1,3770 0,7376 -0,1525 0,9806 5,5920
2,8368 1,8644 0,9633 0,1524 -0,2737 -1,0928 -1,0003 0,4273 1,6144 0,9492
|
-0,3544 -0,3936 -0,3616
-0,8301 0,0000 2,6890 1,4638 0,9878 0,6599 0,3099 0,0000 -0,1787 -0,3229
-0,2514 0,0879 0,2715 0,0000 -0,2734 -0,0908 0,2485 0,3207 0,1775 0,0000
-0,1809
|
0,6262 2,2360 0,9206 0,2950
0,6241 2,7090 1,9133 -0,1112 -0,4831 1,6869 0,7376 0,3312 0,6577 5,3406
2,9247 2,1159 0,9633 -0,1210 -0,3645 -0,8443 -0,6796 0,6048 1,6144 0,7683
|
-0,3229 -0,2514 0,0879
0,2715 0,0000 -0,2734 -0,0908 0,2485 0,3207 0,1775 0,0000 -0,1809 -0,3544
-0,3936 -0,3616 -0,8301 0,0000 2,6890 1,4638 0,9878 0,6599 0,3099 0,0000
-0,1787
|
0,3033 1,9846 1,0085 0,5665
0,6241 2,4356 1,8225 0,1373 -0,1624 1,8644 0,7376 0,1503 0,3033 4,9470 2,5631
1,2858 0,9633 2,5680 1,0993 0,1435 -0,0197 0,9147 1,6144 0,5896
|
Таблица служат исходным материалом при расчёте на прочность шатунных шеек
коленчатого вала многоцилиндрового двигателя
Лекция 15. 8.4. Внешняя неуравновешенность и уравновешивание двигателей
Определение неуравновешенных сил и моментов от системы сил инерции
поступательно-движущихся масс. Под
внешней неуравновешенностью двигателя понимается наличие в нем периодических
сил или моментов сил, передающихся на фундамент. Эти силы вызывают вибрацию. В
СЭУ с ДВС вследствие неуравновешенности возникают вибрация корпуса судна или
отдельных его участков. Причиной внешней неуравновешенности
являются силы инерции приведенных ПДМ и неуравновешенных вращающихся масс КШМ
всех цилиндров, а также опрокидывающие моменты. Силы инерции неуравновешенных вращающихся масс одного цилиндра при
установившемся режиме работы двигателя
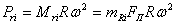
где
i - номер цилиндра.
Вертикальная
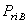 и горизонтальная
и горизонтальная  проекции
этой силы определяются в зависимости от положения кривошипа αi
проекции
этой силы определяются в зависимости от положения кривошипа αi

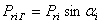
Проекция
силы инерции ПДМ на вертикальную ось найдем по приближенной формуле
Pji=MSiRω2(cosαi + λ
cos2αi)= PI i cosαi + PII i λ
cos2αi,
где
PI i В = PI i
cosαi PII i В = PII i
cosαi
- силы инерции ПДМ первого и второго порядков.
Рассмотрим систему сил инерции многоцилиндрового двигателя на примере
четырехцилиндрового двухтактного ДВС. На
рисунке приняты следующие обозначения: Pr - сила инерции неуравновешенных
вращающихся масс КШМ; PI cos α и PII cos α - сила инерции ПДМ КШМ первого и
второго порядков соответственно. В рассматриваемом примере система сил инерции состоит 12
сил: четыре силы инерции вращающихся масс Pr1, Pr2, Pr3, Pr4 ; четыре силы инерции ПДМ первого
порядка PI cos α1, PI cos α2, PI cos α3, PI cos α4 и четыре силы инерции ПДМ второго
порядка PII cos 2α1, PII cos 2α2, PII cos 2α3, PII cos 2α4 . Кривошипно-шатунный механизм в многоцилиндровых двигателях
обычно выполняют одинаковыми, однородными; поэтому, как правило, для
многоцилиндровых двигателей можно принять
Pr 1= Pr 2 = Pr 3 = Pr
4= Pr
PI 1= PI 2 = PI 3 = PI
4= PI
PII 1= PII 2 = PII 3 = PI
I4= PII

Рис. 8.12 - Системы сил инерции: а - одного цилиндра; б - 4-х
цилиндрового 2-тактного ДВС.
Как следует из рисунка, система сил инерции вращающихся масс представляет
пространственную систему сил, а система сил инерции ПДМ первого и второго
порядков - плоскую систему сил, лежащих в вертикальной плоскости, проходящей
через ось вращения коленчатого вала.
Двигатель считается полностью уравновешенным, если при любом положении
коленчатого вала система сил находится в равновесии. Приведем систему сил к точке ОС, т.е. в середине
оси коленчатого вала. Как известно, любую систему сил можно привести к данной
точке, заменив ее главным вектором всей системы сил, приложенным в точке ОС
приведения и равным геометрической сумме всех сил системы, и главным моментом,
равным геометрической сумме векторов моментов всех сил относительно точки
приведения. Для удобства исследования обычно
отдельно рассматривают:
·
систему сил
инерции вращающихся масс;
·
систему сил
инерции ПДМ первого порядка;
·
систему сил
инерции ПДМ второго порядка.

Рис. 8.13 - Схема систем сил инерции
Силы инерции вращающихся масс Pr i перенесены по линии их действия в точки Оi на оси коленчатого вала и каждая из
сил разложена на две составляющие: вертикальную PriВ и горизонтальную PriГ . Величины составляющих находят по уравнениям
PriВ = Pr icos αi ; PriГ = Pr i sin αi
Плечи сил разных КШМ относительно точки О обозначены
h1 = О1ОС; h2 = О2ОС; h3 = О3ОС; h4 = О4ОС;
Так как моменты сил, приложенных по разные стороны от точки, имеют разные
знаки, будем приписывать плечам сил, расположенным в сторону носовой части
двигателя (h1 и h2) знак плюс, расположенным в сторону
кормовой части двигателя (h1 и h2) - знак минус.
Для того чтобы общая система сил инерции находилась в равновесии при
любом положении коленвала, необходимо обеспечить условия равновесия каждой из
трех систем сил. Условием такого равновесия будет равенство нулю главных
векторов и главных моментов сил инерции у каждой из систем относительно точки ОС.
При исследовании уравновешенности систем сил инерции ПДМ первого и
второго порядков удобнее рассматривать равновесие систем фиктивных сил тех же
порядков. Из равенства нулю, например, главного вектора и главного момента
системы фиктивных сил инерции ПДМ первого порядка, как следствие, вытекает
равенство нулю главного вектора и главного момента действительной системы сил
инерции ПДМ первого порядка. Условия равновесия запишем в следующем виде:


Равенства 8.5, 8.7, 8.9 и 8.11 выражают сумму действительных
составляющих, а равенства 8.6, 8.8, 8.10 и 8.12 - сумму фиктивных составляющих
главного вектора и главного момента сил инерции ПДМ первого и второго порядков.
Уравнения 8.1 - 8.12 являются аналитическим условиями уравновешенности
многоцилиндрового двигателя, записанными в скалярной форме.
При симметричной конструкции остова и коленчатого вала двигателя
положение точки ОС можно принимать в середине коленчатого вала. В
случае несимметричной конструкции остова координату центра масс можно найти из
уравнения статических моментов масс отдельных цилиндров относительно какой-либо
вертикальной оси, например оси первого цилиндра.
Расположение колен коленчатого вала характеризуется диаграммой заклинки
кривошипов, которая иначе называется фазовой диаграммой первого порядка и
представляет собой вид на коленчатый вал со стороны его свободного конца при
положении кривошипа первого цилиндра в ВМТ.

Рис. 8.14 - Схема расположения кривошипов коленчатого вала.

Рис. 8.15 - К определению αi для произвольного положения
коленчатого вала
Очевидно, что в произвольном положении коленчатого вала, когда угол
кривошипа первого цилиндра от своей ВМТ равен α1 , для угла αi справедливо следующее равенство
αi = α1 + βi .
В самом общем случае неуравновешенности системы сил инерции ни одно из
уравнений 0-10 не будет удовлетворяться, и мы получим двенадцать уравнений,
характеризующих неуравновешенные силы и моменты:





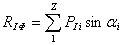
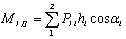

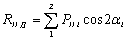



где Rr В и Rr Г - вертикальная и горизонтальная
проекции неуравновешенной силы инерции
(главного вектора) системы сил Pr i ;
Мr Г и Мr В - моменты системы сил Pr i относительно горизонтальной и
вертикальной осей, проходящих через точку ОС (проекция главного момента системы сил Pr i относительно точки ОС соответственно на горизонтальную и вертикальную ось);
R1
Д и R1 Ф - действительная и фиктивная
составляющие главного вектора системы сил инерции ПДМ
первого порядка:
М1 Д и М1 Ф - действительная и фиктивная
составляющие главного момента системы сил инерции ПДМ
первого порядка;
R1I Д и R1I Ф - действительная и фиктивная составляющие главного вектора системы сил инерции ПДМ второго порядка:
М1I Д и М1I Ф - действительная и фиктивная
составляющие главного момента системы сил инерции ПДМ
второго порядка;
Главный
вектор неуравновешенных вращающихся масс, равный геометрической сумме векторов  ,
,  ,
, 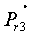 и
и 

будет
вращаться вместе с коленчатым валом с угловой скоростью ω. При любом положении коленвала проекциями этого вектора
на вертикальную и горизонтальную ось будут RrВ и RrГ. Следовательно,
численное значение главного вектора неуравновешенных вращающихся масс можно
определить из выражения

Если
определены проекции главного вектора Rr при положении
коленчатого вала, кргда его первый кривошип находится в своей ВМТ, то угол
между главным вектором и вертикальной осью φr

Справедливо
и обратное: для произвольного положения коленчатого вала, определяемого углом αi,
проекции главного вектора на вертикальную и горизонтальную оси можно найти по
уравнениям
RrВ
= Rr cos (α1 +φr) RrГ = Rr sin (α1 +φr).
Несколько
иначе обстоит дело с неуравновешенными моментами от сил инерции вращающихся
масс. Как известно, момент P·a сил  ,
действующих в плоскости ЕЕ, можно представить вектором
,
действующих в плоскости ЕЕ, можно представить вектором  , перпендикулярным к плоскости ЕЕ. Длина вектора
, перпендикулярным к плоскости ЕЕ. Длина вектора  соответствует в выбранном масштабе величине момента.
Вектор
соответствует в выбранном масштабе величине момента.
Вектор  направлен в ту сторону, откуда пара сил
направлен в ту сторону, откуда пара сил  представляется действующей по часовой стрелке. В
соответствии с этим вектор момента от силы PriВ направлен горизонтально, а вектор момента от силы PriГ -
вертикально.
представляется действующей по часовой стрелке. В
соответствии с этим вектор момента от силы PriВ направлен горизонтально, а вектор момента от силы PriГ -
вертикально.

Рис.
8.16 - Вектор изображения момента пары сил

Рис.
8.17 - Схема моментов неуравновешенных вращающихся масс цилиндра
Момент
от силы Pri
 .
.
Соответственно
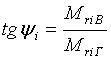 .
.
Обозначим
через ψr
угол между результирующим вектором момента Mr и
горизонтальной осью. Для главного вектора сил инерции вращающихся масс по
аналогии получим
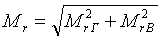 ,
,
 ;
;

Таким
образом
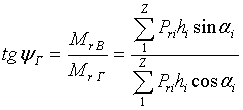 ,
,
откуда
непосредственно следует
Mr Г =
Мr
cos (α1 + ψr);r
В =
Мr
sin (α1 +
ψr),
где
ψr
- начальная фаза момента.
В
дальнейшем будем определять ψr для
положения коленчатого вала при α1 = 0.
Для
сил и моментов сил инерции ПДМ первого и второго порядков получим
соответственно:
 ;
;
 ;
;
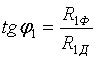 ;
;
 ;
;
R1Д = RI cos (α1 + φ1); M1Д = MI cos (α1 + φ1);
 ;
;
 ;
;
 ;
;
 ;1IД = RII cos (α1 + φ1I); M1IД = MII cos
(α1 + φ1I).
;1IД = RII cos (α1 + φ1I); M1IД = MII cos
(α1 + φ1I).
Лекция 16.
8.4.2. Определение
неуравновешенных сил и моментов от системы сил инерции вращающихся масс
Неуравновешенные силы и моменты принято определять при положении
коленчатого вала, когда кривошип первого цилиндра находится в ВМТ.
Определение неуравновешенной силы графическим способом.
Разберем этот способ на примере 4-х цилиндрового 2-тактного двигателя.
Предположим, что приведенные вращающиеся массы КШМ различных цилиндров различны
и составляют MR2 = 0,5 MR1; MR3 = 1,5 MR1; MR4 = MR1. Для данного двигателя Pr2 = 0,5 Pr1; Pr3 = 1,5 Pr1; Pr4 = Pr1.
Принимаем за силу Pr0 силу инерции вращающихся масс первого цилиндра. Тогда безразмерные силы
инерции
Pr1 = 1,0; Pr2 = 0,5; Pr3 = 1,5; Pr4 = 1,0;
Направление
безразмерных сил инерции соответствует фазовой диаграмме первого порядка
(диаграмма заклинки кривошипов). Выполним геометрическое сложение безразмерных
сил. Многоугольник не замкнулся; неуравновешенная сила представлена
безразмерным главным вектором 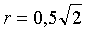 и
фазовым углом φГ = 45˚.
и
фазовым углом φГ = 45˚.

Рис.
8.18 - Графический способ определения rr: а - фазовая
диаграмма сил инерции враща-ющихся масс (фазовая диаграмма первого порядка);
б-многоугольник сил инерции Pri .
При
вращении коленчатого вала многоугольник сил вращается вместе с ним в ту же
сторону и с той же угловой скоростью.
Таким
образом, для графического определения амплитуды безразмерной силы rr на фазовой диаграмме первого порядка следует указать направление
безразмерных сил Pri и cложить эти силы. Замыкающая многоугольника сил
представит амплитуду безразмерной неуравновешенной силы. Абсолютное значение
неуравновешенной силы находят по формуле
Rr = rr Pr0 = rr
MR1
R ω2
Фазовым
углом φr
будет угол между вектором rr и вертикалью. Максимальное значение проекции
неуравновешенной силы как на горизонтальную, так и на вертикальную ось равно Rr.
Если
приведенные массы МRi разных цилиндров будут одинаковыми, то многоугольник
замкнется и, следовательно, силы инерции вращающихся масс уравновесятся. При
равномерной заклинке кривошипов и одинаковой величине вращающихся масс
различных КШМ, как правили силы инерции вращающихся масс оказываются
уравновешенными (за исключением 4-тактного 2-х цилиндрового ДВС).
Определение
неуравновешенной силы Rr аналитическим способом
Для
аналитического определения неуравновешенной силы используем формулы (при α1 = 0)
 ,
, 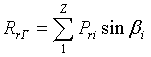 ,
,
или
в безразмерном виде
 ;
;  .
.
Углы
βi
определяют по фазовой диаграмме первого порядка.
Расчет
неуравновешенной безразмерной силы проводим в табличной форме
|
Номер КШМ
|
βi
|
cos βi
|
sin βi
|
pri
|
pricos
βi
|
prisin
βi
|
|
1 2 3 4
|
0 180 90 270
|
1,0 -1,0 0 0
|
0 0 1,0 -1,0
|
1,0 0,5 1,5 1,0 ∑
|
1,0 -0,5 0 0 rr
В = 0,5
|
0 0 1,5 -1,0 rr Г = 0,5
|
|
 ; ;  ; φr = 45˚. ; φr = 45˚.
|
Абсолютная неуравновешенная сила
Rr = rr Pr0 = rr
MR1 R ω2.
Определение неуравновешенных моментов графическим способом
Рассмотрим схему коленчатого вала 2-тактного 4-х цилиндрового двигателя.
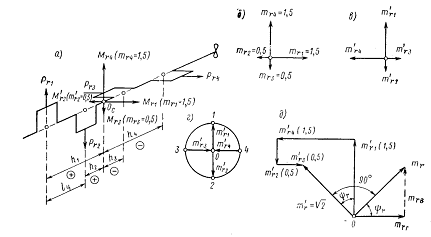
Рис. 8.19 - Графическое определение неуравновешенного момента: а - схема
коленвала; б - направление действительных безразмерных моментов; в -
направление повернутых безразмерных моментов; г - совмещение повернутых
безразмерных моментов с фазовой диаграммой первого порядка; д - многоугольник
моментов.
Следует отметить, что неуравновешенность двигателя не зависит от
направления вращения коленвала. Предполагаем, что двигатель однородный, т.е.
безразмерные амплитуды сил инерции вращающихся масс удовлетворяют равенству
pr1
== pr2 = pr3
= pr4=1,0.
Безразмерные плечи моментов, как следует из рисунка равны:
 ;
;  ;
;  ;
; 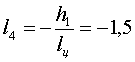 .
.
Безразмерные
моменты (без учета знака) составляют
mr1 = pr1 l1=
1,5; mr2 = pr2 l2 = 0,5; mr3 =
pr3 l3 = 0,5; mr4 = pr4
l4 = 1,5;
Направление
векторов размерных Мri безразмерных mri
моментов соответствует показанному на рисунке 8, б. Если все векторы моментов
повернуть на 90° против часовой стрелки, то они расположатся так как
показано на рис. 8, в. (повернутые моменты обозначатся через 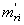 ). Сравнивая фазовую диаграмму первого порядка с
диаграммой повернутых моментов
). Сравнивая фазовую диаграмму первого порядка с
диаграммой повернутых моментов 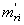 можно
заметить, что линии действия повернутых безразмерных моментов совпадают с
плоскостями соответствующих кривошипов, причем безразмерные повернутые моменты
можно
заметить, что линии действия повернутых безразмерных моментов совпадают с
плоскостями соответствующих кривошипов, причем безразмерные повернутые моменты 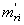 плечи которых положительны, направлены от центра
фазовой диаграммы рис. 8, г к периферии, а безразмерные повернутые моменты
плечи которых отрицательны, - по линии кривошипов от периферии к центру. Схема
рис. 8, г не учитывает величины указанных векторных моментов и показывает
только их направление.
плечи которых положительны, направлены от центра
фазовой диаграммы рис. 8, г к периферии, а безразмерные повернутые моменты
плечи которых отрицательны, - по линии кривошипов от периферии к центру. Схема
рис. 8, г не учитывает величины указанных векторных моментов и показывает
только их направление.
На
рис. д приведено геометрическое суммирование повернутых безразмерных моментов и
найдена их геометрическая сумма  .
Поскольку порядок сложения
.
Поскольку порядок сложения  произволен,
то имеет смысл складывать векторы таким образом, чтобы не накладывать друг на
друга. Фактическое направление суммарного вектора момента найдется поворотом
вектора
произволен,
то имеет смысл складывать векторы таким образом, чтобы не накладывать друг на
друга. Фактическое направление суммарного вектора момента найдется поворотом
вектора  на 90° по часовой стрелке рис. д.
Проекция безразмерного вектора на горизонталь даст
на 90° по часовой стрелке рис. д.
Проекция безразмерного вектора на горизонталь даст 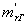 , а на вертикаль -
, а на вертикаль - 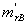 при a = 0. При вращении коленчатого вала вектор
при a = 0. При вращении коленчатого вала вектор  вращается вместе с ним в ту же сторону и с той же
угловой скоростью w. Соответственно изменяются
вращается вместе с ним в ту же сторону и с той же
угловой скоростью w. Соответственно изменяются 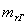 и
и 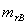 .
Максимальное значение их будет равно
.
Максимальное значение их будет равно  .
.
Абсолютное
значение амплитуды неуравновешенного момента
Mr = mr Pr0 lц ,
Pr0 = MR1 Rr w2
= mR1 FП Rr w2.
Начальную
фазу вектора момента yГ находят
из рис. д. В данном случае mrГ = mrВ , yr = 45°.
Порядок
графического определения  :
:
1) оценивают безразмерные силы pri;
2) выбирают безразмерные плечи с учетом их знака lц;
) находят безразмерные моменты mri = pri;pli;
) на фазовой диаграмме первого порядка указывают направление
повернутых на 90° против
часовой стрелки безразмерных моментов;
) геометрически складывают повернутые безразмерные моменты и
находят их геометрическую сумму;
6) поворачивают
вектор  на на 90° по часовой стрелке
и определяют таким образом вектор
на на 90° по часовой стрелке
и определяют таким образом вектор  ;
;
) снимают
с чертежа угол yr ;
) находят
абсолютное значение амплитуды неуравновешенного момента
Mr = mr Pr0 lц= mR1 FП Rr w2.
Определение неуравновешенного момента аналитическим способом
Для аналитического определения неуравновешенной момента используем
формулы (при α1
= 0°)
 ,
,  ,
,
или
в безразмерном виде
 ;
;  .
.
Углы
βi
определяют по фазовой диаграмме первого порядка. Как следует из рис. б при
вращении коленвала против часовой стрелки β1 = 0°, β2 = 180°, β4 = 270°, β3 = 90°,
Расчет
неуравновешенной безразмерной силы проводим в табличной форме
|
Номер КШМ
|
βi , °
|
cos βi
|
sin βi
|
pri
|
li
|
pri li
cos βi
|
pri li
sin βi
|
|
1 2 3 4
|
0 180 90 270
|
1,0 -1,0 0 0
|
0 0 1,0 -1,0
|
1,0 1,0 1,0 1,0
|
1,5 0,5 -0,5
-1,5
|
1,5 -0,5 0 0
|
0 0 -0,5 1,5
|
|
|
|
|
|
|
S
|
mrГ = 1,0
|
mrВ = 1,0
|
|
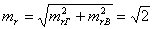 ; ;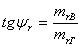 ; yr = 45°. ; yr = 45°.
|
Уравновешивание сил и моментов сил инерции вращающихся масс
Радикальным способом устранения неуравновешенных сил и моментов сил
инерции вращающихся масс является установка противовесов на щеках коленчатого
вала.
Рассмотрим три частных случая уравновешивания вращающихся масс.
Первый
случай Rr  0; Mr = 0.
0; Mr = 0.
Пусть
О-О - ось коленвала (рис. 9, а), Rr - амплитуда неуравновешенной силы. Точки А и В
соответствуют положению середин щек коленчатого вала, на которых мы собираемся
установить противовесы. Рассчитаем силы инерции противовесов Pпр
А и Pпр B
по следующей схеме:
Pпр А + Pпр B = Pпр рез = - Rr ; (1)
Pпр А lB = - Pпр BlB . (2)
Приведенные
условия требуют, чтобы сила Pпр рез
была по величине равна Rr и приложена в точке С. Задаемся значением rпр и определяем mпр А и mпр B из уравнений
Pпр А = mпр А rпр w 2 ;
Pпр B
= mпр B rпр w 2 .
При
присоединении к системе сил Pri еще
двух сил Pпр А и Pпр
B равенство нулю главного момента Mr не нарушится ввиду выполнения условия (2).
Второй
случай Rr = 0; Mr  0.
0.
Для
уравновешивания Mr на
щеках коленвала в точка А и В устанавливаем одинаковые противовесы (mпр
А = mпр В), чтобы
Pпр А АВ = - Mr.
Равные
силы Pпр А и Pпр
B создают момент Mпр, который и уравновешивает Mr. В
результате присоединения к системе сил Pri
двух сил Pпр А и Pпр
B равенство нулю главного вектора не нарушится, так как
Pпр А и Pпр
B равны по величине и противоположны по направлению.
Третий
случай Rr  0; Mr
0; Mr  0.
0.
Раскладываем Rr на
две параллельные силы RА
и RВ, приложенные в точках А и В соответственно. Момент Mr заменяем парой сил R’А и R’В (R’А = R’В). Далее находим
равнодействующие RАS и RВS сил, приложенных в точках А и В, и устанавливаем противовесы mпр А и mпр B с таким расчетом, чтобы Pпр А = RАS, а Pпр В = RВS. После присоединения указанных
противовесов система сил инерции вращающихся масс полностью уравновешенна. Таким образом, во всех случаях система сил инерции неуравновешенных
вращающихся масс может быть уравновешена по меньшей мере двумя противовесами на
щеках коленчатого вала.
Определение неуравновешенных сил и моментов от системы сил инерции ПДМ
первого порядка.
Сил инерции первого
порядка PIcosα можно рассматривать как проекцию на
вертикаль вектора фиктивной ц/б силы, направленного PIi вдоль кривошипа и вращающегося
вместе с ним с угловой скоростью ω. Действительная составляющая главного вектора сил инерции
первого порядка всегда лежит в вертикальной плоскости, а действительная
составляющая вектора главного момента MIД
- в горизонтальной плоскости, так как для системы сил вектор перпендикулярен
плоскости действия сил.
Допустим имеем однородный двигатель
PI1
= PI2 = PI3
= PI4
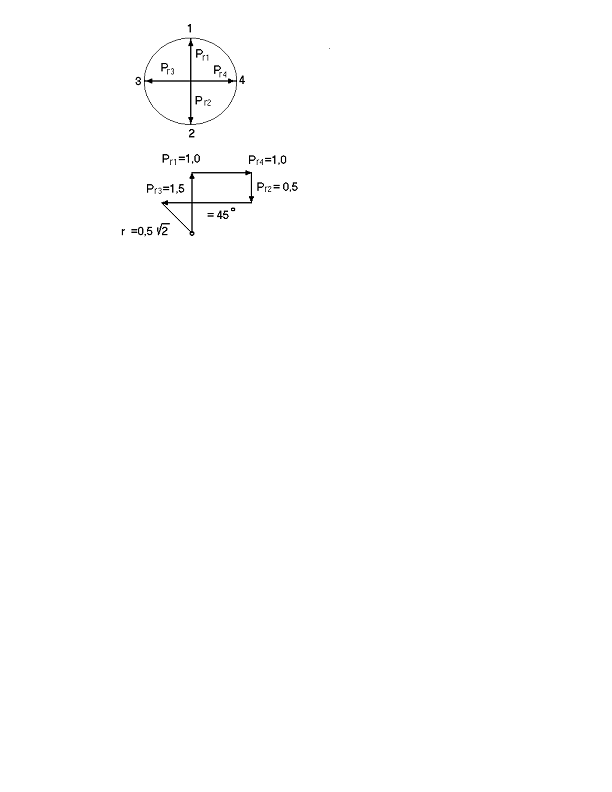
Рис. 8.20 - Фазовая диаграмма
При расчёте аналитическим способом заполняем таблицу
|
№ КШМ
|
βi
|
cos βi
|
sin βi
|
PIi
|
PIi
cos
βi
|
PIi
sin
βi
|
|
1
|
3
|
4
|
5
|
6
|
7
|
|
1 2 3 4
|
0 180 90 270
|
1 -1 0 0
|
0 0 1 -1
|
1 1 1 1
|
1 -1 0 0
|
0 0 1 -1
|
|
|
|
|
∑
|
PIВ
|
PIГ
|
Силы инерции первого порядка уравновешены что наблюдается всегда при
равномерной заклинке кривошипов
Определение безразмерного момента сил инерции ПДМ первого порядка
mI1 = PI1l1 = 1,5; mI2
= PI2l2 = 0,5; mI3 = PI3l3
= 0,5; mI4 = PI4l4 = 1,5;
При расчёте аналитическим способом заполняют таблицу
|
№ КШМ
|
βi
|
cos βi
|
sin βi
|
PIi
|
li
|
PIi li
cos
βi
|
PIi li
sin
βi
|
|
1 2 3 4
|
0 180 90 270
|
1 -1 0 0
|
0 0 1 -1
|
1 1 1 1
|
1,5
0,5 -0,5 -1,5
|
1,5 -0,5 0 0
|
0 0 -0,5 1,5
|
|
|
|
|
|
∑
|
mIГ=1
|
mIВ=1
|
 , ψГ = 45° .
, ψГ = 45° .
Уравновешивание
сил и моментов сил инерции первого порядка
При
равномерной заклинке кривошипа RI как правило равна нулю. Неуравновешенный максимальный
момент от сил инерции первого порядка
MI = mI∙PI0∙lЦ можно уменьшить, если удастся подобрать более
рациональный порядок заклинки кривошипов (фазовую диаграмму первого порядка).
Этот момент можно уменьшить за счёт облегчения одних поршней и утяжеления
других. Однако при этом нарушится уравновешенность сил инерции первого и
второго порядков.
Полностью
уравновесить силы инерции первого порядка обычными противовесами установленными
на щеках колен не удаётся. Можно, например, подобрать массу противовеса mпр так, чтобы PПР = PI и PIcosα = PПРcosα, уравновесив тем самым силы инерции в вертикальной плоскости, но это
взывает появление новой неуравновешенной силы PПРsinα в горизонтальной плоскости, максимальное значение
которой равно PПР = PI.
Следовательно
обычным противовесом можно только перенести неуравновешенную силу инерции ПДМ
первого порядка из вертикальной плоскости в горизонтальную. Однако такой
перенос, как правило, практического смысла не имеет. Иногда, правда переносят
половину силы инерции ПДМ первого порядка в горизонтальную плоскость, но это
конечно нельзя считать кардинальным решением вопроса.
Полностью
уравновесить силу инерции первого порядка можно за счёт специального устройства
- динамического противовеса.
Идея
динамического противовеса заключается в следующем.
В
остов двигателя на подшипниках устанавливают две шестерни вращающиеся в разные
стороны с одинаковой угловой скоростью ω. С шестернями связаны два противовеса (mпр1 и mпр2)
радиусы которых составляют с вертикалью одинаковые углы α. Горизонтальные составляющие сил инерции противовесов
взаимно уравновешиваются, а вертикальная составляющая равная 2РПРcosα приложена в точке "К" может уравновесить
неуравновешенную силу PIcosα, если 2РПР = РI.
Двумя
парами аналогичных динамических противовесов можно создать пару сил 2РПРLсosα лежащих в вертикальной плоскости вектор момента
которой Мпр направленный всегда в горизонтально, изменяясь по закону
косинуса уравновесит неуравновешенный вектор момента 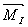 .
.
Библиографический список
. Ваншейдт, В.А. Судовые двигатели внутреннего сгорания
(теория). / В.А. Ваншейдт. - Л.: Судпрогиз, 1950. - 528 с.
. Ваншейдт, В.А. Судовые двигатели внутреннего сгорания. /
В.А. Ваншейдт. - Л.: Судостроение, 1977. - 371 с.
. Самсонов, В.И. Судовые двигатели внутреннего сгорания. /
В.И. Самсонов, Н.И. Худов, А.А. Мирющенко. - М.: Транспорт, 1981. - 490 с.
. Дизели : справочник / Под ред. В.А. Ваншейдта, Н.Н.
Иванченко, Л.К. Коллерова. - Л.: Машиностроение, 1977. - 480 с.
. Возницкий, И.В. Судовые двигатели внутреннего сгорания. Том
2. / И.В. Возницкий, А.С. Пунда. - М,: Моркнига, 2008. - 468 с.