Рекомендации по использованию гуманитаризации при изучении золотого сечения

Рекомендации по использованию гуманитаризации при изучении золотого сечения

Рекомендации по использованию гуманитаризации при изучении золотого сечения

План

золотое сечение преподавание математика

Введение

Глава 1. Золотое сечение и его свойства

.1 История

.2 Определение золотого сечения

.3 Золотые фигуры

.4 Открытие Леонардо Фибоначчи

.5 Золотое сечение, которое нас окружает

.5.1 Раковина

.5.2 Растения и животные

.6 Божественная пропорция в искусстве

.6.1 Золотое сечение в архитектуре

.6.2 «Золотая пропорция» живописи

.7 Золотая пропорция в человеке

.7.1 Пропорция

.7.2 Золотая пропорция в человеке

.7.3 Кровяное давление

.7.4 Сердце и дыхание

.8 Второе золотое сечение

.9 Серебреное сечении

Глава 2. Обучение математике в гуманитарных классах

.1 Место математики в гуманитарных классах

.2 Положение теории гуманитаризации математического

образования

.3 Построение гуманитаризованного курса математики

.4 Психолого-педагогические особенности учащихся гуманитарных классов

.5 Использование золотого сечения при решения задач на построение

Заключение

Список литературы

Приложения

Введение

век. В России и за её пределами в настоящее время учёными самых различных специальностей уделяется непосредственное внимание проблеме гармонии природных и искусственных систем, а так же изучению феномена золотого сечения, тесно связанным с этим. Возникающие при этом вопросы весьма разносторонни и отличаются многогранностью. Включают в себя даже такие вопросы как: структура закономерности Солнечной системы, физиологические функции человека, морфология животных, строение бытовых приборов и т.д.

Как известно, целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения - высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.

Золотая пропорция имеет довольно интересную историю, завораживает своими свойствами, поражает открытиями, которые проводятся благодаря ней. «Божественное сечение» всегда приводило в восторг античных учёных, скульпторов, художников.

Проблема, которая подтолкнула к написанию диплома по этой теме - в век научно-технической революции мы на каждом шагу сталкиваемся с глобальной неграмотностью и отсутствием вкуса, неумением людей использовать программные школьные знания на практике, а так же находить межпредметные связи.

Цель дипломной работы - изучение золотого сечения и его проявление в математике, в окружающего мире, произведениях искусства, бытовых предметах и рассмотрение вопросов гуманитаризации преподавания математики на примере темы золотого сечения.

Для этого поставим следующие задачи:

·   подбор и изучение литературы по этой теме;

·   рассмотрение понятия золотого сечения, его свойств и особенностей;

·   исследование связи золотой пропорции с природой, человеком, искусством;

·   разработка занятий по теме исследования и их апробация на уроках математики в гуманитарном классе;

·   разработка рекомендаций по использованию гуманитаризации при изучении золотого сечения.

Наиболее актуальным на данный момент является гуманитаризация в обучение математике. Ведь гуманитаризация предполагает усиление взаимосвязи естественно-математического образования с гуманитарным - более понятным, близким ребёнку. Так же подразумевается усиление практического и прикладного аспектов преподавания. Это означает, что в обучении математике акцент необходимо ставить на общее развитие учащегося, а именно на развитие абстрактно-логического мышления, математической речи, пространственного воображения, интуиции, эстетического чувства.

Предметом исследования нашей работы является тема золотого сечения на уроках математики в гуманитарных классах.

А.В. Дорофеева выдвигает тезис о том, «что история математики помогает формированию мировоззрения учащихся». Причем, по её мнению, «элементы истории математики привлекают школьников, склонных к гуманитарным наукам» и отстающих учащихся. Сегодня данный тезис представляется актуальным как привлечение внимания школьников с различными способностями и интересами к математике как науке.

Теоретическая значимость исследования заключается в:

разработке модели преподавания математики в гуманитарных классах на примере темы «Золотое сечение»;

выявлении особенностей развития мотивации к изучению математики учащихся старших классов гуманитарного профиля;

определении системы мер, позволяющих актуализировать мотивационный потенциал школьников в ходе реализации коммуникативно-речевых ситуаций в процессе математического образования.

Практическая значимость исследования:

предложенные рекомендации могут быть применены при овладении учащимися основными элементами школьного математического содержания;

разработанная методика может быть использована в процессе совершенствования школьных программ по математике, учебников и учебных пособий, в вузовских методических курсах и в системе повышения квалификации учителей математики.

Глава 1. Золотое сечение и его свойства

.1 Исторические сведения

«О, сколько мы много и, в то же время, так мало знаем о золотом делении», говорили мастера. История этого деления поразительна.

Американский математик Марк Барр 80 лет назад предложил назвать отношение двух отрезков, образующих «золотое сечение», числом Φ. Буква Φ является первой буквой в имени великого Фидия, по преданию, часто использовавший золотое сечение в своих работах. Хотя первый начал использовать пропорцию, работавший вместе с ним, скульптор Мирон. Фидий, Мирон и Поликлет разработали вместе пропорции человека для статуй.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н. э.). Однако есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. Действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления, хотя деление на нём очень уж приблизительные.

Греки были искусными геометрами. Очень интересно, что они обучали своих детей алгебре при помощи геометрических фигур. Квадрат Пифагора и диагональ его были основанием для построения динамических прямоугольников (Рис. 1).

рис. 1 Динамические прямоугольники.

Платон (ок. 427 - 347 гг. до н.э.) также использовал золотое деление. Его диалог "Тимей" посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по "золотому сечению", то получим те или иные выступы фасада. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления (рис. 2).

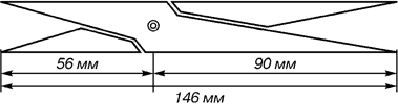
Рис. 2 Античный циркуль золотого сечения.

В дошедшей до нас античной литературе золотое деление впервые упоминается в "Началах" Евклида. Во 2-й книге "Начал" дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам "Начал" Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

Где-то в XIII веке в историю золотого сечения было вплетено имя математика монаха родом из Италии, Леонардо из Пизы. Хотя нам он известен под другим именем, а точнее по прозвищу Фибоначчи (Fibonacci - сокращенное filius Bonacci, то есть сын Боначчи). В 1202г. им была написана книга "Liber abacci", то есть "Книга об абаке". "Liber abacci" представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими ("арабскими") цифрами.

Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением, как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи, художник и ученый, видел, что в итальянских художниках большой эмпирический опыт, но недостаток знаний. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Его называли творцом начертательной геометрии.

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г. по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи.

В 1509 г. в Венеции была издана книга Луки Пачоли «De divina Proportine» ("О Божественной пропорции") с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее "божественную суть" как выражение божественного триединства: бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок - бога отца, а весь отрезок - бога духа святого).

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение, которое держится по наши дни.

В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: "Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать".

Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица - ртом и т.д.

Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

Шел всё тот же XVI век. Астроном Иоган Кеплер первый начинает обращать внимание на золотое сечение как инструмент для ботаники, назвав его одно из сокровищ геометрии.

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы "вместе с водой выплеснули и ребенка". Вновь "открыто" золотое сечение было в середине XIX в.

В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд "Эстетические исследования". В нем он проделал огромную работу, где измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон: деление тела точкой пупа - важнейший показатель золотого сечения. Так же данная пропорция присутствует и в отношении других частей тела - длина плеча, предплечья и кисти, фаланги пальцев.

С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства.

У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях "математической эстетикой".

В ХIХ веке (новый разгар изучения божественной пропорции) появилось огромное количество теорий о применении данного сечения в архитектуре, искусстве. Теперь после развития дизайна его начали применять и в нём: в машинах, мебели и т.д.

.2 Определение золотого сечения

Иоганн Кеплер говорил, что геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением. И если первое из этих двух сокровищ можно сравнить с мерой золота, то второе с драгоценным камнем.

Теорему Пифагора знает каждый школьник, а что такое золотое сечение - далеко не все.

Пропорция - равенство между двумя отношениями четырёх величин: a:b=c:d. Возьмём пример, предлагаемый Васютинским, где АВ, который можно разделить на две равные части №1. Это будет соотношение разных величин - АВ : АС=АВ : ВС. Эту же прямую №2 и №3 можно разделить на две неравные части в любом отношении. Эти части пропорции не образуют. А вот прямую АВ №4 можно разделить по золотому сечению, когда АВ: АС, как АВ : ВС. Это и будет искомым золотым сечением (золотым делением) или деление в крайнем и среднем отношении.

Рис. 3. Деление отрезка прямой на равные части и по золотому сечению:

№1 - АВ : АС;

№2, №3 - пропорция не образуется;

№4 - АВ : АС = АС : ВС или ВС : АС = АС : АВ (золотая пропорция)

Золотое сечение - это такое пропорциональное гармоническое деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей. Или другими словами, меньший отрезок относится к большему, как больший ко всему, т.е. а:в=в:с или с:в=в:а.

Определение в крайнем и среднем отношении становится более понятно, если выразить его геометрически. На рисунке 4 приведено геометрическое изображение золотой пропорции.

Рис. 4, а

Рис. 4, б

Отрезки золотой пропорции, если их, конечно, продолжат (рис. 4,б) дальше, выражаются иррациональной бесконечной дробью 0,618..., если с принять за единицу, а = 0,382.…На этой пропорции базируются основные геометрические фигуры.

Прямоугольник с таким отношением сторон стали называть золотым прямоугольником. Он также обладает интересными свойствами. Если от него отрезать квадрат, то останется вновь золотой прямоугольник. Этот процесс можно продолжать до бесконечности. А если провести диагональ первого и второго прямоугольника, то точка их пересечения будет принадлежать всем получаемым золотым прямоугольникам.

Разумеется, существует и золотой треугольник. Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равно числу Ф (с ним мы встретимся в разделе золотые фигуры).

Астроном Иоганн Кеплер называл эту последовательность продолжающей саму себя. «Устроена она так, - писал Кеплер, - что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причём та же пропорция сохраняется до бесконечности».

Как можно заметить, построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

Практическое знакомство с золотым сечением, как правило, начинается с деления отрезка прямой в золотой пропорции геометрическим способом (рис. 5).

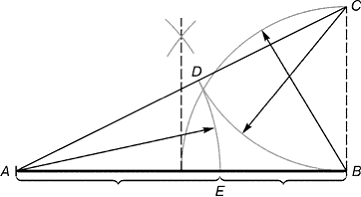
Рис. 5

Из точки. В восстанавливаем перпендикуляр, равный половин АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок равный ВС, заканчивающийся точкой D. Отрезок АD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

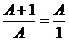
В этом случае геометрическую пропорцию можно выразить следующим образом:

Где АД = х.

Если АВ = а принять за единичный отрезок, то получим следующее числовое выражение:

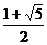
будем обозначать Ф. при этом

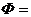
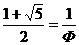
Обратим внимание удивительную инвариантность золотой пропорции:

Такие преобразования как возведение в степень не смогли уничтожить сущность этой уникальной пропорции.

Подобно числу π, Ф можно представить в виде суммы бесконечного ряда многими способами. Одно из них:

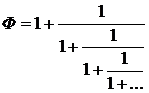
1.3 Открытие Леонардо Фибоначчи

Итальянский купец Леонардо из Пизы (1180-1240), более известный под прозвищем Фибоначчи был, безусловно, самым значительным математиком средневековья. Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.

Жизнь и научная карьера Леонардо теснейшим образом связана с развитием европейской культуры и науки.

В век Фибоначчи возрождение было еще далеко, однако история даровала Италии краткий промежуток времени, который вполне можно было назвать репетицией надвигающейся эпохи Ренессанса. Этой репетицией руководил Фридрих II, император (с 1220 года) Священной Римской империи.

Покровительство Фридриха и стимулировало выпуск научных трактатов Фибоначчи:

· книга абака, написанная в 1202 году, но дошедшая до нас во втором своем варианте, который относится к 1228 г.

· практики геометрии (1220г.)

· книга квадратов (1225г.)

По этим книгам, превосходящим по своему уровню арабские и средневековые европейские сочинения, учили математику, чуть ли не до времен Декарта(XVII в.).

Наибольший интерес представляет для нас сочинение "Книга абака". Эта книга представляет собой объемный труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший значительную роль в развитии математики в Западной Европе в течение нескольких следующих столетий.

Сообщаемый в "Книге абака" материал поясняется на примерах задач, составляющих значительную часть этого тракта.

Как сказано выше, золотая пропорция тесно связана с последовательностью Фибоначчи. А началось всё с того, что Кеплер, спустя четыре столетия после открытия этого ряда установил, что отношение рядом стоящих чисел в пределе стремится к золотой пропорции Ф. Это свойство присуще не только числам Фибоначчи. Начав с любых двух чисел, и построив аддитивный ряд, в котором каждый член равен сумме двух предыдущих (например, ряд 7,2,9,11,20…), мы обнаружим, что отношение двух последовательных членов такого ряда так же стремится к числу Ф: чем дальше будем продвигаться от начала ряда, тем лучше будет приближение.

На страницах 123 - 124 данной рукописи, Фибоначчи поместил следующую задачу:

Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет др. пару, а рождают кролики со второго месяца после своего рождения.

Ясно, что если считать первую пару кроликов новорожденными, то на второй месяц мы будем по прежнему иметь одну пару; на 3-й месяц- 1 + 1 = 2; на 4-й- 2 + 1 = 3 пары (ибо из двух имеющихся пар потомство дает лишь одна пара); на 5-й месяц - 3 + 2 = 5 пар (лишь 2 родившиеся на 3-й месяц пары дадут потомство на 5-й месяц); на 6-й месяц - 5 + 3 = 8 пар (ибо потомство дадут только те пары, которые родились на 4-м месяце) и т. д.

Выглядит это так.

И так далее.

Таким образом, если обозначить число пар кроликов, имеющихся на n-м месяце через F_к, то F₁=1, F₂=1, F₃=2, F₄=3, F₅=5, F₆=8, F₇=13, F₈=21 и т. д., причем образование этих чисел регулируется общим законом: F_n=F_n-1 + F_n-2

При всех n > 2, ведь число пар кроликов на n-м месяце равно числу F_n-1 пар кроликов на предшествующем месяце плюс число вновь родившихся пар, которое совпадает с числом F_n-2 пар кроликов, родившихся на (n-2)-ом месяце (ибо лишь эти пары кроликов дают потомство).

Числа F_n, образующие последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ... называются "числами Фибоначчи", а сама последовательность - последовательностью Фибоначчи.

Суть последовательности Фибоначчи в том, что, начиная с 1, 1 следующее число получается сложением двух предыдущих.

Но почему эта последовательность так важна?

Данная последовательность асимптотически (приближаясь, все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.

Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875...и через раз то превосходящая, то не достигающая его. Но, даже затратив на это Вечность, невозможно узнать соотношение точно, до последней десятичной цифры. Краткости ради, мы будем приводить его в виде 1,618.

Особые названия этому соотношению начали давать еще до того, как Лука Пачоли (средневековый математик) назвал его Божественной пропорцией. Среди его современных названий есть такие, как Золотое сечение, Золотое среднее и отношение вертящихся квадратов. Кеплер назвал это соотношение одним из "сокровищ геометрии". В алгебре общепринято его обозначение греческой буквой фи. Ф = 1,618

Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать более понятными, если показать отношения нескольких первых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:

:1 = 1.0000, что меньше ф на 0.6180;

:1 = 2.0000, что больше ф на 0.3820;

:2 = 1.5000, что меньше ф на 0.1180;

:3 = 1.6667, что больше ф на 0.0486;

:5 = 1.6000, что меньше ф на 0.0180;

По мере нашего продвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим приближением к недостижимому Ф.

Человек подсознательно ищет Божественную пропорцию: она нужна для удовлетворения его потребности в комфорте.

При делении любого члена последовательности Фибоначчи на следующий за ним получается просто обратная к 1.618 величина (1 : 1.618=0.618). Но это тоже весьма необычное, даже замечательное явление. Поскольку первоначальное соотношение - бесконечная дробь, у этого соотношения также не должно быть конца.

При делении каждого числа на следующее за ним через одно, получаем число 0,382.

: 0,382 = 2,618

Подбирая, таким образом, соотношения, получаем основной набор коэффициентов Фибоначчи: 4,235; 2,618; 1,618; 0,618; 0,382; 0,236. Упомянем также 0,5. Все они играют особую роль в природе и в частности в техническом анализе.

Тут необходимо отметить, что Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна еще в древнейшие времена под названием Золотое сечение.

1.4 Золотые фигуры

Отрезки золотой пропорции выражаются иррациональной бесконечной дробью 0,618..., если с принять за единицу.

а = 0,382…как мы уже знаем числа 0.618 и 0.382 являются коэффициентами последовательности Фибоначчи. На этой пропорции базируются основные геометрические фигуры.

Построение золотого прямоугольника:

Если построить квадрат со стороной АВ (рис. 6), найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точки Е, то точка. В разделит отрезок АЕ в среднем и крайнем отношении.

Рис. 6

Рассматривая золотой прямоугольник можно заметить что, если отрезать от него квадрат, сторона которого равна меньшей стороне прямоугольника, то мы снова получим золотой прямоугольник меньших размеров. И если продолжать в таком порядке, то получим совершенно квадратируемый прямоугольник бесконечного порядка. Точки, делящие стороны прямоугольника в среднем и крайнем отношении, лежат на логарифмической спирали, закручивающейся вовнутрь. Полюс спиралей лежит на пунктирных диагоналях (рис. 7).

| | 0.500 | 0.618 |

Рис. 7, а. Золотая спираль

Рис. 7, б. Спираль Фибоначчи.

Спираль золотого сечения закручивается в бесконечность. Но есть ещё одна спираль, спираль Фибоначчи. Она построена из шести квадратов одного размера («конечна»). Возьмём раковину моллюска наутилуса: «Существует неписаное правило, что в любой хорошей книги по сакральной геометрии должна быть раковина нотариуса. Во многих книгах сказано, что это спираль золотого сечения, но это не верно - это спираль Фибоначчи. Можно увидеть совершенства рукавов спирали, но если посмотреть на центр и начало, то он не выглядит таким совершенным. Советую вам увидеть настоящую раковину. Два первых внутренних изгиба фактически равны, и отношение их дли равно 1, что далеко от фи. Второй и третий виток всё ближе и ближе приближается к 1,618. Потом получается эта изящная спираль. Можно подумать, что этот маленький моллюск в самом начале; похоже, он не ведал, что творил. Нет, он творит прекрасно, это не ошибка. Просто он чётко следует математике ряда Фибоначчи» (Друнвало Мелхиседек).

Эта спираль возникает и в других геометрических построениях. Возьмём золотой треугольник, стороны которого находятся в золотом отношении к основанию. Этот треугольник будет равнобедренный (Рис. 8), у которого отношение длины боковой стороны к длине основания равняется 1,618 (приложение 1). Углы при основании такого треугольника равны по 72^о, что вдвое больше угла при вершине, равного 36^о. Точка пересечения биссектрисы угла при основании с противоположной стороной делит эту сторону в среднем и крайнем отношении, при этом весь треугольник разбивается на два меньших, один из которых подобен исходному. Так же и этот треугольник можно разбить на более мелкие. Продолжая это, получим бесконечную последовательность закручивающихся треугольников (логарифмическую).

Логарифмическая спираль - единственный тип спирали, не меняющей своей формы при увеличении размеров.

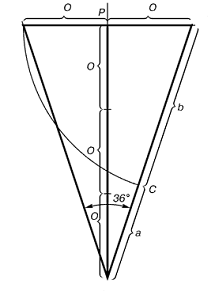
Рис. 9. Золотой треугольник

Есть и золотой кубоид - это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.

В звездчатом пятиугольнике каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются золотыми треугольниками.

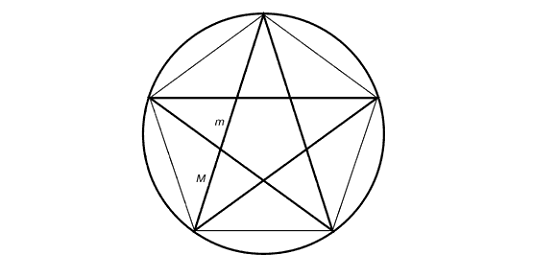
Рис. 9. Построение правильного пятиугольника и пентаграммы (пентакл)

Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком. Бытует легенда о том, что один из пифагорейцев больным попал в дом к незнакомым людям. Они старались его выходить, но болезнь не отступала. Не имея средств заплатить за лечение и уход, больной перед смертью попросил хозяина дома нарисовать у входа пятиконечную звезду, объяснив, что по этому знаку найдутся люди, которые вознаградят его. И на самом деле, через некоторое время один из путешествующих пифагорейцев заметил звезду и стал расспрашивать хозяина о том, каким образом она появилась у входа. После рассказа хозяина гость щедро вознаградил его. Пентаграмма была хорошо известна и в Древнем Египте. Но непосредственно как эмблема здоровья она была принята лишь в Древней Греции.

Существует гипотеза, что пентаграмму никто не изобретал, ее только скопировали с натуры. Вид пятиконечной звезды имеют пятилепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет, поэтому естественно предположить, что геометрический образ этих объектов - пентаграмма - стала известна раньше, чем "золотая" пропорция.

Рассмотрим теперь, как Евклид использует золотое сечение для построения угла равного 72^о, именно под таким углом видна сторона правильного пятиугольника из центра описанной вокруг него окружности. Начнём с отрезка АВЕ, разделённого в крайнем и среднем отношении точкой В (рис.10).

Рис. 10

Проведём далее дуги окружностей с центрами в точках В и Е и радиусом АВ, пересекающиеся в точке С. Пусть АС = АЕ. Обозначим через α равные углы ЕВС и СЕВ. Так как АС = АЕ, то угол АСЕ равен α. Теорема о том, что сумма углов треугольника равна 180^о, позволяет найти угол ВСЕ: он равен 180^о - 2α, а угол ЕАС равен 3α - 180^о. Но тогда угол АВС равен 180^о - α, и, суммируя углы треугольника АВС, получаем:

^о = (3α - 180^о) + (3α - 180^о) + (180^о - α),

откуда

5α = 360^о и α = 72^о.

Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36^о. Следовательно, что бы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую сторону ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; обойдя вокруг всей окружности, можно найти и все остальные стороны.

Число Ф, например, является отношением радиуса окружности к стороне правильного вписанного десятиугольника. Расположим три золотых прямоугольника (стороны которых находятся в золотом отношении) так, чтобы каждый симметрично пересекался с двумя другими (под прямым углом к каждому из них), видно, что вершины золотых прямоугольников совпадают с вершинами правильного икосаэдра и в то же время указывают положение центров 12 граней правильного додекаэдра. См. (приложение 2, 3)

Использование золотого сечения при решении задач на построение

Задача №1.

С помощью циркуля и линейки построить прямоугольник с отношением сторон 1 : (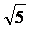 - 1 ) / 2.

Решение

Поделим отрезок АВ точкой С в отношении золотого сечения. Из точки А восстановим окружность радиуса (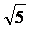- 1 ) / 2. Она пересекает перпендикуляр АК в точке D. Последующие построения очевидны. Они завершают чертёж прямоугольника АВЕD, отношение сторон которого 1 : (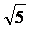- 1 ) / 2.

Задача №2

Построить прямоугольник отношением сторон 1 : (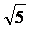 - 5 ) / 2.

Решение

Проводим отрезок АВ = 1, точкой С делим его в золотом отношении. Тогда АС = 1 - (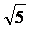- 1 ) / 2 = ( 3 -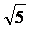) / 2. Продолжим отрезок АВ за точку А, и из точки А проведём окружность радиуса АС. Пересечение с продолжением АВ будет точка D. Из точки В восстановим перпендикуляр ВМ к АВ. Строим окружность с центром в точке В радиусом ВD.

ВD = 1 + ( 3 -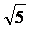) / 2 = ( 5 -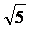) / 2.

Окружность пересекает перпендикуляр ВМ в точке Е, длина стороны прямоугольника равна ( 5 -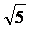) / 2.

Задача №3

Построить правильный пятиугольник по данной стороне АВ = 1.

Решение

Находим на отрезке АВ точку С золотого сечения. Из точки В как из центра проводим окружность радиусом АС, которая пересекает продолжение отрезка АВ в точке D.

Строим две окружности с центром А и В радиусом

AD = 1 + (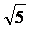- 1 ) / 2 = (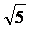+ 1 ) / 2.

Одна из точек пересечения - точка Е, третья вершина пятиугольника. Потом из точки В чертим окружность радиусом АВ. Она пересекается с предыдущей окружностью в точке N, четвёртой вершине пятиугольника. Из точек А и Е проводим окружности, радиусы которых равны длине отрезка АВ (стороне правильного пятиугольника). Две последние окружности пересекаются в пятой вершине К пятиугольника.

1.5 Золотое сечение, которое нас окружает

Книга природы написана на языке математики.

Галилео Галилей (1564 - 1646).

Живой организм, вытянутый в длину, таит для его владельца много опасностей. Змея погибает чаще из-за своего длинного тела. Ящерица отбрасывает хвост, если ей грозит опасность или её схватили за него. Раковина закручивается по спирали. Винтообразное и спиралевидное распределение листьев.

Спирали очень распространены в природе: в семенах подсолнечника и шишках сосны, ананасах и кактусах.

Однако только совместная работа ботаников и математиков пролила свет на эти удивительные проявления природы.

Выяснилось, что в расположении листьев на ветке (Филотаксис), семя подсолнечника, шишак сосны представляет собой ряд Фибоначчи, и, стало быть, проявляет себя закон золотой пропорции.

Паук плетёт паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. ДНК закручиваются двойной спиралью.

1.5.1 Раковина

Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе.

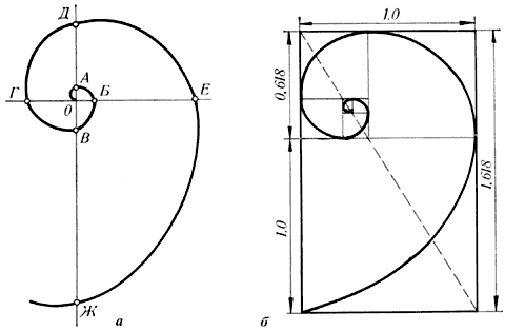
спираль Архимеда

Рис. 11

ОБ : ОА = ОВ : ОБ = ОГ : ОВ = ... = 1.618

(ОБ + ОГ) : (ОВ + ОА) = ... = 1.618.

Форма спирально завитой раковины привлекла внимание Архимеда (рис. 11). Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.

1.5.2 Растения и животные

Еще Гете подчеркивал тенденцию природы к спиральности. Гете называл спираль "кривой жизни".

Среди придорожных трав растет особо не примечательное растение - цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок

Цикорий

Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий - 38, четвертый - 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

В частности, было показано, что угловое расхождение ветвей многих растений определяется так называемым идеальным углом, величина которого равна 360° : Ф - 2 = 137° 30'.

Проявление чисел Фибоначчи наблюдается в числе пазух на стебле растения во время его роста. Идеальный случай можно увидеть в стеблях и цветах sneezewort'а. Каждая новая ветка прорастает из пазухи и дает начало другим веткам. Если рассмотреть вместе старые и новые ветки, в каждой горизонтальной плоскости обнаруживается число Фибоначчи.

Ирис - 3 лепестка;

Примула - 5 лепестков;

Амброзия полыннолистная - 13 лепестков;

Нивяник обыкновенный - 34 лепестка;

Астра - 55 и 89 лепестков;

Число и расположение цветков в головке того или иного представителя сложноцветных - прекрасный пример золотых чисел, находимых в природе.

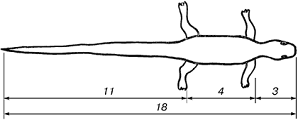
Ящерица живородящая

В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции - длина ее хвоста так относится к длине остального тела, как 62 к 38.

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы - симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.

Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.

Яйцо птицы

Великий Гете, поэт, естествоиспытатель и художник (он рисовал и писал акварелью), мечтал о создании единого учения о форме, образовании и преобразовании органических тел. Это он ввел в научный обиход термин морфология.

Пьер Кюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды.

Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как будет указано ниже, есть в строении отдельных органов человека и тела в целом.

Суммируя известные данные о формообразовании в природе можно отметить:

·   «Золотое число», равное 1,618, передаёт математически своеобразную ритмичность функциональных структур.

·   Принцип «золотой симметрии» действует и на уровне неживой природы как определённый инструмент её упорядочения и прогрессивной эволюции.

·   Числа Фибоначчи математически выражают собой определённые принципы природного развития, связанные с общим законом сохранения. Эти принципы имеют место, как на организменном, так и на молекулярном уровне развития живых систем.

·   В то время как ряды Фибоначчи математически характеризуют прогрессивную тенденцию природного отбора, т.е. стремление природы к оптимальному функционированию её систем, принцип «золотого сечения» - экстремальное (высшее) проявление структурного и функционального совершенства этих стилей.

·   «Золотая» спираль с модулем Ф является математическим смыслом тайны жизни, которая оптимально выявляет себя и в растительном и в животном мире, потому что она проявление закона гармонического возрастания пульсаций.

В итоге можно заметить, что среди бесчисленного разнообразия форм в природе, с которым встречается зодчий, царит закономерность и системность, связывающая нитью, которая является золотой пропорцией.

Существует пять принципов формирования в природе:

1. целостность (человек, дерево, рыба…) добавляя или удаляя какую-то часть от целого, получим дефект. Происходит нарушение гармонии.

2. пропорции. Целое всегда состоит из частей. Части разной величины в определённом отношении находятся друг к другу и к целому.

3. Симметрия. Пропорциональные отношения ведут к симметрии, ритму, гармонии и красоте.

.6 Божественная пропорция в искусстве

.6.1 Золотое сечение в архитектуре

Рис. 12

В книгах о золотом сечении можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что если некоторые пропорции в здании кажутся образующими золотое сечение, то с других точек зрения они будут выглядеть иначе. Золотое сечение дает наиболее спокойное соотношение размеров тех или иных длин.

Золотое сечение можно обнаружить в архитектуре здания Сената в Кремле. Еще один архитектурный шедевр Москвы - дом Пешкова - является одним из наиболее совершенных произведений архитектуры Баженова. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 году. При восстановлении здание приобрело более массивные формы. Не сохранилась внутренняя планировка здания, о которой дают представления только чертежи нижнего этажа.

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).

Рис. 13. Парфенон.

Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.

Существуют математические закон архитектурной гармонии. В приложении приведён анализ трёх сооружений, принадлежащих разным эпохам и стилям в архитектуре, с помощью золотого сечения: храм Агии Софии в Константинополе - памятник Византии (приложение 4), Смольный собор в. Санкт - Петербурге (приложение 5), собор в Ульме в Германии (приложение 6). Как видно из рисунков, большинство пропорциональных соотношений этих зданий являются соотношениями золотого сечения.

Римский архитектор Ветрувий написал сочинение «Об архитектуре», включающее в себя десять книг. Особое внимание в этих книгах уделено пропорциям человеческого тела, которое Ветрувий перенёс на здания. Он считал, что без симметрии и пропорции строение храма лишено правильности, свойственно хорошо сложенному человеку.

Меры длины у различных народов являются производными от размеров члена человеческого тела, которые постоянно служили основой производимых при строительстве измерений. Длина стопы человека - фут (0,3087 м) была одна из основной античных мер.

При строительстве храма в честь Дианы, греки для колоннады взяли пропорции, свойственные стройной женщине. Толщина колонны в этой колоннаде составляла 1/8 высоты, а высота капители - 1/3 толщины. Новый ордер получил название ионический, а колонны, возводимые по канонам этого ордера, напоминали изяществом, украшениями и пропорциями стройную женщину.

Зодчие и архитекторы древности знали о золотой пропорции и сознательно применяли её. Однако теорию гармонизации пропорции в строительстве создал известный французский архитектор Ле Корбюзье. В системе, названной «Модулор», он объединил существующее предложение о пропорциях человеческого тела с математическими принципами золотого сечения.

1.6.2 «Золотая пропорция» живописи

Долгое время считали, что в изобразительном искусстве теория художнику не нужна, а знакомство с наукой не обязательно. Многие даже считали, что это мешает свободному индивидуальному творчеству. Но мастера древней Греции, умевшие сознательно пользоваться законами золотого сечения применяли их для создания гармонии в произведениях и добились такого совершенств строения форм, выражающие их общественные идеалы, какое редко встречается в практике мирового искусства. Вся античная культура прошла под знаком золотой пропорции. Знали эту пропорцию и в древнем Египте. Знание законов золотого сечения или непрерывного деления помогает художнику творить осознанно и свободно. Используя закономерности золотого деления можно исследовать пропорциональную структуру любого художественного произведения.

В. И. Суриков говорил, что в композиции есть свой закон, благодаря которому в картину ничего нельзя добавить и ничего нельзя от неё отнять.

При переносе геометрического способа деления на картину или эскиз поступают так: половину длины картины или эскиза откладывают на высоту или на продолжение высоты, если эскиз узкого формата. Полученную точку С соединяют с левым нижним углом картины, и т. д.(рис. 14)

(Рис. 14)

Линия золотого сечения в левой части картины будет находится на таком же расстоянии от левого края, как и в правой, от правого (показано пунктиром)

Фигура А.С. Пушкина в картине И.Е. Репина «А.С. Пушкин на акте в лицее 8 января 1815 год» помещена художником на линию золотого сечения в правой части картины (приложение 7).

Левая часть картины, в свою очередь, тоже разделена в пропорции золотого сечения. От головы А.С. Пушкина Г.Р. Державина и от неё до левого края картины. Расстояние от головы Державина до правого края картины разделено на две равные части линией золотого сечения. В нижней части картины глаз улавливает деление на три равные части. Их образует стол в левой части картины, нога Пушкина правее линии золотого сечения и правый край картины.

Если необходимо найти золотое сечение по горизонтали, то новое деление геометрическим способом высоты картины нет необходимости. Достаточно провести диагонали картины. Их пересечения с линиями золотого сечения по вертикали укажут точки, через которые следует провести горизонтальные линии золотого сечения (приложение 8). Эти линии ещё могут понадобиться при построении пейзажа.

При нахождении Φ, картина делится, в основании, на 100 частей.

Недостаток деления на 10 или 5 заключён в том, что даёт довольно приблизительные отрезки золотого сечения: 60, 40, 20 (таблица 1, ряд 1).

Таблица 1. Величины нисходящего ряда золотой пропорции

Фигура А.С. Пушкина в картине «Александр Сергеевич Пушкин в селе Михайловском» поставлена художником на линии золотого сечения в левой части полотна (приложение 9).

Но и все остальные величины по ширине вовсе не случайны: ширина печи равна 24 частям от ширины картины, этажерка - 14 частям, расстояние от этажерки до печи тоже 14 частей и - т.д. Такие же величина присутствуют и в картине Репина (приложение 7): от левого края до головы Державина 24 части, от стола до носка правой ноги Пушкина - 24 части. Такое расстояние от головы Пушкина до головы военного, с восторгом слушающего чтение поэта. От головы Пушкина до головы молодой женщины в правой части картины, с умилением слушающей декламацию, тоже 24 части, а от её головы до правого края картины - 10 частей и т.д.

Повторение равных величин, чередование равных и неравных величин в пропорциях золотого сечения создаёт в картине определённый ритмический строй, вызывающий у зрителя то или иное настроение и втягивающий его в рассмотрение картины.

Достоинство пропорции золотого сечения заключается в том, что раз поделив отрезок прямой или сторону картины геометрическим способом, получают отрезки любого уменьшения. В практической же работе художника достаточно величин, соответствующим числовым значениям: 62,38,24,14 и 10.

Но, всё же, какова бы не была прекрасна эта пропорция, рассматривать её отдельно от симметрии нельзя. Художественная форма, в основе построения которой лежит пропорции золотого сечения, и особенно сочетания симметрии и золотого сечения, является высокоорганизованной формой, способствующей наиболее ясному выражению содержания, наилучшему зрительному восприятию и появлению у зрителей ощущения красоты.

Вот несколько картин, которые были представлены мне для нахождение в них золотого сечения:

И.Е. Репин.

«Осенний букет», 1892 г. На полотне изображена дочь Репина Вера. Браслет на левой руке делит картину в золотой пропорции по горизонтали.

«Портрет П.М. Третьякова». Глаз Третьякова делит картину по золотому сечению (по вертикали).

«Садко в подводном царстве» (1876 г.). Ярко выраженная представительница подводного царства делит картину по вертикали в золотом сечении. По горизонтали - борода Садко.

«Приготовление к экзамену». Герой, заснувший с книгой в руках, делит по вертикали.

На панораме Флоренции 1490 года река разделяла город по золотому сечению.

На следующих работах можно видеть композиционный анализ картин (приложения 10,11,12,13,14,15).

.7 Золотая пропорция в человеке

.7.1 Пропорция

Пропорции человека с древних времён привлекали учёных, художников, скульпторов, биологов. Они искали закономерности пропорций человеческого тела. Существует свидетельство Плиния о том, что скульптор Поликлет написал статью о правилах пропорции человеческого тела, и вылепил по ним знаменитую статую Доридофа (приложение 15), хорошо сохранившуюся до наших дней. Долгое время эта фигура служила каноном человеческого тела.

Римский архитектор Ветрувий говорил, что природа создала человека, соблюдая постоянное отношение отдельных частей к целому, так:

·   лицо, считая от подбородка до лба, включительно, составляет 1 / 10 части всей высоты человека;

·   столько же составляет длина кисти руки;

·   часть тела, считая от груди до начала волос равна 1/6 общей высоте фигуры человека;

·   высота всей фигуры, от подбородка - 1/8 всей высоты человека;

·   лицо состоит из трёх разных частей: первая, от подбородка до начала носа, вторая - до средней линии бровей, третья - от линии бровей до начала корней волос;

·   ступня ноги составляет 1/6 от всей длинны человека;

·   длина руки от локтя, а так же ширина груди между плечами, составляет ¼ высоты человека.

.7.2 Золотая пропорция в человеке

Вообще все части человека находятся в определённом численном отношении к общей его высоте.

Рассмотрим классический пример Адольфа Цейзинга, его труд (457 страниц), под названием «Der golden Schnitt» («золотое сечение»), опубликованный в 1884 году. Цейзинг доказывает, что из всех пропорций именно золотое сечение даёт художественный наибольший эффект доставляет наибольшее удовольствие при восприятии. Он формулировал закон пропорциональности следующим образом: «Для того, что бы целое, разделённое на две неравные части, казалось прекрасным с точки зрения формы, между меньшей и большей частями должно быть тоже самое отношение, что между большей частью и целым».

Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа - важнейший показатель золотого сечения (рис. 15). Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела:

Рис. 15, а

Отношение расстояния от головы до кончиков средних пальцев, когда руки опущены вдоль тела, и расстояние от кончиков пальцев до подошвы тоже равно золотой пропорции; высота лица (до корней волос) относится к вертикальному расстоянию между дугами бровей о нижней частью подбородка, как расстояние между нижней частью носа и нижней частью подбородка относится к расстоянию между разрезом губ и нижней частью подбородка.

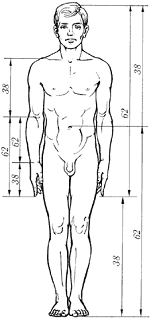
(рис. 15, б)

Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского, Венеры Медицейской и т.д. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название "Золотое деление как основной морфологический закон в природе и искусстве". В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга.

В том же духе выдержанны и книги «Nature’s Harmonic Unity» («Гармоническое единство природы») С. Колмена (1913 г.) и «the Curves of Life» («Кривые жизни») Т. Кука (1914 г.). Последний сравнивал различные стадии и картины художников эпохи Возрождения и создаёт идеальный канон женского тела. (Приложение 17).

Вертикальная шкала справа от женской фигуры разделена сверху вниз на части в соответствии с членами возрастающего ряда от φ¹ до φ⁷. Нетрудно заметить, что эти деления совпадают с основными членениями человеческого тела.

Много размышлял на тему о Ф и Фрэнк А. Лонк. Измерив, рост 65 женщин и сравнив полученные данные с расстоянием от пупка соответствующей особы до пола. Среднее отношение оказалось равным 1,618…и было названо «относительной постоянной Лонка». Субъекты, у которых отношение данных не совпадало, говорили, что перенесли в детстве вывих бедра или стали жертвой несчастного случая, повлекшего за собой деформацию тела. Он произвёл более точные вычисления числа π. Лонк возвёл в квадрат число Ф умножив результат на 6 и поделив затем полученное число на 5. По его расчётам, значение π выражается десятичным числом 3,14164078644620550.

Если поставить открытую ладонь вертикально перед собой, направив большой палец к лицу, и, начиная с мизинца, последовательно сжимать пальцы в кулак, получается движение, которое и есть спираль Фибоначчи.

.7.3 Кровяное давление

При работе сердца в сосудах создаётся гидродинамическое давление, вызываемое сопротивлением стенок сосудов. Для взрослого человека условно нормальным считается артериальное давление: максимальное (систолическое) -100 - 140 мм рт. ст. и минимальное (диастолическое) - 70 - 90 мм рт. ст.

Таким образом, диапазон возможных давлений у человека составляет

- 100 - 140 мм рт. ст.

Разделим этот диапазон в отношении 1,618 : 1, получим

/ 1,618 = 61,8 мм рт. ст.;

/ 1,618 = 86,5 мм рт. ст.

Что очень хорошо приближается к параметрам диастолического давления.

При заболевании гипертонической болезнью или при повышенных физических нагрузках артериальное давление повышается. Максимально возможное систолическое давление у человека может достигать 230 мм рт. ст.

Предельное значение артериального давления отличается от нормального систолического в покое в 1,618 раза:

* 1,618 = 226,5 мм рт. ст.

Связь с золотой пропорцией очевидна.

.7.4 Сердце и дыхание

Частота сокращения сердечной мышцы (частота пульса) и частота дыхание характеризуют состояние органов кровообращения и поэтому являются важным показателем здоровья человека.

Нормальный сердечный ритм в покое составляет 70-75 сокращений в минуту, а ритм дыхания 16-17 дыханий в минуту. Предельно возможные минимальные показатели этих двух ритмов соответствуют состоянию смерти и равны нулю. Предельно допустимые максимальные показатели этих двух ритмов для абсолютного большинства людей равны соответственно 190 - 200 сокращений сердца в минуту и 42-45 дыханий в минуту.

Таким образом, возможный диапазон числа сердечных сокращений составляет 0 - 190 - 200 сокращений в минуту, а сокращений лёгкого -

- 42 - 45 дыханий в минуту.

Разделим эти диапазоны золотым сечением:

(190-200) / 2,618 = 72,6-76,4, что приблизительно равно 73-74 сокращений в минуту;

(42-45) / 2,618 = 16,04-17,19, что приблизительно равно 16-17 дыханий в минуту.

На приведённых примерах показано, что физиологические функции связанны с золотым сечением.

.8 Второе золотое сечение

Болгарский журнал "Отечество" (№10, 1983 г.) опубликовал статью Цветана Цекова-Карандаша "О втором золотом сечении", которое вытекает из основного сечения и дает другое отношение:

: 56.

Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.

Деление осуществляется следующим образом. Отрезок АВ делится в пропорции золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой угол АСD делится пополам. Из точки С проводится линия до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56 : 44.

На рисунке 16 показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.

Таким образом, было доказано, что разделить отрезок в крайнем и среднем отношении можно не единственным способом.

Рис. 16.

.9 Серебряное сечение

История о невостребованном числе (Иэн Стюарт).

Архитектор Ричард Падован обнаружил некую последовательность целых чисел, которую, не обладай она весьма интересной геометрической метафоричностью и не допускай некоторых поразительных параллелей с золотым сечением, можно было бы счесть достаточно тривиальной - в связи с чем злые языки поспешили обозвать её «искусственной» и «пластмассовой». Эта последовательность является рекуррентным соотношением

Р_i+3 = P_i + P_i+1

Причём

Р₀ = Р₁ = 0, Р₂ = 1.

Уравнение этой последовательности будет выглядеть

p ³ - p - 1 = 0

Уравнение аналогично

φ ² - φ - 1 = 0

решением которого является золотое сечение φ.

Приблизительное значение р можно вычеслить до любого желаемого знака посредством интеграции выражения:

где р = 1,324717957.

Глава 2. Обучение математике в гуманитарных классах

2.1 Место математики в гуманитарных классах

Математику обычно относят к естественнонаучным дисциплинам, и из всех других наук наиболее близкой к ней считается физика. Достаточно вспомнить об ученых степенях кандидата и доктора физико-математических наук.

Однако за последнее время появились и другие классификации. Физик Л.Д. Ландау шутил, что все науки делятся на естественные (физика и др.), неестественные (история и др.) и противоестественные (математические). Математик И.М. Яглом уже всерьез отделял математику от всех остальных наук: “Естественные науки - физика, химия, астрономия, биология, медицина... - изучают окружающий нас мир; гуманитарные - история, литература, филология, юриспруденция, социология,... - человеческое общество, также представляющее собой реальность, поддающуюся наблюдениям и даже эксперименту; математика же (ибо группа математических наук сводится к одной науке - математике) изучает самое себя. С этой, безусловно, самой основной точки зрения различие между математикой и “нематематикой” оказывается несравненно более глубоким, чем различие между естественными и гуманитарными дисциплинами”[8,С.6].

В той же книге И.М. Яглом приводит как дискуссионное мнение А.В. Гладкого о том, что математика - это наука гуманитарная. С этим мнением нельзя не согласиться, ибо, изучая саму себя, математика имеет своим объектом результаты деятельности человеческого разума, что роднит ее с искусствознанием и науковедением.

Обратимся к проблеме математического образования в гуманитарных классах. Каким должно быть преподавание математики в классах с различной профильной направленностью? Что общего и чем отличается обучение математике в этих классах? Нужна ли вообще математика в гуманитарных классах?

Хорошо известно, что математика является объектом общей культуры человека. Она нужна и художнику, и биологу, и музыканту. Это связано с тем, что рациональные (мышление) и иррациональные (ощущение) психические функции у большинства людей взаимосвязаны, поэтому подавление одних может немедленно ослабить и другие. Проблемы обучения математике в классах гуманитарного профиля, а также изучение индивидуальных особенностей учеников-гуманитариев (преобладание наглядно-образного мышления, богатое воображение, ярко выраженная эмоциональность восприятия окружающей действительности, интерес к вопросам истории математики, занимательному материалу, проявлению красоты математики в произведениях искусства, явлениях живой и неживой природы) разрабатываются в течении серидины ХХ - ХХI.

Однако в этих исследованиях далеко не в полной мере учтен разнородный состав школьников, избравших конкретный раздел гуманитарного профиля образования. В частности, то, что справедливо относительно будущих историков или, например, художников, может быть не вполне приемлемо для учащихся классов сугубо лингвистической направленности (иностранные и родной языки, литература, журналистика), в последнее время приобретающих все большее распространение в современной школе. При этом недостаточно учитывается, например, тот факт, что математика произошла из языка и до сих пор является своеобразным языком, строящимся по специфическим правилам и предназначенным для максимально точного описания определенных характеристик (пространственных, количественных) действительного мира. Такая общность реального языка и математических конструкций не только говорит о возможности развития языкознания путем его формализации, но и должна вносить соответствующие коррективы в процесс усвоения содержания затрагиваемых предметов.

Математическая память.

В результате многочисленных специальных экспериментов выяснилось, что все способности человека имеют некую общую основу, важную для развития и проявления практически любой из них. Общие способности определяют уровень и своеобразие любой умственной деятельности, именно поэтому их часто и называют умственными способностями. Можно привести много впечатляющих примеров того, как один и тот же человек с успехом занимался различными видами деятельности. Например, А.С. Пушкин был не только гениальным поэтом, но и признанным мастером портретной графики. Он в совершенстве владел французским языком, глубоко изучал историю и вообще, по мнению современников, был одним из умнейших людей своего времени. Создатель "Горя от ума" А.С. Грибоедов известен еще как дипломат и музыкант. Крупнейший ученый древности Архимед соединял в себе математика, механика, физика, инженера. Великие художники эпохи Возрождения Леонардо да Винчи и Альбрехт Дюрер не просто увлекались математикой, но и добились известных результатов в теории многогранников и теории перспективы. Этот ряд примеров далеко не заканчивается перечисленными персоналиями.

Для того чтобы способности дали о себе знать, нужна соответствующая среда, соответствующее обучение. Если этого нет, то возможности человека могут и не проявиться. К сожалению, довольно часто человек даже не подозревает о своих способностях. История знает много ярких примеров того, когда только случайность помогла человеку найти свой путь. Например, знаменитый математик, создатель московской математической школы Н.Н. Лузин рассказывал, что в гимназии плохо успевал по математике, пока отец не нашел ему репетитора, который начал занятия с самых азов и постепенно внушил своему подопечному глубокое понимание красоты математики.

Приведенные примеры указывают на недопустимость ранней специализации. Психологи называют определенные возрастные периоды, наиболее благоприятные для развития специальных способностей. Для различных способностей такие периоды неодинаковы. Наиболее ранний период имеют способности музыкальные и лингвистические. Они ярко проявляются уже в начальных классах. Математические же способности обнаруживаются позже, в среднем школьном возрасте, приблизительно к 14-15 годам. Они могут проявиться немного раньше, но могут и позже. Отсюда вывод: нельзя исключать из школьных программ предметы, носящие общекультурный, развивающий характер, к которым, безусловно, относится и математика.

При введении курса математики в гуманитарном классе мы развиваем не только логическое мышление, но и понятийный аппарат учащихся.

Существует распространенное мнение, что математика в гуманитарных классах - это просто математика для неспособных к ней, математика для слабых. И что состоять она должна лишь из обязательного минимума («задач на тройку»). Якобы, изучая ту или иную теорему в гуманитарном классе, ее не обязательно доказывать, а надо лишь научить простейшим применениям этой теоремы. Известны школы с сильными гуманитарными классами, в которых математику преподают именно так. Нам известно, какое отвращение к математике испытывают ученики этих классов.

Представление о математике как о науке гуманитарной в корне меняет такой взгляд. С этой точки зрения рассматривают математику в гуманитарных классах А.В. Гладкий и Г.Е. Крейдлин в журнале «Математика в школе»: “...в гуманитарной школе математика не должна быть падчерицей среди других дисциплин. Но преподавать ее следует именно в гуманитарном аспекте, вынося на первый план ее общечеловеческий характер. Этим должны определяться и содержание курса, и конкретные способы преподавания. Говоря о содержании любого курса математики (независимо от особенностей школы), можно выделить три основных аспекта: логический, образный и технический. Для гуманитарной школы наиболее важен первый из них. Формировать понятия, строить классификации, отделяя существенные признаки от несущественных, проводить строгие рассуждения - вот главное, чему должен научиться в курсе математики ученик такой школы” [11,С.6 - 7].

Итак, здесь же рекомендуют следующие принципиальные задачи преподавания математики в гуманитарных классах:

· усилить (а не ослаблять) идейную сторону преподавания математики;

· ослабить (а не усиливать) рутинную техническую сторону преподавания.

Иначе говоря, в гуманитарных классах нужно преподавать математику более для головы, чем для рук.

Основные принципы обучения «для головы, а не для рук»:

. Направленность обучения на развитие личности ученика, формирование для каждого школьника своего собственного индивидуального стиля деятельности.

. Вариативность обучения, т.е. разнообразие его содержания, форм и методов. Этот принцип обеспечивает каждому учащемуся возможность выбрать учебный материал в соответствии со своими индивидуальными возможностями и интересами, предпочтительными формами и методами работы. При этом основное содержание обучения, конечно, не может быть свободным, добровольным или выборочным.

. Валидность обучения, означающая достаточно высокую значимость математического материала для достижения результатов обучения.

. Успешность обучения, понимаемая нами в том, что у каждого ученика должен быть свой, пусть маленький, но собственный успех в обучении. Успех рождает вдохновение, уверенность в своих силах. Задача учителя - помочь каждому ученику достичь такого успеха.

. Открытость методической работы учителя. Речь идет не только о понимании учениками целей обучения, но и о том, чтобы учащиеся представляли себе, почему, например, они доказывают какую-либо теорему или решают определенную задачу, или чем хорошо предложенное индивидуальное задание и т.д. Ученикам должно нравиться построение уроков, их основные этапы, техника проведения каждого из них.

Необходимо ввести понятийный аппарат, раскрывающий теорию гуманитаризации школьного математического образования.

Математические объекты - «все математические понятия, имеющие самостоятельный смысл и употребление». Утверждения о математических объектах и их свойствах, различные связи между объектами и утверждениями будем называть логическими конструкциями .

Гуманитарные объекты представляют собой элементы различных систем гуманитарной культуры - истории, музыки, искусства, архитектуры, скульптуры, различных жанров литературы и т.д.

Изучение математических объектов и логических конструкций происходит на когнитивном уровне; изучение же гуманитарных объектов - преимущественно на эмоционально- ценностном, чувственном уровне.

Составные объекты - органически взаимосвязанные между собой математические объекты, логические конструкции и гуманитарные объекты. Взаимосвязи между перечисленными объектами и конструкциями осуществляются в большей степени на эмоционально-ценностном уровне, хотя и не без участия когнитивных процессов познания.

.2 Положение теории гуманитаризации математического образованя

Теория носит название гуманитаризации школьного математического образования. Данное название отражает характер основных направлений модернизации системы обучения.

Идентификация:

- по уровню применения данная технология обучения является частно-предметной, так как раскрывает особенности обучения математике;

- по отношению к ребёнку - личностно-ориентированная;

  по направлению модернизации традиционной системы обучения технология основывается на конкретной реализации идеи гуманитаризации школьного математического образования, раскрытой ранее.

Концептуальная часть: позиция ребёнка. Рассмотрим законы высшей нервной деятельности, объясняющие процессы познания. Первый закон взаимной индукции. Суть его в следующем: «если возбуждаются одни участки головного мозга, то в других в это время идут процессы торможения». Например, когда решается математическая задача, все знания о литературе, театре как бы «замирают». Второй закон - закон динамического стереотипа: «при частых, постоянных раздражениях одних участков головного мозга и столь же постоянных раздражениях других происходит устойчивое распределение очагов возбуждения. М.Л. Портнов подмечает важную закономерность: «чем больше очагов возбуждения, тем больше их может появиться - возможности головного мозга во много раз выше, чем кажется».

Описанные характеристики познавательного процесса дают возможность предположить, что обучение учащихся будет носить более продуктивный характер, если при изучении дисциплин естественно-математического цикла мы по возможности активно будем воздействовать на различные участки головного мозга, используя органические части гуманитарных и негуманитарных дисциплин.

Среди целей, положенных в основу технологии гуманитаризации школьного математического образования, можно выделить следующие:

учебные цели в когнитивной (мыслительной) области:

формировать умения учащихся строить новые сочетания математических знаний со знаниями, полученными из системы гуманитарной культуры;

формировать умения учащихся транслировать математический материал из одной формы выражения в другую, т.е. умение интерпретировать учеником математический материал с помощью гуманитарных объектов;

формировать умения учащихся использовать изученный математический и гуманитарный материал в конкретных условиях и новых ситуациях, отыскивать точки соприкосновения математической и гуманитарной культур.

Заметим, что, сформулированные выше цели не касаются теоретических основ математики, поскольку задача предлагаемой технологии гуманитаризации - не вносить изменения в действующую систему математических знаний, а обогащать её гуманитарными объектами.

Учебные цели в эмоционально-ценностной области:

формировать восприятие учащимися целостной картины мира, а не разделённой на различные области человеческого познания;

формировать эмоционально-личностное отношение учащихся к таким составным частям культуры, как математика и гуманитарные науки;

способствовать концептуализации ценностных ориентаций учащихся к составным частям культуры, организации собственной системы ценностей;

развивать правополушарные и левополушарные возможности учащихся как одного из условий формирования необходимого уровня усвоения ценностей, на котором они устойчиво определяют поведение индивида, входят в привычный образ действий или жизненный стиль.

Для гуманитаризации школьного математического образования осуществляется системный подход. Элементами этой системы являются цели и содержание школьного математического образования, раскрывающее связи с предметами гуманитарного цикла; законы высшей нервной деятельности, объясняющие процессы познания, методы и средства обучения. Функционирование указанных элементов системы должно основываться на следующих основополагающих принципах: принципах гуманизации; принципе личностно-ориентированного подхода; принципе целостности; принципе выделения основной структуры системы и принципе органичности.

Остановимся подробнее на принципах, положенных в основу технологии школьного математического образования, подчеркивая еще раз, что эти принципы должны представлять технологию как педагогическую систему с необходимым перечнем принципов, присущих системному подходу.

Принцип целостности

Это означает, что при разработке педагогической системы необходимо добиваться гармонического взаимодействия всех компонентов педагогической системы как по горизонтали (в рамках одного периода обучения - четверти, учебного года), так и по вертикали (на весь период обучения).

Принцип выделения основной структуры системы

Важность данного принципа обосновывается в теории систем И.Д. Пехлецкого. Исследователь считает, что это один из основных принципов, который должен «наложить свой отпечаток на все фундаментальные определения и понятия теории системы». Причем смысл принципа выделения основной структуры системы состоит в том, что «всякое научное рассмотрение, анализ или моделирование достаточно сложной, абстрактной или реальной системы не возможны без процесса выдвижения на первый план некой части структуры системы».

С позиций целей исследования основной частью такой педагогической системы будет являться математическое содержание, ко всей же остальной структуре педагогической системы относятся гуманитарные и составные объекты.

Принцип органичности

Он означает, что при разработке технологии гуманитаризации школьного математического образования необходимо достичь органичного взаимодействия между математическими и гуманитарными системами культуры. Гуманитарные объекты должны естественным образом включаться в математическое содержание.

2.3 Построение гуманитаризованного курса математики

Рассматривая конкретные пути построения программы курса математики для гуманитарных классов, нужно принять во внимание мнение самих гуманитариев. Правильным, но трудоемким делом было бы проведение подробной анкеты среди них.

Многое можно почерпнуть и из литературы. Например, из воспоминаний А.И. Цветаевой, удалось понять разницу между восприятием гуманитариями двух основных предметов школьной математики - алгебры и геометрии. Оказывается, геометрия воспринимается лучше и сознательнее. Тут играют роль и более удачная организация курса, и его наглядность, логичность, доказательность, опора на историю науки и большее разнообразие задач (меньшее количество однотипных упражнений).

Возможными путями построения программы по математике для гуманитарных классов являются следующие:

· оставить неприкосновенным курс геометрии, отведя на него большее число часов за счет сокращения курса алгебры;

· курс алгебры существенно упростить в техническом отношении, оставив неприкосновенной его теоретическую глубину.

Учебная программа лицеев строится таким образом, чтобы обеспечить углубленную гуманитарную подготовку учащихся. Предметы математического цикла, реализующие общеобразовательную программу полного среднего образования, вызывают у учащихся, проявляющих склонности и способности к изучению иностранных языков, литературы и истории, целый ряд трудностей, связанных с индивидуально-психологическими особенностями личности и мотивацией к обучению. Для учащихся лицеев в большей степени свойственны эмоциональное отношение к событиям, образность и живость мышления. Для них трудна деятельность, связанная с оперированием абстрактным материалом, математическими понятиями и выражениями.

Внедрение современных компьютерных технологий в курс математики позволяет учащимся повысить интерес к изучаемому предмету и успешно освоить ряд тем обязательного минимума образования по математике. На наш взгляд, наиболее удачными темами таких уроков являются:

Организованные межпредметные связи помогают учащимся не только лучше усвоить некоторые темы по математике, но и совершенствовать свои навыки работы с компьютером при решении математических задач.

В результате этого взаимодействия значительно возрастает интерес и к математике, и к информатике.

Гуманитарное образование - база для широкого диапазона возможностей профессионального выбора учащихся. Среди выпускников гуманитарного профиля - учителя и журналисты, психологи и юристы, филологи, историки и экономисты.

Нестандартные уроки - уроки, проводимые в игровой форме: занятия с элементами игры, соревнования, содержащие игровые ситуации.

Игровые формы должны включаться не для того, чтобы развлечь учащихся, а с целью формирования у них мотивации к обучению. Так же нестандартными уроками по математике будут являться уроки, направленные на историческое значение данной темы.

.4 Психолого-педагогические особенности учащихся гуманитарных классов

Исходя из анализа наблюдений, анкетирования, опыта преподавания в профильных классах, исследователи выделяют следующие психолого-педагогические особенности учащихся гуманитарных классов:

. У учащихся гуманитарных классов преобладает наглядно-образное мышление, а математических - абстрактно-логическое.

. У школьников-гуманитариев восприятие красоты математики направлено на ее проявление в живой природе, в произведениях искусства, в конкретных математических объектах. Учащиеся математических классов интерес математики видят в необычных, неожиданных решениях задачи.

. На уроке в гуманитарных классах внимание может быть устойчивым в среднем 12 - 15 минут.

. Из форм работы на уроке гуманитарии предпочитают объяснение учителем нового материала, деловые игры, выполнение индивидуальных заданий с использованием справочной литературы. Математики - решение нестандартных, проблемных, исследовательских задач.

. Из методов самостоятельной работы гуманитарии выбирают коллективные. Математики чаще действуют индивидуально.

. У гуманитариев богаче воображение, чем у математиков, сильнее проявляются эмоции.

. В гуманитарных классах по составу учащихся больше девочек (в математических - мальчиков). Этот фактор не нашел в нашей школе пока должного внимания и учета.

Глава 3. Факультативные занятия

Важнейшим фактором успеха в будущем обучении является интерес учеников к предмету. Поэтому деятельность учителя, урок, задания на нём должны быть интересными и увлекательными. Интерес школьников к предмету является всё же ведущим фактором обучения. Но нехватка времени на уроке приводит к тому, что «самое интересное» в понимании школьников остаётся неохваченным. Поэтому внеклассная работа имеет немаловажное значение. Основным видом внеклассной работы по математике в школе являются кружки и факультативные занятия. Вызывая интерес у школьников они помогают развить творческие способности учеников, прививают самостоятельность и переносят заинтересованность к этому предмету на урок.

Золотое сечение имеет интересную историю, которая захватывает не только математику, но и другие области знания. Соответствующая тема обладает занимательностью и математической красотой, и поэтому имеет полное право быть рассматриваемой на математических факультативах. При планировании данной темы необходимо иметь в виду уровень подготовленности учащихся. Исходя из этого, считаю, что тема «Золотое сечение» может быть рассмотрена в девятом классе.

К этому возрасту ребята уже знакомы с построением середины отрезка, биссектрисы угла, перпендикулярных прямых, треугольника по трём элементам. Так же знакомятся на уроках геометрии с теоремой о сумме углов в треугольнике, с теоремой Пифагора и Фалеса, изучают тему «Подобные треугольники», где знакомятся с признаками подобия треугольника и рассматривают пропорциональные отрезки в прямоугольном треугольнике.

На уроках эти темы рассматриваются в полной мере, что позволяет больше времени уделить на новые темы на факультативах.

Можно выделить несколько целей факультативного курса:

обучение школьников делению отрезка в крайнем и среднем отношении;

овладение практическими навыками использования геометрических инструментов для изображения фигур;

формирование представлений о математике как о части общечеловеческой культуры, о значимости математики в других сферах деятельность.

Ниже предоставляется тематическое планирование, рассчитанное на 8 академических часов.

Заседание №1

Определение золотого сечения. История возникновения и применения его на практике.

Цели:

Образовательная: дать понятие золотого сечения; способы построения золотого сечения построения отрезка .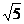

Развивающая: формирование чертёжных навыков.

Воспитательная: точность при выполнении чертежей; аккуратность.

Оборудование: линейка, карандаш, циркуль.

Форма проведение урока: «Суд над золотым сечением»

Оформление класса: судейский стол, плакаты, столик поменьше с книгой на нём для клятвы. Половина классного кабинета освобождена от стульев и парт - своеобразная сцена.

Действующие лица: председатель суда, присяжный заседатель, свидетели, обвинитель и обвиняемый, находящиеся по разным сторонам сцены.

Ход урока.

Председатель суда начинает: сегодня в этом зале происходит слушанье дела по обвинению золотой пропорции в бесполезности её существования, а так же присвоение её таких имён как: «золотое деления», «божественная пропорция», «золотое сечение».

подсудимая, прошу встать! Ваше имя?

Золотая пропорция.

повернитесь к залу, что бы Вас все увидели и запомнили.

Рис. 1 (Показывают плакат с изображённой на ней золотой пропорцией)

Год рождения. Национальность.

Для ответов на эти вопросы приглашается свидетели, которые расскажут биографию подсудимой.

(выступают подготовленные ученики с докладами об истории золотого сечения)

Свидетели: клянусь говорить правду, только правду и ничего, кроме правды.

Доклад №1

Золотое сечение было известно древним грекам. Вряд ли можно сомневаться в том, что некоторые древнегреческие архитекторы и скульпторы сознательно использовали его в своих творениях. Примером может служить хотя бы Парфенон. Именно это обстоятельство и имел в виду американский математик Марк Барр, лет так 85 назад, когда предложил называть отношение двух отрезков, образующих золотое сечение, числом j. Буква j (фи) - первая буква в имени великого Фидия, который, по преданию, часто использовал золотое сечение в своих скульптурах. Одной из причин, по которой пифагорейцы (последователи Пифагора) избрали пентаграмму, или пятиконечную звезду, символом своего тайного ордена, является то обстоятельство, что любой отрезок в этой фигуре находится в золотом отношении к наименьшему соседнему отрезку.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н. э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. Действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

Греки были искусными геометрами. Очень интересно, что они обучали своих

детей алгебре при помощи геометрических фигур. Квадрат Пифагора и диагональ его были основанием для построения динамических прямоугольников (Рис. 2)

Рис. 2 Динамические прямоугольники.

Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

Доклад №2

Где-то в XIII веке в историю золотого сечения было вплетено имя математика монаха родом из Италии, Леонардо из Пизы. Хотя нам он известен под другим именем, а точнее по прозвищу Фибоначчи (Fibonacci - сокращенное filius Bonacci, то есть сын Боначчи). В 1202г. им была написана книга "Liber abacci", то есть "Книга об абаке". "Liber abacci" представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими ("арабскими") цифрами.

Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением, как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи, художник и ученый, видел, что в итальянских художниках большой эмпирический опыт, но недостаток знаний. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Его называли творцом начертательной геометрии.

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г. по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи.

Леонардо да Винчи много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение, которое держится по наши дни.

В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: "Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать".

Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица - ртом и т.д. Известен пропорциональный циркуль Дюрера.

хорошо, свидетели. Обвиняемая, считаете ли Вы себя виновной?

нет!

в таком случае слово предоставляется обвинению. Господин обвинитель, прошу встать.

Обвинитель. Клянусь говорить правду, только правду и ничего, кроме правды.

Милые господа, прошу внимания. Золотая пропорция является, скорее всего, одной из самых известных пропорций в математике, может даже и самая шикарная и красивая, очень правильная, везде встречающая. И, наверное, никакая больше пропорция не имеет в себе столько ужасных штрихов, как она. На вопрос: «Что такое «Золотая пропорция»?» большинство людей даже предположить не могут. Итак, первым обвинением будет то, что завоевав Наше доверие, вскружила голову даже не представилось. У меня всё, господа!

Судья. Слово для защиты предоставляется подсудимой. Подсудимая, что Вы можете сказать в своё оправдание? (Учитель даёт определение золотого сечения, исполняя роль золотой пропорции).

Пропорция. Господа судьи, меня здесь обвиняют в бесполезности и вредности. Обидно мне слышать такие слова. Вы оглянитесь, посмотрите, везде увидите моё существование, и этим существованием я даю красивую жизнь для очень многого на земле! Я в цветах и, вообще, в растениях; я в шедеврах мировой архитектуры, да и вообще в строительстве; я в музыке, в поэзии, в анатомии. Даже астрономам не чужда я. А свойства мои - это моё богатство, не зная их, плохо бы пришлось человеку. Сейчас расскажу Вам по подробней. Но сперва, можно более точно преставиться?

Судья. Разрешаю.

Обвиняемая (Гордо). Деление отрезка в крайнем и среднем отношении!

Меня надо понимать так: разделить данный отрезок, на такие две части, что бы меньшая относилась к большей так, как большая ко всему отрезку!

Но для этого надо найти хотя бы один отрезок. Попробуем отыскать больший отрезок. Допустим, что сначала речь пойдёт не о построении отрезка, а о нахождении его длины. Этот вопрос (задача) будет решаться приблизительно так: если длину всего отрезка обозначим за а, а длину большей части х, то длина другой части будет равна а - х, то есть

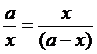
Отсюда, х² = а(а - х) или х² + ах - а² = 0

Решив уравнение, получим

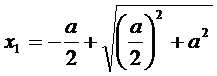
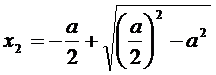
Возьмём положительный корень уравнения:

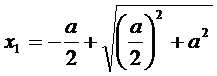
Получим

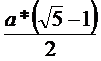
Таким образом, задача всегда имеет единственное решение.

Исходя из теоремы Пифагора, то выражение, находящееся под корнем можно расценивать как гипотенузу треугольника с катетами равными а и а/2, тогда х - разность между гипотенузой и а/2, то есть что бы разделить отрезок в заданном отношении, нужно построить треугольник с катетами а и 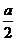. затем из гипотенузы этого треугольника вычесть а/2 и оставшийся отрезок равный

отложим на первоначальном отрезке а (Рис. 1).

Если принять отрезок а за единичный, то получим следующее числовое выражение:

Число j - называется коэффициентом золотого сечения.

Мне кажется, я привела достаточно доказательств своей невинности.

Обвинитель. Господин судья, прошу слово.

Судья. Разрешаю.

Обвинитель. Допустим Вы везде по всюду, но какова же Ваша причастность к геометрии. Можете привести конкретный пример?

В защиту вызываются свидетели для решения этого вопроса.

Задача 1.

Построить правильный пятиугольник по данной стороне АВ = 1.

Решение:

Находим на отрезке АВ точку С золотого сечения. Из точки В как из центра проводим окружность радиусом АС, которая пересекает продолжение отрезка АВ в точке D.

Строим две окружности с центром А и В радиусом

AD = .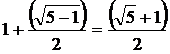

Одна из точек пересечения - точка Е, третья вершина пятиугольника. Потом из точки В чертим окружность радиусом АВ. Она пересекается с предыдущей окружностью в точке N, четвёртой вершине пятиугольника. Из точек А и Е проводим окружности, радиусы которых равны длине отрезка АВ (стороне правильного пятиугольника). Две последние окружности пересекаются в пятой вершине К пятиугольника.

Судья. Заседание продолжается. Слово предоставляется обвиняемой.

Обвиняемая. Что бы вспомнить меня надо проводить построения каждый раз. Что бы избежать этого воспользуемся теоремой Фалеса. Сначала вспомним, как она звучит: если параллельные прямые, пересекающие стороны угла, отсекают на другой его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Обвинитель. Протестую. Каким образом эта теорема причастна к делению отрезка на n равных частей, допустим на 3?

Обвиняемая. Давайте посмотрим на рисунок.

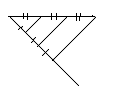
Возьмём теперь другой отрезок и разделим его в соответствии с золотым сечением, используя теорему Фалеса и отрезок, уже разделённый в золотом сечении. С этим отрезком поступим как и в предыдущем случае.

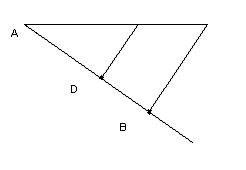
Судья. (Читает приговор). Именем Высших Адептов Света Великий Суд постановляет:

Золотую пропорцию считать полностью оправданной ввиду её необходимости в жизни и в математике в частности. Суд считает, что обвинение, выдвинутое против Золотой пропорции, не обоснованно.

Вывод.

Идёт знакомство с новым материалом. Показывается важность математики в жизни.

Заседание 2

Тема: Построение правильных треугольников

Цели: обобщение изученного материала, применение математических знаний к решению задач, овладение практическими навыками использования геометрических инструментов для изображения фигур.

Форма проведения: математический вечер.

Оформление: плакаты с высказываниями о математики, в частности о золотом сечении, на люстры надеты плафоны в виде геометрических (Платоновых тел), карточки с заданиями.

На входе участников встречает учитель, на время взявший на себя ответственность швейцара. Билеты в виде золотых прямоугольников и треугольников раздаются на входе.

Приветствие ведущего:

Да здравствует, всяк сюда вошедший!

Правильные многогранники уже в глубокой древности считались символом красоты. Ведь правильно, что из всех многоугольников с заданным числом сторон наиболее приятен для глаз правильный многоугольник, у которого все стороны и углы равны.

На нашем вечере Мы будем подчиваться следующими блюдами. Первое:

Лёгкое блюдо для разжигания аппетита.

Теперь предлагаю отведать второе блюдо.

(задание раздаются каждой команде. Победа за той, кто быстрей справиться с задачей)

1.  построить правильный выпуклый шестиугольник. (Рис. 3. 1)

2.   построить правильный выпуклый треугольник. (Рис. 3. 2)

. построить правильный выпуклый двенадцатиугольник. (Рис. 3. 3)

. построить правильный выпуклый восьмиугольник. (Рис. 3. 4)

. построить правильный выпуклый шестиугольник, описанный около окружности. (Рис. 3, 5)

Рис. 3(проверка жюри)

Ведущий. Спасибо за то, что по достоинству оценили наше блюдо.

Теперь немного салатов. Будем украшать их.

(раздаётся материал для «украшения салатов» - задача)

Задача.

Построить правильный двенадцатиугольник со стороной, равный данному отрезку.

Решение

Построим равносторонний треугольник АВС, равный данному отрезку АВ. Через точку С проведём прямую, перпендикулярную отрезку АВ. Отложим на этой прямой отрезок СО, равный АВ. Тогда отрезок ОА является радиусом окружности, описанного около правильного двенадцатиугольника со стороной АВ.

Для этого достаточно доказать, что угол АОВ = 30⁰. точка С равноудалена от А, В и О, то есть является центром окружности, описанного около треугольника АОВ. Следовательно угол АОВ = ½ угла АСВ = 30⁰. теперь на окружности радиуса АО от любой точки последовательно отложим 11 дуг, каждая из которых равна дуге АВ. Получим вершины правильного двенадцатиугольника.

Ведущий. Теперь специальное блюдо. Заливное из шестнадцатиугольника.

Построить правильный шестнадцатиуголькик со стороной, равный заданному.

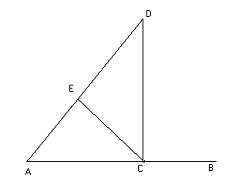
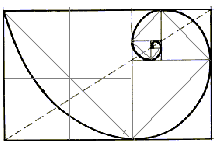
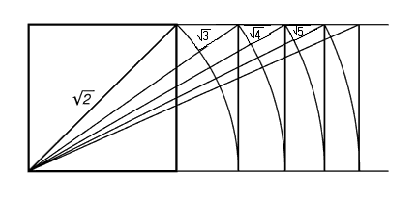
Решение:

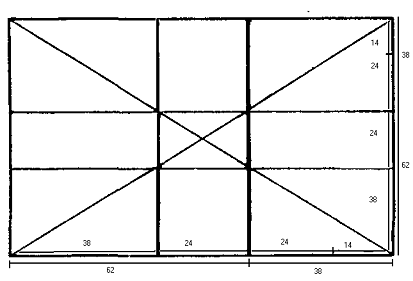
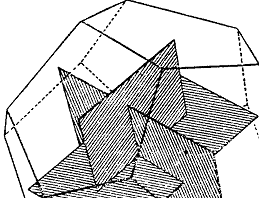
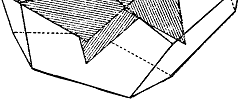
Из середины С отрезка АВ восстановим перпендикуляр и на нём отложим отрезок CD, равный ½ АВ. Затем отрезок DE, равный AD и ЕО, равный АЕ. Тогда отрезок АО является радиусом окружности, описанного около правильного шестнадцатиугольника со стороной АВ. (Рис. 4)

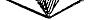
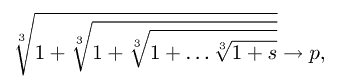
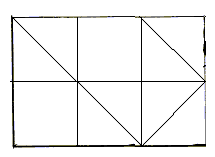
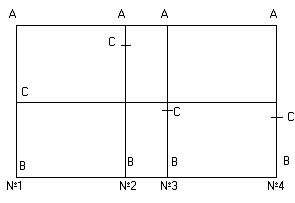
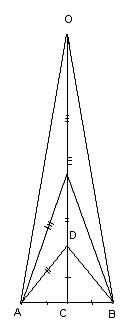
АЕВ = ½ ADB = 45⁰

АОВ = ½ АЕВ = 45⁰/2

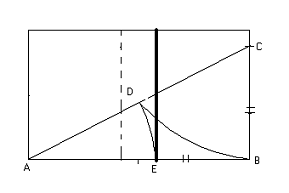т.е. АОВ = 360⁰/16.

Рис. 4

Ведущий. К сожалению наша встреча подходит к концу!

Идёт подсчёт баллов.

Всё, что хотели мы, сделали и огромное спасибо за посещения нашего вечера!!!

Заседание 3

Тема: Применение золотого сечения при построении правильных многоугольников.

Цели: овладение практическими навыками использование геометрических инструментов при построении правильных многоугольников; развитие самостоятельности и математической речи.

Форма проведения: математическая игра.

Ведущий. (приветствие. Говорит о том, что сегодняшняя игра посвящается правильным пятиугольникам и десятиугольникам.)

Наши команды уже подготовились к трудным, но интересным этапам. Они стремятся к победе. Мы начинаем первый раунд.

Первый раунд «Тёмная лошадка»

Ведущий задаёт наводящие вопросы, игроки должны угадать о каком предмете идёт речь. Задаётся 8 вопросов. (в чёрном ящике вносят циркуль)

Вопросы:

1.  (10 очков) Существует легенда о греческом изобретателе Дедале (мастер, сделавший крылья Икару) и его племяннике, очень талантливом юноше, который придумал гончарный круг, первую в мире пилу и то, что лежит в этом ящике. За это он расплатился собственной жизнью, которую отнял у него дядя в порыве зависти. Дедал столкнул его с большого вала.

2.   (9 очков) Самый древний предмет пролежал под землёй 2000 лет.

. (8 очков) Под пеплом Помпеи археологи обнажили много таких предметов. Изготовлены из бронзы. В нашей стране это впервые было обнаружено при раскопках в Нижнем Новгороде.

. (7 очков) За многие сотни лет конструкция этого предмета практически не изменилась, настолько совершенна она.

. (6 очков) В древней Греции умение пользоваться этим предметам считалось верхом совершенства, а умение решать задачи с помощью него, признаком большого ума и высокого положения.

. (5 очков) Этот предмет незаменим в архитектуре и строительстве.

. (4 очка) Писатель Ю. Олеша, автор «Трёх толстяков», писал: «В бархатном ложе лежит, плотно сжав ноги, холодный и сверкающий. У него тяжёлая голова. Я намереваюсь поднять его, он неожиданно раскрывается и производит укол в руку».

. (3 очка) «Сговорились две ноги делать дуги и круги».

Второй раунд: «Заморочки из бочки».

Ведущий. Предлагаю решить следующую задачу.

(решение будет разбираться на доске)

Задача. Доказать, что сторона правильного вписанного в окружность десятиугольника равна большей части золотого сечения радиуса этой окружности. Вписать данную окружность в правильный десятиугольник.

Решение

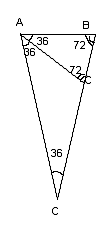
Пусть АВ - сторона правильного вписанного в окружность десятиугольника. Тогда

 АОВ = 36⁰, а каждый из углов АОВ и АВО = 72⁰.

Проведём биссектрису АС угла А треугольника АОВ. Так как АСВ = 72⁰, то из равнобедренных треугольников АВС и АСО получим АВ = АС = ОС.

По свойству биссектрисы треугольника получаем:

ОС : ВС = ОВ : ОС, то есть ОС² = ВС*ОВ, а это и означает, радиус ОВ разделён точкой С в золотом сечении, причём ОС - большая часть радиуса (потому что АСВ >

) ВАС, откуда ОС = АВ > ВС). Таким образом, разделив радиус ОВ в золотом сечении и взяв большую его часть, мы найдём длину стороны АВ правильного вписанного в окружность десятиугольника.

Теперь от любой точки данной окружности последовательно отложим 9 хорд, равных АВ.

Раунд 3. «Ты - мне, я - тебе».

Команды обмениваются вопросами в виде заранее приготовленных задач, связанные с построением правильного пятиугольника с помощью циркуля и линейки.

Например.

Построить прямоугольник отношением сторон 1 : .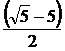

Решение:

Проводим отрезок АВ = 1, точкой С делим его в золотом отношении. Тогда АС = 1 - 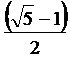 = 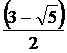. Продолжим отрезок АВ за точку А, и из точки А проведём окружность радиуса АС. Пересечение с продолжением АВ будет точка D. Из точки В восстановим перпендикуляр ВМ к АВ. Строим окружность с центром в точке В радиусом ВD.

ВD = 1 +  =.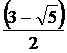

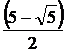Окружность пересекает перпендикуляр ВМ в точке Е, длина стороны прямоугольника равна .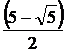

По окончанию игры подводятся итоги и раздаются дипломы.

Заседание 4

Тема: Золотое сечение вокруг нас.

Цели: 1. Воспитание интереса к предмету у учащихся.

. Расширение кругозора. Показ связи математики с другими науками.

Форма проведения: математический вечер.

Действующие лица: королева - пропорция, докладчики: профессор Цейзинг, Иоганн Кеплер, Леонардо да Винчи, композитор Л. Сабанеев, искусствовед Розенов.

Ход занятия

Пропорция. Здравствуйте. Кто-то называет меня «Пропорция», а Лука Пачоли назвал меня однажды «Божественная Пропорция». Я та, кто вносит гармонию и красоту в шедевры мировых произведений, в окружающую природу, в строение человеческого тела. Мой один из наиболее горячих поклонников Адольф Цейзинг говорит, что я «господствую» в природе.

Профессор Цейзинг. (доклад одного из ученика)

Давайте поговорим о строении человеческого тела. То, что части красиво сложенного нашего тела находятся в определенной пропорции. Нам это известно, ведь недаром мы употребляем термин «пропорционально сложенная фигура». Но далеко не всем известно, что здесь речь идёт о золотом сечении. Очень хорошим примером являются античные статуи для изображения человеческого тела и нахождения пропорции в нём. Идеально сложенное тело полностью отвечает этому принципу. Если разделить хорошо сложенного человеческого тела в крайнем и среднем отношении, то линия разделения окажется на уровне талии, а точнее пупа. Особенно хорошо эта пропорция видна на мужском теле.

Деление тела точкой пупа - важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела.

Но не только тело целиком делится, ещё и отдельные части его находятся в зависимости (голова, рука, кисть). Разделив в крайнем и среднем отношении голову человека, увидим, что раздел приходится на линию бровей. При дальнейшем делении образовавшихся частей последовательно получим: кончик носа, кончик подбородка и т.д.

Рука тоже делится с помощью золотого деления: плечо, предплечье, кисть, фаланги пальцев.

Пропорция. А сейчас давайте посмотрим как это правило действует на Нас. (практическая работа)

Пропорция. Дальше пожалуйста Иоган Кеплер. (золотое сечение в растительном мире)

Расположение листьев на деревьях не случайно, а подчиняется определённому математическому закону. Рассмотрим вот что. Если внимательно рассмотреть веточку с листьями, то можно заметить, что основания черенков располагаются по винтовой линии. Если соединить последовательно основания листьев ниткой, то она обовьётся вокруг стебля. Проследить расположение листьев на этой спирали, мы непременно увидим листья расположенные один над другим. Часть спирали, заключённая между такими листьями в ботанике называется «циклом».

Для краткости и удобства обозначим листорасположение в виде дроби, в числителе которого число оборотов, в знаменателе - число листьев в этом цикле. Так, дробь 3/8 показывает, что один цикл спирали трижды огибает стебель, и что в этом цикле 8 листьев. Эта же дробь показывает расхождение двух соседних листьев.

Каждый вид растений имеет своё листорасположение. И этот угол всегда подчиняется определённому закону.

Пропорция. С помощью измерения веточек растений вычислить подчиняется ли Ваша веточка этому правилу.

(выполняется второе практическое задание)

Пропорция. Наш вечер почтил своим присутствием сам Леонардо ди Сьер Пьеро да Винчи. Ему предоставляется слово.

(«Золотое сечение в эстетике»)

Долгое время считали, что в изобразительном искусстве теория художнику не нужна, а знакомство с наукой не обязательно. Многие даже считали, что это мешает свободному индивидуальному творчеству. Но мастера древней Греции, умевшие сознательно пользоваться законами золотого сечения применяли их для создания гармонии в произведениях и добились такого совершенств строения форм, выражающие их общественные идеалы, какое редко встречается в практике мирового искусства. Вся античная культура прошла под знаком золотой пропорции. Знали эту пропорцию и в древнем Египте. Знание законов золотого сечения или непрерывного деления помогает художнику творить осознанно и свободно. Используя закономерности золотого деления можно исследовать пропорциональную структуру любого художественного произведения.

Но давайте поговорим о времени, которое ближе к Нам. В 60-х годах прошлого столетия члены Рижского общества естествоиспытателей провели следующее исследование: они собрали несколько тысяч визитных карточек различных людей и определили отношение длин их неравных сторон. Среднее отношение довольно сильно подходило к золотому сечению. Прямоугольная форма книг, бумажников, окон, рамок для картин - более или менее удовлетворяет пропорции золотого деления.

В архитектуре уже сталкиваемся с более точным и сознательным применением того же принципа. Рассмотрим известную фигуру зодчества - Парфенон (Рис. 6).Длина - 31,2 метра, высота - 19,3. Отношение высоты здания к его длине равно 0,618. Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным.

Рис. 6

Пропорция. Ребята, я даю Вам на дом задание: измерить множество предметов и взять среднее от их величин. Допустим, аудио кассету, отношение длинной к короткой стороне.

А мы продолжаем. Далее будет выступать композитор Сабанеев и искусствовед Розенов.

Композитор. Я занимался исследованиями музыкальных произведений классиков и пришёл к такому выводу, что отдельные интервалы соответствуют золотому сечению. Оно присутствовало в таком огромном количестве объектов моего исследования, что их количество перевалила за 50% от всего мною разобранного, так сказать.

Искусствовед. Золотое сечение обнаружено и в поэтических произведениях. Экспериментами стиховедов и физиологов установлено, что если единица ритма стихотворения короче 0,1 с, то слух человека не фиксирует разрыв речи и речевой поток кажется непрерывным; если период превышает 10 с, то восприятие периодичности тоже прекращается. Следовательно, оптимальное время единицы ритма расположено в границах от 0,1 до 10 с.

Найдём продолжительность единицы стихотворного ритма по закону золотого сечения, исходя из границ.

T_опт = 0,1 +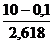

 3,88

И действительно, в основном столько и затрачивается на произнесения одной строки.

Пропорция. И так, я встречаюсь в изобразительном искусстве и прикладном, в архитектуре и музыкальных произведениях, в литературе и предметах быта.

Заседание 6

Тема: Многоугольник своими руками.

Цель: 1. Воспитание интереса к предмету у учащихся.

. Выработка навыков работы с бумагой.

. развитие познавательного интереса и эрудиции учащихся.

Форма проведения: интеллектуальная игра.

Оборудования: плакаты, наглядные пособия.

Ход занятия

Раунд 1

Ведущий.(интеллектуал 1 категории)

ВОВ началась 22 июня 1941 г. Узнать, сколько дней продолжалась война Вам поможет волшебный квадрат, но для начала решите пожалуйста следующую задачку.

Задача. Как из бумажного прямоугольника получить квадрат?

Решение. Возьмём лист бумаги (прямоугольный). Складываем, что бы одна из коротких сторон лежала на длинной стороне. Тот кусочек (прямоугольник), что остался не согнутым, можно отрезать. (Рис. 7)

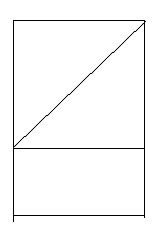
Место пере-

гиба

Часть, которую

можно отрезать.

Рис. 7

Ведущий. А вот и квадрат, который поможет Нам узнать ответ на вопрос. (Рис. 8)

Рис. 8

Выберите из каждой строки и каждого столбца по одному числу, найдите сумму выбранных чисел, и вы получите ответ на вопрос. (1418)

Раунд 2. «Хочу всё знать»

Ведущий. На земном шаре обитают птицы, которые безошибочно составляют погоду на лето. Название их Вы узнаете решив следующую задачу.

Задача. Как из бумажного квадрата сгибанием получить равносторонний треугольник. (Рис. 9)

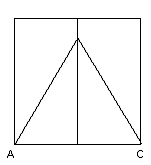
Рис. 9

Решение. Возьмём на средней линии квадрата такую точку, что бы её расстояние от двух вершин квадрата были ровны его стороне, и сделаем перегибы, которые проходят через эту точку и углы квадрата, лежащие по обеим сторонам средней линии. В этом случае получаем р/с треугольник.

Ведущий. Молодцы! Птица-метеоролог - фламинго. Они строят гнёзда из песка в виде усечённого конуса, в верхнем основании делая углубления для яиц.

Высота гнезда зависит от того каким будет лето: сухим - низкое гнездо, дождливое - гнездо высокое, что бы не затопило водой.

Раунд 3. биология

Ведущий. Тихий океан. На его островах живут черепахи-гиганты. Они такой величины, что дети могут кататься на них верхом.

Название самой большой черепахи узнаете, если решите следующую задачу. А так же расскажу об одной из самых странных работ на земле.

Задание. Как из квадрата получить правильный шестиугольник? (Рис. 10)

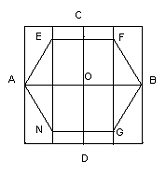
Рис. 10

Решение

Перегибанием квадрата через середину противоположных сторон. получаем линии АОВ и СОD. На сгибах АО и ОВ строим известным уже способом р/с треугольники АЕО, АОN, ВОF, ВОG. Делаем перегибы ЕF и NG. Многоугольник и будет правильным шестиугольником.

Ответ на этот вопрос - дермохеликс.

Раунд 4. «Это интересно знать»

Ведущий. Однажды в английском графстве Камберленд разразилась гроза, сильный ветер вырывал деревья с корнями, образуя воронки. В одной из воронок жители обнаружили какое-то чёрное вещество. Название Вы узнаете после очередного задания.

Задание. Как в данном квадрате построить правильный восьмиугольник. (Рис. 11)

Решение

Возьмём данный нам квадрат и впишем в него другой квадрат.

Разделим пополам углы между сторонами данного и вписанного квадрата (Рис. 11. 1). Пусть сгибы, делящие эти углы пополам, пересекаются в точках E, F, G, H. Полученный многоугольник и есть искомый восьмиугольник (Рис. 11. 2).

Ведущий. Это вещество - графит.

Кусочками графита начали метить овец, а торговцы делали надписи на корзинах и ящиках. Но это первые использования графита…дальше - больше.

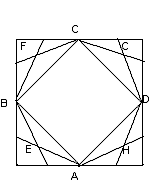
В конце учитель-ведущий подводит итог.

Рис. 11.1                  Рис. 11.2

Заседание 7

Тема: Оригами и золотое сечение.

Цели: 1. научится делать из бумаги фигуры.

. рассмотреть некоторые золотые фигуры (золотой прямоугольник, спираль, пятиконечная звезда)

Ход занятия

1.   Организационный момент

Сегодня мы научимся делать из простых листов бумаги настоящие звёзды и рассмотрим их прекрасные свойства.

2.   Звёзды из бумаги.

Известно, что, складывая лист бумаги можно получить какую-нибудь фигуру, допустим с острыми концами. Возьмём пятиконечную звезду.

Она представляет собой десятиугольник, вершины которого чередуются через одну, определяют лучи (концы) нашей звезды.

Но давайте сначала рассмотрим четырёхконечную и трехконечную звезду. Разрешается сделать один прямой разрез.

Сложим бумагу 1 раз (Рис. 12 а). Затем ещё раз, получим квадрат (Рис. 12 б). квадрат не является звездой, так как углы при его вершине не острые.

Третье складывание (Рис. 13 а) - получаем настоящую четырёхугольную звезду (Рис. 13 б), а если сделать перегибы в разные стороны (Рис. 13 в) получаем трёхконечную звезду (Рис. 13 г).

Задание. Получить с помощью четырёх складываний пятиконечную и шестиконечную звезду.

Как сделать шестиконечную звезду, показано на рисунке 14 а.

Пятиконечную построить труднее. Смотрите рисунок 15.

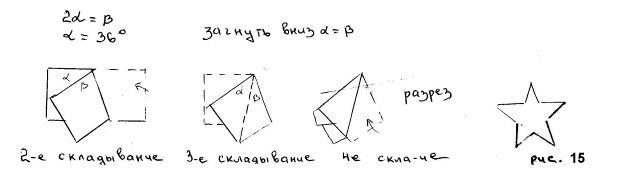
3.   Свойство пятиконечной звезды

Проведём в правильном пятиугольнике диагонали. Они образуют пятиконечную звезду и обладают удивительными свойством: точки пересечения делят диагонали в золотом сечении.

Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком. Бытует легенда о том, что один из пифагорейцев больным попал в дом к незнакомым людям. Они старались его выходить, но болезнь не отступала. Не имея средств заплатить за лечение и уход, больной перед смертью попросил хозяина дома нарисовать у входа пятиконечную звезду, объяснив, что по этому знаку найдутся люди, которые вознаградят его. И на самом деле, через некоторое время один из путешествующих пифагорейцев заметил звезду и стал расспрашивать хозяина о том, каким образом она появилась у входа. После рассказа хозяина гость щедро вознаградил его.

4.   Оригами и золотое сечение

) Дан прямоугольник 1х2. складывая прямоугольник только два раза получаем золотое сечение. (Рис 16 а, б)

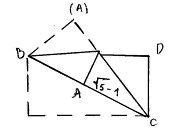
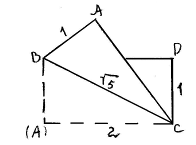
Рис. 16 а                                               Рис. 16 б

Решение

Сложите прямоугольник по диагонали СВ. Загните угол А так, чтобы сторона легла на сторону BD. СВ = 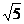 (по т. Пифагора), АВ = 1 => СА = 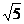 - 1, DB = 2.

2)   Взяв квадратный лист бумаги и сделать не более 4 складок, проведите складку (рис. 17), отсекающую у нашего квадрата прямоугольник, отношение сторон которого равнялись бы числу ф.

Решение

Пусть сторона исходного квадрата равна 2. на рисунке 18 а) мы с помощью одного складывание находим середину стороны квадрата, вторая складка представляет собой диагональ прямоугольника 1х2. Загнём угол А вниз (Рис. 18 б) так, чтобы АС лёг вдоль второй складки, образуя третью складку BD параллельно АС (Рис. 18 в), совмещая ED c EC, тогда АВ: АС = ф.

А Рис. 18. Б

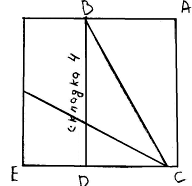
В

Прямоугольник, который мы получили в последней задаче, называется золотым, так как его отношение сторон образует золотое сечение.

Эта фигура обладает многими интересными свойствами. Если, например, от золотого прямоугольника отрезать квадрат со стороной, равной меньшей стороне прямоугольника, то снова получим золотой прямоугольник, но меньших размеров. Если этот процесс продолжать, то получим , так называемые, вращающие квадраты.

Если соединить противоположные вершины квадратов, то получим кривую, называемую золотой спиралью. Такую спираль можно заметить в природе: раковины моллюсков, улиток. Семечки в подсолнечнике располагаются по золотой спирали.

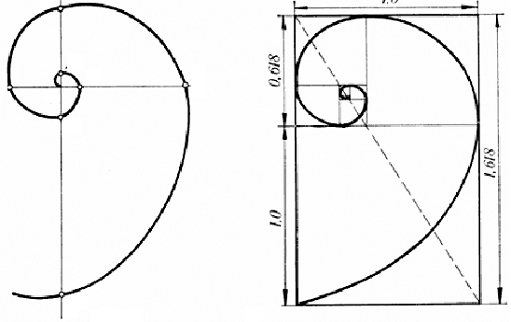
Ведущий. На этом наше занятие подошло к концу.

Заключение

Понимание математики как науки гуманитарной, изучающей особое направление деятельности человеческого разума, играет важную роль в уточнении всех компонентов методической системы преподавания математики в школе.

В работе были рассмотрены основные положения и принципы теории гуманитаризации. Внедрение элементов технологии гуманитаризации может проводить каждый учитель, обладающий творческим потенциалом, любящий свой предмет и относящийся к ученикам как к субъектам обучения. Но чтобы правильно строить процесс обучения, учителя всегда должны помнить, что человеческое мышление изначально двустороннее: логическая и эмоционально-образная стороны существуют как равноправные части.

Список литературы

1. Азевич А.И. Двадцать уроков гармонии. М., 1998 г.

2. Беспалько В.П. Слагаемые педагогической технологии М., Педагогика, 1989.

3. Васютинский Н.А. Золотая пропорция. - М.: Молодая гвардия, 1990 г.

. Волошинов А.В. Математика и искусство. - М. Просвещение, 1992 г.

. Воробьёв Н.Н. Числа Фибоначчи. - М.: Наука, 1969 г.

. Газале М. Гномон. От фараонов до фракталов.

. Гарднер М. Математические досуги. М.: Мир, 1972 г.

. Гладкий А.В., Крейдлин Г.Е. // Математика в школе. - 1994. - № 2.

. Гика М. Эстетика пропорции искусства. - М.,1972 г.

. Гримм Г. Д. Пропорциональность в архитектуре. - М.,1935 г.

. Душенко К. В. «Всё по науке». - 2-е, перераб. Издание. - М.: Изд-во Эксмо, 2005.

. // Математика в школе. - 1994, № 3.

. // Художественная галерея №36, 2005, стр. 4, 5, 7, 15.

. // Художественная галерея №7, 2005, стр. 14.

. Кеплер И. О шестиугольных снежинках. - М.: Наука, 1982 г.

. Ковалёв И.О. Золотое сечение в живописи. - Киев: Высшая школа, 1989 г.

. Лихачев Б.Т. Педагогика. - М.: Прометей, 1993

. Нафиков Н.Н. Гипотеза об истоке золотого сечения.//Математика в школе 1994, №3, стр. 76-77.

. Оценка качества занятий по математике. - М: Дрофа, 2000.

. Пидоу Д. Геометрия и искусство. - М., 1979 г.

. Полякова Т.С., Кондрашова З.И., Герасимова О.С. Гуманитаризация школьного образования, использование литературы в обучении математике. Изд-во РГПУ, 1997.

. Рошаль В.М. Энциклопедия символов. - М.: аст; СПб.: Сова, 2005 г.

. Стахов А. Коды золотой пропорции. - М.: Мир, 1979.

. Стратилатова П. Из опыта проведения внеклассной работы по математике в средней школе. Сб. статей под ред. - М.: Учпедгиз, 1955.

. Шевелёв И.Ш. Золотое сечение.//Квант, 1997, №6.

. Яглом И.М. Математические структуры и математическое моделирование. - М., 1980.

Приложение 1

золотой треугольник

приложение 2

Вершины золотых прямоугольников совпадает с вершинами икосаэдра

Приложение 3

Вершины тех же «золотых» прямоугольников, что и во втором приложении, совпадает с центрами додекаэдра.

Приложение 4

Храм Агии Софии в Константинополе

Приложение 5

Приложение 6

Приложение 7

Приложение 8

Линии золотого сечения и диагонали на картине

Приложение 16

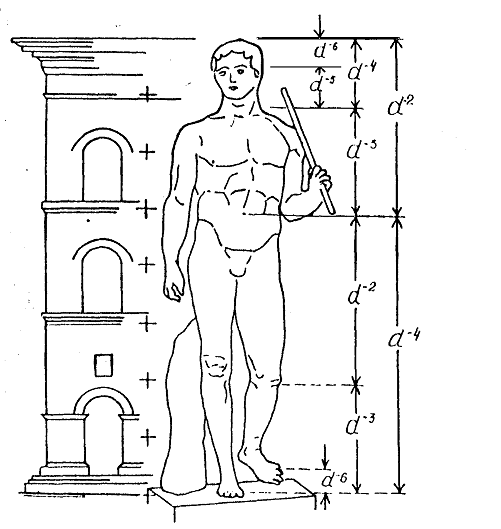
приложение 17

"Vetruvio architetto mette nelle sue opera d’architettura che le misure dell’omo…”

" Архитектор Ветрувий заложил в своей архитектуре измерения человека..."