Приложения качественной теории дифференциальных уравнений к биологическим задачам
Выпускная работа
Приложения
качественной
теории
дифференциальных уравнений
к
биологическим задачам
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
ГЛАВА 1.
1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ТЕОРЕМЫ, ИСПОЛЬЗУЕМЫЕ В ДАЛЬНЕЙШЕМ.
1.1 СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ И СИСТЕМ.
1.2 ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ.
2. ОСНОВЫ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ.
2.1 АВТОНОМНЫЕ УРАВНЕНИЯ
2.2 АВТОНОМНЫЕ СИСТЕМЫ НА ПЛОСКОСТИ
3. ЛИНЕЙНЫЕ СИСТЕМЫ
3.1 ЛИНЕЙНАЯ ЗАМЕНА ПЕРЕМЕННЫХ
3.2 ФАЗОВЫЕ ПОРТРЕТЫ ДЛЯ КАНОНИЧЕСКИХ СИСТЕМ НА ПЛОСКОСТИ
4. НЕЛИНЕЙНЫЕ СИСТЕМЫ НА ПЛОСКОСТИ
4.1 ЛОКАЛЬНОЕ И ГЛОБАЛЬНОЕ ПОВЕДЕНИЕ ФАЗОВЫХ ПОРТРЕТОВ НЕЛИНЕЙНЫХ
СИСТЕМ
4.2 ЛИНЕАРИЗАЦИЯ СИСТЕМ В ОКРЕСТНОСТИ ОСОБОЙ
ТОЧКИ
4.3 СЛОЖНЫЕ ОСОБЫЕ ТОЧКИ
4.4 ОБЫКНОВЕННЫЕ ТОЧКИ
5. ПРИМЕРЫ, ИЛЛЮСТРИРУЮЩИЕ
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ.
ГЛАВА 2.
1. ПРИЛОЖЕНИЕ КАЧЕСТВЕННОЙ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ К
БИОЛОГИЧЕСКИМ ЗАДАЧАМ.
1.1 ФАЗОВЫЕ ПОРТРЕТЫ И ДИНАМИКА.
1.2 КОНКУРИРУЮЩИЕ ВИДЫ.
1.3 УРАВНЕНИЯ ВОЛЬТЕРРА - ЛОТКА.
1.4 МОДЕЛЬ ХОЛЛИНГА - ТЭННЕРА.
2. ДРУГИЕ МОДЕЛИ.
СПИСОК ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
Моя выпускная квалификационная работа посвящена
изучению основ качественной теории дифференциальных уравнений и ее приложений к
биологическим задачам и имеет следующую структуру:
В первой главе я рассматриваю теоремы о
существовании и единственности решений дифференциальных уравнений и систем,
геометрическую интерпретацию решений, автономные уравнения и системы на
плоскости, линейные системы и линейную замену переменных, типы фазовых
портретов для канонических систем, нелинейные системы на плоскости и их
линеаризацию в окрестности особой точки, локальное и глобальное поведение их
фазовых портретов, сложные особые точки и обыкновенные точки. В конце главы я привожу
примеры, иллюстрирующие теоретический материал, в которых исследую на
устойчивость решения дифференциальных систем, нахожу положения равновесия
уравнений, исследую особые точки и рисую фазовые плоскости траекторий уравнений
и систем.
Вторая глава посвящена приложениям теории
дифференциальных уравнений в биологии. Здесь я рассматриваю дифференциальные
уравнения, моделирующие динамику популяций конкурирующих видов, их решения и
фазовые портреты. Более подробно изучаю уравнения Вольтерра - Лотка, модель
Холлинга - Теннера. В конце главы исследую другие модели, описывающие
конкуренцию двух видов, рассматриваю уравнение типа «хищник - жертва» и рисую
типичные фазовые портреты для этих моделей. Примеры и модели я подбирала и
исследовала самостоятельно.
Работа состоит из 80 страниц машинописного
текста, список литературы содержит 5 наименований.
Теория дифференциальных уравнений возникла из
прикладных задач в области механики и астрономии и в настоящее время самым
тесным образом связана с приложениями. Она оказывает большое влияние на
развитие других областей математики. Характеризуя математику как метод
проникновения в тайны природы, можно сказать, что основным путем применения
этого метода является формирование и изучение математических моделей реального мира.
Изучая какие-либо физические и биологические явления, исследователь прежде
всего создает его математическую идеализацию или, другими словами,
математическую модель, то есть, пренебрегая второстепенными характеристиками
явления, он записывает основные законы, управляющие этим явлением, в
математической форме. Очень часто эти законы можно выразить в виде
дифференциальных уравнений. Такими оказываются модели различных явлений
механики сплошной среды, химических реакций, электрических, магнитных и биологических
явлений и др.
Исследуя полученные дифференциальные уравнения
вместе с дополнительными условиями, которые, как правило, задаются в виде
начальных и граничных условий, математик получает сведения о происходящем
явлении, иногда может узнать его прошлое и будущее. Изучение математической
модели математическими методами позволяет не только получить качественные
характеристики физических явлений и рассчитать с заданной степенью точности ход
реального процесса, но и дает возможность проникнуть в суть физических явлений,
а иногда предсказать и новые физические эффекты. Бывает, что сама природа
физического явления подсказывает и подходы, и методы математического
исследования. Критерием правильности выбора математической модели является
практика, сопоставление данных математического исследования с
экспериментальными данными.
Для составления математической модели в виде
дифференциальных уравнений нужно, как правило, знать только локальные связи и
не нужна информация обо всем физическом явлении в целом. Математическая модель
дает возможность изучать явление в целом, предсказать его развитие, делать
количественные оценки изменений, происходящих в нем с течением времени.
Как известно, теория обыкновенных
дифференциальных уравнений начала развиваться в XVII веке одновременно с
возникновением дифференциального и интегрального исчисления.
Обыкновенные дифференциальные уравнения
возникают тогда, когда неизвестная функция зависит лишь от одной независимой
переменной. Соотношение между независимой переменной, неизвестной функцией и ее
производными до некоторого порядка составляет дифференциальное уравнение. В
настоящее время теория обыкновенных дифференциальных уравнений представляет
собой богатую, широко разветвленную теорию. Одними из основных задач этой
теории являются существование у дифференциальных уравнений таких решений,
которые удовлетворяют дополнительным условиям (начальные данные Коши, когда
требуется определить решение, принимающее заданные значения в некоторой точке и
заданные значения производных до некоторого конечного порядка, краевые условия
и другие), единственность решения, его устойчивость. Под устойчивостью решения
понимают малые изменения решения при малых изменениях дополнительных данных
задачи и функций, определяющих само уравнение. Важными для приложений являются
исследование характера решения, или, как говорят, качественного поведения
решения, нахождение методов численного решения уравнений.
Важно отметить, что для проверки правильности
математической модели очень важны теоремы существования решений соответствующих
дифференциальных уравнений, так как математическая модель не всегда адекватна
конкретному явлению и из существования решения реальной задачи (физической,
химической, биологической) не следует существование решения соответствующей
математической задачи.
Начало качественной теории дифференциальных
уравнений было положено в работах знаменитого французского математика Пуанкаре.
В настоящее время теория дифференциальных уравнений представляет собой
исключительно богатый содержанием, быстро развивающийся раздел математики,
тесно связанный с другими областями математики и с ее приложениями.
Многие разделы теории дифференциальных уравнений
так разрослись, что стали самостоятельными науками. Можно сказать, что большая
часть путей, связывающих абстрактные математические теории и естественнонаучные
приложения, проходит через дифференциальные уравнения. Все это обеспечивает
теории дифференциальных уравнений почетное место в современной науке.
Известно много приложений математики в биологии.
В первую очередь это исследования по физиологическим проблемам, относящимся к
ощущениям, кровообращению, движению животных; эти исследования можно
рассматривать как разделы оптики, акустики, гидродинамики, механики твердого
тела.
Мы будем рассматривать биологические сообщества.
Они состоят из нескольких популяций биологических видов, живущих в общей среде.
Обычно индивидуумы этих сообществ оспаривают одну и ту же пищу, или же одни
виды живут за счет других, которыми они питаются. Так же они могут и взаимно
оказывать друг другу помощь. Все это входит в общее явление борьбы за
существование. Количественный характер этого явления проявляется в заданной
среде в виде изменений численности индивидуумов, составляющих различные
популяции. В определенных условиях эти изменения состоят в колебаниях числа
индивидуумов около некоторых средних значений, в других случаях они вызывают
исчезновение или прогрессирующее увеличение некоторых видов.
Изучение этих вариаций и разнообразных изменений
является важным теоретически, но во многих случаях это изучение представляет и
огромную практическую важность, как это мы имеем в случае живущих в одних и тех
же морях разных видов рыб, изменение числа которых интересует промышленность.
Точно так же изменение числа паразитов растений интересует агрономию в том
случае, когда эти паразиты ведут борьбу за существование с их собственными
паразитами. Инфекционные болезни, например, малярия, показывают также
изменения, которые зависят, по всей вероятности, от подобных же причин.
Борьба за существование относится к тем
вопросам, о которых в конце позапрошлого века очень много спорили, но не делали
почти никаких попыток узнать, что она в действительности собой представляет. В XX
веке несколько выдающихся людей ясно чувствовали необходимость математической теории
борьбы за существование и делали определенные шаги в этой области. При этом
часто один исследователь не знал о работах другого, но приходил к тем же самым
выводам, что и его предшественник. По-видимому, всякое серьезное размышление
над процессом конкуренции заставляет человека охватить этот процесс в его
целом, а это неизбежно ведет к математике, так как простое описание и даже
количественное выражение данных еще недостаточно для ясного представления о
взаимоотношении конкурирующих компонентов в процессе их роста.
Первый шаг в этой области был сделан Рональдом
Россом в 1911 году, который интересовался в это время распространением малярии.
Размышляя над процессом распространения, Росс пришел к заключению, что он имеет
дело со своеобразным случаем борьбы за существование между малярийным
плазмодием и человеком при участии комара. Росс математически сформулировал
уравнение борьбы за существование для малярии, которое по своей идее довольно
близко к тем уравнениям борьбы за существование, которые были предложены в 1926
г. итальянским математиком Вольтерра, не знавшим об исследованиях Росса. В то
время как Росс работал над вопросом о распространении малярии, американский
математик Лотка теоретически исследовал ход определенных химических реакций и
должен был здесь иметь дело с уравнениями такого же типа. Позже Лотка
заинтересовался проблемой борьбы за существование, и в 1920 г. сформулировал
уравнение, описывающее взаимодействие между хозяевами и паразитами, причем он
представил обильный и интересный материал в своей ценной книге "Элементы
физической биологии" (1925). Не будучи знаком с этими исследованиями,
итальянский математик Вито Вольтерра предложил в 1926 г. довольно сходные
уравнения борьбы за существование. В то же самое время он способствовал значительному
продвижению вперед в области всей этой проблемы, впервые проведя исследования
многочисленных важных вопросов теории конкуренции с теоретической точки зрения.
Таким образом, три видных исследователя пришли к весьма сходным теоретическим
уравнениям практически в одно и то же время, однако за счет совершенно разных
подходов. Также интересно отметить, что экспериментальное изучение борьбы за
существование началось только после того, как почва для этого была подготовлена
чисто теоретическими исследованиями.
Исследования борьбы за существование несомненно
будут в будущем быстро прогрессировать, однако этим исследованиям придется
преодолеть определенный разрыв между исследованиями современных биологов и
математиков. Нет сомнения, что борьба за существование представляет собой
биологическую проблему, и она должна решаться экспериментальным путем, а не за
столом математика. Однако, для того, чтобы глубже проникнуть в природу этих
явлений, ученые должны объединить экспериментальный метод с математической теорией,
возможность которой создана блестящими исследованиями Лотки и Вольтерры.
Соединение экспериментального метода с количественной теорией вообще является
одним из самых мощных средств современной науки.
ГЛАВА 1.
. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ТЕОРЕМЫ, ИСПОЛЬЗУЕМЫЕ
В ДАЛЬНЕЙШЕМ
1.1 СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ РЕШЕНИЙ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И СИСТЕМ.
Определение. Пусть 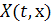 -
действительнозначная функция действительных переменных t и х с областью
определения
-
действительнозначная функция действительных переменных t и х с областью
определения 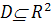 . Функция
. Функция 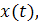 где
t принадлежит некоторому интервалу
где
t принадлежит некоторому интервалу 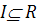 ,
для которой всюду на I
выполняется равенство
,
для которой всюду на I
выполняется равенство
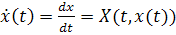 (1.1)
(1.1)
называется решением дифференциального уравнения
(1.1).
Чтобы функция  была
решением, необходимо выполнение условия
была
решением, необходимо выполнение условия  для
любого
для
любого  ;
таким образом, область D ограничивает как область определения, так и область
значений функции
;
таким образом, область D ограничивает как область определения, так и область
значений функции  .
.
Предложение 1 Если функция X непрерывна в
открытой области  , то для любой
точки
, то для любой
точки 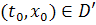 существует
решение
существует
решение  ,
,
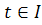 ,
уравнения
,
уравнения 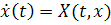 такое, что
такое, что 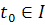 и
и
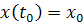 .
.
Замечание. Это предложение не исключает случая,
когда 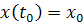 более
чем для одного решения
более
чем для одного решения  .
.
Предложение 2. Если X и  непрерывны
в некоторой открытой области
непрерывны
в некоторой открытой области  , то для любой заданной
точки
, то для любой заданной
точки 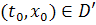 существует
единственное решение
существует
единственное решение 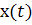 уравнения
уравнения 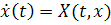 такое,
что
такое,
что 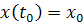 .
.
Замечание. Предложение 1.2 дает достаточное
условие, при котором каждой точке из 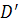 соответствует
только одно решение.
соответствует
только одно решение.
1.2 ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ РЕШЕНИЙ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИ.
Решение  уравнения
уравнения
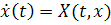 представляется
геометрически графиком функции
представляется
геометрически графиком функции  . Этот график
определяет интегральную кривую на плоскости
. Этот график
определяет интегральную кривую на плоскости  .
.
Если X непрерывна в D, то предложение 1 утверждает,
что интегральные кривые заполняют область D плоскости  .
Это следует из того, что каждая точка D должна лежать, по крайней мере, на
одной интегральной кривой. Таким образом, решения дифференциального уравнения
представляются семейством интегральных кривых в D (рис. 1.1-1.3).
.
Это следует из того, что каждая точка D должна лежать, по крайней мере, на
одной интегральной кривой. Таким образом, решения дифференциального уравнения
представляются семейством интегральных кривых в D (рис. 1.1-1.3).
Eсли обе функции X и
 непрерывны
в D, то из предложения 2 следует, что существует единственная интегральная
кривая, проходящая через каждую точку D.
непрерывны
в D, то из предложения 2 следует, что существует единственная интегральная
кривая, проходящая через каждую точку D.
Примеры.
1. Рассмотрим
уравнение
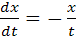 (1.2)
(1.2)
в области D плоскости (t,
x).
Интегрируя его, мы получим
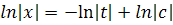
следовательно

Когда 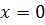 ,
,
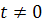 .
.
Для точек 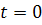 ,
,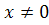 будем рассматривать перевернутое уравнение
будем рассматривать перевернутое уравнение
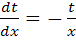 (1.2’)
(1.2’)
Как мы видим, интегральными кривыми уравнения
(1.2) являются гиперболы:

верхняя и нижняя части оси Ox.
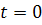 ,(
,(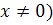
тоже являются интегральными кривыми, что вытекает
из рассмотрения уравнения (1.2’).
Интегральные кривые следующих уравнений
исследуем с помощью метода изоклин. Это метод позволяет, не интегрируя
уравнение, увидеть, как ведут себя его решения.
2. Рассмотрим
уравнение
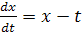 (1.3)
(1.3)
Дифференциальное уравнение задает наклон
интегральных кривых
(т.е. угловой коэффициент касательных к ним) во
всех точках области D. Так, в частности, в точках пересечения с кривой 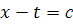 (где
(где
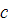 -
некоторая постоянная) интегральные кривые имеют наклон
-
некоторая постоянная) интегральные кривые имеют наклон 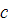 .
Такая кривая называется изоклиной наклона
.
Такая кривая называется изоклиной наклона .
Множество изоклин, которое получается, когда мы придаем
.
Множество изоклин, которое получается, когда мы придаем 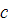 различные
действительные значения, - это семейство прямых:
различные
действительные значения, - это семейство прямых:
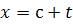
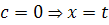 ,
,
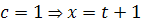
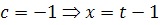 .
.
А угол наклона касательных к интегральным кривым
можно найти из
формулы: 
Таким образом, при 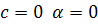
при 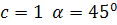

3. Сделаем
набросок интегральных кривых уравнения
 (1.4)
(1.4)
в области D плоскости t, х, где 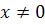 .
.
) В этом случае интегральные кривые имеют
наклон 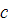 в
точках
в
точках
пересечения с кривой 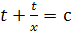 .
.
А множество изоклин, которое получается, когда
мы придаем с различные действительные значения, - это семейство гипербол:
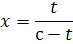
с асимптотами 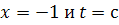 .
.
Множество изоклин: 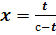
) Знак 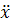 определяет,
в каких точках D интегральные кривые выпуклы, а
определяет,
в каких точках D интегральные кривые выпуклы, а
в каких вогнуты. Если 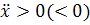 ,
то функция
,
то функция 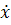 возрастает
(убывает) при возрастании t и интегральная кривая вогнута (выпукла). Таким
образом, область D можно разбить на два подмножества, на каждом из которых
интегральные кривые либо выпуклы, либо вогнуты; эти множества разделяются
кривой
возрастает
(убывает) при возрастании t и интегральная кривая вогнута (выпукла). Таким
образом, область D можно разбить на два подмножества, на каждом из которых
интегральные кривые либо выпуклы, либо вогнуты; эти множества разделяются
кривой  .
Для уравнения (1.4) получается
.
Для уравнения (1.4) получается
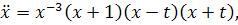
и D
разбивается на области 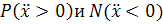 .
.
) Изоклины расположены симметрично
относительно прямой 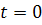 , и,
, и,
значит, интегральные кривые тоже должны быть
относительно ее симметричны. Функция 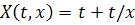 удовлетворяет
соотношению
удовлетворяет
соотношению 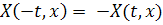 , из которого
следует, что если
, из которого
следует, что если 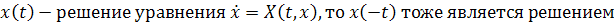 .
.
Эти три замечания позволяют сделать набросок
интегральных кривых для уравнения (1.4) вогнутости (P)
интегральных дифференциального уравнения кривых уравнения 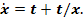
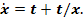
Можно увидеть, что обе функции  непрерывны
в
непрерывны
в 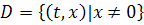 ,
так что через каждую точку проходит единственная интегральная кривая.
,
так что через каждую точку проходит единственная интегральная кривая.
Так же решения  можно
найти с помощью разделения переменных. Семейство интегральных кривых состоит из
кривых, заданных уравнением
можно
найти с помощью разделения переменных. Семейство интегральных кривых состоит из
кривых, заданных уравнением
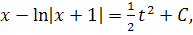 (1.5)
(1.5)
где С - постоянная, и решения  .
Однако нарисовать интегральные кривые непосредственно по уравнению (1.5)
труднее, чем по самому дифференциальному уравнению (1.4).
.
Однако нарисовать интегральные кривые непосредственно по уравнению (1.5)
труднее, чем по самому дифференциальному уравнению (1.4).
2
ОСНОВЫ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
.1 АВТОНОМНЫЕ УРАВНЕНИЯ
Определение 1. Дифференциальное уравнение вида
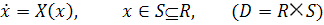 (2.1)
(2.1)
называется автономным.
Это название оправдано тем, что 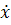 определяется
одним только х, и, таким образом, решение само управляет своим изменением.
определяется
одним только х, и, таким образом, решение само управляет своим изменением.
Решения автономных уравнений обладают следующим
важным свойством:
Если 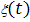 -решение
уравнения (2.1) с областью определения I
и
-решение
уравнения (2.1) с областью определения I
и
областью значений x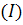 ,
то h
,
то h при любом действительном С также является решением с той же областью значений и
с областью определения
при любом действительном С также является решением с той же областью значений и
с областью определения 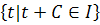 . Это следует из
того, что
. Это следует из
того, что
 .
.
Интегральная кривая  получается
из интегральной кривой
получается
из интегральной кривой 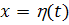 сдвигом по
сдвигом по 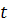 в
положительном направлении, на величину С.
в
положительном направлении, на величину С.
Кроме того, если через каждую точку полосы 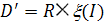 проходит
только одна интегральная кривая, то все решения в полосе
проходит
только одна интегральная кривая, то все решения в полосе 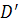 получаются
сдвигами
получаются
сдвигами  .
Таким образом, область D разделяется на полосы, в которых интегральные кривые
получаются из какой-нибудь одной кривой сдвигом вдоль оси t.
.
Таким образом, область D разделяется на полосы, в которых интегральные кривые
получаются из какой-нибудь одной кривой сдвигом вдоль оси t.
Рассмотрим примеры автономных дифференциальных
уравнений.
. Возьмем уравнение
 ,
,
можем записать его как
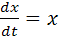 (2.2)
(2.2)
Интегрируя уравнение (2.2), получим: 
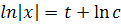
т.е. 
. Посмотрим, как получаются интегральные
кривые уравнения
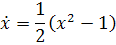
Запишем его в виде
 (2.3)
(2.3)
Проинтегрировав уравнение (2.3):
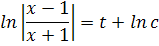
видим, что решения имеют такой вид:
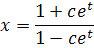
Это позволяет сделать набросок интегральных
кривых данного уравнения:
Для семейств интегральных кривых, в которых
кривые получаются одна из другой сдвигами, качественное поведение семейства
определяется качественным поведением каждого индивидуального решения, а оно в
свою очередь определяется функцией Х(х). Если 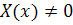 ,
то решения либо возрастают, либо убывают; если же Х(с) = 0, то существует
решение
,
то решения либо возрастают, либо убывают; если же Х(с) = 0, то существует
решение 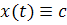 .
.
Эти свойства решений удобнее изображать на оси
х, чем на плоскости t, x.
Если 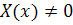 для
для
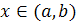 ,
то на этом интервале рисуется стрелка, показывающая направление изменения х.
,
то на этом интервале рисуется стрелка, показывающая направление изменения х.
Определение 2.Если Х(с) = 0, то решение 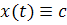 изображается
точкой
изображается
точкой 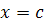 .
Такие решения называются особыми точками или положениями равновесия уравнения,
так как
.
Такие решения называются особыми точками или положениями равновесия уравнения,
так как 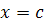 для
всех значений t.
для
всех значений t.
Определение 3. Геометрическое изображение
качественного поведения решений уравнения  называется
фазовым портретом.
называется
фазовым портретом.
Если решение х не является особой точкой, то оно
должно быть либо возрастающим, либо убывающим; таким образом, если число особых
точек конечно, то может существовать только конечное число «различных» фазовых
портретов. Под словом «различные» подразумеваются «отличающиеся набором
областей, в которых х возрастает или убывает».
На каждой из получаемых полупрямых 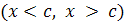 функция
X может быть либо положительной, либо отрицательной. Следовательно, фазовый
портрет должен соответствовать одному из четырех случаев, изображенных на рис.
2.5. Это значит, что качественное поведение любого автономного
дифференциального уравнения с одной особой точкой должно соответствовать одному
из фазовых портретов на рис. 2.5 при некотором значении с.
функция
X может быть либо положительной, либо отрицательной. Следовательно, фазовый
портрет должен соответствовать одному из четырех случаев, изображенных на рис.
2.5. Это значит, что качественное поведение любого автономного
дифференциального уравнения с одной особой точкой должно соответствовать одному
из фазовых портретов на рис. 2.5 при некотором значении с.
Различные дифференциальные уравнения с одной
особой точкой, имеющие один и тот же фазовый портрет, считаются качественно
эквивалентными.
Замечание. Соображения, которые использовались
при получении рис. 2.5, сохраняют свою силу, если точка х = с - одна из многих
особых точек на фазовом портрете. Другими словами, качественное поведение х в
окрестности любой особой точки должно быть таким же, как в одном из случаев на
рис. 2.5. Это поведение определяет характер особой точки.
Из сказанного можно сделать вывод, что фазовый
портрет любого автономного уравнения полностью определяется видом его особых
точек.
Определение 4. Два дифференциальных уравнения
вида  качественно
эквивалентны, если они имеют равное количество особых точек одинакового
характера, расположенных в одинаковом порядке на фазовой прямой.
качественно
эквивалентны, если они имеют равное количество особых точек одинакового
характера, расположенных в одинаковом порядке на фазовой прямой.
2.2 АВТОНОМНЫЕ СИСТЕМЫ НА ПЛОСКОСТИ
Рассмотрим дифференциальное уравнение
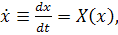 (2.4)
(2.4)
где 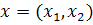 -вектор
в
-вектор
в 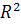 .
Такое уравнение эквивалентно системе двух связанных уравнений:
.
Такое уравнение эквивалентно системе двух связанных уравнений:
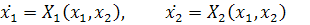 (2.5)
(2.5)
причем  ,
так как
,
так как 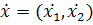 .
Решение уравнения (2.4) является парой функций
.
Решение уравнения (2.4) является парой функций 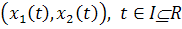 ,
удовлетворяющих системе уравнений (2.5).
,
удовлетворяющих системе уравнений (2.5).
Вообще говоря, решение 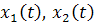 содержит
две произвольные постоянные, так что возникает двупараметрическое семейство
решений.
содержит
две произвольные постоянные, так что возникает двупараметрическое семейство
решений.
Качественное поведение этого семейства
определяется тем, как ведут себя  с
увеличением времени. Вместо того чтобы просто указывать на фазовой прямой,
увеличивается или уменьшается величина х, мы должны показать как изменяется
положение точки х на фазовой плоскости. Поэтому фазовый портрет будет
двумерным, а качественное поведение определяется семейством кривых с указанием
направления движения по этим кривым при возрастании t.
Такие кривые называются траекториями.
с
увеличением времени. Вместо того чтобы просто указывать на фазовой прямой,
увеличивается или уменьшается величина х, мы должны показать как изменяется
положение точки х на фазовой плоскости. Поэтому фазовый портрет будет
двумерным, а качественное поведение определяется семейством кривых с указанием
направления движения по этим кривым при возрастании t.
Такие кривые называются траекториями.
Качественное исследование уравнений на плоскости
начинается с изучения особых точек уравнения (2.4). Особым точкам соответствуют
решения вида 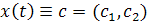 , и они возникают в
случае, когда
, и они возникают в
случае, когда
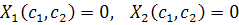
Соответствующая траектория - это точка  на
фазовой плоскости.
на
фазовой плоскости.
) Система

имеет особую точку (0,0) и решения
 (2.6)
(2.6)
где 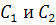 -
некоторые действительные постоянные. Любое решение из семейства (2.6) при
-
некоторые действительные постоянные. Любое решение из семейства (2.6) при 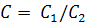 удовлетворяет
для всех t уравнению
удовлетворяет
для всех t уравнению

Таким образом, каждая траектория семейства (2.6)
лежит на некоторой прямой, проходящей через начало координат. Из уравнений
(2.6) видно, что при любых ненулевых 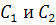 значения
значения
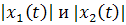 убывают
при возрастании t и стремятся к нулю при
убывают
при возрастании t и стремятся к нулю при  .
На рисунке 2.6 это показано с помощью стрелок на траекториях; если
.
На рисунке 2.6 это показано с помощью стрелок на траекториях; если  представляет
собой положение фазовой точки х в момент t, то с ростом времени t она движется
по направлению к началу координат. Чтобы изобразить это, достаточно нарисовать
направленный луч.
представляет
собой положение фазовой точки х в момент t, то с ростом времени t она движется
по направлению к началу координат. Чтобы изобразить это, достаточно нарисовать
направленный луч.
) На рис. 2.7 показана еще одна
возможность. Здесь при возрастании
t величина  убывает,
а
убывает,
а 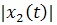 возрастает.
Система
возрастает.
Система
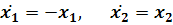
имеет решения
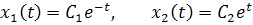
где 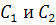 -
действительные числа.
-
действительные числа.
Тогда 
с 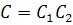 .
В этом случае только две траектории стремятся, к особой точке (0, 0), а все
остальные от нее рано или поздно уходят, причем
.
В этом случае только две траектории стремятся, к особой точке (0, 0), а все
остальные от нее рано или поздно уходят, причем  при
при
 ,
и наоборот. Качественное поведение здесь сильно отличается от того, что
представлено на рис. 2.6.
,
и наоборот. Качественное поведение здесь сильно отличается от того, что
представлено на рис. 2.6.
Уравнения траекторий можно часто найти, решая
уравнение
 (2.7)
(2.7)
Иногда необходимо получить фазовый портрет,
когда невозможно записать обозримые явные формулы для решений. Это можно
сделать, обобщив метод изоклин на случай плоскости. Во всех точках плоскости,
где задана векторная функция 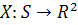 , она задает вектор
х (векторное поле). Для качественного исследования обычно достаточно знать
направление Х(х). Это направление постоянно на изоклинах уравнения (2.7).
Особенно интересны точки, где
, она задает вектор
х (векторное поле). Для качественного исследования обычно достаточно знать
направление Х(х). Это направление постоянно на изоклинах уравнения (2.7).
Особенно интересны точки, где 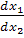 обращается в нуль
или в бесконечность, т. е. изоклины, где
обращается в нуль
или в бесконечность, т. е. изоклины, где  или
или
 .
.
Если для любой точки 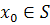 и
любого
и
любого  существует
единственное решение x(t) уравнения
существует
единственное решение x(t) уравнения 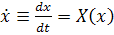 такое,
что
такое,
что 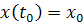
то через каждую точку 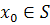 проходит
в точности одна траектория. Если же возникает неединственность, то обычно она
бывает сосредоточена на некоторых линиях в S,
и только в их окрестности поведение траекторий не сразу можно определить по
виду функции.
проходит
в точности одна траектория. Если же возникает неединственность, то обычно она
бывает сосредоточена на некоторых линиях в S,
и только в их окрестности поведение траекторий не сразу можно определить по
виду функции.
) Будем решать систему
 ,
,
записав ее в виде уравнения
 (2.8)
(2.8)
т.е.  .
.
Это уравнение является однородным. Чтобы
привести его к уравнению с разделяющимися переменными, сделаем замену:

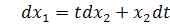
Тогда наше уравнение примет вид:
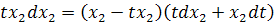 ,
,
преобразуя его, получим

Следовательно
 (2.9)
(2.9)
где 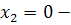 не
решение, а
не
решение, а 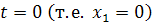 и
и 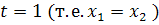
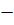 решения
уравнения. Траектории, лежащие на прямых
решения
уравнения. Траектории, лежащие на прямых  и
и
 ,
проходят через особую точку системы (0,0).
,
проходят через особую точку системы (0,0).
Проинтегрировав уравнение (2.9), имеем

откуда, возвращаясь к переменным 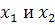 ,
найдем общий интеграл
,
найдем общий интеграл
уравнения (2.8)
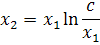
Две траектории, которые лежат на прямой  стремятся
к особой точке (0,0), а все остальные от нее рано или поздно уходят.
стремятся
к особой точке (0,0), а все остальные от нее рано или поздно уходят.
При рассмотрении следующей системы уравнений,
воспользуемся методом изоклин.
) Систему уравнений

запишем в виде
 (2.10)
(2.10)
Интегральные кривые имеют наклон 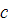 в
точках пересечения с кривой
в
точках пересечения с кривой
 .
.
А множество изоклин, которое получается, когда
мы придаем с различные действительные значения, - это семейство парабол:
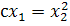
и прямая 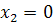 .
.
Некоторые из этих изоклин изображены на рисунке
2.9 красным цветом.
А угол наклона касательных к интегральным кривым
найдем из формулы:

Получается при 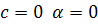
при 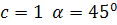
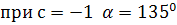 .
.
Особой точкой уравнения является точка(0,0)
Используя достаточно густое семейство изоклин,
мы может получить отчетливое представление о траекториях уравнения (2.10). Одна
траектория (лежащая на прямой  ) стремится к
особой точке, а все остальные от нее уходят.
) стремится к
особой точке, а все остальные от нее уходят.
Эти примеры показывают, что качественно
различные решения приводят к траекториям с различными геометрическими
свойствами. Проблема выделения различных видов особых точек сводится к проблеме
выделения различных геометрических конфигураций, составленных траекториями.
Здесь показано только несколько фазовых портретов на плоскости, имеющих одну
особую точку.
3
ЛИНЕЙНЫЕ СИСТЕМЫ
Определение 1. Система 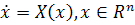 ,
называется линейной системой размерности n,
если отображение
,
называется линейной системой размерности n,
если отображение 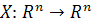 линейно. Для
линейных систем существует только конечное число качественно различных фазовых
портретов. Чтобы установить это, надо рассмотреть, как на такую систему влияет
линейная замена переменных.
линейно. Для
линейных систем существует только конечное число качественно различных фазовых
портретов. Чтобы установить это, надо рассмотреть, как на такую систему влияет
линейная замена переменных.
3.1 ЛИНЕЙНАЯ ЗАМЕНА ПЕРЕМЕННЫХ
Линейное отображение: 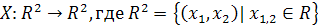 ,
,
можно записать в матричной форме:
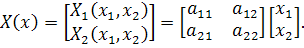
Соответственно дифференциальное уравнение  принимает
вид
принимает
вид
 (3.1)
(3.1)
Где A-
матрица коэффициентов. Каждая компонента 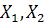 производной
производной
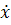 является
линейной функцией переменных
является
линейной функцией переменных  . Эти переменные
являются просто координатами точки
. Эти переменные
являются просто координатами точки 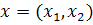 относительно
базиса в
относительно
базиса в 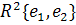 ,
где
,
где 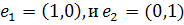 .
.
Следовательно,
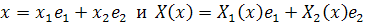
Чтобы сделать замену переменных, надо координаты
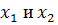 представить
как функцию новых переменных.
представить
как функцию новых переменных.
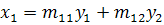
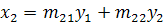
 (3.2)
(3.2)
где 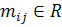 для
всех i и j.
Конечно, одному набору старых координат
для
всех i и j.
Конечно, одному набору старых координат  должен
соответствовать один набор новых координат
должен
соответствовать один набор новых координат 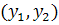 и
наоборот. Это значит, что отображение (3.2) должно быть взаимно однозначным, и,
следовательно, М должна быть обратимой матрицей. Отсюда следует, что столбцы
и
наоборот. Это значит, что отображение (3.2) должно быть взаимно однозначным, и,
следовательно, М должна быть обратимой матрицей. Отсюда следует, что столбцы  матрицы
М должны быть линейно независимы.
матрицы
М должны быть линейно независимы.
Из формулы (3.2) вытекает, что
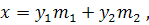
и мы видим, что 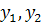 -
это координаты точки
-
это координаты точки 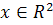 относительно
нового базиса
относительно
нового базиса 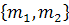 . Уравнение (3.1)
легко можно записать через новые переменные; получим
. Уравнение (3.1)
легко можно записать через новые переменные; получим
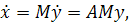
так что
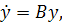
где
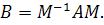
Таким образом, матрица коэффициентов В подобна
А.
Подобие является отношением эквивалентности
между  матрицами;
отсюда следует, что множество таких матриц по этому отношению распадается на
классы эквивалентности. Для любых двух матриц
матрицами;
отсюда следует, что множество таких матриц по этому отношению распадается на
классы эквивалентности. Для любых двух матриц 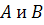 ,
принадлежащих одному классу эквивалентности, системы
,
принадлежащих одному классу эквивалентности, системы  и
y
и
y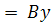 связаны
соотношением
связаны
соотношением 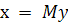 , где
, где  .
Таким образом, если одна из этих систем решена, то можно получить решения для
любой системы с матрицей того же класса.
.
Таким образом, если одна из этих систем решена, то можно получить решения для
любой системы с матрицей того же класса.
Предложение 3.1 Пусть 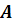 -
действительная 2´2-матрица. Тогда существует
действительная неособая матрица M
такая, что
-
действительная 2´2-матрица. Тогда существует
действительная неособая матрица M
такая, что 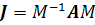 принадлежит одному
из нижеперечисленных типов:
принадлежит одному
из нижеперечисленных типов:
(a)
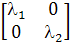 ,
,
 ;
(b)
;
(b) 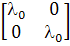 ;
(3.3)
;
(3.3)
(c)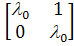 (d)
(d)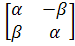 ,
,
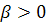
Где 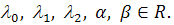
Определение 2. Матрица 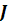 называется
жордановой формой матрицы
называется
жордановой формой матрицы 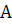 . Собственные
значения матрицы
. Собственные
значения матрицы 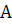 (и
(и 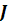 )
- это значения
)
- это значения  , для которых
, для которых
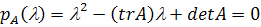 .
.
Здесь 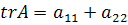 -
след матрицы А, а
-
след матрицы А, а 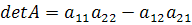 - ее определитель.
Таким образом, собственными значениями являются
- ее определитель.
Таким образом, собственными значениями являются
 (3.4)
(3.4)
где
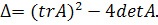 (3.5)
(3.5)
Именно характер собственных значений определяет
тип, к которому относится матрица 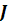 .
.
Жорданова форма 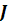 зависит
от вида собственных значений, являются ли они действительными различными (
зависит
от вида собственных значений, являются ли они действительными различными (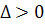 ),
действительными совпадающими (
),
действительными совпадающими ( ) или комплексными
(
) или комплексными
(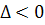 ).
).
(a) Действительные
различные собственные значения (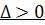 )
)
Собственные векторы 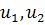 матрицы
А определяются из уравнений
матрицы
А определяются из уравнений
 (i=1,
2),
(i=1,
2),
где 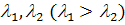 -
различные собственные значения.
-
различные собственные значения.
Пусть
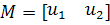
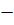 матрица, столбцами
которой являются собственные векторы. Тогда
матрица, столбцами
которой являются собственные векторы. Тогда
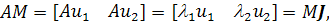
где
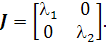
В случае различных действительных собственных
значений собственные векторы 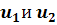 линейно независимы
и, следовательно, матрица М неособая. Так что
линейно независимы
и, следовательно, матрица М неособая. Так что
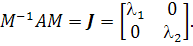
(b) Совпадающие
собственные значения (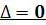 )
)
Из уравнения (3.4) получаем, что 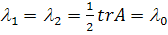 .
В этом случае мы должны рассмотреть две возможности.
.
В этом случае мы должны рассмотреть две возможности.
(i) Матрица 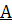 диагональная
диагональная
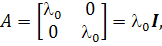
что соответствует случаю (3.3(b)). Здесь для
любой неособой матрицы М мы имеем 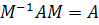 .
Следовательно,
.
Следовательно, 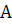 подобна только
самой себе и является единственной в своем классе эквивалентности.
подобна только
самой себе и является единственной в своем классе эквивалентности.
(ii) Матрица А недиагональная
В этом случае, так как  ,
rank (А -
,
rank (А - )
= 1 и не существует двух линейно независимых собственных векторов. Пусть
)
= 1 и не существует двух линейно независимых собственных векторов. Пусть 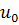 -
некоторый собственный вектор А. Если мы положим
-
некоторый собственный вектор А. Если мы положим 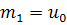 и
выберем
и
выберем  так,
чтобы матрица
так,
чтобы матрица  была неособой, то
была неособой, то
 ,
,
где 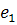 -
первый столбец единичной матрицы I.
-
первый столбец единичной матрицы I.
Матрицы А и  имеют
одинаковые собственные значения, так что
имеют
одинаковые собственные значения, так что
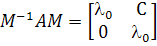 ,
,
где  .
Однако переход от М к
.
Однако переход от М к

дает
 ,
,
что соответствует случаю (3.3 (с)).
(c) Комплексные
собственные значения (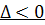 )
)
Можно обозначить 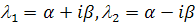 ,
где
,
где 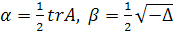 .
Надо показать, что существует неособая матрица
.
Надо показать, что существует неособая матрица 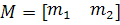 такая,
что
такая,
что 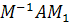 имеет
вид (3.3(d)), или, что равносильно,
имеет
вид (3.3(d)), или, что равносильно,
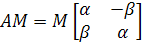 .
.
Записав матрицу М через ее столбцы, получим
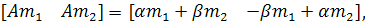
или
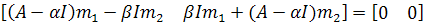
Это матричное уравнение можно записать как
систему четырех линейных однородных уравнений относительно неизвестных
элементов матрицы М:
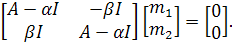 (3.6)
(3.6)
Пусть P
- матрица коэффициентов в (3.5), а
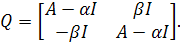
Получается, что
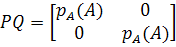 ,
,
где 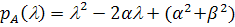 - характеристический полином матрицы
A. По теореме
Кэли - Гамильтона, утверждающей, что всякая квадратная матрица является корнем
своего характеристического многочлена
<#"556021.files/image235.gif">, так что
- характеристический полином матрицы
A. По теореме
Кэли - Гамильтона, утверждающей, что всякая квадратная матрица является корнем
своего характеристического многочлена
<#"556021.files/image235.gif">, так что

здесь 0 - нулевая 4´4-матрица.
Таким образом, столбцы матрицы Q являются решениями уравнения (3.6). Первый
столбец Q дает
 (3.7)
(3.7)
Заметим, что дискриминант 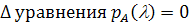 имеет вид
имеет вид
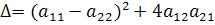
Если 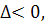 то
то  , следовательно,
, следовательно,  . Тогда и
. Тогда и 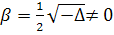 , и мы
получаем, что
, и мы
получаем, что 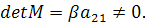 Таким
образом (3.7) дает неособую матрицу М такую, что
Таким
образом (3.7) дает неособую матрицу М такую, что  имеет вид (3.3(d)).
имеет вид (3.3(d)).
Любая действительная 2´2-матрица А
попадает в один, и только один, из указанных в (3.3) классов.
3.2 ФАЗОВЫЕ ПОРТРЕТЫ ДЛЯ КАНОНИЧЕСКИХ СИСТЕМ
НА ПЛОСКОСТИ
Рассмотрим простые линейные системы.
Определение 3. Линейная система  называется
простой, если матрица А неособая, т. е.
называется
простой, если матрица А неособая, т. е. 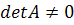 и
А не имеет нулевых собственных значений. Тогда единственным решением уравнения
и
А не имеет нулевых собственных значений. Тогда единственным решением уравнения
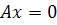
является х = 0 и система имеет единственную
изолированную особую точку в начале координат фазовой плоскости. Каноническая
система, соответствующая простой линейной системе, так же является простой, так
как А и J имеют одинаковые собственные значения.
(а) Различные действительные
собственные значения
В этом случае 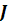 задается
формулой (3.3(a)) с ненулевыми
задается
формулой (3.3(a)) с ненулевыми 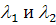 . Тогда система
. Тогда система  после
замены примет вид:
после
замены примет вид:
 (3.8)
(3.8)
и, следовательно,
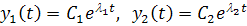 (3.9)
(3.9)
где 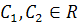 .
.
Если 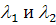 одного
знака, то фазовые портреты имеют вид, изображенный на рис. 3.1 (а) и (b).
особая точка в начале координат плоскости
одного
знака, то фазовые портреты имеют вид, изображенный на рис. 3.1 (а) и (b).
особая точка в начале координат плоскости 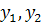 называется
узлом. Если все траектории направлены к началу координат (от него), то узел
называется устойчивым (неустойчивым). Форма траекторий определяется отношением
называется
узлом. Если все траектории направлены к началу координат (от него), то узел
называется устойчивым (неустойчивым). Форма траекторий определяется отношением 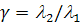 .
Из (3.8), (3.9) следует уравнение
.
Из (3.8), (3.9) следует уравнение
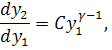
где  .
Следовательно, при
.
Следовательно, при 
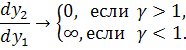
Если 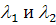 имеют
противоположные знаки, то возникает фазовый портрет. В этом случае особая точка
называется седлом. На осях координат (исключая начало) лежат особые траектории,
которые называются сепаратрисами седла. Это единственные траектории, имеющие
вид радиальных лучей. На одной координатной оси лежат две сепаратрисы (начало
координат также является отдельной траекторией). Эти сепаратрисы направлены к
началу координат (от него), если соответствующее собственное значение
отрицательно (положительно). Остальные траектории имеют сепаратрисы в качестве
асимптот; сначала они подходят к некоторой точке при возрастании t от
имеют
противоположные знаки, то возникает фазовый портрет. В этом случае особая точка
называется седлом. На осях координат (исключая начало) лежат особые траектории,
которые называются сепаратрисами седла. Это единственные траектории, имеющие
вид радиальных лучей. На одной координатной оси лежат две сепаратрисы (начало
координат также является отдельной траекторией). Эти сепаратрисы направлены к
началу координат (от него), если соответствующее собственное значение
отрицательно (положительно). Остальные траектории имеют сепаратрисы в качестве
асимптот; сначала они подходят к некоторой точке при возрастании t от 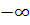 ,
лежащей ближе всего к началу координат, а затем снова удаляются.
,
лежащей ближе всего к началу координат, а затем снова удаляются.
(b)
Равные собственные значения
Если матрица J диагональная, то каноническая
система задается формулой (3.8) с  .
Таким образом, случай (3.3(b)) соответствует узлу специального вида, который
называется дикритическим узлом. Этот узел устойчив при
.
Таким образом, случай (3.3(b)) соответствует узлу специального вида, который
называется дикритическим узлом. Этот узел устойчив при  ,
неустойчив при
,
неустойчив при  ; все его
траектории являются радиальными лучами.
; все его
траектории являются радиальными лучами.
Если матрица J недиагональная, т. е. имеет вид
(3.3(c)), то система
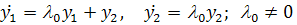
имеет решения
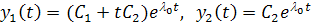
В этом случае начало координат называется вырожденным
узлом; он устойчив при  и неустойчив при
и неустойчив при  .
Кривая, на которой траектории меняют свое направление, - геометрическое место
точек экстремума для
.
Кривая, на которой траектории меняют свое направление, - геометрическое место
точек экстремума для 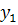 . Оно задается
уравнением
. Оно задается
уравнением 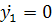 , т. е.
, т. е.
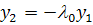
(с) Комплексные собственные значения
Жорданова матрица задается в этом случае
формулой (3.3(d)), так что каноническая система имеет вид
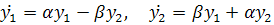
Систему такого вида можно проинтегрировать, перейдя
к полярным координатам на плоскости  Þ
Þ
 .
Если продифференцировать эти выражения по t
и подставить
.
Если продифференцировать эти выражения по t
и подставить 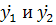 , то получится
, то получится
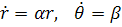
и решение будет иметь вид:
 .
.
Если 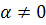 ,
то начало координат называется фокусом (устойчивым при
,
то начало координат называется фокусом (устойчивым при 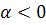 ,
неустойчивым при
,
неустойчивым при 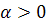 ). Параметр
). Параметр 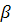 >
0 определяет угловую скорость точки на спирали.
>
0 определяет угловую скорость точки на спирали.
Если 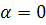 ,
то начало координат называется центром и фазовый портрет состоит из континуума
концентрических кругов. Это единственный случай, когда в линейных системах
возникает повторяющееся, или периодическое, движение. Каждая точка (за
исключением начала координат) снова проходится через время
,
то начало координат называется центром и фазовый портрет состоит из континуума
концентрических кругов. Это единственный случай, когда в линейных системах
возникает повторяющееся, или периодическое, движение. Каждая точка (за
исключением начала координат) снова проходится через время 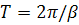 .
Решения системы периодичны по t с периодом T
и определяются формулами:
.
Решения системы периодичны по t с периодом T
и определяются формулами:
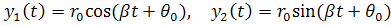 .
.
В случае, когда система 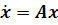 является
вырожденной (
является
вырожденной (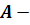 вырожденная
матрица, т. е.
вырожденная
матрица, т. е.  ), хотя бы одно из
собственных значений А равно нулю. Тогда существуют нетривиальные решения
уравнения
), хотя бы одно из
собственных значений А равно нулю. Тогда существуют нетривиальные решения
уравнения 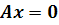 кроме
кроме  ,
и система имеет другие особые точки. Для линейных систем на плоскости
существуют только две возможности: или ранг А равен единице, или А - нулевая
матрица. В первом случае имеется прямая, состоящая из особых точек, проходящая
через начало координат; во втором случае все точки плоскости являются особыми
точками. Ранг А равен рангу J,
так что то же самое справедливо для канонической системы.
,
и система имеет другие особые точки. Для линейных систем на плоскости
существуют только две возможности: или ранг А равен единице, или А - нулевая
матрица. В первом случае имеется прямая, состоящая из особых точек, проходящая
через начало координат; во втором случае все точки плоскости являются особыми
точками. Ранг А равен рангу J,
так что то же самое справедливо для канонической системы.
(а) 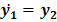
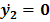 т.е.
т.е. 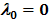 .
.
все точки оси  являются
неподвижными точками; это предельный случай
являются
неподвижными точками; это предельный случай
(а) при 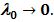
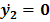 т.е.
т.е. 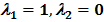 .
.
все точки оси 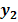 являются
неподвижными точками; это предельный случай
являются
неподвижными точками; это предельный случай
(а) при 
Рассмотрим сначала случай вещественных различных
 .
.
В этом случае 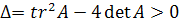 ,
то есть
,
то есть 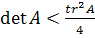 .
.
Если 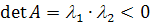 ,
то собственные числа
,
то собственные числа 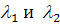 разных знаков и
особая точка является седлом.
разных знаков и
особая точка является седлом.
Если 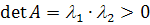 ,
то собственные числа
,
то собственные числа 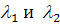 одного знака. При
этом если
одного знака. При
этом если 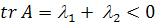 , то
, то 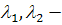 отрицательные,
и особая точка является устойчивым узлом, а если
отрицательные,
и особая точка является устойчивым узлом, а если 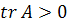 ,
то
,
то 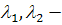 положительные,
и особая точка - неустойчивый узел.
положительные,
и особая точка - неустойчивый узел.
Когда 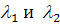 совпадают,
совпадают,
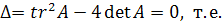
 .
.
В этом случае 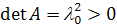 ,
где
,
где 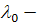 собственное
значение матрицы
собственное
значение матрицы  . Если
. Если  ,
то
,
то 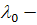 отрицательное,
и особая точка является устойчивым дикритическим или вырожденным узлом, а если
отрицательное,
и особая точка является устойчивым дикритическим или вырожденным узлом, а если 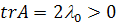 ,
то
,
то 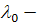 положительное
и особая точка является неустойчивым дикритическим или вырожденным узлом.
положительное
и особая точка является неустойчивым дикритическим или вырожденным узлом.
Теперь рассмотрим случай комплексных собственных
значений 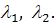
В этом случае 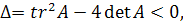 то
есть
то
есть 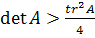 .
.
Если обозначить 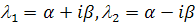 ,
то
,
то 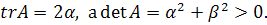 Если
Если
 то
то
 отрицательное,
и особая точка является устойчивым фокусом. Если
отрицательное,
и особая точка является устойчивым фокусом. Если  то
то
 положительное,
и особая точка - неустойчивый фокус. А если
положительное,
и особая точка - неустойчивый фокус. А если  ,
и особая точка является центром.
,
и особая точка является центром.
Определение 4. Две системы дифференциальных
уравнений называются качественно эквивалентными, если существует непрерывное
взаимно однозначное преобразование, которое переводит фазовый портрет одной
системы в фазовый портрет другой, так что сохраняется ориентация траектории.
Так же эта эквивалентность называется топологической эквивалентностью.
Выше мы показали, что любая простая линейная
система на плоскости качественно эквивалентна одной из систем. Десять изображенных
там фазовых портретов представляют алгебраические типы линейных систем.
Качественная эквивалентность дает менее
подробную классификацию. Можно показать, что все устойчивые (неустойчивые)
узлы, вырожденные узлы, фокусы эквивалентны друг другу в смысле определения 4.
Это означает, что классы алгебраически эквивалентных систем можно далее
группировать в классы качественно (или топологически) эквивалентных. В таком
смысле существует только четыре типа качественного поведения: устойчивость,
центр, седло и неустойчивость.
Фазовый портрет в окрестности произвольной
особой точки принадлежит одному и только одному из указанных трех типов:
асимптотически устойчивому, нейтрально устойчивому или неустойчивому.
Дадим строгое определение устойчивой особой точки.
Определение 5. Особая точка 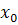 системы
системы
 называется
устойчивой, если для любой окрестности V
точки
называется
устойчивой, если для любой окрестности V
точки 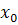 существует
некоторая меньшая окрестность этой точки
существует
некоторая меньшая окрестность этой точки 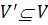 такая,
что любая траектория, проходящая через
такая,
что любая траектория, проходящая через  ,
остается в
,
остается в  при возрастании t.
при возрастании t.
Определение 6. Особая точка 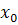 системы
системы
 называется
асимптотически устойчивой, если она устойчива и, кроме того, существует
окрестность V точки
называется
асимптотически устойчивой, если она устойчива и, кроме того, существует
окрестность V точки 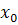 такая,
что любая траектория, проходящая через V,
стремится к
такая,
что любая траектория, проходящая через V,
стремится к 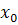 при стремлении t к
бесконечности.
при стремлении t к
бесконечности.
Замечание. Любая асимптотически устойчивая
особая точка устойчива. Но обратное неверно.
Определение 7. Особая точка системы  ,
которая устойчива, но не асимптотически устойчива, называется нейтрально
устойчивой.
,
которая устойчива, но не асимптотически устойчива, называется нейтрально
устойчивой.
Определение 8. Особая точка системы  ,
которая не является устойчивой, называется неустойчивой.
,
которая не является устойчивой, называется неустойчивой.
Это значит, что существует такая окрестность V
особой точки, что для любой окрестности 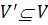 имеется
по крайней мере одна траектория, которая проходит через
имеется
по крайней мере одна траектория, которая проходит через  и
не остается в
и
не остается в  . Например, седло
неустойчиво, так как существует сепаратриса, содержащая точки, сколь угодно
близкие к началу координат, причем при движении по этой сепаратрисе точка
стремится к бесконечности при возрастании времени.
. Например, седло
неустойчиво, так как существует сепаратриса, содержащая точки, сколь угодно
близкие к началу координат, причем при движении по этой сепаратрисе точка
стремится к бесконечности при возрастании времени.
Типы устойчивости простых линейных особых точек:
a) Устойчивый
узел, вырожденный узел и фокус обладают следующим
свойством: при 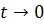 траектории
стремятся к началу координат. Таким образом,
траектории
стремятся к началу координат. Таким образом,  удовлетворяет
требованиям определения 5, и эти особые точки асимптотически устойчивы.
удовлетворяет
требованиям определения 5, и эти особые точки асимптотически устойчивы.
Центр не является асимптотически устойчивым, но
он устойчив. Это следует из определения 6 с

Таким образом, центр нейтрально устойчив.
Неустойчивые узел, вырожденный узел и фокус, а
также седло неустойчивы.
4
НЕЛИНЕЙНЫЕ СИСТЕМЫ НА ПЛОСКОСТИ
В этом параграфе будем рассматривать фазовые
портреты систем  - непрерывно
дифференцируемая нелинейная функция. Такие фазовые портреты не всегда
определяются характером особых точек системы.
- непрерывно
дифференцируемая нелинейная функция. Такие фазовые портреты не всегда
определяются характером особых точек системы.
4.1 ЛОКАЛЬНОЕ И ГЛОБАЛЬНОЕ ПОВЕДЕНИЕ
ФАЗОВЫХ ПОРТРЕТОВ НЕЛИНЕЙНЫХ СИСТЕМ
При исследовании нелинейных систем часто
приходится встречаться с сужениями полных, или глобальных фазовых портретов на
некоторую окрестность точки 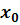 , которую мы можем
выбирать сколь угодно малой. Такое сужение называется локальным фазовым
портретом в точке
, которую мы можем
выбирать сколь угодно малой. Такое сужение называется локальным фазовым
портретом в точке 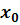 .
.
Замечание. Качественный портрет простой линейной
системы определяется характером особой точки. Другими словами, локальный
фазовый портрет в начале координат качественно эквивалентен глобальному фазовому
портрету системы.
Нелинейные системы могут иметь более одной
особой точки, и часто можно для каждой из них построить локальный фазовый
портрет. Однако, локальные фазовые портреты не всегда определяют глобальный
фазовый портрет.
Определение 1. Замкнутая траектория С на фазовом
портрете называется предельным циклом, если она изолирована от всех остальных
замкнутых траекторий; точнее, если существует трубчатая окрестность С, не
содержащая других замкнутых траекторий.
Типы предельных циклов:
Предельный цикл называется
) Устойчивым, если траектории, проходящие
через окрестность V
предельного цикла остаются в этой же окрестности при всех 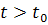 ;
;
) Неустойчивым предельным циклом, если
траектории, проходящие через окрестность V
предельного цикла покидают ее при всех 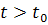 ;
;
) Полуустойчивым предельным циклом, если
траектории, проходящие через окрестность V
предельного цикла, с одной стороны остаются в этой окрестности, а с другой
стороны выходят за ее пределы при возрастании 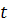 .
.
Признак отсутствия предельных циклов
(Бендиксона):
Запишем  в
виде системы уравнений:
в
виде системы уравнений:
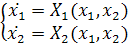
Если правые части этих уравнений имеют
непрерывные частные производные первого порядка в односвязной области D
и выражение
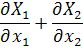
нигде не меняет знак и не равно тождественному
нулю, то в области D нет
предельных циклов.
4.2 ЛИНЕАРИЗАЦИЯ СИСТЕМ В ОКРЕСТНОСТИ ОСОБОЙ
ТОЧКИ
Рассмотрим нелинейные системы, имеющие особую
точку в начале координат.
Определение 2. Допустим, что систему 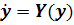 можно
записать в виде
можно
записать в виде
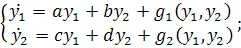 (4.1)
(4.1)
где 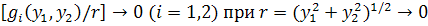 .
.
Линейная система
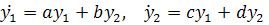 (4.2)
(4.2)
называется линеаризацией системы (3.1) (или
линеаризованной системой, соответствующей (4.1)) в начале координат. Компоненты
линейного векторного поля системы (4.2) называются линейной частью (4.1).
Замечание. Определение 2 можно также применить к
особым точкам, отличным от начала координат, введя локальные координаты.
Пусть 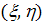 -особая
точка нелинейной системы
-особая
точка нелинейной системы
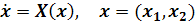 .
.
При замене переменных

точка 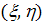 перейдет
в начало координат. Координаты
перейдет
в начало координат. Координаты 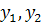 называются
локальными координатами в точке
называются
локальными координатами в точке 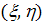 .
.
В этих координатах система имеет вид
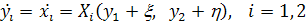 (4.3)
(4.3)
где 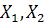 -
компоненты вектора X.
-
компоненты вектора X.
Если мы положим
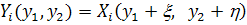
то (4.3) преобразуется в систему
 (4.4)
(4.4)
Для системы (4.4) интересующая нас особая точка
находится в начале координат, и в ней можно строить линеаризацию.
Определение 3. Говорят, что начало координат
является простой особой точкой системы  ,
если соответствующая линеаризованная система проста.
,
если соответствующая линеаризованная система проста.
Теорема о линеаризации. Пусть нелинейная система
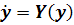
имеет простую особую точку  .
Тогда в окрестности начала координат фазовые портреты этой системы и ее
линеаризации качественно эквивалентны, если только особая точка линеаризованной
системы не является центром.
.
Тогда в окрестности начала координат фазовые портреты этой системы и ее
линеаризации качественно эквивалентны, если только особая точка линеаризованной
системы не является центром.
Если собственные значения линеаризованной
системы имеют действительную часть, отличную от нуля, то фазовые портреты
нелинейной системы и ее линеаризации качественно эквивалентны в окрестности
особой точки. Такие особые точки называются гиперболическими.
Эта теорема устанавливает связь фазового
портрета нелинейной системы в окрестности некоторой особой точки с фазовым
портретом ее линеаризации.
Аналогия между особыми точками нелинейных систем
и их линеаризацией более тонкая, чем просто качественная эквивалентность, и не
сводится к окончательной классификации особых точек на устойчивые, седловые и
неустойчивые, приведенной на рис. 3.7. Внутри устойчивых и неустойчивых классов
для особых точек нелинейных систем также можно определить узлы, вырожденные
узлы и фокусы таким образом, что если особая точка линеаризации является узлом,
вырожденным узлом или фокусом, то такой же характер имеет особая точка исходной
нелинейной системы.
Траектории, представляющие собой лучи для
линеаризованной системы в некоторой особой точке являются касательными к
соответствующим траекториям нелинейной системы.
Если для линеаризованной системы особая точка -
центр, то для исходной нелинейной системы она может быть центром или фокусом.
Если траектории системы 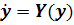 имеют ось
симметрии, проходящую через исследуемую особую точку, то последняя будет
центром для этой системы. Фокус имеется тогда и только тогда, когда нулевое
решение системы
имеют ось
симметрии, проходящую через исследуемую особую точку, то последняя будет
центром для этой системы. Фокус имеется тогда и только тогда, когда нулевое
решение системы 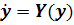 будет
асимптотически устойчиво при
будет
асимптотически устойчиво при 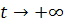 или при
или при 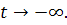
4.3 СЛОЖНЫЕ ОСОБЫЕ ТОЧКИ
Определение 4. Особая точка нелинейной системы
является сложной, если соответствующая линеаризованная система является
вырожденной.
Такие линейные системы имеют целую прямую, а
иногда и целую плоскость, особых точек. Нелинейные члены 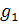 и
и
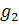 могут
существенно изменить это поведение.
могут
существенно изменить это поведение.
Систему уравнений 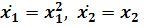 исследуем
методом изоклин.
исследуем
методом изоклин.
Запишем в виде
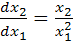 (4.5)
(4.5)
Интегральные кривые имеют наклон 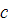 в
точках пересечения с кривой
в
точках пересечения с кривой
 .
.
А множество изоклин, которое получается, когда
мы придаем с различные действительные значения, - это семейство парабол:
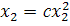
и прямая  .
.
Некоторые из этих изоклин изображены на рисунке
4.1 (а) красным цветом.
А угол наклона касательных к интегральным кривым
можно найти из формулы: 
Получаем при 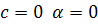
при 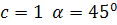
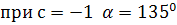 .
.
Особой точкой уравнения является точка(0,0)
Используя достаточно густое семейство изоклин,
мы может получить отчетливое представление о траекториях уравнения (4.5). Как
мы видим на рисунке (4.1(а)), только одна траектория (лежащая на прямой 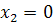 )
стремится к особой точке, а все остальные рано или поздно от нее уходят.
)
стремится к особой точке, а все остальные рано или поздно от нее уходят.
Характер локального фазового портрета
определяется теперь нелинейными членами. Поэтому в отличие от простых особых
точек, существует бесконечно много различных типов локальных фазовых портретов.
Линеаризации многих систем имеют на своих
фазовых портретах по крайней мере одну прямую, состоящую из особых точек. Так
же линии, состоящие из особых точек, могут возникать и в нелинейных системах;
они не обязаны быть прямыми и всегда состоят из непростых особых точек.
В силу сделанных выше замечаний неудивительно,
что не существует
подробной классификации непростых особых точек.
Однако определения устойчивости (применимые как к простым, так и к непростым
особым точкам)
позволяют дать грубую классификацию
качественного поведения.
Теорема 1. Всякая достаточно малая окрестность
особой точки системы
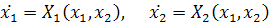
не являющаяся центром или топологическим узлом,
состоит из конечного числа эллиптических, параболических и гиперболических
областей (в частных случаях области некоторых типов могут отсутствовать),
примыкающих последовательно одна к другой, а так же из точек траектории, отделяющих
эти области одной от другой и из самой особой точки.
Сложные особые точки с нулевыми
характеристическими корнями.
Рассмотрим систему
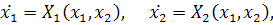 (4.6)
(4.6)
где 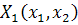 и
и
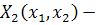 аналитические
функции, не имеющие общего множителя, отличного от постоянного. В разложениях
этих функций по степеням
аналитические
функции, не имеющие общего множителя, отличного от постоянного. В разложениях
этих функций по степеням  и
и 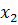 хотя
бы один из линейных членов не равен нулю.
хотя
бы один из линейных членов не равен нулю.
Пусть начало координат является сложной особой
точкой этой системы, т.е.

и определитель матрицы коэффициентов
линеаризованной системы, соответствующей системе (4.6) в начале координат равен
нулю:
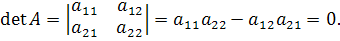 (4.7)
(4.7)
Следовательно, хотя бы одно из собственных
значений матрицы  равно нулю. Среди
сложных особых точек, для которых выполняется условие (4.7), выделяются два
случая в зависимости от следа матрицы
равно нулю. Среди
сложных особых точек, для которых выполняется условие (4.7), выделяются два
случая в зависимости от следа матрицы  :
:
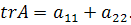
Так как характеристическое уравнение имеет вид

то, в случае, когда  ,
только один характеристический корень равен нулю, второй же равен
,
только один характеристический корень равен нулю, второй же равен 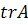 .
А в случае, когда trA
.
А в случае, когда trA ,оба
характеристических корня равны нулю.. Рассмотрим случай, когда
,оба
характеристических корня равны нулю.. Рассмотрим случай, когда 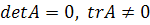 .
.
В этом случае систему (4.6) в окрестности начала
координат можем представить в каноническом виде:
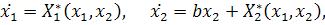
где  ,
а разложения по степеням
,
а разложения по степеням  функций
функций 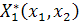 и
и
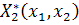 начинаются
с членов не менее чем второго порядка.
начинаются
с членов не менее чем второго порядка.
Введем в рассмотрение функцию
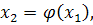
являющуюся решением уравнения
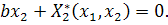
Подставим функцию  в
в
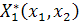 и
введем обозначение
и
введем обозначение
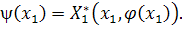
Так как функции 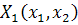 и
и
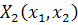 не
имеют общего множителя, отличного от постоянного, то
не
имеют общего множителя, отличного от постоянного, то 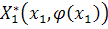 не
может быть тождественно равна нулю и, следовательно, в разложении функции
не
может быть тождественно равна нулю и, следовательно, в разложении функции 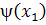 по
степеням
по
степеням  будут
отличные от нуля члены.
будут
отличные от нуля члены.
Таким образом, мы можем написать
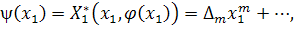
где  (так
как разложение
(так
как разложение 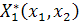 по степеням
по степеням  и
и
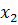 начинается
с членов не ниже второй степени и
начинается
с членов не ниже второй степени и  ).
Число
).
Число 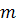 характеризует
красность общей точки кривых
характеризует
красность общей точки кривых
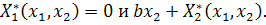
Теорема 2. Особая точка  ,
для которой
,
для которой  , может иметь
следующий качественный характер:
, может иметь
следующий качественный характер:
а) характер седла ( при 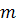 нечетном
и
нечетном
и 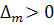 );
);
б) характер узла ( при 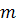 нечетном
и
нечетном
и 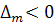 );
причем при
);
причем при 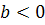 узел устойчивый, а
при
узел устойчивый, а
при 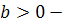 неустойчивый.
неустойчивый.
в) особая точка с одним узловым сектором и двумя
седловыми ( при 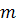 четном и любом
знаке
четном и любом
знаке 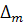 ).
При
).
При 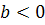 узловой
сектор устойчивый, при
узловой
сектор устойчивый, при 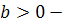 неустойчивый.
Кроме того, если
неустойчивый.
Кроме того, если  , то траектории
узлового сектора стремятся к
, то траектории
узлового сектора стремятся к 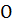 (при
(при 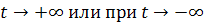 в
зависимости от знака
в
зависимости от знака 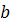 ) слева от оси
) слева от оси 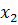 (рис.
4.3 (а)), а если
(рис.
4.3 (а)), а если  , то справа оси
, то справа оси 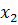 (рис.
4.3 (б)).
(рис.
4.3 (б)).
В случае, когда рассматриваемая система не имеет
канонического вида, направления, в которых траектории стремятся к началу
координат, могут быть отличны от направления осей. . Теперь рассмотрим
случай, когда  .
.
В этом случае оба характеристических корня
особой точки равны нулю.
Систему (4.6) можем привести к виду:
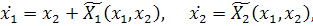
где 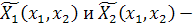 аналитические
функции, разложения которых по степеням
аналитические
функции, разложения которых по степеням 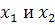 начинаются
с членов не менее чем второго порядка.
начинаются
с членов не менее чем второго порядка.
Рассмотрим следующие функции:
) функцию  ,
являющуюся решением уравнения
,
являющуюся решением уравнения

) функцию  ,
определяемую формулой
,
определяемую формулой
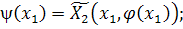
эта функция тождественно не равна нулю (в силу
предположения об отсутствии общих множителей, отличных от постоянных у правых
частей рассматриваемой системы), поэтому в разложении 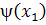 по
степеням
по
степеням  будут
отличные от нуля члены, и мы можем написать
будут
отличные от нуля члены, и мы можем написать

3) функцию
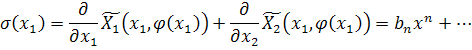
Функция  ,
в отличие от
,
в отличие от 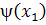 , может
тождественно обращаться в нуль.
, может
тождественно обращаться в нуль.
Рассмотрим сначала случай, когда 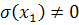 ,
так что при некотором
,
так что при некотором  Числа
Числа  и
коэффициенты
и
коэффициенты 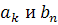 характеризуют
качественную структуру особой точки.
характеризуют
качественную структуру особой точки.
Теорема 3. Пусть 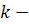 четное,
четное,
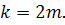
Тогда: 1) в случае, если 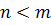 ,
особая точка
,
особая точка  имеет качественный
характер седло-узла;
имеет качественный
характер седло-узла;
) в случае, когда 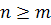 ,
существует одна полутраектория, стремящаяся к
,
существует одна полутраектория, стремящаяся к 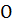 при
при
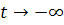 ,
и одна полутраектория, стремящаяся к
,
и одна полутраектория, стремящаяся к при
при 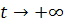 ,
все остальные траектории и при возрастании, и при убывании
,
все остальные траектории и при возрастании, и при убывании 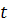 выходят
из окрестности
выходят
из окрестности 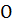 (т.е. окрестность
особой точки
(т.е. окрестность
особой точки 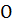 состоит из двух
седловых секторов). Такая особая точка называется вырожденным седло-узлом.
состоит из двух
седловых секторов). Такая особая точка называется вырожденным седло-узлом.
Теорема 4. Пусть 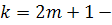 нечетное
число и
нечетное
число и 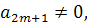 и
пусть
и
пусть 
Тогда: 1) если 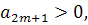 то
особая точка
то
особая точка  имеет качественный
характер седла (рис. 4.6);
имеет качественный
характер седла (рис. 4.6);
) если 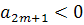 ,
то особая точка имеет:
,
то особая точка имеет:
а) характер фокуса или центра при 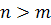 ,
о также при
,
о также при 
б) характер узла, если 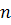 четное
и при этом
четное
и при этом 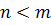 или
или 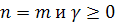 ;
;
в) одну замкнутую узловую область, две
сопровождающие ее узловые области и одну седловую область (рис 4.7), если 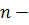 нечетное
число и при этом
нечетное
число и при этом  и
и 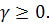
Рисунки 4.4 - 4.7 выполнены при условии 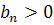 ;
в случае
;
в случае 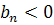 на
рисунках 4.6 и 4.7 расположение траекторий получается симметричным относительно
оси
на
рисунках 4.6 и 4.7 расположение траекторий получается симметричным относительно
оси  .
Все стремящиеся к особой точке с определенным направлением траектории стремятся
к ней, касаясь оси
.
Все стремящиеся к особой точке с определенным направлением траектории стремятся
к ней, касаясь оси  . Однако если
особая точка является фокусом или центром, то нет траекторий, стремящихся к
особой точке, а все траектории в достаточно малой окрестности являются
спиралями или замкнутыми траекториями.
. Однако если
особая точка является фокусом или центром, то нет траекторий, стремящихся к
особой точке, а все траектории в достаточно малой окрестности являются
спиралями или замкнутыми траекториями.
4.4 ОБЫКНОВЕННЫЕ ТОЧКИ
Определение 5. Любая точка фазовой плоскости,
которая не является особой точкой системы  ,
называется обыкновенной точкой этой системы.
,
называется обыкновенной точкой этой системы.
Таким образом, если 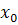 -
обыкновенная точка, то
-
обыкновенная точка, то 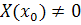 , и в силу
непрерывности функции X существует некоторая окрестность точки
, и в силу
непрерывности функции X существует некоторая окрестность точки 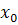 ,
содержащая только обыкновенные точки. Это означает, что локальный фазовый
портрет в обыкновенной точке не содержит особых точек. Существует важный
результат относительно качественной эквивалентности таких локальных фазовых
портретов-теорема о выпрямлении векторного поля или теорема о трубке траекторий
.
,
содержащая только обыкновенные точки. Это означает, что локальный фазовый
портрет в обыкновенной точке не содержит особых точек. Существует важный
результат относительно качественной эквивалентности таких локальных фазовых
портретов-теорема о выпрямлении векторного поля или теорема о трубке траекторий
.
На рис. 4.8- 4.11 показаны локальные фазовые
портреты в типичных обыкновенных точках 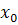 .
Для каждой из рассмотренных точек
.
Для каждой из рассмотренных точек 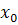 выделена
некоторая специальная окрестность, называемая трубкой траекторий. Траектории
системы входят в окрестность на одном ее конце и выходят на другом; ни одна
траектория не может покинуть эту окрестность через ее боковые стороны. Для
каждого из фазовых портретов, изображенных на рисунках, можно найти такие новые
координаты на плоскости,
выделена
некоторая специальная окрестность, называемая трубкой траекторий. Траектории
системы входят в окрестность на одном ее конце и выходят на другом; ни одна
траектория не может покинуть эту окрестность через ее боковые стороны. Для
каждого из фазовых портретов, изображенных на рисунках, можно найти такие новые
координаты на плоскости,
Типичной трубкой траекторий. В полярных
координатах это
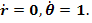
При замене переменных 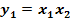 и
гарантирует существование системы
и
гарантирует существование системы
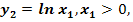 она имеет вид
координат, в которой локальный фаз
она имеет вид
координат, в которой локальный фаз
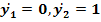 . вый портрет в
точке
. вый портрет в
точке 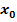 принимает
вид, изображенный на рис. 4.8.
принимает
вид, изображенный на рис. 4.8.
Например, на рис. 4.9 надо перейти к полярным
координатам r, q.
На плоскости( r, q),
окружности (r = const)
превратятся в прямые, параллельные оси q,
а радиальные прямые (q = const) станут
прямыми, параллельными оси r.
Таким образом, трубка траекторий на рис. 4.9 примет в полярных координатах
такой вид, как на рис. 4.8.
На рис. 4.10 траектории в окрестности точки 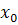 лежат
на гиперболах
лежат
на гиперболах 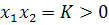 . Если мы введем
переменные
. Если мы введем
переменные 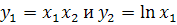 , то трубка
траекторий будет ограничена координатными линиями
, то трубка
траекторий будет ограничена координатными линиями  ,
,
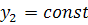 и на плоскости
и на плоскости 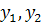 локальный
фазовый портрет снова имеет такой вид, как на рис. 4.8.
локальный
фазовый портрет снова имеет такой вид, как на рис. 4.8.
Теорема о трубке траекторий или о выпрямлении
векторного поля. В достаточно малой окрестности обыкновенной точки 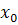 системы
х = Х(х) существует дифференцируемая взаимно однозначная замена переменных у =
у(х), переводящая исходную систему в систему
системы
х = Х(х) существует дифференцируемая взаимно однозначная замена переменных у =
у(х), переводящая исходную систему в систему  .
.
Теорема о трубке траекторий гарантирует существование
новых координат, обладающих указанным выше свойством, по крайней мере в
некоторой окрестности произвольной обыкновенной точки любой системы. Таким
образом, все локальные фазовые портреты в обыкновенных точках качественно
эквивалентны.
5
ПРИМЕРЫ, ИЛЛЮСТРИРУЮЩИЕ ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
1) Исследуем
на устойчивость нулевое решение системы
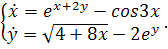 (5.1)
(5.1)
Выделяя линейную часть функций по формуле
Тейлора, получаем
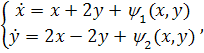
 функции
функции 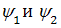 равны
равны
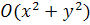 и,
значит, линеаризация системы (5.1) будет выглядеть так:
и,
значит, линеаризация системы (5.1) будет выглядеть так:

Теперь находим собственные значения матрицы
коэффициентов

 .
.
Они вещественные и один из них положителен,
значит, особая точка является седлом, и нулевое решение неустойчиво.
2)
Выясним, при каких значениях параметров a
и b нулевое решение
данной системы устойчиво.
 (5.2)
(5.2)
Как и в прошлом примере рассмотрим линеаризацию
системы (5.2)

и найдем собственные значения матрицы
коэффициентов
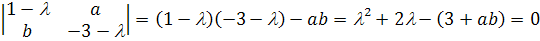
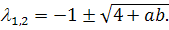
Мы знаем, что нулевое решение устойчиво тогда и
только тогда, когда корни отрицательны.
Рассмотрим, при каких значениях 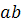 корни
будут удовлетворять этому
корни
будут удовлетворять этому
условию.
Когда 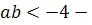 корни
комплексные с отрицательной вещественной частью.
корни
комплексные с отрицательной вещественной частью.
Когда  корни
вещественные, и отрицательными будут при
корни
вещественные, и отрицательными будут при
 .
.
Следовательно, нулевое решение системы (5.2)
устойчиво при  .
.
3) Исследуем,
устойчиво ли решение 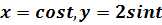 системы
системы
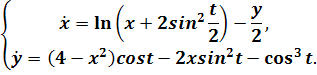
Для этого сначала переведем решение в нулевое.
Сделаем замену  При
этом данная система примет вид:
При
этом данная система примет вид:
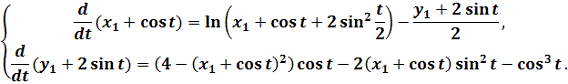
После преобразований и линеаризации получим:

Теперь найдем корни характеристического
уравнения

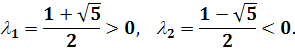
Они вещественные и разных знаков, значит,
решение 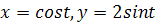 неустойчиво.
неустойчиво.
В четвертом и пятом примерах найдем все
положения равновесия и исследуем их на устойчивость.
4) Рассмотрим
систему:
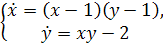
Чтобы найти ее положения равновесия надо решить
систему уравнений:
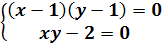
Получаем две особые точки 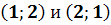 .
.
Перенесем точку  в
начало координат.
в
начало координат.
При замене 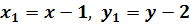 система
примет вид:
система
примет вид:
 .
.
Теперь линеаризуем ее и получим:
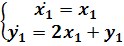 .
.
Найдем собственные значения матрицы
коэффициентов:

 .
.
Они равные и положительные, следовательно, в
точке  положение
равновесия является неустойчивым вырожденным узлом.
положение
равновесия является неустойчивым вырожденным узлом.
Теперь точку  переведем
в
переведем
в  заменой
заменой

Получим систему:

которая после линеаризации будет иметь вид
 .
.
Корни характеристического уравнения

вещественные и разных знаков:  ,
следовательно, в точке
,
следовательно, в точке 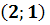 положение равновесия
неустойчиво и является седлом.
положение равновесия
неустойчиво и является седлом.
5) Теперь
найдем положения равновесия системы
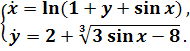 (5.3)
(5.3)
Из уравнения

находим, что
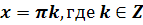 .
.
Подставив найденные  в
уравнение:
в
уравнение:
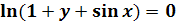 ,
,
получаем точки вида ( ),
),
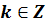 ,
в которых данная система находится в равновесии.
,
в которых данная система находится в равновесии.
Для исследования этих точек на устойчивость надо
перенести их в начало координат.
Сделаем замену
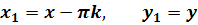
и рассмотрим два случая, когда 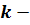 четные
числа и когда нечетные.
четные
числа и когда нечетные.
(a) При
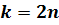 после
замены система (5.3) останется прежней:
после
замены система (5.3) останется прежней:
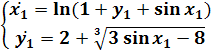 ,
,
и ее линеаризация имеет вид:

Найдем корни характеристического уравнения:
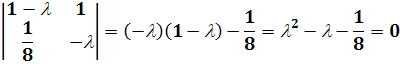

 .
.
Они вещественные и разных знаков. Поэтому в
точках вида ( положение
равновесия неустойчиво и является седлом.
положение
равновесия неустойчиво и является седлом.
(b) При
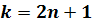 после
замены система (5.3) примет вид
после
замены система (5.3) примет вид
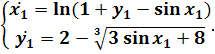
После линеаризации получим:
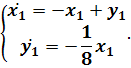
Корни характеристического уравнения
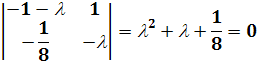
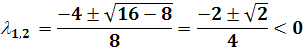
вещественные и меньше нуля, следовательно, в
точках вида 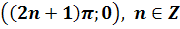 положение
равновесия является устойчивым узлом.
положение
равновесия является устойчивым узлом.
6) Исследуем
особую точку (0,0) уравнения:
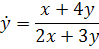
Составим и решим характеристическое уравнение:
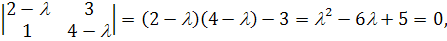
значит 
Корни вещественные, различные и положительные.
Следовательно, особая точка - неустойчивый узел.
Чтобы начертить траектории, находим для 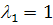 собственный
вектор
собственный
вектор  ,
а для
,
а для  вектор
вектор
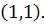 На
плоскости
На
плоскости 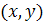 строим прямые,
направленные вдоль этих векторов, а затем кривые, касающиеся в начале координат
первой из этих прямых, так как
строим прямые,
направленные вдоль этих векторов, а затем кривые, касающиеся в начале координат
первой из этих прямых, так как  .
.
7) Найдем
и исследуем особые точки уравнения
 (5.4)
(5.4)
Его можно записать в виде системы:
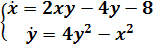 (5.5)
(5.5)
Особыми точками уравнения (5.4) являются точки,
в которых
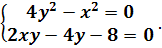
Следовательно, уравнение имеет две особые точки 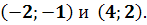
Исследуем особую точку  .
.
Перенесем ее в начало координат с помощью
замены:
 ,
,  .
.
и линеаризуем:
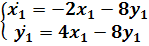
Найдем корни характеристического уравнения
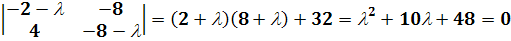
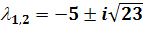 .
.
Значит, особая точка - фокус.
Строим в точке 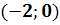 вектор
скорости
вектор
скорости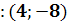 .
Следовательно, возрастанию t
соответствует движение по траекториям по часовой стрелке. Так как вещественная
часть корней l равна
.
Следовательно, возрастанию t
соответствует движение по траекториям по часовой стрелке. Так как вещественная
часть корней l равна  ,
то особая точка устойчива, следовательно, при возрастании t
решения приближаются к особой точке
,
то особая точка устойчива, следовательно, при возрастании t
решения приближаются к особой точке  ,
как показано на рис. 5.2.
,
как показано на рис. 5.2.
Особую точку 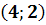 исследуем
аналогично.
исследуем
аналогично.
Система (5.5) после замены  ,
,
 и
линеаризации примет вид:
и
линеаризации примет вид:
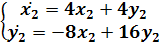
Решим характеристическое уравнение:

Собственные числа: 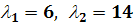 .
.
Значит, особая точка 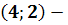 неустойчивый
узел (рис. 5.2).
неустойчивый
узел (рис. 5.2).
Разделив  получим
уравнение вида
получим
уравнение вида

Прямые, проходящие через особую точку, ищем в
виде 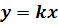 .
.
Здесь 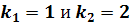 .
.
Значит,  искомые
прямые.
искомые
прямые.
8) Найдем
и исследуем особые точки системы

Система уравнений
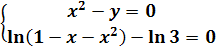
имеет решения  .
Следовательно, точки
.
Следовательно, точки  особые.
особые.
Исследуем каждую из этих точек.
С помощью замены

данную систему приводим к виду:
 .
.
Отсюда, применяя формулу Тейлора и отбрасывая
нелинейные члены, получаем:
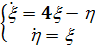 .
.
Решив характеристическое уравнение
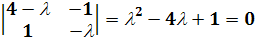

видим, что первая особая точка 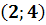 -
неустойчивый узел.
-
неустойчивый узел.
Для  находим
собственный вектор
находим
собственный вектор 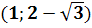 , а для
, а для 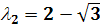 -
вектор
-
вектор 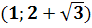 .
На плоскости строим прямые, направленные вдоль этих векторов, а затем кривые,
касающиеся своими вершинами с обеих сторон второй из этих прямых в точке
.
На плоскости строим прямые, направленные вдоль этих векторов, а затем кривые,
касающиеся своими вершинами с обеих сторон второй из этих прямых в точке  ,
так как
,
так как 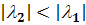 ,
как показано на рис.5.3.
,
как показано на рис.5.3.
Положив

из данной системы аналогично предыдущему случаю
получаем:
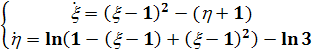 .
.
И после аналогичных выкладок приводим ее к
линеаризованной:
 .
.
Корни характеристического уравнения: 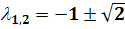 вещественные
и разных знаков, следовательно, вторая особая точка
вещественные
и разных знаков, следовательно, вторая особая точка 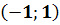 -
седло.
-
седло.
Теперь находим собственные вектора, и по ним
устанавливаем направление движения по траекториям.
В примерах 9,10 и 11 исследуем особые точки.
9) Система
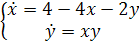
имеет две особые точки: 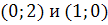 .
.
Аналогично предыдущим задачам получим, что в
особой точке 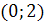 линеаризованная
система имеет вид:
линеаризованная
система имеет вид:
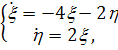
Корни характеристического уравнения:  равные
и отрицательные, значит, особая точка
равные
и отрицательные, значит, особая точка 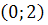 является
устойчивым вырожденным узлом. По теореме о линеаризации особая точка данной
системы будет того же типа, что и особая точка линеаризованной системы. Более
того, картины расположения интегральных кривых данной системы и укороченной
системы в малой окрестности особой точки будут примерно одинаковы.
является
устойчивым вырожденным узлом. По теореме о линеаризации особая точка данной
системы будет того же типа, что и особая точка линеаризованной системы. Более
того, картины расположения интегральных кривых данной системы и укороченной
системы в малой окрестности особой точки будут примерно одинаковы.
Собственный вектор для  .
Прямая, направленная вдоль этого вектора является интегральной и ее касаются
все интегральные кривые в точке
.
Прямая, направленная вдоль этого вектора является интегральной и ее касаются
все интегральные кривые в точке 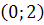 .
.
Теперь исследуем интегральные кривые уравнения
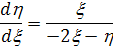
с помощью метода изоклин. В точках пересечения с
кривой
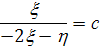
(где 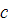 - некоторая
постоянная) интегральные кривые имеют наклон
- некоторая
постоянная) интегральные кривые имеют наклон 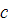 .
.
При 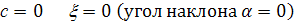
При 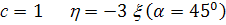
При 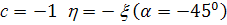
Линеаризация системы в окрестности особой точки 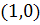 имеет
вид:
имеет
вид:
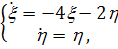 .
.
Корни характеристического уравнения:
вещественные и разных знаков, следовательно,
особая точка 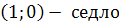 . Аналогично
предыдущему случаю, точка
. Аналогично
предыдущему случаю, точка 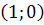 будет седлом и для
исходной системы.
будет седлом и для
исходной системы.
Для 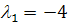 собственный
вектор равен
собственный
вектор равен 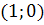 , а для
, а для  равен
равен
 .
.
Значит, по прямой  интегральные
прямые входят в седло, а по прямой
интегральные
прямые входят в седло, а по прямой 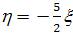 выходят
из него.
выходят
из него.
10) Рассмотрим
систему:
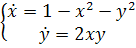
Поскольку эта система при замене x
на -x, y
на -y вида не меняет, то
картина фазовых траекторий симметрична как относительно оси Ox,
так и относительно оси Oy.
Данная система имеет четыре особые точки: 
Рассмотрим точки 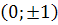
После замены 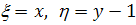
и линеаризации, получим систему:

Поскольку корни характеристического уравнения
этой системы:

комплексные и чисто мнимые, то особая точка  -
центр. Для исходной системы эта точка может быть фокусом или центром. В силу
симметрии интегральных кривых относительно оси Ox,
точка
-
центр. Для исходной системы эта точка может быть фокусом или центром. В силу
симметрии интегральных кривых относительно оси Ox,
точка 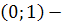 центр,
аналогично точка
центр,
аналогично точка  тоже является
центром.
тоже является
центром.
Направление движения по траекториям определим по
вектору скорости.
Для точки 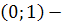 вектор
скорости в точке
вектор
скорости в точке 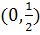 равен
равен  ,
следовательно, движение идет по положительному направлению.
,
следовательно, движение идет по положительному направлению.
Теперь рассмотрим точку 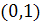 .
.
Сделаем замену 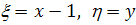 .
.
Укороченная система имеет вид:
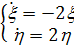 .
.
Корни характеристического уравнения: 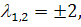 следовательно
особая точка
следовательно
особая точка  седло.
седло.
Найдем собственные векторы для  и
и
 :
:
Для 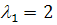 собственный
вектор равен
собственный
вектор равен 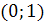 , и по прямой
, и по прямой 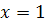 интегральные
прямые выходят из седла.
интегральные
прямые выходят из седла.
Для  вектор
равен
вектор
равен 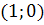 ,
значит, по прямой
,
значит, по прямой 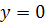 интегральные
прямые входят в седло.
интегральные
прямые входят в седло.
В силу симметричности траекторий относительно
оси Oy, точка 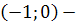 также
седло, и из нее наоборот интегральные прямые выходят по оси Ox,
а входят по прямой
также
седло, и из нее наоборот интегральные прямые выходят по оси Ox,
а входят по прямой 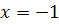 .
.
11) Исследуем
особые точки системы:
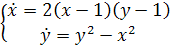 .
.
Из системы уравнений
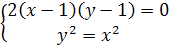
находим координаты особых точек: 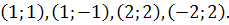
Полагая 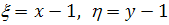 ,
приводим систему дифференциальных уравнений к укороченному виду:
,
приводим систему дифференциальных уравнений к укороченному виду:
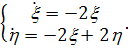
Из характеристического уравнения
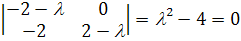
видим, что собственные числа  вещественные
и разных знаков, значит, точка
вещественные
и разных знаков, значит, точка  седло.
седло.
Найдем собственные векторы для 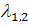 .
.
Для  -
это вектор
-
это вектор 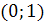 ,
,
а для  -
вектор
-
вектор 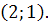
Аналогично, положив 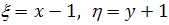 и
удержав линейные члены, из данной системы получаем укороченную:
и
удержав линейные члены, из данной системы получаем укороченную:
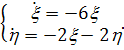
Решив характеристическое уравнение
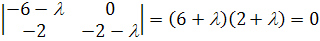

заключаем, что точка 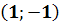 является
устойчивым узлом.
является
устойчивым узлом.
Так же найдем для  собственный
вектор
собственный
вектор 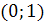 и
для
и
для 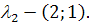 Следовательно,
все интегральные кривые касаются вектора
Следовательно,
все интегральные кривые касаются вектора 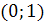 ,
так как
,
так как 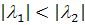 .
.
Теперь сделаем замену  ,
и как в предыдущих случаях рассмотрим укороченную систему, получившуюся из
данной:
,
и как в предыдущих случаях рассмотрим укороченную систему, получившуюся из
данной:
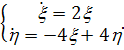
Поскольку корни уравнения

равны 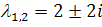 ,
то особая точка
,
то особая точка 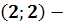 неустойчивый
фокус.
неустойчивый
фокус.
Для выяснения направления закручивания
интегральных кривых (спиралей) построим вектор скорости в точке 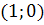 :
:
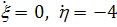 .
.
Приняв во внимание, что фокус неустойчивый,
видим, что при движении по спиралям от особой точки будет происходить вращение
по часовой стрелке.
Для рассмотрения оставшейся точки 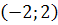 сделаем
замену
сделаем
замену

и приведем данную систему к укороченной:
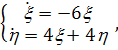
характеристическое уравнение которой имеет корни
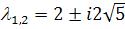 .
И, значит, точка
.
И, значит, точка  тоже неустойчивый
фокус.
тоже неустойчивый
фокус.
В этом случае построим вектор скорости в точке 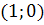 :
:
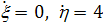 .
.
И так как фокус неустойчивый, будет происходить
вращение по спиралям от особой точки против хода часовой стрелки.
12) Начертим
на фазовой плоскости траектории системы, записанной в полярных координатах, и
исследуем, имеются ли предельные циклы.
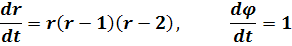
Для этого нужно правую часть прировнять к нулю и
найти корни.
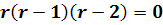
получаем 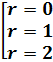
Посмотрим, где функция возрастает, а где
убывает.
Так как 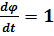 ,
возрастанию t соответствует
движение по траекториям против часовой стрелки.
,
возрастанию t соответствует
движение по траекториям против часовой стрелки.
Получается, что к предельному циклу с радиусом  траектории
неограни-ченно приближаются с обеих сторон при
траектории
неограни-ченно приближаются с обеих сторон при 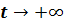 ,
то есть он устойчивый.
,
то есть он устойчивый.
А от предельного цикла с радиусом  траектории
неограниченно удаляются с обеих сторон при
траектории
неограниченно удаляются с обеих сторон при 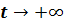 ,
то есть он неустойчивый.
,
то есть он неустойчивый.
13) Начертим
на фазовой плоскости траектории системы:
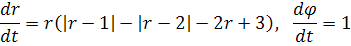
и исследуем, имеются ли предельные циклы.
Сначала раскроем модули. Обозначим
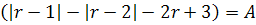
Когда 

Когда 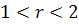

И когда 
 .
.
Получается:

Существуют замкнутые траектории, заданные
уравнениями
 .
.
Кроме того,
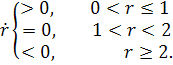
Так как 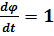 ,
возрастанию t соответствует движение
по траекториям против часовой стрелки.
,
возрастанию t соответствует движение
по траекториям против часовой стрелки.
Мы видим, что траектории неограниченно
приближаются при 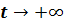 к предельному
циклу с радиусом
к предельному
циклу с радиусом  при
при 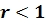 и
к предельному циклу с радиусом
и
к предельному циклу с радиусом  при
при 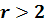 ,
значит они устойчивые.
,
значит они устойчивые.
При 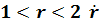 не
меняется, следовательно, в этом промежутке лежит множество замкнутых
траекторий, которые не являются предельными циклами, и каждая из этих
траекторий является устойчивой.
не
меняется, следовательно, в этом промежутке лежит множество замкнутых
траекторий, которые не являются предельными циклами, и каждая из этих
траекторий является устойчивой.
дифференциальный
уравнение популяция фазовый
ГЛАВА 2
1. ПРИЛОЖЕНИЕ КАЧЕСТВЕННОЙ ТЕОРИИ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ К БИОЛОГИЧЕСКИМ ЗАДАЧАМ
1.1 ФАЗОВЫЕ ПОРТРЕТЫ И ДИНАМИКА
В различных приложениях дифференциальное
уравнение 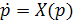
моделирует изменение какого-нибудь параметра х
некоторой физической системы в зависимости от времени. Мы говорим, что состояние
системы определяется значением величины х. Например, уравнение
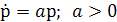 (1.1)
(1.1)
моделирует рост популяции р некоторого
изолированного вида. В рамках этой модели состояние вида в момент времени t
задается количеством индивидуумов 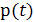 ,
существующих в момент t.
,
существующих в момент t.
Фазовый портрет фиксирует только направление
скорости фазовой точки и, следовательно, отражает лишь качественную картину
динамики. Такая качественная информация может оказаться полезной при построении
моделей. Например, рассмотрим (1.1) - модель роста изолированной популяции.
Заметим, что  для всех
для всех  ,
и фазовый портрет на рис. 1.1 показывает, что популяция растет неограниченно.
Это свойство выглядит неправдоподобно: та среда, в которой живет этот вид,
имеет свои ограничения и не может обеспечить ресурсами неограниченно растущую
популяцию.
,
и фазовый портрет на рис. 1.1 показывает, что популяция растет неограниченно.
Это свойство выглядит неправдоподобно: та среда, в которой живет этот вид,
имеет свои ограничения и не может обеспечить ресурсами неограниченно растущую
популяцию.
Предположим, что окружающая среда может
обеспечивать существование популяции  .
Очевидно, неограниченный рост р должен быть чем-то остановлен. Одна из
возможностей - ввести устойчивую неподвижную точку
.
Очевидно, неограниченный рост р должен быть чем-то остановлен. Одна из
возможностей - ввести устойчивую неподвижную точку  ,
как показано на рис. 1.1(б). Это значит, что популяции, большие чем
,
как показано на рис. 1.1(б). Это значит, что популяции, большие чем  ,
уменьшаются, меньшие чем
,
уменьшаются, меньшие чем  , растут, а
равновесие достигается при
, растут, а
равновесие достигается при 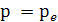 . Чтобы могли
существовать две неподвижные точки при
. Чтобы могли
существовать две неподвижные точки при  и
и
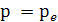 ,
функция
,
функция  в
(1.1) должна быть нелинейной. Уравнение
в
(1.1) должна быть нелинейной. Уравнение
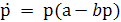
хорошо тем, что при  оно
сводится к (1.1); в противном случае оно имеет неподвижную точку
оно
сводится к (1.1); в противном случае оно имеет неподвижную точку 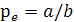 .
.
(a)
(b)
Рис. 1.1. Фазовые портреты для уравнений (a)
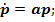 (b)
(b)

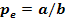 . В обоих случаях
нас интересует только поведение неотрицательных популяций (
. В обоих случаях
нас интересует только поведение неотрицательных популяций ( ).
Уравнение (b) называется
логистическим законом роста популяции.
).
Уравнение (b) называется
логистическим законом роста популяции.
Конечно, чаще в моделях биологических систем
состояние системы определяется более чем одной переменной, и в дальнейшем мы
будем рассматривать именно такие системы.
.2 КОНКУРИРУЮЩИЕ ВИДЫ
Два сходных вида животных конкурируют друг с
другом на некоторой территории с ограниченными запасами пищи. Возможны
различные исходы их конкурентной борьбы:
(a) вид 1 выживает, а вид 2 вымирает;
(b) вид 2 выживает, а вид 1 вымирает;
(c) оба вида сосуществуют;
(d)
оба вида вымирают.
Каждый из этих исходов соответствует некоторому
положению равновесия для популяций  и
и
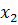 двух
рассматриваемых видов. Поэтому дифференциальные уравнения, моделирующие
динамику популяций
двух
рассматриваемых видов. Поэтому дифференциальные уравнения, моделирующие
динамику популяций  и
и 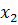 ,
должны иметь четыре изолированные особые точки.
,
должны иметь четыре изолированные особые точки.
Рассмотрим следующие нелинейные динамические
уравнения:
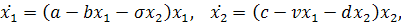 (1.2)
(1.2)
где  Заметим,
что прирост на особь
Заметим,
что прирост на особь  состоит из трех
слагаемых: скорости размножения изолированной популяции a;
члена, соответствующего внутривидовой конкуренции
состоит из трех
слагаемых: скорости размножения изолированной популяции a;
члена, соответствующего внутривидовой конкуренции  члена,
соответствующего межвидовой конкуренции
члена,
соответствующего межвидовой конкуренции  .
Аналогично интерпретируются члены
.
Аналогично интерпретируются члены  в
уравнении для
в
уравнении для 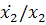 . Необходимое
условие для возможности выживания обоих видов состоит в том, что должна
существовать неподвижная точка уравнений (1.2), обе координаты которой
положительны. Такая неподвижная точка для уравнений (1.2) существует тогда и
только тогда, когда линейные уравнения
. Необходимое
условие для возможности выживания обоих видов состоит в том, что должна
существовать неподвижная точка уравнений (1.2), обе координаты которой
положительны. Такая неподвижная точка для уравнений (1.2) существует тогда и
только тогда, когда линейные уравнения
 (1.3)
(1.3)
имеют решение с положительными координатами. Мы
будем предполагать, что система (1.3) имеет единственное решение в первом
квадранте плоскости  ,
, 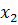 .
В этом случае неподвижная точка имеет координаты
.
В этом случае неподвижная точка имеет координаты
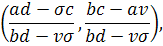
причем либо
 (1.4)
(1.4)
либо
 (1.4’)
(1.4’)
Сейчас рассмотрим характер изменения величин  ,
,
 при
условиях (1.4).
при
условиях (1.4).
Начнем с того, что произведем линеаризацию
системы во всех четырех неподвижных точках. Каждую из линеаризованных систем мы
обозначим 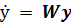 , где у - локальные
координаты в окрестности соответствующей неподвижной точки. Ниже для каждой из
неподвижных точек указана ее матрица
, где у - локальные
координаты в окрестности соответствующей неподвижной точки. Ниже для каждой из
неподвижных точек указана ее матрица 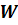 :
:
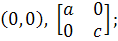 (1.5)
(1.5)
 (1.6)
(1.6)
 (1.7)
(1.7)
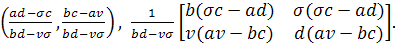 (1.8)
(1.8)
Все неподвижные точки простые, а их вид определяется
собственными значениями соответствующих матриц 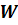 .
Для (1.5) это числа
.
Для (1.5) это числа 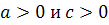 ,и по теореме о
линеаризации начало координат - неустойчивый узел. Собственные значения
,и по теореме о
линеаризации начало координат - неустойчивый узел. Собственные значения  из
(1.6) тоже легко усматриваются, так как матрица
из
(1.6) тоже легко усматриваются, так как матрица  треугольная,
и оба значения отрицательны (по (1.4)). То же справедливо относительно
треугольная,
и оба значения отрицательны (по (1.4)). То же справедливо относительно  из
(1.7), и в каждом из этих случаев теорема о линеаризации позволяет сделать
вывод, что эти точки - устойчивые или вырожденные узлы (заметим, что возможны
равенства
из
(1.7), и в каждом из этих случаев теорема о линеаризации позволяет сделать
вывод, что эти точки - устойчивые или вырожденные узлы (заметим, что возможны
равенства 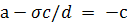 или
или 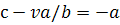 ).
).
Наконец, неподвижная точка (1.8) является седлом,
поскольку
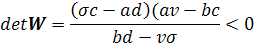
(по условиям (1.4)), и собственные значения  должны
обладать противоположными знаками (как видно на рис. 3.7. первой главы).
должны
обладать противоположными знаками (как видно на рис. 3.7. первой главы).
Теперь видно, что сосуществование является чрезвычайно
маловероятным, так как при  в седло входят
только две сепаратрисы. Неподвижные точки
в седло входят
только две сепаратрисы. Неподвижные точки  устойчивы
и соответствуют вымиранию видов 1 и 2. Начало координат является неустойчивым узлом,
так что возможность вымирания обоих видов исключена, поскольку все траектории
удаляются от точки
устойчивы
и соответствуют вымиранию видов 1 и 2. Начало координат является неустойчивым узлом,
так что возможность вымирания обоих видов исключена, поскольку все траектории
удаляются от точки 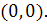 Предполагая, что
все начальные положения в первом квадранте равновероятны, мы видим, что
наиболее вероятным исходом является вымирание одного из видов. Полученный нами
результат находится в соответствии с «принципом конкурентного исключения»,
согласно которому в таких ситуациях конкурентной борьбы один из видов вымирает.
Предполагая, что
все начальные положения в первом квадранте равновероятны, мы видим, что
наиболее вероятным исходом является вымирание одного из видов. Полученный нами
результат находится в соответствии с «принципом конкурентного исключения»,
согласно которому в таких ситуациях конкурентной борьбы один из видов вымирает.
Дальнейшие подробности относительно эволюции
этих двух видов можно получить, нарисовав фазовый портрет рассмотренной модели.
Заметим, что прямые из уравнений (1.3) - это изоклины направлений 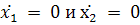 соответственно.
Направление векторного поля
соответственно.
Направление векторного поля 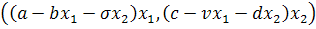 можно получить,
исследуя знаки
можно получить,
исследуя знаки 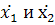 , как это показано
на рис. 1.3. Этой информации вместе со сведениями о характере неподвижных точек
достаточно для того, чтобы построить фазовый портрет, изображенный на рис. 1.4.
Различные детали, например какой оси касаются траектории, выходящие из начала
координат, зависят уже от величин собственных значений. Например, на рис. 1.4
предполагается, что
, как это показано
на рис. 1.3. Этой информации вместе со сведениями о характере неподвижных точек
достаточно для того, чтобы построить фазовый портрет, изображенный на рис. 1.4.
Различные детали, например какой оси касаются траектории, выходящие из начала
координат, зависят уже от величин собственных значений. Например, на рис. 1.4
предполагается, что  и поэтому
траектории на рисунке касаются оси
и поэтому
траектории на рисунке касаются оси 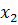 .
.
.3 УРАВНЕНИЯ ВОЛЬТЕРРА - ЛОТКА
Самые общие колебания, которые могут возникнуть
при рассмотрении автономных линейных уравнений на плоскости, имеют вид
 (1.9)
(1.9)
им соответствуют замкнутые эллиптические
траектории на фазовом портрете. Кривые, заданные уравнениями (1.9), сильно
симметричны, и, хотя изменение параметров 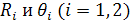 допускает
изменение амплитуды и сдвиг начального положения точки, форма траекторий
остается неизменной.
допускает
изменение амплитуды и сдвиг начального положения точки, форма траекторий
остается неизменной.
В динамике популяций существует много примеров,
когда изменение численности популяций во времени носит колебательный характер.
Однако эти колебания заметно отличаются от гармонических, и для того, чтобы их
промоделировать, необходимы нелинейные уравнения. Одним из самых известных
примеров уравнений описания динамики взаимодействующих популяций являются
уравнения Вольтерра - Лотка.
Рассмотрим модель, содержащую два вида, один вид
- хищники, а другой - их добыча. Пусть  и
и
 -
популяции жертв и хищников соответственно. Предположим, что между особями
одного вида нет соперничества. Пусть прирост на особь
-
популяции жертв и хищников соответственно. Предположим, что между особями
одного вида нет соперничества. Пусть прирост на особь  для
жертв составляет
для
жертв составляет 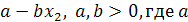 - скорость размножения
жертв в отсутствие хищников,
- скорость размножения
жертв в отсутствие хищников, 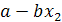 есть член,
учитывающий потери от хищников. Популяция хищников уменьшалась бы в отсутствие
их пищи (т. е. жертв), так что
есть член,
учитывающий потери от хищников. Популяция хищников уменьшалась бы в отсутствие
их пищи (т. е. жертв), так что 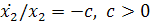 при
при  .
Однако наличие жертв в случае удачной охоты на них компенсирует это уменьшение,
так что при
.
Однако наличие жертв в случае удачной охоты на них компенсирует это уменьшение,
так что при 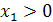 имеем
имеем  Таким
образом, система имеет вид
Таким
образом, система имеет вид
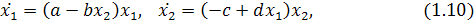
где 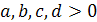 .
Это и есть уравнения Вольтерра - Лотка. Система (1.10) имеет две неподвижные
точки:
.
Это и есть уравнения Вольтерра - Лотка. Система (1.10) имеет две неподвижные
точки:  .
Первая из этих точек - седло, для которого оси
.
Первая из этих точек - седло, для которого оси 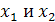 являются
сепаратрисами, причем ось
являются
сепаратрисами, причем ось  устойчивая.
Линеаризованная система в нетривиальной неподвижной точке
устойчивая.
Линеаризованная система в нетривиальной неподвижной точке 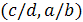 имеет
центр, и, следовательно, теорема о линеаризации не дает возможности определить
характер этой точки для исходной системы.
имеет
центр, и, следовательно, теорема о линеаризации не дает возможности определить
характер этой точки для исходной системы.
Дифференциальное уравнение

является уравнением с разделяющимися
переменными, и его решения удовлетворяют равенству
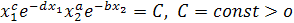 .
.
Следовательно система (4.9) имеет первый
интеграл

Здесь функции 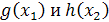 одного
и того же вида: обе они положительны на полуоси
одного
и того же вида: обе они положительны на полуоси 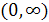 и
имеют на ней один максимум.
и
имеют на ней один максимум.
Функции 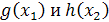 принимают
максимальные значения при
принимают
максимальные значения при 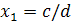 и
и 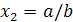 соответственно,
и, таким образом, функция
соответственно,
и, таким образом, функция 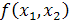 принимает
максимальное значение
принимает
максимальное значение 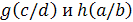 в точке
в точке 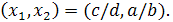 Следовательно,
линии уровня функции
Следовательно,
линии уровня функции 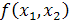 являются
замкнутыми кривыми, окружающими точку
являются
замкнутыми кривыми, окружающими точку 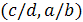 .
Траектории системы (1.10) совпадают с этими линиями уровня, и точка
.
Траектории системы (1.10) совпадают с этими линиями уровня, и точка 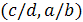 является
центром.
является
центром.
Функции 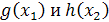 не
симметричны относительно своих максимальных значений и, следовательно,
замкнутые траектории не являются эллипсами. Обе функции
не
симметричны относительно своих максимальных значений и, следовательно,
замкнутые траектории не являются эллипсами. Обе функции 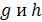 имеют
крутой подъем и относительно пологий спуск (см. рис. 1.5); это значит, что
траектории имеют форму, указанную на рис. 1.6. Неэллиптическая форма траекторий
этого нелинейного центра отражает негармонический характер колебаний
численности популяций (рис. 1.7).
имеют
крутой подъем и относительно пологий спуск (см. рис. 1.5); это значит, что
траектории имеют форму, указанную на рис. 1.6. Неэллиптическая форма траекторий
этого нелинейного центра отражает негармонический характер колебаний
численности популяций (рис. 1.7).
.4 МОДЕЛЬ ХОЛЛИНГА - ТЭННЕРА
Хотя незатухающие негармонические колебания
встречаются для нелинейных систем с центрами на фазовых портретах, неизвестно,
являются ли такие колебания устойчивыми относительно возмущений самой модели.
Если модифицировать уравнения Вольтерра - Лотка (1.10) таким образом, чтобы
учитывалась внутривидовая конкуренция, на фазовом портрете измененной таким
образом системы уже не будет центра, он превратится в фокус, и колебания
популяции будут затухать. Способность к легкому разрушению вообще является
характерным свойством центров; говорят, что они структурно неустойчивы.
Другая возможность, при которой в нелинейных
системах возникают незатухающие колебания, - это наличие предельных циклов на
их фазовых портретах. Предельные циклы являются структурно устойчивыми и,
следовательно, представляют собой более «постоянную» характерную черту фазового
портрета системы: они не имеют тенденции исчезать при относительно малых
возмущениях модели. Модели, не чувствительные к малым возмущениям, называются
грубыми. Поскольку большинство моделей являются идеализациями, в которых
внимание сосредоточено только на некоторых основных переменных и соотношениях
между ними, такой вид устойчивости чрезвычайно важен.
Система «хищник - жертва» для двух видов
является, конечно, именно такой идеализацией, и модель Вольтерра - Лотка не
является грубой. Поэтому возникает сомнение, отражает ли система (1.10)
настоящий механизм колебаний численности популяций. Модель, в которой возникают
структурно устойчивые колебания численности популяций для системы «хищник -
жертва», - это модель Холлинга - Тэннера. Динамические уравнения этой модели
имеют вид
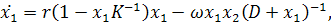 (1.11)
(1.11)
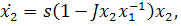
где 
Скоростью роста популяции жертв 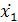 является
разность двух членов:)
является
разность двух членов:)  , задающего
скорость размножения жертв в отсутствие хищников. Сюда включен член, соответствующий
межвидовой конкуренции в условиях ограниченных ресурсов ;)
, задающего
скорость размножения жертв в отсутствие хищников. Сюда включен член, соответствующий
межвидовой конкуренции в условиях ограниченных ресурсов ;) 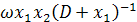 ,
описывающего влияние хищников.
,
описывающего влияние хищников.
Чтобы объяснить вид члена 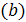 ,
надо понять влияние хищников в терминах «коэффициента хищничества». Это -
количество жертв, убиваемых одним хищником в единицу времени. В уравнениях
(1.10) коэффициент хищничества равен
,
надо понять влияние хищников в терминах «коэффициента хищничества». Это -
количество жертв, убиваемых одним хищником в единицу времени. В уравнениях
(1.10) коэффициент хищничества равен 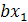 .
Это значит, что количество жертв, убиваемых одним хищником в единицу времени,
неограниченно растет вместе с популяцией жертв.
.
Это значит, что количество жертв, убиваемых одним хищником в единицу времени,
неограниченно растет вместе с популяцией жертв.
Более разумным представляется предположение, что
существует верхний предел коэффициента хищничества, т. е. что хищник перестает
убивать, когда насыщается. Это учитывается видом члена 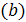 ,
в котором коэффициент хищничества равен
,
в котором коэффициент хищничества равен 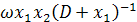 (см.
рис. 1.8).
(см.
рис. 1.8).
Скорость роста популяции хищников 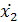 такая
же, как в (1.11), в предположении, что жертвы достаточно редки. Допустим, что
количество жертв, необходимых для поддержания жизни одного хищника, равно
такая
же, как в (1.11), в предположении, что жертвы достаточно редки. Допустим, что
количество жертв, необходимых для поддержания жизни одного хищника, равно  .
Таким образом, популяция из
.
Таким образом, популяция из  жертв может
поддерживать не более чем
жертв может
поддерживать не более чем 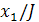 хищников. Мы
должны построить модель таким образом, чтобы количество хищников не превышало
критическую величину
хищников. Мы
должны построить модель таким образом, чтобы количество хищников не превышало
критическую величину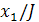 ; это достигается
при
; это достигается
при

Именно это уравнение задано в (1.11).
Как видно на чертеже, существует неподвижная
точка с положительными значениями 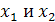 ;
обозначим ее
;
обозначим ее 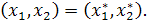 Чтобы определить
характер этой неподвижной точки, удобно в уравнениях (1.11) изменить масштаб
переменных, разделив их на
Чтобы определить
характер этой неподвижной точки, удобно в уравнениях (1.11) изменить масштаб
переменных, разделив их на 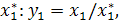
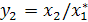 .
Получим уравнения
.
Получим уравнения
 (1.12)
(1.12)
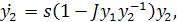
где 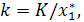 а
а
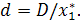 Кроме
того, на плоскости
Кроме
того, на плоскости 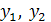 неподвижная точка
имеет координаты
неподвижная точка
имеет координаты
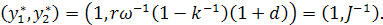 (1.13)
(1.13)
Матрица коэффициентов линеаризованной в точке 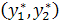 системы
имеет вид
системы
имеет вид
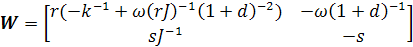
Заметим, что
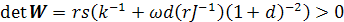
так что 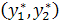 никогда
не может быть седлом. Однако, подставив
никогда
не может быть седлом. Однако, подставив 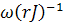 из
(1.13), получим, что
из
(1.13), получим, что
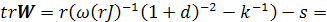
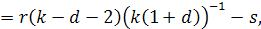
а это выражение может быть как положительным,
так и отрицательным.
Если  то
то
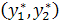 является
неустойчивой неподвижной точкой. Так же, если набор параметров
является
неустойчивой неподвижной точкой. Так же, если набор параметров  удовлетворяет
условию
удовлетворяет
условию

то на фазовом портрете системы (1.12) имеется
устойчивый предельный цикл, как показано на рис. 1.10. А если точка 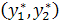 лежит
левее максимума на нулевой изоклине
лежит
левее максимума на нулевой изоклине 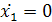 ,
то она является просто устойчивым фокусом.
,
то она является просто устойчивым фокусом.
2. ДРУГИЕ МОДЕЛИ
1. Исследуем
характер неподвижных точек модели, описывающей конкуренцию видов
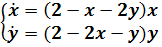 .
.
Из системы
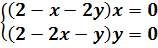
Найдем особые точки: 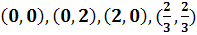 .
.
Рассмотрим точку 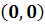 .
Линеаризация данной системы имеет вид:
.
Линеаризация данной системы имеет вид:
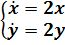
Составив и решив характеристическое уравнение:

видим, что корни  одинаковые
и положительные, значит, особая точка - неустойчивый дикритический узел. То
есть множество интегральных прямых вида
одинаковые
и положительные, значит, особая точка - неустойчивый дикритический узел. То
есть множество интегральных прямых вида 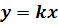 выходят
из точки
выходят
из точки 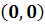 .
.
При рассмотрении точки 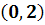 сделаем
замену:
сделаем
замену:
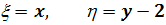
и приведем исходную систему к укороченной:
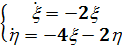
Из уравнения

находим  и,
следовательно, точка
и,
следовательно, точка 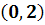 является
устойчивым вырожденным узлом. Собственный вектор для l
равен
является
устойчивым вырожденным узлом. Собственный вектор для l
равен 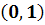 .
Таким образом, прямая
.
Таким образом, прямая 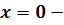 интегральная, и ее
касаются все интегральные кривые в точке
интегральная, и ее
касаются все интегральные кривые в точке 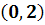 .
Если рассмотреть векторы скорости, например, в точке
.
Если рассмотреть векторы скорости, например, в точке 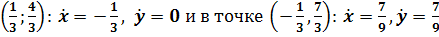 ,
то можно построить поле направлений, и затем начертить интегральные кривые, как
показано на рисунке 2.1.
,
то можно построить поле направлений, и затем начертить интегральные кривые, как
показано на рисунке 2.1.
Далее, сделаем замену
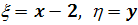 ,
,
и получим для особой точки 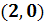 укороченную
систему:
укороченную
систему:
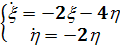 .
.
Характеристическое уравнение имеет корни 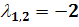 .
Как и в предыдущем случае, точка
.
Как и в предыдущем случае, точка 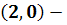 тоже
устойчивый вырожденный узел. Здесь собственный вектор для l
равен
тоже
устойчивый вырожденный узел. Здесь собственный вектор для l
равен 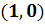 ,
и интегральная прямая, которую касаются все кривые - это
,
и интегральная прямая, которую касаются все кривые - это  .
Построив векторы скорости в точке
.
Построив векторы скорости в точке  ,
строим интегральные кривые.
,
строим интегральные кривые.
Осталось рассмотреть точку 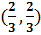 .
.
Укороченная система имеет вид:
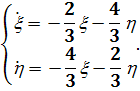
Корни характеристического уравнения
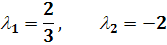
вещественные и разных знаков, значит, особая
точка  седло.
седло.
Для 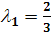 собственный
вектор равен
собственный
вектор равен  Следовательно,
прямые
Следовательно,
прямые  интегральные,
а остальные кривые в окрестности особой точки их касаются.
интегральные,
а остальные кривые в окрестности особой точки их касаются.
Интерпретация фазового портрета в терминах
поведения вида:
Мы рассматриваем взаимодействие двух видов,
численности которых x и y,
описаны уравнениями 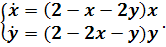
Начало координат является неустойчивым
дикритическим узлом, значит, все траектории удаляются от точки 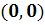 ,
поэтому возможность вымирания обоих видов исключена. Неподвижные точки (0, 2) и
(2, 0) - устойчивые узлы и соответствуют вымиранию одного из видов 1 и 2. Точка
,
поэтому возможность вымирания обоих видов исключена. Неподвижные точки (0, 2) и
(2, 0) - устойчивые узлы и соответствуют вымиранию одного из видов 1 и 2. Точка
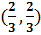 является
седлом и она характеризует сосуществование двух видов. Из рисунка видно, что
она неустойчива, в нее входят только две сепаратрисы, отделяющие области
выживания каждого из видов, а все остальные траектории от нее удаляются.
Сместившись от этой особой точки даже на маленькое расстояние, мы сразу попадем
либо в точку (0,2), либо в (2,0), то есть один из видов вымирает.
является
седлом и она характеризует сосуществование двух видов. Из рисунка видно, что
она неустойчива, в нее входят только две сепаратрисы, отделяющие области
выживания каждого из видов, а все остальные траектории от нее удаляются.
Сместившись от этой особой точки даже на маленькое расстояние, мы сразу попадем
либо в точку (0,2), либо в (2,0), то есть один из видов вымирает.
2. Исследуем
поведение особых точек системы, описывающих конкуренцию видов
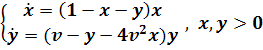 (2.1)
(2.1)
при изменении параметра 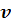 для
всех
для
всех 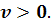
Приравняем к нулю правые части уравнений системы

и найдем особые точки: 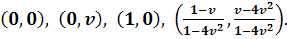
Матрицы для каждой из неподвижных точек:
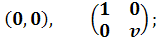
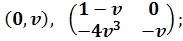
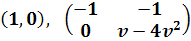
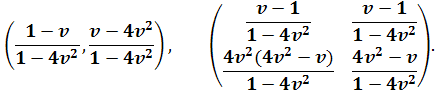
Рассмотрим характер неподвижных точек при
различных значениях 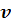 .) Когда
.) Когда 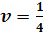 у
системы
у
системы
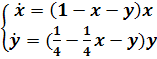 (2.2)
(2.2)
будет три особые точки: 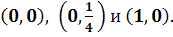
Начало координат является неустойчивым узлом,
так как собственные значения матрицы  вещественные
и положительные. Собственный вектор для
вещественные
и положительные. Собственный вектор для 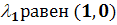 ,
для
,
для 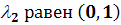
Собственные значения матрицы  вещественные
и разных знаков, значит, особая точка
вещественные
и разных знаков, значит, особая точка 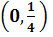 является
седлом. А собственные векторы для
является
седлом. А собственные векторы для 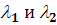 равны
равны
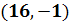 и
и
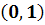 соответственно.
соответственно.
Теперь рассмотрим точку 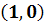 .
Собственные значения ее матрицы:
.
Собственные значения ее матрицы: 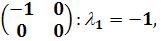
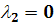 .
То есть особая точка сложная. Определитель ее равен нулю, а след ненулевой. Мы
рассматривали такие сложные особые точки в параграфе 4, это случай I.
Перенеся точку
.
То есть особая точка сложная. Определитель ее равен нулю, а след ненулевой. Мы
рассматривали такие сложные особые точки в параграфе 4, это случай I.
Перенеся точку 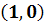 в начало координат
и поменяв местами оси, представим систему (2.2) в виде:
в начало координат
и поменяв местами оси, представим систему (2.2) в виде:
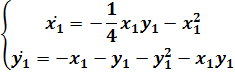
Обозначим 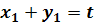 и
получим систему:
и
получим систему:
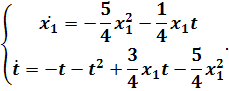
Мы видим, что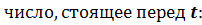
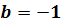 .
Введем в рассмотрение функцию
.
Введем в рассмотрение функцию
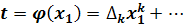
И подставив ее в 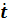 увидим,
что
увидим,
что  .
Теперь подставим найденное
.
Теперь подставим найденное 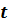 в
в  и
введем обозначение
и
введем обозначение

Получается 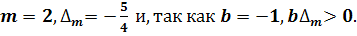 По
теореме 2 из параграфа 4, особая точка является седло-узлом с устойчивым
узловым сектором и, кроме того, траектории узлового сектора стремятся к этой
точке справа от оси
По
теореме 2 из параграфа 4, особая точка является седло-узлом с устойчивым
узловым сектором и, кроме того, траектории узлового сектора стремятся к этой
точке справа от оси 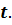 Изображение особой
точки
Изображение особой
точки 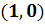 на
плоскости
на
плоскости 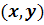 представлено на
рисунке 2.2.
представлено на
рисунке 2.2.
Поведение фазовых траекторий системы дает
наглядное представление о возможных исходах конкуренции.
Найдем уравнения для главных изоклин системы
(2.2):
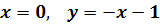
уравнения изоклин вертикальных касательных.
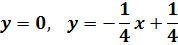
- уравнения изоклин горизонтальных касательных.
Мы видим, что если скорость размножения
изолированной популяции  больше скорости
размножения популяции
больше скорости
размножения популяции  в 4 раза, а
внутривидовая конкуренция
в 4 раза, а
внутривидовая конкуренция  меньше чем у
конкуренции
меньше чем у
конкуренции  тоже в 4 раза, то
выживает популяция
тоже в 4 раза, то
выживает популяция  , а популяция
, а популяция  вся
вымирает.) При
вся
вымирает.) При 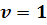 данная система
примет вид:
данная система
примет вид:
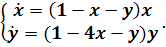 (2.3)
(2.3)
Особых точек у нее тоже 3, как и в предыдущем
случае: 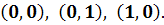
Начало координат является неустойчивым
дикритическим узлом. Собственные значения его матрицы:
Для матрицы 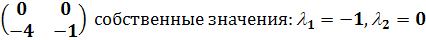 .
Одно из них равно нулю и, значит, особая точка
.
Одно из них равно нулю и, значит, особая точка 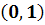 сложная.
сложная.
Как и в предыдущем случае, определитель матрицы
нулевой, а след не равен нулю. Перенесем точку 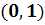 в
начало координат и получим систему:
в
начало координат и получим систему:
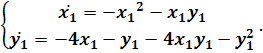
После замены 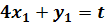 эта
система примет вид:
эта
система примет вид:
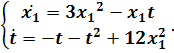
Подставив функцию  в
в
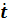 ,
найдем
,
найдем 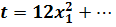 и
подставим его в
и
подставим его в  , после чего найдем
, после чего найдем
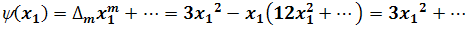
Следовательно, 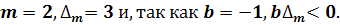 По
теореме 2 из параграфа 4, особая точка является седло-узлом с устойчивым
узловым сектором, траектории которого стремятся к этой точке слева от оси
По
теореме 2 из параграфа 4, особая точка является седло-узлом с устойчивым
узловым сектором, траектории которого стремятся к этой точке слева от оси 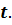
Для матрицы: вещественные и отрицательные, следовательно, особая точка
вещественные и отрицательные, следовательно, особая точка 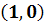 -
устойчивый узел.
-
устойчивый узел.
Собственный вектор для 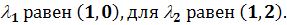
Для построения интегральных кривых найдем
уравнения для главных изоклин системы (2.3):

- уравнения изоклин вертикальных касательных.

- уравнения изоклин горизонтальных касательных.
Из рисунка видно, что выживает популяция  ,
это случается, потому что внутривидовая конкуренция у популяции
,
это случается, потому что внутривидовая конкуренция у популяции  больше
чем у популяции
больше
чем у популяции  и популяция
и популяция  вся
вымирает.) Посмотрим характер особых точек системы при
вся
вымирает.) Посмотрим характер особых точек системы при
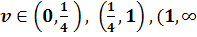 ).
).
Особая точка 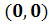 при
всех значениях
при
всех значениях  является
неустойчивым узлом, так как собственные значения ее матрицы:
является
неустойчивым узлом, так как собственные значения ее матрицы:  вещественные
и положительные.
вещественные
и положительные.
Особая точка  является
седлом при
является
седлом при 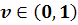 и устойчивым узлом
при
и устойчивым узлом
при 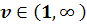 ,
так как собственные значения ее матрицы
,
так как собственные значения ее матрицы вещественные и разных знаков, когда
вещественные и разных знаков, когда 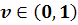 ,
и оба отрицательные, когда
,
и оба отрицательные, когда 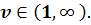
Особая точка 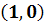 является
седлом при
является
седлом при 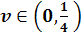 и устойчивым узлом
при
и устойчивым узлом
при 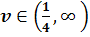 ,
так как собственные значения ее матрицы равны
,
так как собственные значения ее матрицы равны 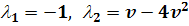 вещественные
и разных знаков при
вещественные
и разных знаков при 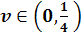 и оба
отрицательные при
и оба
отрицательные при 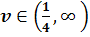 .
.
Особая точка  при
при
 не
находится в первом квадранте, и поэтому мы не рассматриваем этот случай.
не
находится в первом квадранте, и поэтому мы не рассматриваем этот случай.
Матрица для этой точки имеет след
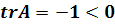 ,
,
определитель
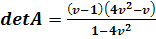 ,
,
который при 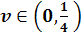 положительный,
а при
положительный,
а при 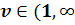 )
отрицательный, и
)
отрицательный, и  , которая при любых
, которая при любых
 положительная.
положительная.
Таким образом, исследуемая особая точка при 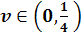 является
устойчивым узлом, при
является
устойчивым узлом, при 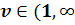 ) - седлом.
) - седлом.
Случай (а) соответствует сосуществованию видов 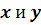 ,
случай (b) - выживанию вида
,
случай (b) - выживанию вида  ,
а в случае (c) исход конкуренции
зависит от начальных условий, так как ненулевая особая точка для обоих видов
является неустойчивым седлом, через которое проходит сеператриса, отделяющая области
выживания каждого из видов.
,
а в случае (c) исход конкуренции
зависит от начальных условий, так как ненулевая особая точка для обоих видов
является неустойчивым седлом, через которое проходит сеператриса, отделяющая области
выживания каждого из видов.
3. Рассмотрим
уравнение типа «хищник - жертва» с «логистической» поправкой

для 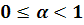 .
.
При 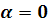 данная
система примет вид:
данная
система примет вид:
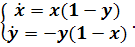
У этой системы две неподвижные точки -  .
.
Особая точка 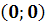 является
седлом с собственными значениями матрицы коэффициентов линеаризованной системы:
является
седлом с собственными значениями матрицы коэффициентов линеаризованной системы:
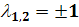 .
.
Собственный вектор для 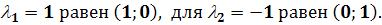
Переведем точку 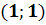 в
начало координат заменой:
в
начало координат заменой:

Получим систему:
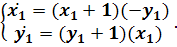
Решив характеристическое уравнение укороченной
системы

мы видим, что собственные значения комплексные с
нулевой вещественной частью, следовательно, особая точка  центр.
центр.
Следовательно, в точке  сосуществование
обоих популяций, остальные траектории движутся вокруг нее. Если рассматривать
точку
сосуществование
обоих популяций, остальные траектории движутся вокруг нее. Если рассматривать
точку 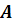 ,
соответствующую моменту, когда численность жертв
,
соответствующую моменту, когда численность жертв  минимальна,
то можно увидеть, что по мере возрастания количества жертв, численность хищников
минимальна,
то можно увидеть, что по мере возрастания количества жертв, численность хищников
 потихоньку
убывает, потому что им пока нечем питаться. Когда количество жертв доходит до
определенного числа
потихоньку
убывает, потому что им пока нечем питаться. Когда количество жертв доходит до
определенного числа 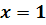 , которое
необходимо для того чтобы рождаемость хищников превышала их смертность,
популяция хищников начинает возрастать. Но в определенный момент, когда
, которое
необходимо для того чтобы рождаемость хищников превышала их смертность,
популяция хищников начинает возрастать. Но в определенный момент, когда 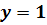 ,
хищников становится настолько много, что численность жертв начинает убывать, но
хищникам пока пищи достаточно и их количество, все еще, растет. Через некоторое
время число жертв уменьшится настолько, что хищникам будет нечем питаться, их
численность начнет убывать и в конце концов мы придем в первоначальную точку
,
хищников становится настолько много, что численность жертв начинает убывать, но
хищникам пока пищи достаточно и их количество, все еще, растет. Через некоторое
время число жертв уменьшится настолько, что хищникам будет нечем питаться, их
численность начнет убывать и в конце концов мы придем в первоначальную точку 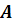 ,
и все начнется заново.
,
и все начнется заново.
Чем дальше мы берем точку 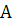 от
положения равновесия системы, тем больше времени требуется на прохождении
цикла.
от
положения равновесия системы, тем больше времени требуется на прохождении
цикла.
При  система
система

имеет четыре неподвижные точки:
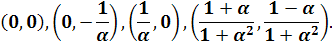
Особая точка 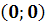 ,
как и при
,
как и при 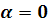 является седлом с
собственными значениями:
является седлом с
собственными значениями: 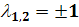 .
.
Особая точка 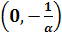 является
неустойчивым узлом, так как собственные значения ее матрицы:
является
неустойчивым узлом, так как собственные значения ее матрицы: 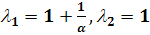 вещественные
положительные.
вещественные
положительные.
Особая точка 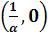 является
седлом, так как собственные значения ее матрицы:
является
седлом, так как собственные значения ее матрицы:  вещественные
и разных знаков.
вещественные
и разных знаков.
Линеаризация системы в особой точке 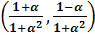 :
:
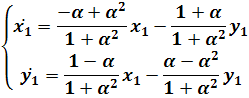
имеет след 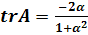 ,
который при
,
который при  принимает
отрицательные значения, определитель
принимает
отрицательные значения, определитель 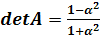 ,
который при
,
который при  отрицательный и,
отрицательный и,  .
Значит, исследуемая особая точка является устойчивым фокусом.
.
Значит, исследуемая особая точка является устойчивым фокусом.
Траектории движутся против часовой стрелки к
особой точке 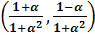 , которая является
фокусом, аналогично тому как двигалась точка
, которая является
фокусом, аналогично тому как двигалась точка 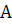 по
окружности, в предыдущем случае, только здесь точка движется по спирали и в
конечном итоге приходит в положение равновесия системы, то есть жертвы и
хищники сосуществуют. Вымирание обоих видов или одного из видов невозможно,
потому что особые точки
по
окружности, в предыдущем случае, только здесь точка движется по спирали и в
конечном итоге приходит в положение равновесия системы, то есть жертвы и
хищники сосуществуют. Вымирание обоих видов или одного из видов невозможно,
потому что особые точки 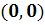 и
и 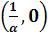 являются
сёдлами, а точка
являются
сёдлами, а точка  , и все траектории
от нее удаляются.
, и все траектории
от нее удаляются.
СПИСОК ЛИТЕРАТУРЫ:
. Баутин
Н.Н. Леонтович Е.А. Методы и приемы качественного исследования динамических
систем на плоскости. - Москва, «Наука», 1990. - 486 с.
. Матвеев
Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. - Москва,
«Высшая школа», 1967. - 564 с.
. Филиппов
А.Ф. Сборник задач по дифференциальным уравнениям. Ижевск, 2000. - 176 с.
. Эрроусмит
Д., Плейс К. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями.
- Москва, «Мир», 1986. - 243 с.
. Гаузе
Г.Ф. Борьба за существование. - Москва, 2002. - 160 с.