Решение задачи разгона и торможения судна в процессе его эксплуатации

Решение задачи разгона и торможения судна в процессе его эксплуатации

Курсовая работа

Решение задачи разгона и торможения судна в процессе его эксплуатации

Содержание

Введение

. Постановка задачи и ее математическая модель

. Методика и алгоритмы решения задачи

. Формирование исходных данных

. Модельная задача №1

.1 Линейная аппроксимация

.2 Нахождение стационарной скорости

.3 Нахождение времени разгона судна

.4 Нахождение пути разгона судна

.5 Нахождение энергии разгона судна

. Модельная задача №2

.1 Аппроксимация полиномом 2-й степени

.2 Нахождение стационарной скорости

.3 Нахождение времени разгона судна

.4 Нахождение пути разгона судна

.5 Нахождение энергии разгона судна

. Модельная задача №3

.1 Аппроксимация полиномом 3-й степени

.2 Нахождение стационарной скорости

.3 Нахождение времени разгона судна

.4 Нахождение пути разгона судна

.5 Нахождение энергии разгона судна

.6 Нахождение времени торможения судна

.7 Нахождение пути торможения судна

.8 Нахождение энергии торможения судна

Результаты расчетов

Общие выводы

Список литературы

Введение

Значительные резервы в повышении скоростей судов появились при использовании новых принципов движения, в частности основанных на применении гидродинамических сил поддержания. Наиболее полно и эффективно используются гидродинамические силы в случае применения подводных крыльев в качестве несущей системы судна. С их помощью корпус судна поднимается над поверхностью воды, способствуя тем самым существенному уменьшению сопротивления воды движению судна. В данной курсовой работе решается задача для СПК, так как это наиболее распространенный тип судна с динамическими принципами поддержания.

гидродинамика скорость судно подводные крылья

1. Постановка задачи и ее математическая модель

1.1Общая задача описания динамики разгона (торможения) судна

Из курса теоретической механики известно, что в соответствии с принципом Даламбера неустановившееся движение тела описывается вторым законом Ньютона. Поскольку в данной задаче рассчитывается движение лишь в направлении одной из осей координат (в данном случае оси X), то достаточно записать уравнения движения в проекции на ось X и решать его относительно скорости V в направлении оси X и пройденного по этой координате пути S.

1.2. Физическая и математическая модели неустановившегося движения судна.

Основным уравнением задачи в этом случае является уравнение второго закона Ньютона в проекции на ось координат Х

ma=F

т - масса тела (судна),

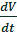
a =  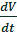- ускорение тела (судна) (1)

F - сумма всех сил, действующих на судно, в проекции на ось X. Равнодействующая сила F складывается из двух сил:

F = T + R (2)

R - сопротивления движению судна,

Т- тяги движителя (как правило, гребного винта).

Из физических соображений понятно, что сопротивление R зависит от скорости движения (чем больше скорость V, тем больше сопротивление R) и направлена против скорости V, т.е. в отрицательном направлении оси

Тяга T, создаваемая гребным винтом, также зависит от скорости движения судна, но действует в противоположном силе сопротивления R направлении, т.е. направлена в положительном направлении оси X. С учетом сказанного, уравнение (1) можно записать в виде

m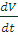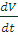= T(V)-R(V)(3)

Таким образом, получено обыкновенное дифференциальное уравнение 1-го порядка относительно скорости движения судна V.

Для определения пройденного за время разгона пути S к этому Уравнению (2) необходимо добавить уравнение  = V, являющееся определением понятия - «скорость».

Математической моделью задачи является система из двух

дифференциальных уравнений 1-го порядка, записанных в каноническом

виде:

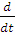
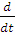V(t)[T(V)-R(V)] (4)

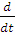
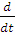S(t)= V(t)

Здесь функции R(V) и T(V) являются заданными и находятся по испытаниям моделей судна и гребного винта. Как правило, эти функции задаются либо графически, либо таблично.

Для решения системы уравнений (4) необходимо задать начальные условия. Обычно они задаются в виде t=0, V=0 или V=V_n.

2. Методика и алгоритмы решения задачи

2.1 Формирование исходных данных

В данной работе исходными данными являются функции R(V) и T(V), которые представлены в графическом виде (см. [1], с. 9, рис. 2). Решением данной задачи является снятие контрольных точек с графиков (R(V) - 16-20 точек и Т(V) - 8-10 точек) и заполнение таблиц исходных данных. Расчеты производятся в системе СИ.

2.2 Аппроксимация исходных данных

По сформированным таблицам этих функций необходимо:

• Определить коэффициенты аппроксимации.

• Рассчитать и вывести на дисплей графики аппроксимирующих функций.

Модельная задача 1

Линейная аппроксимация исходных функций R(V) и Т(V) на всём участке по первой и последней точкам.

Модельная задача 2 Кусочно-линейная аппроксимация исходных функций R(V)(3 участка) и T(V) (2 участка).

Модельная задача 3. Аппроксимация исходных функций R(V) и T(V) на всем участке, полиномом третьей степени.

2.3 Численное решение системы дифференциальных уравнений

Осуществить численное решение системы (4) методом Эйлера. В каждом случае необходимо вычислить значение стационарной скорости V_ст, время разгона судна Т_разг и пройденный путь.

Для определения стационарной скорости V_CT необходимо задать степень точности расчета.

При решении 3-й модельной задачи кроме разгона необходимо рассчитать задачу торможения судна при выключенном двигателе Т(V)=0.

2.4 Вычисление кинетической энергии

Запишем теорему об изменении кинетической энергии в

интегральной форме:

_N

W-W₀=∑A_k ^k=1

Получаем:

_N

W=∑A_k(5)

^k=1

Находим работу:

dA = T(V)-dS

 _N

∑A_k   = (6)

^k=1

где Sr - путь разгона.

Подставим значение работы из (8) в (7):

E_разг = (7)

Получили формулу для расчета кинетической энергии, затрачиваемой на разгон судна.

При торможении T(V) = 0, работу совершает сила сопротивления R(V). Поэтому формула для расчета кинетической энергии для торможения примет вид:

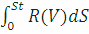
E_разг = 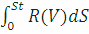(8)

где St - тормозной путь.

3. Формирование исходных данных

Даны графики зависимости сопротивления и тяги от скорости, полученные экспериментальным путем. На кривой R(V) возьмем 18 контрольных точек, на кривой T(V) - 9. С интервалами 4 км/ч и 8,5 км/ч соответственно. Занесем данные в таблицу 1, переведем в СИ.

Исходные данные

4. Модельная задача 1

4.1 Линейная аппроксимация функций T(V) и R(V)

Аппроксимацию производим с помощью команды "Добавить линию тренда" в программе Excel.

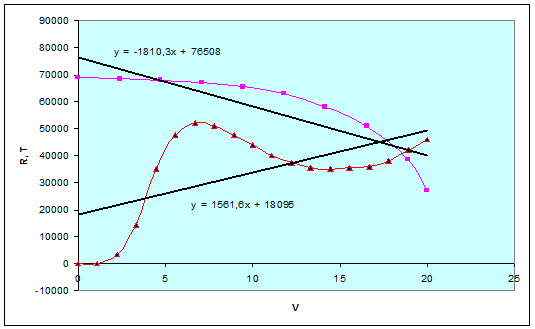
Графики зависимости T(V), R(V) и аппроксимирующие прямые

4.2 Нахождение стационарной скорости

Находим стационарную скорость (скорость, при которой сопротивление равно тяге, решаем уравнение R(V)=T(V) ) .

F(x)=-3371,9x+58413

Отделение корня шаговым методом:

Результат программы:

vvedi a,b,h

.1

.30

.40

В результате вычислений шаговым методом получаем интервал изоляции корня [17,3;17,4]

Уточнение корня методом Ньютона:

program nuton;

var a,b,x,x0,e:real;:integer;y(x:real):real;:=-3371.9*x+58413;;u(x:real):real;:=-3371.9;;z(x:real):real;:=0;;('vvedi a,b,e');(a,b,e);u(a)<>0 thenu(a)*z(a)>0x:=ax:=b;:=0;abs(y(x))>e do:=i+1;:=x-y(x)/u(x);;('x =',x:8:3);.

Результат программы:

vvedi a,b,e

.3

.4

.001

x = 17.323

стационарная скорость Vст = 17,323м/c

4.3 Нахождение времени разгона судна

Определяем время разгона судна - время за которое судно выходит за стационарную скорость:

t=∫1/F(V) ,где F(V) =T(V)-R(V)/m.

t = ∫40400/(-3371,9*x+58413)

Метод центральных прямоугольников:

Program metodcentrpr;a,b,h,n,x,S:real;:integer;:array [1..51] of real;;('vvedite a');(a);('vvedite b');(b);:=(b-a)/50;:=(a+h)/2;:=0;i:=1 to 51 do[i]:=40400/(-3371.9*x+58413);:=x+h;:=S+c[i];;:=h*S;('S=',S:6:3);;.

Результат программы:

vvedite a

vvedite b

.323

S=46.290

Время разгона до Vст t = 46,29 сек.

4.4 Нахождение пути разгона судна

Вычисляем путь разгона, путь который пройдет судно за время разгона.

Решаем систему дифференциальных уравнений:

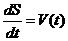
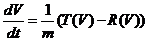
Метод Эйлера:

Program eiler;,xn,h,y0,N,D,z0,kp:real;,y,z,y1,V,z1:real;f(x,z:real):real;:=(-3010.9*x+56297)/40400;;('Vvedi x0,xn,y0,z0,V,D ');(x0,xn,y0,z0,V,D);:=x0; y:=y0; z:=z0;:=V/D;:=xn/D;x<=xn do;('t=',x:8:4 ,' S=',y:8:4 ,' V=',z:8:4);:=x+h;:=y+h*z;

z:=z+N;;

readln;

end.

Результат программы:

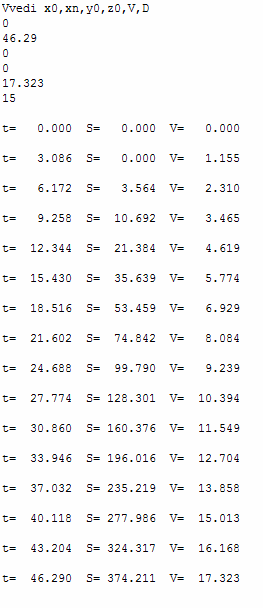
Путь разгона до Vст S=374,211м

График S(t)

График V(t)

4.5 Нахождение энергии разгона судна

Вычисляем энергию разгона по формуле:

E=m/2∫v²(t)dt

V(t) = 0,37423t

Метод центральных прямоугольников:

Program metodcentrpr;a,b,h,n,x,S:real;

i:integer;

c:array [1..51] of real;;('vvedite a');(a);('vvedite b');(b);:=(b-a)/50;:=(a+h)/2;:=0;i:=1 to 51 do[i]:=40400/2*sqr(0.374*x);:=x+h;:=S+c[i];;:=h*S;('S=',S:6:3);

readln;.

Результат программы:

vvedite a

vvedite b

.29

S=99127380.931

Энергия разгона судна до Vст E = 99,1 МДж

5. Модельная задача 2

5.1 Кусочно-линейная аппроксимация функций R(V) и T(v)

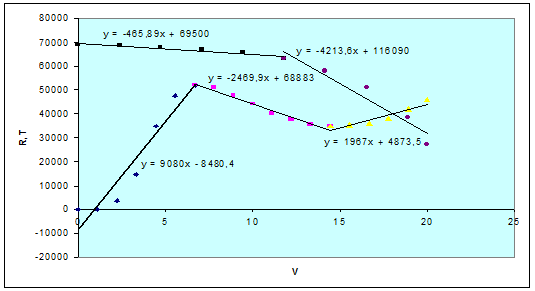
5.2 Нахождение стационарной скорости

F(x)=-6180,6x+111216,5

Отделение корня шаговым методом:

program shag;

Результат программы:

vvedi a,b,h

.1

.90

.00

В результате вычислений шаговым методом получаем интервал изоляции корня [17,9;18]

Уточнение корня методом половинного деления:

program polovina;a,b,e,af,bf,xf,z,absxf,x:real;('vvedite a,b,e');(a,b,e);:=(a+b)/2;:=-6180.6*a+111216.5;:=-6180.6*b+111216.5;:=-6180.6*x+111216.5;:=abs(xf);abs(xf)>=e then:=af*xf;z<0 then b:=xa:=xwriteln('x = ',x:4:3)abs(xf)<e;;.

Результат программы:

vvedite a,b,e

.9

.001

x = 17.994

стационарная скорость Vст = 17,994 м/c

5.3 Нахождение времени разгона судна

Метод трапеций:

program tr_s;,b:real;:real;:integer;f(x:real):real;:=abs(40400/(-6180.6*x+111216.5));;trap(a,b:real;n:integer):real;

s:real;

h:real;

m:integer;:=(b-a)/n;:=(f(a)+f(b))/2;m:=1 to n-1 do s:=s+f(a+m*h);:=s*h;;('vvedi A,B ');(a,b);:=100;:=trap(a,b,n);('r = ',r:6:3);;.

Результат программы:

vvedi A,B

.994

r = 49.111

Время разгона до Vст t = 49,111 сек.

5.4 Нахождение пути разгона судна

Метод Эйлера 1 модификация:

Program eiler1;,xn,h,y0,N,D,z0:real;,y,z,y1,V,z1,x1:real;f(x,z:real):real;:=(-6810.6*x+111216.5)/40400;;('Vvedi x0,xn,y0,z0,V,D ');(x0,xn,y0,z0,V,D);('Ti vvel x0=',x0:6:2,' xn=',xn:6:2,' D=',D:6:2,' y0=',y0:6:2,' z0=',z0:6:2,' V=',V:6:2);:=x0; y:=y0; z:=z0;:=V/D;:=xn/D;x<=xn do;('t=',x:8:4 ,' S=',y:8:4 ,' V=',z:8:4);:=x+h/2;:=y+h/2*z;:=z+N/2;:=x+h;:=y+h*z1;:=z+N;

end;;.

Результат программы:

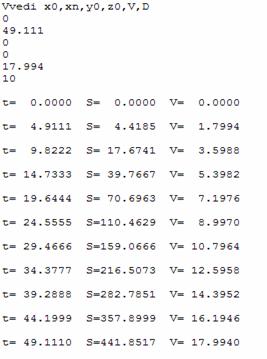
Путь разгона до Vст S = 441,8517 м

График S(t)

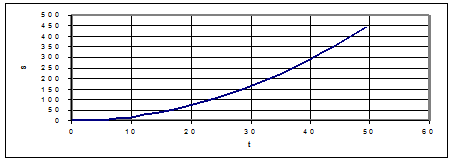
График V(t)

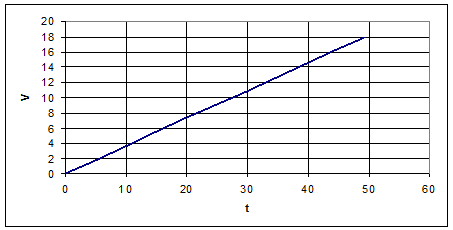
5.5 Нахождение энергии разгона судна

Вычисляем энергию разгона по формуле: E=m/2∫v²(t)dt

V(t) = 0,36639t

Метод трапеций:

program tr_s;,b:real;:real;:integer;f(x:real):real;:=40400/2*sqr(0.36639*x);;trap(a,b:real;n:integer):real;:real;:real;:integer;:=(b-a)/n;:=(f(a)+f(b))/2;m:=1 to n-1 do s:=s+f(a+m*h);:=s*h;;('vvedi A,B ');(a,b);:=100;:=trap(a,b,n);('r = ',r:6:3);;.

Результат программы:

vvedi A,B

.111

r = 107071869.240

Энергия разгона судна до Vст E = 107,1 МДж

6. Модельная задача 3

6.1 Аппроксимация функций R(V) и T(v) полиномом 3 степени

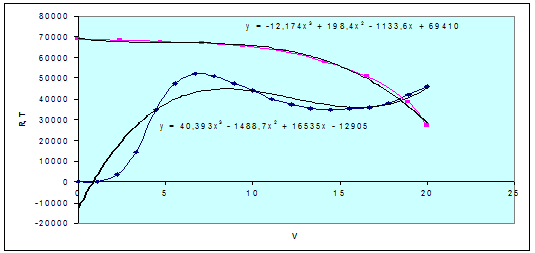
6.2 Нахождение стационарной скорости

F(x)=-52,567x³+1687,1x²-17668,6x+82315

Отделение корня шаговым методом:

program shag;

var a,b,h,x,x1,x2:real;,y2:real;:byte;y(x:real):real;:=-52.567*exp(ln(x)*3)+1687.1*sqr(x)-17668.6*x+82315;;('vvedi a,b,h');(a,b,h);:=0;:=a+h;x<=b do:=x-h;:=x;:=y(x1);:=y(x2);y1*y2<0 then:=k+1;(x1:5:2);(x2:5:2);;:=x+h;;k=0 then('korney net');.

Результат программы:

vvedi a,b,h

.1

.50

.60

В результате вычислений шаговым методом получаем интервал изоляции корня [18,5;18,6]

Уточнение корня методом половинного деления:

program polovina;a,b,e,af,bf,xf,z,absxf,x:real;('vvedite a,b,e');(a,b,e);:=(a+b)/2;:= -52.567*exp(ln(a)*3)+1687.1*sqr(a)-17668.6*a+82315;:= -52.567*exp(ln(b)*3)+1687.1*sqr(b)-17668.6*b+82315;:= -52.567*exp(ln(x)*3)+1687.1*sqr(x)-17668.6*x+82315;:=abs(xf);abs(xf)>=e then:=af*xf;z<0 then b:=xa:=xwriteln('x = ',x:4:3)abs(xf)<e;;.

Результат программы:

vvedite a,b,e

.5

.6

.001

x = 18.502

стационарная скорость Vст = 18,502 м/c

Определяем время разгона судна - время за которое судно выходит за стационарную скорость:

t=∫1/F(V) , где F(V) =T(V)-R(V)/m.

Метод Симпсона:

program simpson;,b:real;:integer;:real;:real;:real;:integer;:integer;(' vvodim A,B: ');(a,b);:=30;:=(b-a)/n;:=40400/(-52.567*a*a*a+1687.1*a*a-17668.6*a+82315)+40400/(-52.567*b*b*b+1687.1*b*b-17668.6*b+82315);:=4;m:=1 to n-1 do:=s+mn*(40400/(

.567*(a+h*m)*(a+h*m)*(a+h*m)+1687.1*(a+h*m)*(a+h*m)

.6*(a+h*m)+82315));mn=4 then mn:=2 else mn:=4;:=s*h/3;('t = ',simpson:6:3);;

end.

Результат программы:

vvodim A,B:

.502

t = 52.337

Время разгона до Vст t=52,337 сек.

6.4 Нахождение пути разгона судна

Вычисляем путь разгона, путь который пройдет судно за время разгона.

Метод Эйлера 2 модификация:

Program eiler2;

Var,xn,h,y0,N,D,z0:real;,y,z,y1,V,z1,x1:real;f(x,z:real):real;:=(-52.567*x*x*x+1687.1*x*x-17668.6*x+82315)/40400;;('Vvedi x0,xn,y0,z0,V,D ');(x0,xn,y0,z0,V,D);:=x0; y:=y0; z:=z0;:=V/D;:=xn/D;x<=xn do;('t=',x:8:4 ,' S=',y:8:4 ,' V=',z:8:4);:=x+h;:=y+h*z;:=z+N;:=x1;:=y+h*z1;:=z+N;;;.

Результат программы:

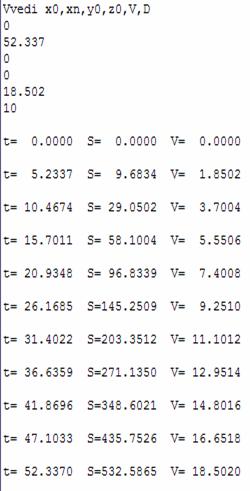
Путь разгона до Vст S = 532,5865 м

График S(t)

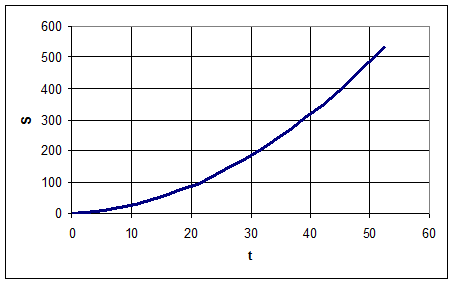
График V(t)

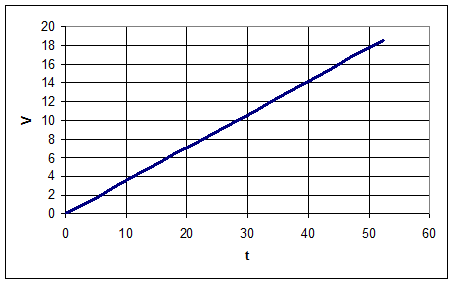
6.5 Нахождение энергии разгона судна

Вычисляем энергию разгона по формуле:

E=m/2∫v²(t)dt

V(t) = 0,35352t

Метод Симпсона:

program simpson;,b:real;:integer;:real;:real;:real;:integer;:integer;(' vvodim A,B: ');(a,b);:=30;:=(b-a)/n;:=40400/2*sqr(0.35352*a)+40400/2*sqr(0.35352*b);:=4;m:=1 to n-1 do:=s+mn*(40400/2*sqr(0.35352*(a+h*m)));mn=4 then mn:=2 else mn:=4;:=s*h/3;('E = ',simpson:6:3);

readln;.

Результат программы:

vvodim A,B:

.337

E = 120638121.642

Энергия разгона судна до Vст E = 120,6 МДж

6.6 Нахождение времени торможения судна

t=∫m/R(V)

Метод Симпсона:

program simpson;,b:real;:integer;:real;:real;:real;:integer;:integer;(' vvodim A,B: ');(a,b);:=30;:=(b-a)/n;:=40400/(40.393*a*a*a-1488.7*a*a+16535*a-12905)+40400/(40.393*b*b*b-1488.7*b*b+16535*b-12905);:=4;m:=1 to n-1 do:=s+mn*(40400/(40.393*(a+h*m)*(a+h*m)*(a+h*m)-1488.7*(a+h*m)*(a+h*m)+16535*(a+h*m)-12905));mn=4 then mn:=2 else mn:=4;:=s*h/3;('t = ',simpson:6:3);;

end.

Результат программы:

vvodim A,B:

.502

t = 12.491

Время торможения = 15.72 сек.

6.7 Нахождение пути торможения судна

Метод Эйлера:

Program eiler;,xn,h,y0,N,D,z0:real;,y,z,y1,V,z1,x1:real;f(x,z:real):real;:=(40.393*x*x*x-1488.7*x*x+16535*x-12905)/40400;;('Vvedi x0,xn,y0,z0,V,D ');(x0,xn,y0,z0,V,D);:=x0; y:=y0; z:=z0;:=z/D;:=xn/D;x<=xn do;('t=',x:8:4 ,' S=',y:8:4 ,' V=',z:8:4);:=x+h;:=y+h*z;:=z-N;:=x1;:=y+h*z1;:=z-N;;

readln;.

Результат программы:

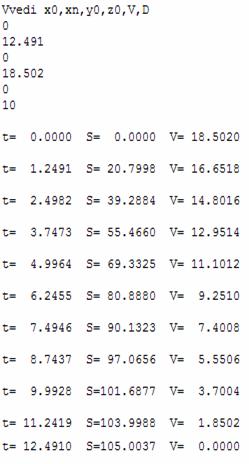
Путь, пройденный до полного торможения S = 105,0037 м

График S(t)

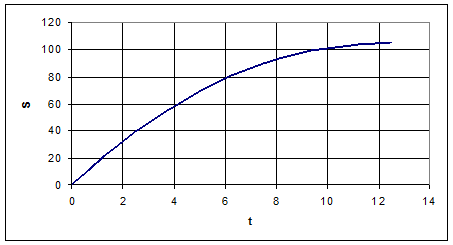
График V(t)

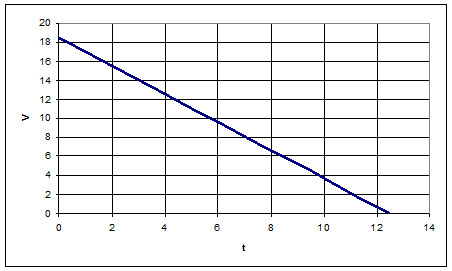
6.8 Нахождение энергии торможения судна

V(t) = -1,4812t+18,502

Метод Симпсона:

program simpson;,b:real;:integer;:real;:real;:real;:integer;:integer;(' vvodim A,B: ');(a,b);:=30;:=(b-a)/n;:=40400/2*sqr(-1.4812*a+18.502)+40400/2*sqr(-1.4812*b+18.502);:=4;m:=1 to n-1 do:=s+mn*(40400/2*sqr(-1.4812*(a+h*m)+18.502));mn=4 then mn:=2 else mn:=4;:=s*h/3;('E = ',simpson:6:3);;

end.

Результат программы:

vvodim A,B:

.491

E = 28792040.279

Энергия торможения судна Е = 28,8 МДж

Таблица результатов:

Общие выводы

При выполнении работы использовались три вида аппроксимации функций. В данном случае стационарная скорость была определена с приблизительно одинаковой точностью по всем методам.

Наиболее точными являются результаты аппроксимации полиномом 3^-й степни. Линейная аппроксимация была самым грубым методом расчёта, однако результаты 1-й модельной задачи оказались близкие к истине, как и результаты 2-й, полученные по методу кусочно-линейной аппроксимации.

При решении подобных задач методы линейной и кусочно-линейной аппроксимации могут использоваться лишь для качественного описания процесса. Для количественного описания необходимо применять метод аппроксимации полиномом 3^-й степни.