Исследование случайных процессов

ТАГАНРОГСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Контрольная работа

ПО КУРСУ

“Прикладные математические методы в статистической радиотехнике”

«Анализ случайных процессов»

Вариант №13.1

Таганрог 2002 г.

Задание

1.       По отсчетным значениям, применяя линейную интерполяцию, построить реализацию х(t) случайного процесса X(t).

2.       Выполнить глазомерную классификацию случайного процесса по его реализации с целью определения стационарности по математическому ожиданию и дисперсии, а так же спектральных свойств центрированного СП.

.        Для нестационарного СП оценить математическое ожидание методом текущего среднего или рекуррентного усреднения.

.        По известной форме реализации х(t) определить математическое ожидание, считая заданную реализацию, соответствующей стационарному эргодическому процессу, методом среднего арифметического и по размаховой оценке, оценить погрешность и сравнить результаты вычислений.

.        Определить дисперсию и среднеквадратическое отклонение заданного процесса различными методами, оценить погрешность вычислений, оценить коэффициенты асимметрии и эксцесса.

.        Рассчитать и построить гистограмму плотности вероятности процесса, используя методы экспресс анализа, определить вид плотности вероятности.

.        Рассчитать корреляционную функцию методом условного среднего и построить график, определить интервал корреляции по среднему значению интервалов пересечения уровня математического ожидания.

.        Определить спектральную плотность мощности процесса и определить эффективную полосу, занимаемой случайным процессом.

.        Произвести нелинейное преобразование заданного случайного процесса, определить плотность вероятности процесса после преобразования.

.        Изобразить полученную плотность вероятности.

.        Построить возможный вид реализации случайного процесса после нелинейного преобразования.

.        Определить основные параметры этой плотности вероятности: математическое ожидание и дисперсию.

Значения случайного процесса

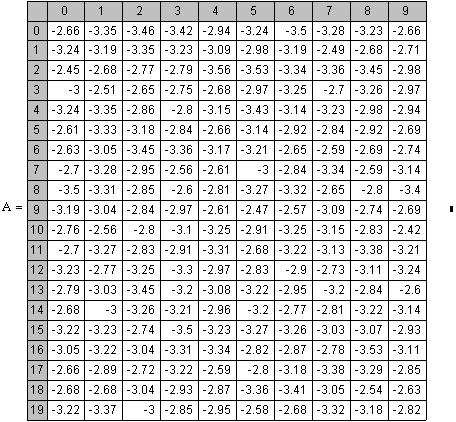
Время отсчета случайного процесса t=10 мкс

Функция нелинейного преобразования: z=a½y½

Расчет

1.       По отсчетным значениям, применив линейную интерполяцию построим реализацию случайного процесса Рис. 1.

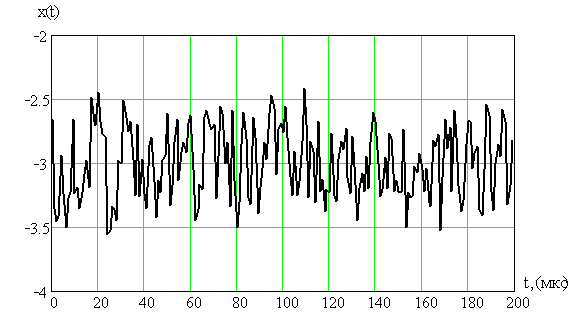
Рис.1 Реализация случайного процесса

Выполним глазомерную классификацию сделаем вывод,что имеем случайный процесс стационарный по математическому ожиданию и СП широкополосный.

Найдем математическое ожидание методом среднего арифметического.

Найдем математическое ожидание методом размаховой оценки

Оценим погрешность вычислений

переведем в проценты

Можно сделать вывод, что можно пользоваться методом размаховой оценки, так как этот метод достаточно точный, но объем вычислений по сравнению с методом среднего арифметического намного меньше.

Определим дисперсию и среднеквадратическое отклонение.

Среднеквадратическое отклонение равно:

Вычислим СКО по размаховой оценке

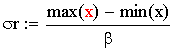
где β=5,8 это число определяется по номограмме Рис.9.1 в методическом пособии 2265

Теперь по СКО найдем дисперсию

Определим погрешность вычисления среднеквадратического отклонения методом размаховых оценок, принимая, что среднеквадратическое отклонение, вычисленное по равноотстоящим отсчётам точно

В процентах

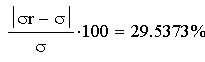
Найдем коэффициент асимметрии

Найдем эксцесс

Определим максимальное и минимальное значение процесса:

Максимум равняется -2.42

Минимум равняется -3.56

Для построения гистограммы нужно выбрать количество интервалов.

Количество интервалов найдем из графика 7.2 Числовые характеристики распределения стр.16 в методическом пособии №2265.

Определяем m=10.

Найдем размер интервала : h = (Xmax - Xmin)/m

h = 0.114

Имеем интервалы:

Построим гистограмму Рис.2

математический ожидание среднеквадратический отклонение

Рис.2 Гистограмма плотности вероятности

Построение НКФ

Для стационарного СП корреляционная функция определяется выражением

где τ - интервал корреляции выбирается минимальное временное расстояние между двумя точками отсчета реализации .Для наглядности отцентрируем СП.

τ = 10 мкс

Список литературы

1.   Конспект лекций по Математике(спец.) Лектор Федосов В.П. 2002г.

.     Методические указания к расчетному заданию по курсу “Прикладные математические методы в статистической радиотехнике” на тему Анализ случайных процессов. Федосов В.П. 1996г. Таганрог