Изучение темы 'Многоугольники' в школьном курсе геометрии
Содержание
Введение
§1.
Роль и место темы «Многоугольники» в школьном курсе геометрии
§2.
Анализ содержания темы «Многоугольники» в школьных учебниках геометрии
§3.
Методика изучения темы «Многоугольники»
.1
Определения равных треугольников
3.2
Признаки равенства треугольников
3.3 Методика введения понятия теоремы обратной
данной
§4. Методика изучения темы «Четырехугольники»
.1 Параллелограмм
4.2
Прямоугольник
4.3 Квадрат
4.4
Ромб
4.5 Трапеция
§5. Методика изучения темы «Многоугольники»
.1 Выпуклые многоугольники
.2 Правильные многоугольники
§6. Организация обобщающего повторения темы
«Многоугольники» в курсе геометрии 9 класса
§7. Задачи по теме «Многоугольники» в материалах
ЕГЭ по математике
Заключение
Литература
Введение
Школьный курс геометрии занимает
важное место в математическом образовании учащихся. В ходе изучения геометрии у
школьников развивается пространственное воображение, логическое мышление. Они
приобретают навыки использования линейки, циркуля, прямого угла. Учащиеся
убеждаются, что теоретические положения, изучаемые ими, являются отражением
реальной действительности и находят отражение в практической деятельности
людей.
В курсе геометрии 7-9 классов
изучаются геометрические фигуры на плоскости, причём основное внимание
уделяется изучению многоугольников и их свойств.
В ходе изучения темы
«Многоугольники» вводится много новых понятий, изучаются теоремы, вводятся
понятие теоремы обратной данной, решение задач требует от школьника
актуализации имеющихся теоретических знаний.
Этот раздел школьного курса
геометрии выполняет и определенные мировоззренческие функции.
Проблемам совершенствования
методики обучения школьников геометрии посвящены многочисленные исследования
математиков-методистов Александров А.Д. (2), Аргунов Б.И. (3), Балк М.Б. ( 3),
Бескин Н.М., Болтянский В.Г. (6), Гусев В.А. (9), Киселёв А.П.(11), Колягин
Ю.М. (15), Лянин С.Е., Погорелов А.В.(18), Саранцев Г.И. ( 21), и другие.
Аргунов Б.И., Балк М.Б., Бескин
Н.М., Гусев В.А., Колягин Ю.М., Миншин В.И., Саранцев Г.И. и др. рассматривают
методику изучения основных тем школьного курса геометрии, анализируют пути и
способы обучения учащихся решению геометрических задач.
Киселев А.П., Черкасов Р.С.
(22), Погорелов А.В., Атанасян (4), Александров А.Д. и др. являются авторами
школьных учебников как для обычных, так и для профильных классов.
В тоже время анализ программ по
геометрии, результатов ЕГЭ по математике свидетельствует о непрочном овладении
школьников планиметрическим материалом. В частности, решаемость задач
составляет до 10% от решавших. Как правило, задачи по геометрии решают до 60%
школьников.
Именно поэтому весьма актуален
поиск путей совершенствования методики обучения учащихся решению задач по теме
«Многоугольники».
Гипотеза выпускной
квалификационной работы заключается в том, что если в ходе изучения каждого
вида многоугольников учитель будет подбирать систему задач, направленную на
усвоение теоретических положений и выработку у школьников умений и навыков
решать задачи на вычисление и доказательство, использовать наглядность,
осуществлять дифференцированный подход к организации индивидуальной работы с
учащимися. То это будет способствовать повышению качества их знаний.
Сформулированная гипотеза
потребовала решения следующих задач:
1. Рассмотреть роль и место
темы «Многоугольники» в школьном курсе геометрии.
2. Раскрыть методику работ
учителя по изучению темы «Многоугольники» в курсе геометрии 7-9 классов.
Поставленные задачи были решены
при помощи следующих методов исследования:
1. Теоретический (изучение и
анализ математической и методической литературой).
2. Эмпирический
(наблюдение за учебной деятельностью учащихся, знакомство с передовым
педагогически опытом)
. Статистический (анализ
результатов контрольных работ)
Дипломная работа состоит из
введения, семи параграфов, заключения, списка литературы.
Во введении обосновывается
актуальность выбранной темы, формулируется гипотеза выпускной квалификационной
работы, перечисляются задачи и методы исследования.
В основной части
рассматривается методика обучения школьников применять теорию к решению задач
на вычисление и доказательство по теме «Многоугольники».
В заключении подводится итого
проведенной работы. Список литературы состоит из наименований.
§1. Роль и место темы
«Многоугольники» в школьном курсе геометрии
В курсе геометрии VII-IX
классов систематически изучаются геометрические фигуры на плоскости, причем
большое внимание уделяется многоугольникам, изучению их свойств, рассмотрению
величин, характеризующих плоский многоугольник. В решении задач на
многоугольники находят применение различные методы.
Систематическое изучение
плоских многоугольников базируется на сформированных в I-III
классах представлениях о простейших геометрических фигурах и служит средством
развития логического мышления учащихся. Здесь вводится много определений,
доказываются содержательные теоремы, введется работа по формированию понятий
«свойство» и «признак». Уже в I-III
классах они знакомы учащимся и служат хорошим дидактическим средством изучения
арифметики. В I классе дети
считают элементы многоугольников: вершины, стороны,..., углы, измеряют их
стороны. Разбитый на равные квадраты прямоугольник используется во II
классе для иллюстрации переместительного закона умножения, задача на нахождение
периметра прямоугольного закона умножения относительно сложения. В III
классе формируются представления о площади фигуры, основное внимание при этом
уделяется вычислению площади прямоугольника и квадрата.
При обучении элементам
геометрии в IV-V
классах многоугольник выступает не только как средство изучения арифметики и
элементов алгебры, но и как объект изучения. Большое внимание при этом
уделяется развитию пространственных представлений учащихся, работе с
изображением отрезка, ломанной, угла, многоугольника, многогранника
(прямоугольного параллелепипеда, куба). Основным для получения результатов
является конкретно-индуктивный метод. Эпизодически вводятся элементы дедукции:
формулируются некоторые определения (длина ломаной, дополнительные лучи,
квадрат, куб и т.п.), отдельные свойства (отрезок АВ короче любой линии,
соединяющий точки А и В, свойства измерения углов и др.), на которые учащиеся
ссылаются при решении задач типа «Объясните, почему...»
Этот раздел школьного курса
геометрии выполняет и определенные мировоззренческие функции. В процессе его
рассмотрения ученики знакомятся с историей отдельных вопросов, узнают об их
месте и роли в практической деятельности человека.
Вместе с тем при изучении
многоугольников идет формирование знаний, умений и навыков, необходимых для
изучения смежных дисциплин: физики, черчения, трудового обучения и др.
Изучение в курсе планиметрии
свойства и признаки многоугольников находят широкое применение в курсе
стереометрии. Учителю необходимо помнить об этом при организации текущего и
итогового повторения.
В различных школьных курсах
планиметрии понятие многоугольников трактуется неодинаково.
В одних курсах многоугольник А1,
А2, ..., Аn
трактуется как фигура, состоящая из отрезков A1A2,
A2A3,
..., An-1An,
АnА1
любые два из которых, имеющие общий конец, не лежат на одной прямой (4),
(18). В этом случае при рассмотрении площади многоугольников (прямоугольника,
параллелограмма, треугольника и др.) под каждым из них понимается
соответствующий плоский многоугольник (конечная часть плоскости, ограниченная
многоугольником).
В других курсах простой
многоугольник (треугольник, четырехугольник и др.) трактуется с самого начала
как часть плоскости, ограниченная простой замкнутой ломаной (2).
Если перечень вопросов курса,
их объем предопределены программой, то структура материала внутри каждой темы,
последовательность изучаемых вопросов обычно характерны для каждого отдельного
учебника.
Так, учебники геометрии
А.Д.Александрова и др. (2) и Л.С.Атанасяна и др. (4) отличает широкое
использование практического опыта учащихся, различные приложения изучаемой
теории.
Кроме того, нельзя не сказать о
роли наглядности при изучении многоугольников. Наличие в учебнике большого
числа рисунков ни в коем случае не ограничивает творчество учителя. В то же
время это дает возможность ученику, вынужденному в силу сложившихся
обстоятельств самостоятельно изучать тот или иной раздел, следить на хорошем
иллюстративном материале за логикой рассуждений, «увидеть» идею и путь
доказательства.
§2. Анализ содержания темы
«Многоугольники» в школьных учебниках геометрии
В курсе геометрии 7-9 классов
систематически изучаются геометрические фигуры на плоскости, причем большое
внимание уделяется многоугольникам, изучению их свойств, рассмотрению величин
характеризующих плоский многоугольник.
Курс геометрии 7 класса - это, по
существу, геометрия треугольника.
Основное внимание при изучении
темы следует уделить формированию умений доказывать равенство треугольников.
Введение понятий медианы, биссектрисы и высоты треугольника, свойств
равнобедренного треугольника расширяет класс задач на доказательство.
Темы «Четырехугольники»
изучаются в курсе геометрии 8 класса. Здесь получают дальнейшее развитие умения
учащихся проводить доказательные рассуждения. Основу для этого составляет
изучение и применение признаков и свойств рассматриваемых в теме видов
четырехугольников.
Доказательства большинства
теорем данного раздела проводятся с опорой на признаки равенства треугольников,
которые используются и при решении задач в совокупности с применением новых
теоретических фактов.
Основное внимание при изучении
темы отводится выработке у школьников умений применять многочисленные
теоретические сведения при решении задач.
В 9 классе завершается изучение
темы «Многоугольники». Сведения о многоугольниках обобщают известные учащимся
факты о треугольниках и четырехугольниках. Большое практическое значение имеют
теоремы о правильных многоугольниках. Особое внимание необходимо уделить выводу
формул, связывающих стороны правильных многоугольников с радиусами вписанных в
них и описанных около них окружностей и решению задач на вычисление элементов
правильных многоугольников, длин окружностей и их дуг, что подготавливает
аппарат решения задач, связанных с многогранниками и телами вращения в курсе
стереометрии.
§3. методика
изучения темы «Треугольники»
.1 Определения
равных треугольников
Треугольник
- самый «экономный» вид многоугольника. Для его задания достаточно указать его
вершины - три точки, не лежащие на одной прямой, или три попарно пересекающиеся
прямые.
Классифицируют треугольники
также по степени их симметричности или по числу равных сторон.
|
Треугольник
|
Количество
осей симметрии
|
Количество
пар разных сторон
|
|
|
Равносторонний
Равнобедренный Разносторонний
|
3
1 Нет
|
3
1 Нет
|
|
В школе принята также
классификация треугольников по углам: остроугольные, прямоугольные и
тупоугольные.
Изучение треугольников в
соответствии с программой распределено практически по всем классам неполной
средней школы. Курс 7 класса - это, по существу, геометрия треугольника.
Треугольник - одна из основных
«рабочих» фигур изучаемого в школе курса планиметрии. Установление цепочек
равных треугольников - широко используемый прием доказательства различных
геометрических утверждений.
Главная цель изучения признаков
равенства треугольников - добиться активного владения им, обратив особое
внимание на отработку навыков использования признаков равенства треугольников в
решении задач.
Равенство традиционно изучается
в курсе планиметрии. Однако трактовка этого понятия, методика введения разные
для различных учебников. Так, в учебниках А.Н. Колмагорова и Л.С. Атанасяна (4)
равные треугольники - частный случай равных фигур, т.е. фигур, которые можно
совместить наложением. Такие понятия, как «совмещение» и «наложение», считаются
интуитивно понятными учащимся и в курсе не определяются.
В учебнике «Геометрия 7-11»
А.В. Погорелова (18) понятие «равные треугольники» вводится в §1 «Основные
свойства простейших геометрических фигур» п.9 «Треугольник».
Сначала дается определение
треугольника: треугольником называется фигура, которая состоит из трех
точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти
точки. Точки называются вершинами треугольника, а отрезки - сторонами.
Затем рассматривают что такое
угол треугольника, равные отрезки и равные углы: «Углом треугольника ABC
при вершине А называется угол, образованный полупрямыми АВ и АС. Так же
определяются углы треугольника при вершинах В и С.
Два отрезка называются
равными, если они имеют одинаковую длину. Два угла называются равными,
если они имеют одинаковую угловую меру в градусах».
И только после введения выше
перечисленных понятий дается определение «равные треугольники»: Треугольники
называются равными, если них соответствующие стороны равны и
соответствующие углы равны.
В учебнике «Геометрия 7-9» Л.С
Атанасяна (4) понятие «равные треугольники» вводится в §1 «Первый признак
равенства треугольников» п. 14 «Треугольник», следующим образом:
«Отметим какие-нибудь три
точки, не лежащие на одной прямой, и соединим их отрезками. Получим
геометрическую фигуру, которая называется треугольником. Отмеченные три
точки называются вершинами, а отрезки - сторонами треугольника.
Три угла - ВАС, СВА и АСВ -
называются углами треугольника ABC.
Сумма длин трех сторон треугольника называется его периметром». Затем
говорится, что две фигуры, в частности два треугольника, называются равными,
если их можно совместить наложением.
Рассмотрим методику введения
понятия «равные треугольники» на примере учебника геометрии А.В. Погорелова
(29).
После введения перечисленных
выше понятий и их определений школьники решают задачи:
3адача 1.
Треугольники ABC и PQR
равны. Известно, что сторона АВ равна 10 см, а угол С равен 900.
Чему равны сторона PQ
и угол R? Объясните ответ.

Дано: ∆АВС=∆PQR, AB=10 см,  С=900.
С=900.
|
Найти:
PQ,  R R
|
|
Решение.
Так как ∆АВС=∆PQR, то у них AB= PQ=10 см,  С=
С= R=90.
R=90.
Ответ: PQ=10 см,  R=900.
R=900.
3адача 2. Треугольники
ABC и PQR равны. Углы
второго треугольника известны:  P=400 ,
P=400 ,  Q=600
,
Q=600
,  R=800.
Найти углы ∆АВС.
R=800.
Найти углы ∆АВС.
 Дано: ∆АВС=∆PQR,
Дано: ∆АВС=∆PQR,  P=400
,
P=400
,  Q=600
,
Q=600
,  R=800
R=800
Найти:  А,
А,  В,
В,  С.
С.
Решение.
По условию ∆АВС=∆PQR, значит у
них и соответствующие углы равны, получаем:  Р=
Р= А=400 ,
А=400 ,  Q=
Q= В = 600
,
В = 600
,  R=
R= С=800
С=800
Ответ:  А=400,
А=400,
 В=600,
В=600,
 С=800.
С=800.
Затем им можно предложить систему
задач, направленную на выработку соответствующих умений и навыков.
1). Треугольники MPQ
и NPQ равны. Перечислите
шесть пар равных друг другу элементов (сторон, углов) этих двух треугольников.
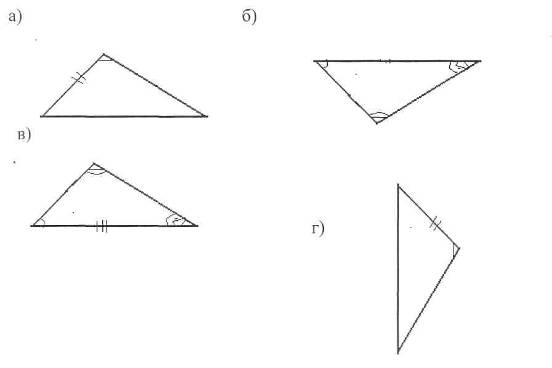
). Для каждого из изображенных
треугольников найти равный ему.

3.2 Признаки равенства треугольников
Основная идея доказательства I
и II признаков
равенства треугольников в учебнике Атанасяна (4) и др. Атанасян Л.С. состоит в
последовательном осуществлении наложения одного из данных треугольников на
другой и доказательства совмещения их при таком наложении. В доказательстве III
признака существенно используется свойство углов при основании равнобедренного
треугольника.
Доказательство первых двух
признаков равенства треугольников в учебном пособии А.В. Погорелова (18) и
пробном учебнике А. Д. Александрова (2) и др. Бевз Г.П. (5) сводится к
доказательству совпадения некоторого третьего треугольника, равного первому и
определенным образом расположенного относительно второго, с этим вторым данным
треугольником. При доказательстве первых двух признаков равенства можно
использовать серию рисунков, отражающих динамику доказательства, отдельные его
этапы. Так, при рассмотрении первого признака полезно использовать серию
рисунков.
Рассмотрим методику изучения
признаков равенства треугольников по учебнику А.В.Погорелова.
Тема: «Первый
признак равенства треугольников». Чтобы подвести к
формулировке теоремы, можно в начале урока предложить учащимся следующее
задание практического характера:
1)
Начертите
треугольник ABC.
2)
Проведите
луч MN и отложите
от него угол KMN, равный
углу ВАС. На луче МК отложите отрезок MP,
равный отрезку АВ, а на луче MN
- отрезок ME, равный
отрезку АС.
3)
Соедините
точки Р и Е.
4)
Измерьте
и сравните отрезки ВС и РЕ, углы ABC
и МРЕ, углы АСВ и МЕР.
5)
Запишите
равные между собой элементы построенных треугольников.
По ходу выполнения задания
ставятся вопросы:
1)
Сколько
равных между собой углов можно отложить от данного луча?
2)
Что
значит «Треугольник МРЕ равен треугольнику ABC»?
3)
Сформулируйте
аксиому существования треугольника, равного данному, если считать данными
треугольник ABC и
полупрямую MN.
В результате выполнения задания
на доске и в тетрадях появляется чертеж (рис.1) и запись:
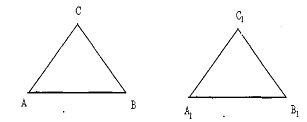
Рис. 1
По условию AB=МР, AC=МЕ,  ВАС=
ВАС= РМЕ.
Результаты измерений
РМЕ.
Результаты измерений
 АСВ=
АСВ= МЕР,
МЕР,  АВС=
АВС= МРЕ, ВС=РЕ.
МРЕ, ВС=РЕ.
Опираясь на определение равных
треугольников, из того, что все шесть элементов одного треугольника
соответственно равны мести элементам другого, делается вывод: АВС=МРЕ.
Это задание подводит учащихся к
формулировке первого признака равенства треугольников.
Теорема 3.1: (признак
равенства треугольников по двум сторонам и углу между ними). Если две
стороны и угол между ними одного треугольника равны соответственно двум
сторонам и углу между ними другого треугольника, то такие треугольники равны.
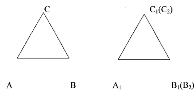 Дано: ∆АВС и ∆А1В1С1,
АВ=А1В1 , АС=А1С1,
Дано: ∆АВС и ∆А1В1С1,
АВ=А1В1 , АС=А1С1,  А=
А= А1
А1
Доказать: ∆АВС = ∆А1В1С1
Доказательство:
. Пусть Дано: ∆АВС и ∆А2В2С2,
(по аксиоме IV).
Причем расположен он может быть
следующим образом: одна его вершина совпадает с вершиной А1 другая
(В2) лежит на луче А1В1 a
третья - (С2) лежит в той же полуплоскости относительно прямой А1В1,
что и вершина С.
2. Т.к. А1В1=AB
(по условию), то AB=A1B2
(из п.1), следовательно В2 совпадает с вершиной В1.
3. Т.к.  B1A1C1 =
B1A1C1 =  BAC (по
условию), то
BAC (по
условию), то  B2A1С2=
B2A1С2= BAC (из п.1), следовательно,
BAC (из п.1), следовательно,
 B1A1C1 = B2A1С2
B1A1C1 = B2A1С2
Тогда луч A1С2
совпадает с лучом A1C1.
4. AC= A1C1 (по
условию), A1С2=AC (из п.1),
следовательно A1C1= A1С2.
Тогда вершина С2 совпадет с вершиной С1.
Таким образом, ∆АВС = ∆А1В1С1
Ч.т.д.
После доказательства теоремы о
первом признаке равенства треугольников предлагаются задачи:
Задача 1.В каждой из
изображенных на рисунке пар треугольников равные элементы треугольников указаны
пометками. Какие треугольники равны по первому признаку?

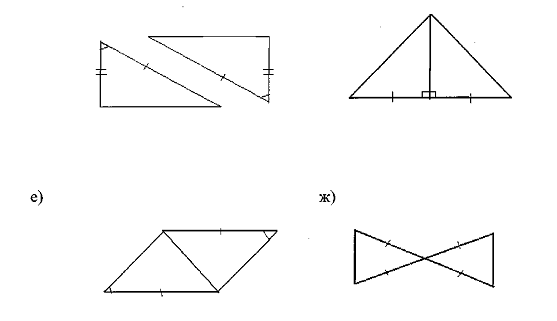
Задача 2.Отрезки
AR и ВН делят друг
друга пополам в точке F.
Доказать, что AB=RH.

3адача 3.
Отрезки АВ и CD
пересекаются в точке О, которая является серединой каждого из них. Чему равен
отрезок BD, если
отрезок АС=10м?
Дано:
АВUCD=0,AO=OB,
CO=OD, АС=10м.
Найти: BD.

Решение.
∆AOC=∆BOD
(по I признаку равенства
треугольников).
1) AOC =
AOC =  BOD -
вертикальные углы.
BOD -
вертикальные углы.
2)ОА=ОВ и OC=OD
(т.к. точка О - середина отрезков АВ и CD).
Из равенства треугольников АОС
и BOD следует равенство
их сторон
АС и BD.
А т.к. АС=10м (по условию), то и BD=10m.
Ответ:
BD=1 Ом.
3адача 4. На стороне
ВС ∆АВС отмечена точка D, а на стороне B1С1 ∆А1В1С1
- точка D1, причем  BAD=
BAD= B1A1D1. Докажите,
что если ∆ADC=∆A,D1C1, то ∆АВС=∆А1В1С1.
B1A1D1. Докажите,
что если ∆ADC=∆A,D1C1, то ∆АВС=∆А1В1С1.
Дано: ∆АВС и ∆А1В1С1,
 BAD=
BAD= B1A1D1, ∆ADC=∆A,D1C1.
B1A1D1, ∆ADC=∆A,D1C1.
Доказать: ∆ABC=∆A1B1C1.
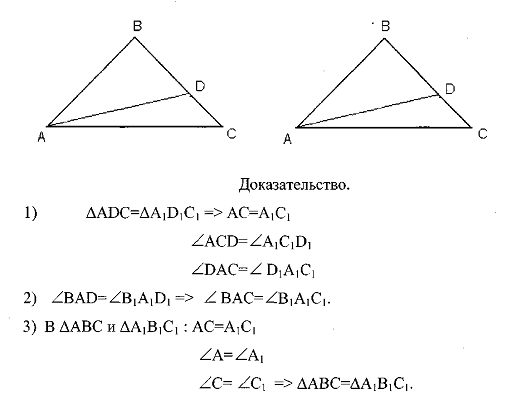
Ч.т.д.
Затем учащимся можно предложить
систему задач:
1. Докажите равенство
треугольников ADC и ABC,
изображенных на рисунке, если AD=AB и  1=
1= 2. Найдите:
2. Найдите:  ADC и
ADC и  ACD, если
ACD, если  ACB=380,
ACB=380,
 ABC=1020.
ABC=1020.

2.Известно, что ∆АВС=∆А1В1С1,
причем  A=
A= A1,
A1,  B=
B= B1. На
сторонах АС и A1C1 отмечены
точки D и D1 так, что CD=C1 D1. Докажите,
что ∆CBD=∆C1B1 D1.
B1. На
сторонах АС и A1C1 отмечены
точки D и D1 так, что CD=C1 D1. Докажите,
что ∆CBD=∆C1B1 D1.
.Известно, что ∆МКР=∆М1К1Р1
причем  M=
M= M1,
M1,  K=K1. На сторонах
MP и M1P1 отмечены
точки Е и Е1 так, что МЕ=М1Е1.
Докажите, что ∆МЕК=∆М1Е1К1.
K=K1. На сторонах
MP и M1P1 отмечены
точки Е и Е1 так, что МЕ=М1Е1.
Докажите, что ∆МЕК=∆М1Е1К1.
.Через середину О отрезка АВ
проведена прямая, перпендикулярная прямой АВ. Докажите, что каждая точка X этой прямой
одинаково удалена от точек А и В.
Аналогично рассматриваются
доказательства II и III признаков.
Теорема 3.2
(признак равенства треугольников по стороне и прилежащим к ней углам). Если
сторона и прилежащие к ней углы одного треугольника равны соответственно
стороне и прилежащим к ней углам другого треугольника, то такие треугольники
равны.
Теорема 3.3 (признак
равенства треугольников по трем сторонам). Если три стороны одного
треугольника соответственно равны трем сторонам другого треугольника, то такие
треугольники равны.
И можно привести следующую систему
задач, направленную на выработку соответствующих умений и навыков:
. В каждой из изображенных на
рисунке пар треугольников равные элементы треугольника указаны пометками. Какие
треугольники равны по II
признаку, а какие равны по III
признаку?
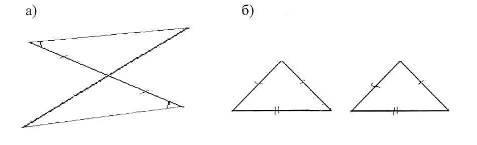

2.В треугольниках МРК и XYZ  РМК=
РМК= ZYX,
ZYX,  MKP=
MKP=  YXZ и сторона
РК равна стороне XY. Докажите равенство сторон РК и ZX.
YXZ и сторона
РК равна стороне XY. Докажите равенство сторон РК и ZX.
3.На рисунке AB=CD
и BD=AC.
Докажите, что:
a)  CAD =
CAD = ADB;
ADB;
б)  BAO =
BAO =  CDB.
CDB.

4.В треугольнике DEC и D1E1С1 DE= D1E1,  D=
D= D1,
D1,  E=
E= E1. На
сторонах DE и D1E1 отмечены
точки Р и P1 так, что
E1. На
сторонах DE и D1E1 отмечены
точки Р и P1 так, что  DCP=
DCP= D1С1
P1. Докажите,
что:
D1С1
P1. Докажите,
что:
a) ∆DCP=∆D1C1P1;
б) ∆СРЕ=∆С1Р1Е1.
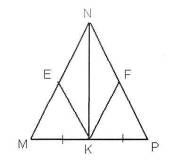
.На рисунке, треугольник MNP
равнобедренный с основанием MP, точка К - середина отрезка MP,  MKE=
MKE= PKF. Докажите,
что ∆NEK=∆NFK.
PKF. Докажите,
что ∆NEK=∆NFK.
3.3 Методика
введения понятия теоремы обратной данной
В учебнике «геометрия 7-11»
А.В. Погорелова (18) после доказательства теорем Т.3.3 («В равнобедренном
треугольнике углы при основании равны») §3 «Признаки равенства треугольников»
п.23 «Равнобедренный треугольник» и Т.3.4 («Если в треугольнике два угла равны,
то он равнобедренный»), того же параграфа п.24 «Обратная теорема», говорится,
что Т.3.4 называется обратной Т.3.3.
В учебнике «Геометрия 7-9» Л.С.
Атанасяна (4), сначала изучаются теоремы п.25 §1 «Признаки параллельности двух
прямых» главы III. т.е.:
Теорема: Если
при пересечении двух прямых секущей накрест лежащие углы равны, то прямые
параллельны.
Теорема: Если
при пересечении двух прямых секущей соответственные углы равны, то прямые
параллельны.
Теорема: Если
при пересечении двух прямых секущей сумма односторонних углов равна 180, то
прямые параллельны.
Затем в §2 этой главы «Аксиома
параллельных прямых» в п.29 вводят определение:
теоремой, обратной
данной, называется такая теорема, в которой условием является заключение данной
теоремы, а заключением - условие данной теоремы.
После чего школьникам
предлагают доказать теоремы, обратные теоремам п.25.
Рассмотрим методику введения
понятия «обратная теорема» на примере учебника А.В. Погорелова.
1способ: Вначале
учащиеся доказывают Т.3.3: «В равнобедренном треугольнике углы при основании
равны», затем Т.3.4: «Если в треугольнике два угла равны, то он
равнобедренный». После чего учащиеся говорят «Теорема 3.4 называется обратной
теореме 3.3. Заключение теоремы 3.3 является условием теоремы 3.4. А условие
теоремы 3.3 является заключением теоремы 3.4. Не всякая теорема имеет обратную,
т.е. если данная теорема верна, то обратная теорема может быть неверна. Поясним
это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать
так: если два угла вертикальные, то они равны. Обратная ей теорема была бы
такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два
равных угла вовсе не обязательно быть вертикальными».
В то же время в методической
литературе перечисляют затруднения, которые испытывают учащиеся.
1)
школьнику
кажется, что прямая и обратная теоремы выражают одну и ту же мысль;
2)
если
ученик различает содержание каждой теоремы, то убежден, что справедливость
одной влечет за собой справедливость другой;
3) не вполне ясное выделение
в теореме условия и заключения приводит к тому, что ученики часто смешивают
прямую и обратную теоремы;
4) большинству учащихся
кажется, что обе записи выражают одну и ту же мысль.
Поэтому можно предложить второй
способ изложения этого материала.
II
способ: Перед доказательством Т.3.4 учитель предлагает
учащимся самостоятельно сформулировать ту теорему, которая получается из Т.3.3,
если в ней поменять условие и заключение.
Учащиеся заполняют таблицу:
|
Прямая
теорема
|
Обратная
теорема
|
|
Условие
|
Если в треугольнике две стороны равны,
Если треугольник равнобедренный,
|
Если в треугольнике два угла равны, Если
углы при основании равны,
|
|
Заключение
|
то углы, лежащие против этих сторон
равны, то углы при основании равны.
|
то стороны, лежащие против этих
углов, равны. то треугольник равнобедренный.
|
Учитель предлагает доказать эту
теорему. После доказательства возвращается к первой строчке таблицы, вводятся
термины «прямая теорема», «обратная теорема».
После доказательства Т.3.4 надо
предложить учащимся ряд упражнений на образование обратных теорем:
Например, составить для каждой
из теорем обратную:
1. Если сумма цифр числа
нацело делится на 9, то само число делится на 9.
2. Если число оканчивается
двумя нулями, то оно нацело делится на 4.
3. Если в одном и том же
круге центральные углы равны, то и соответственные им дуги равны.
Ученик, составляя обратную
теорему, должен сказать верна ли она.
В упражнениях полезно ввести и
жизненные примеры: образовать обратное утверждение к следующему: если ученик
болен, то он пропускает уроки.
Также полезно предложить
учащимся привести примеры доказанных ранее теорем сформировать для них
обратные. При этом лучше переформулировать теоремы таким образом, чтобы они
читались: «Если ..., то ...». Можно взять в качестве примера теорему о
вертикальных углах, I и II
признаки равенства треугольников и теорему о смежных углах.
На примере теорем 3.3 и 3.4 и
признаков равенства треугольников показывается, что в этих случаях наряду с
исходной теоремой верна и обратная; на примере теоремы о вертикальных углах -
что возможен случай, когда прямая теорема верна, а обратная утверждение
неверно.
Можно также предложить ученикам
сформировать теорему обратную к теореме 3.4 (или к любой другой, которую они
формировали как обратную), и убедиться в том, что теорема, обратная обратной,
есть прямая теорема.
многоугольник
геометрия методика школьный
§4. методика
изучения темы «Четырехугольники»
Четырехугольники - традиционный
для курса планиметрии материал. Как и треугольник, четырехугольник трактуется в
одних учебниках как простая замкнутая четырехзвенная ломаная, в других - как
часть плоскости, ограниченная такой ломаной. Из всевозможных четырехугольников
выделяют выпуклые. Во всех действующих в настоящее время пособиях
осуществляется одинаковый подход во введении частных видов параллелограммов:
прямоугольников и ромбов. Квадрат в одних учебниках вводится как
четырехугольник, который одновременно является прямоугольником и ромбом. В
других квадрат определяется как частный вид прямоугольника. Трапеция
рассматривается после параллелограммов.
При установлении различных
свойств и признаков параллелограмма широко используются свойства и признаки
равных треугольников, свойств углов, образованных при пересечении двух
параллельных прямых третьей, признаки параллельности прямых. Материал о
параллелограммах и их частных видах очень удобен для формирования и развития
логического мышления учащихся. Именно здесь учитель имеет широкие возможности
по работе с определениями: предложить, например, ученику дать определение
прямоугольника через понятие прямоугольника, параллелограмма и т.д.
4.1 Параллелограмм
В учебнике «Геометрия 7-11»
А.В. Погорелова (18) тема «Параллелограмм» изучается в 6 параграфе
«Четырехугольники» в трех пунктах.
В п.51 «Параллелограмм» в
начале вводится определение параллелограмма: «Параллелограмм - это
четырехугольник, у которого противолежащие стороны параллельны, т.е. лежат на
параллельных прямых», а затем рассматривают и доказывают признак
параллелограмма (Т.6.1).
Теорема 6.1: Если диагонали
четырехугольника пересекаются и точкой пересечения делятся пополам, то этот
четырехугольник -параллелограмм.
В п.52 «Свойство диагоналей
параллелограмма» и п.53 «Свойство противолежащих сторон и углов
параллелограмма» изучаются свойства параллелограмма:
1. Диагонали параллелограмма
пересекаются и точкой пересечения делятся пополам. (Т.6.2, которая является
обратной теореме 6.1).
2. У параллелограмма
противолежащие стороны равны, противолежащие углы равны. (Т.6.3)
В учебнике «Геометрия 7-9» Л.
С. Атанасяна (5) тема «Параллелограмм» рассматривается в §2 «Параллелограмм и
трапеция» в пунктах 42 и 43.
Определение и свойства
параллелограмма даются в п.42 «Параллелограмм»:
Опр.: Параллелограммом
называется четырехугольник, у которого противолежащие стороны попарно
параллельны. Свойства:
1. В параллелограмме
противолежащие стороны и противолежащие углы равны.
2. Диагонали параллелограмма
точкой пересечения делятся пополам.
Л.С. Атанасян выделяет три
признака параллелограмма, которые изучаются в 43 пункте «Признаки
параллелограмма»:
1.
Если
в четырехугольнике две стороны равны и параллельны, то этот четырехугольник -
параллелограмм.
2.
Если
в четырехугольнике противолежащие стороны попарно равны, то этот
четырехугольник - параллелограмм.
3. Если в четырехугольнике
диагонали пересекаются и точкой пересечения делятся пополам, то этот
четырехугольник - параллелограмм.
Рассмотрим методику изучения
темы «Параллелограмм» на примере геометрии А.В. Погорелова. Понятие
параллелограмма вводится с помощью таблицы «Четырехугольники».

В таблице показаны два вида
четырехугольников: параллелограммы и не параллелограммы.
Параллелограмм иллюстрируется
не одним объектом, входящим в объем этого понятия, что дает возможность с
первого урока учащимся не приписывать этому понятию несущественные признаки:
один угол острый, а другой - тупой, стороны не равны и т.д.
Классу задается вопрос: по
какому признаку разделили все четырехугольники на два вида? (У
четырехугольников справа противолежащие стороны параллельны.)
Составляется определение
параллелограмма: параллелограммом называется четырехугольник, у которого
противолежащие стороны параллельны, т.е. лежат на параллельных прямых.
Термин «параллелограмм»
происходит от объединения греческих слов «параллелос» - то, что идет рядом, и
«грамма» - черта, линия (этот термин ввел Евклид).
После введения определения
параллелограмма школьники решают следующие задачи:
3адача 1.
При пересечении двух прямых а и b
прямыми с и d образуется
четырехугольник ABCD.
Определите в каком случае четырехугольник является параллелограммом?
Ответ: a)
a||b,
с||d; б) a||b,
c||d;
в) а||b; г) с||d.
Задача 2.
В
треугольнике ABC параллельно
сторонам АВ и АС проведены прямые DG
и FG. Определите вид
четырехугольника AFGD.
Решение.
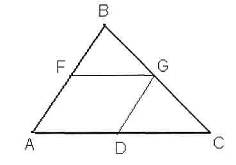
Т.к. AF||DG.
AD||FG
( по условию), следовательно AFGD-
параллелограмм ( по определению).
Ответ: AFGD-параллелограмм.
Задача 3.В
параллелограмме ABCD
параллельно стороне АВ проведена прямая FG.
Определите вид четырехугольника ABFG.

AB||GF,
BF||AG,
следовательно ABFG -
параллелограмм (по определению параллелограмма).
Ответ: ABFG
- параллелограмм.
Задача 4.
В
треугольнике ABC проведена
медиана BF. На ее
продолжении за точку F
отложен отрезок FD,
равный BF. Докажите,
что четырехугольник ABCD
- параллелограмм.
Дано: BF-медиана
∆АВС, FD=BF.
Доказать: ABCD-параллелограмм.
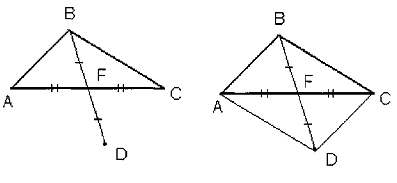
Решение. AF=CF,
так как BF - медиана ∆АВС.
FD=BF
по условию.
Следовательно, в
четырехугольнике ABCD
диагонали АС и BD
пересекаются и точкой пересечения F
делятся пополам. Следовательно, по признаку параллелограмма четырехугольник ABCD
- параллелограмм.
Ч.т.д.
Признаки
параллелограмма
Для «открытия» теоремы 6.1
учащимся предлагается в тетрадях выполнить следующие построения: провести две
пересекающиеся прямые, отложить на них точки пересечения соответственно равные
отрезки АО=ОС, OB=OD
(AO не равен ОВ) и
полученные точки А, В, С, D
последовательно соединить отрезками. Такой подход дает возможность учащимся
лучше понять и запомнить содержание теоремы, не путать ее условие и заключение.
Классу задается вопрос: Какой
же получился четырехугольник? Формулируется теорема 6.1, записывается ее
условие.
Теорема: Если
диагонали четырехугольника пересекаются и точкой пересечения делятся пополам,
то этот четырехугольник - параллелограмм.
Дано: ABCD
- четырехугольник, ACUBD=0,AO=OC,
BO=OD.

Доказать: ABCD-параллелограмм.
Доказательство.
ABCD
- четырехугольник, точка О - точка пересечения его диагоналей.
Рассмотрим ∆AOD
и ∆СОВ, они равны, т.к.
 AOD=
AOD=  COB
(вертикальные), OD=OB ( по
условию теоремы), ОА=ОС ( по условию теоремы).
COB
(вертикальные), OD=OB ( по
условию теоремы), ОА=ОС ( по условию теоремы).
=>  OBC=
OBC= ODA, а они
являются внутренними накрест лежащими для прямых AD и ВС и
секущей BD.
ODA, а они
являются внутренними накрест лежащими для прямых AD и ВС и
секущей BD.
=> AD||BC ( по
признаку параллельности прямых).
Аналогично доказывается
параллельность прямых АВ и CD
=> ABCD -
параллелограмм (по определению).
Ч.т.д.
Свойства
параллелограмма
После введения определения
параллелограмма и его признака, изучают свойства.
Свойство диагоналей
параллелограмма учащиеся легко обнаружат, выполнив соответствующий рисунок.

Теорема 6.2
(обратная теореме 6.1): Диагонали параллелограмма пересекаются
и точкой пересечения делятся пополам.
Дано: ABCD-параллелограмм,
АС и BD-диагонали.
Доказать: AC⋂BD
и точкой пересечения делятся пополам.
Доказательство.
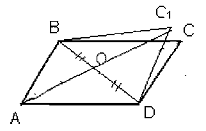
Пусть ABCD
- данный параллелограмм.
BD
- диагональ, точка О ее середина. Предположим, что существует точка d,
такая что АО=ОС1.
Получаем, что ABС1D
-
параллелограмм (по Т.6.1).
=>BC||AD.
Получили противоречие, т.к. через точку можно провести только одну прямую,
параллельную данной. Значит ВС1 совпадает с ВС.
Точно так же доказывается, что
прямая DC1
совпадает с прямой DC.
Значит, что C1
совпадает с точкой С => ABCD
совпадает с ABC1D.
Поэтому его диагонали пересекаются и точкой пересечения делятся пополам.
Ч.т.д.
Теорема 6.3: У
параллелограмма противолежащие стороны равны, противолежащие углы равны.
Дано: ABCD-параллелограмм,
АС и BD-диагонали, AC⋂BD=0
Доказать: AB=CD,
AD=BC,
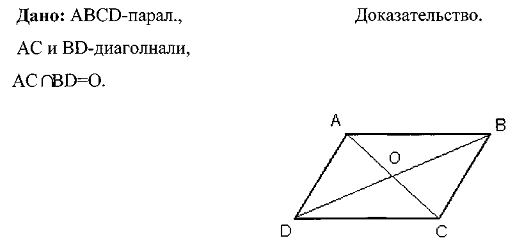
Доказать: AB=CD, AD=BC,  B=
B= D.
D.
. Рассмотрим ∆АОВ и ∆DOC, они равны,
т.к. ОА=ОС, OB=OD (свойство
диагоналей),  AOB=
AOB= COD
(вертикальные) => AB=CD.
COD
(вертикальные) => AB=CD.
Равенство AD и ВС
доказывается аналогично из треугольников AOD и СОВ.
. ∆ABC=∆CDA (по III признаку
равенства треугольников) AB=CD BC=DA
АС - общая, => ABC=
ABC= CDA. Равенство
углов BCD и DAB
доказывается аналогично.
CDA. Равенство
углов BCD и DAB
доказывается аналогично.
Ч.т.д.
После этого учащиеся приступают к
решению задач.
Задача 1: Через
точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что
отрезок ее, заключенный между параллельными сторонами, делятся этой точкой
пополам.
Дано: ABCD-параллелограмм,
АС, BD-диагонали, AC⋂BD = 0, FE-прямая, OЄFE.
Доказать: FO=OE.
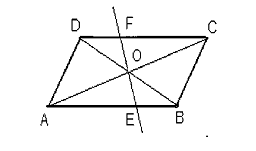
Доказательство.
ABCD:
EF⋂АВ
= Е
EF⋂DC
= F
∆ОАЕ = ∆OCF(по
II признаку)
О А = ОС (т.к. О - середина
диагонали АС)
 O =
O = О (вертикальные)
О (вертикальные)
 EA О =
EA О =  FCO (внутренние
накрест лежащие при параллельных прямых АВ, CD и секущей
АС)
FCO (внутренние
накрест лежащие при параллельных прямых АВ, CD и секущей
АС)
=>ОЕ = OF.
Ч.т.д.
Задача 2: Докажите,
что если у четырехугольника две стороны параллельны и равны, то он является
параллелограммом.
Дано: ABCD -
четырехугольник, АВ||CD, AB=CD.
Доказать: ABCD -
параллелограмм.

Доказательство.
Через вершину В проведем прямую
b, b||AD,
b⋂DC
= Cl.
ABC1D
- параллелограмм (т.к.у параллелограмма противолежащие
стороны равны), то C1D
= AB.
Т.к.
AB = CD=>DC = DC1=>C = C1
=> ABCD
совпадает с ABC1D
=> ABCD -
параллелограмм.
Ч.т.д.
После введения перечисленных
свойств и признаков параллелограмма учащимся можно предложить систему задач,
направленную на выработку соответствующих умений и навыков.
1. Сторона AD
параллелограмма ABCD
равна 9см, а его диагонали равны 14см и 10см. О - точка пересечения диагоналей.
Чему равен периметр AAOD?
2. В параллелограмме ABCD
диагонали равны, О - точка пересечения диагоналей. Докажите, что∆AOD-равнобедренный.
3. Стороны АВ и ВС
параллелограмма ABCD
равны 9см и 6см. Чему равны стороны CD
и AD?
4. В параллелограмме сумма
двух углов равна 120. Могут ли эти углы прилежать к одной стороне
параллелограмма.
. В равнобедренный
треугольник вписан параллелограмм так, что угол параллелограмма совпадает с
углом при вершине треугольника, а вершина противолежащего угла лежат на
основании. Докажите, что периметр параллелограмма есть величина постоянная для
данного треугольника.
Конспект урока по
теме «Параллелограмм. Свойства параллелограмма».
Цели урока:
образовательные цели
направлены на усвоение и закрепление понятия параллелограмма, его свойств,
навыка построения параллелограмма и применения его свойств при решении задач;
развивающие цели
данного урока направлены на развитие пространственного воображения учащихся,
логического мышления; совершенствование графической культуры, формирование
навыков осмысленного понимания теорем и быстрого их запоминания, развитие
умений применять знания в различных ситуациях; умений самостоятельной работы;
Исходя из типа урока, целей урока, содержания
учебного материала на уроке используются следующие методы и приемы
обучения:
· эвристический (постановка
проблемы и организация деятельности по ее решению);
· практический
(закрепление умений и навыков происходит в ходе выполнения практических
заданий);
· словесный;
· наглядный.
формы обучения
· общеклассная (на
этапе изучения нового материала ведется работа со всем классом, что необходимо
для закрепления материала обязательного уровня всеми учениками класса);
· индивидуальная и групповая (учащиеся
работают самостоятельно, в парах, исходя из своих возможностей).
Обрудование: компьютер,
мультимедийный проектор или интерактивная доска, линейки, угольники, циркули,
нелинованная бумага, рабочая карта урока.
Урок проводится в сопровождении мультимедийной
презентации PowerPoint.
Ход урока:
|
Деятельность учителя
|
Деятельность учащихся
|
Комментарий к слайдам
|
|
1. Организационный момент. Слайд 2. Учитель
сообщает тему урока, формулирует цели урока.
|
|
Слайд 2 
|
|
2. Актуализация опорных знаний. - Повторим
свойства параллельных прямых. Как называются углы, изображенные на рисунках?
Сформулируйте свойства параллельных прямых. Слайд 3
|
Учащиеся
после просмотра каждого рисунка формулируют свойства параллельных прямых
|
Слайд 3 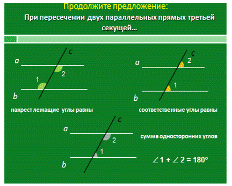
|
|
-
Повторим признаки равенства треугольников. Слайд 4
|
Учащиеся
формулируют признаки равенства треугольников.
|
Слайд 4 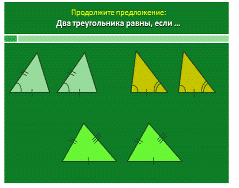
|
|
Устная
работа с рисунком на Слайде 5. 1) Назовите пары параллельных прямых;
2) укажите четырехугольники, у которых не более двух параллельных прямых; 3)
укажите четырехугольники, у которых стороны попарно параллельны.
|
Ответы
учащихся: 1)
AB êêCD,
AB êêEF,
AE êêKO,
NR êêBF;
2) KMPN, MPRO, KNRO и т.д.;
3) AKMC, CMOE, NPBD, PDFR, AKOE, NBFR и т.д.
|
Слайд 5 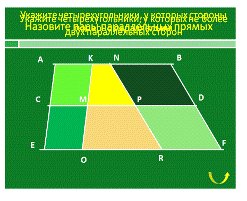 После
ответов учащихся 2) и 3) четырехугольники по клику мышки меняют цвет. По
гиперссылке возвращаемся на слайд с целями урока Слайд 2. После
ответов учащихся 2) и 3) четырехугольники по клику мышки меняют цвет. По
гиперссылке возвращаемся на слайд с целями урока Слайд 2.
|
|
3. Изучение нового материала. -
Четырехугольники, у которых стороны попарно параллельны, являются
параллелограммами. Запишите это определение в тетрадь (Слайд 6).
Назовите противоположные стороны параллелограмма.
|
|
Слайд 6 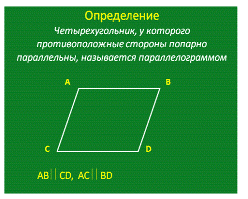 По клику
мышки появляется запись: пары параллельных сторон - противоположных сторон. По клику
мышки появляется запись: пары параллельных сторон - противоположных сторон.
|
|
-
Ребята, как вы предполагаете, какими свойствами обладает параллелограмм?
|
Предположения
учащихся: ü диагональ
делит параллелограмм на равные треугольники; ü противоположные стороны равны; ü противоположные
углы равны; ü
стороны
параллельны Þ сумма
односторонних углов равна 180°;
ü вторая
диагональ делит параллелограмм на 4 попарно равных треугольника; ü диагонали
в точке пересечения делятся пополам.
|
Слайд 7 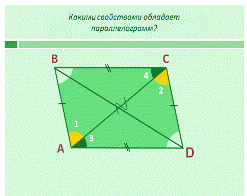
|
|
-
Но пока это только наши утверждения, которые требуют доказательства.
Давайте попытаемся вместе доказать Свойство 1 (Слайд 8) и Свойство 2 (Слайд
10)
|
По
ходу доказательства теорем, учащиеся делают записи в тетради
|
Слайд 8 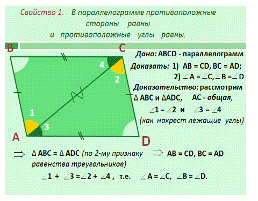 Все
необходимые элементы чертежа и записи теоремы появляются по клику мыши. Все
необходимые элементы чертежа и записи теоремы появляются по клику мыши.
|
|
-
Теперь, ребята, я предлагаю вам повторить доказательство с помощью
анимированного чертежа (Слайд 9, 11)
|
Учащиеся
повторяют доказательства ( учитель помогает, руководя анимацией)
|
Слайд 9  Теперь
записей на чертеже нет. Теперь
записей на чертеже нет.
|
|
|
Слайд 9 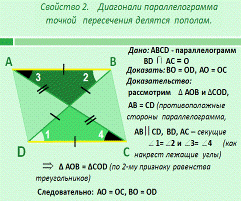
|
|
|
Слайд 10 
|
|
4. Физкультминутка (1,5-2
мин) 5. Практическая работа. - Ребята, сейчас вы делали чертежи
параллелограммов в тетради с помощью клеточек. А как построить параллелограмм
на нелинованной бумаге? Как могут свойства параллелограмма вам в этом помочь?
|
Ответы
учащихся: - Так как у параллелограмма противоположные стороны параллельны,
то параллельные прямые можно построить с помощью угольника и линейки.
|
Слайд 11 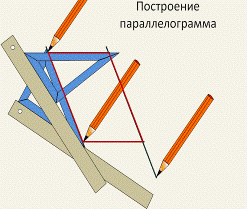
|
|
Можно
предложить учащимся: 1)посмотреть готовые анимации построения на Слайдах
11,12; 2) построить на доске мелом или интерактивной доске маркером.
|
-
Так как диагонали параллелограмма в точке пересечения делятся пополам, то
можно на пересекающихся прямых от точки пересечения отложить парные равные
отрезки с помощью циркуля, а потом последовательно соединить полученные точки
пересечения. Учащиеся строят параллелограммы на доске и на нелинованных
листах. Работают в парах: проверяют друг у друга выполненные работы.
|
Слайд 12 
|
|
6. Закрепление полученных знаний и умений.
Решение задач. (Слайды
13, 14)
|
Сильные
учащиеся решают задачи самостоятельно, остальные - с помощью учителя.
Решение: MNPK -
параллелограмм Þ NP=MK=7см, PK=NM=4 см Þ P= (7+4)2 =
22 см Ð M
= Ð
P = 70°
Ð
N = Ð
K = 180°-
70°=
110°
|
Слайд 13 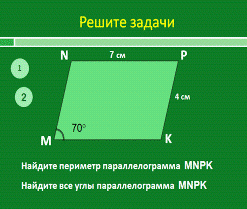
|
|
Решение: по свойству
параллелограмма ВО = ОD, Ð ВОМ =Ð КОD -
вертикальные, Ð
МВО = Ð
DОК -
накрест лежащие углы при параллельных прямых ВМ и DК и
секущей ВD
Þ
∆OMB = ∆OKD (по
стороне и двум прилежащим углам). Решение задач проверяются и обсуждаются
совместно с учителем
|
Слайд 14 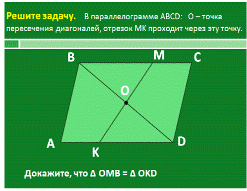
|
|
Подведение итогов. Задание на дом. Подведем
итоги нашего урока. 1. Достигли ли мы поставленной цели? 2. Какой
главный итог нашего урока? 3. Что мы использовали для достижения цели
урока? Запишите домашнее задание. Благодарю всех за урок. Молодцы.
|
Да,
мы узнали определение и свойства параллелограмма, научились строить
параллелограмм. Изученные свойства параллелограмма можно применить в
различных ситуациях: помогают решать задачи, делать построения. Свойства
параллельных прямых, признаки равенства треугольников, формула периметра. Домашнее
задание п. 42, теоремы о свойствах параллелограмма, № 371 б), 372 в), 376
а),в).
|
Слайд 15 
|
4.2 Методика
изучения темы «Прямоугольник»
В учебнике «Геометрия 7-11»
А.В. Погорелова (18) понятие «прямоугольник» вводится в §6 «Четырехугольники» в
пункте 54 «Прямоугольник»: Прямоугольник - это параллелограмм, у
которого все углы прямые.
В учебнике «Геометрия 7-9» Л.С.
Атанасяна (4) тема «Прямоугольник рассматривается в §3 «Прямоугольник, ромб,
квадрат» в п.45 «Прямоугольник»: в начале параграфа вводится определение:
«прямоугольником называется параллелограмм, у которого все углы прямые», а
затем рассматривают свойство прямоугольника (диагонали прямоугольника равны) и
признак прямоугольника (если в параллелограмме диагонали равны, то этот
параллелограмм - прямоугольник).
Рассмотрим методику изучения
темы «Прямоугольник» на примере учебника А.В. Погорелова.
Прямоугольник - это
параллелограмм, у которого все углы прямые.
Для изучения свойства
прямоугольника, классу можно предложить вопросы:
1. Равны ли диагонали у
произвольного параллелограмма? (на доске нарисован параллелограмм, не
являющийся прямоугольником).
2. Равны ли диагонали у
прямоугольника?
. Докажите равенство
диагоналей прямоугольника ABCD,
рассмотрев треугольники BAD
и CDA.
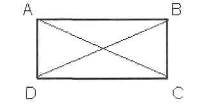
. Сформулируйте теорему о свойствах
прямоугольника.
Теорема 6.4.
Диагонали прямоугольника равны.
После введения определения и
свойства прямоугольника школьники решают задачи.
Задача 1.
Докажите, что если у параллелограмма все углы равны, то он является
прямоугольником.
Дано: ABCD-параллелограмм,
 A=
A= B=
B= С=
С= D.
D.
Доказать: ABCD-прямоугольник.
Доказательство.

 A+
A+ B=180, т.к. они являются внутренними
односторонними при параллельных прямых ВС и AD и секущей
АВ. =>
B=180, т.к. они являются внутренними
односторонними при параллельных прямых ВС и AD и секущей
АВ. =>  A=
A= B=90.
B=90.
=> ABCD -
прямоугольник.
Задача 2. В
параллелограмме из вершин углов на противолежащие стороны опущены
перпендикуляры. Докажите, что полученный четырехугольник - прямоугольник.
Дано: GBFD-параллелограмм,
BA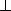 GD,DC
GD,DC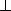 BF.
BF.
Доказать: ABCD-прямоугольник.
Доказательство.

BC||AD,
так как GBFD -
параллелограмм;
 BAD=90, так как BA
BAD=90, так как BA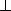 GD.
GD.
 АВС=90, так как
АВС=90, так как  BAD и
BAD и  ABC- внутренние
односторонние углы при BF||GD и секущей
АВ.
ABC- внутренние
односторонние углы при BF||GD и секущей
АВ.
 BCD=90, так как DC
BCD=90, так как DC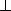 BF.
BF.
 CAD=90, так как
CAD=90, так как  CAD и
CAD и  BCD -
внутренние односторонние углы при BF||GD и секущей DC.
BCD -
внутренние односторонние углы при BF||GD и секущей DC.
BA||DC, так как  BAD и
BAD и  CDA -
внутренние односторонние углы при прямых АВ и CD и секущей AD и
CDA -
внутренние односторонние углы при прямых АВ и CD и секущей AD и  BAD+
BAD+ CDA=180.
CDA=180.
Следовательно, ABCD -
параллелограмм, у которого все углы равны.
Значит, ABCD -
прямоугольник.
Задача 3.В прямоугольнике
ABCD диагональ
АС образует со стороной AD угол, равный 37. найдите
градусную меру угла ACD. (решение устно)
Ответ:  ACD=53.
ACD=53.
Затем им можно предложить систему
задач, направленную на выработку соответствующих умений и навыков.
1. В параллелограмме KLMN
каждый из углов LKM
и MNL равен 57.
определите, является ли параллелограмм KLMN
прямоугольником.
2. Докажите, что если в
четырехугольнике три угла прямые, то он является прямоугольником.
3. ABCD
- прямоугольник. О - точка пересечения диагоналей. Докажите, что ААОВ -
равнобедренный.
. В прямоугольный
равнобедренный треугольник вписан прямоугольник так, что угол прямоугольника
совпадает с углом при вершине треугольника, а вершина противолежащего угла
лежит на гипотенузе. Докажите, что периметр прямоугольника есть величина
постоянная для данного треугольника.
. Стороны прямоугольника
равны 5см и 4см. биссектрисы углов, прилежащих к большей стороне, делят
противолежащую сторону на три части. Найдите длины этих частей.
Конспект урока по теме
«Прямоугольник».
Цели урока:
повторить понятие прямоугольника, опираясь на полученные
ранее знания учащихся;
рассмотреть свойства прямоугольника как частного
вида параллелограмма и научить учащихся применять их в процессе решения задач.
Ход урока. Организационный момент:
Сообщать цель урока, тему урока.. Актуализация
знаний учащихся
) Практическое задание:
Разделить данный отрезок на 7 равных частей.
) Проверить Д/з №393(б),398
) Решение задач на готовых чертежах.
Работа проводится с целью подготовки учащихся к
восприятию нового материала.
а) Найдите углы выпуклого четырёхугольника, если
их градусные меры пропорциональны числам 1,2,3,4
б)

Докажите, что расстояния АМ и СN от вершин. А и.
С параллелограмма ABCD до прямой BD равны.
в) Найдите углы параллелограмма ABCD, если A =
3B. Изучение нового материала
. Ввести понятие прямоугольника можно в процессе
ответов на вопросы (работа парами 3-5 мин.)
а) Какой четырёхугольник называется
прямоугольником?
б) Можно ли утверждать, что прямоугольник - это
параллелограмм, и почему?
в) Чем отличается произвольный параллелограмм от
прямоугольника?
г) Закончите предложение: «Прямоугольник - это
параллелограмм, у которого…»
д) Сформулируйте свойства прямоугольника.
На доске кратко все ответы фиксируем.
. Рассмотреть особое свойство диагонали
прямоугольника:
а) (самостоятельно в группах по 4 человека)
Исследуйте стороны, углы и диагонали
прямоугольника и заполните таблицу:
|
Параллелограмм
|
Прямоугольник
|
|
Стороны
|
1
2
|
1
2
|
|
Углы
|
1
2
|
1
2 3
|
|
диагонали
|
1
|
1
2
|
3. Рассмотреть признак прямоугольника.
Как определить, является ли данный
параллелограмм прямоугольником? Ответ обоснуйте.
(Работа в парах 3-5 мин. на обдумывание.)
Выберете верные утверждение (каждому даётся
листок с вопросами).
а) Если в четырёхугольнике диагонали равны и
делятся точкой пересечения пополам, то этот четырёхугольник - прямоугольник.
б) Если в четырёхугольнике противоположные
стороны параллельны, а все углы прямые, то этот четырёхугольник -
прямоугольник.
в) Если в четырёхугольнике диагонали равны, то
этот четырёхугольник - прямоугольник.
г) Если в параллелограмме два прямых угла, то
этот параллелограмм - прямоугольник.
д) Если в четырехугольнике два прямых угла и две
стороны равны, то этот четырехугольник - прямоугольник.
е) Если в четырехугольнике диагонали равны, а
один угол прямой, то этот четырехугольник - прямоугольник.
Ответы проверяем, ставим + или -
Что общего между свойствами параллелограмма и
прямоугольника?. Закрепление изученного материала.
№304
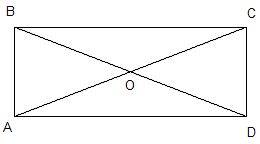
Дано: ABCD - прямоугольник= 30° АС = 12 см
Найти: РAOB
Решение:
∆АСD - прямоугольный, в нем CAD= 30°,
значит СD = ½ АС = 6 см, тогда АВ
= СD = 6 см.
В прямоугольнике диагонали равны и точкой
пересечения делятся пополам, т.к. АО = ½ АС
= ½
ВD
= ВО = 6см
РAOB = АО + ВО + АВ = 6 + 6 + 6 = 18см
Ответ : РAOB = 18см
№ 401(б) - самостоятельно.
Проверить на доске этот номер.. Подведение
итогов урока.
Выслушаем учеников.
Что нового мы узнаем, какие ошибки были в
решении задач и в работе на листах.
Д/з п.45 в.12,13
№399, 401(а).
4.3 Квадрат
В учебнике «Геометрия 7-11»
А.В. Погорелова (18) понятие «квадрат» вводится в §6 «Четырехугольники» в п.56
«квадрат».
Квадрат -
это прямоугольник, у которого все стороны равны.

Так как стороны квадрата равны,
то он является также ромбом. Поэтому квадрат обладает свойством прямоугольника
и ромба:
1.
У
квадрата все углы прямые.
2.
Диагонали
квадрата равны.
3.
Диагонали
квадрата пересекаются под прямым углом и являются биссектрисами его угла.
4.
В учебнике «Геометрия 7-9» Л.С.
Атанасяна (5) понятие «квадрат» вводится в п.46 «Ромб и квадрат» 3 параграфа
после изучения «ромба».
Квадратом называется
прямоугольник, у которого все стороны равны. Затем формулируются основные
свойства квадрата:
1.
Все
углы квадрата прямые.
2.
Диагонали
квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и
делят углы квадрата пополам.
Рассмотрим методику изучения
темы «Квадрат» на примере учебника А.В. Погорелова.
После введения свойств и
определения квадрата школьники решают задачи.
3адача 1.
Докажите, что если диагонали прямоугольника пересекаются под прямым углом, то
он есть квадрат.
Дано: ABCD-прямоугольник,
AC, BD
- диагонали, AC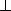 BD.
BD.
Доказать: ABCD-квадрат.
Доказательство.
Так как прямоугольник есть
параллелограмм, а параллелограмм с перпендикулярными диагоналями есть ромб, то
у ABCD все стороны равны
=> ABCD - квадрат (по
определению).
3адача 2.
Докажите, что ромб, у которого один угол - прямой, является квадратом.
Дано: ABCD-
ромб,
 AB=90.
AB=90.
Доказать: ABCD - квадрат.
Доказательство.
Так как ABCD - ромб,
значит ABCD -
параллелограмм.
ABCD -
параллелограмм, у которого  АВС=90.
АВС=90.
Следовательно, ABCD -
прямоугольник.
А прямоугольник, у которого все
стороны равны (ABCD - ромб), по определению является
квадратом.
Следовательно, ABCD - квадрат.
Ч.т.д.
Далее ученикам можно предложить систему
задач, направленную на выработку соответствующих умений и навыков.
1.
Периметр
квадрата равен 28см. Найдите его сторону.
2.
В
квадрате ABCD проведена
диагональ BD.
Определите:
а) вид треугольника ABD;
б) углы AABD.
3.
В
равнобедренный прямоугольный треугольник, каждый катет которого 2м, вписан
квадрат, имеющий с ним общий угол. Найдите периметр квадрата.
4.
Диагональ
квадрата равна 4 м. сторона его равна диагонали другого квадрата. Найдите
сторону последнего.
5.
В
квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна
вершина прямоугольника и стороны прямоугольника параллельны диагоналям
квадрата. Найдите стороны прямоугольника, зная, что одна из них вдвое больше
другой и что диагональ квадрата равна 12 м.
Конспект урока по
теме «Параллелограмм, прямоугольник, ромб, квадрат».
Цели урока: Систематизировать, обобщить знания о
четырех фигурах - параллелограмме, прямоугольнике, ромбе, квадрате, их
свойствах, признаках.
Девиз урока:
«Математику уже затем учить надо, что она ум в
порядок приводит.»
(М. В. Ломоносов).
План урока:
Загадки.
Беседа с классом по вопросам.
Работа по готовым чертежам (работа в парах).
Применение в жизни (сообщение).
Физкультминутка («истинно - ложно»).
Тест (2 варианта).
Домашнее задание: п. 45, 46, № 406, № 411, на
оценку «5» № 412.
Самостоятельная работа
Итоги урока.
1. Загадки:
УЧИТЕЛЬ: Вспомним определения четырехугольников.
В этих загадках используются их свойства. Я читаю загадку, а вы поднимаете
карточку с верным ответом (у каждого ученика карточки: параллелограмм, квадрат,
ромб, прямоугольник).
. Знаете ли вы меня
Хочу проверить,
Любую площадь я могу измерить,
Ведь у меня четыре стороны
И все они между собой равны.
И у меня равны еще диагонали,
Углы мне они делят пополам, и ими
На части равные разбит я сам.
(Квадрат)
. И у меня равны диагонали,
Хочу сказать я, хотя меня не называли,
И хоть я не зовусь квадратом
Он мне приходится родным братом.
(Прямоугольник)
. Хоть стороны мои
Попарно и равны, и параллельны,
Все ж я в печали, что не равны мои диагонали,
Да и углы они не делят пополам
Но все ж, скажи, дружок, кто я?
(Параллелограмм)
. Мои хотя и не равны диагонали,
По значимости всем я уступлю едва ли.
Ведь под прямым углом они пересекаются,
И каждый угол делят пополам,
И очень важная фигура я, скажу я вам.
(Ромб)
2. Беседа с классом по вопросам:
К какому виду четырехугольников относятся
прямоугольник, ромб, квадрат?
Назовите свойства параллелограмма?
Назовите признаки параллелограмма?
Назовите особое свойства прямоугольника?
Назовите особое свойства ромба?
Назовите основные свойства квадрата?
3. Работа по готовым чертежам
(работа в парах):
Задание: Указать вид четырехугольника на
рисунках. Объяснить почему?
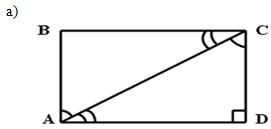

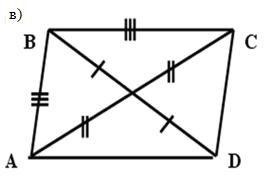
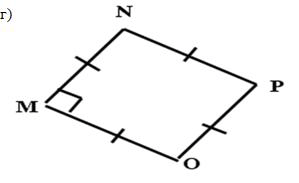
Двое учащихся выполняют это задание на откидной
доске (работают в паре). Учитель проверяет задание, остальные учащиеся
оценивают друг друга, выставляется вторая оценка в «Карточку самооценки».
4. Применение в жизни. (Сообщение):
Параллелограмм дает определение прямоугольнику,
ромбу. В жизни параллелограмм - это рамы велосипедов, мотоциклов, где для
жесткости проведена диагональ.
Прямоугольник несет красоту, стройность,
четкость. Это стены домов, пол, потолок, грани карандашей.
Реечный домкрат для легковых автомобилей имеет
форму ромба. Плиточники укладывают плитки в виде ромба, квадрата - из них
получаются красивые узоры.
В хирургическом отделении для пересадки кожи
применяют специальную машинку, которая вырезает кожу в виде квадратов. Их
располагают на обожженном участке в шахматном порядке, так как кожа имеет
свойство расти во всех направлениях, со временем промежутки между квадратами
зарастают.
В сельском хозяйстве применяют квадратно - гнездовой
способ посадки культур - урожай при этом лучше, этот способ хорош тем, что
можно применять механизированную обработку.
В физике применяют параллелограмм при изучении
разложения сил, при нахождении равнодействующей силы.
5. Физкультминутка («истинно -
ложно»):
Учитель: Я скажу несколько предложений. Если
предложение ложное, то вы встаете, если верное, то поднимаете руку.
Диагонали прямоугольника равны.
Все углы квадрата прямые.
Диагонали параллелограмма равны.
В ромбе все стороны равны.
Диагонали прямоугольника перпендикулярны.
В параллелограмме противоположные стороны равны.
Диагонали ромба равны.
6. Тест
(2 варианта)

Результаты заносятся в таблицу, расположенную в
конце теста, который содержит пять заданий. Выполнив тест, учащиеся
обмениваются результатами, учитель называет правильные ответы. За верно
выполненное задание - 1 балл.
7. Домашнее задание: п. 45, 46, №
406, № 411, на оценку «5» № 412.
. Самостоятельная работа.
I вариант:
Вычислить углы параллелограмма, если его углы,
прилежащие к одной стороне, относятся как 2:7.
В ромбе периметр равен 24 см, один из углов
120°. Чему равна длина меньшей диагонали.- параллелограмм. Доказать: ECFB -
параллелограмм.
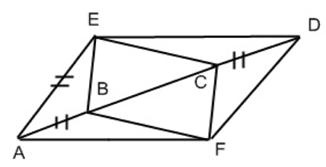
вариант:
Вычислить углы параллелограмма, если его углы,
прилежащие к одной стороне, относятся как 4:5.
В ромбе один из углов 120°, длина меньшей
диагонали 5 см, найти периметр ромба.- параллелограмм. Доказать: ACDF -
параллелограмм.
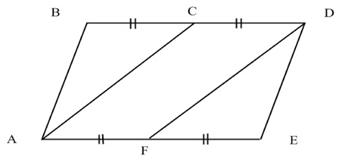
Двое учащихся выполняют самостоятельную работу
по вариантам на откидных досках. По окончанию работы ученики сверяют свои решения
с доской.
9. Подведение итогов урока.
Рефлексия:
Если было хорошо у нас - улыбнись и покажи
квадрат.
Если было скучно вам - покажи параллелограмм.
Если ждешь таких уроков - хлопни.
Если больше ничего не хочешь - топни.
Спасибо за внимание!
4.4 Ромб
В учебнике «Геометрия
7-9» Л.С. Атанасяна (4) понятие «ромб» вводится в §3 п.46 «Ромб и квадрат»:
Ромбом называется параллелограмм, у которого все стороны равны. Далее
рассматривают и доказывают свойство ромба: «Диагонали ромба взаимно
перпендикулярны и делят его углы пополам.»
А.В. Погорелов (18) тему «Ромб»
выделяет в отдельный пункт (п.55).
В начале пункта дается
определение: Ромб - это параллелограмм, у которого все стороны равны. А
затем вводит свойство ромба как теорему 6.5: «Диагонали ромба пересекаются под
прямым углом. Диагонали ромба являются биссектрисами его углов».
Дано: ABCD-ромб,
AC,
BD - диагонали.
Доказать: AC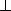 BD,
BD,
AC,
BD - биссектрисы.
Доказательство.
1)
Пусть
АС⋂ВD=O,
2)
ААВС
- равнобедренный, т.к. АВ=ВС (ABCD-ромб).
АО=ОС (по свойству
параллелограмма) => ВО - медиана, а => и биссектриса, и высота.
А значит BD
- биссектриса угла В и перпендикулярна АС.
Ч.т.д.
Рассмотрим методику изучения
темы «Ромб» на примере учебника А.В. Погорелова.
После введения свойств и
определения ромба школьники решают задачи.
Задача 1.
Докажите, что если у параллелограмма диагонали перпендикулярны, то он является
ромбом.
Дано: ABCD-параллелограмм,
АС, BD-диагонали, AC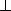 BD.
BD.
Доказать: ABCD-ромб.
Доказательство.
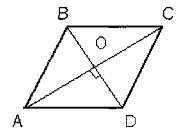
Пусть О - точка пересечения
диагоналей. ∆АОВ = ∆AOD (по I признаку),  AOB=
AOB= AOD=90 (по
условию), ОА - общая, OB=OD (по
свойству диагоналей параллелограмма).
AOD=90 (по
условию), ОА - общая, OB=OD (по
свойству диагоналей параллелограмма).
=>AB=AD. А по
свойству противолежащих сторон параллелограмма AD=BC, AB=CD.
=> ABCD-ромб.
3адача 2. Периметр
ромба ABCD равен 56см.
Найдите углы ромба, (устно).
Ответ: AB=BC=CD=AD=14cm.
3адача 3. Один из
углов ромба ABCD равен 72.
найдите углы ромба (устно).
 Ответ:
Ответ:  A=
A= C=72,
C=72,  B=
B= D=108.
D=108.
Затем
им можно предложить систему задач:
1. В ромбе ABCD
проведена диагональ АС. Докажите, что треугольник ABC
- равнобедренный.
2. Две окружности с
центрами в точках О и O1
и равными радиусами пересекаются в точках А и В. Докажите, что четырехугольник
АО1ВО - параллелограмм.
. Сторона ромба равна
18см, а один из углов равен 150. найдите расстояние между его противолежащими
сторонами.
. Докажите, что точка
пересечения диагоналей ромба равноудалена от его сторон.
.5 Трапеция
В учебнике «Геометрия 7-11»
А.В. Погорелова (18) тема «Трапеция» изучается в §6 п.59 «Трапеция».
Определение трапеции вводится в началепункта: Трапецией называется
четырехугольник, у которого только две противолежащие стороны параллельны. Эти
параллельные стороны называются основаниями трапеция. Две другие стороны
называются боковыми сторонами.
Далее вводится понятия
«равнобедренная трапеция» и «средняя линия трапеции», и рассматривается теорема
6.8 (о средней линии трапеции): «Средняя линия трапеции параллельна
основаниям и равна их полусумме».
В учебнике «Геометрия 7-9» Л.С.
Атанасяна (4) понятие «трапеция» вводится в §2 «Параллелограмм и трапеция» в
пункте 44 «Трапеция»:
«Трапецией называется
четырехугольник, у которого две стороны параллельны, а две другие стороны не
параллельны. Параллельные стороны трапеции называются ее основаниями, а
две другие стороны - боковыми сторонами.
Трапеция называется равнобедренной,
если ее боковые стороны равны. Трапеция, один из углов которой прямой,
называется прямоугольной».
Рассмотрим методику изучения
темы «Трапеция» на примере учебника А.В. Погорелова.
Трапецией называется
четырехугольник, у которого только две противолежащие стороны параллельны. Эти
параллельные стороны называются основаниями трапеции. Две другие стороны
называются боковыми сторонами.
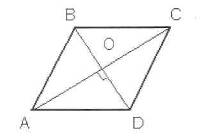
На рисунке вы видите трапецию ABCD
с основаниями АВ и CD
и боковыми сторонами ВС и AD.
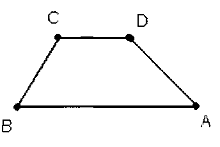
Трапеция, у которой боковые
стороны равны, называется равнобокой. Отрезок, соединяющий середины
боковых сторон, называется средней линией трапеции.
Теорема 6.8: Средняя
линия трапеции параллельна основаниям и равна их полусумме.
Дано: ABCD-трапеция,
QP-средняя
линия.
Доказать: QР||ВС,
QP||AD,
QP=½ (BC+AD).
Доказательство.
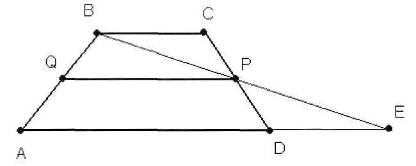
BP⋂AD=E, ∆PBC=∆PED (по второму
признаку равенства треугольников) CP=DP (по
построению),  PCB=
PCB= PDE (внутренние
накрест лежащие при параллельных прямых ВС и AD и секущей CD),
PDE (внутренние
накрест лежащие при параллельных прямых ВС и AD и секущей CD), BPC=
BPC= EPD
(вертикальные).
EPD
(вертикальные).
Из равенства треугольников =>
РВ=РЕ, BC=ED.
Значит средняя линия PQ трапеции
является средней линией ∆АВЕ. По свойству сред, линии треугольника PQ||AE и отрезок
pq = ½АЕ=
½(ad+bc).
Ч.т.д.
После введения выше перечисленных понятий
школьники решают задачи.
Задача1.В трапеции
ABCD углы,
прилежащие к стороне AD, равны 74 и 81. Определите
углы прилежащие к стороне ВС. (устно).
Ответ:  ABC=106,
ABC=106,  BCD=99.
BCD=99.
Дано: ABCD-равнобокая
трапеция,
АВ, CD-основания.
Доказать:  A=
A= B,
B,  D=
D= C.
C.

Доказательство.
BP||AD, ABED -
параллелограмм => BE=AD (по
свойству параллелограмма) AD=BC (по
условию) => ∆ВСЕ - равнобедренный с основанием ЕС. Углы треугольника и
трапеции при вершине С совпадают, а углы при вершине Е и D равны как
соответственные углы при пересечении параллельных прямых секущей. Поэтому  ADC=
ADC= BCD.
BCD.
Ч.т.д.
Затем ученикам можно предложить систему
задач, направленную на выработку соответствующих умений и навыков.
1. В равнобокой трапеции ABCD
углы, прилежащие к стороне AD,
равны 45. Найдите высоту трапеции, если основания равны 13 см и 27 см.
2.
Докажите,
что если в трапеции диагонали равны, то трапеция равнобокая.
3.
В
трапеции, одно из оснований которой равно 5 см проведена средняя линия, длина
которой равна 6 см. Чему равно другое основание трапеции?
4.
Диагонали
трапеции ABCD пересекают
среднюю линию RP в точках М
и N. Докажите, что RM=NP.
5.
Докажите,
что середины сторон равнобокой трапеции являются вершинами ромба.
Конспект урока по
теме: «Трапеция. Средняя линия трапеции»
Цели урока.
Образовательные:закрепит
знания изученных свойств трапеции и теорему о средней линии трапеции, научить
определять условия существования трапеции; научить применять формулу нахождения
средней линии трапеции при решении простейших задач, а также в сходных и новых
ситуациях.
Развивающие:
развить навыки самоконтроля и взаимоконтроля, развитие логического мышления,
грамотного и аккуратного выполнения работ.
Воспитательные: воспитание
самостоятельности и коллективизма культуры речи.
Оборудование:
2 половины листа и 1 лист копировальной бумаги, каждому ученику письменные
принадлежности, лист учёта у каждого ученика.
Ход урока.
1. Организационный момент урока.
Перед введением определения трапеции полезно
вспомнить определение параллелограмма и рассмотреть такой вид четырехугольника,
у которого только две противоположные стороны параллельны. (Определение
трапеции сопровождается рисунком на доске).
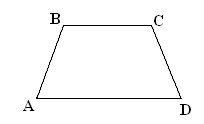
ВС//АD
2.
Закрепление понятия трапеции идет через готовые
рисунки на доске и вопросы к ним:

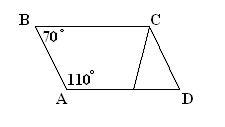
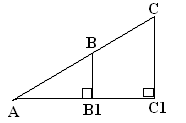
) Какие четырехугольники на рис. а), б), в)
являются трапециями?
Назовите их основания и боковые стороны.
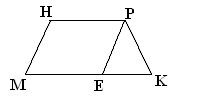
В трапеции МНРК проведен отрезок РЕ//МН.
Определите вид четырехугольника МНРЕ.
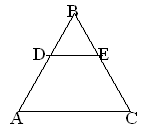
В равностороннем треугольнике АВС со стороной 8
см проведена средняя линия DE. Определите вид четырехугольника АDЕС. Чему равны
стороны этого четырехугольника?
Рассмотреть и назвать элементы трапеции, виды
трапеции.
3. Рассмотрение доказательства
теоремы о средней линии трапеции.
После изложения доказательства теоремы полезно
зафиксировать его этапы:
Дополнительное построение: отрезок ВЕ;
ΔРВС=ΔРЕD.
РО - средняя линия ΔАВЕ.
Вывод: РО//АD, РО= 1/2 (АD+ВС)
Замечание:(РО - средняя линия трапеции, отрезок
РО - можно было рассматривать как среднюю линию ΔАВЕ)
. Первичное закрепление теоремы о средней
линии идет через решение задач типа:
) Основания трапеции 7 и 9 см. Чему равна
средняя линия трапеции?
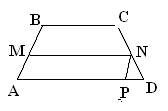
МN - средняя линия трапеция АВСD. Через т. N
проведена прямая, параллельная стороне АВ и пересекает стороны АD в точке Р.
Докажите, что МNРА - параллелограмм.
) В трапеции АВСD известны стороны: АВ=4 см,
ВС=6 см, СD=5 см, АD=10 см. Чему равны стороны трапеции АЕFD, если ЕF - средняя
линия трапеции?
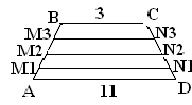
Каждая из боковых сторон трапеции АВСD разделена
на 4 равные части. Чему равны отрезки М N , М N и М N, если АD=11 см, ВС=3 см?
) РМ - средняя линия трапеции АВСD с основаниями
АD=а и ВС=в. Она пересекает диагональ АС в точке К. чему равны отрезки РК и КМ?
.Средняя линия трапеции равна 8 см, а одно из
оснований равно 6 см. Чему равно другое основание?
Закрепление нового материала через предложенные
задачи, показывает - насколько понят и усвоен новый материал.
. Подведение итогов урока:
определение трапеции;
названия ее элементов;
виды трапеций;
формулировка теоремы о средней линии.
2.
Постановка
домашнего задания: § 59 стр. 92-93, вопросы 17-19, зад. №59 стр.100.
Контроль за усвоением материала осуществляется
через тестирование (предполагается дифференцированный контроль знаний
учащихся).
В обязательной части предлагаются задания, для
успешного выполнения которых учащиеся должны применять знания на уровне
минимальных программных требований. Дополнительная часть содержит два задания
среднего уровня сложности, что соответствует большинству основных задач
учебника, и два задания для более подготовленных учащихся.
Время, необходимое для тестирования,
определяется исходя из возможностей конкретного класса.
|
Оценка
|
3
|
4
|
5
|
|
Обязательная
часть
|
10
|
11
|
11
|
|
Дополнительная
часть
|
-
|
4
|
9
|
) (1) Заполните пропуски, чтобы получилось
верное высказывание.
Средняя линия трапеции параллельна основаниям и
_____________
__________________________________________________________
) (1) Если МN - средняя линия трапеции АВСD, то
длина отрезка МN равна ________________________________________________
АD и ВС - основания трапеции.
) (2) Установите истинность или ложность
следующих утверждений:
А) Отрезок, соединяющий боковые стороны
трапеции, называется ее средней линией ________________
Б) Если основания трапеции равны 4 см и 8 см, то
ее средняя линия равна 4 см ___________________
) (2) Найдите МN.
а) 7 см; б) 5 см; в) 3 см.

5) (3)В трапеции одно из
оснований больше другого в 2 раза. Средняя линия трапеции = 15 см. Найдите ее
основание.
а) 5 см; 10 см; б) 10 см; 20
см; в) 15 см; 30 см.
) (3) Меньшее основание
трапеции относится к ее средней линии как 2:3. Найдите длину меньшего
основания, если большее основание равно 16 см.
а) 8 см; 12 см; б) 10 см; 15
см; в) 4 см и 6 см.
Дополнительная часть
3)
(4)
Дано: АВСD - трапеция. АМ=ВМ, ВN= ND. Докажите, что МР - средняя линия трапеции
АВСD.
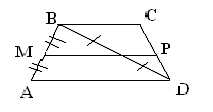
) (4) Средняя линия трапеции на
2 см меньше большего основания. Найдите среднюю линию трапеции, если меньшее
основание равно 6 см.
а) 8 см; б) 10 см; в) 5 см.
) (5) В равнобедренной трапеции
АВСD перпендикуляр, опущенный из вершины В на большее основание ВD, делит его
на отрезке, равные 4 см и 7 см. Найдите среднюю линию и меньшее основание
трапеции.
а) 10 см; б) 4 см; в) 8 см.
) (5) В равнобедренной трапеции
АВСD МN - средняя линия, ВС=6 см, МN=14 см. Вычислите длину отрезка, который
является частью средней линии и лежит между диагоналями трапеции.
а) 10 см; б) 4 см; в) 8 см.
§5. Методика
изучения темы «Многоугольники»
В курсе геометрии VI-VIII
классов систематически изучаются геометрические фигуры на плоскости, причем
большое внимание уделяется многоугольникам, изучению их свойств, рассмотрению
величин, характеризующих плоский многоугольник. В решении задач на
многоугольники находят применение различные методы.
В различных школьных курсах
планиметрии понятие многоугольников трактуется неодинаково.
В одних курсах многоугольник А1,
А2, ..., Аn
трактуется
как фигура, состоящая из отрезков A1A2,
A2A3,
..., An-1An,
АnА1
любые два из которых, имеющие общий конец, не лежат на одной прямой (4), (18).
В этом случае при рассмотрении площади многоугольников (прямоугольника,
параллелограмма, треугольника и др.) под каждым из них понимается
соответствующий плоский многоугольник (конечная часть плоскости, ограниченная
многоугольником).
В других курсах простой
многоугольник (треугольник, четырехугольник и др.) трактуется с самого начала
как часть плоскости, ограниченная простой замкнутой ломаной (3).
.1 Выпуклые
многоугольники
В учебнике «Геометрия 7-11»
Г.П.Бевза (5) «выпуклые многоугольники» рассматриваются в §42 «Многоугольники».
Определение «выпуклого многоугольника» дается в конце параграфа: «Если все углы
многоугольника меньше развернутого, его называют выпуклым». Затем
рассматривается теорема: «Сумма углов выпуклого n-угольника
равна 180 (n-2)».
В учебнике «Геометрия 7-11»
А.В.Погорелова (18) тема «Выпуклые многоугольники» изучается в §13
«Многоугольники» п. 144.
В начале пункта вводится
определение замкнутой: «Ломаная называется замкнутой, если у нее концы
совпадают». Затем дается определение многоугольника: «Простая замкнутая ломаная
называется многоугольником, если ее соседние звенья не лежат на одной
прямой. Вершинами ломаной называются вершинами многоугольника, а звенья
ломаной - сторонами многоугольника. Отрезки, соединяющие не соседние
вершины многоугольника, называются диагоналями».
После чего рассматривается
определение «выпуклого многоугольника»
и доказывается теорема 13.2: Сумма
углов выпуклого п-уголъника равна 180(п-2).
В учебнике «Геометрия 7-9»
Л.С.Атанасяна (4) тема «Выпуклые
многоугольники» рассматривается
в п.40 §1 «Многоугольник» главы 5.
Определение «выпуклого
многоугольника» дается в начале пункта: «Многоугольник называется выпуклым, если
он лежит по одну сторону от каждой прямой, проходящей через две его соседние
вершины». Затем рассматривается свойство: «Сумма углов выпуклого n-угольника
равна (п-2)180.
Рассмотрим методику изучения
темы «Выпуклый многоугольник» на примере учебника геометрии А.В.Погорелова.
При изучении нового материала
учащиеся должны познакомиться с несколькими новыми понятиями, уметь дать каждому
определение, проиллюстрировать на рисунке.
Классу можно задать вопросы
(рисунки к вопросам заготовлены заранее):
. Назовите концы ломаных А1А2А3А4А5
и B1B2B3B4B5,
изображенных на данном рисунке (рис.1).

Рис. 1.
2. Чем отличаются друг от
друга данные ломаные? [Концы ломаной А1А2А3А4А5
не совпадают, а ломаной B1B2B3B4B5
совпадают].
Дается название ломаной B1B2B3B4B5,
- замкнутая ломаная. Составляется определение замкнутой ломаной.
3.
Какие
из известных фигур можно назвать замкнутыми ломаными? [Треугольник,
четырехугольник].
4.
Чем
отличаются замкнутые ломаные, изображенные на рисунке 2, а, б, от
замкнутой ломаной, изображенной на рисунке 2, в? [а) и б) без самопересечения;
в) с самопересечением].
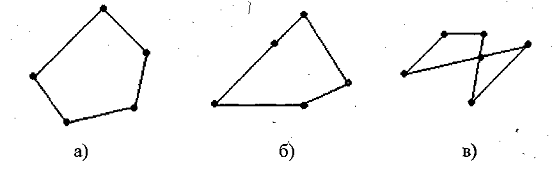
Рис. 2.
5. Чем отличаются друг от
друга замкнутые ломаные, изображенные на рисунках 2, а, б? [а) Никакие
соседние звенья не лежат на одной прямой].
Дается название: замкнутая
ломаная, изображенная на рисунке 2, а, называется многоугольником.
Составляется определение многоугольника. Вводятся понятия: вершина, сторона,
диагональ.
5.
Назовите
на рисунке 3 выпуклые четырехугольники. Какой четырехугольник называется
выпуклым?
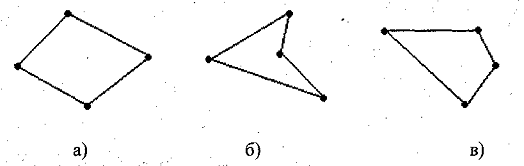
Рис. 3.
7. Составляется определение
выпуклого многоугольника: многоугольник называется выпуклым, если он лежит в
одной полуплоскости относительно любой прямой, содержащей его сторону. Вводится
понятие угла выпуклого многоугольника: углом выпуклого многоугольника при
данной вершине называется угол, образованный его сторонами, сходящимися в этой
вершине.
Затем рассматривается теорема
13.2.
Теорема 13.2: Сумма
углов выпуклого п-уголъникаравна 180(п-2).
Дано:
A1A2...An-выпуклый,
п>3.
Доказать:  A1
+
A1
+  A2
+... +
A2
+... +  An
=180° *(n - 2).
An
=180° *(n - 2).
Доказательство:
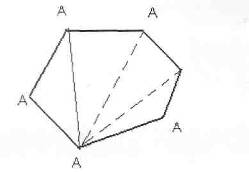
Если n=3, то теорема
справедлива.
1. Пусть А1А2...Аn
- данный выпуклый многоугольник и n>3.
А1А3, A1A4,...,
A1An-1
-
диагонали.
Т.к. многоугольник выпуклый, то
диагонали разбивают его на n-2
треугольника: ∆A1A2A3,
∆A1A3A4,...,
∆A1An-1An.
Сумма углов многоугольника
равна сумме углов треугольников. Сумма углов треугольника =180, число
треугольников = n-2.
=>  A1 +
A1 +  A2 +... +
A2 +... +  An =180° *(n - 2).
An =180° *(n - 2).
Ч.т.д.
.2 Правильные многоугольники
В учебнике «Геометрия 7-11»
А.В.Погорелова (18) тема «Правильные многоугольники» изучается в §13 «Многоугольники»
п. 115.
Определение «правильного
многоугольника» рассматривается в начале пункта: «Выпуклый многоугольник
называется правильным, если у него все стороны равны и все углы равны». Затем
даются определения «вписанного» и «описанного» многоугольника и рассматривается
теорема: «Правильный выпуклый многоугольник является вписанным в окружность и
описанным около окружности».
В учебнике «Геометрия 7-9»
Л.С.Атанасяна (4) тема «Правильные многоугольники» рассматривается в п. 105 §1
«Правильные многоугольники» главы 12.
Определение «правильного
многоугольника» дается в начале пункта:
«Правильным многоугольником
называется выпуклый многоугольник, у которого все углы равны и все стороны
равны». Затем выводят формулу для вычисления угла αn правильного
n-угольника:
ап= *180°.
*180°.
В учебнике «Геометрия 7-9»
И.М.Смирновой, В.А.Смирнова «правильный многоугольник» изучается в п.6 «Ломаные
и многоугольники».
В начале пункта вводятся
определение «ломаной»: «Фигура, образованная отрезками, расположенными так, что
конец первого является началом второго, конец второго - началом третьего и
т.д., называется ломаной линией или просто ломаной».
Затем даются определения
простой, замкнутой и многоугольника: «Ломаная называется простой, если она не
имеет точек самопересечения». «Если начало первого отрезка ломаной совпадает с
концом последнего, то ломаная называется замкнутой». «Фигура, образованная
простой замкнутой ломаной и ограниченной его частью плоскости, называется
многоугольником».
После чего рассматривается
определение «правильного многоугольника»: «Многоугольник называется правильным,
если у него все стороны и все углы равны».
Рассмотрим методику изучения
темы «Правильные многоугольники» на примере учебника геометрии А.В.Погорелова.
В начале пункта вводится
определение «правильного многоугольника»: «Выпуклый многоугольник называется
правильным, если у него все стороны равны и все углы равны», затем вводятся
определения «вписанного» и «описанного» многоугольников: «Многоугольник
называется вписанным в окружность, если все его вершины лежат на некоторой
окружности»; «Многоугольник называется описанным около окружности, если все его
стороны касаются некоторой окружности».
Перед изучением теоремы 13.3 с
целью подготовки класса к доказательству можно задать учащимся вопросы на
повторение:
1.
Какая
прямая называется касательной к окружности?
2.
Каково
может быть взаимное расположение прямой и окружности? В классе проводится
беседа, которая состоит из двух частей: сначала
речь идет об окружности,
описанной около многоугольника, а затем об окружности, вписанной в
многоугольник.
Ответы учащихся сопровождаются
последовательным показом серии рисунков.
Какой треугольник называется
вписанным в окружность или какая окружность называется описанной около
треугольника (рис.1)?

Рис. 1.
Можно ли
около произвольного треугольника описать окружность?
Как найти центр окружности,
описанной около треугольника? (Рис.2) Что является радиусом? (Рис.3)
Всегда ли можно описать
окружность около многоугольника? (Нет. Пример: ромб, если он не квадрат. Рис.4)
Можно ли описать окружность
около правильного многоугольника? (Рис.5)
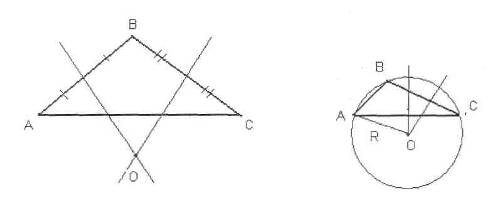
Рис. 2.
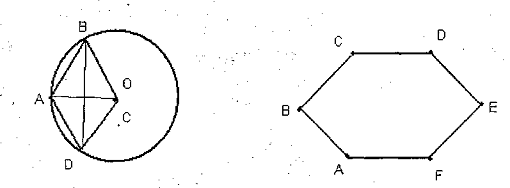
Рис. 3.
Формулируется первая часть
теоремы 13.3. Делается предположение, что около правильного многоугольника
можно описать окружность. Стоит заметить, что этот факт будет доказан позднее.
Аналогичная работа проводится
относительно возможности вписать окружность в многоугольник. Классу те же 5
вопросов относительно окружности, вписанной в многоугольник. При этом по
аналогии с первой частью беседы используется серия рисунков, аналогичных
предыдущим.
Учитель обращает внимание
учащихся на возможность вписать окружность в правильный многоугольник.
Формулируется и доказывается теорема 13.3: «Правильный выпуклый многоугольник
является вписанным в окружность и описанным около окружности».
Доказательство теоремы ведется
по учебнику. Полезно подчеркнуть, что центры вписанной и описанной окружностей
в правильном многоугольнике совпадают и данная точка называется центром
многоугольника.
После доказательства теоремы
предлагаются задачи:
.Сторона правильного вписанного
в окружность треугольника равна а. Найдите сторону квадрата, вписанного
в эту окружность.
Дано: Окружность (0;R),
ΔАВС
- правильный, вписанный,
АВ = a,
КМРЕ - вписанный квадрат.
Найти: KM.
Решение.
ΔАВС - правильный, вписанный: R =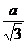 KMPE - вписанный
квадрат в окружность (0;R).
KMPE - вписанный
квадрат в окружность (0;R).
Пусть х =КМ - сторона квадрата,
тогда
R = 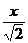
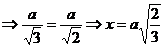 .
.
Ответ: KM =  .
.
2. В окружность, радиус которой
4 дм, вписан правильный треугольник, на стороне которого построен квадрат.
Найдите радиус окружности, описанной около квадрата.
Дано: окружность (0;R),
R=4
дм,
ΔАВС
- правильный, вписанный,
Oкр.1
(O;R1),
ABDE
- вписанный квадрат в Oкр.1
Найти: R1.
Решение.
1.ΔАВС
- правильный, вписанный:
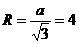 , a=
, a=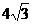 дм.
дм.
1.
ABDE - вписанный
квадрат в Oкр.1 :
R =
=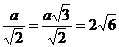 дм.
дм.
Ответ: 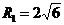 дм.
дм.
3. Сторона
правильного многоугольника равна а, а радиус описанной окружности R.
Найдите радиус вписанной окружности. Дано: Окр.(0;R),
A1A2...An
-
правильный, вписанный,
A1A2=а,
радиус=R,
Окр.(0;г).
Найти: г.
Решение.
ОС - радиус вписанной
окружности.
ΔОСВ
- прямоугольный (ZC
= 90°)

OB=R, СВ=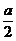 .
.
ОС2 = ОВ2 - ВС2
ОС=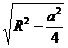 .
.
Ответ: ОС=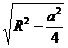 .
.
.Сторона правильного многоугольника равна
а, а радиус вписанной окружности г. Найдите радиус описанной окружности.
Дано: окружность(0;г),
A1A2...An - пpaвильный.,
описанный,
А1А2=а,
радиус=г,
Окружность (0;R).
Найти: R.

Решение. OB
- радиус описанной окружности.
ΔОСВ
- прямоугольный (ZC
= 90°)
ОС=г, СВ=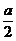
ОВ2=ОС2+СВ2
R2= .
.
Ответ: R = 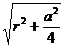 .
.
Затем учащимся можно предложить
систему задач:
. В правильном шестиугольнике
А1А2А3А4А5А6 сторона
равна 8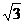 . Отрезок ВС
соединяет середины сторон А3А4 и А5Аб.
Найдите длину отрезка, соединяющего середину стороны А1А2
с серединой отрезка ВС.
. Отрезок ВС
соединяет середины сторон А3А4 и А5Аб.
Найдите длину отрезка, соединяющего середину стороны А1А2
с серединой отрезка ВС.
. Сторона правильного
шестиугольника ABCDEF равна 32 . Найдите
радиус окружности, вписанной в треугольник МРК, если М, Р и К -середины сторон
АВ, CD. EF
соответственно.
. Найдите
радиус окружности, вписанной в треугольник МРК, если М, Р и К -середины сторон
АВ, CD. EF
соответственно.
3.
Выразите
сторону b правильного
описанного многоугольника через радиус R
окружности и сторону а правильного вписанного многоугольника с тем же числом
сторон.
4.
Периметры
двух правильных n-угольников
относятся как а:b. Как
относятся радиусы их вписанных и описанных окружностей?
5.
Сколько
сторон имеет правильный многоугольник, каждый из внутренних углов которого
равен: 1) 135; 2) 150?
§6. Организация обобщающего
повторения темы «Многоугольники» в курсе геометрии 9 класса
При обобщающем повторении темы
«Многоугольники» происходит сопоставление понятий треугольник, параллелограмм,
прямоугольник, ромб, квадрат, трапеция, выясняются связи между ними. Эти
понятия включаются в новые отношения, учащиеся устанавливают иерархию понятий.
Результатом обобщения может служить схема.
Методы работы с таблицами и
схемами различны: учитель проводит беседу, выразив ее результаты в виде схемы;
знакомит учащихся с планом беседы, а затем по этому плану проводит ее; знакомит
учащихся со схемой, по которой они самостоятельно проводят обобщение,
предлагает учащимся самостоятельно обобщить материал и выразить результаты в
виде схемы.
Рассмотрев эту схему с
учащимися, учитель предлагает серию вопросов:
1.Как определить ромб через
четырехугольник, квадрат через четырехугольник, квадрат через ромб?
. Можно ли определить ромб
через прямоугольник?
. Что является пересечением
множества всех прямоугольников и множества всех ромбов?
Методика организации работы
учащихся по данной теме может быть и другой. Например, учитель может лишь
определить цель работы и указать основные вопросы, на которые учащиеся должны
найти ответы; определить не только цель работы и перечень вопросов, но и
раскрыть этапы и методику работы над этими вопросами.
При обобщающем повторении на
уровне теорий дается определенная трактовка изученным понятиям с позиции тех
или иных фундаментальных теорий, входящих в содержание математических курсов,
при этом строится единая, общая форма многообразия частных фактов, явлений
понятий. Значительное внимание уделяется происхождению понятий. Школьники
устанавливают общие закономерности, причинно-следственные отношения, обобщают и
конкретизируют материал, применяют общие положения к конкретным фактам.
Материал, выносимый на обобщающее повторение на уровне теорий, должен
представлять собой логическую систему, вопросы которой объединены той или иной
фундаментальной теорией.
Обобщающее повторение на уровне
теорий освещает полученные знания не только в плане внутрипредметных, но и
межпредметных связей, так как многие понятия различных учебных предметов
получают единую трактовку с позиций одной какой-либо теории.
Методика организации урока
повторения по данной теме представлена к конспекте урока.
Урок обобщения и систематизации
знаний по теме "Многоугольники"
Место урока в учебном плане: итоговое повторение
по геометрии.
Тип урока: урок обобщения и систематизации
знаний.
Цели урока: повторение изученного материала по
теме "Многоугольники", подготовка к курсу стереометрии по теме
"Многогранники", отработка навыков применения формул для нахождения
площадей.
Задачи урока:
Образовательные: закрепление определений по
данной теме, формирование умений и навыков нахождения площадей.
Развивающие: развитие логического мышления,
памяти, внимания, познавательного интереса.
Воспитательные: воспитание активности,
настойчивости в достижении цели; привитие учащимся навыков самостоятельной работы.
Форма работы на уроке: индивидуальная,
групповая, коллективная, устная, письменная.
Оборудование урока: карточки с заданиями.
План урока
. Сообщение темы и постановка целей урока. - 1
мин.
. Актуализация знаний учащихся. - 5 мин.
. Практическая работа. - 15-20 мин.
. Рекламная пауза. - 5 мин.
. Закрепление знаний. Конкурс "Самый
находчивый". 10 мин.
. Подведение итогов урока. - 3 мин.
. Домашнее задание - 1 мин.
Ход урока
. Сообщение темы и постановка целей урока.
Учитель: Здравствуйте, ребята! Сегодня на уроке мы вспомним определения
многоугольников, их свойства, признаки, будем совершенствовать навыки
распознавания на чертежах многоугольников, их элементов, совершенствовать
навыки в измерениях необходимых элементов для нахождения площадей многоугольников;
учиться отстаивать свою точку зрения в конкурсе "Самый находчивый".
. Актуализация знаний учащихся. Проводится
фронтальная устная работа (учитель отмечает "+" за правильный ответ).
Вопросы.
) Какая фигура называется многоугольником и
n-угольником, их виды?
) Что такое вершины, стороны, диагонали и
периметр многоугольника?
) Является ли треугольник примером
многоугольника?
) Назовите виды треугольников, перечислите их
признаки?
) Дайте определения четырехугольников: ромба,
прямоугольника, квадрата, параллелограмма в такой последовательности, чтобы
одно определение следовало из другого?
) Перечислите три признака параллелограмма,
признак прямоугольника, назовите особое свойство ромба?
) Почему квадрат обладает всеми свойствами
прямоугольника и ромба?
) Сформулируйте основные свойства квадрата?
) Назовите значения синуса, косинуса и тангенса
для углов 30°, 45°, 60°?
) Сформулируйте теоремы, следствия, формулы для
нахождения площадей многогранников (всего 10)?
. Практическая работа. Учитель раздает бланки с
построенными в нем многоугольниками (квадрат, прямоугольник, прямоугольный
треугольник, равносторонний треугольник, тупоугольный треугольник,
равнобедренный треугольник, параллелограмм, ромб, трапеция, прямоугольная
трапеция).
Задание. Пронумеруйте каждый многогранник.
Запишите его название, измерьте необходимые данные для нахождения площади,
подставьте в формулу, вычислите.
Замечания: каждую формулу для нахождения площади
применять один раз.
Ответы: квадрат стороны; произведение смежных
сторон; половина произведения катетов; половина произведения стороны в квадрате
на синус 60°; половина произведения большей стороны на высоту, опущенную из
тупого угла или формула Герона; произведение его основания на высоту; половина
произведения диагоналей; произведение средней линии трапеции на высоту;
произведение полусуммы её оснований на высоту, содержащую боковую сторону.
Дополнительная задача: Найдите площадь
равнобедренной трапеции с диагональю 20 мм., высотой 16мм., и ответ выразите в
квадратных сантиметрах.
(Краткое решение: подкоренное выражение (202 -
162 )умножить на высоту 16, т.е. 2*6*16 равно 192 мм2. Ответ: 1,92 см2).
. Рекламная пауза. Каждый ученик по очереди
выходит к доске, схематически чертит один из изученных углов, одновременно
рассказывая определение и свойства (острый, тупой, развернутый, внешний,
вертикальные, смежные, внутренние накрест лежащие, внутренние односторонние,
соответственные). И угол в 30°,45°,60° с помощью треугольника и линейки
(прямоугольный треугольник с катетом в два раза меньшим гипотенузы,
прямоугольный равнобедренный треугольник).
. Закрепление знаний. Конкурс "Самый
находчивый". Каждый правильный ответ - 1 балл, если утверждение доказано -
2 балла, если четко сформулировано - 3 балла.
Задание 1. Какое слово из перечисленных (квадрат,
параллелограмм, прямоугольник, ромб) является обобщающим для всех остальных и
почему? (параллелограмм, т.к. остальные фигуры являются параллелограммами по
определению).
Задание 2. Можно ли описать окружность около
любого четырехугольника, если сумма его противоположных углов равна 180° и
почему? (можно, потому что вписанные углы опираются на дуги, сумма которых
равна 360°).
Задание 3. При каком условии можно вписать в
окружность выпуклый четырехугольник и почему? (если суммы противоположных
сторон равны; доказывается с помощью равных отрезков касательных, проведенных
из одной вершины).
Задание 4. Как относятся площади треугольников,
если угол одного треугольника равен углу другого треугольника и какая теорема
доказывается с помощью этого отношения? (как произведение сторон, заключающие
равные углы. Теорема: отношение площадей двух подобных треугольников равно
квадрату коэффициента подобия).
Задание 5. Назовите формулу для вычисления суммы
углов выпуклого n-угольника, и выведите её? ((n-2)*180°. Любой n-угольник
содержит n-2 треугольника, сумма углов, которых равна сумме углов n-угольника).
. Подведение итогов урока. Какие затруднения
возникли при выполнении практической работы? По наличию "+" и
количеству баллов выставляется первая оценка по результатам фронтальной устной
работы и конкурса "Самый находчивый", а на следующем уроке
выставляется вторая оценка по результатам практической работы.
. Домашнее задание. В ходе урока каждый из вас
выявил пробелы в своих знаниях, дома необходимо каждому индивидуально
поработать над устранением этих пробелов. Повторить пункт 108 (Формулы для
вычисления площади правильного многоугольника, его стороны и радиуса вписанной
окружности).
§7. Задачи по теме «Многоугольники»
в материалах ЕГЭ по математике
Задачи по теме «Многоугольники»
традиционно встречаются на выпускных экзаменах и в 9 классах и в 11 классах.
С 2008 года математика включена
в список предметов, по которым государственная итоговая аттестация по курсу
основной школы стала проводиться в новой форме.
Особенности содержания и
структуры экзаменационной работы определяется целью проведения экзамена -
оценить образовательную подготовку выпускников 9-х классов по курсу геометрии с
целью их итоговой аттестации.
Приведем примеры тестов по
геометрии.
Все задания в тесте
распределены по уровню сложности и видам деятельности.
Вариант 1. ЧАСТЬ 1
1.В ромбе ABCD проведена
диагональ BD. Найдите  АВС если
известно, что
АВС если
известно, что  ABD = 20°.
ABD = 20°.
1)20 2)70 3)40
4)140
4. Четырехугольник ABCD
- трапеция. Используя данные, указанные на рисунке, найдите длину отрезка AD.
1)15 2)16 3)17
4)22
8. Найдите сторону ВС
треугольника BCD, если
известно, что CD= = , AB = 30°, a
, AB = 30°, a  D = 45° .
D = 45° .
Ответ:
ЧАСТЬ 2
. В прямоугольнике ABCD
проведены биссектрисы углов А и D,
которые пересекаются в точке на стороне ВС. Найдите периметр прямоугольника ABCD,
если АВ =8.
Ответ:
.В квадрате ABCD
точка К - середина стороны ВС, точка М - середина стороны АВ. Докажите, что
прямые АК и MD взаимно
перпендикулярны, а треугольники АЕМ (Е - точка пересечения прямых АК и MD)
и АВК подобны.
ЧАСТЬ 3
14.
В
равнобедренный треугольник ABC
с основанием ВС вписана окружность. Она касается стороны АВ в точке М. Найдите
радиус окружности, если АМ=12 и ВМ=18.
Высоты треугольника ABC
пересекаются в точке Н, а медианы - в точке М. Точка К - середина отрезка МН.
Найдите площадь треугольника АКС, если известно, что AB=18 , СН=12
, СН=12 ,
,  BAC = 45°.
BAC = 45°.
Вариант 2
ЧАСТЬ 1
1. Диагональ трапеции
образует с меньшим основанием угол, равный 42. Найдите величину угла, который
эта диагональ образует с большим основанием.
1)21 2)58 3)42 4)138
2. Используя данные,
указанные на рисунке, найдите площадь
параллелограмма.
) 21м2
2)
42
м2
3)
34
м2
4)
68
м2
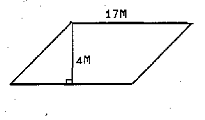
Используя данные, указанные на
рисунке, найдите периметр четырехугольника ABCD, если
известно, что  АВС =
АВС = CBD.
CBD.
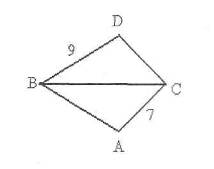
Ответ:.
Часть 2
10. Найдите площадь равнобедренной
трапеции, если ее диагональ равна 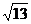 , а высота равна 2.
, а высота равна 2.
Ответ:
13. В ромбе ABCD
из вершины тупого угла В к стороне AD
проведена высоты ВК и к стороне CD
- высота ВР. Докажите равенство треугольников АВК и СВР, и равенство углов КВР
и BAD.
ЧАСТЬ 3
15. В треугольнике ABC проведены
высоты AN и ВМ и
отмечена точка К - середина стороны АВ. Найдите АВ, если известно, что  ACB = 105°, а
площадь треугольника MNK равна 4.
ACB = 105°, а
площадь треугольника MNK равна 4.
Кроме этого в содержании контрольных
измерительных материалов по математике к итоговой аттестации выпускников входят
задачи по планиметрии (в любом тесте это задачи В11). Приведем примеры таких
задач:
2007г.
В11. Дан ромб ABCD с острым
углом В. Площадь ромба равна 320, а синус угла В равен 0,8. Высота СН
пересекает диагональ BD в точке К. Найдите длину
отрезка СК.
В11. В ромбе ABCD синус
острого угла С равен 0,6. Площадь ромба равна 135. Высота ВК пересекает
диагональ АС в точке Р. Найдите длину отрезка РК.
В11. В равнобедренном треугольнике ABC с
основанием АС высоты ВМ и АН пересекаются в точке К, причем АК равно 5, КН
равно 3. Найдите площадь треугольника ABC.
2008г.
В11. В параллелограмме ABCD биссектриса
угла В пересекает сторону CD в точке Т и прямую AD в точке М.
Найдите периметр треугольника АВМ, если ВС равно 15, ВТ равно 18, ТМ равно 12.
В11. В равнобедренном треугольнике ABC с основанием
АС высоты BE и СН
пересекаются в точке К, причем ВН=6, КН=3. Найдите площадь треугольника СВК.
В11. Сторона правильного
шестиугольника ABCDEF равна. Найдите радиус окружности,
вписанной в треугольник МРК, если М, Р и К -середины сторон АВ, CD, EF
соответственно.
2009г.
В11. В правильном шестиугольнике A1A2A3A4A5A6 сторона
равна . Отрезок ВС соединяет середины сторон А3А4 и А5А6.
Найдите длину отрезка, соединяющего середину стороны А1А2
с серединой отрезка ВС.
В11. Найдите периметр
параллелограмма ABCD, если AD=10, BD=8, a
отрезок, соединяющий вершину В с
серединой стороны AD, равен VI5 .
В11. Из вершины С параллелограмма ABCD проведен
луч, который пересекает сторону AD в точке Т и диагональ BD в точке Р.
Площадь треугольника CDP равна 10, а площадь
треугольника DPT равна 8.
Найдите площадь параллелограмма.
2010 г.
В4. В треугольнике ABC проведены
биссектрисы AK и BM (рис. 1). Известно, что угол ABM равен 15°, а угол KAM
равен 18°. Найти внешний угол BCD при вершине C.
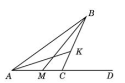
Рис. 1.
С4. Дан параллелограмм ABCD, AB = 2,
BC = 5,  A = 600.
Окружность с центром в точке О касается биссектрисы угла D и двух сторон
параллелограмма, исходящих из вершины одного его острого угла. Найдите площадь
четырёхугольника ABOD.
A = 600.
Окружность с центром в точке О касается биссектрисы угла D и двух сторон
параллелограмма, исходящих из вершины одного его острого угла. Найдите площадь
четырёхугольника ABOD.
В4. В треугольнике ABC проведены
биссектрисы AK и BM (рис. 1). Известно, что угол ABM равен 13° , а угол KAM
равен 19°. Найти внешний угол BCD при вершине C.
С4. Дан параллелограмм ABCD, ABCD,
AB = 3, BC = 7,  A = 600.
Окружность с центром в точке О касается биссектрисы угла D и двух сторон
параллелограмма, исходящих из вершины одного его острого угла. Найдите площадь
четырёхугольника ABOD.
A = 600.
Окружность с центром в точке О касается биссектрисы угла D и двух сторон
параллелограмма, исходящих из вершины одного его острого угла. Найдите площадь
четырёхугольника ABOD.
B4. В
треугольнике АВС АС=ВС, АD- высота, угол BAD равен 280.
Найдите угол C. Ответ
дайте в градусах.
B4. В
треугольнике АВС АС=ВС, угол C равен 620. Найдите
внешний угол CBD. Ответ
дайте в градусах.

B4. В треугольнике
ABC угол C равен 58◦, AD и BE - биссектрисы, пересекающиеся в точке O.
Найдите угол AOB. Ответ дайте в градусах
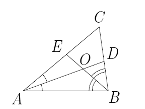
Литература
1. Автономова
Т.В., Аргунов Б.И. Основы понятия и методы школьного курса геометрии. - М.:
Просвещение, 1988.Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия для 7-9
классов: Учебное пособие для учащихся школ и классов с углубленным изучением
математики.- М.: Просвещение, 2002.
2. Александров
А.Д., Вернер А.Л., Рыжик В.И. Геометрия: 7-9 кл. - М.: Просвещение, 2002.
. Аргунов
Б.И. и Балк М.Б. Элементарная геометрия. - М.: Просвещение, 1966.
. Атанасян
Л.С. и др. Геометрия: Учеб. Для общеобразоват. учреждений: базовый профил.
уровни 7-9 кл. - М.: Просвещение, 2002.
. Бевз Г.П.,
Бевз В.Г., Владимирова Н.Г. Геометрия: Учеб. для 7-11 классов сред, школы. -
М.: Просвещение, 1992.
. Болтянский
В.Г. Элементарная геометрия. - М.: Просвещение, 1985.
. Геометрия
в 6 классе: пособие для учителя Н.Б. Мельникова. И.Л. Никольевская, Л.Ю.
Чернышева. - М.: Просвещение, 1982.- 160 с.
. Геометрия
в 7-9 классах (Методические рекомендации к преподаванию курса геометрии и по
учебному пособию А.В. Погорелова) Л.Ю. Березина,Н.Б. Мельникова и др. М.:
Просвещение, 2000.
. Гусев В.А.
Практикум по решению математических задач и геометрии - М.: Просвещение, 1985.
. Карнацевич
Л.С., Грушин А.И. Изучение геометрии в 7 кл.: Из опыта работы. - М.:
Просвещение, 2000.
. Киселев
А.П. Геометрия, ч.1 и 4.2-М.: Учпедгиз, 1957. Лабораторные и практические работы
по методике преподавания математики: Учебное пособие для студентов физ-мат.
спец. пед.институтов (Е.И. Лященко, К.В. Зобкова и др.; Под редакцией Е.И.
. Лященко.-
М.: Просвещение, 1988. Методика преподавания математики в средней школе: Общая
методика. Учебное пособие для студентов пед. институтов/ Л.Я. Блох, Е.С. Канин,
Н.Г. Килина и др.; Сост. Р.С. Черкасов, Л.А. Столяр.- М.: Просвещение, 1985.
. Методика
преподавания математики в средней школе: Частная методики: Учебное пособие для
студентов пед. институтов/ А.Я. Блох, В.А. Гусев, Г.В. Дорофеев и др., Сост.
В.И. Мишин.- М.: Просвещение, 1987.
. Методика
преподавания математики в средней школе: Общая методика: Учебное пособие для
физ-мат. факультета пед. институтов/ Ю.М. Колягин, В.А. Оганесян, В.Я. Санинский,
Г.Л. Луканкин.-М.: Просвещение, 1980.
. Методика
преподавания математике в средней школе: Частные методики: Учебное пособие для
физ-мат фак. институтов/ Ю.М. Колягин, Г.Л. Луканкин, Е.Л. Мокрушин и др.- М.:
Просвещение, 1977.
. Методические
рекомендации к курсу геометрии 6-8 классов: Пособие для учителя/ Л.С. Киселева,
И.И. Бутузова_ М.: Просвещение, 1987.
. Монахова
Н.А. Из опыта обучения геометрии в старших классах.- М.: Просвещение, 1979.
. Погорелов
А.В. Геометрия: Учебное пособие для 7-11 классов. - М.: Просвещение, 2002.
. Преподавание
геометрии в 6-8 кл. Сб. статей/ Сост. В.А. Гусев. - М.: Просвещение, 1979.
. Тесленко
И.Ф. О преподавании геометрии в средней школе. Книга для учителя - М.:
Просвещение, 1985.
. Саранцев
Г.И. Упражнения в обучении математике. - М.: Просвещение, 1995.-240с.
. Семенович
А.Ф., Черкасов Р.С. Геометрия: Учебное пособие для ~-: кл. средней
школы. - М: Просвещение, 1985.
. Смирнова
И.М., Смирнов В.А. Геометрия. Учеб. для 7-9 кл. общеобразоват. учреждений. -
М.: Просвещение, 2001.