Исследование трехслойных ИНС
Контрольная работа
Исследование трехслойных
ИНС
Брест 2007
Введение
Целью контрольной работы является исследование обучения,
работы и прогнозирования многослойных ИНС, в данном случае 3-слойной.
Для изучения ИНС нам необходимо разработать программу,
моделирующую процессы обучения, работы и прогнозирования ИНС. За основу возьмем
программу, написанную в процессе выполнения лабораторной работы №2, с
доработками. В результате получили программу с интерфейсом, представленным
ниже:

Рисунок 1 - Интерфейс программы
Величину среднеквадратической ошибки примем равной 0,05.
Функции активации слоев для простоты работы с ними примем сигмоидные.
В процессе исследования ИНС мы выполним:
· поиск наиболее оптимальных ALFA для каждого слоя при
постоянном шаге обучения и непосредственно само обучение;
· прогнозирование на базе результатов
обучения с постоянным шагом обучения;
· обучение ИНС с помощь адаптивного шага
обучения;
· прогнозирование на базе результатов
обучения с адаптивным шагом обучения.
Также мы произведем изменение количества входов и проверим
реакцию ИНС данные действия.
1.
Обучение ИНС с использованием постоянного шага обучения
Обучение будем производить путем поэтапного изменения
величины ALFA для каждого слоя с шагом 0,05. Наиболее оптимальными будут те ALFA, при которых количество
шагов обучения (по 30 итераций) будет минимальным.
В следствии того, что нам необходимо менять ALFA для каждого слоя в
отдельности, построение графиков зависимости количества шагов обучения от ALFA становится
затруднительным. Приведем результат поиска оптимальных ALFA:
ALFA_1 = 0.45 - ALFA для первого слоя
ALFA_2 = 0.50 - ALFA для второго слоя
ALFA_3 = 0.45 - ALFA для третьего слоя
N = 3 - Кол-во шагов обучения
При данных ALFA произведем обучение ИНС:
|
№ шага
|
Yрасч.
|
Yэтал
|
E
|
|
1
|
0.202811
|
0.201410
|
0.001402
|
|
2
|
0.201563
|
0.201541
|
0.000022
|
|
3
|
0.201611
|
0.201670
|
-0.000059
|
|
4
|
0.201734
|
0.201797
|
-0.000063
|
|
5
|
0.201861
|
0.201923
|
-0.000062
|
|
6
|
0.201985
|
0.202047
|
-0.000061
|
|
7
|
0.202108
|
0.202169
|
-0.000060
|
|
8
|
0.202230
|
0.202289
|
-0.000059
|
|
9
|
0.202349
|
0.202407
|
-0.000058
|
|
10
|
0.202466
|
0.202524
|
-0.000057
|
|
11
|
0.202582
|
0.202638
|
-0.000056
|
|
12
|
0.202696
|
0.202751
|
-0.000055
|
|
13
|
0.202808
|
0.202862
|
-0.000054
|
|
14
|
0.202918
|
0.202971
|
-0.000053
|
|
15
|
0.203026
|
0.203079
|
-0.000052
|
|
16
|
0.203133
|
0.203184
|
-0.000051
|
|
17
|
0.203237
|
0.203288
|
-0.000051
|
|
18
|
0.203340
|
0.203390
|
-0.000050
|
|
19
|
0.203441
|
0.203490
|
-0.000049
|
|
20
|
0.203541
|
0.203588
|
-0.000048
|
|
21
|
0.203638
|
0.203684
|
-0.000047
|
|
22
|
0.203733
|
0.203779
|
-0.000046
|
|
23
|
0.203827
|
0.203872
|
-0.000045
|
|
24
|
0.203919
|
0.203963
|
-0.000044
|
|
25
|
0.204009
|
0.204052
|
-0.000043
|
|
26
|
0.204097
|
0.204139
|
-0.000042
|
|
27
|
0.204184
|
0.204224
|
-0.000041
|
|
28
|
0.204268
|
0.204308
|
-0.000040
|
|
29
|
0.204351
|
0.204389
|
-0.000039
|
|
30
|
0.204432
|
0.204469
|
-0.000038
|
E = 0.00000011859
Далее проведем прогнозирование на основании полученных
результатов обучения:
|
№ шага
|
Yрасч.
|
Yэтал
|
E
|
|
1
|
0.204511
|
0.204547
|
-0.000037
|
|
2
|
0.204553
|
0.204624
|
-0.000070
|
|
3
|
0.204595
|
0.204698
|
-0.000103
|
|
4
|
0.204635
|
0.204770
|
-0.000135
|
|
5
|
0.204675
|
0.204841
|
-0.000166
|
|
6
|
0.204714
|
0.204910
|
-0.000196
|
|
7
|
0.204752
|
0.204977
|
-0.000225
|
|
8
|
0.204789
|
0.205042
|
-0.000253
|
|
9
|
0.204825
|
0.205105
|
-0.000280
|
|
10
|
0.204860
|
0.205167
|
-0.000307
|
|
11
|
0.204894
|
0.205226
|
-0.000332
|
|
12
|
0.204927
|
0.205284
|
-0.000356
|
|
13
|
0.204960
|
0.205340
|
-0.000380
|
|
14
|
0.204991
|
0.205394
|
-0.000402
|
|
15
|
0.205022
|
0.205446
|
-0.000424
|
E=0.00000026073
Приведем график зависимости величины ошибки от шага обучения:
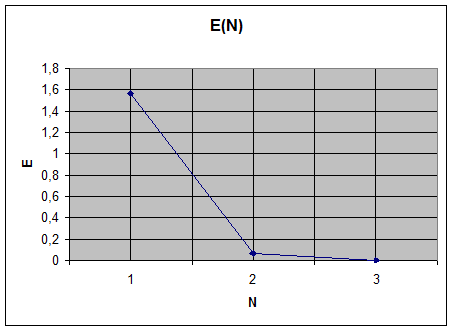
График зависимости ошибки от шага
2.
Обучение ИНС с использованием адаптивного шага обучения
Для достижения заданной точности оказалось достаточно 2 шага
обучения (по 30 итераций). При этом на последнем шаге были получены следующие
значения ALFA:
ALFA_1 = 0.57891 - ALFA для первого слоя
ALFA_2 = 0.02568 - ALFA для второго слоя
ALFA_3 = 0.40045 - ALFA для третьего слоя
Результат последнего шага обучения приведен ниже:
|
№ шага
|
Yрасч.
|
Yэтал
|
E
|
|
1
|
0.124568
|
0.205843
|
-0.081275
|
|
2
|
0.205849
|
0.205411
|
0.000439
|
|
3
|
0.205413
|
0.204793
|
0.000620
|
|
4
|
0.204794
|
0.203991
|
0.000803
|
|
5
|
0.203991
|
0.203006
|
0.000986
|
|
6
|
0.203005
|
0.201838
|
0.001167
|
|
7
|
0.201836
|
0.200488
|
0.001348
|
|
8
|
0.200485
|
0.198958
|
0.001527
|
|
9
|
0.198953
|
0.197249
|
0.001705
|
|
10
|
0.197243
|
0.195362
|
0.001881
|
|
11
|
0.195355
|
0.193299
|
0.002056
|
|
12
|
0.193291
|
0.191063
|
0.002228
|
|
13
|
0.191053
|
0.188654
|
0.002399
|
|
14
|
0.188643
|
0.186076
|
0.002567
|
|
15
|
0.186063
|
0.183330
|
0.002733
|
|
16
|
0.183316
|
0.180420
|
0.002896
|
|
17
|
0.180404
|
0.177347
|
0.003057
|
|
18
|
0.177329
|
0.174114
|
0.003215
|
|
19
|
0.174094
|
0.170725
|
0.003370
|
|
20
|
0.170703
|
0.167182
|
0.003521
|
|
21
|
0.167158
|
0.163488
|
0.003669
|
|
22
|
0.163462
|
0.159648
|
0.003814
|
|
23
|
0.159619
|
0.155664
|
0.003955
|
|
24
|
0.155632
|
0.151539
|
0.004093
|
|
25
|
0.151504
|
0.147279
|
0.004226
|
|
26
|
0.147241
|
0.142885
|
0.004355
|
|
27
|
0.142844
|
0.138364
|
0.004480
|
|
28
|
0.138318
|
0.133717
|
0.004601
|
|
29
|
0.133667
|
0.128951
|
0.004717
|
|
30
|
0.128896
|
0.124068
|
0.004828
|
E=0.00023145
Далее проведем прогнозирование на основании полученных
результатов обучения:
|
№ шага
|
Yрасч.
|
Yэтал
|
|
1
|
0.124008
|
0.119074
|
0.004935
|
|
2
|
0.123943
|
0.113972
|
0.009971
|
|
3
|
0.123871
|
0.108768
|
0.015103
|
|
4
|
0.123792
|
0.103466
|
0.020326
|
|
5
|
0.123706
|
0.098071
|
0.025635
|
|
6
|
0.123610
|
0.092588
|
0.031022
|
|
7
|
0.123505
|
0.087021
|
0.036484
|
|
8
|
0.123389
|
0.081376
|
0.042013
|
|
9
|
0.123261
|
0.075658
|
0.047604
|
|
10
|
0.123121
|
0.069871
|
0.053249
|
|
11
|
0.122966
|
0.064022
|
0.058944
|
|
12
|
0.122795
|
0.058115
|
0.064680
|
|
13
|
0.122607
|
0.052156
|
0.070451
|
|
14
|
0.122400
|
0.046150
|
0.076250
|
|
15
|
0.122172
|
0.040103
|
0.082069
|
E=0.0189632
Приведем график зависимости величины ошибки от шага обучения:

График зависимости ошибки от шага
3.
Исследование поведения системы в зависимости от количества входов при
постоянном шаге обучения
программа обучение прогнозирование трехслойный
Проведем исследование поведения системы 6±4 входа. Будем
проводить обучение для 2, 6 и 10 входовых ИНС, прогнозирование. По результатам
исследования построим графики зависимости ошибки от количества входов.
. Количество входов равно 6 - см. раздел 1.
. Количество входов равно 2.
Процесс обучения:
|
№ шага
|
Yрасч.
|
Yэтал
|
E
|
|
1
|
0.203088
|
0.200868
|
0.002221
|
|
2
|
0.201210
|
0.201006
|
0.000204
|
|
3
|
0.201076
|
0.201142
|
-0.000066
|
|
4
|
0.201176
|
0.201277
|
-0.000101
|
|
5
|
0.201305
|
0.201410
|
-0.000105
|
|
6
|
0.201437
|
0.201541
|
-0.000104
|
|
7
|
0.201568
|
0.201670
|
-0.000102
|
|
8
|
0.201697
|
0.201797
|
-0.000101
|
|
9
|
0.201824
|
0.201923
|
-0.000099
|
|
10
|
0.201949
|
0.202047
|
-0.000098
|
|
11
|
0.202072
|
0.202169
|
-0.000096
|
|
12
|
0.202194
|
0.202289
|
-0.000095
|
|
13
|
0.202314
|
0.202407
|
-0.000093
|
|
14
|
0.202432
|
0.202524
|
-0.000092
|
|
15
|
0.202548
|
0.202638
|
-0.000091
|
|
16
|
0.202662
|
0.202751
|
-0.000089
|
|
17
|
0.202775
|
0.202862
|
-0.000088
|
|
18
|
0.202885
|
0.202971
|
-0.000086
|
|
19
|
0.202994
|
0.203079
|
-0.000085
|
|
20
|
0.203101
|
0.203184
|
-0.000083
|
|
21
|
0.203206
|
0.203288
|
-0.000082
|
|
22
|
0.203310
|
0.203390
|
-0.000080
|
|
23
|
0.203411
|
0.203490
|
-0.000079
|
|
24
|
0.203511
|
0.203588
|
-0.000077
|
|
25
|
0.203609
|
0.203684
|
-0.000076
|
|
26
|
0.203705
|
0.203779
|
-0.000074
|
|
27
|
0.203799
|
0.203872
|
-0.000073
|
|
28
|
0.203891
|
0.203963
|
-0.000071
|
|
29
|
0.203982
|
0.204052
|
-0.000070
|
|
30
|
0.204071
|
0.204139
|
-0.000068
|
E=0,0000762556
Прогнозирование на основании полученных результатов обучения:
|
№ шага
|
Yрасч.
|
Yэтал
|
E
|
|
1
|
0.204157
|
0.204224
|
-0.000067
|
|
2
|
0.204185
|
0.204308
|
-0.000123
|
|
3
|
0.204211
|
0.204389
|
-0.000178
|
|
4
|
0.204237
|
0.204469
|
-0.000232
|
|
5
|
0.204262
|
0.204547
|
-0.000285
|
|
6
|
0.204287
|
0.204624
|
-0.000336
|
|
7
|
0.204312
|
0.204698
|
-0.000386
|
|
8
|
0.204335
|
0.204770
|
-0.000435
|
|
9
|
0.204358
|
0.204841
|
-0.000482
|
|
10
|
0.204381
|
0.204910
|
-0.000529
|
|
11
|
0.204403
|
0.204977
|
-0.000574
|
|
12
|
0.204425
|
0.205042
|
-0.000617
|
|
13
|
0.204446
|
0.205105
|
-0.000659
|
|
14
|
0.204466
|
0.205167
|
-0.000700
|
|
15
|
0.204486
|
0.205226
|
-0.000740
|
E=0.00000166694
3. Количество входов равно 10.
Процесс обучения:
|
№ шага
|
Yрасч.
|
Yэтал
|
E
|
|
1
|
0.203332
|
0.200442
|
0.002891
|
|
2
|
0.200981
|
0.200586
|
0.000396
|
|
3
|
0.200678
|
0.200727
|
-0.000050
|
|
4
|
0.200740
|
0.200868
|
-0.000128
|
|
5
|
0.200866
|
0.201006
|
-0.000140
|
|
6
|
0.201001
|
0.201142
|
-0.000141
|
|
7
|
0.201137
|
0.201277
|
-0.000139
|
|
8
|
0.201272
|
0.201410
|
-0.000138
|
|
9
|
0.201405
|
0.201541
|
-0.000136
|
|
10
|
0.201536
|
0.201670
|
-0.000134
|
|
11
|
0.201665
|
0.201797
|
-0.000132
|
|
12
|
0.201793
|
0.201923
|
-0.000130
|
|
13
|
0.201919
|
0.202047
|
-0.000128
|
|
14
|
0.202042
|
0.202169
|
-0.000126
|
|
15
|
0.202164
|
0.202289
|
-0.000124
|
|
16
|
0.202285
|
0.202407
|
-0.000123
|
|
17
|
0.202403
|
0.202524
|
-0.000121
|
|
18
|
0.202520
|
0.202638
|
-0.000119
|
|
19
|
0.202634
|
0.202751
|
-0.000117
|
|
20
|
0.202747
|
0.202862
|
-0.000115
|
|
21
|
0.202858
|
0.202971
|
-0.000113
|
0.202968
|
0.203079
|
-0.000111
|
|
23
|
0.203075
|
0.203184
|
-0.000109
|
|
24
|
0.203181
|
0.203288
|
-0.000107
|
|
25
|
0.203284
|
0.203390
|
-0.000105
|
|
26
|
0.203386
|
0.203490
|
-0.000104
|
|
27
|
0.203486
|
0.203588
|
-0.000102
|
|
28
|
0.203585
|
0.203684
|
-0.000100
|
|
29
|
0.203681
|
0.203779
|
-0.000098
|
|
30
|
0.203776
|
0.203872
|
-0.000096
|
E=0, 000004
Прогнозирование на основании полученных результатов обучения:
|
№ шага
|
Yрасч.
|
Yэтал
|
E
|
|
1
|
0.203869
|
0.203963
|
-0.000094
|
|
2
|
0.203882
|
0.204052
|
-0.000169
|
|
3
|
0.203896
|
0.204139
|
-0.000243
|
|
4
|
0.203909
|
0.204224
|
-0.000315
|
|
5
|
0.203922
|
0.204308
|
-0.000386
|
|
6
|
0.203934
|
0.204389
|
-0.000455
|
|
7
|
0.203947
|
0.204469
|
-0.000523
|
|
8
|
0.203959
|
0.204547
|
-0.000589
|
|
9
|
0.203971
|
0.204624
|
-0.000653
|
|
10
|
0.203982
|
0.204698
|
-0.000716
|
|
11
|
0.203993
|
0.204770
|
-0.000777
|
|
12
|
0.204004
|
0.204841
|
-0.000837
|
|
13
|
0.204015
|
0.204910
|
-0.000895
|
|
14
|
0.204025
|
0.204977
|
-0.000951
|
|
15
|
0.204036
|
0.205042
|
-0.001006
|
E=0.00000306659
Получили зависимость среднеквадратической ошибки при
прогнозировании от количества входов сети. Построим график зависимости:

График зависимости ошибки от количества входов при постоянном
шаге обучения
4.
Исследование поведения системы в зависимости от количества входов при
адаптивном шаге обучения
Проведем исследование поведения системы 6±4 входа. Будем
проводить обучение для 2, 6 и 10 входовых ИНС, прогнозирование. По результатам
исследования построим графики зависимости ошибки от количества входов.
. Количество входов равно 6 - см. раздел 2.
. Количество входов равно 2.
Процесс обучения:
|
№ шага
|
Yрасч.
|
Yэтал
|
E
|
|
1
|
0.203819
|
0.200868
|
0.002952
|
|
2
|
0.200876
|
0.201006
|
-0.000130
|
|
3
|
0.201019
|
0.201142
|
-0.000123
|
|
4
|
0.201156
|
0.201277
|
-0.000121
|
|
5
|
0.201290
|
0.201410
|
-0.000120
|
|
6
|
0.201423
|
0.201541
|
-0.000118
|
|
7
|
0.201554
|
0.201670
|
-0.000116
|
|
8
|
0.201683
|
0.201797
|
-0.000115
|
|
9
|
0.201810
|
0.201923
|
-0.000113
|
|
10
|
0.201935
|
0.202047
|
-0.000112
|
|
11
|
0.202059
|
0.202169
|
-0.000110
|
|
12
|
0.202181
|
0.202289
|
-0.000108
|
|
13
|
0.202301
|
0.202407
|
-0.000107
|
|
14
|
0.202419
|
0.202524
|
-0.000105
|
|
15
|
0.202535
|
0.202638
|
-0.000103
|
|
16
|
0.202649
|
0.202751
|
-0.000102
|
|
17
|
0.202762
|
0.202862
|
-0.000100
|
|
18
|
0.202873
|
0.202971
|
-0.000098
|
|
19
|
0.202982
|
0.203079
|
-0.000097
|
|
20
|
0.203089
|
0.203184
|
-0.000095
|
|
21
|
0.203195
|
0.203288
|
-0.000093
|
|
22
|
0.203298
|
0.203390
|
-0.000092
|
|
23
|
0.203400
|
0.203490
|
-0.000090
|
|
24
|
0.203500
|
0.203588
|
-0.000088
|
|
25
|
0.203598
|
0.203684
|
-0.000087
|
|
26
|
0.203694
|
0.203779
|
-0.000085
|
|
27
|
0.203788
|
0.203872
|
-0.000083
|
|
28
|
0.203881
|
0.203963
|
-0.000082
|
|
29
|
0.203972
|
0.204052
|
-0.000080
|
|
30
|
0.204060
|
0.204139
|
-0.000079
|
E=0.000005
Прогнозирование на основании полученных результатов обучения:
|
№ шага
|
Yрасч.
|
Yэтал
|
E
|
|
1
|
0.204147
|
0.204224
|
-0.000077
|
|
2
|
0.204156
|
0.204308
|
-0.000152
|
|
3
|
0.204164
|
0.204389
|
-0.000226
|
|
4
|
0.204172
|
0.204469
|
-0.000298
|
|
5
|
0.204179
|
0.204547
|
-0.000368
|
|
6
|
0.204187
|
0.204624
|
-0.000437
|
|
7
|
0.204194
|
0.204698
|
-0.000504
|
|
8
|
0.204201
|
0.204770
|
-0.000569
|
|
9
|
0.204208
|
0.204841
|
-0.000633
|
|
10
|
0.204215
|
0.204910
|
-0.000695
|
|
11
|
0.204222
|
0.204977
|
-0.000755
|
|
12
|
0.204228
|
0.205042
|
-0.000813
|
|
13
|
0.204235
|
0.205105
|
-0.000870
|
|
14
|
0.204241
|
0.205167
|
-0.000926
|
|
15
|
0.204247
|
0.205226
|
-0.000979
|
E=0.00000287983
3. Количество входов равно 10.
Процесс обучения:
|
№ шага
|
Yрасч.
|
Yэтал
|
E
|
|
1
|
0.202954
|
0.200442
|
0.002512
|
|
2
|
0.200444
|
0.200586
|
-0.000141
|
|
3
|
0.200625
|
0.200727
|
-0.000102
|
|
4
|
0.200766
|
0.200868
|
-0.000101
|
|
5
|
0.200906
|
0.201006
|
-0.000100
|
|
6
|
0.201044
|
0.201142
|
-0.000099
|
|
7
|
0.201180
|
0.201277
|
-0.000097
|
|
8
|
0.201314
|
0.201410
|
-0.000096
|
|
9
|
0.201446
|
0.201541
|
-0.000095
|
|
10
|
0.201577
|
0.201670
|
-0.000093
|
|
11
|
0.201705
|
0.201797
|
-0.000092
|
0.201832
|
0.201923
|
-0.000091
|
|
13
|
0.201957
|
0.202047
|
-0.000089
|
|
14
|
0.202081
|
0.202169
|
-0.000088
|
|
15
|
0.202202
|
0.202289
|
-0.000087
|
|
16
|
0.202322
|
0.202407
|
-0.000085
|
|
17
|
0.202440
|
0.202524
|
-0.000084
|
|
18
|
0.202556
|
0.202638
|
-0.000083
|
|
19
|
0.202670
|
0.202751
|
-0.000081
|
|
20
|
0.202782
|
0.202862
|
-0.000080
|
|
21
|
0.202893
|
0.202971
|
-0.000079
|
|
22
|
0.203001
|
0.203079
|
-0.000077
|
|
23
|
0.203108
|
0.203184
|
-0.000076
|
|
24
|
0.203213
|
0.203288
|
-0.000075
|
|
25
|
0.203316
|
0.203390
|
-0.000073
|
|
26
|
0.203418
|
0.203490
|
-0.000072
|
|
27
|
0.203517
|
0.203588
|
-0.000071
|
|
28
|
0.203615
|
0.203684
|
-0.000069
|
|
29
|
0.203711
|
0.203779
|
-0.000068
|
|
30
|
0.203805
|
0.203872
|
-0.000067
|
E=0,000003
Прогнозирование на основании полученных результатов обучения:
|
№ шага
|
Yрасч.
|
Yэтал
|
E
|
|
1
|
0.203897
|
0.203963
|
-0.000065
|
|
2
|
0.203921
|
0.204052
|
-0.000130
|
|
3
|
0.203945
|
0.204139
|
-0.000194
|
|
4
|
0.203968
|
0.204224
|
-0.000257
|
|
5
|
0.203990
|
0.204308
|
-0.000317
|
|
6
|
0.204012
|
0.204389
|
-0.000377
|
|
7
|
0.204034
|
0.204469
|
-0.000435
|
|
8
|
0.204055
|
0.204547
|
-0.000492
|
|
9
|
0.204076
|
0.204624
|
-0.000548
|
|
10
|
0.204096
|
0.204698
|
-0.000602
|
|
11
|
0.204116
|
0.204770
|
-0.000655
|
|
12
|
0.204135
|
0.204841
|
-0.000706
|
|
13
|
0.204154
|
0.204910
|
-0.000756
|
|
14
|
0.204172
|
0.204977
|
-0.000805
|
|
15
|
0.204190
|
0.205042
|
-0.000852
|
E=0.00000216793
Получили зависимость среднеквадратической ошибки при
прогнозировании от количества входов сети. Построим график зависимости:
Заключение
В ходе проведения контрольной работы было установлено:
· 3-слойная нейронная сеть во многом похожа
на 2-слойную (способы обучения аналогичны, отличаются лишь особенностями
реализации);
· 3-слойная нейронная сеть является более
точной по сравнению с 2-слойной (если сравнивать результаты лабораторной работы
№2, то видно, что 3-слойная ИНС обладает большей скоростью обучения, большей
точностью);
· в 3-слойных ИНС в процессе обучения
наблюдается «эффект уточнения» - на каждом последующем шаге величина
среднеквадратической ошибки уменьшается;
· в ходе работы было рассмотрено влияние
изменения количества входов на точность ИНС и построены графики зависимости.
При анализе данных графиков можно предположить, что данная точность не
максимальна и путем увеличения количества входов точность можно увеличить.
Однако из графика также видно, что при добавлении очередного количества входов
эффект от них гораздо меньше, чем от предыдущих. В соответствии с этим встает
вопрос о целесообразности наращивания количества входов.
· как и в 1- и 2-слойных ИНС, адаптивный шаг
обучения является более эффективным по скорости получения результата (3 шага -
при обучении с постоянным шагом, 2 шага - при обучении с адаптивным шагом), но
мене точным (E=0,00000026073
- при обучении с постоянным шагом; E=0,0189632 - при обучении с адаптивным шагом).