Творческая тетрадь как средство обеспечения выполнения творческих работ по математике для учащихся 6 классов
Творческая
тетрадь как средство обеспечения выполнения творческих работ по математике для
учащихся 6 классов
Дипломная
работа
Оглавление
Введение
Глава 1. О значении творческих работ для школьного
математического образования
§ 1 Задачи математического образования в подростковой школе
§ 2 Математическое творчество подростков
.2.1 Характеристика детского математического творчества
.2.2 Творческая работа по математике в 6 - 8 классах.
Особенности выполнения творческих работ шестиклассниками
Глава 2. Средства обеспечения выполнения творческих работ по
математике
§1. Творческая тетрадь для шестого класса по теме “Признак
делимости на 11 натуральных чисел”
.1.1 Материал и содержание творческой работы
.1.2 Характеристика творческой тетради
.1.2.1 Структура творческой тетради
.1.2.2 Особенности оформления
.1.2.3 Действия детей с материалом тетради
.1.3 Анализ результатов апробации творческой тетради
.1.4 Методическое обеспечение работы учителя с творческой
тетрадью
.1.4.1 Методические рекомендации
.1.4.2 Описание организационной формы передачи учителям
методики работы с творческими работами
§ 2 Комплект материалов для обеспечения творческой работы по
теме “Некоторые вопросы, связанные с изучением бинома Ньютона”
.2.1 Общая характеристика материалов
.2.2 Возможное содержание творческой работы
Заключение
Литература
Введение
Многие исследователи развивающего обучения (Воронцов А.Б, Эльконин Б.Д,
Поливанова К.Н.) отмечают, что инициация детского творчества является особенно
важной при обучении подростков, поскольку творчество способствует личностному
росту ученика, развитию его мыслительных способностей, способностей к его
самостоятельной деятельности и планированию [15]. Разработчики программ
развивающего обучения математики г. Красноярска отмечают, что уже в шестом
классе появляется возможность детского научного (математического) творчества
[1]. Сравнивая представления о творчестве, как рассматривал его А.Т. Шумилин,
математическом творчестве, сформулированном в монографии [1] и об
учебно-исследовательской задаче в подростковой школе, описанной Юдиной Ю.Г., мы
обнаружили, что под математическим творчеством в подростковой школе можно
понимать исследовательскую деятельность учащегося, процесс которой
характеризуется:
· самостоятельной постановкой учащимся задачи, поиском средств
и способов ее решения;
· эмоциональной вовлеченностью учащегося в работу с проблемой;
· значимостью полученного результата для самого учащегося и его
новизна относительно материала школьной программы.
При выполнении творческой работы по математике в шестом классе перед
учеником встают различные трудности, которые он сам преодолеть еще не может,
поскольку не умеет оформлять свои мысли и испытывает большие трудности при
написании текста творческой работы. Поэтому большое значение имеет руководство
учителя при написании творческой работы.
Отметим, что руководство творческой работой является достаточно новой, не
освоенной учителями II ступени
деятельностью. Учитель, как правило, испытывает трудности, впервые столкнувшись
с задачами руководителя творческой работы, а именно, с удержанием логики
исследования, помощью ребенку в оформлении его мыслей, представлением норм
изложения работы. Поэтому возникла необходимость создания учебно-методического
обеспечения, которое поможет учителю в разрешении возникающих у него проблем.
Цель работы: разработать учебно-методическое средство, обеспечивающее
выполнение шестиклассниками творческой работы по теме “Признаки делимости на 11
натуральных чисел”.
Гипотеза: Специально организованный текст, названный нами творческой
тетрадью может являться методическим средством, обеспечивающим руководство
учителя, который только начинает пробовать себя в роли руководителя творческой
работы, поскольку содержит логику разворачивания исследовательской задачи.
Также этот текст может инициировать творческое отношение учащегося к задаче,
поскольку содержит ловушки, специальным образом представленные задания.
Для достижения цели решались следующие задачи:
· Провести анализ материала и выделить содержание творческой
работы по указанной теме.
· Разработать творческую тетрадь для 6-х классов, а именно:
задания и структуру тетради; форму предъявления заданий и оформление тетради.
· Разработать методику работы с творческой тетрадью.
Во время работы над дипломом возникли дополнительные задачи, связанные с
динамикой учебно-методических средств от 6 к 9 классу. Появилась гипотеза, что
для обеспечения выполнения творческой работы по математике в 7 - 8 классах,
необходимо учебно-методическое средство по форме отличное от творческой тетради
для 6 классов, поскольку к 7 классу учащийся уже имеет опыт выполнения
творческой работы. На данном этапе учебно-методическое средство должно
предполагать большую самостоятельность ребенка при выполнении творческой
работы. Таким средством может являться, например, комплект материалов,
содержащих список возможных тем творческих работ с рекомендациями и выделением
возможных трудностей в материале, а также аннотированный список литературы по
заданной теме для учителя и ученика.
Дополнительные задачи:
· Провести анализ материала и выделить содержание творческой
работы по теме “Некоторые вопросы, связанные с изучением бинома Ньютона”.
· Разработать комплект материалов по теме “Некоторые вопросы,
связанные с изучением бинома Ньютона”, организующий исследование школьников 7 -
8 классов.
Работа состоит из введения, двух глав, заключения, списка литературы и
приложений.
В первой главе дипломной работы обсуждаются задачи математического
образования в подростковой школе (актуальность творчества), и понятие математического
творчества учащегося. Выделяются общие принципы создания творческих работ, типы
творческих работ и соответствующие им цели и содержание. Определяется специфика
и трудности выполнения творческих работ шестиклассниками.
Вторая глава полностью посвящена разработке учебно-методических средств
для 6-х классов и 7-8 классов.
Разработка
творческой тетради. В качестве материала для творческой тетради был выбран
признак делимости на 11 в десятичной системе счисления. Нами он был обобщен и
доказан признак делимости на 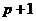 в
системе счисления по основанию
в
системе счисления по основанию  . Кроме
этого, был проведен анализ детских творческих работ по теме “Признак делимости
на 11 натуральных чисел”. Было определено, что дети могут вывести признаки
делимости на 11 для двузначных, трехзначных чисел и обобщить их для чисел с
большим количеством знаком, при этом двигаясь путем эмпирических обобщений.
. Кроме
этого, был проведен анализ детских творческих работ по теме “Признак делимости
на 11 натуральных чисел”. Было определено, что дети могут вывести признаки
делимости на 11 для двузначных, трехзначных чисел и обобщить их для чисел с
большим количеством знаком, при этом двигаясь путем эмпирических обобщений.
В
ходе анализа детских работ были выделены “ловушки”, провоцирующие детей на
формальный перенос признака. Была разработана система заданий, выполняя которые
учащийся проходит все этапы исследования. Задания в тетради представлены в виде
вопросов, либо особым образом расположенного материала, провоцирующего ребенка
на вопрос. Для усиления свободы оперирования с тетрадью, материал сформулирован
таким образом, чтобы содержание каждой страницы было логически завершенным,
подводящим итог какого-либо из этапов исследования.
Разработанная нами творческая тетрадь полностью готова к изданию. Она
прошла апробацию, в которой принимали участие учителя и учащиеся шестых
классов. В процессе апробации было отмечено, что, проводя исследование, ребенок
действительно двигается путем эмпирических обобщений, о чем свидетельствует его
попадание в ловушки. Учащимся интересна работа с тетрадью, кроме имеющихся в
тетради вопросов они начинают ставить свои вопросы, придумывать задачи, которые
с интересом решают. По материалам апробации написаны методические рекомендации
для индивидуальной и групповой работы с творческой тетрадью.
Разработка учебного комплекта по теме “Некоторые вопросы, связанные с
изучением бинома Ньютона” для 7 - 8 классов. Были разработаны:
· Содержание
творческой работы по теме “Некоторые вопросы, связанные с изучением бинома
Ньютона”. Творческих работ по данной теме учащимися ранее написано не было,
поэтому нами было проведено собственное исследование, в результате которого
выведено разложение формул бинома и тринома Ньютона, правило нахождения
биномиальных коэффициентов в треугольнике и триномиальных коэффициентов в
пирамиде Паскаля, а также формулы нахождения биномиальных коэффициентов через
число сочетаний  . В процессе работы были выделены трудности, связанные
с исследованием материала. Полученные результаты исследования сопоставлены и
дополнены материалом книг по этим вопросам и оформлены в виде описания
возможного содержания творческой работы.
. В процессе работы были выделены трудности, связанные
с исследованием материала. Полученные результаты исследования сопоставлены и
дополнены материалом книг по этим вопросам и оформлены в виде описания
возможного содержания творческой работы.
· Пробная форма учебного комплекта, организующего творчество
подростка, в который входит: 1) учебная тетрадь, приводящая к постановке задачи
творческой работы; 2) список тем творческих работ и описанием возможных путей
исследования материала; 3) аннотация к литературе по заданной теме.
В заключении описываются основные результаты работы.
В приложениях приводятся: творческая тетрадь по теме “Признаки делимости
на 11 натуральных чисел” для 6 класса; учебная тетрадь для 7-го класса,
аннотация к литературе для творческой работы по теме “Некоторые вопросы,
связанные с изучением бинома Ньютона” для 7 - 8 классов; список тем творческих
работ.
Местами для апробации, разработанной нами творческой тетради, явились
средняя общеобразовательная школа № 14 г. Назарово и семинар института психологии
и педагогики развития (ИППР) г. Красноярска.
Результаты работы были доложены на краевой научной конференции молодых
ученых и студентов, а также на рабочем семинаре лаборатории развивающего
обучения математике института психологии и педагогики развития.
Глава 1. О
значении творческих работ для школьного математического образования
§ 1 Задачи
математического образования в подростковой школе
Исследователи развивающего обучения Б.Д. Эльконин и И.Д. Фрумин полагают,
что “учебная деятельность в подростковом возрасте должна быть продолжена как
учебно-эксперементальная”, в которой предметом являются условия существования и
границы предметной области, описываемой через некое исходное отношение. “Учеба
подростка должна быть в основном игрой с границами понятия как системы,
своеобразной игрой в допущения, гипотезы и их проверку” [1]. На материале
математики это означает, что подростковая школа должна стать этапом освоения
учебно-исследовательской деятельности, которая предполагает пробность и
поисковость. На этом этапе развития учебной деятельности изменяется содержание
математического образования, его целью становится освоение математики как вида
деятельности. Кроме этого подростковая школа должна стать этапом постепенного
выращивания из коллективного субъекта учебной деятельности индивидуального
субъекта [6].
Заметим, что учебная деятельность не является ведущей в подростковом
возрасте и не определяет развития. Психологи утверждают, что «для подростка
…ведущей воспроизводящей деятельностью является общественно-значимая
деятельность» [8]. Основные интересы подростка лежат либо в «пространстве
общения», либо в таких предметах учебного пространства, которые отличаются
прагматичностью (обучение езде на машине) или психологичностью (обучение
ответственности, «урок разговора по душам»). И, конечно, обучение математике не
лежит в области запросов подростков, а сама математика не рассматривается ими
как значимая деятельность. Анализ областей интересов, предложенных самими
подростками, позволяет предположить, что интересными и значимыми для них
являются такие формы взрослых деятельностей, которые в современной
социокультурной ситуации естественным образом представлены как взрослые. По
отношению к ним можно построить образование как удовлетворение запросов
подростка.
Однако, математическая деятельность относится к тем профессиональным
деятельностям, которые требуют специальной работы взрослого по их
представленности [1].
Позитивное здесь - готовность подростка к тем видам учебной деятельности,
которые делают его более взрослым в его собственных глазах. Такая готовность
может быть одним из мотивов учения. Одной из возрастных особенностей учащихся
является утрата интереса подростка к классно-урочной форме работы и освоенным
учебным отношениям [1]. Для подростков становятся привлекательными
самостоятельные формы занятий. Подростку это импонирует, и он легче осваивает
новые способы действия, когда учитель лишь помогает ему.
В соответствии с представлениями о ведущей деятельности
учебно-исследовательская математическая деятельность может быть освоена
подростком только как общественно значимая. Для младших подростков (6 класс)
общую значимость можно создать внутри школы, посредством разработки “мест”,
задающих значимость [1].
Таким образом, задачами математического образования в подростковом
периоде являются:
1. Введение новых основных средств изучения понятий.
2. Включение подростка в такие формы, где бы формировался интерес к
занятию математическим исследованием (такой формой может являться
математический клуб).
. Формирование образовательного запроса, который не складывается
стихийно.
Реализация этих задач возможна в рамках математического творчества.
§ 2
Математическое творчество подростков
.2.1
Характеристика детского математического творчества
Последнее время термин “математическое творчество” все чаще употребляется
при попытках описания содержания математического образования в средней ступени
школы. Для того, чтобы говорить о детском математическом творчестве, сначала
определимся с тем, что мы будем под этим понимать.
Мы будем следовать пониманию математического творчества, представленному
в [20]. Согласно этому пониманию творчество обладает следующими важными
характеристиками:
· Творчество тесно связано с познавательной деятельностью.
Математическое творчество - это форма овладения математическими знаниями.
· Необходимым условием начала творческого поиска (исследования)
является осознание проблемы, ее постановка; процесс творчества - это процесс
решения проблемы. В процессе творчества формулировка проблемы претерпевает изменения,
уточняется, ее решение распадается на ряд задач. Разными авторами отмечается
этапность, цикличность в решении проблемы, то есть наличие истории творческого
поиска.
Отметим, что творчество в математике связано с получением новых
утверждений о свойствах математических объектов (этапом выдвижения и проверки
гипотез), формулированием новых теорем и поиском способов доказательства и
(лишь на последнем этапе) проведением строгих доказательств.
· В процессе творчества всегда создается новая вещь (получается
новый математический результат), совершается открытие, применяются либо новые
средства, способы.
А.Т. Шумилин выделяет четыре этапа движения творчества (которые зависят
от того, какие задачи на нем решаются) [18]:
1. осознание, постановка, формулирование проблемы.
2. нахождение принципа решения проблемы, нестандартной задачи
(решающая гипотеза, идея изобретения, замысел).
. обоснование и развитие найденного принципа, теоретическая
разработка, конкретизация и доказательство гипотезы (научное творчество). А
также разработка плана экспериментальной проверки гипотезы, реализации замысла,
идеи и т.д.
. практическая проверка гипотезы, реализация изобретения,
объективизация результатов.
Заметим, что вышеперечисленные этапы тесно связаны с этапами решения учебно-исследовательских
задач в подростковой школе, сформулированными Ю.Г. Юдиной в [19]. Приведем эти
этапы:
1. Постановка проблемы в исследовании предмета (фиксация
затруднений, появление у учащихся проверки и обоснования).
2. Гипотезирование (переформулировка проблемы в форме гипотез,
требующих проверки и обоснования).
. Формулировка и обоснование утверждений, появление теорем.
Построение «маленькой теории».
. Оформление полученных знание для применения(описание логики
рассуждений, составление культурного текста, написание «статьи» по предмету).
. Практическое применение полученных знаний (решение класса
аналогичных задач, перенос полученных способов исследования на другой
материал).
В случае математического творчества эти этапы фактически идентичны, т.е. предполагают
постановку проблемы, процесс продуцирования правдоподобных утверждений
(гипотез) и их обоснование, презентацию результатов либо как теоретического
знания, либо как практического. Таким образом, подростковое математическое
творчество, есть фактически осуществление исследовательской деятельности.
Однако нужно выделить некоторые отличия математического творчества от
решения учебно-исследовательской задачи. А именно:
· Творчество учащегося отмечено наличием активной личностной
позиции по отношению к познанию, личной заинтересованностью в творческой
деятельности, эмоционально окрашенным отношением к исследуемому материалу[10].
· При решении учебно-исследовательских задач для учащегося
важно приобрести умение решать подобные задачи, а сам результат является
второстепенным.
Отличительной характеристикой математического творчества является
значимость результата для учащегося. Однако результат творчества подростка
обычно является объективно известным в науке, но как индивидуально,
“психологически новым”, т.е. достигнутым собственными силами ребенка [16]. Либо
объективно новым по отношению к материалу школьной программы.
Таким образом, под математическим творчеством подростков будем понимать
исследовательскую деятельность с высокой мотивацией, для которой характерна
ярко выраженная авторская позиция учащегося и высокий уровень
самостоятельности, результат, полученный в процессе этой деятельности, является
объективно новым по отношению к школьной программе, выходит за ее рамки.
.2.2
Творческая работа по математике в 6 - 8 классах. Особенности выполнения
творческих работ шестиклассниками
Практика выполнения творческих работ, начиная с 6 класса, существует в
гимназии №1 “Универс” г. Красноярска, а также начинает складываться в других
школах, в которых присутствует развивающее обучение. В гимназии “Универс”, для
организации творчества подростков 7 - 9 классов организовано специальное
образовательное пространство “Школа молодого ученого”, где происходит встреча
ребенка с ученым. Темы творческих работ в “Школе молодого ученого” учащимся
могут представить как учителя, так и ученые (преподаватели университета), в
процессе прочтения лекций, при этом представленные темы, обычно выходят за
рамки школьной программы. Результаты творческих работ учащиеся представляют на
конференции, куда могут прийти все желающие, и в виде правильно оформленных
текстов. А для организации творчества в 6 - 7 классах разработана методика.
Чтобы творчество шестиклассников стало возможным необходимо создание
особых условий организации обучения математике [1]. Такие условии были выделены
сотрудниками лаборатории развивающего обучения математике института психологии
и педагогики развития г. Красноярска О.В. Знаменской, Ю.Г. Юдиной и описаны в
методике руководства творческими работами. Они выделяют следующие условия
творческого самоопределения учащихся [19]:
1. Открытость обучения предмету, понимаемую как “особый стиль работы
учителя, содержания образования, общения между учащимися и т.д. ”, оставляющие
за учащимся возможность выбора и свободного планирования собственной
деятельности.
2. Определенная поляризация образовательного пространства класса,
предполагающая наличие различных мест содержательного общения подростков с
взрослым, позволяющем создать, с одной стороны, особую эмоциональную атмосферу
отношения к предметам в классе, с другой стороны, представляет различное
предметное видение действительности разными взрослыми, например, ученым -
исследователем, учителем - предметником, ведущим предметного клуба.
. Построение подростком совместно с учителем индивидуального
маршрута собственной творческой деятельности. Составление гибкого плана и
прохождение определенных этапов выполнения творческой работы как средство
построения подростком индивидуального маршрута. Демонстрация подростком
продуктов собственной творческой деятельности.
Согласно третьему условию творческого самоопределения, выполнение
творческой работы учащимся происходит в сотрудничестве с учителем, который
должен создать такие условия, при которых стало возможным самостоятельное
движение учащихся, включающее выбор темы, формулирование и решение задачи,
оформление и защиту работы. В деятельности учителя выделяют 4 этапа [1, 19]:
1. Подготовительная работа. Цель педагога на этом этапе - создание
на уроке условий для возникновения предметного творчества подростков, т.е.
“мест” где возможно возникновение интереса и вопроса учащегося.
2. Этап обмена письменными текстами. Цель педагога на этом этапе -
помочь учащемуся сформулировать собственную проблему и поставить задачу, а
также задать образцы изложения своих мыслей.
. Этап работы по плану в режиме консультаций с учителем. Задача
педагога на данном этапе - “поддержать пробу учащегося, сохранив при этом
авторский подход учащегося к теме, помочь ему осознать, что он пытается узнать
нового о предмете и о себе”.
. Защита работы. Задача педагога на данном этапе - создание
условий для демонстрации подростками результатов их личного творчества с
выходом на коллективное обсуждение работы, оценку работы участниками
обсуждения, самооценку самого ученика. Должна быть официально организована в
школе и представлена учащимся как особый этап демонстрации, презентации
результатов их творческой работы, а также получения коллективной оценки
качества творческой работы.
Описание выделенных этапов деятельности учителя относится к организации
детского творчества в шестом классе, когда подросток только начинает
знакомиться с новой для него деятельностью. В шестом классе ученик еще
действительно нуждается в помощи со стороны учителя, она особенно ему
необходима в процессе оформления своих мыслей, написания текста (поэтому иногда
оформление работы, написание текста может быть выполнено ребенком в седьмом
классе).
Данная методика предполагает выбор учащимся темы творческой работы,
источником которой является вопрос, возникший в процессе урока, что накладывает
некоторые ограничения на возможность выбора подростка. Также хочется отметить о
трудностях реализации методики, связанных с организацией первого этапа, на
котором происходит творческое самоопределение учащегося. Эти трудности могут
возникнуть у учителя при выполнении условия открытости обучения предмету, и
быть связаны со сложностью и отсутствием опыта создания особой среды на уроках.
Как говорилось выше, текст творческой работы должен быть “культурно”
оформлен. Сотрудниками лаборатории развивающего обучения математике института
психологии и педагогики развития г. Красноярска: О.В. Знаменской, О. И.
Белоконь, Ю.Г. Юдиной были проанализированы реальные творческие работы учащихся
6 - 9 классов, в результате чего были выделены их жанры. Обнаружены не только
чисто исследовательские творческие работы, но и работы основной целью которых
являлось проведение анализа, однако средством для его проведения служило
исследование [19]:
Виды аналитических работ
Реферативная работа преследует цель научиться чему-то новому,
сформировать свое отношение к определенной теме. В подобной работе существенным
является фиксация разрывов в понимании, систематизация знаний. Работа
обязательно включает в себя изучение и проведение анализа литературы по данной
теме: обнаружение общего и особенного по данной тематике, применение полученных
знаний по теме в решении задач, оформление собственного отношения к данной
теме, выявление связей со школьной программой.
Работа
по обобщению и систематизации знаний преследует цель определения границ знания
- незнания об объекте, выявления связей имеющихся знаний. Работа включает в
себя описание системы знаний, типов связей на начало работы:  ,
, 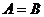 ,
, 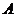 обосновывает
обосновывает 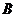 ,
,  ,
, 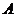 частный
случай
частный
случай 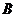 , а также обнаружение незнания за счет фиксации
несвязности знаний. Результатом может являться обзор, либо постановка
исследовательской задачи.
, а также обнаружение незнания за счет фиксации
несвязности знаний. Результатом может являться обзор, либо постановка
исследовательской задачи.
Аналитическая
работа преследует цель восстановления логики предметного содержания,
обнаружение “разрывов” в самой логике изложения содержания. Работа включает в
себя обязательное изучение литературы. Результатом является формулировка
возможных тем для исследования.
Таким
образом, аналитические работы связаны с рефлексией своей прошлой деятельности,
своих знаний, анализом литературы, и как правило результатом таких работ
является постановка исследовательской задачи. Выполнение таких работ характерно
для 8 - 9 классов.
Виды
исследовательских работ
Исследовательские
виды работ связаны либо с исследованием объекта, либо способа.
Исследовательская
работа направлена на решение предметной проблемы, построение “маленькой” теории
об объекте. Работа включает в себя исследование некоторого свойства
математического объекта. Исследование, если оно самостоятельное, как правило,
носит характер эмпирических обобщений некоторых свойств объектов, а лишь затем
попыток теоретического обоснования. Если полученный результат является
“переоткрытием” известного в литературе результата, то работа должна
обязательно содержать описание хода открытия.
Работа
по изучению способа связана с изобретением, применением, обобщением, развитием
методов и способов. Работа включает в себя описание известного способа,
обоснование, выделение класса задач. которые решаются данным способом, изучение
границ применимости данного способа и возможности его распространения на более
широкий класс объектов.
Основная
масса работ в 6 - 7 классах являются исследовательскими, поэтому остановимся на
них подробнее. В качестве примера приведем содержание двух работ.
Работа
на перенос способа
Известен
способ деления угла пополам при помощи циркуля и линейки. Он состоит в
следующем: чтобы разделить угол пополам, нужно из вершины угла провести дугу
произвольного радиуса. Соединить между собой точки, полученные при пересечении
дугой сторон угла. Чтобы разделить угол пополам, отметим середину полученного
отрезка. Соединим середину отрезка с вершиной угла, в результате получим два
равных угла (рис. 1.1 а).
Возможно ли распространение этого способа на случай деления угла на
большее количество равных частей? Рисунок 1.1 б наводит нас на мысль, что да,
деля АВ на три равные части, мы, и угол делим на три равные части. Это
гипотеза. Один из способов проверки - мысленный эксперимент. Раздвинем мысленно
угол, превратив его почти в развернутый, и получим контрпример (см. рис. 1.1
в).
Направлением
дальнейшего исследования может являться выделение класса углов, для которых
способ дает верное решение (последовательно его применяя, получим 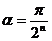 ).
).
Изучение
объекта:
Известны
тройки взаимно простых чисел 3, 4, 5; 5, 12, 13; 7, 24, 25; 9, 40, 41; 11, 60,
61; удовлетворяющих равенству 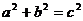 (Пифагоровы
тройки). Как найти все такие тройки чисел?
(Пифагоровы
тройки). Как найти все такие тройки чисел?
Проводя
исследование можно получить формулы для всех таких чисел:  ,
, 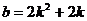 ,
, 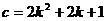 , где
, где  . Это
гипотеза. Общие они или нет? Оказывается можно привести пример тройки, которая
не описывается такими формулами - 8, 15, 17. Направлением дальнейшего
исследования может являться обобщение формулы для всех троек.
. Это
гипотеза. Общие они или нет? Оказывается можно привести пример тройки, которая
не описывается такими формулами - 8, 15, 17. Направлением дальнейшего
исследования может являться обобщение формулы для всех троек.
Отметим,
что описанная выше методика организации выполнения учащимися 6 классов
творческих работ по математике является трудно воспроизводимой для учителя
математики из-за трудности создания условий для возникновения творчества
(создания особой среды на уроках). Кроме этого, у данной методики существует
ограничение, связанное с тем, что она предполагает выбор учащемуся темы
творческой работы, источником которой может являться только вопрос, возникший в
процессе урока. Это не дает возможности для возникновения вопросов, связанных с
областью, лежащей вне школьной программы.
Поскольку
деятельность руководителя творческой работой является пока не освоенной
учителями, однако у многих есть желание заниматься творчеством с детьми.
Поэтому есть необходимость в создании методического средства, которое помогло
бы учителям в освоении идеи руководства творческой работой детей, а в частности
руководства детским математическим исследованием.
Глава 2.
Средства обеспечения выполнения творческих работ по математике
§1.
Творческая тетрадь для шестого класса по теме “Признак делимости на 11
натуральных чисел”
Настоящий параграф посвящен одному из средств обеспечения выполнения
творческих работ по математике, которое мы назвали творческой тетрадью.
Творческая тетрадь - это особым образом оформленная система заданий и мест для
решения, выстроенная в соответствии с логикой разворачивания исследовательской
задачи. Далее будет описано содержание тетради, ее структура, нормы оформления,
а также анализ апробации и методика работы с ней.
.1.1 Материал
и содержание творческой работы
Особое место в школьной программе занимает изучение теории целых чисел.
Признаки делимости чисел являются важным элементом этой теории. Они быстро
позволяют определить, делится ли одно число на другое в том случае если не
нужно знать результата деления. В школьной программе признаки делимости
изучаются в пятом классе. Поэтому можно ожидать, что шестикласснику постановка
задачи поиска признака делимости является знакомой и понятной, а поиск новых признаков
может быть интересным и полезным. Т.е. не потребуется особых действий по
включению ребенка в проблему. Поэтому мы решили в качестве темы для творческой
работы выбрать признак делимости на число, который шестикласснику еще не
известен, а именно делимости на 11.
В [11] мы нашли идею доказательства этого признака и его словесную
формулировку:
Если сумма цифр данного числа через одну равна сумме остальных цифр через
одну или разность этих сумм делится на 11, то и данное число делится на 11.
Мы сформулировали этот признак на математическом языке, используя
позиционную запись числа, и получили строгое доказательство, следующего
утверждения.
Пусть
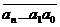 произвольное натуральное число.
произвольное натуральное число.
Теорема
1. Если, при  ,
, 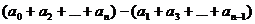 делится
на 11;
делится
на 11;
при
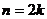 ,
, 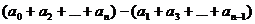 делится
на 11,
делится
на 11,
то
число 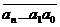 делится на 11.
делится на 11.
Пытаясь
провести строгое доказательство теоремы 1, мы заметили, что признак можно легко
распространить на произвольную систему счисления, т.е. получить признак
делимости на 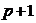 в системе счисления по основанию
в системе счисления по основанию 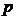 .
.
Пусть
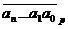 произвольное число,
произвольное число, 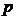 -
основание системы счисления,
-
основание системы счисления, 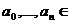
 {0, 1, …,
{0, 1, …,
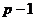 }.
}.
Теорема
2. Если, при  ,
, 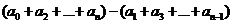 делится
на
делится
на 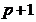 ;
;
при
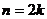 ,
, 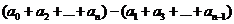 делится
на
делится
на 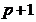 ,
,
то
число 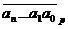 делится на
делится на 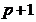 .
.
Доказательство
теоремы 2. По условию 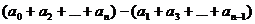 делится на
делится на 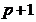 при
при 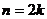 . Докажем, что число
. Докажем, что число 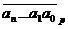 делится
на
делится
на 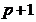 .
.
Рассмотрим
позиционную запись числа:
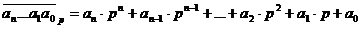 .
.
Из
условия известно, что 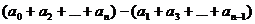 делится на
делится на 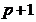 . Выделим
в позиционной записи числа
. Выделим
в позиционной записи числа 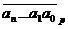 слагаемое
слагаемое
 . Имеем:
. Имеем:

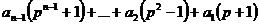 .
Полученное выражение делится на
.
Полученное выражение делится на 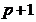 .
Действительно, делится на
.
Действительно, делится на 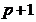 по условию. Оставшиеся слагаемы, также делятся на
по условию. Оставшиеся слагаемы, также делятся на 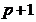 .
.
Действительно,
распишем  при помощи формулы разности квадратов,
при помощи формулы разности квадратов, 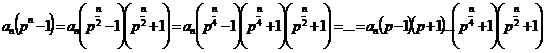 . Видим, что один из множителей делится на
. Видим, что один из множителей делится на 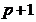 значит, произведение делится на
значит, произведение делится на 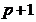 . Разложим
. Разложим 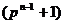 в
произведение двух множителей при помощи формулы суммы нечетных степеней
в
произведение двух множителей при помощи формулы суммы нечетных степеней  формула заимствована из [5], получим
формула заимствована из [5], получим 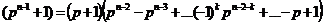 . Видим, что один из множителей произведения делится
на
. Видим, что один из множителей произведения делится
на 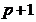 значит, произведение делится на
значит, произведение делится на 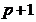 , значит и
, значит и 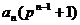 делится
на
делится
на 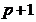 . Проведя аналогичные рассуждения для остальных слагаемых
. Проведя аналогичные рассуждения для остальных слагаемых
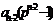 ,
, 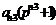 , …,
, …, 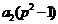 ,
, 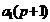 получим,
что они делятся на
получим,
что они делятся на 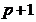 .
.
Итак,
 делится на
делится на 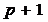 , а
, а 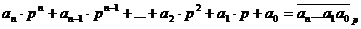 значит,
значит, 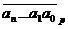 делится
на
делится
на 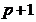 .
.
Доказательство
теоремы 2 для  в точности повторяет доказательство теоремы 2 для
в точности повторяет доказательство теоремы 2 для 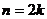 .
.
Заметим,
что доказательство теоремы 1 получается из доказательства теоремы 2
подстановкой вместо 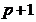 числа 11, а вместо
числа 11, а вместо  числа
10.
числа
10.
Заметим,
что, вообще говоря, признак выполняется и в другую сторону, т.е. справедливо
Утверждение.
Если 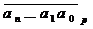 делится на
делится на 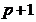 , то
, то
при
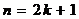 ,
, 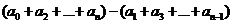 делится
на
делится
на 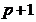 ,
,
а
при 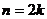 ,
, 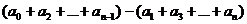 делятся
на
делятся
на 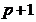 .
.
Помимо
обобщения и обоснования признака делимости для определения содержания
творческой работы был выполнен анализ нескольких творческих работ по теме
“Признаки делимости на 11”, выполненных учащимися 6 -7 классов гимназии
“Универс” г. Красноярска. Анализ работ показал, что шестиклассники могут
провести исследование и вывести признаки делимости на 11 для двузначных,
трехзначных, четырехзначных чисел, например, анализируя числа: 121, 484, 308,
616, 242, 209. Также они могут обобщить полученные признаки для чисел с большим
количеством знаков. При этом, ребенок, проводя исследование, двигается путем
эмпирического обобщения. Было выделено, что обосновать признаки делимости для
двухзначных, трехзначных чисел дети могут посредством полного перебора. Нам
кажется, что доказательство признаков в общем виде от шестиклассников требовать
еще преждевременно, потому, что оно опирается на позиционную запись числа,
которая им еще не известна. Однако нужно отметить, что в работах детей,
обучавшихся в шестом классе по курсу “Начала алгебры”, где вводится позиционная
запись числа, мы обнаружили попытки обоснования признаков в общем виде. Поэтому
у нас появилась гипотеза, что если ввести форму записи числа в общем виде,
которая используется в доказательстве признаков, то дети освоив ее и идею
доказательства, смогут перенести их на числа с большим количеством знаков.
Таким
образом, материалом для творческой работы доступным шестикласснику может
являться вид записи числа, а содержанием вывод признака делимости на 11,
обоснование его полным перебором, освоение идеи доказательства и перенос на
числа с большим числом знаков.
Преимуществом
данной творческой работы является то, что она может быть продолжена и в более
старших классах, возможность этого продолжения связана с возможностью обобщения
признака в произвольной системе счисления.
.1.2
Характеристика творческой тетради
Разработанная нами творческая тетрадь состоит из двух частей:
1. Вводная часть, содержащая задачи, привлекающие внимание ребенка к
проблеме.
2. Основная часть:
· Исследовательская часть, посвященная выводу правдоподобных утверждений,
т.е. выдвижению гипотез, их подтверждению и опровержению.
· Часть, посвященная обоснованию выведенных утверждений.
Тетрадь выполняет функции:
1. Обеспечение эмпирического исследования.
2. Введения нормативного языка описания процесса исследования и его
результатов.
. Обеспечение условий для осознания возникновения необходимости
идеи доказательства (ее частичного освоения).
.1.2.1
Структура творческой тетради
Вводная часть тетради содержит четыре задачи. Две задачи связаны с
делимостью чисел на 5, решить которые шестиклассник может либо при помощи
непосредственного деления чисел, либо при помощи известного ему признака
делимости на 5. Оставшиеся задачи связаны с делимостью чисел на 11, которые он
может решить уже только одним способом, используя непосредственное деление чисел.
При этом ребенку предлагается оценить способы решения задач, выделить более
простой способ решения, определить дефицит своих знаний. Таким образом, вводная
часть тетради привлекает внимание ребенка к проблеме, приводит к постановке
задачи, которую он будет решать в процессе работы с тетрадью. В принципе, эту
часть можно опустить.
Остановимся подробнее на структуре основной части. Исследовательская
часть тетради представлена заданиями, выполняя которые ребенок проходит все
этапы исследования: наблюдение, выделение свойств объекта; выдвижение гипотез и
проверка их правдоподобности, записывая результаты в виде гипотез (догадок) и
теорем (признаков). При этом ребенку сначала предлагается сформулировать
признаки делимости для двузначных, трехзначных чисел, и затем перенести эти
признаки на числа с большим количеством знаков. Таким образом, выполняя
предложенные в тетради задания, ребенок двигается путем эмпирических обобщений.
Важную роль в исследовательской части тетради играют ловушки. Они создают
интригу движения в материале, приводят к пониманию того, что утверждения
нуждаются в обосновании и доказательстве. Ловушки представляют собой
специальным образом представленный материал, провоцирующий и обнаруживающий
формальный перенос признака на более широкий класс чисел. Ряд ловушек был
выделен в результате анализа детских творческих работ по данной теме. Например,
на стр. 4 творческой тетради [9 или приложения 2], ловушка, провоцирует ребенка
на перенос признака делимости на 11 для двузначных чисел на трехзначные: “Верно
ли, что трехзначное число делится на 11, если оно записывается одинаковыми
цифрами?” При попадании в эту ловушку ребенку предлагается проверить выдвинутое
им предположение на числах посредством деления. Однако, выполняя проверку,
ребенок может попасть еще в одну ловушку. Среди чисел, предложенных для
проверки, встретятся: 484, 242, 121, 535, 636, имеющие, с первого взгляда общий
вид: крайние цифры этих чисел равны. При этом первые три числа делятся на 11,
из этого ребенок может предположить, что числа, имеющие такой вид, а значит и
числа 535, 636, делятся на 11. Однако это не так, и проверив их, ребенок
убедиться в этом. Еще одна ловушка, задуманная в тетради (смотри стр.5 [9]),
провоцирует ребенка на то, чтобы он догадку, выдвинутую для части трехзначных
чисел, без обоснования принял в качестве признака делимости для всех
трехзначных чисел. Попав в эту ловушку, ребенку, в который раз придется
проверить выдвинутое им предположение при помощи деления. Подчеркнем, что цель
ловушек состоит в том, чтобы ребенок осознал необходимость обоснования своих
гипотез.
Осознав необходимость обоснования, учащийся может на начальном этапе
обосновать свою гипотезу о делимости только одним способом - полным перебором
чисел. Таким способом ему и предлагается обосновать гипотезу о делимости
трехзначных чисел на 11 (смотри стр. 7 - 8 [9]). Далее ребенок сталкивается с
тем, что доказательство полным перебором становится трудоемким, в связи с
увеличением количества чисел, которые придется проверять. Трудоемкость
провоцирует желание найти другой способ обоснования. Таким образом, создаются
условия для того, чтобы у ребенка возникло желание и необходимость в другом
способе доказательства.
Освоение идеи доказательства признака для всех чисел требует от ребенка
знания позиционной записи числа, которое, как правило, ему еще не известно,
если он не обучается по специальной программе развивающего обучения. Поэтому
встает необходимость введения нового материала (см. стр. 11 творческой тетради
[9]). Идея обоснования признака в общем виде (для всех чисел) вводится на
примере признаков, истинность которых уже известна, т.е. признаков для
двухзначных и трехзначных чисел. Задача учащегося - перенести этот способ на
числа с большим количеством знаков. Необходимо отметить, что по мере продвижения
по творческой тетради постепенно увеличивается число действий, которые должен
ребенок провести самостоятельно.
Творческая тетрадь содержит два типа текстов:
· Описывающих образ действий (схема описания этапов
исследования).
· Описывающих идею доказательства.
Разработка тетради преследовала несколько целей, поэтому мы получили
сложную структуру тетради. Итак, сначала происходит работа со словесной
формулировкой в процессе вывода гипотез для двузначных и трехзначных чисел,
обнаруживается необходимость в обосновании; на следующем этапе вводятся
общепринятые термины для описания процесса исследования (гипотеза,
обоснование); далее выводится признак для четырехзначных чисел, при этом уже
используется введенная терминология. На следующем этапе проблематизируется
обоснование полным перебором и последний этап представлен введением идеи
доказательства и переносом его на доказательства признаков для чисел с большим
количеством знаков.
2.1.2.2
Особенности оформления
Вторая задача, которая стояла перед автором - разработка оформления
тетради. Необходимо было разработать форму предъявления заданий, форму для
обратной связи (того, что пишут дети) и структуру страницы.
Первоначально мы придерживались способу оформления принятому для рабочих
тетрадей [14, 17]. Тетрадь представляла собой сборник пронумерованных заданий,
имеющих прямую формулировку, а также места для записи решений, представленных в
виде пустых мест [см. приложение 1]. Однако монотонная, “скучная” тетрадь не
вызывает интерес, ребенок не воспринимает ее как занимательную. Кроме этого,
недостатком такой тетради являлась прямая формулировка заданий, взятая из
рабочих тетрадей, которая приводит ребенка лишь к исполнительским действиям, и
не вызывая у него своих вопросов, не представленных автором. Поэтому необходимо
было переоформить тетрадь.
Таким образом, была разработана особая форма тетради, привлекающая к себе
интерес, как со стороны ребенка, так и со стороны взрослого, позволяющая
удерживать интерес к материалу при работе с ней; а также, которая, решает проблемы,
связанные с представлением культурных норм оформления творческой работы.
А именно, в творческой тетради задания оформлены в виде вопросов или
особым образом организованного материала (красочных схем), провоцирующего
ребенка на вопрос (см. стр. 6, 9 творческой тетради[9]).
Так как тетрадь должна решать проблемы связанные с нормотивным
представлением результатов, то были введены тексты с “пробелами”, в которых был
задан образец оформления утверждений.
Все ключевые места в тетради выделены в рамочку и отмечены
восклицательным знаком, который обозначает, что на это необходимо обратить
внимание. Также специальным образом выделены задания (звезда и солнышко),
которые ребенок может захотеть выполнить самостоятельно.
Особое внимание было уделено организации страницы. Для усиления свободы
оперирования с тетрадью, материал скомпонован таким образом, чтобы содержание
каждой страницы было логически завершенным, каждая страница заканчивалась
некоторым утверждением, подводящим итог какого-либо из этапов исследования. Это
позволяет начинать работу с тетрадью, практически с любой страницы, но не
отменяет необходимости возвращения к началу.
2.1.2.3
Действия детей с материалом тетради
Процесс работы ребенка с тетрадью требует от него выполнения разных
действий с материалом. Ему приходится не только применять имеющиеся у него
знания, но также осваивать новые.
Работа ребенка с введением тетради требует от него решения задач,
проверки правильности и анализа полученных решений. Работа в тетради посвящена
проведению исследования, поэтому действия связаны с проведением этапов этого
исследования. Этап наблюдения и выделения свойств объектов, связан с анализом
чисел. Однако, если в начале тетради некоторые из чисел, анализ которых
необходимо выполнить даны в готовом виде, то далее ребенку уже приходится
самому их находить, например, посредством умножения. На этапе проверки и
обоснования гипотез возможно применение уже выведенных утверждений. В процессе
работы с тетрадью происходит введение новых терминов и знаковых средств, при
помощи текста, который ребенку необходимо понять и научиться использовать в
процессе работы с тетрадью.
.1.3 Анализ
результатов апробации творческой тетради
Творческая тетрадь прошла апробацию, в которой принимали участие учителя
и учащиеся шестых классов. Основными местами для апробации детьми явилась
средняя общеобразовательная школа № 14 г. Назарово, а учителями семинар
института психологии и педагогики развития (ИППР) г. Красноярска. В результате
работы с тетрадью детьми было проведено исследование и выведен признак
делимости на 11 для произвольного натурального числа, который был ими доказан
для четырехзначных и пятизначных чисел. Итоги работы были представлены детьми в
виде докладов на отчетном занятии, на которое были приглашены их одноклассники.
При работе с тетрадью у детей было отмечено эмоциональное отношение к
материалу, что свидетельствует о том, что тетрадь действительно
заинтересовывает детей.
В процессе работы детей с тетрадью было отмечено, что они попадали в
запроектированные нами ловушки. Из этого можно сделать вывод, что, проводя
исследование, ребенок действительно двигается путем эмпирических обобщений.
Также эмпирический характер исследования подтверждается тем, что дети выводя
признаки делимости, опирались при этом на математическую запись имеющихся
признаков. Это подтвердило нашу гипотезу о способе движения ребенка.
Также можно отметить высокую степень самостоятельности детей во время
проведения исследования, участие учителя при работе ребенка с тетрадью
определялось его помощью при оформлении мыслей, а также организацией
коммуникации между детьми во время работы.
Было подтверждено наше предположение, связанное с возможностью
возникновения у детей в процессе работы с тетрадью своих вопросов, задач. Так в
процессе работы с тетрадью у детей кроме гипотез, логика дальнейшего
исследования которых заложена в тетради, была получена гипотеза, которая не
была учтена при разработке тетради. Ребенком была предложена догадка о
делимости на 11 трехзначных чисел:
Пусть
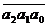 - произвольное трехзначное число. Если
- произвольное трехзначное число. Если  делится на 11, то
делится на 11, то 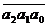 делится
на 11.
делится
на 11.
Данная
гипотеза верна для всех трехзначных чисел, и может быть обобщена для чисел с
большим количеством знаков. Таким образом, тетрадь может являться источником
нового детского исследования.
Также
в процессе работы с тетрадью детьми были решены свои задачи, не сформулированные
в тетради. Например, при обосновании гипотезы для трехзначных чисел полным
перебором, детьми был обнаружен способ выделения трехзначных чисел делящихся на
11 среди всех остальных: отметем первое число, делящееся на 11, каждое
следующее число, которое делится на 11, будет стоять на каждом одиннадцатом
месте в ряду всех трехзначных чисел. Еще был определен способ нахождения числа
всех трехзначных чисел без их полного пересчета: необходимо посчитать, сколько
чисел делящихся на 11 находится между 101 и 200, а их получается 9 и умножить
на количество сотен среди трехзначных чисел, которых тоже 9; получаем, что
число трехзначных чисел делящихся на 11 равно 81.
Учителям
в на семинаре, посвященном детским творческим работам, была предложена работа с
тетрадью. Одним из заданий было: поработать с тетрадью с позиции ребенка, после
чего попробовать выделить ловушки, заложенные в материале, и структуру тетради.
Учителя довольно легко справились с заданием, ими были выделены все ловушки, а
также адекватно определена структура тетради. Таким образом, наша цель -
прозрачность структуры для учителя также была достигнута. У учителей появился
интерес к использованию творческой тетради при работе с детьми, это значит, что
учителя видят в тетради методическое средство, которое способствует выполнению
творческих работ детьми.
В
процессе работы с тетрадью была обнаружена творческая активность учителей, в
процессе работы с тетрадью у них появилась новая задача, выделенная из
материала тетради: определить способ нахождения по виду числа 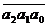 , сомножителя числу 11 при получении данного
трехзначного числа. При решении этой задачи ими была замечена закономерность
для трехзначных чисел, у которых сумма крайних цифр числа равна средней:
сомножитель числу 11 при нахождении числа
, сомножителя числу 11 при получении данного
трехзначного числа. При решении этой задачи ими была замечена закономерность
для трехзначных чисел, у которых сумма крайних цифр числа равна средней:
сомножитель числу 11 при нахождении числа 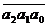 равен
числу
равен
числу 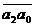 . Это говорит о том, что творческий характер тетради
может также проявляться в процессе работы с ней учителя.
. Это говорит о том, что творческий характер тетради
может также проявляться в процессе работы с ней учителя.
Результатом
апробации творческой тетради явился заказ от учителей на создание методики
работы с творческой тетрадью.
Таким
образом, в процессе апробации были подтверждены наши гипотезы, а именно:
· Об эмпирическом характере обобщений.
· О форме предъявления заданий, провоцирующих собственные
вопросы детей.
· О том, что логика изложения исследовательской задачи служит
методическим средством для учителя.
2.1.4
Методическое обеспечение работы учителя с творческой тетрадью
.1.4.1
Методические рекомендации
Данный пункт представляет собой готовые методические рекомендации по
работе с творческой тетрадью. Рекомендации представлены в виде ограничений
действий учителя, как учитель может помогать учащемуся при работе с тетрадью.
В процессе апробации были выделены формы работы с творческой тетрадью:
индивидуальная и групповая, соответственно разработано два варианта
рекомендаций.
Индивидуальная работа
Учитель предлагает ребенку самостоятельно заполнить тетрадь, после чего
встретится на консультации. Консультации происходят в форме свободной беседы с
учеником, в процессе которой происходит обсуждение того, что ему удалось
сделать, и что вызвало у него трудности.
Работа с тетрадью начинается с выполнения заданий предложенных во
введении. Учитель может регулировать количество решаемых задач в зависимости от
возможностей и желания ребенка, но ни в коем случае учитель не должен решать
задачи вместо ребенка, а также объяснять ему их решения. Не обязательно решать все
четыре задачи, пусть ребенок решит одну задачу с делимостью на 5, а другую с
делимостью на 11. Этого ему хватит, чтобы ответить на предложенные во введении
вопросы. Также может возникнуть такая ситуация, что ребенок захочет начать
работу сразу с исследования, не выполняя задания из введения. В этом случае
нельзя запрещать ему этого делать, к задачам из введения он сможет вернуться
позже.
Далее начинается работа с основной частью тетради (Приложение 2), в
которой можно выделить несколько ключевых этапов:
1. Гипостазирование (стр. 4 -6).
2. Проблематизация способа обоснования (стр. 7, 8, 10 - 12).
. Введение культурного языка (стр. 9).
. Обобщение (стр. 13 -15).
Гипостазирование. В начале этого этапа необходимо договориться с ребенком
о способе работы с тетрадью:
· Выделить в материале “порции”, например, две - три страницы тетради, с
которыми ребенок будет работать в промежутках между встречами с учителем.
· Договориться с ребенком о ведении записей в тетради.
Например, для работы иметь два экземпляра творческой тетради: чтобы с одной
ребенок работал дома и записывал в нее, как сможет, появляющиеся идеи, а вторую
тетрадь использовать во время работы с учителем для записи уже обоснованных
мыслей. Либо, договориться, чтобы в процессе самостоятельной работы записи в
тетради ребенок делал карандашом или в “месте для твоих мыслей”, а
окончательную запись делать в тетради ручкой в процессе работы с учителем.
Работая с тетрадью, учитель должен постоянно обращать ребенка к вопросам
и к выбору, которые содержатся в тетради. Все гипотезы и ответы на вопросы
должны быть обязательно оформлены. Однако если ребенок не может пока объяснить
свой выбор или ответ, не нужно его торопить или отвечать вместо него; можно
пока оставить место для ответа не заполненным, а спустя некоторое время вернуть
к нему ребенка. Нельзя игнорировать мысли, высказываемые ребенком, а также
останавливать его рассуждения, тем самым, прерывая инициативу, даже если они
неверные. Необходимо обращать внимание ребенка на дополнительные сведения,
которые предлагаются в тетради и являются важными для дальнейшей работы. Также
нужно обратить внимание ребенка на форму записи догадки: “Число делится на 11,
если …” и обсудить на что нужно ПОСМОТРЕТЬ в задании, чтобы сформулировать ее.
Если для выделения догадки ребенку не хватает числового материала, то, в
зависимости от его возможностей, либо дать ему этот материал, либо обсудить
способ получения материала, чтобы он сам смог его найти.
Проблематизация способа обоснования. Учитель должен обсудить с ребенком
текст о необходимости обоснования полученных догадок. Обсудить имеющийся у
ребенка опыт, связанный с необходимостью обоснования, если он был. Если нет, то
пусть ребенок на опыте работы с тетрадью рассудит, приведет пример, что
обоснование является важным. Учителю нужно обсудить способ действия ребенка в
процессе проверки догадки полным перебором чисел. Если во время проведения
полного перебора чисел ребенок, посмотрев на другой способ обоснования на
странице 12, решает разобрать его, то необходимо помочь ему в этом. Сначала
обратить его внимание на текст на странице 11, разобрать на примерах новый
способ записи чисел, и дать при помощи него записать уже выведенные
утверждения. В процессе разбора доказательств, нужно объяснить введение
сокращающихся слагаемых. Можно показать новый способ доказательства на примерах
доказательств известных ребенку признаков делимости на 5 и на 3, оформляя их
таким же способом как в тетради. После разбора приведенных доказательств
необходимо вернуть ребенка обратно, для продолжения исследования. После
доказательства признака делимости на 11 для трехзначных чисел в тетради
предлагается вернуться к введению и попробовать решить задачи при помощи уже
обоснованного признака. В этом случае необходимо обсудить с ребенком, какие
задачи он сможет выполнить при помощи выведенного признака, а также определить,
какие еще признаки ему необходимы для решения задач из введения. В процессе
дальнейшего исследования, обсудить с ребенком способ работы с тетрадью на
странице 10. При работе с этой страницей возможно два способа движения, либо
сверху вниз, заполнив сначала свое облачко числами; либо снизу вверх, т.е.
разбив сначала имеющиеся числа в облачке на две группы. Обсудить также с
ребенком, какие числа он объединил в одну группу с числом 1210. Здесь может
быть два варианта: 1) четырехзначное число, образованное от трехзначного,
делящегося на 11, приписыванием к нему нуля, например, 3520; 2) четырехзначные
числа, у которых сумма цифр, стоящих на четных местах равна сумме цифр, стоящих
на нечетных местах, тогда это и 3520, и 3333 и т.д. Также учитель должен
обсудить с ребенком выполнение отдельно выделенных заданий (солнышко и
звездочку). Необходимо обсудить с ребенком проблематизацию старого способа
обоснования (полным перебором), которая возникает при доказательстве чисел с
большим количеством знаком, и затем, если это не было сделано ранее перейти к
разбору нового способа доказательства. Однако учитель не должен настаивать на
разборе нового способа доказательства, если ребенок не хочет этого делать, можно
остановиться с ним на обсуждении границ старого способа. Необходимо удержать
эмоциональный фон, сложившийся в процессе исследования, который может снижаться
у ребенка, если он сталкивается с трудностями, которые не может преодолеть.
Поэтому, возможность работы с новым способом доказательства учитель должен
регулировать в зависимости от способностей ребенка: сильный ребенок может
разобрать с учителем доказательства признаков для двухзначных и трехзначных
чисел, а затем самостоятельно провести доказательства для четырехзначных чисел
и т.д. Более слабые дети могут остановиться на совместном с учителем разборе
доказательств, либо же не разбирать новый способ доказательства, но при этом
нужно обсудить с ребенком, что если он не докажет свою гипотезу каким-либо
способом, то останется на уровне правдоподобных рассуждений.
Введение нормативного языка. В процессе работы с тетрадью посредством
текста вводится культурный язык. Нужно обсудить с ребенком текст, разобрать
введенную в нем схему исследования, соотнести ее с проводимой в тетради
работой. Учитель должен настаивать на культурном оформлении исследования,
должен выдерживать форму общения с ребенком в процессе работы на введенном
нормативном языке.
В конце работы с тетрадью учитель должен помочь ребенку представить
полученные им в процессе работы с тетрадью результаты. Для этого можно устроить
презентацию, на которую пригласить одноклассников ребенка, возможно, других
учителей математики, на которой ребенок расскажет о проведенной им работе.
Необходимо отметить о недостатках, которые выделяются в процессе
индивидуальной работы ребенка с тетрадью:
1. Процесс индивидуальной работы с тетрадью не позволяет ребенку
видеть возможности представленности других гипотез (версий).
2. Мотивация движения ребенка к доказательству может быть небольшой,
когда он двигается один, так как в процессе индивидуальной работы отсутствует
дух сотрудничества, соревновательности.
. Темп работы может быть низким, так как отсутствует дух
соревновательности.
Групповая работа.
Для работы с тетрадью дети могут объединяться в группы по 2 - 4 человека.
Работу с тетрадью можно организовывать как в одной группе, так и между
несколькими группами. Учителю необходимо договориться с детьми о способе работы
с тетрадью:
· Выделить в материале “порции”, например, две - три страницы тетради, с
которыми дети будут работать в промежутках между встречами с учителем.
· Договориться о ведении записей в тетради. Необходимо, чтобы
творческая тетрадь была у каждого из детей работающих в группе, с которой ребенок
мог бы заниматься в процессе самостоятельного исследования, записывая свои
мысли, как сможет. Также необходимо, чтобы у учителя был еще один экземпляр
тетради, в которую будут вноситься уже окончательно оформленные, прошедшие
обсуждение утверждения.
В процессе групповой работы выделяется три основных этапа:
. Индивидуальный этап, во время которого дети работают с тетрадью
самостоятельно.
. Обсуждение проведенной работы, полученных версий:
· Представление всех версий.
· Сопоставление версий в процессе дискуссии между детьми.
· Оформление окончательного варианта, который заносится в
тетрадь.
. Выбор направления дальнейшего творчества, переход к следующему этапу
работы.
Задачей учителя в процессе групповой работы с творческой тетрадью
является организация общих занятий, на которых бы происходило обсуждение
работы, которую дети проводили самостоятельно. Можно выделить следующие
ключевые занятия:
1. Работа с догадками (гипотезами).
2. Введение нормативного языка.
. Проблематизация старого способа обоснования, введение
доказательства.
Опишем идеи ключевых занятий.
Занятие 1. Работа с догадками (стр. 4 - 6).
Цель: Обсудить все гипотезы, оценить корректность формулировки, записать
наиболее корректную формулировку гипотез.
Задачи: 1. Организовать сравнение содержания утверждений и формулировок.
Обнаружить, что одно и тоже содержание может быть по-разному оформлено.
. Записать оптимальную формулировку гипотез.
Начать занятие можно с обсуждения того, какой признак делимости на 11 для
двухзначных чисел дети получили, записать его формулировку. Обсудить, как
ответили на вопрос: “Есть ли еще двухзначные числа, делящиеся на 11?”.
Обсуждение результатов вывода признака для трехзначных чисел нужно начать
с того, что узнать какой выбор сделали при ответе на вопрос: “Как тебе сейчас
кажется, трехзначное число делится на 11, если оно записывается одинаковыми
цифрами?”. Обсудить с детьми, почему они сделали тот или иной выбор. Если все
ответили одинаково, обсудить с ними вопрос: “Как мог рассуждать тот, кто выбрал
другой ответ?”. Обсудить их действия после выбора.
Узнать у детей, какие догадки у них получились и на что они смотрели,
чтобы их получить. Записать все догадки на доске. Обсудить, что общего и что
разное в догадках. Сформулировать оптимальный вариант записи догадки, записать
чистовой вариант в тетрадь.
Обратить внимание детей на следующий выбор. Обсудить какой они сделали
выбор, почему, как рассуждал человек сделавший другой выбор. Обсудить с детьми,
нужно ли проверять свой выбор. Обсудить их действия после выбора. Узнать какие
закономерности выделили у чисел из облачка. Обсудить какие догадки получились,
сформулировать общий вариант догадки, записать в тетрадь. Обсудить с детьми,
нужно ли проверять получившийся результат.
Занятие 2. Введение нормативного языка (стр. 7 - 11).
Цель: Ввести нормативный язык.
Задачи: 1. Прочитать и обсудить текст.
. Вывести признак делимости для четырехзначных чисел, проводя рассуждения
на нормативном языке.
. Ввести общую запись числа.
Начать занятие с прочтения текста на стр. 7 вслух, обсудить, как дети его
поняли, почему текст выделен восклицательным знаком, что важного хотел сказать
автор. Далее обсудить обоснование признака делимости трехзначных чисел, каким
способом его проводили. Записать окончательный вариант признака делимости на 11
для трехзначных чисел.
Прочитать текст на стр. 9 (индивидуально), обсудить, что нового дети
узнали, что поняли. Вернуться к выводу признака для трехзначных чисел, чтобы
дети определили, где гипотезы, выделили этапы исследования.
Перейти к выводу признака для четырехзначных чисел, с условием, что
обсуждения проходят на культурном языке, в процессе выделять этапы
исследования. Обсудить с детьми как они работали с облачком, сначала нашли свои
числа и разделили их на две группы или разделили числа из заполненного облачка.
Обсудить, каким способом дети находили четырехзначные числа для своего
множества. Выделить, какие числа входят в одну группу с числом 1210, выдвинуть
гипотезу о делимости для этих чисел. Провести проверку гипотезы - пусть каждый
ребенок предложит свое число. Обсудить задания обозначенные солнышком и
звездочкой.
Прочитать текст в рамочке на стр. 11 и обсудить, что дети поняли,
попросить детей записать числа с разным количеством знаков. Записать уже
выведенные признаки и гипотезы, используя новую форму запись числа.
Занятие 3. Проблематизация старого способа обоснования, введение
Доказательства (стр. 12 - 15).
Цель: Ввести общий способ доказательства.
Задачи: 1. Обсудить недостатки обоснования гипотез с помощью полного
перебора чисел.
. Разобрать доказательство для двухзначных и трехзначных чисел.
. Провести доказательство для четырехзначных чисел, заполнив текст с
пробелами.
. Вывести признак делимости для пятизначных чисел, доказать его.
В начале занятия вспомнить, что записали гипотезу о делимости для
четырехзначных чисел, обсудить нужно ли ее доказывать и каким способом.
Обсудить недостатки полного перебора. Прочитать текст, обозначенный
восклицательным знаком.
Разобрать доказательство признака для двухзначных чисел, определить, что
понятно, а что нет. Разобрать непонятные моменты в доказательстве. Предложить
детям объяснить друг другу доказательство для трехзначных чисел, выделить
основные этапы доказательства. Заполнить пустые места в доказательстве гипотезы
о делимости для четырехзначных чисел.
Вывести признак делимости для пятизначных чисел, обсудить каким способом
был он выведен. Записать гипотезу. Дать задание по группам, чтобы дети
проверили гипотезу, каждой группе свой способ. Записать признак в тетрадь.
Предложить детям провести доказательство признака для пятизначных чисел.
Вывести и записать признак делимости для произвольного числа, обсудить способ
вывода признака.
В заключение работы с творческой тетрадью проводится защита, презентация
полученных детьми результатов, а именно, того, что они смогли сделать, чего
нет, какие дополнительные задачи они решали в процессе работы с творческой
тетрадью. Защита проводится в форме образовательного праздника. На нее
приглашаются как одноклассники, не принимавшие участия в работе, так и внешние
слушатели: старшеклассники, другие учителя, директор, родители. В процессе
защиты дети представляют результаты в виде выступлений с плакатами. Работа
детей оценивается компетентным жюри по номинациям: “ Самый эмоциональный
доклад”, ”Самая интересная гипотеза”, и т.д., дети награждаются.
Необходимо выделить некоторые достоинства и недостатки групповой формы
работы. Достоинством является то, что, работая в коллективе, ребенок начинает
видеть свое движение, результаты; выделять индивидуальный, авторский характер
своих гипотез. В качестве недостатка можно выделить сложность организации
работы с тетрадью, которая выражается в необходимости проектировать занятия.
математический творчество школа тетрадь
2.1.4.2
Описание организационной формы передачи учителям методики работы с творческими
работами
В 2002 - 2003 годах на базе гимназии №1 “Универс” по заказу института
повышения квалификации проходил семинар для учителей по теме: “Руководство
творческими работами по математике в 6 и 7 классах”, проводимый сотрудниками
лаборатории развивающего обучения математике института психологии и педагогики
развития: О.И. Белоконь, О.В. Знаменская, Ю.Г. Юдина. Вела семинар О.В.
Знаменская. В создании проекта семинара также принимали участие студенты
психолого-педагогического факультета, обучающиеся по специальности “Математик.
Преподаватель”. Семинар состоял из двух частей, одна из которых была посвящена
творческой тетради и методике работы с ней.
Первая часть семинара состоялась осенью 2002 года и проходила в течение
двух дней. Целью данной части семинара было познакомить учителей с детским
математическим творчеством. Первый день семинара начался со знакомства с
учителями, которые должны были рассказать о школе, в которой они работают, о
том, что интересного происходит в их школе, связанного с математическим
образованием. После этого учителям было дано задание: написать, что, по их
мнению, является математическим творчеством, а что им не является, с вынесением
ответов на доску, подведением итогов. У учителей получилось, что к математическому
творчеству относятся: решение нестандартных задач, исследовательская
деятельность, сопровождающаяся эстетическими переживаниями, в результате
которой происходит развитие мышления, воображения, “математической зоркости”; в
качестве особенности детского математического творчества было выделено умение
использовать литературу, а также обязательное наличие у ребенка базового уровня
предметной подготовки. При этом к математическому творчеству нельзя отнести
действие по образцу. После подведения итогов, состоялась лекция, на которой
были сообщены характеристики детского математического творчества, а также,
откуда берутся творческие задачи. Например, для нахождения задачи выделяются
следующие этапы:
1. Решаем какую-либо известную задачу:
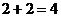 и
и 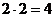 ;
; 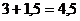 и
и  ;
; 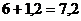 и
и 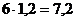
2. Происходит удивление, формулируется задача: есть ли еще такие
числа?
3. Происходит постановка творческой задачи: как найти все такие
числа.
Далее было дано задание для работы в группах: несколько задач, которые
нужно решить, затем чему-то удивиться и сформулировать задачу для творческой
работы. После выполнения работы группы делают доклады о получившихся
результатах, о трудностях с которыми они столкнулись при выполнении задания;
происходит общее обсуждение решения задач. В конце первого дня семинара учителя
получили тексты, с которыми необходимо было разобраться.
Второй день семинара начался с работы в группах, обсуждения текстов,
после чего состоялась лекция, в которой говорилось о возможности использования
разного рода текстов при выполнении творческой работы. Далее учителям был
предложен текст с описанием типов творческих работ, которые обсуждались в
течение лекции-беседы. Затем давалось задание (в группах): прочитать детскую
творческую работу, определить какого она типа и представить ее от лица ребенка
так, чтобы всем было понятно, какого типа работу выполнял ребенок. После этого
происходило обсуждение каждого из представлений. И, в заключение этой части
семинара были подведены итоги и дано задание учителям: попробовать себя в роли
руководителя творческой работы по решению одной из разобранных на семинаре
творческих задач.
Вторая часть семинара состоялась весной. Целью этой части семинара было
познакомить учителей с творческой тетрадью и методикой работы с ней. В начале
семинара была прочитана лекция, содержащая общие характеристики детского
математического творчества, а также особенности выполнения творческих работ
шестиклассниками. После этого учителям была предложена работа с творческой
тетрадью. Им было необходимо (работая в группах) приняв позицию ребенка
заполнить творческую тетрадь, при этом выделяя задуманные в тетради ловушки и
ключевые места. Результаты работы были представлены на общем заседании.
Например, в качестве ловушки была выделена следующая провокация: в процессе
доказательства признака делимости на 11 полным перебором, ребенку предлагается
рассмотреть другой способ доказательства, который ему пока непонятен; однако
если ребенок решится в нем сразу разобраться, чтобы не продолжать проверять
оставшиеся числа, вернувшись обратно на исходную страницу тетради, он обнаружит
задание, в котором необходимо записать количество трехзначных чисел, делящихся
на 11, для выполнения которого необходимо до конца разобраться с
доказательством признака полным перебором. В качестве ключевых мест учителя
выделили места, имеющие значение для продолжения работы:
· Текст в рамочке, в котором говорится о необходимости обязательного
обоснования гипотез.
· Схема, определяющая этапы исследования.
· Переход к
позиционной записи числа: 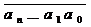
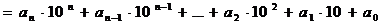 .
.
Итоги данного задания подводила лекция о содержании и структуре
творческой тетради. Далее учителям была предложена лекция о методике работы с
творческой тетрадью, после которой было дано последнее задание: спроектировать
ключевые занятия, которые необходимы при работе с творческой тетрадью.
Результаты были представлены группами на общем заседании, на котором были
доработаны прожекты групп к ключевым занятиям, связанным с работой детей с
догадками на начальном этапе исследования и с введением новых терминов. Семинар
закончился итоговой лекцией.
Проведя анализ вышеописанного семинара, можно выделить следующие
организационные формы работы, необходимые для освоения учителями методики
работы с творческими работами, в частности с творческой тетрадью:
· Представление творческой работы от лица ребенка.
· Работа с творческой тетрадью с позиции ребенка.
· Анализ творческой тетради, выделение ключевых мест, ловушек
структуры.
· Проектирование ключевых занятий.
§ 2 Комплект
материалов для обеспечения творческой работы по теме “Некоторые вопросы,
связанные с изучением бинома Ньютона”
Настоящий параграф посвящен описанию второго из разработанных нами
средств, которое представляет собой комплект учебно-исследовательских
материалов, обеспечивающих постановку подростком творческой задачи, а также
процесс ее решения.
1. Учебную тетрадь по теме: “Обобщение распределительного закона.
Доказательство истинности полученных в результате обобщения утверждений”.
2. Список тем творческих работ и описание возможных путей
исследования материала.
. Аннотацию к литературе по темам творческих работ.
Разработанная нами учебная тетрадь организует учебно-исследовательскую
деятельность подростка и приводит учащихся к постановке задачи творческой
работы. Кроме этого, в процессе работы с тетрадью создаются условия для
осуществления выбора учащимися уровня самостоятельности в исследовании, средств
для исследования.
Список тем творческих работ и указанием на возможные пути исследования
материала. Список тем дает ученику свободу выбора темы для творческой работы,
которая будет ему интересна, а также будет соответствовать уровню его
подготовки. Кроме этого, список с описанием путей исследования дает возможность
знать ребенку о имеющихся путях развития выбранной им темы.
Аннотация к литературе. Представлен список аннотированной литературы, в
которой содержатся ответы на некоторые вопросы по заданной теме. Каждый из
источников имеет подробную характеристику, с описанием вопросов, которые
освещаются в книге и имеют непосредственное отношение к творческой работе.
.2.2
Возможное содержание творческой работы
Одной из главных задач разработки учебно-исследовательского комплекта
была разработка содержания творческой работы по теме: “Некоторые вопросы,
связанные с изучением бинома Ньютона”. Так как творческих работ на эту тему
написано не было, то встала необходимость в проведении самостоятельного
исследования, чтобы выделить возможные пути обобщения формул сокращенного
умножения по степени, по количеству слагаемых, а также трудности, которые могут
возникнуть в процессе исследования материала. Описание данного исследования с
выделением трудностей и будет представлено в данном пункте.
В
седьмом классе на уроках математики изучаются формулы сокращенного умножения: 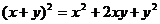 и
и  . Эти
равенства могут быть обобщены школьниками по степени до формулы, дающей
разложение для
. Эти
равенства могут быть обобщены школьниками по степени до формулы, дающей
разложение для  . Выпишем ряд формул, являющихся частными случаями для
. Выпишем ряд формул, являющихся частными случаями для
 , которые можно получить раскрыв скобки и приведя
подобные слагаемые:
, которые можно получить раскрыв скобки и приведя
подобные слагаемые: 

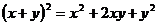
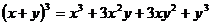 (2.1)
(2.1)
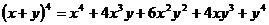

Проведя
анализ этих формул, можно выделить следующие свойства:
. Количество
слагаемых в правой части равенства на единицу больше степени, в которую был
возведен двучлен - бином (от латинского bis - дважды и
греческого “номос” - член) [7] - сумма двух членов. Поэтому, при возведении
бинома в n-ю степень число слагаемых будет равно 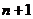 .
.
. Сумма
степеней членов бинома при разложении равна степени, в которую возводился
бином. Например:
 , видим,
что
, видим,
что 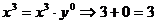 ;
;
 ;
; 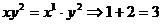 ;
; 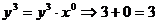 .
.
3. В правой части равенства степень у одного из членов бинома от
наибольшей постепенно уменьшается на 1 до нулевой степени, а у другого
одновременно с этим увеличивается с нулевой степени до степени, в которую
возводился бином.
4. Коэффициенты при членах бинома с наибольшей степенью равны 1.
Зная
эти свойства, получаем следующее разложение для формулы 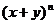 , биномиальные коэффициенты которой пока неизвестны:
, биномиальные коэффициенты которой пока неизвестны:
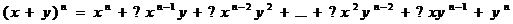
Для
получения полного разложения формулы необходимо найти, чему равны биномиальные
коэффициенты.
Продолжая
анализ формул (2.1), выпишем все биномиальные коэффициенты в виде треугольной
таблицы:
 или
или 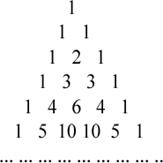
Данная
таблица называется “арифметическим треугольником” или, треугольником Паскаля, в
честь выдающегося французского математика и философа XVII века Блез
Паскаля (1623-1662) [3]. Она является одной из самых знаменитых таблиц в
истории математики. Паскаль посвятил ей специальный “Трактат об арифметическом
треугольнике”. Однако эта треугольная таблица была известна задолго до 1665
года, даты выхода труда Паскаля. Так, в 1529 году треугольник Паскаля был
воспроизведен на титульном листе учебника арифметики, написанного Петром
Апианом, астрономом из Ингольштадского университета. Изображен треугольник и на
иллюстрации в книге “Яшмовое зеркало четырех элементов” китайского математика
Чжу Шицзе, выпущенной в 1303 году. Омар Хайям, не только поэт и философ, но и
математик, знал о существовании треугольника коло 1100 года, а в свою очередь
заимствовал его из более ранних китайских или индийских источников. Но именно
Паскаль обобщил известные и привел много новых свойств треугольника, которые
сформулированы в девятнадцати теоремах [12].

рис.
2.1
Рассмотрим
арифметическую таблицу, выписанную в виде равнобедренного треугольника (рис.
2.1.) Видим, что в нем на вершине и по боковым сторонам стоят единицы, а каждое
из остальных чисел равно сумме двух чисел, стоящих над ним слева и справа в
предшествующей строке. Треугольник можно продолжать неограниченно. Он обладает
симметрией относительно вертикальной оси, проходящей через его вершину. Строка
с номером n состоит из коэффициентов разложения бинома 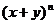 .
.
Треугольник Паскаля содержит и другие свойства, о которых можно прочитать
в [2, 12]. Например, вдоль диагоналей, параллельных сторонам треугольника,
выстроены треугольные числа и их обобщения на случай пространств всех
размерностей (рис. 2.2). Суммы чисел, стоящих вдоль восходящих диагоналей,
образуют последовательность чисел Фибоначчи. Если, спускаясь по центральному
столбцу, из каждого числа вычитать соседнее справа (или слева), то возникает
последовательность чисел Каталана.
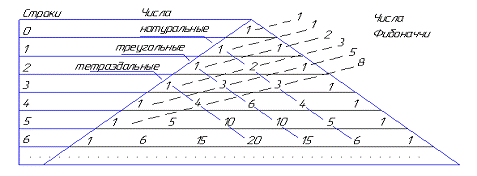
рис. 2.2
Таким образом, биномиальные коэффициенты можно найти при помощи
треугольника Паскаля и выведенного правила. Однако этот способ не всегда удобен
для получения биномиальных коэффициентов.
Разберем
второй способ нахождения биномиальных коэффициентов, связанный с поиском числа
сочетаний, которые принято обозначать  или
или  - число сочетаний из n по k
элементов.
- число сочетаний из n по k
элементов.
Рассмотрим известные формулы:
 и
и 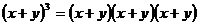
Раскроем
скобки в правой части этих равенств, причем будем записывать все множители в
том порядке, в котором они нам встретятся:
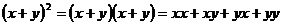
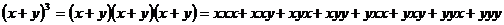
Видно,
что в формулу квадрата суммы входят все сочетания, составленные из букв a и b по
две буквы, а в формулу куба суммы - сочетания из тех же букв, но состоящие из
трех букв каждое. То же самое будет и в общем случае:
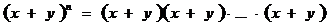
мы получим всевозможные сочетания с повторениями букв x и y, состоящие из n
элементов[4].
Теперь найдем формулу для получения числа сочетаний, т.е. биномиальных
коэффициентов. Для этого рассмотрим уже известные формулы. Однако так как
сочетания для x и y повторяются, то будем рассматривать сочетания по числу
вхождений в них х.
Итак,
для  получаем, что в рассматриваемом множестве два элемента
получаем, что в рассматриваемом множестве два элемента
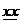 , тогда получаем число сочетаний из двух элементов по
два равно единице (два элемента из двух мы можем выбрать только единственным
образом); число сочетаний из двух элементов по одному равно двум, число
сочетаний из двух элементов по нулю элементов равно единице:
, тогда получаем число сочетаний из двух элементов по
два равно единице (два элемента из двух мы можем выбрать только единственным
образом); число сочетаний из двух элементов по одному равно двум, число
сочетаний из двух элементов по нулю элементов равно единице: 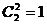 ,
, 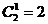 ,
, 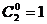 - биномиальные коэффициенты. Получили формулу:
- биномиальные коэффициенты. Получили формулу:
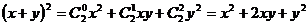
Для
 получаем множество из трех элементов
получаем множество из трех элементов  , тогда получаем, что число сочетаний из трех
элементов по три равно единице
, тогда получаем, что число сочетаний из трех
элементов по три равно единице 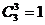 ; число
сочетаний из трех элементов по два равно трем
; число
сочетаний из трех элементов по два равно трем 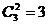 , число
сочетаний из трех элементов по одному равно трем
, число
сочетаний из трех элементов по одному равно трем 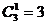 , число
сочетаний из трех элементов по нулю элементов равно
, число
сочетаний из трех элементов по нулю элементов равно 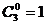 . Получили формулу:
. Получили формулу:
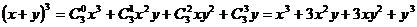 .
.


рис. 2.3
Теперь
проведем рассуждения для  . Рассмотрим множество из пяти элементов
. Рассмотрим множество из пяти элементов  . Найдем число сочетаний из пяти элементов по два,
рассуждая следующим образом: во множестве пять элементов, каждый из которых
может быть взят в паре с другими, четырьмя способами (рис. 2.3), но среди
получившихся сочетаний встречаются повторяющиеся, каждая пара повторяется еще
раз, поэтому получаем формулу:
. Найдем число сочетаний из пяти элементов по два,
рассуждая следующим образом: во множестве пять элементов, каждый из которых
может быть взят в паре с другими, четырьмя способами (рис. 2.3), но среди
получившихся сочетаний встречаются повторяющиеся, каждая пара повторяется еще
раз, поэтому получаем формулу: 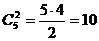 .
Подобные рассуждения проводятся и для сочетаний с другим количеством элементов.
.
Подобные рассуждения проводятся и для сочетаний с другим количеством элементов.
Рассмотрим
общий случай, т.е. множество из  элементов.
Найдем число сочетаний из
элементов.
Найдем число сочетаний из  элементов по два: во множестве
элементов по два: во множестве  элементов, каждый из которых может быть взят в паре с
другим
элементов, каждый из которых может быть взят в паре с
другим 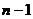 способом (рис. 2.4), но среди них есть повторяющиеся,
каждая пара повторяется еще раз, поэтому получаем формулу:
способом (рис. 2.4), но среди них есть повторяющиеся,
каждая пара повторяется еще раз, поэтому получаем формулу:
 .
.
Проводя
рассуждения при выводе общей формулы для числа сочетаний  , где k большое число, легко запутаться. Поэтому предлагаем
проводить рассуждения для k = 3, 4, 5, 6,7.
, где k большое число, легко запутаться. Поэтому предлагаем
проводить рассуждения для k = 3, 4, 5, 6,7.
Проводя
подобные рассуждения для других случаев будем получать следующие формулы:
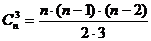 ;
; 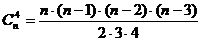
 ; … … …
…;
; … … …
…;  =
=
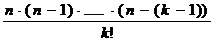 =
= =
= .
.
Формулы
для 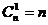 ,
, 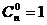 ,
, 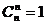 ,- очевидны.
,- очевидны.
Таким
образом, формулы биномиальных коэффициентов найдены. Получаем следующее
разложение для формулы 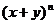 :
:
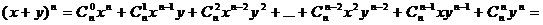
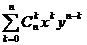 .
.
Данное
разложение называется формулой бинома Ньютона.
Формулу
 называют формулой бинома Ньютона, но это название с
точки зрения истории неверно. Формулу для
называют формулой бинома Ньютона, но это название с
точки зрения истории неверно. Формулу для  хорошо
знали среднеазиатские математики Омар Хайям, Гиясэддин и др. Заслуга же Ньютона
в том, что ему удалось обобщить формулу на случай нецелых показателей [4].
хорошо
знали среднеазиатские математики Омар Хайям, Гиясэддин и др. Заслуга же Ньютона
в том, что ему удалось обобщить формулу на случай нецелых показателей [4].
Таким
образом, мы вывели разложение формулы бинома Ньютона, которая является
обобщением формул 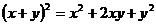 и
и 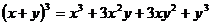 ; два
способа нахождения биномиальных коэффициентов: через треугольник Паскаля и
формулу числа сочетаний
; два
способа нахождения биномиальных коэффициентов: через треугольник Паскаля и
формулу числа сочетаний  .
.
Бином
Ньютона можно обобщить по количеству слагаемых, т.е. найти разложение для  , однако вывод данной формул является довольно сложным
для школьника. Поэтому рассмотрим частный случай формулы, формулу для суммы
трех переменных, т.е. для тринома. Выведем разложение для тринома
, однако вывод данной формул является довольно сложным
для школьника. Поэтому рассмотрим частный случай формулы, формулу для суммы
трех переменных, т.е. для тринома. Выведем разложение для тринома 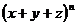 , а также арифметическую таблицу триномиальных
коэффициентов.
, а также арифметическую таблицу триномиальных
коэффициентов.
Рассмотрим
ряд формул, являющихся частными случаями для 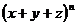 , которые
можно получить раскрыв скобки и приведя подобные слагаемые:
, которые
можно получить раскрыв скобки и приведя подобные слагаемые:




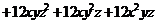
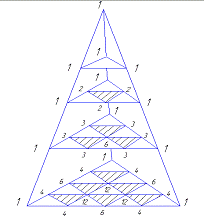

рис. 2.5
Построим
арифметическую таблицу из триномиальных коэффициентов, данная таблица будет
представлять собой пирамиду, которую называют пирамидой Паскаля (рис. 2.5).
Видим, что по трем внешним ребрам пирамиды стоят единицы. Каждая из трех
боковых граней представляет собой треугольник Паскаля. В n-ом
сечении (треугольнике) пирамиды (n ≥
0), параллельном основанию, располагаются триномиальные коэффициенты (которые
обозначаются  ) подобно биномиальным коэффициентам в треугольнике
Паскаля.
) подобно биномиальным коэффициентам в треугольнике
Паскаля.
Рассмотрим
сечения пирамиды для  ,
,  и
и 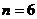 (рис. 2.6):
(рис. 2.6):



рис.
2.6
Видим, что коэффициенты, лежащие внутри сечения пирамиды в углу, равны
сумме двух коэффициентов располагающихся на внешней стороне сечения, которые
лежат на одной прямой с этим коэффициентом. Правило для нахождения
триномиальных коэффициентов, стоящих внутри сечения пирамиды, вызвало большие
трудности, поэтому правило вывода триномиальных коэффициентов было взято из
литературы [12].
Известно,
что любой внутренний элемент пирамиды Паскаля, стоящий в n -ом
сечении, равен сумме трех элементов, расположенных в углах элементарного
треугольника 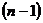 - го сечения пирамиды [2]. Построение n-го
сечения связывают с равенством :
- го сечения пирамиды [2]. Построение n-го
сечения связывают с равенством :
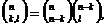
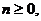
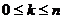 ;
; 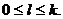
Сечение
получается из треугольника Паскаля, основанием которого служит  -я строка треугольника, умножением элементов его строк
почленно на элементы основания, повернутого против часовой стрелки на угол
-я строка треугольника, умножением элементов его строк
почленно на элементы основания, повернутого против часовой стрелки на угол  . Рис. 2.7, а иллюстрирует построение сечения при n=4.
Расположение элементов
. Рис. 2.7, а иллюстрирует построение сечения при n=4.
Расположение элементов  сечения показано на рис. 2.7, б [12, 13].
сечения показано на рис. 2.7, б [12, 13].

рис. 2.7
Получим
разложение тринома 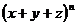 . Для этого воспользуемся полученными формулами:
формулой бинома Ньютона и формулой биномиальных коэффициентов.
. Для этого воспользуемся полученными формулами:
формулой бинома Ньютона и формулой биномиальных коэффициентов.
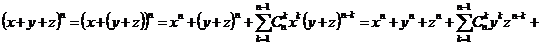
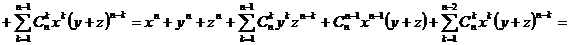
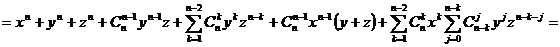

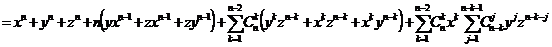
В
полученной формуле часть:
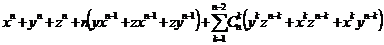
выражает
основание треугольника Паскаля, т.е. триномиальные коэффициенты, которые лежат
на внешней стороне  -го сечения пирамиды. А часть полученной формулы:
-го сечения пирамиды. А часть полученной формулы: 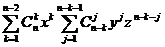 выражает триномиальные коэффициенты, лежащие внутри
выражает триномиальные коэффициенты, лежащие внутри  -го сечения пирамиды.
-го сечения пирамиды.
В
литературе разложение тринома 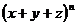 представляют
в виде:
представляют
в виде:
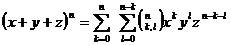 ,
,
где
 - триномиальные коэффициенты,
- триномиальные коэффициенты,  ,
, 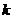 ,
, 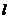 - неотрицательные целые числа, которые выражаются
формулой:
- неотрицательные целые числа, которые выражаются
формулой:
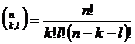
Для
триномиальных коэффициентов справедлива рекуррентная формула:
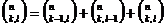
с
начальными условиями 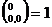 ;
; 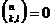 .
.
Триномиальные коэффициенты удовлетворяют условиям:
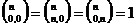
и равенствам
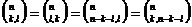 ,
,
указывающих
на наличие трех осей симметрии [12].
Итак,
наше исследование показало, что можно обобщить формулы квадрата суммы и куба
суммы по степени, получив разложение формулы бинома Ньютона. Биномиальные
коэффициенты можно найти либо при помощи треугольника Паскаля, записав
коэффициенты разложения в виде треугольной таблицы и выведя очевидное правило,
либо посредством формул числа сочетаний  , которые
возможно вывести. Также оказался возможным построение пирамиды Паскаля и вывод
разложения для тринома. При этом нужно отметить, что если для вывода разложения
бинома литература является средством подтверждения полученных результатов, то
для разложения тринома литература является дополняющим средством к полученным
результатам. Полученные результаты исследования были сопоставлены и дополнены
материалом книг по этим вопросам.
, которые
возможно вывести. Также оказался возможным построение пирамиды Паскаля и вывод
разложения для тринома. При этом нужно отметить, что если для вывода разложения
бинома литература является средством подтверждения полученных результатов, то
для разложения тринома литература является дополняющим средством к полученным
результатам. Полученные результаты исследования были сопоставлены и дополнены
материалом книг по этим вопросам.
Заключение
Моя работа была направлена на разрешение проблем, возникающих у учителей,
которые не имеют опыта работы с детскими творческими работами, но хотели бы
заниматься ими со своими учениками. Для этого было разработано
учебно-методическое средство, которое мы назвали творческой тетрадью - особым
образом оформленная тетрадь, содержащая логику предъявления исследовательской
задачи и специальным образом представленные задания. Используя эту тетрадь,
учитель может освоить идею руководства детским исследованием в математике.
Кроме этого, тетрадь также должна обеспечивать эмоциональную включенность и
сохранение устойчивого интереса к теме у шестиклассника, инициировать
возникновение у него своих вопросов, творческое отношение к предложенным
задачам.
Итак, была разработана творческая тетрадь по теме “Признаки делимости на
11 натуральных чисел”. Результаты проведенной апробации подтвердили, что она
действительно является средством обеспечения выполнениям ребенком творческой
работы по математике. Действительно, учащимся интересна работа с тетрадью,
кроме имеющихся в тетради вопросов, они начинают ставить свои вопросы,
придумывать задачи, которые с интересом решают.
Также в процессе работы учащихся с тетрадью было отмечено, что они
действительно попадают в придуманные нами ловушки. Это подтвердило выдвинутую
нами гипотезу о преобладании эмпирического обобщения при решении учащимися подобных
задач. И детям, и учителям работа с тетрадью понравилась. По материалам
апробации была написана методика работы с творческой тетрадью.
В процессе работы нами также были решены дополнительные задачи. Был
разработан учебный комплект по теме “Некоторые вопросы, связанные с изучением
бинома Ньютона”, организующий исследование учащихся 7-8 классов. Однако
апробации разработанного комплекта проведено не было.
Возможными направлениями дальнейших исследований связанных с творческой
тетрадью может быть, например, исследование специфики работы с тетрадью детьми,
обучающимися по программам традиционного и развивающего обучения; предметно
сильных и слабых детей; исследование, связанное с выделением особенностей
ловушек, содержащихся в творческой тетради по сравнению с ловушками в
программах по математике начальной школы развивающего обучения.
Литература
1. Аронов
А.М., Ермаков С.В., Знаменская О.В. Учебно-образовательное пространство в
педагогике развития: математическое образование: Монография / КГУ, 2001.
2. Бондаренко
Б.А. Обобщенные треугольники и пирамиды Паскаля, их фрактали, графы и
приложения. Ташкент: “Фан”, 1990.
. Бородин
А.И., Бугай А.С. Биографический словарь деятелей в области математики. Киев: “Радянська школа”, 1979.
. Виленкин
Н.Я. Комбинаторика. М.: “Наука”, 1969.
. Виленкин
Н.Я., Сурвилло Г.С., Дробышев Ю.А., Кудрявцев А.И. Алгебра-8. Учебное пособие
для школ и классов с углубленным изучением математики. Новосибирск: “Наука”,
1992.
. Воронцов
А.Б., Заславский В.М., Егоркина С.В., Захарова О.А. Учебная самостоятельность
подростка как одно из условий организации образовательного процесса в основной
школе.
. Глейзер
Г.И. История математики в школе. М., 1983.
. Давыдов
В.В. Виды обобщения в обучении. М., 1972.
. Знаменская
О.В., Юшкова Е.В. Признаки делимости на 11 натуральных чисел: творческая
тетрадь для учащихся 6 классов. На правах рукописи, 2002.
.
Кашапов М.М., Табаков Ю.А. Обучение творческому решению проблемных ситуаций в
процессе преподавания психологии как средство формирования интеллектуальных
способностей старшеклассников // Педагогика развития: проблемы современного
детства и задачи школы: Материалы III науч.-практ. конф. Красноярск, 1996, Ч. 2.
.
Кордемский Б.А. Математическая смекалка., 2000.
.
Кузьмин О.В. Обобщенные пирамиды Паскаля и их приложения. Новосибирск: “Наука”,
2000.
.
Кузьмин О.В. Треугольник Паскаля: свойства и обобщения //Соросовский
образовательный журнал. Том 6, № 5, 2000.
.
Миндюк М.Б., Рудницкая В.Н. Математика. Рабочая тетрадь для 6 класса. Часть 1.
М.: “Генжер”, 2001.
.
Поливанова К.Н. Психологическое содержание подросткового возраста // Вопросы
психологии. 1996, № 1.
.
Табидзе О.И. Ценностный аспект творчества // Вопросы философии. 1981, №6.
.
Щетников А.И. Арифметика по Пифагору. Рабочая тетрадь. : издательство гимназии
“Открытый мир”,
.
Шумилин А.Т. Проблемы теории творчества: Монография. М.: Высшая школа, 1989.
.
Юдина Ю.Г. Организация творческой деятельности подростков. Методическое пособие
для педагогов и студентов педагогических специальностей университета.
Красноярск, 2003.
.
Яковлева О.В., Торопова Ю.Г. Педагогические условия выполнения учащимися 6
класса творческих работ по математике // Педагогический ежегодник. Красноярск,
1996.