Решение систем уравнений
Задача 1.16
Доказать совместность системы линейных уравнений и решить ее двумя
методами:
) методом Крамера,
) методом Гаусса,
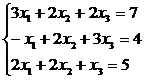
Решение:
Система
является совместной, если определитель матрицы, составленной из ее
коэффициентов, не равен 0
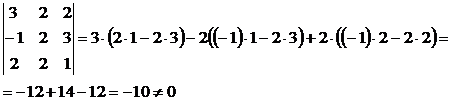
.
Метод Крамера.
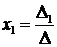
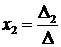
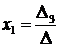
Где
Δ
- определитель матрицы, составленный из
коэффициентов системы; Δ1 ,Δ2 ,Δ3 - определители матриц, составленных из коэффициентов
системы при замене соответственного столбца на столбец свободных коэффициентов.
Δ = - 10
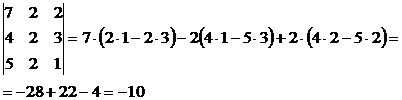
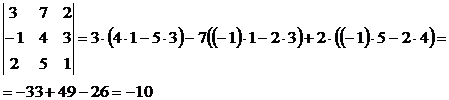

Отсюда
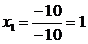
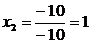
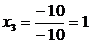
.
Метод Гаусса. Основан на преобразованиях, которые не изменяют множество решений
системы:
перестановка
уравнений;
умножения
уравнения на число, отличное от нуля;
замена
уравнения на сумму этого уравнения и другого из этой же системы.
Посредством
этих преобразований приводим систему к треугольному виду.
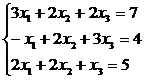
Умножаем
второе уравнение на 3 и складываем с первым. Умножаем первое уравнение на 2,
третье - на (- 3) и складываем их

Умножаем
третье уравнение на 4 и складываем со вторым.

Мы
привели систему к треугольному виду. Отсюда получаем решение:
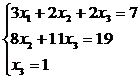

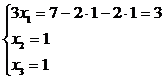
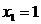
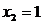
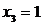
Задача 2.16
Найти общее и одно частное решение системы линейных уравнений
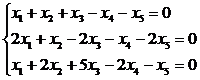
Решение:
Найдем
ранг матрицы
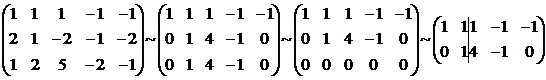
вычтем
из третьей строки первую, затем умножим вторую строку на 2 и вычтем из нее
первую;
вычтем
из третьей строки вторую.
Ранг
матрицы равен r = 2 < 3, следовательно выполняется условие
существования ненулевого решения однородной системы уравнений.
Выберем
в качестве базисного минора
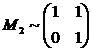
Запишем
укороченную систему

В
качестве базисных выберем неизвестные х1 и х2. Тогда х3, х4, х5- свободные
неизвестные. Полагая х3 = с3, х4 = с4, х5 = с5, получим

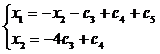
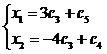
Таким
образом, общее решение будет
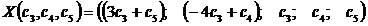
Частное
решение найдем, придав сi любые значения, например 1. Тогда частное решение
будет
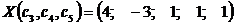
Задача 3.16
Даны координаты вершин пирамиды АВСD.
1.
Найти модуль вектора 
.
Найти площадь грани АВС
.
Найти длину высоты, опущенной из вершины D.
.
Найти косинус угла между векторами 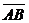 и
и 
.
Записать уравнение плоскости АВС
.
Записать уравнение высоты, опущенной из вершины D на грань АВС.
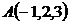 ,
,  ,
,  ,
, 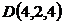
Решение
.
Найти модуль вектора 

.
Найти площадь грани АВС. Площадь треугольника АВС численно равна половине
модуля векторного произведения любых двух сторон треугольника АВС:
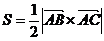
Найдем
векторное произведение.
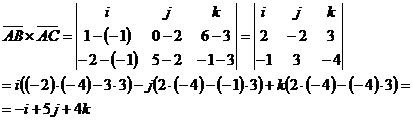
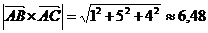

.
Найти длину высоты, опущенной из вершины D
Найдем
уравнение плоскости АВС. Для этого подставим координаты точек А, В, С в общее
уравнение плоскости  и решим получившуюся систему уравнений
и решим получившуюся систему уравнений
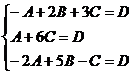
Решим
систему методом Гаусса
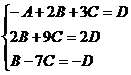
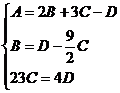

В
результате имеем уравнение плоскости АВС
Длину
высоты находим как расстояние от точки D до плоскости
АВС по формуле

.
Найти косинус угла между векторами 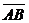 и
и 
Косинус
угла между векторами находим как скалярное произведение этих векторов, деленное
на произведение их длин

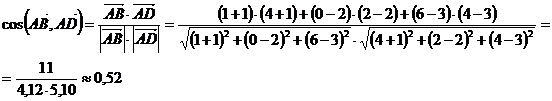
.
Записать уравнение плоскости АВС
Уравнение
плоскости АВС нашли в п.3
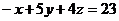
.
Записать уравнение высоты, опущенной из вершины D на грань АВС.
Уравнение
высоты находим из тех соображений, что ее направляющий вектор должен быть перпендикулярен
плоскости, а, следовательно, совпадать с нормалью. Вектор нормали к плоскости
запишем из уравнения плоскости: (- 1, 5, 4)
Тогда
уравнение высоты, т.е. прямой, перпендикулярной плоскости с нормалью (- 1, 5,
4) и проходящей через точку 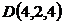 будет
(исходя из общего уравнения прямой)
будет
(исходя из общего уравнения прямой)

Задача 4.16
Даны две смежные вершины квадрата А(1, - 3), В(2, 1). Составить уравнения
его сторон.
Решение:
Составим сначала уравнение стороны АВ, исходя из общего уравнения прямой

Прямые
АD и BC перпендикулярны прямой АВ, следовательно, их угловой
коэффициент будет равен
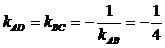 , а
уравнения этих прямых будет
, а
уравнения этих прямых будет
АD: 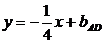 BC:
BC: 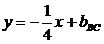
Свободные
члены уравнений найдем, подставив в уравнения координаты точек:
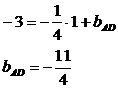
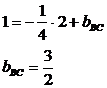
Уравнения,
следовательно, будут
АD: 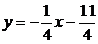 BC:
BC: 
Уравнение
прямой СD будет иметь угловой коэффициент такой же как и
уравнение прямой АВ и будет иметь вид
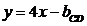
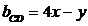
Чтобы
найти свободный член, найдем длину стороны квадрата АВ
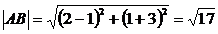
Найдем
расстояние l от прямых АВ и CD до начала
координат. Для этого найдем координаты точек пересечения этих прямых и
перпендикуляра, опущенного из начала координат:
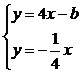
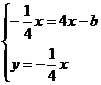
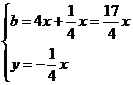
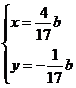
Тогда
расстояние до начала координат будет
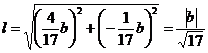
Так
как для прямой АВ b = - 7 , то

Расстояние
между прямыми АВ и CD равно стороне квадрата. Следовательно, расстояние от
прямой CD до начала координат, можем найти:
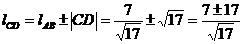
Будем
учитывать, что сторона СD может лежать как с одной стороны от стороны АВ, так и
с другой, поэтому задача решается неоднозначно.
Но
 , откуда
, откуда 
В
результате имеем уравнение прямой СD
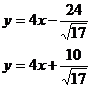
Ответ:
Уравнения сторон квадрата будут:АВ: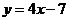 ; АD:
; АD: 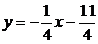 ; BC:
; BC:  ; СD
; СD 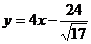 или
или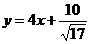
Задача 5.16
Привести уравнение кривой второго порядка f(x, y) к каноническому виду. Определить
вид кривой и построить ее график.

Решение:
Выделим
полные квадраты


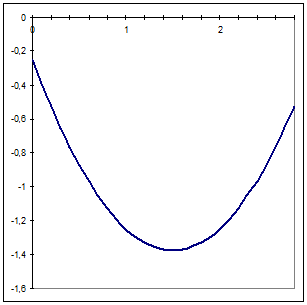
Т.е.
мы получили параболу, ось которой параллельна оси у, а вершина лежит в точке 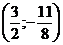
Задача 6.16
Найти указанные пределы, не пользуясь правилом Лопиталя
а)
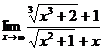
Имеем
неопределенность типа  . Для устранения ее разделим числитель и знаменатель
на х
. Для устранения ее разделим числитель и знаменатель
на х
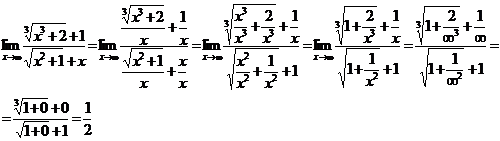
б)
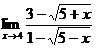
уравнение векторный тригонометрический функция
Для
устранения неопределенности умножим числитель и знаменатель на сопряженные
множители

в)
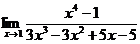
Разложим
числитель и знаменатель на множители

г)
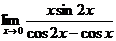
С
помощью тождественных преобразований приведем предел к первому замечательному
пределу
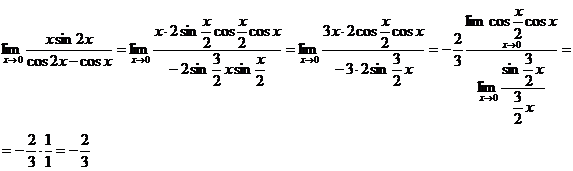
д)

С
помощью тождественных преобразований приведем выражение ко второму
замечательному пределу
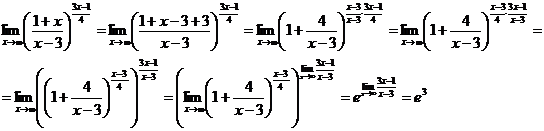
Задача 7.16
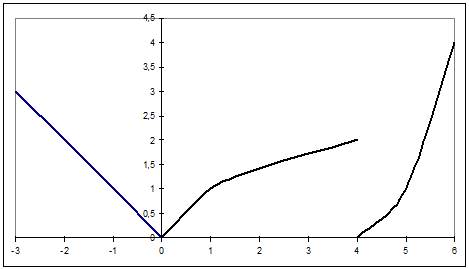
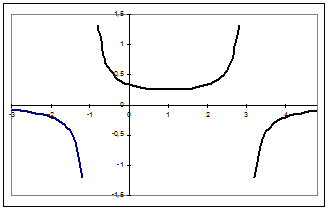
Исследовать функцию y = f(x) на непрерывность, найти точки разрыва функции и определить
их тип. Построить схематический график функции.
а)
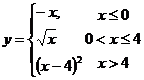
Найдем
пределы справа и слева от предполагаемых точек разрыва
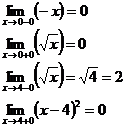
б)
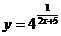
Функция
имеет разрыв в точке х = - 5/2
Найдем
пределы справа и слева от предполагаемых точек разрыва
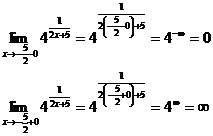
Функция
имеет разрыв второго рода
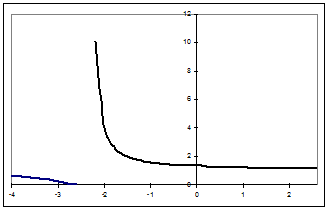
б)

Найдем
корни знаменателя.
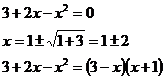
Следовательно,
функция имеет разрыв в точках х = 3 и х = - 1. Найдем пределы функции справа и
слева в этих точках
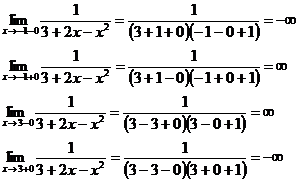
Т.е.
функция имеет в этих точках разрывы второго рода
Задача 8.16
Дано комплексное число z.
Найти:
а) модуль числа z,
аргумент z;
б) записать z в
тригонометрической и показательной формах;
в)
найти все значения 
г)
изобразить точками плоскости числа z и 
z =- 64i
Решение:
а)
модуль числа z r = 64, аргумент числа z 
б)
Тригонометрическая форма числа z:
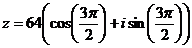
Показательная
форма числа z
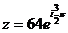
в)
найдем все значения 
Применим
формулу Муавра

При
k = 0 
При
k = 1 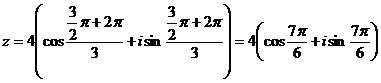
При
k = 2 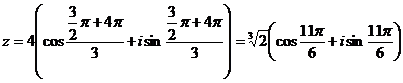
Изобразим
корни уравнения на рисунке:

Список
литературы
1. Фихтенгольц
Г.М. Курс дифференциального и интегрального исчисления. Т.1. М., 1997 г.
2. Фихтенгольц
Г.М. Курс дифференциального и интегрального исчисления. Т.2. М., 1998 г.