Математическое моделирование в энергетике

Математическое моделирование в энергетике

Курсовая работа

«Математическое моделирование в энергетике»

1. Формирование узловых и контурных уравнений установившихся режимов электрической сети

.1 Составление схемы замещения электрической сети, определение ее параметров и нагрузок в узлах

Балансирующий узел по условию: Г

Нагрузки: Г+2=Е, Г+4=И, Г+5=А.

Генерирующий источник: Г+3=Ж.

X-число букв в фамилии (Нистюк)

Y-число букв в имени (Сергей);

Z-число букв в отчестве (Николаевич);

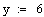
Базовая длина участка:

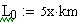
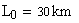
Базовая мощность:

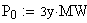
Напряжение в балансирующем узле:

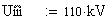
Пронумеруем схему в соответствии с принципом ярусности. Получаем 8 узлов, 7 ветвей дерева, 3 хорды.

Длины первого и последнего участков соответственно:

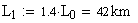
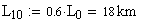
Зная удельное сопротивление ветвей х0=0,4Ом/км и длины всех участков сети, найдем их сопротивления по формуле:

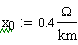
Вычисляем мощности в заданных узлах по формуле:

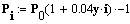 где 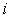 - номер узла.

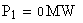
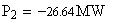
1.2 Составление элементарных матриц параметров режима сети и матриц соединений

Матрицу параметров режима составим по уже известным мощностям в узлах сети:

По формуле 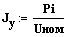 найдем задающие токи. В первом приближении.

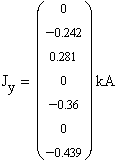
Составляем диагональную матрицу сопротивлений. Затем находим обратную ей матрицу, которую будем называть матрицей проводимостей ветвей:

Составим матрицу соединения ветвей в независимые контуры N или вторую матрицу инциденций, которая позволяет сформировать контурную модель электрической сети. Матрица N будет составной. Её элементами будут матрицы N_α - матрица соединений для ветвей дерева и N_β - матрица соединений для хорд схемы.

Выделим из матрицы N матрицы N_α и N_β.

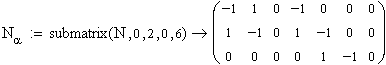
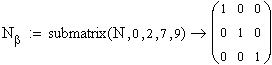
2. Расчет режима электрической сети по линейным узловым и контурным уравнениям при задании нагрузок в токах, анализ результатов расчета

.1 Расчет режима электрической сети по линейным узловым уравнениям

Произведем расчет режима нашей электрической сети.

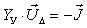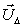Узловое уравнение в матричной форме имеет вид . При помощи этого уравнения мы можем найти напряжения в узлах схемы. Для этого из уравнения найдем матрицу-столбец падений напряжения  в узлах схемы относительно балансирующего узла (элементы матрицы 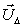 будут иметь отрицательное значения), а затем для получения матрицы-столбца узловых напряжений Uу сложим матицы-столбцы падений напряжения и напряжения в балансирующем узле.

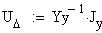
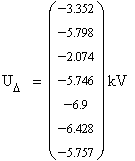
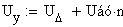
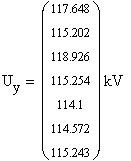
Из полученных значений узловых напряжений видно, что напряжение значительно падает в тех узлах, которые имеют большую нагрузку и имеют малое число связей с соседними узлами. Генерирующий узел (узел 3) имеет тенденцию к повышенному напряжению. Это можно объяснить тем, что в генерирующем узле мощность не потребляется из сети, а наоборот, поступает в сеть.

При помощи матрицы падений напряжений в узлах схемы и матрицы M^T мы можем найти падения напряжений уже на ветвях схемы.

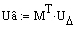
Зная падения напряжений на ветвях схемы легко можно найти токи в ветвях. Для этого умножим обратную диагональную матрицу dZв на падения напряжения в ветвях:

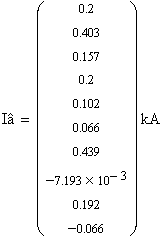
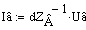
Как видно, значения полностью идентичные. Следовательно, можно смело утверждать, что проведенные ранее расчеты верны.

2.2 Произведем расчет режима электрической сети на основе контурных уравнений

Контурное уравнение в матричной форме имеет вид:

.

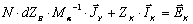В нашей схеме нет ЭДС в контурах, поэтому .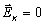

.

Так как обратная матрица Mα (Mα^-1) имеет размерность (7*7), а произведение - N*dZв имеет размерность (10*3), то перемножить их не можем. Однако мы можем дополнить матрицу Mα^-1 нулевыми элементами (обозначим ее Mα1), которые не повлияют на результат, но дадут нам возможность перемножить матрицы.

Выразим контурный ток из уравнения: .

Контурный ток находится как: .

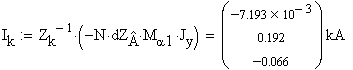
Ток в хорде схемы равен контурному току, протекающем в контуре, содержащем данную хорду. Обозначим токи в хордах как I_β.

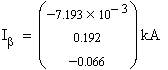
Зная токи в хордах схемы и задающие токи в узлах, найдем токи в ветвях дерева схемы Iα:

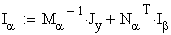
Для вычисления напряжений в узлах схемы Uу, необходимо найти падения напряжения в узлах схемы относительно балансирующего, а затем для получения самих узловых напряжений взять сумму матриц напряжений в балансирующем узле и падений напряжений в узлах схемы. Причем значения матрицы падений напряжения в узлах имеют отрицательные значения.

Для нахождения падений напряжения в узлах относительно балансирующего, возьмем пять первых значений падений напряжения (в ветвях дерева) из матрицы UΔв. Для получения падений напряжения в узлах UΔ, умножим матрицу Mα^T-1 на пять первых значений матрицы UΔв.

Так как для нахождения задающих токов в узлах мы брали номинальное напряжение, а это напряжение в узлах не соответствует действительным напряжениям, то необходимо проверить точность произведенных расчетов. Для этого определим небаланс задающих мощностей.

Для этого найдем ток в узлах схемы, зная ток ветвях I в и первую матрицу инциденций M.

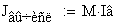
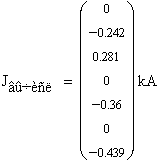
Вычисляем небаланс в МВт и%.

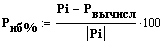
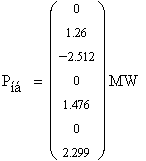
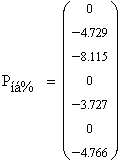
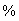
Небаланс мощности во всех узлах превышает допустимое значение в 1%. Для увеличения точности расчета режима уточним задающие токи в узлах сети. Для этого вместо номинального напряжения в формуле для вычисления задающих токов подставим значения напряжений в узлах, полученные при расчете первого приближения.

Так как оба метода (метод контурных уравнений и метод узловых уравнений) дают идентичные результаты, то рассчитаем режим сети во втором приближении лишь методом узловых уравнений.

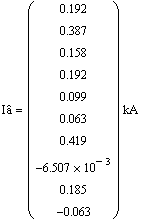
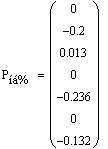
Небаланс мощности составляет менее 1%. В пределах данной задачи нас это вполне удовлетворяет. Следовательно, расчет режима сети по методам контурных и узловых уравнений окончен.

Как видно из расчетов, методы контурных уравнений и узловых уравнений дают совершенно идентичные результаты. Однако метод узловых уравнений оказался более быстрым и удобным в использовании, по сравнению с методом контурных уравнений.

3. Расчет режима электрической сети по узловым уравнениям в форме баланса токов при их решении методом ускоренной итерации

.1 Расчет режима по узловым уравнениям в форме баланса токов при их решении методом простой итерации

электрический сеть уравнение нагрузка

 (3.1.1)

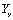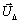где  - матрица узловых проводимостей без учета балансирующего узла,  - вектор-столбец падений напряжений, относительно балансирующего, 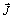 - вектор-столбец задающих токов (содержащих свой знак).

Правую часть уравнения (3.1.1) представим в виде:

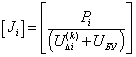 (3.1.2)

где 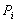 - задающая мощность в i-том узле,  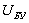- напряжение в балансирующем узле,  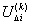- падение напряжения в i-том узле при k-том приближении.

Приравняем левую часть уравнения (3.1.1) и правую часть уравнения (3.1.2):

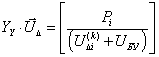 (3.1.3)

На основе уравнения (3.1.3) составим систему уравнений, применительно к нашей сети, представив левую часть в алгебраической форме, а правую оставив без изменения:

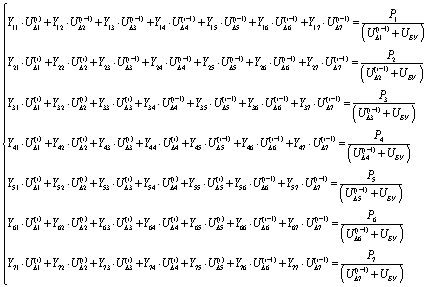
Уравнения системы разрешим относительно диагональных неизвестных 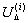. Для этого необходимо перенести все элементы каждого уравнения вправо, оставив слева лишь произведение, содержащее 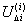, где i - номер уравнения в системе. Затем разделим обе части уравнения на 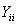(диагональные элементы в матрице узловых проводимостей 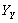не могут равняться нулю, следовательно, такое деление возможно), стоящий при 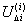, где i - номер уравнения в системе.

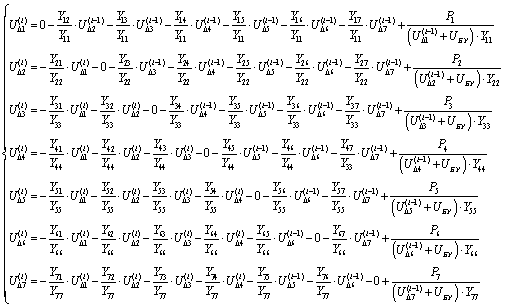
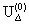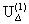Для итерационного процесса необходимо выбрать начальное приближение падений напряжений  и подставить в правую часть данной системы. Получим , затем подставим его в правую часть, получим  и т.д. Процесс может вестись по методу простой или ускоренной итерации.

Мы будем вести итерационный процесс по методу ускоренной итерации, т.е. для нахождения k-ой переменной в i-ой итерации используются переменные , 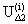… 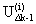, вычисленные на этой же i-ой итерации и переменные k+1, k+2,…, n, вычисленные на предыдущей (i-1) - ой итерации.

начальное значение падения напряжения в узлах схемы.

Матрица узловых проводимостей.

Принимая во внимание однотипность формул итерационного процесса, сами вычисления последующих итераций отображать не будем, а только некоторые рассчитанные значения.

Вторая итерация:

точность не удовлетворяет заданной

Произведем построение графика сходимости итераций U=f(I), где I - номер итерации:

На основе проведенного итерационного процесса, производим расчет режима сети.

Падение напряжения в узлах относительно балансирующего:

Определяем токи в ветвях схемы:

Определяем падения напряжения в ветвях схемы:

Рассчитаем небаланс мощности.

Как видно, небаланс мощности менее 1%. Это свидетельствует о том, что заданная точность итерационного процесса нас полностью удовлетворяет.

3.2 Расчет режима электрической сети по обращенным узловым уравнениям

Организуем итерационный процесс на базе матричного уравнения:

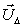где  - матрица узловых проводимостей без учета балансирующего узла,  - вектор-столбец падений напряжений в узлах сети, относительно балансирующего узла, 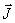 - вектор-столбец задающих токов (токи содержат свой знак).

Оставим в левой части уравнения (3.2.1) лишь вектор-столбец падений напряжений.

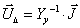
Распишем 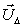 как разность напряжений в узлах  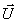и напряжения в балансирующем узле :

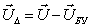
Приравняем правые части уравнений (3.2.2) и (3.2.3):

Выразим вектор-столбец напряжений в узлах:

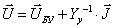
Выразим 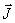 через задающую мощность в узлах и напряжения в узлах схемы:

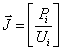
Подставим выражение (3.2.6) в выражение (3.2.5):

Обратную матрицу 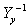 в выражении (3.2.7) обозначим через Z. Она носит название - матрица собственных и взаимных сопротивлений. Элементы матрицы узловых сопротивлений Z_ij представляют собой коэффициенты частичного падения напряжения, или коэффициенты влияния тока нагрузки в j-том узле на напряжение в i-том узле.

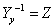
С учетом нового обозначения (3.2.8), уравнение (3.2.7) примет вид:

Итерационная процедура определения напряжения по обращенным уравнениям может быть ускорена, если на k-той итерации для расчета i-того неизвестного принимать 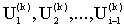 из этой же k-той итерации, а остальные неизвестные U_i+1 брать из (k-1) итерации, то есть вести процесс по методу ускоренной итерации. Так и поступим.

На основе уравнения (3.2.9) составим систему уравнений для итерационного процесса:

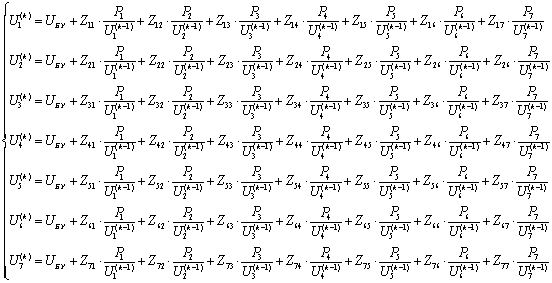
Точность итерационного процесса будет равна: ε= U_i+1-U_i ≤0.01 кВ, где i - номер итерации.

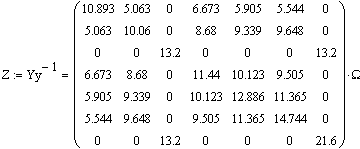
Вычислим обратную матрицу узловых проводимостей .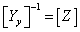

Определяем токи в ветвях схемы:

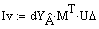
Определяем падения напряжения в ветвях схемы:

Определяем потоки мощности в ветвях схемы:

Определим потери мощности в ветвях сети:

Определяем суммарные потери мощности в ветвях:

Определим токи в узлах схемы:

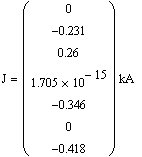
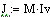
Определим мощности в узлах сети:

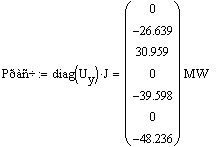
Рассчитаем небаланс мощности. Как уже говорилось ранее, он не должен превышать 1%.

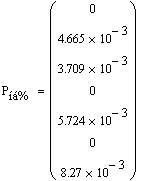
Как видно, небаланс мощности менее 1%. Это свидетельствует о том, что заданная точность итерационного процесса нас полностью удовлетворяет как по напряжению, так и по мощности.

Литература

1)      Электрические системы, т. 1. Математические задачи энергетики. Под ред. В.А. Веникова. Учебное пособие для электроэнергетических вузов. М., «Высшая школа», 1981, 336 с.

)        Идельчик В.И. Электрические системы и сети. М., Энергоатомиздат, 1989

)        Веников В.А. Математические задачи электроэнергетики. М., «Высшая школа «, 1981

)        Расчет и анализ режимов работы сетей. Под ред. В.А. Веникова, Москва, Энергия, 1974

)        Передача и распределение электрической энергии: учеб. пособие / А.А. Герасименко, В.Т. Федин. - Красноярск: ИПЦ КГТУ; Минск: БНТУ, 2006. - 808 с.