Математическая модель складского хозяйства
Контрольная
работа
Предмет:
Предметно-ориентированное программное обеспечение
Тема:
Математическая модель складского хозяйства
Введение
математический модель мathcad
складской хозяйство
В своей контрольной работе, на тему
«Математическая модель складского хозяйства», я решил для начала раскрыть
понятие «Математическая модель».
Никакое определение не может в полном объёме
охватить реально существующую деятельность по математическому моделированию.
Несмотря на это, определения полезны тем, что в них делается попытка выделить
наиболее существенные черты.
Вкратце - же математическая модель - это
математическое представление реальности
Все естественные и общественные науки,
использующие математический аппарат, по сути, занимаются математическим моделированием:
заменяют реальный объект его математической моделью и затем изучают последнюю.
По учебнику Яковлева: «модель (лат. modulus -
мера) - это объект-заместитель объекта-оригинала, обеспечивающий изучение
некоторых свойств оригинала. » «Замещение одного объекта другим с целью
получения информации о важнейших свойствах объекта-оригинала с помощью
объекта-модели называется моделированием. ««Под математическим моделированием
будем понимать процесс установления соответствия данному реальному объекту некоторого
математического объекта, называемого математической моделью, и исследование
этой модели, позволяющее получать характеристики рассматриваемого реального
объекта. Вид математической модели зависит как от природы реального объекта,
так и задач исследования объекта и требуемой достоверности и точности решения
этой задачи».
По учебнику Самарскому и Михайлову,
математическая модель - это «„эквивалент“ объекта, отражающий в математической
форме важнейшие его свойства - законы, которым он подчиняется, связи, присущие
составляющим его частям, и т.д.» Существует в триадах
«модель-алгоритм-программа». «Создав триаду „модель-алгоритм-программа“,
исследователь получает в руки универсальный, гибкий и недорогой инструмент,
который вначале отлаживается, тестируется в пробных вычислительных
экспериментах. После того, как адекватность (достаточное соответствие) триады
исходному объекту установлена, с моделью проводятся разнообразные и подробные
„опыты“, дающие все требуемые качественные и количественные свойства и характеристики
объекта».
Несколько менее общее определение математической
модели, основанное на идеализации «вход - выход - состояние», заимствованной из
теории автоматов, даёт Wiktionary: «Абстрактное математическое представление
процесса, устройства или теоретической идеи; оно использует набор переменных,
чтобы представлять входы, выходы и внутренние состояния, а также множества
уравнений и неравенств для описания их взаимодействия».
Типы моделей
Тип 1: Гипотеза (такое могло бы быть)
Тип 2: Феноменологическая модель (ведем себя
так, как если бы…)
Тип 3: Приближение (что-то считаем очень большим
или очень малым)
Тип 4: Упрощение (опустим для ясности некоторые
детали)
Тип 5: Эвристическая модель (количественного
подтверждения нет, но модель способствует более глубокому проникновению в суть
дела)
Тип 6: Аналогия (учтём только некоторые
особенности)
Тип 7: Мысленный эксперимент (главное состоит в
опровержении возможности)
Тип 8: Демонстрация возможности (главное -
показать внутреннюю непротиворечивость возможности)
Важнейшие математические модели обычно обладают
важным свойством универсальности: принципиально разные реальные явления могут
описываться одной и той же математической моделью. Скажем, гармонический
осциллятор описывает не только поведение груза на пружине, но и другие
колебательные процессы, зачастую имеющие совершенно иную природу: малые
колебания маятника, колебания уровня жидкости в U-образном сосуде или изменение
силы тока в колебательном контуре. Таким образом, изучая одну математическую
модель, мы изучаем сразу целый класс описываемых ею явлений.
В основном математическая модель чего либо проще
строится на программе Mathcad, поскольку я упомянул эту программу, то предлагаю
ознакомится с ней поближе.
Mathcad
- программа для выполнения и документирования
инженерных и научных расчётов. Появившись в 1986 году для платформы MS-DOS,
Mathcad впервые среди программ подобного рода использовал наборную
математическую нотацию, совмещённую с автоматической системой вычислений. Кроме
того, впервые было реализовано автоматическое вычисление и проверка единиц
измерения. Например, СИ. На сегодняшний день Mathcad включает некоторые
возможности алгебраических систем для ЭВМ, но при этом сохраняет ориентацию на
инженерные приложения. Изначально Mathcad был создан Алэном Рэздоу из
Массачусетского технологического института (MIT), который впоследствии стал
одним из основателей фирмы Mathsoft, ныне являющейся частью корпорации
Parametric Technology Corporation.
Рабочая область программы представляется как
обыкновенный лист, на котором уравнения и выражения отображаются графически, а
не в текстовом виде.
Основные возможности Mathcad
Решение дифференциальных уравнений различными
численными методами.
Построение двух- и трёхмерных графиков функций.
Использование греческого алфавита как в
уравнениях, так и в тексте.
Выполнение вычислений в символьном режиме.
Выполнение операций с векторами и матрицами.
Символьное решение систем уравнений.
Аппроксимация кривых.
Выполнение подпрограмм.
Поиск корней многочленов и функций.
Проведение статистических расчётов и работа с
распределением вероятностей.
Поиск собственных чисел и векторов.
Вычисления с единицами измерения.
Интеграция с САПР системами, использование
результатов вычислений в качестве управляющих параметров.
Несмотря на то, что данная программа
ориентирована на пользователей, мало знакомых с программированием, она всё же
находит применение в достаточно сложных проектах для визуализации результатов
математического моделирования с использованием распределённых вычислений и
традиционных языков программирования. Также Mathcad часто используется в
крупных инженерных проектах, где большое значение имеет трассируемость и
соответствие стандартам.
Математическая модель складского
хозяйства без очереди на Mathcad
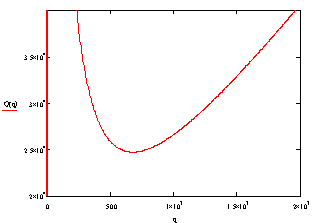
Рис. 1
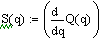
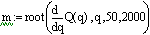
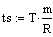
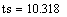
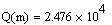
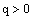
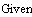
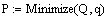
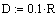
. При любом R > R1 выполняется условие
D-Q0(q) > 0
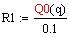
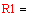
. Модель с очередью
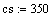
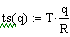
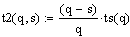
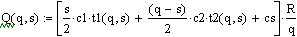
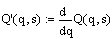
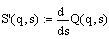
Пояснения
А теперь поясню, что конкретно вписывалось в
Mathcad и для чего.
Пусть предприниматель должен поставлять своим
клиентам R изделий равномерно в течение интервала времени Т. Тем самым спрос на
его продукцию фиксирован и известен. Нехватка товара не допускается, т.е. штраф
при неудовлетворенном спросе бесконечно велик. Затраты на производство
складываются из следующих компонентов: с1 - стоимость хранения одного изделия в
единицу времени, сs - стоимость запуска в производство одной партии изделия.
Под запуском в производство может пониматься как собственное производство, так
и доставка партии товара на склад. Тем самым кривая запасов на складе описана
на рис.1
Рис. 2 - Кривая запасов
Следует найти, как часто необходимо организовать
выпуск или доставку партий и каким должен быть размер партии.
. Задаем исходные параметры для задачи.
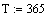
. Пусть q - размер партии, ts - интервал времени
между запусками в производство партий, а R - полный спрос за все время
планирования Т. Тогда R/q - число партий за время T и
.
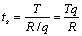Если интервал ts начинается, когда
на складе имеется q изделий, и заканчивается при отсутствии запасов, тогда q/2
- средний запас в течение ts,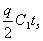 
- затраты на хранение в интервале ts
. Общая стоимость создания запасов
равна сумме стоимости хранения и стоимости запуска в производство
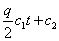
Для вычисления полной стоимости
запасов за время Т следует эту величину умножить на общее число партий за это
время:
,
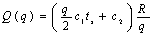Подставим в это выражение ts и
получим:
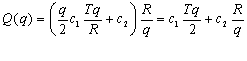
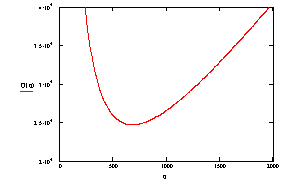
Рис. 3
Построим график общей стоимости от
величины партии
Вычислим минимальное значение
функции Q(q). Воспользуемся хорошо известным фактом, что в точке экстремума
функции производная равна нулю. Решим нашу задачу двумя способами.
-ый способ - с использованием
функции root.
. Функция root позволяет решать
простейшие уравнения вида F(x) = 0. Решение находится с помощью выражения
root(F(x), x). Эта функция возвращает значение переменной х, при котором
выражение F(x) равно 0
. Далее вычисляем затраты при m =
678.433.
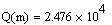
. Временной интервал определяется
подстановкой значения m в выражение для ts.
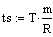
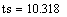
-ой способ - с использованием
функции Minimize.
. Вначале определяем функцию затрат
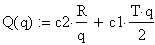
2. Затем задаем начальную точку, с
которой начинается вычисление решения.
. Определяем вычислительный блок и
находим решение.
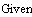
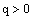
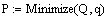
Как видно и второе решение приводит
к тому же результату.
Заключение
Итак решив одну из множества задач
«Математическая модель складского хозяйства без очереди» мы можем с
уверенностью подчеркнуть следующие достоинства этой программы.
Во-первых, это универсальность
пакета MATHCAD ,который может быть использован для решения самых разнообразных
инженерных, экономических, статистических и других научных задач.
Во-вторых, программирование на
общепринятом математическом языке позволяет преодолеть языковой барьер между
машиной и пользователем. Потенциальные пользователи пакета - от студентов до
академиков.
В-третьих, совместно применение
текстового редактора, формульного транслятора и графического процессора
позволяет пользователю в ходе вычислений получить готовый документ. Но, к
сожалению, популярный во всем мире пакет MATHCAD фирмы MathSoft , в России
распространен еще слабо, как и все программные продукты подобно рода. Наверное,
это оттого, что люди, живущие в России, ещё не привыкли к тому, что решить
систему дифференциальных уравнений из пяти переменных шестого порядка можно не
только с помощью карандаша и бумаги, но и с помощью компьютера и MATHCAD`a .
Приятно быть сильным физически, но
быть сильным интеллектуально не менее приятно. Именно эти чувства испытываешь
при работе с MATHCAD`ом.
Список используемой литературы
1. Лекции
Попова С.В.
2. Сайт
Интернета: <http://wikipedia.net>
. Советов
Б.Я., Яковлев С.А. Моделирование систем, 2001, 399 с.
. Самарский
А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры 2002,
431 с.