Исследование работы алгоритма Мамдани в системах нечеткого вывода

Исследование работы алгоритма Мамдани в системах нечеткого вывода

Введение

Так уж повелось, что любую статью о нечеткой логике принято начинать с упоминания имени Лотфи Заде. И я не стану исключением. Дело в том, что этот человек стал не только отцом-основателем целой научной теории, написав в 1965 году фундаментальный труд «Fuzzy Sets», но и проработал различные возможности ее практического применения. Он описал свой подход в 1973 году в тексте «Outline of a New Approach to the Analysis of Complex Systems and Decision Processes» (опубликованном в журнале IEEE Transactions on Systems). Примечательно, что сразу после его выхода одна предприимчивая датская фирма весьма успешно применила изложенные в нем принципы для усовершенствования своей системы управления сложным производственным процессом.

Но при всех заслугах Л. Заде, не менее важный вклад внесли последователи этой теории. Например, английский математик Э. Мамдани (Ebrahim Mamdani). В 1975 году он разработал алгоритм, который был предложен в качестве метода для управления паровым двигателем. Предложенный им алгоритм, основанный на нечетком логическом выводе, позволил избежать чрезмерно большого объема вычислений и был по достоинству оценен специалистами. Этот алгоритм в настоящее время получил наибольшее практическое применение в задачах нечеткого моделирования.

1. Начальное представление систем нечеткого вывода

Для успешного применения на практике алгоритмов управления они должны быть достаточно простыми для реализации и понимания. По последним данным, на 84% японских предприятий всё ещё используются обычные PID контроллеры. Кроме того, они должны обладать способностью к обучению, гибкостью, устойчивостью, нелинейностью. Алгоритмы, основанные на нечёткой логике, обладают некоторыми из указанных свойств, благодаря чему они получили в настоящее время достаточно широкое распространение.

Для многих производственных процессов сложно обеспечить точное управление. Они обычно являются многомерными, нелинейными и изменяются во времени. Управление на основе нечёткой логики может успешно применятся для таких сложных процессов. Кроме того, нечёткие контроллеры могут работать с трудноформализуемыми и не полностью определёнными системами потому, что для них (в отличие от традиционных адаптивных контроллеров) не требуется строгая математическая модель объекта управления. Другим преимуществом нечётких контроллеров является то, что они могут быть легко реализованы на цифровых или аналоговых СБИС.

Нечётко - логический контроллер разрабатывается по лингвистическим правилам, что тесно связано с технологией основанной на знаниях.

Построение систем интеллектуального управления по этой технологии предполагает выполнение следующих этапов:

) определение входов и выходов создаваемой системы управления;

) задание для каждой из входных и выходных переменных функции принадлежности;

) разработка базы нечётких правил;

) выбор и реализация алгоритма нечёткого логического вывода;

) анализ процесса управления созданной системы.

Общий логический вывод осуществляется по схеме, представленной на рисунке 1.

Рисунок 1. Общая схема логического вывода

Рассмотрим эту схему более подробно.

Нечёткость (введение нечёткости, фаззификация)

Функции принадлежности, определённые на входных переменных, применяются к их фактическим значениям для определения степени истинности каждой предпосылки каждого правила.

1.1 Логический вывод

Вычисленное значение истинности для предпосылок каждого правила применяется к заключениям каждого правила. Это приводит к одному нечёткому подмножеству, которое будет назначено каждой переменной вывода для каждого правила. В качестве правил логического вывода обычно используются только операции min (минимум) или prod (умножение). В логическом выводе prod функция принадлежности вывода отсекается по высоте, соответствующей вычисленной степени истинности предпосылки правила (нечёткая логика «И»). В логическом выводе prod функция принадлежности вывода масштабируется при помощи вычислений степени истинности предпосылки правила.

Композиция

Нечёткие подмножества, назначенные для каждой переменной вывода (во всех правилах) объединяются вместе, чтобы сформировать одно нечёткое подмножество для каждой переменной вывода. При подобном объединении обычно используется max (максимум) или sum (сумма). При композиции max комбинированный вывод нечёткого подмножества конструируется как поточечный максимум по всем нечётким подмножествам (нечёткая логика «ИЛИ»). При композиции sum комбинированный вывод нечёткого подмножества конструируется как поточечная сумма по всем нечётким подмножествам, назначенным переменной вывода правилами логического вывода.

Приведение к чёткости (дефаззификация)

Это дополнительный этап, который полезно использовать, когда полезно преобразовать нечёткий набор выводов в чёткое число.

Общий вид системы интеллектуального управления объектом на основе нечёткой логики приведён на рисунке 1.2.

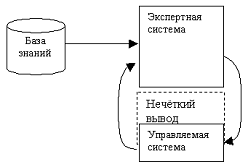
Рисунок 1.2 Общая схема управления объектом на основе нечёткой логики

1.2 База знаний в системах управления

Под базой знаний принято понимать совокупность знаний о предметной области, используемых для построения систем интеллектуального управления объектами. Используемый в различного рода экспертных системах механизм нечётких выводов имеет в своей основе базу знаний, формируемую специалистами предметной области в виде совокупности нечётких предикатных правил вида:

П1: если х есть А1, то y есть В1,

П2: если х есть А2, то y есть В2,

…

Пn: если х есть Аn, то y есть Вn.

Где х - входная переменная (имя для известных значений данных), y - переменная вывода (имя для значений данных, которое будет вычислено); А и В-функции принадлежности, определённые, соответственно на х и у.

Пример подобного правила:

Если х - низко, то у - высоко.

Также к базе знаний принято относить и функции принадлежности входных и выходных переменных, которые принято либо выбирать из типового набора (треугольная, колокольная,…), либо задавать самостоятельно.

Существует несколько алгоритмов нечёткого вывода. Рассмотрим самый используемый из них: алгоритм Мамдани.

2. Алгоритм Мамдани в системах нечеткого вывода

нечеткий вывод мамдани алгоритм

Предположим, что базу знаний образуют два нечётких правила:

П₁: если х есть А₁ и y есть В₁, то z есть С₁,

П₂: если х есть А₂ и y есть В₂, то z есть С₂,

где х и у - имена входных переменных, z - имя переменной вывода, А₁, А₂, В₁, В₂, С₁, С₂ - некоторые заданные функции принадлежности, при этом чёткое знание z₀ необходимо определить на основании приведённой информации и чётких знаний x₀, y₀.

Данный алгоритм математически может быть описан следующим образом.

. Нечёткость: находятся степени истинности для предпосылок каждого правила: А₁(х₀), А₂(х₀), В₁(х₀), В₂(х₀).

. Нечёткий вывод: находятся уровни отсечения для предпосылок каждого из правил (с использованием операции минимума):

                     (1)

где через «» обозначена операция логического минимума.

Затем находят усечённые функции принадлежности:

                                                           (2)

3. Композиция: с использованием операции max производится объединение найденных усеченных функций, что приводит к получению итогового нечёткого подмножества для переменной выхода с функцией принадлежности

. Приведение к чёткости (для нахождения z₀) производится, например, центроидным методом

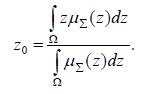                                                       (3)    

2.1 Принцип работы

Нечеткая переменная - это кортеж вида <α, X, Α>, где:

α - имя нечеткой переменной;- её область определения;- нечеткое множество на универсуме X.

Пример: Нечеткая переменная < «Тяжелый бронежилет», {x| 0 кг < x < 35 кг}, B={x, μ(x)}> характеризует массу военного бронежилета. Будем считать его тяжелым, если его масса > 16 кг (рисунок 1.3).

Рисунок 1.3. График функции принадлежности μ(x) для нечеткого множества B.

Лингвистическая переменная есть кортеж <β, T, X, G, M>, где:

β - имя лингвистической переменной;- множество её значений (термов);- универсум нечетких переменных;- синтаксическая процедура образования новых термов;- семантическая процедура, формирующая нечеткие множества для каждого терма данной лингвистической переменной.

Пример: Допустим, мы имеем субъективную оценку массы бронежилета. Она, например, может быть получена от военнослужащих (выступающих в роли экспертов), которые непосредственно имеют дело с подобной амуницией. Формализовать эту оценку можно с помощью следующей лингвистической переменной <β, T, X, G, M> (рис. 4), где:

β - Бронежилет;- {«Легкий бронежилет (Light)», «Бронежилет средней массы (Medium)», «Тяжелый бронежилет (Heavy)»};= [0; 35];- процедура образования новых термов при помощи логических связок и модификаторов. Например, «очень тяжелый бронежилет»;- процедура задания на универсуме X=[0; 35] значений лингвистической переменной, т.е. термов из множества T.

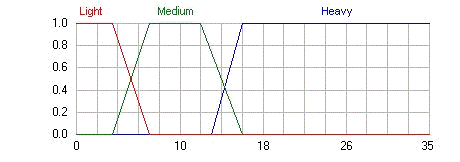
Рисунок 1.4. Графики функций принадлежности значений лингвистической переменной «Бронежилет»

Нечетким высказыванием будем называть высказывание вида «β IS α», где:

β - лингвистическая переменная;

α - один из термов этой переменной

Упрощенно говоря, правилом нечетких продукций (далее просто правилом) будем называть классическое правило вида «ЕСЛИ… ТО…», где в качестве условий и заключений будут использоваться нечеткие высказывания. Записываются такие правила в следующем виде:

IF (β1 IS α1) AND (β2 IS α2) THEN (β3 IS α3).

Кроме «AND» также используются логическая связка «OR». Но такую запись обычно стараются избегать, разделяя такие правила на несколько более простых (без «OR»). Также каждое из нечетких высказываний в условии любого правила будем называть подусловием. Аналогично, каждое из высказываний в заключении называется подзаключением.

Пример: Следующие примеры помогут зафиксировать определение:

) IF (Бронежилет тяжелый) THEN (Солдат уставший);

) IF (Муж трезвый) AND (Зарплата высокая) THEN (Жена довольная).

Все. Этого минимума достаточно для понимая принципов работы алгоритма

2.2 Принцип Работы Алгоритм Мамдани

Данный алгоритм описывает несколько последовательно выполняющихся этапов (рисунке 1.5). При этом каждый последующий этап получает на вход значения полученные на предыдущем шаге.

Рисунок 1.5. Диаграмма деятельности процесса нечеткого вывода

Алгоритм примечателен тем, что он работает по принципу «черного ящика». На вход поступают количественные значения, на выходе они же. На промежуточных этапах используется аппарат нечеткой логики и теория нечетких множеств. В этом и состоит элегантность использования нечетких систем. Можно манипулировать привычными числовыми данными, но при этом использовать гибкие возможности, которые предоставляют системы нечеткого вывода.

Для реализации алгоритма использовался объектно-ориентированный подход. Исходный код написан на языке программирования Java. Диаграмма (рисунке 1.6) показывает наиболее существенные связи и отношения между классами, задействованными в алгоритме.

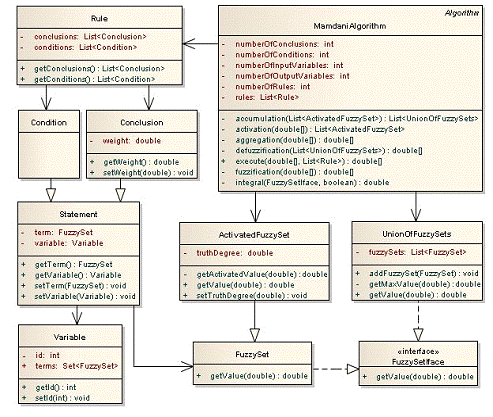
Рисунок 1.6. Диаграмма классов реализации алгоритма Мамдани

Правила (Rule) состоят из условий (Condition) и заключений (Conclusion), которые в свою очередь являются нечеткими высказываниями (Statement). Нечеткое высказывание включает в себя лингвистическую переменную (Variable) и терм, который представлен нечетким множеством (FuzzySet). На нечетком множестве определена функция принадлежности, значение которой можно получить с помощью метода getValue(). Это метод определенный в интерфейсе FuzzySetIface. При выполнении алгоритма необходимо будет воспользоваться «активизированным» нечетким множеством (ActivatedFuzzySet), которое некоторым образом переопределяет функцию принадлежности нечеткого множества (FuzzySet). Также в алгоритме используется объединение нечетких множеств (UnionOfFuzzySets). Объединение также является нечетким множеством, и поэтому имеет функцию принадлежности (определенную в FuzzySetIface).

Алгоритм Мамдани (MamdaniAlgorithm), включает в себя все этапы (рис. 3) и использует базу правил (List<Rule>) в качестве входных данных. Также алгоритм предполагает использование «активизированных» нечетких множеств (ActivatedFuzzySet) и их объединений (UnionOfFuzzySets).

Итак, этапы нечеткого вывода выполняются последовательно. И все значения, полученные на предыдущем этапе, могут использоваться на следующем.

2.3 Формирование базы правил

База правил - это множество правил, где каждому подзаключению сопоставлен определенный весовой коэффициент.

База правил может иметь следующий вид (для примера используются правила различных конструкций):

RULE_1: IF «Condition_1» THEN «Conclusion_1» (F1) AND «Conclusion_2» (F2);_2: IF «Condition_2» AND «Condition_3» THEN «Conclusion_3» (F3);

…_n: IF «Condition_k» THEN «Conclusion_(q-1)» (Fq-1) AND «Conclusion_q» (Fq);

Где Fi - весовые коэффициенты, означающие степень уверенности в истинности получаемого подзаключения (i = 1..q). По умолчанию весовой коэффициент принимается равным 1. Лингвистические переменные, присутствующие в условиях называются входными, а в заключениях выходными.

Обозначения:- число правил нечетких продукций (numberOfRules).- кол-во входных переменных (numberOfInputVariables).- кол-во выходных переменных (numberOfOutputVariables).- общее число подусловий в базе правил (numberOfConditions).- общее число подзаключений в базе правил (numberOfConclusions).

Примечание: Данные обозначения будут использоваться в последующих этапах. В скобках указаны имена соответствующих переменных в исходном коде.

2.4 Фаззификация входных переменных

Этот этап часто называют приведением к нечеткости. На вход поступают сформированная база правил и массив входных данных А = {a1,…, am}. В этом массиве содержатся значения всех входных переменных. Целью этого этапа является получение значений истинности для всех подусловий из базы правил. Это происходит так: для каждого из подусловий находится значение bi = μ(ai). Таким образом получается множество значений bi (i = 1..k).

Реализация:

private double[] fuzzification (double[] inputData) {i = 0;[] b = new double[numberOfConditions];(Rule rule: rules) {(Condition condition: rule.getConditions()) {j = condition.getVariable().getId();term = condition.getTerm();[i] = term.getValue (inputData[j]);

i++;

}

}b;

}

Примечание: Массив входных данных сформирован таким образом, что i-ый элемент массива соответствует i-ой входной переменной (номер переменной храниться в целочисленном поле «id»).

2.5 Агрегирование подусловий

Как уже упоминалось выше, условие правила может быть составным, т.е. включать подусловия, связанные между собой при помощи логической операции «AND». Целью этого этапа является определение степени истинности условий для каждого правила системы нечеткого вывода. Упрощенно говоря, для каждого условия находим минимальное значение истинности всех его подусловий.

Формально это выглядит так:

cj = min{bi}.

Где:= 1..n;- число из множества номеров подусловий в которых участвует j-ая входная переменная.

Реализация:double[] aggregation (double[] b) {i = 0;j = 0;[] c = new double[numberOfInputVariables];(Rule rule: rules) {truthOfConditions = 1.0;(Condition condition: rule.getConditions()) {= Math.min (truthOfConditions, b[i]);++;

}[j] = truthOfConditions;++;

}c;

}

2.6 Активизация подзаключений

нечеткий вывод мамдани алгоритм

На этом этапе происходит переход от условий к подзаключениям. Для каждого подзаключения находится степень истинности di = ci*Fi, где i = 1..q. Затем, опять же каждому i-му подзаключению, сопоставляется множество Di с новой функцией принадлежности. Её значение определяется как минимум из di и значения функции принадлежности терма из подзаключения. Этот метод называется min-активизацией, который формально записывается следующим образом:

μ'i(x) = min {di, μi(x)}.

Где:

μ'i(x) - «активизированная» функция принадлежности;

μi(x) - функция принадлежности терма;- степень истинности i-го подзаключения.

Итак, цель этого этапа - это получение совокупности «активизированных» нечетких множеств Di для каждого из подзаключений в базе правил (i = 1..q).

Реализация:

private List<ActivatedFuzzySet> activation (double[] c) {i = 0;<ActivatedFuzzySet> activatedFuzzySets = new ArrayList<ActivatedFuzzySet>();[] d = new double[numberOfConclusions];(Rule rule: rules) {(Conclusion conclusion: rule.getConclusions()) {[i] = c[i]*conclusion.getWeight();activatedFuzzySet = (ActivatedFuzzySet) conclusion.getTerm();.setTruthDegree (d[i]);.add(activatedFuzzySet);++;

}

}activatedFuzzySets;

}double getActivatedValue (double x) {Math.min (super.getValue(x), truthDegree);

}

2.7 Акумуляция заключений

Целью этого этапа является получение нечеткого множества (или их объединения) для каждой из выходных переменных. Выполняется он следующим образом: i-ой выходной переменной сопоставляется объединение множеств Ei = ∪ Dj. Где j - номера подзаключений в которых участвует i-aя выходная переменная (i = 1..s). Объединением двух нечетких множеств является третье нечеткое множество со следующей функцией принадлежности:

μ'i(x) = max {μ1 (x), μ2 (x)}, где μ1 (x), μ2 (x) - функции принадлежности объединяемых множеств.

Реализация:

private List<UnionOfFuzzySets> accumulation (List<ActivatedFuzzySet> activatedFuzzySets) {<UnionOfFuzzySets> unionsOfFuzzySets =ArrayList<UnionOfFuzzySets>(numberOfOutputVariables);(Rule rule: rules) {(Conclusion conclusion: rule.getConclusions()) {id = conclusion.getVariable().getId();.get(id).addFuzzySet (activatedFuzzySets.get(id));

}

}unionsOfFuzzySets;

}double getMaxValue (double x) {result = 0.0;(FuzzySet fuzzySet: fuzzySets) {= Math.max (result, fuzzySet.getValue(x));

}result;

2.8 Вывод

Алгоритм Мамдани и многие другие алгоритмы нечеткого вывода уже реализованы в таких замечательных продуктах как Fuzzy Logic Toolbox (расширение для MatLab), fuzzyTECH и многих других. Поэтому столь детальное рассмотрение алгоритма, как в данной статье, носит больше теоретическую ценность, чем практическую. Однако замечу, что только имея под собой прочный фундамент из знаний и понимания основ работы алгоритма появляется возможность применять его с максимальным эффектом.

Заключение

Влияние нечеткой логики оказалось, пожалуй, самым обширным. Подобно тому, как нечеткие множества расширили рамки классической математическую теорию множеств, нечеткая логика «вторглась» практически в большинство методов Data Mining, наделив их новой функциональностью. Ниже приводятся наиболее интересные примеры таких объединений.

Триумфальное шествие нечеткой логики по миру началось после доказательства в конце 80-х Бартоломеем Коско знаменитой теоремы FAT (Fuzzy Approximation Theorem). В бизнесе и финансах нечеткая логика получила признание после того как в 1988 году экспертная система на основе нечетких правил для прогнозирования финансовых индикаторов единственная предсказала биржевой крах. И количество успешных фаззи-применений в настоящее время исчисляется тысячами.

Список использованных источников

1. Леоненков А.В. Нечеткое моделирование в среде MATLAB и fuzzyTECH / А. Леоненков. - СПб: БХВ-Петербург, 2003. - 736 с.

. Штовба С.Д. Проектирование нечетких систем средствами MATLAB / С. Штовба. - М: Горячая линия-Телеком, 2007. - 288 с.

. В. Дьяконов, В. Круглов. Математические пакеты расширения MATLAB. Специальный справочник. - Санкт-Петербург: Питер, 2001 - 480 с.

. Р.А. Алиев. Управление производством при нечёткой исходной информации, М.: Энергоатомиздат, 1991.

. А. Гультяев. Визуальное моделирование в среде MATLAB: учебный курс. - Санкт-Перербург: Питер, 2000.

. Н.Н. Мартынов, А.П. Иванов. MATLAB 5.x. Вычисление, визуализация, программирование. - М.: КУДИЦ-ОБРАЗ, 2000.

7. Орлов А.И. Теория принятия решений. Учебное пособие / А.И. Орлов. - М.: Издательство «Март», 2004. - 656 с.

. Нейронные сети, генетические алгоритмы и нечеткие системы. Д. Рутковская, M. Пилиньский, Л. Рутковский. 1999.

. Понятие лингвистической переменной и его применение к принятию приближенных решений. - Заде Л.А.М.: Мир, 1976.

Приложение 1

fcltClusters =

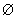
FOR_EACH f IN closedFacilitiesList:.add (new Cluster({f}))

WHILE есть существенный прогресс AND время не истекло:

FOR_EACH clstr IN fcltClusters:= [empty]                ==!! fuzzy set ==

FOR_EACH enemy IN openFacilitiesList:

IF enemy хорошо заменяется на clstr OR

цена enemy велика THEN:.add(enemy)IS false

FOR_EACH c IN citiesList:

FOR_EACH f IN clstr:

IF fwtn[c] ∈ activEnemies ANDдешевле для c чем fwtn[c] THEN:IS true

IF goodChange OR

стоимость activEnemies больше стоимости clstr

THEN:

open(clstr).remove(clstr)(activEnemies)

FOR_EACH aEnm IN activEnemies:.add (new Cluster({aEnm}))

FOR_EACH clstr1 IN fcltClusters:

FOR_EACH clstr2 IN fcltClusters:

IF clstr1 похож на clstr2 AND

(стоимость clstr1 не слишком велика OR

стоимость clstr2 не слишком велика) THEN:

join (clstr1, clstr2)

<fuzzy condition> THEN var_out IS val_out

<fuzzy condition> -

<fuzzy condition> =

<fuzzy check>

<fuzzy condition> <operator> <antecedent>

<antecedent> = <fuzzy variable> IS <linguistic variable>

<operator> = OR AND

<fuzzy variable<linguistic variable>

public interface INegotiatingAgent {void onNegotiationStart (INegotiationContext context);

/**

* returns true if wants to continue negotiation

*/boolean negotiate (INegotiationContext context);

} interface INegotiationContext {

public <ServT extends IService> ServT getService (<ServT> clazz

);

public <ServT extends IService> void registerService (<ServT> clazz,service

);

}

private void analiseUtilities (context,<INegotiatingAgent> agents

) {minUtilAgent = null;

double minUtility = Double.MAX_VALUE;<IUtilityFuncNegotiationAgent> ufagents =(agents);

for (IUtilityFuncNegotiationAgent agent: ufagents) {

double utility = agent.computeUtility(context);

if (utility < minUtility) {= utility;= agent;

}

}

if (minUtilAgent == null) {

return;

}

.negotiatePrivileged(context);

}

private void extractUFAgents (<INegotiatingAgent> agents)

{End}