Разработка экономико-математической модели по оптимизации отраслевой структуры производства
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное
образовательное учреждение высшего профессионального образования
«Воронежский государственный аграрный
университет им. К.Д. Глинки»
Кафедра информационного обеспечения и
моделирования агроэкономических систем
КУРСОВОЙ ПРОЕКТ
по дисциплине
«Моделирование
социально-экономических систем и процессов»
На тему: «Разработка
экономико-математической модели по оптимизации отраслевой структуры
производства»
Выполнила:
студентка заочница Э-4
Байрамова О. Г. 08409
Проверил:
Воронеж 2011
Содержание
1. Решение экономико-математических задач методами линейного
программирования (ЛП)
.1 Математическая формулировка задачи линейного
программирования
- основная задача линейного программирования;
- приведение системы неравенств к основной задаче ЛП
1.2 Геометрическая интерпретация и решение задачи линейного
программирования в случае двух переменных
- математические основы решения задачи графическим способом;
- этапы решения задач графическим способом;
1.3 Алгоритм симплексного метода решения задач ЛП
- формирование первого опорного плана;
- структура симплексной таблицы;
- исследование опорного плана на оптимальность;
2. Порядок разработки экономико-математической модели
оптимизации отраслевой структуры производства
.1 Экономико-математическая модель по оптимизации отраслевой
структуры производства
. Решение задач линейного программирования с помощью Microsoft Excel
.1 Пример решения задачи линейного программирования
.2 Анализ результатов решения задачи на основе стандартных
отчетов Microsoft Excel
Список литературы
Приложение
Введение
Развитие современного общества характеризуется повышением технического
уровня, усложнением организационной структуры производства, углублением общественного
разделения труда, предъявлением высоких требований к методам планирования и
хозяйственного руководства. В этих условиях только научный подход к руководству
экономической жизнью общества позволит обеспечить высокие темпы развития
народного хозяйства.
Одним из необходимых условий дальнейшего развития экономической науки
является применение точных методов количественного анализа, широкое
использование математики. В настоящее время новейшие достижения математики и
современной вычислительной техники находят все более широкое применение в
экономических исследованиях и планировании. Этому способствует развитие таких
разделов математики, как математическое программирование, теория игр, теория
массового обслуживания, а также бурное развитие быстродействующей электронно-вычислительной
техники. Уже накоплен достаточный опыт постановки и решения экономических задач
с помощью математических методов. Особенно успешно развиваются методы
оптимального планирования, которые и составляют сущность математического программирования.
Одной из основных становится задача создания единой системы оптимального
планирования и управления народным хозяйством на базе широкого применения
математических методов и электронно-вычислительной техники в экономике.
Основной целью написания курсовой работы является всесторонний анализ
применения линейного программирования для решения экономических задач.
1. Решение экономико-математических
задач методами линейного программирования (ЛП)
.1 Линейное программирование
Линейное программирование -математическая дисциплина, посвященная теории
и методам решения задач об экстремумах линейных функций на множествах n-мерного
векторного пространства, задаваемых системами линейных уравнений и неравенств.
Линейное программирование является частным случаем математического
программирования. Одновременно оно - основа нескольких методов решения задач
целочисленного и нелинейного программирования.
Математическое
программирование, математическая
дисциплина, посвященная теории и методам решения задач о нахождении экстремумов
функций на множествах, определяемых линейными и нелинейными ограничениями
(равенствами и неравенствами). Математическое программирование - раздел
науки об исследовании операций , охватывающий широкий класс задач управления,
математическими моделями которых являются конечномерные экстремальные задачи.
Задачи Математическое программирование находят применение в различных
областях человеческой деятельности, где необходим выбор одного из возможных
образов действий, например, при решении многочисленных проблем управления и
планирования производственных процессов, в задачах проектирования и
перспективного планирования. Наименование «Математическое программирование»
связано с тем, что целью решения задач является выбор программы действий.
Математическая формулировка задачи Математическое программирование:
минимизировать скалярную функцию j(x) векторного аргумента х на
множестве X = {x: gi(x) ³ 0, hi(x)
= 0, <#"512816.files/image001.gif"> при линейных ограничениях 
, i = 1, 2, …, m, либо все величины cj,
aij, bi, либо часть из них случайны. Задачи
перечисленных разделов обладают общим свойством: всякая точка локального
минимума является оптимальной точкой. Несколько в стороне находятся так
называемые многоэкстремальные задачи - задачи, для которых указанное свойство
не выполняется. В основе теории выпуклого программирования и, в частности,
линейного и квадратичного, лежит теорема Куна - Таккера о необходимых и
достаточных условиях существования оптимальной точки x*: для того чтобы
точка х* была оптимальной, то есть 
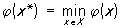, X
= {x: gi(x) ³ 0, i = 1, 2,
..., k}, необходимо и достаточно, чтобы существовала такая точка у*
= (у*1, у*2, ..., у*k),
чтобы пара точек х*, у* образовывала седло функции Лагранжа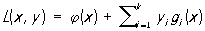 
Последнее означает, что L(x*, y) £ L(x*, y*) £ L(x, у*)
для любых х и всех у ³ 0. Если ограничения gi(x)
нелинейны, то теорема справедлива при некоторых дополнительных предположениях о
допустимом множестве. Если функции j(x) и gi(x)
дифференцируемы, то следующие соотношения определяют седловую точку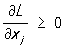 
, j = 1, 2, …, n; 
; 
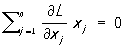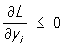; i
= 1, 2, …, k; 
, yi ³ 0, i = 1, 2, …,
k. Таким образом, задача выпуклого программирования сводится к решению
системы уравнений и неравенств. На основе теоремы Куна - Таккера разработаны
различные итерационные методы минимизации, сводящиеся к поиску седловой точки
функции Лагранжа. В Математическое программирование одно из главных мест
принадлежит вычислительным методам решения экстремальных задач. Широким классом
таких методов являются методы проектирования. Идея этих методов состоит в следующем.
В точке xk Î X выбирается направление спуска sk,
то есть одно из направлений, по которому функция j(x) убывает, и
вычисляется xk+1 = p(xk + aksk),
где p(xk + aksk) означает
проекцию точки xk + aksk на
множество X: 
, число ak > 0 выбирается при этом так,
чтобы j(xk +1) < j(xk).
Существуют различные варианты методов проектирования. Наиболее распространённым
из них является метод проекции градиента, когда sk = -grad j(xk).
В Математическое программирование доказано, что при определённых
условиях на целевую функцию и допустимое множество, последовательность {хk},
построенная методом проекции градиента, такова, что 
стремится к нулю со скоростью геометрической
прогрессии. Характерной особенностью вычислительной стороны методов решений
задач Математическое программирование является то, что применение этих
методов неразрывно связано с использованием электронных вычислительных машин, в
первую очередь потому, что задачи Математическое программирование,
связанные с ситуациями управления реальными системами, являются задачами
большого объёма, недоступными для ручного счёта. Важным направлением
исследования в Математическое программирование являются проблемы
устойчивости. Здесь существ. значение имеет изучение класса устойчивых задач -
задач, для которых малые возмущения (погрешности) в исходной информации влекут
за собой малые возмущения и в решении. В случае неустойчивых задач большая роль
отводится процедуре аппроксимации неустойчивой задачи последовательностью
устойчивых задач - так называемому процессу регуляризации.
Многие свойства задач линейного программирования можно интерпретировать
также как свойства многогранников и таким образом геометрически формулировать и
доказывать их.
Математическая формулировка задачи линейного программирования
Нужно максимизировать
при условиях при i = 0, 1, 2, . . . , m .
Иногда на xi также накладывается некоторый набор ограничений в
виде равенств, но от них можно избавиться, последовательно выражая одну переменную
через другие и подставляя ее во всех остальных равенствах и неравенствах (а
также в функции f).
Такую задачу называют "основной" или "стандартной" в
линейном программировании.
1.2 Формулировка задачи
Даны линейная функция
=С1х1+С2х2+...+СNxN
(1.1)
и система линейных ограничений
11x1 + a22x2 + ... + a1NХN = b121x1 + a22x2
+ ... + a2NХN = b2
. . . . . . . . . . . . . . .i1x1 + ai2x2
+ ... + aiNХN = bi (1.2) . .
. . . . . . . . . . . . .M1x1 + aM2x2
+ ... + aMNХN = bMj 0 (j = 1, 2, ... ,n)
(1.3)
экономика математическая задача линейное программирование
где аij, bj и Сj - заданные постоянные
величины.
Найти такие неотрицательные значения х1, х2, ..., хn,
которые удовлетворяют системе ограничений (1.2) и доставляют линейной функции
(1.1) минимальное значение.
Общая задача имеет несколько форм записи.
Векторная форма записи. Минимизировать линейную функцию Z = СХ при
ограничениях А1х1 + А2x2 + ... + АNxN
= Ао, X0 (1.4)
где С = (с1, с2, ..., сN); Х = (х1,
х2, ..., хN); СХ - скалярное произведение; векторы A1
= A2 = ,..., AN состоят соответственно из
коэффициентов при неизвестных и свободных членах.
Матричная форма записи. Минимизировать линейную функцию, Z = СХ при
ограничениях АХ = А0Х0, где С = (с1, с2,
..., сN) - матрица-cтрока; А = (аij) - матрица системы; Х
=(xij)- матрица-столбец, А0 = (аi)
матрица-столбец
Запись с помощью знаков суммирования. Минимизировать линейную функцию Z =
Сjхj при ограничениях
пределение 1. Планом или допустимым решением задачи линейного
программирования называется Х = (х1, х2, ..., хN),
удовлетворяющий условиям (1.2) и (1.3).
пределение 2. План Х = (х1, х2, ..., хN)
называется опорным, если векторы А (i = 1, 2, ..., N), входящие в разложение
(1.4) с положительными коэффициентами х , являются линейно независимыми.
Так как векторы А являются N-мерными, то из определения опорного плана
следует, что число его положительных компонент не может превышать М.
пределение 3. Опорный план называется невырожденным, если он содержит М
положительных компонент, в противном случае опорный план называется
вырожденным.
пределение 4. Оптимальным планом или оптимальным решением задачи
линейного программирования называется план, доставляющий наименьшее
(наибольшее) значение линейной функции.
В дальнейшем рассмотрено решение задач линейного программирования,
связанных с нахождением минимального значения линейной функции. Там, где
необходимо найти максимальное значение линейной функции, достаточно заменить на
противоположный знак линейной функции и найти минимальное значение последней функции.
Заменяя на противоположный знак полученного минимального значения, определяем
максимальное значение исходной линейной функции.
1.3 Основные понятия линейной алгебры
и выпуклого анализа, применяемые в теории математического программирования
Кратко напомним некоторые фундаментальные определения и теоремы линейной
алгебры и выпуклого анализа, которые широко применяются при решении проблем как
линейного, так и нелинейного программирования.
Фундаментальным понятием линейной алгебры является линейное (вещественное)
пространство. Под ним подразумевается множество некоторых элементов (именуемых
векторами или точками), для которых заданы операции сложения и умножения на
вещественное число (скаляр), причем элементы, являющиеся результатом выполнения
операций, также в соответствии с определением должны принадлежать исходному
пространству.
Частными случаями линейных пространств являются вещественная прямая,
плоскость, геометрическое трехмерное пространство.
Вектор л1a1 + л2a2 + …+ лmam
называется линейной комбинацией векторов а1 а2,..., аm
с коэффициентами л1, л2, лm,
Система векторов линейного пространства а1 а2,...,
аm называется линейно зависимой, если существуют такие числа л1,
л2, лm не равные одновременно нулю, что их линейная
комбинация л1a1 + л2a2 + …+ лmam
равняется нулевому вектору (вектору, все компоненты которого равны нулю). В
противном случае систему а1, а2,..., аm
называют линейно независимой, т. е. линейная комбинация данных векторов может
быть равна нулевому вектору только при нулевых коэффициентах л1, л2,
…, лm
Максимально возможное количество векторов, которые могут образовывать
линейно независимую систему в данном линейном пространстве, называют
размерностью пространства, а любую систему линейно независимых векторов в
количестве, равном размерности, -- базисом пространства.
Линейное пространство обычно обозначают как Rn, где n -- его
размерность.
Любое подмножество данного линейного пространства, которое само обладает
свойствами линейного пространства, называется линейным подпространством. Множество
Н, получаемое сдвигом некоторого линейного подпространства L € Rn на
вектор a € Rn: H=L+a, называется аффинным множеством
(пространством). Если фундаментальным свойством любого линейного пространства
или подпространства является принадлежность ему нулевого вектора, то для
аффинного множества это не всегда так. На плоскости примером подпространства
является прямая, проходящая через начало координат, а аффинного множества --
любая прямая на плоскости. Характеристическим свойством аффинного множества является
принадлежность ему любой прямой, соединяющей две любые его точки. Размерность
аффинного множества совпадает с размерностью того линейного подпространства,
сдвигом которого оно получено.
Если рассматривается некоторое линейное пространство Rn, то
принадлежащие ему аффинные множества размерности 1 называются прямыми, а
размерности (n-1)--гиперплоскостями. Так, обычная плоскость является
гиперплоскостью для трехмерного геометрического пространства R3, а
прямая -- гиперплоскостью для плоскости R2. Всякая гиперплоскость
делит линейное пространство на два полупространства.
Множество V векторов (точек) линейного пространства Rn
называется выпуклым, если оно содержит отрезок прямой, соединяющей две его
любые точки, или, другими словами, из того, что a €V и b€V , следует, что х =
(1- л) х а+ л х b € V , где 0 ? л ? 1.
Линейная комбинация векторов а1, а2... аm
называется выпуклой, если лi ?0, i €1:m и
Множество, содержащее все возможные выпуклые комбинации точек некоторого
множества М, называют выпуклой оболочкой данного множества. Можно показать, что
выпуклая оболочка множества М является наименьшим выпуклым множеством,
содержащим М.
Выпуклая оболочка конечного множества точек называется выпуклым
многогранником, а непустое пересечение конечного числа замкнутых полупространств
-- многогранным выпуклым множеством. В отличие от выпуклого многогранника
последнее может быть неограниченным.
Точка v выпуклого множества V называется его угловой (крайней) точкой,
если она не является внутренней точкой ни для какого отрезка, концы которого
принадлежат множеству V. Угловые точки выпуклого многогранника являются его
вершинами, а сам он -- выпуклой оболочкой своих вершин.
Множество К называется конусом с вершиной в точке x0, если x0
€ К , и из того, что некоторая точка х принадлежит К ( х € К ), следует,
что в К содержится и луч, начинающийся в х0 и проходящий через х, т.
е.
или
Выпуклая оболочка конечного множества лучей, исходящих из одной точки,
называется многогранным выпуклым конусом с вершиной в данной точке.
1.4 Математические основы решения
задачи линейного программирования графическим способом
.4.1 Математический аппарат
Для понимания всего дальнейшего полезно знать и представлять себе
геометрическую интерпретацию задач линейного программирования, которую можно
дать для случаев n = 2 и n = 3.
Наиболее наглядна эта интерпретация для случая n = 2, т.е. для случая
двух переменных x1 и x2. Пусть нам задана задача
линейного программирования в стандартной форме
Возьмём на плоскости декартову систему координат и каждой паре чисел (x1,x2)поставим
в соответствие точку на этой плоскости.
Обратим прежде всего внимание на ограничения x1 ?0 и x2
? 0. Они из всей плоскости вырезают лишь её первую четверть (см. рис. 1).
Рассмотрим теперь, какие области соответствуют неравенствам вида a1
x1 + a2 x2 ? b. Сначала рассмотрим область,
соответствующую равенству a1 x1 + a2 x2
= b. Как Вы, конечно, знаете, это прямая линия. Строить её проще всего по двум
точкам.
Пусть b ? 0. Если взять x1 = 0, то получится x2 =
b/a2. Если взять x2 = 0, то получится x1 = b/a1.
Таким образом, на прямой лежат две точки (0, b/a2) и (b/a1,
0). Дальше через эти две точки можно по линейке провести прямую линию (рисунок
2).
Если же b=0, то на прямой лежит точка (0,0). Чтобы найти другую точку,
можно взять любое отличное от нуля значение x1 и вычислить
соответствующее ему значение x2.
Эта построенная прямая разбивает всю плоскость на две полуплоскости. В
одной её части a1x1 + a2x2 < b,
а в другой наоборот a1x1 + a2x2
> b. Узнать, в какой полуплоскости, какой знак имеет место проще всего
посмотрев, какому неравенству удовлетворяет какая-то точка плоскости, например,
начало координат, т.е. точка (0,0).
1.4.2 Геометрическая интерпретация
задачи линейного программирования
Рассмотрим задачу ЛП в стандартной форме записи:
f(X) = с1х1 + с2х2 + ... + спхп
(*)
при ограничениях
а11х1 + а12х2 + … + а1nхn
? b1
а21х1 + а22х2 + … + а2nхn
? b2
……………………………..
аm1х1 + аm2х2 + … + аmnхn
? bm
хj ? 0, j = 1, 2, …, n.
Рассмотрим эту задачу на плоскости, т.е. при п = 2. Пусть система
неравенств (**), (***) совместна (имеет хотя бы одно решение):
а11х1 + а12х2 ? b1
а21х1 + а22х2 ? b2
…………..
аm1х1 + аm2х2 ? bm1
? 0; х2 ? 0.
Каждое неравенство этой системы геометрически определяет полуплоскость с
граничной прямой аi1х1 + аi2х2 ?
bi i = 1, m. Условия неотрицательности определяют
полуплоскости соответственно с граничными прямыми x1 = 0; х2
= 0.. Система совместна, поэтому полуплоскости, как выпуклые множества,
пересекаясь, образуют общую часть, которая является выпуклым множеством и
представляет собой совокупность точек, координаты каждой из которых составляют
решение данной системы. Совокупность этих точек называют многоугольником
решений. Это может быть точка, отрезок, луч, замкнутый многоугольник,
неограниченная многоугольная область.
Если в системе ограничений (**) - (***) n = 3, то каждое неравенство
геометрически представляет полупространство трехмерного пространства, граничная
плоскость которого аi1х1 + аi2х2 +
аi3х1 ? bi, а условия
неотрицательности -- полупространства с граничными плоскостями соответственно xi
= 0 (i = 1, 2, 3). Если система ограничений совместна, то эти полупространства,
как выпуклые множества, пересекаясь, образуют в трехмерном пространстве общую
часть, которая называется многогранником решений.
Пусть в системе (**) - (***) п > 3, тогда каждое неравенство
определяет полупространство n-мерного пространства с граничной гиперплоскостью
аi1х1 + аi2х2 + … + аinхn
? bi i = 1, т , а условия неотрицательности --
полупространства с граничными гиперплоскостями xj = 0, j = 1, n.
Если система ограничений совместна, то по аналогии с трехмерным
пространством она образует общую часть n-мерного пространства, называемую
многогранником решений, так как координаты каждой его точки являются решением.
Таким образом, геометрически задача линейного программирования
представляет собой отыскание такой точки многогранника решений, координаты
которой доставляют линейной функции минимальное значение, причем допустимыми
решениями служат все точки многогранника решений.
1.4.2 Этапы решения графического метода
задач линейного программирования
Графический метод основан на геометрической интерпретации задачи
линейного программирования и применяется в основном при решении задач
двумерного пространства и только некоторых задач трехмерного пространства, так
как довольно трудно построить многогранник решений, который образуется в
результате пересечения полупространств. Задачу пространства размерности больше
трех изобразить графически вообще невозможно.
Пусть задача линейного программирования задана в двумерном пространстве,
т. е. ограничения содержат две переменные.
Если в ЗЛП ограничения заданы в виде неравенств с двумя переменными, она
может быть решена графически. Графический метод решения ЗЛП состоит из
следующих этапов.
Этап 1.
Сначала на координатной плоскости x1Ox2 строится
допустимая многоугольная область (область допустимых решений, область
определения), соответствующая ограничениям:
Не приводя строгих доказательств, укажем те случаи, которые тут могут
получится.
. Основной случай - получающаяся область имеет вид ограниченного
выпуклого многоугольника (рис. 1а).
. Неосновной случай ? получается неограниченный выпуклый многоугольник,
имеющий вид, подобный изображенному на рис. 1б. Подобная ситуация, например,
получится, если в рассмотренном выше примере убрать ограничение х1 +
х 2 ? 3. Оставшаяся часть будет неограниченным выпуклым
многоугольником.
Наконец, возможен случай, когда неравенства (1.6) противоречат друг
другу, и допустимая область вообще пуста.
Рассмотрим теорию на конкретном примере:
Найти допустимую область задачи линейного программирования, определяемую
ограничениями
Решение:
. Рассмотрим прямую -x1+x2 = 1. При x1 =
0, x2 = 0, а при x2= 0, x1= -1. Таким образом,
эта прямая проходит через точки (0,1) и (-1,0). Беря x1 = x2
= 0, получим, что -0+0<1 и поэтому интересующая нас полуплоскость лежит ниже
прямой, изображенной на рис. 4.а.
. Рассмотрим прямую . При , а при . Таким образом, эта прямая проходит
через точки (0, -1/2) и (1,0). так как (4.б).
. Наконец, рассмотрим прямую . Она проходит через точки (0,3) и (3,0) и
так как 0+0<3, то интересующая нас полуплоскость лежит ниже прямой,
изображенной на рис. 4.в.
Сводя все вместе и добавляя условия х1 ? 0,х2 ? 0
получим рисунок 5, где выделена область, в которой выполняются одновременно все
ограничения (1.32). Обратим внимание на то, что получившаяся область имеет вид
выпуклого многоугольника.
Этап 2.
Вернёмся теперь к исходной задаче линейного программирования. В ней,
кроме системы неравенств, есть еще целевая функция с1х1+с2х2
=>max.
Рассмотрим прямую с1х1+с2х2 =
L. Будем увеличивать L. Что будет происходить с нашей прямой?
Легко догадаться, что прямая будет двигаться параллельно самой себе в том
направлении, которое дается вектором (с1,с2), так как это
? вектор нормали к нашей прямой и одновременно вектор градиента функции
(х1,х2) = с1х1+с2х2
.
.3 Симплекс метод - метод линейного программирования, который реализует
рациональный перебор базисных допустимых решений, в виде конечного итеративного
процесса, необходимо улучшающего значение целевой функции на каждом шаге.
Применение симплекс-метода для задачи линейного программирования
предполагает предварительное приведение ее формальной постановки к канонической
форме с n неотрицательными переменными: (X1, ..., Xn),
где требуется минимизация линейной целевой функции при m линейных
ограничениях типа равенств. Среди переменных задачи выбирается начальный базис
из m переменных, для определенности (X1, ..., Xm),
которые должны иметь неотрицательные значения, когда остальные (n-m)
свободные переменные равны 0. Целевая функция и ограничения равенства
преобразуются к диагональной форме относительно базисных переменных,
переменных, где каждая базисная переменная входит только в одно уравнение с
коэффициентом 1.
Данная формальная модель задачи линейного программирования обычно
задается в форме, так называемой симплекс-таблицы, удобной для
выполнения операций симплекс-метода:
Симплекс-таблица
|
|
|
1
|
X1
|
X2
|
...
|
Xm
|
Xm+1
|
...
|
Xn
|
|
|
X0
|
A0,0
|
0
|
0
|
...
|
0
|
A0,m+1
|
...
|
A0,n
|
|
|
X1
|
A1,0
|
1
|
0
|
...
|
0
|
A1,m+1
|
...
|
A1,n
|
|
|
X2
|
A2,0
|
0
|
1
|
...
|
0
|
A2,m+1
|
...
|
A2,n
|
|
|
...
|
...
|
...
|
...
|
...
|
...
|
...
|
...
|
...
|
|
|
Xm
|
Am,0
|
0
|
0
|
...
|
1
|
Am,m+1
|
...
|
Am,n
|
|
|
|
|
|
|
|
|
|
|
|
Верхняя строка симплекс-таблицы представляет целевую функцию задачи.
Каждая строка симплекс-таблицы, кроме первой, соответствует определенному
ограничению-равенству задачи. Свободные члены ограничений составляют крайний
левый столбец таблицы. Слева от таблицы записаны текущие базисные переменные (X1,
..., Xm). Сверху от таблицы приведен набор всех переменных
задачи, где Xm+1, ..., Xn - свободные переменные
задачи.
На начальном шаге алгоритма симплекс-метода должно быть выбрано базисное
допустимое решение (X1, ..., Xm) >= 0 при Xj
= 0 (j = m+1, ..., n), следовательно, все свободные члены ограничений Ai,0
>= 0 (i = 1, ..., m). Когда это условие выполнено, симплекс-таблица
называется прямо-допустимой, так как в этом случае базисные переменные,
равные Ai,0, определяют допустимое решение прямой задачи
линейного программирования. Если все коэффициенты целевой функции A0,j
>= 0 (j = 1, ..., m), то симплекс-таблица называется двойственно-допустимой,
поскольку соответствующее решение является допустимым для двойственной задачи
линейного программирования.
Если симплекс-таблица является одновременно прямо и двойственно
допустимой, т.е. одновременно все Ai,0 >= 0 и A0,j
>= 0, то решение оптимально.
Действительно, поскольку допустимыми являются лишь неотрицательные
значения управляемых параметров, то изменение целевой функции за счет вариации
свободных переменных, через которые она выражена, возможно только в сторону
увеличения, т.e. будет ухудшаться. Если среди ее коэффициентов имеются A0,j
< 0, то значение целевой функции еще можно уменьшить (т.e. улучшить),
увеличивая значение любой свободной переменной Xj с
отрицательным коэффициентом A0,j при побочном уменьшении
базисных переменных, чтобы оставались справедливы ограничения задачи.
Теоретически можно использовать любую свободную переменную Xj
с A0,j < 0, но на практике обычно действуют в соответствии
со стратегией наискорейшего спуска, выбирая минимальный элемент A0,p
< 0 из всех отрицательных A0,j < 0:
0,p = min A0,j < 0.
j
Столбец p симплекс-таблицы, соответствующий выбранному
коэффициенту A0,p < 0, называется ведущим столбцом.
Свободная переменная ведущего столбца должна быть введена в базис вместо одной
из текущих базисных переменных. Очевидно, из базиса следует исключить такую
переменную Xq, которая раньше других обращается в нуль при
увеличении переменной Xp ведущего столбца.
Её индекс легко определить, если среди положительных элементов ведущего
столбца p найти элемент, минимизирующий отношение (Ai,0 /
Ai,p):
Aq,0 Ai,0
----- = min ------ , i = 1,...,m.q,p i Ai,p
Элемент Aq,p называется ведущим элементом,
cтрока q симплекс-таблицы, содержащая ведущий элемент, называется,
соответственно, ведущей строкой. Переменная ведущей строки Xq
заменяется в базисе переменной ведущего столбца Xp и
становится свободной переменной с значением 0, в то время как новая базисная
переменная Xp достигнет максимально возможного значения,
равного: max Xp = ( Aq,0 / Aq,p).
После указанного взаимообразного обмена переменными Xp
и Xq между наборами свободных и базисных переменных нужно
модифицировать исходную каноническую модель задачи путем приведения ее к
диагональной форме относительно нового множества базисных переменных. Для
указанного преобразования можно формально использовать процедуру исключения
Гаусса, которая, как известно, состоит из двух элементарных операций,
применяемых к системе алгебраических уравнений ( в данном случае ограничений -
равенств):
· умножение уравнения E1(X) = 0 на константу K1
и замена уравнения E1(X) = 0 уравнением K1*E1(X)
= 0;
· сложение уравнений E1(X) = 0 и E2(X) =
0 c последующей заменой уравнения E2(X) = 0 уравнением E1(X)
+ E2(X) = 0.
Исключения Гаусса позволяют привести систему уравнений к диагональной
форме относительно желаемого множества переменных. В данном случае исключение
Гаусса применяется так, чтобы все элементы симплекс-таблицы в ведущем столбце,
кроме ведущего элемента Aq,p, стали нулевыми, а ведущий
элемент стал равным единице:
Ai,p = 0, если i не равно q
иi,p = 1, если i = q.
Указанные шаги симплекс-метода повторяются, пока не будет получена
симплекс-таблица, которая одновременно является прямо и двойственно допустимой.
Если положит в такой симплекс-таблице текущие базисные переменные равными Ai,0,
а свободные - нулю, то будет получено оптимальное решение.
Практика применения симплекс метода показала, что число итераций,
требуемых для решения задачи линейного программирования обычно колеблется от 2m
до 3m, хотя для некоторых специально построенных задач вычисления по
правилам симплекс метода превращаются в прямой перебор базисных допустимых
решений.
Ограничения задачи вырезают на плоскости некоторый многоугольник. Пусть
при некотором L прямая с1х1+с2х2 =
L пересекает допустимую область. Это пересечение дает какие-то значения
переменных (х1,х2), которые являются планами.
Увеличивая L мы начнем двигать нашу прямую и её пересечение с допустимой
областью будет изменяться (см. рис. 7). В конце концов эта прямая выйдет на
границу допустимой области ? как правило, это будет одна из вершин
многоугольника. Дальнейшее увеличение L приведёт к тому, что пересечение прямой
с1х1+с2х2 = L с допустимой областью
будет пустым. Поэтому то положение прямой с1х1+с2х2
= L, при котором она вышла на граничную точку допустимой области, и даст
решение задачи, а соответствующее значение L и будет оптимальным значением
целевой функции.
2.
ПОРЯДОК РАЗРАБОТКИ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПО ОПТИМИЗАЦИИ ОТРАСЛЕВОЙ
СТРУКТУРЫ ПРОИЗВОДСТВА
2.1 Экономико-математическая
модель по оптимизации отраслевой структуры производства
Постановка задачи
Большинство современных сельскохозяйственных предприятий развивает
совокупность отраслей, рациональное сочетание которых в значительной степени
определяет эффективность всей производственно-финансовой деятельности
хозяйствующего субъекта. Очевидно, что есть отрасли более эффективные, чем
другие. Но отдать доминирующий приоритет самым эффективным отраслям невозможно
иногда в силу агротехнических или зооветеринарных, иногда в силу
организационно-экономических требований. Именно поэтому проблема поиска
оптимального сочетания развиваемых в предприятии отраслей действительно
актуальна.
Постановку данной задачи сформулируем следующим образом: исходя из
наличия ресурсов необходимо найти такое сочетание отраслей, которое обеспечило
бы получение максимальной суммы чистого дохода при условии соблюдения всех
агротехнических и зооветеринарных требований, выполнения договорных
обязательств по реализации продукции, гарантированного обеспечения отраслей
животноводства кормами.
Входная информация.
Для разработки экономико-математической модели данной задачи необходимо
иметь следующую информацию:
· площадь пашни, имеющуюся у предприятия;
· перечень сельскохозяйственных культур, которые планируется
возделывать;
· урожайность основной и побочной продукции, нормы высева семян
(по культурам, по которым используются семена собственного производства),
нормативы отходов;
· производственные затраты и затраты труда в расчете на 1 га
посева;
· агротехнические требования по насыщению севооборотов
отдельными культурами и группами культур;
· поголовье имеющихся у предприятия сельскохозяйственных
животных;
· структуру стада, продуктивность скота, затраты корма на
единицу продукции;
· рационы кормления скота;
· питательность кормов, включенных в рационы кормления;
· выход продукции в расчете на 1 структурную голову;
· производственные затраты в расчете на 1 структурную голову
без учета стоимости кормов;
· цену приобретения покупных кормов;
· цену реализации реализуемой продукции.
Основными источниками получения информации являются фактические данные,
получаемые в хозяйствах, справочная литература, информация о нормативной или
фактической питательности кормов. Подготовку входной информации и построение
экономико-математической модели рассмотрим на конкретном примере.
Условия задачи и подготовка входной информации.
В ООО «Простор» имеется 5 800 га пашни. Продуктивные сенокосы и пастбища
отсутствуют. Планируется возделывать следующие сельскохозяйственные культуры:
озимую пшеницу, ячмень, сою, горчицу, сахарную свеклу, подсолнечник, кукурузу
на силос и зеленый корм, однолетние травы, многолетние травы. В соответствии с
потребностями отрасли животноводства травы будут выращиваться на сено, сенаж и
зеленый корм.
Исходя из запланированного уровня урожайности и на основании рассчитанных
технологических карт были определены размеры затрат материально-денежных
средств и затраты труда в расчете на 1 га посева сельскохозяйственных культур.
Результаты расчетов приведены в таблице 1.
Таблица 1. Информация об урожайности, затратах материально-денежных
средств и затратах труда в расчете на 1 га посева сельскохозяйственных культур
|
Сельскохозяйственные
культуры
|
Планируемая урожайность,
ц/га
|
Материально-денежные затраты
в расчете на 1 га, тыс.руб.
|
|
основной продукции
|
побочной продукции
|
|
|
Озимая пшеница
|
38
|
57
|
10,1
|
|
Ячмень
|
34
|
34
|
8,5
|
|
Соя
|
15
|
11
|
8,9
|
|
Горчица
|
15
|
11
|
7,9
|
|
Сахарная свекла
|
400
|
160
|
44,9
|
|
Подсолнечник
|
18
|
|
7,2
|
|
Кукуруза на силос
|
297
|
|
10,8
|
|
Кукуруза на зеленый корм
|
287
|
|
10,2
|
|
Однолетние травы на сено
|
29
|
|
5,6
|
|
Однолетние травы на сенаж
|
48
|
|
5,4
|
|
Однолетние травы на зеленый
корм
|
144
|
|
5,2
|
|
Многолетние травы на сено
|
48
|
|
6,7
|
|
Многолетние травы на сенаж
|
78
|
|
6,5
|
|
Многолетние травы на
зеленый корм
|
238
|
|
6,2
|
|
Озимые на зеленый корм
|
105
|
|
4,6
|
|
Пар
|
|
|
2,7
|
Хозяйством заключены договора на реализацию 23 000 ц озимой пшеницы, 12
000 ц ячменя, 195 000 ц сахарной свеклы и 20 000 ц молока.
Исходя из агротехнических требований заданы следующие границы насыщения
севооборота отдельными культурами и группами культур.
Таблица 2. Пределы насыщения севооборота отдельными культурами и группами
культур
|
Сельскохозяйственные
культуры
|
Нижняя граница
|
Верхняя граница
|
|
%
|
га
|
%
|
га
|
|
Всего пашни
|
100,0%
|
5 800
|
100,0%
|
5 800
|
|
Зерновые и зернобобовые
|
50,0%
|
2 900
|
60,0%
|
3 480
|
|
Озимые
|
20,0%
|
1 160
|
30,0%
|
1 740
|
|
Соя и горчица
|
0,0%
|
0
|
20,0%
|
1 160
|
|
Сахарная свекла
|
0,0%
|
0
|
15,0%
|
870
|
|
Подсолнечник
|
0,0%
|
0
|
12,5%
|
725
|
|
Пар
|
5,0%
|
290
|
10,0%
|
В хозяйстве развивается молочное скотоводство. Оборот стада предусматривает
реализацию всего сверхремонтного молодняка в 20-ти дневном возрасте населению и
предприятиям, специализирующимся на выращивании, доращивании и откорме крупного
рогатого скота.
При описании животноводческих отраслей для упрощения расчетов, связанных
с подготовкой исходной информации, в качестве единицы измерения используются
структурные головы. За структурную голову в молочном скотоводстве принимаются
фуражная корова.
Информация о среднегодовом поголовье крупного рогатого скота, полученная
на основе составленного оборота стада исходя из фактического поголовья фуражных
коров, приведена в таблице 3.
Таблица 3. Информация о среднегодовом поголовье крупного рогатого скота
|
Половозрастные группы
|
Поголовье, гол
|
Структура стада, %
|
|
Коровы
|
425
|
77.4
|
|
Нетели
|
25
|
4,6
|
|
Телочки до 20 дней
|
7
|
1,3
|
|
Бычки до 20 дней
|
7
|
1,3
|
|
Телочки с 20 дней до 6
месяцев
|
25
|
4,6
|
|
Телки с 6 месяцев до 1 года
|
25
|
4,6
|
|
Телки с 1 года до 18
месяцев
|
25
|
4,6
|
|
Выбракованный скот на
откорме
|
10
|
1,8
|
|
Всего крупного рогатого
скота
|
549
|
100,0
|
Посредством расчета оборота стада была получена следующая информация.
Валовое производство прироста по стаду крупного рогатого скота составило 276,0
ц (или 276,0/425=0,65 ц в расчете на 1 структурную голову). Реализация прироста
крупного рогатого скота составляет 452 ц (или 452,0/425=1,06 ц в расчете на 1
структурную голову). Превышение объемов реализации над объемами производства
прироста связано с тем, что в расчет прироста не входит вес приплода и коров,
который они набирают, находясь в основном стаде. Надой на 1 фуражную корову
планируется на уровне 5110 кг. Исходя из рыночной конъюнктуры планируются
следующие цены реализации продукции животноводства: молоко - 920, прирост КРС -
5 800 руб. за 1 ц. В этом случае стоимость товарной продукции в расчете на 1 структурную
голову составит: 51,10·920 + 1,06·5800 = 53.160 тыс. руб.
Исходя из фактических рационов кормления по каждой половозрастной группе
и количества кормодней пребывания была определена годовая потребность в кормах
и структура рациона кормления в расчете на 1 структурную голову (таблица 4).
Таблица 4. Расчет потребности в кормах на 1 структурную голову КРС
|
Корма и кормовые добавки
|
Годовая потребность в
кормах
|
|
всего
|
на 1 структурную голову,
ц.к.ед.
|
|
Ц
|
ц.к.ед
|
|
|
основное стадо
|
молодняк и скот на откорме
|
основное стадо
|
молодняк и скот на откорме
|
на молоко
|
на прирост
|
всего
|
|
Комбикорм
|
2920
|
354
|
3212
|
389
|
7,56
|
0,92
|
8,47
|
|
Пшеница
|
1216
|
|
1557
|
|
3,66
|
|
3,66
|
|
Ячмень
|
1216
|
|
1398
|
|
3,29
|
|
3,29
|
|
Сено
|
6448
|
249
|
3095
|
120
|
7,28
|
0,28
|
7,56
|
|
Солома
|
|
164
|
|
41
|
|
0,10
|
0,10
|
|
Сенаж
|
19 025
|
2237
|
6 088
|
716
|
14,32
|
1,68
|
16,01
|
|
Силос
|
23 844
|
1663
|
4 769
|
333
|
11,22
|
0,78
|
12,00
|
|
Зеленые корма
|
|
2316
|
|
510
|
|
1,20
|
1,20
|
|
Патока
|
1824
|
|
1 386
|
|
3,26
|
|
3,26
|
|
Премикс
|
158
|
20
|
79
|
10
|
0,19
|
0,02
|
0,21
|
|
Молоко
|
|
125
|
|
43
|
|
0,10
|
0,10
|
|
Обрат
|
|
365
|
|
48
|
|
0,11
|
0,11
|
|
ЗЦМ
|
|
28
|
|
67
|
|
0,16
|
0,16
|
|
Всего
|
|
|
21 584
|
2275
|
50,79
|
5,35
|
56,14
|
Исходя из зооветеринарных требований в 1 ц корма, направляемого на
производство молока, должно содержаться не менее 0,101 кг, а в 1 ц корма,
направляемого на производство прироста, - 0,107 кг переваримого протеина.
Материально-денежные затраты в расчете на 1 структурную голову (без
стоимости кормов) составляют 23,4 тыс. руб. Материально-денежные затраты
включаются в модель без учета стоимости кормов для того, чтобы избежать двойного
счета, поскольку затраты на производство кормов и их приобретение определяются
уже в ходе решения экономико-математической задачи.
Молоко на корм собственного производства потребляется по складывающейся
себестоимости, а остальные корма и кормовые добавки приобретаются по следующим
ценам: комбикорм - 7,20; обрат - 1,00; заменитель цельного молока (ЗЦМ) -
33,60; патока - 1,50; премикс - 5,50 руб. за 1 кг.
Для разработки экономико-математической модели необходимо провести
дополнительные расчеты. Первая расчетная таблица связана с обоснованием
распределения продукции в расчете на 1 га посева отдельных сельскохозяйственных
культур.
Таблица 5. Распределение продукции в расчете на 1 га посева
сельскохозяйственных культур
|
Сельскохозяйственные
культуры
|
Выход продукции с 1 га, ц
|
Отходы, ц
|
Семена со страховым
фондом, ц
|
На корм скоту, ц
|
Товарная продукция
|
|
основной
|
побочной
|
|
|
основной
|
побочной
|
в натуральном выражении, ц
|
в денежном выражении,
тыс.руб.
|
|
Озимая пшеница товарная
|
38
|
57,0
|
0,76
|
2,50
|
0,76
|
|
34,74
|
16,68
|
|
Озимая пшеница фуражная
|
38
|
57,0
|
0,76
|
2,50
|
35,50
|
|
|
|
|
Ячмень товарный
|
34
|
34,0
|
0,68
|
3,30
|
0,68
|
34,00
|
30,02
|
12,31
|
|
Ячмень фуражный
|
34
|
34,0
|
0,68
|
3,30
|
30,70
|
34,00
|
|
|
|
Соя
|
15
|
11,3
|
0,30
|
|
0,30
|
11,25
|
14,70
|
17,64
|
|
Горчица
|
15
|
11,3
|
0,30
|
|
|
|
14,70
|
19,26
|
|
Сахарная свекла
|
400
|
160,0
|
|
|
|
|
400,00
|
44,00
|
|
Подсолнечник
|
18
|
|
0,36
|
|
|
|
17,64
|
16,76
|
|
Кукуруза на силос
|
297
|
|
74,25
|
|
222,75
|
|
|
|
|
Кукуруза на зеленый корм
|
287
|
|
|
|
287,00
|
|
|
|
|
Однолетние травы на сено
|
29
|
|
|
|
29,00
|
|
|
|
|
Однолетние травы на сенаж
|
48
|
|
|
|
48,00
|
|
|
|
|
Однолетние травы на зеленый
корм
|
144
|
|
|
|
144,00
|
|
|
|
|
Многолетние травы на сено
|
48
|
|
|
|
48,00
|
|
|
|
|
Многолетние травы на сенаж
|
78
|
|
|
|
78,00
|
|
|
|
|
Многолетние травы на
зеленый корм
|
238
|
|
|
|
238,00
|
|
|
|
|
Озимые на зеленый корм
|
104
|
|
|
|
104,00
|
|
|
|
Данные о выходе продукции с 1 га посева берутся из таблицы 1.
Норматив отходов по группе зерновых и зернобобовых, горчице и
подсолнечнику устанавливается на уровне 2% от урожайности в физическом весе.
Норматив угара силосной массы берется на уровне 25% от урожайности кукурузы на
силос.
Семена озимой пшеницы и ячменя производятся непосредственно в хозяйстве.
Формирование семенного фонда по данным сельскохозяйственным культурам
происходит исходя из следующих норм высева семян: озимая пшеница - 2,5 ц на 1
га, ячмень - 3,0 ц на 1 га. При этом по ячменю предусматривается создание
страхового фонда семян в размере 10% семенного фонда
Объем продукции, направляемой на корм скоту, по озимой пшенице и ячменю
товарным определяется на уровне отходов, а по этим же культурам, посеянным на
фуражные цели, - как разница между урожайностью и нормой высева семян с учетом
страхового фонда. Выход готового силоса в расчете на 1 га посева кукурузы на
силос рассчитывается с учетом угара силосной массы при хранении этого корма. Из
побочной продукции на корм скоту предполагается использовать солому ячменя и
сои.
Выход товарной продукции в натуральном выражении с 1 га посева
определяется по товарным культурам как разница между урожайностью, количеством
отходов и нормой высева семян с учетом страхового фонда.
Исходя из рыночной конъюнктуры планируются следующие цены реализации
производимой продукции: озимая пшеница - 480, ячмень - 410, соя - 1 200,
горчица - 1 310, сахарная свекла - 115, подсолнечник - 950 руб. за 1 ц.
На основании данных таблицы 24 и питательности кормов заполняется таблица
25.
Для равномерного обеспечения отрасли животноводства зелеными кормами
необходимо провести планирование зеленого конвейера (табл. 26).
Таблица 7. Схема зеленого конвейера
|
Источники зеленого корма
|
Выход с 1 га, ц.к.ед.
|
Сроки использования зеленых
кормов, ц к.ед. с 1га
|
|
|
2-я половина мая
|
1-я половина июня
|
2-я половина июня
|
июль
|
август
|
Сентябрь
|
|
А
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
Кукуруза 1 срока сева
|
60,3
|
|
|
|
60,3
|
|
|
Кукуруза 2 срока сева
|
60,3
|
|
|
|
|
|
60,3
|
|
Многолетние травы на
зеленый корм
|
52,4
|
|
31,4
|
|
20,9
|
|
|
|
Однолетние травы 1 срока
сева
|
25,9
|
|
|
25,9
|
|
|
|
|
Однолетние травы 2 срока
сева
|
25,9
|
|
|
|
25,9
|
|
|
|
Озимые на зеленый корм
|
20,8
|
20,8
|
|
|
|
|
|
По многолетним травам планируется провести два укоса. На первый укос
приходится 60% их урожайности, на второй - 40%.
Определение потребности в кормах в расчете на 1 структурную голову с
учетом страхового фонда приведено в таблице 27 при проектируемом уровне затрат
корма на производство 1 ц молока и прироста КРС соответственно 1,06 и 8,24
ц.к.ед.
В связи с тем, что потребность в молоке на корм будет удовлетворяться за
счет молока собственного производства, необходимо провести корректировку суммы
выручки от реализации продукции животноводства в расчете на 1 структурную
голову. Исходя из данных таблицы 4 в расчете на 1 структурную голову требуется
0,11 ц молока, что в физическом весе составит: 0,11 ц к.ед. / 0,34 ц к.ед. =
0,32 ц. То есть в расчете на 1 структурную голову будет реализовано продукции
не на 53,57 тыс. руб., а на 294,40 руб. меньше (0,32 ц*920 руб. = 294,40 руб.),
или 53,27 тыс. руб.
Построение экономико-математической модели
Система переменных данной экономико-математической задачи представлена
основными и вспомогательной переменными. За основные переменные принимаются:
-
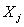площадь посева j-ой сельскохозяйственной культуры;
-
поголовье j-го вида сельскохозяйственных животных;
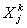- объем
приобретения j-го вида корма или кормовой добавки;
|
x1
|
-
|
Озимая пшеница товарная
|
|
x2
|
-
|
Озимая пшеница фуражная
|
|
x3
|
-
|
Ячмень товарный
|
|
x4
|
-
|
Ячмень фуражный
|
|
x5
|
-
|
Соя
|
|
x6
|
-
|
Горчица
|
|
x7
|
-
|
Сахарная свекла
|
|
x8
|
-
|
Подсолнечник
|
|
x9
|
-
|
Кукуруза на силос
|
|
x10
|
-
|
Кукуруза на зеленый корм 1
срока сева
|
|
x11
|
-
|
Кукуруза на зеленый корм 2
срока сева
|
|
x12
|
-
|
Однолетние травы на сено
|
|
x13
|
-
|
Однолетние травы на сенаж
|
|
x14
|
-
|
Однолетние травы на зеленый
корм 1 срока сева
|
|
x15
|
-
|
Однолетние травы на зеленый
корм 2 срока сева
|
|
x16
|
-
|
Многолетние травы на сено
|
|
x17
|
-
|
Многолетние травы на сенаж
|
|
x18
|
-
|
Многолетние травы на
зеленый корм
|
|
x19
|
-
|
Озимые на зеленый корм
|
|
x20
|
-
|
Пар
|
|
x21
|
-
|
Комбикорм
|
|
x22
|
-
|
Патока
|
|
x23
|
-
|
Премикс
|
|
x24
|
-
|
Молоко на корм
|
|
x25
|
-
|
Обрат
|
|
x26
|
-
|
ЗЦМ
|
|
x27
|
-
|
Поголовье крупного рогатого
скота
|
|
x28
|
|
Производственные затраты
|
Вспомогательная
переменная (
) используется для определения суммы производственных
затрат по предприятию.
Все
условия задачи записаны в виде линейных уравнений и неравенств (ограничений),
которые можно разбить на группы:
· по использованию ресурсов;
· по выполнению агротехнических требований возделывания
сельскохозяйственных культур;
· по выполнению договорных обязательств по реализации
продукции;
· по обеспеченности потребностей животноводства кормами
собственного производства;
· по определению стоимости производственных затрат.
Основными ограничениями (с 1 по 2) являются условия, ограничивающие
систему фактическим наличием ресурсов. В данном конкретном примере
ограничивающими факторами будут являться площадь пашни и поголовье сельскохозяйственных
животных.
В общем виде ограничение по использованию ресурсов записывается следующим
образом:
,
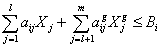где
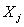- площадь посева j-ой сельскохозяйственной
культуры;
-
поголовье j-го вида скота;
-
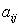затраты ресурсов i-го вида в расчете на 1 га посева j-ой
сельскохозяйственной культуры;
-
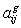затраты ресурсов i-го вида в расчете на 1 структурную голову j-го
вида скота;
-
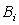наличие ресурсов i-го вида.
Поскольку
по условиям задачи рассматривается только два вида ресурсов, то будут
рассмотрены два частных случая ограничения по ресурсам
,
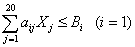где
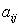- затраты пашни в расчете на 1 га посева j-ой
сельскохозяйственной культуры;
-
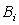наличие пашни в хозяйстве.
Таким
образом, ограничение, гарантирующее, что площадь посева всех
сельскохозяйственных культур и пара не превысит площади пашни, имеющейся в
наличии, будет записано в следующем виде
X1+1X2+1X3+1X4+……+1X17+1X18+1X19+1X20<=5800
i=1.
Коэффициенты
при Xj означают, что для возделывания 1 га каждой
сельскохозяйственной культуры необходимо затрачивать 1 га пашни.
Так
как по условию задачи поголовье сельскохозяйственных животных должно быть
сохранено на фактическом уровне, то второе основное ограничение в структурном
виде записывается как:
,
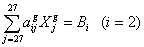где
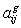- бинарные коэффициенты связи (равны либо 0, либо 1)
по i-му виду сельскохозяйственных животных;
-
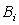фактическое поголовье i-го вида сельскохозяйственных животных в
хозяйстве.
То
есть сохранение существующего поголовья крупного рогатого скота обеспечивается
через реализацию условия
X27=425
i=2.
При
необходимости в систему основных ограничений могут быть введены условия по
использованию сенокосов, пастбищ, трудовых и других ресурсов.
Первую
группу дополнительных ограничений (с 3 по 12) составляют ограничения по
выполнению агротехнических требований, соблюдение которых необходимо для
соблюдения научно обоснованного чередования сельскохозяйственных культур.
Эти
требования представлены условиями двух видов: во-первых, по насыщению
севооборота отдельными культурами или группами культур; во-вторых, по обеспечению
озимых культур хорошими предшественниками.
Ограничение
по насыщению севооборота отдельными культурами или группами культур в
структурном виде может быть записано как
,
где
Qi -
верхние или нижние пределы насыщения севооборотов отдельными
сельскохозяйственными культурами или группами культур.
Например,
ограничение по насыщению севооборота зерновыми и зернобобовыми культурами может
быть записано следующим образом:
1X1+1X2+1X3+1X4+1X5+1X19
>=2900 i=3,
X1+1X2+1X3+1X4+1X5+1X19
<=3480 i=4.
Ограничение
по насыщению севооборота озимыми:
X1+1X2+1X19
>=1160 i=5,
X1+1X2+1X19
<=1740 i=6.
Аналогично
заполняются ограничения по насыщению севооборота горчицей и соей, сахарной
свеклой, подсолнечником, паром.
Информация
о пределах насыщения севооборота отдельными сельскохозяйственными культурами
или группами культур берется из таблицы 21 (столбцы 2 и 4).
Ограничение
по обеспечению озимых культур предшественниками в структурном виде может быть
записано как:
,
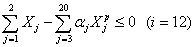где
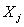- площадь посева j-ой озимой культуры;
-
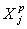площадь посева j-ой сельскохозяйственной культуры;
-
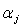коэффициент возможного использования посевов j-ой сельскохозяйственной
культуры в качестве предшественника под озимые.
Данное
ограничение может быть записано следующим образом
1X1+1X2-1X5-1X10-1X12-1X13-1X14-1X15-0,33X16-0,33X17-0,33X18-1X20<=0
i=12.
Коэффициент
0,33 при переменных, означающих многолетние травы, означает, что планируемый
срок использования многолетних трав в хозяйстве составляет три года, поэтому
ежегодно третья часть многолетних трав запахивается и может быть использована в
качестве предшественника под озимые. Если срок эксплуатации многолетних трав
будет равен четырем годам, то данный коэффициент будет равен 0,25.
Вторую
группу дополнительных ограничений (с 13 по 16) составляют ограничения по
выполнению договорных обязательств по реализации продукции.
Эти
ограничения гарантируют, что товарной продукции по тем ее видам, на реализацию
которой заключены договора, будет произведено не менее заданных объемов
,
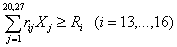где
Xj - площадь посева j-ой сельскохозяйственной
культуры или поголовье j-го вида скота;
rij - выход
продукции i-го вида в расчете на 1 га посева j-ой
сельскохозяйственной культуры или 1 структурную голову j-го вида скота;
-
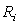минимально необходимый объем производства товарной продукции i-го вида.
По
условиям задачи хозяйство заключило договора на реализацию трех видов
продукции: пшеницы, ячменя, сахарной свеклы и молока. Первые три ограничения
будут записаны следующим образом:
,74X1>=23000
i=13,
,02X3>=12000
i=14,
X7>=195000
i=15.
Ограничение
по реализации молока будет иметь несколько иной вид
X24+51,10X27>=20000
i=16.
Поскольку
потребность в молоке на корм планируется удовлетворять за счет молока
собственного производства, а его объем будет определяться в ходе решения
задачи, то в данном ограничении из объема валового производства молока (51,10X27)
необходимо вычесть потребность в молоке на корм (X24).
Информация
о выходе товарной продукции с 1 га посева соответствующих сельскохозяйственных
культур берется из столбца 7 таблицы 24.
Третью
группу дополнительных ограничений (с 17 по 36) составляют ограничения по
обеспечению потребности отрасли животноводства в кормах. Эти ограничения
гарантируют, что эти потребности будут удовлетворены как за счет собственных,
так и приобретенных кормов.
,
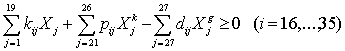где
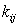- выход корма i-го вида в расчете на 1 га
посева j-ой сельскохозяйственной культуры;
-
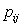содержание питательных веществ i-го вида в единице приобретаемого j-ого
вида корма или j-ой кормовой добавки;
-
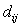потребность в корме i-го вида в расчете на 1 структурную голову j-ого
вида сельскохозяйственных животных.
Ограничение
по удовлетворению общей потребности отрасли животноводства в кормах может быть
записано следующим образом
.97X1+45,44X2+10,30X3+44,83X4+…….+0,34X24+0,13X25+2,40X26-59,14X27>=0 i=17.
По
обеспечению рациона кормления переваримый протеином
,08X1+3,76X2+0,43X3+2,98X4+…….+0,05X24+0,04X25+42,60X26-5.73X27>=0 i=18.
В
ограничениях 17 и 18 информация о выходе корма (с учетом основной и побочной
продукции) берется из столбцов 11 и 12 таблицы 6.
В
ограничениях 20-22 и 24-25 - из столбца 11 таблицы 6. Например, ограничение по
удовлетворению потребности в комбикорме запишется
,10X21-8.47X27>=0 i=20
Ограничение
по удовлетворению потребности в концентрированных кормах собственного
производства будет записано как
,97X1+45,44X2+0,78X3+35,31X4+0,39X5-6.97X27>=0 i=21.
В
ограничении по соломе (23) информация о выходе соломы с 1 га посева зерновых и
зернобобовых культур берется из столбца 9 таблицы 25
,60X3+9,60X4+3,60X5-0,10X27>=0 i=23.
С
помощью ограничений 26-31 происходит моделирование так называемого «зеленого
конвейера», позволяющего обеспечить равномерное поступление зеленых кормов. По
условиям задачи хозяйство не располагает пастбищами, поэтому выход зеленых
кормов планируется только с посевных площадей соответствующих
сельскохозяйственных культур.
Схема
зеленого конвейера приведена в таблице 26. Например, ограничение по
удовлетворению потребности в зеленых кормах в июле запишется следующим образом
.90X15+20.90X18-0,30X27>=0 i=29.
Вспомогательным
является ограничение по определению стоимости производственных затрат в целом
по предприятию:
,
где
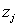- материально-денежные затраты в расчете на 1 га
посева j-ой сельскохозяйственной культуры;
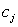- цена
приобретения j-ого вида корма или j-ой кормовой добавки;
-
материально-денежные затраты без учета стоимости кормов в расчете на 1
структурную голову j-ого вида сельскохозяйственных животных.
Это
ограничение может быть записано следующим образом
10,10X1+10,10X2+8,50X3+8,50X4+…+0,72X21+…+29.40X27 - 1X28=0 i=37.
Значения
переменных должны быть неотрицательными
, 
, 
, 
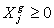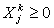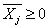
Поскольку
в качестве критерия оптимальности в данной задаче выбрана максимизация сумма
чистого дохода (разница между стоимостью товарной продукции и общей суммой
производственных затрат по предприятию), то целевая функция примет вид:
,
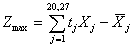где
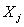- площадь посева j-ой сельскохозяйственной
культуры или поголовье j-го вида скота;
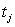- выход
товарной продукции в стоимостном выражении в расчете на 1 га посева j-ой
сельскохозяйственной культуры или 1 структурную голову j-го вида скота.
Целевая
функция может быть записана следующим образом:
Zmax=16,68X1+12,31X3+17,64X5+19,26X6+44.00X7+16.76X8+53,30X27
-X28.
В
матричном виде экономико-математическая модель по оптимизации отраслевой
структуры производства представлена в таблице 8 (при распечатке курсового
проекта целесообразно распечатать модель из MS Excel
и поместить ее в текст в виде приложения.
Реализация
разработанной экономико-математической модели производства осуществляется с
помощью надстройки Поиск решения пункта меню Сервис Microsoft
Excel.
Порядок
работы с данной надстройкой описан в подразделе 4.1. настоящих методических
указаний.
Таблица
8. Экономико-математическая модель по оптимизации отраслевой структуры
производства (часть 1)
|
№
|
Ограничения
|
Единица измерения
|
Переменные
|
|
|
|
Озимая пшеница
|
Ячмень
|
Соя
|
Горчица
|
Сахарная свекла
|
Подсолнечник
|
Кукуруза
|
|
|
|
товарная
|
фуражная
|
товарный
|
фуражный
|
|
|
|
|
на силос
|
на зеленый корм
|
|
|
|
|
|
|
|
|
|
|
|
|
1 срока сева
|
2 срока сева
|
|
|
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
x9
|
x10
|
x11
|
|
|
Значения по решению =
>
|
1285.8
|
0,0
|
1323..1
|
9.5
|
858.4
|
301.6
|
487.5
|
725.0
|
114.5
|
2,1
|
1,1
|
|
1
|
Пашня
|
га
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
2
|
Поголовье КРС
|
стр.гол.
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
Площадь зерновых и
зернобобовых min
|
га
|
1
|
1
|
1
|
1
|
1
|
|
|
|
|
|
|
|
4
|
Площадь зерновых и
зернобобовых max
|
га
|
1
|
1
|
1
|
1
|
1
|
|
|
|
|
|
|
|
5
|
Площадь озимых min
|
1
|
1
|
|
|
|
|
|
|
|
|
|
|
6
|
Площадь озимых max
|
га
|
1
|
1
|
|
|
|
|
|
|
|
|
|
|
7
|
Площадь горчицы и сои
|
га
|
|
|
|
|
1
|
1
|
|
|
|
|
|
|
8
|
Площадь сахарной свеклы
|
га
|
|
|
|
|
|
|
1
|
|
|
|
|
|
9
|
Площадь подсолнечника
|
га
|
|
|
|
|
|
|
|
1
|
|
|
|
|
10
|
Площадь пара min
|
га
|
|
|
|
|
|
|
|
|
|
|
|
|
11
|
Площадь пара max
|
га
|
|
|
|
|
|
|
|
|
|
|
|
|
12
|
Обеспеченность озимых
предшественниками
|
га
|
1
|
1
|
|
|
-1
|
|
|
|
|
-1
|
|
|
|
Объем реализации по
договорам:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13
|
Пшеница
|
ц
|
34.74
|
|
|
|
|
|
|
|
|
|
|
|
14
|
Ячмень
|
ц
|
|
|
30,02
|
|
|
|
|
|
|
|
|
|
15
|
сахарная свекла
|
ц
|
|
|
|
|
|
|
400
|
|
|
|
|
|
16
|
Молоко
|
ц
|
|
|
|
|
|
|
|
|
|
|
|
|
17
|
Требуется корма всего
|
ц.к.ед.
|
0.97
|
45,44
|
10,30
|
44,83
|
3.99
|
|
|
|
44.55
|
60.27
|
60,27
|
|
18
|
Требуется переваримого
протеина
|
кг
|
0.08
|
3,76
|
0,43
|
2,98
|
0,21
|
|
|
|
3,12
|
4,02
|
4,02
|
|
19
|
Концентраты всего:
|
ц.к.ед.
|
0,97
|
45,44
|
0,78
|
35,31
|
0,39
|
|
|
|
|
|
|
|
20
|
в т.ч. комбикорм
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
|
|
21
|
прочие концентраты
|
ц.к.ед.
|
0,97
|
45,44
|
0,78
|
35,31
|
0,39
|
|
|
|
|
|
|
|
22
|
Сено
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
|
|
23
|
Солома
|
ц.к.ед.
|
|
|
9,52
|
9,52
|
3,60
|
|
|
|
|
|
|
|
24
|
Сенаж
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
|
|
25
|
Силос
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
44.55
|
|
|
|
26
|
Зеленый корм во 2-ой
половине мая
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
|
|
27
|
в 1-й половине июня
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
|
|
28
|
во 2-й половине июня
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
|
|
29
|
в июле
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
|
30
|
в августе
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
60.30
|
|
|
31
|
в сентябре
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
60,30
|
|
32
|
Патока
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
|
|
33
|
Премикс
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
|
|
34
|
Молоко
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
|
|
35
|
Обрат
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
|
|
36
|
ЗЦМ
|
ц.к.ед.
|
|
|
|
|
|
|
|
|
|
|
|
|
37
|
Производственные затраты
|
тыс.руб.
|
10,10
|
10,10
|
8,58
|
8,50
|
8,90
|
7,90
|
44,90
|
7,20
|
10,80
|
10,20
|
10,20
|
|
Zmax
|
|
16,68
|
|
12,31
|
|
17,64
|
19,26
|
44.00
|
16.76
|
|
|
|
|
№
|
Переменные
|
Сумма произведений
|
Тип ограничений
|
Объем ограничений
|
|
Однолетние травы
|
Многолетние травы
|
Озимые на зеленый корм
|
Пар
|
Комбикорм
|
Патока
|
Премикс
|
Молоко на корм
|
Обрат
|
ЗЦМ
|
Поголовье крупного рогатого
скота
|
Производственные затраты
|
|
|
|
|
на сено
|
на сенаж
|
на зеленый корм
|
на сено
|
на сенаж
|
на зеленый корм
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 срока сева
|
2 срока сева
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x12
|
x13
|
x14
|
x15
|
x16
|
x17
|
x18
|
x19
|
x20
|
x21
|
x22
|
x23
|
x24
|
x25
|
x26
|
x27
|
x28
|
|
|
bi
|
|
0,0
|
0,0
|
2.5
|
3,3
|
133.9
|
256.6
|
2,0
|
3,1
|
290,0
|
0.0
|
1823.9
|
178.0
|
125,0
|
365,4
|
28,0
|
425,0
|
76472.4
|
|
|
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
|
|
|
|
|
|
5 800,0
|
=
|
5 800
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
425,0
|
=
|
425
|
|
3
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
3480,0
|
>=
|
2 900
|
|
4
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
3480,0
|
<=
|
3 380
|
|
5
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
1 288
|
>=
|
1 160
|
|
6
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
1 288
|
<=
|
1740
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 160
|
<=
|
1 160
|
|
8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
487.5
|
<=
|
870
|
|
9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
725
|
<=
|
725
|
|
10
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
290
|
>=
|
290
|
|
11
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
290
|
<=
|
580
|
|
12
|
-1
|
-1
|
-1
|
-1
|
-0,33
|
-0,33
|
-0,33
|
|
-1
|
|
|
|
|
|
|
|
|
0,0
|
<=
|
0
|
|
13
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44669.4
|
>=
|
23 000
|
|
14
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39720.30
|
>=
|
12 000
|
|
15
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
195000
|
>=
|
195 000
|
|
16
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
51,10
|
|
21592.5
|
>=
|
20 000
|
|
17
|
13,05
|
15,36
|
26,10
|
26,10
|
24,00
|
26,52
|
52.36
|
20.80
|
|
1,10
|
0,76
|
0,50
|
0,34
|
0,13
|
2,40
|
-56.14
|
|
12135.2
|
>=
|
0
|
|
18
|
1,94
|
1,58
|
3,48
|
3,48
|
3,94
|
3,28
|
7,38
|
2,60
|
|
11,00
|
6,00
|
5,50
|
0,05
|
0,04
|
42,60
|
-5.73
|
|
13366.9
|
>=
|
0
|
|
19
|
|
|
|
|
|
|
|
|
|
1,10
|
|
|
|
|
|
1.52
|
|
3601.4
|
>=
|
0
|
|
20
|
|
|
|
|
|
|
|
|
|
1,10
|
|
|
|
|
|
8.47
|
|
0,0
|
>=
|
0
|
|
21
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.95
|
|
0,0
|
>=
|
0
|
|
22
|
13,05
|
|
|
|
24,00
|
|
|
|
|
|
|
|
|
|
|
7.56
|
|
0.0
|
>=
|
0
|
|
23
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,10
|
|
15736.5
|
>=
|
0
|
|
24
|
|
15,36
|
|
|
|
26,86
|
|
|
|
|
|
|
|
|
|
-16.01
|
|
0,0
|
>=
|
0
|
|
25
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-12.00
|
|
0,0
|
>=
|
0
|
|
26
|
|
|
|
|
|
|
|
20.80
|
|
|
|
|
|
|
|
-0,15
|
|
0,0
|
>=
|
0
|
|
27
|
|
|
|
|
|
|
31,40
|
|
|
|
|
|
|
|
|
-0,15
|
|
0,0
|
>=
|
0
|
|
28
|
|
|
26,10
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,15
|
|
0,0
|
>=
|
0
|
|
29
|
|
|
|
26,10
|
|
|
20.90
|
|
|
|
|
|
|
|
|
-0,30
|
|
0,0
|
>=
|
0
|
|
30
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,15
|
|
0,0
|
>=
|
0
|
|
31
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,15
|
|
0,0
|
>=
|
0
|
|
32
|
|
|
|
|
|
|
|
|
|
|
0,76
|
|
|
|
|
-3,26
|
|
0,0
|
=
|
0
|
|
33
|
|
|
|
|
|
|
|
|
|
|
|
0,50
|
|
|
|
-0,21
|
|
0,0
|
=
|
0
|
|
34
|
|
|
|
|
|
|
|
|
|
|
|
|
0,34
|
|
|
-0,10
|
|
0,0
|
=
|
0
|
|
35
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,13
|
|
-0,11
|
|
0,0
|
=
|
0
|
|
36
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,40
|
-0,16
|
|
0,0
|
=
|
0
|
|
37
|
5,60
|
5,40
|
5,20
|
5,20
|
6,70
|
6,50
|
6,20
|
4,62
|
2,70
|
0,72
|
0,15
|
0,55
|
|
0,10
|
0,00
|
23,40
|
-1
|
0,0
|
=
|
0
|
|
Zmax
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
53,277
|
-1
|
38456.0
|
max
|
|
Анализ результатов решения задачи
Результаты реализации экономико-математической модели по оптимизации
отраслевой структуры производства приведены в таблице 9.
Таблица 9. Результаты решения задачи по оптимизации отраслевой структуры
производства
|
Номер переменной
|
Наименование переменной
|
Значение по решению
|
|
x1
|
Озимая пшеница товарная
|
1285.8
|
|
x2
|
Озимая пшеница фуражная
|
0,0
|
|
x3
|
Ячмень товарный
|
1323.1
|
|
x4
|
Ячмень фуражный
|
9.5
|
|
x5
|
Соя
|
858.4
|
|
x6
|
Горчица
|
301.6
|
|
x7
|
Сахарная свекла
|
487.5
|
|
x8
|
Подсолнечник
|
725.0
|
|
x9
|
Кукуруза на силос
|
114.5
|
|
x10
|
Кукуруза на зеленый корм
1-го срока сева
|
2,1
|
|
x11
|
Кукуруза на зеленый корм
2-го срока сева
|
1,1
|
|
x12
|
Однолетние травы на сено
|
0,0
|
|
x13
|
Однолетние травы на сенаж
|
0,0
|
|
x14
|
Однолетние травы на зеленый
корм 1 срока сева
|
2,5
|
|
x15
|
Однолетние травы на зеленый
корм 2 срока сева
|
3,3
|
|
x16
|
Многолетние травы на сено
|
133.9
|
|
x17
|
Многолетние травы на сенаж
|
256.6
|
|
x18
|
Многолетние травы на
зеленый корм
|
2,0
|
|
x19
|
Озимые на зеленый корм
|
3,1
|
|
x20
|
Пар
|
290.0
|
|
x21
|
Комбикорм
|
0.0
|
|
x22
|
Патока
|
1 823.9
|
|
x23
|
Премикс
|
178.0
|
|
x24
|
Молоко на корм
|
|
x25
|
Обрат
|
365,4
|
|
x26
|
ЗЦМ
|
28,0
|
|
x27
|
Поголовье крупного рогатого
скота
|
425.0
|
|
x28
|
Сумма производственных
затрат
|
76472.4
|
В результате решения задачи были определены площади посева
сельскохозяйственных культур, объемы приобретаемых кормов и кормовых добавок,
поголовье крупного рогатого скота (в структурных головах) и сумм
производственных затрат по предприятию.
Все ограничения выполнены. Анализируя результаты, представленные в
столбце «Сумма произведений» можно сделать следующие выводы.
Имеющаяся в хозяйстве пашня используется полностью.
Площадь посева зерновых и зернобобовых (ограничения 3 и 4) берется по
минимальной границе и составляет 2 500 га. Площадь озимых культур (ограничения
3 и 4) формируется на уровне 1251,4 га (при нижней и верхней границе
соответственно 1 000 и 1 500 га). Максимально возможных значений достигает
площадь подсолнечника и суммарная площадь посевов сои и гречихи (соответственно
625 и 1 000 га). Площадь свеклы составляет 649,3 га при максимально возможной -
750 га. Площадь пара берется по минимально допустимой границе в 250 га.
Все озимые культуры размещены по хорошим предшественникам. Излишки
площадей по таким культурам отсутствуют.
Таблица 10. Выполнение договорных обязательств по реализации продукции, ц
|
Продукция
|
Объемы реализации по
плану
|
Объемы реализации по
решению
|
Объемы реализации сверх
плана
|
|
Пшеница
|
23 000,0
|
43 366,0
|
20 366,0
|
|
Ячмень
|
12 000,0
|
12 000,0
|
0,0
|
|
Сахарная свекла
|
95 000,0
|
292 188,4
|
97 188,4
|
|
Молоко
|
20 000,0
|
20 314,8
|
314,8
|
Если реализация пшеницы и сахарной свеклы сверх плана объясняется
выгодностью данных видов продукции, то перевыполнение плана по молоку связано с
тем, что поголовье крупного рогатого скота было зафиксировано на фактическом
уровне.
Анализ обеспеченности отрасли животноводства кормами показывает, что по
оптимальному решению излишек кормов составит 15736.5 к.ед. Этот излишек
образуется за счет соломы, которая является побочной продукцией при
производстве зерновых и зернобобовых культур. Наблюдается избыток в рационе
переваримого протеина (около 63 т), что свидетельствует о необходимости
корректировки рационов кормления.
Сумма чистого дохода по оптимальному решению составляет 38456.0 тыс.
руб., а уровень рентабельности - 50.3%.
Литература
1.
В.А. Колемаев,
О.В. Староверов, В.Б. Турундаевский “Теория вероятностей и математическая
сатистика”/ М., 1991.
2.
“Теория
Статистики” под редакцией Р.А. Шмойловой/ “ФиС”, 1998.
3.
“Многомерный
статистический анализ на ЭBM с
использованием пакета Microsoft Excel”/ М., 1997.
4.
А.А. Френкель,
Е.В. Адамова “Корреляционно регрессионный анализ в экономических приложениях”/
М., 1987.
5.
И.Д.Одинцов
“Теория статистики”/ М., 1998.
6.
А.Н. Кленин, К.К.
Шевченко “Математическая статистика для экономистов-статистиков”/ М., 1990.