Прогноз облікової ставки на основі методу найменших квадратів
Міністерство освіти і науки
України
Чернігівський державний
технологічний університет
Кафедра ФІНАНСИ
Контрольна робота
з дисципліни: “Прогнозування
фінансової діяльності”
на тему: ПРОГНОЗ ОБЛІКОВОЇ
СТАВКИ НА ОСНОВІ МЕТОДУ НАЙМЕНШИХ КВАДРАТІВ
Чернігів 2008
ЗМІСТ
ЗАВДАННЯ 1
ЗАВДАННЯ 2
ЗАВДАННЯ 3
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
Завдання 1
Варіант
2, Б1, 138 (00010001010)
Розробити прогноз
облікової ставки на наступні два роки і вкажіть точність прогнозу, виходячи з
наступних ретроспективних даних :
Таблиця 1.1 - Дані про облікову ставку, відсоток
|
Найменування
країни
|
1970
|
1975
|
1980
|
1985
|
1990
|
1995
|
2000
|
2001
|
2002
|
2003
|
2004
|
|
США
|
4,50
|
5,50
|
6,00
|
11,00
|
7,50
|
6,20
|
5,80
|
4,15
|
3,90
|
3,70
|
2,75
|
|
ФРН
|
4,00
|
6,00
|
3,50
|
8,10
|
4,00
|
4,30
|
5,10
|
5,20
|
4,84
|
4,30
|
3,65
|
Прогноз
зробити на основі методу найменших квадратів, по США перевірити прогноз методом
змінної середньої.
Головною метою методу найменших
квадратів є виконання умови
 ,
,
де у – фактичне
значення варіації,
У – розрахункове
значення варіації ряду.
Для аналізу
використаємо лінійну функцію
У =  .
.
Дана умова
рівносильна системі нормальних рівнянь:
 (1)
(1)
Визначимо таку
систему для динамічного ряду облікової ставки США
|
роки
|
t
|

|
y
|
y*t
|
|
1970
|
1
|
1
|
4,5
|
4,5
|
|
1975
|
5
|
25
|
5,5
|
27,5
|
|
1980
|
10
|
100
|
6,0
|
60,0
|
|
1985
|
15
|
225
|
11,0
|
165,0
|
|
1990
|
20
|
400
|
7,5
|
150,0
|
|
1995
|
25
|
625
|
6,2
|
155,0
|
|
2000
|
30
|
900
|
5,8
|
174,0
|
|
2001
|
31
|
961
|
4,2
|
130,2
|
|
2002
|
32
|
1024
|
3,9
|
124,8
|
|
2003
|
33
|
1089
|
3,7
|
122,1
|
|
2004
|
34
|
1156
|
2,8
|
95,2
|
|
Всього:
|
236
|
6506
|
61,1
|
1208,3
|
Отже маємо
наступну систему рівнянь:


-15870 =1128,3
=1128,3
 = - 0,071;
= - 0,071;
11 = 77,86
= 77,86
 = 7,078
= 7,078
Таким чином
отримали рівняння лінії тренду: Y(t)=-0,071t+7,078
Прогноз облікової
ставки США (%) на наступні два роки:
На 2005р.: t =35, Y = -0,071*35+7,078=4,593%
На 2006р.: t =36, Y = -0,071*36+7,078=4,522%
Аналогічний
розрахунок зробимо для облікової ставки ФРН.
Визначимо систему
рівнянь для динамічного ряду облікової ставки ФРН
|
роки
|
t
|

|
y
|
y*t
|
|
1970
|
1
|
1
|
4,00
|
4,0
|
|
1975
|
5
|
25
|
6,00
|
30,0
|
|
1980
|
10
|
100
|
3,50
|
35,0
|
|
1985
|
15
|
225
|
8,10
|
121,5
|
|
1990
|
20
|
400
|
4,00
|
80,0
|
|
1995
|
25
|
625
|
4,30
|
107,5
|
|
2000
|
30
|
900
|
5,10
|
153,0
|
|
2001
|
31
|
961
|
5,20
|
161,2
|
|
2002
|
32
|
1024
|
4,84
|
154,9
|
|
2003
|
33
|
1089
|
4,30
|
141,9
|
|
2004
|
34
|
1156
|
3,65
|
124,1
|
|
Всього:
|
236
|
6506
|
52,99
|
1113,1
|
Маємо систему:


-15870 =261,54
=261,54  = -
0,016
= -
0,016
11 = 56,77
= 56,77  =5,161
=5,161
Таким чином
отримали рівняння лінії тренду: Y(t)=-0,016t+5,161
Прогноз облікової
ставки США (%) на наступні два роки:
На 2005р.: t =35, Y = -0,016*35+5,161=4,60%
На 2006р.: t =36, Y = -0,016*36+5,161=4,59%
Перевірку
прогнозу по США зробимо методом змінної середньої.
Метод змінної
середньої базується на методі плинної середньої, яка дозволяє прогнозувати дані
на основі вирівняного ряду, що найбільш точно характеризує тенденцію розвитку.
Виберемо за критерій згладжування три роки, матимемо такий вирівняний ряд:
|
Рік
|
Значення у
|
Згладжені значення у
|
|
1970
|
4,5
|
|
|
1975
|
5,5
|
5,3
|
|
1980
|
6,0
|
7,5
|
|
1985
|
11,0
|
8,2
|
|
1990
|
7,5
|
8,2
|
|
1995
|
6,2
|
6,5
|
|
2000
|
5,8
|
5,4
|
|
2001
|
4,2
|
4,6
|
|
2002
|
3,9
|
3,9
|
|
2003
|
3,7
|
3,5
|
|
2004
|
2,8
|
3,3
|
За допомогою
методу найменших квадратів зробимо прогноз по згладжених значеннях:
|
роки
|
t
|

|
y
|
y*t
|
|
1975
|
1
|
1
|
5,3
|
5,3
|
|
1980
|
5
|
25
|
7,5
|
187,5
|
|
1985
|
10
|
100
|
8,2
|
820,0
|
|
1990
|
15
|
225
|
8,2
|
1845,0
|
|
1995
|
20
|
400
|
6,5
|
2600,0
|
|
2000
|
25
|
625
|
5,4
|
3375,0
|
|
2001
|
30
|
900
|
4,6
|
4140,0
|
|
2002
|
31
|
961
|
3,9
|
3747,9
|
|
2003
|
32
|
1024
|
3,5
|
3584,0
|
|
2004
|
33
|
1089
|
3,3
|
3593,7
|
|
Всього:
|
202
|
5350
|
59,60
|
23898,4
|
Отже маємо
наступну систему рівнянь:
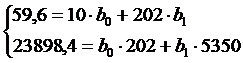

-12696 =-226944,8
=-226944,8
 = 17,86;
= 17,86;
10 = -3548,12
= -3548,12
 = -354,8
= -354,8
Таким чином
отримали рівняння лінії тренду: Y(t)=17,86t-354,8
Прогноз облікової
ставки США (%) на наступні два роки:
На 2005р.: t =34, Y = 17,86*34-354,8=252,44%
На 2006р.: t =35, Y = 17,86*35-354,8=270,3%
Завдання 2
23×7
(0000111×111).
Знайдіть лінійну
залежність рентабельності фірми від наявних сумарних активів і середньорічної
вартості нормованих обертових засобів, використовуючи методику множинної
регресії і визначити прогнозні значення рентабельності при наступних значеннях:
а) сума активів б)
вартість обертових засобів
1. 3,8 0,7
2. 9,8 1,7
3. 19,4 8,9
4. 32,2 17,1
5. 100,4 20,8
Таблиця 2.1 - Значення показників по різним підприємствам
|
№ п/п
|
Сумарні активи, млн.грн.
|
Середньорічна вартість обертових
засобів, млн. грн.
|
Рентабельність, проценти
|
|
1
|
16,2
|
4,2
|
18
|
|
2
|
30,1
|
6,1
|
27
|
|
3
|
2,7
|
10
|
|
4
|
100,1
|
36,2
|
45
|
|
5
|
30,6
|
11,1
|
25
|
|
6
|
2,8
|
1,3
|
11
|
|
7
|
3,8
|
1,5
|
19
|
Зробити висновки
по визначеній моделі:
а) оцінити вплив
незалежних змінних на залежну;
б) визначити
множинні коефіцієнти детермінації та кореляції;
в) побудувати
точковий та інтервальний пронози для знайденої моделі
Лінійна
залежність рентабельності (Y) від сумарних активів (X1) та середньорічної вартості обертових
засобів (Х2) матиме вигляд :
У=а0+а1х1+а2х2.
Для визначення
коефіцієнтів регресії складемо і розв’яжемо систему нормальних рівнянь:

Таблиця 2.2 -
Проміжні
розрахунки
|
номер
|
х1
|
х2
|
у
|
х1*х1
|
х2*х2
|
х1*х2
|
у*х1
|
у*х2
|
|
1
|
16,2
|
4,2
|
18
|
262
|
17,64
|
68,04
|
291,6
|
75,6
|
|
2
|
30,1
|
6,1
|
27
|
906
|
37,21
|
183,61
|
812,7
|
164,7
|
|
3
|
2,7
|
0,7
|
10
|
7
|
0,49
|
1,89
|
27
|
7
|
|
4
|
100,1
|
36,2
|
45
|
10020
|
1310,44
|
3623,62
|
4504,5
|
1629
|
|
5
|
30,6
|
11,1
|
25
|
1310
|
123,21
|
339,66
|
765
|
277,5
|
|
6
|
2,8
|
1,3
|
11
|
8
|
1,69
|
3,64
|
30,8
|
14,3
|
|
7
|
3,8
|
1,5
|
19
|
14
|
2,25
|
5,7
|
72,2
|
28,5
|
|
Всього
|
186,3
|
61,1
|
155
|
12527
|
1492,93
|
4226,16
|
6503,8
|
2196,6
|
Отримаємо
наступну систему лінійних рівнянь:
|
7,00а0
|
+ 186,3 а1
|
+ 61,1 а2
|
= 155
|
|
186,3 а0
|
+ 1492,93 а1
|
+4226,16 а2
|
= 6503,8
|
|
61,1 а0
|
+ 4226,16 а1
|
+1492,93 а2
|
= 2196,6
|
Запишемо матриці
А та C:
|
7,00
|
186,3
|
61,1
|
|
А =
|
186,3
|
1492,93
|
4226,16
|
|
61,1
|
4226,16
|
1492,93
|
С =  ;
;
|
7.00
|
227.2
|
51.1
|
|
|
D=detA=
|
227.2
|
1086.35
|
4520.05
|
= ‑ 70598524,46
|
|
51.1
|
4520.05
|
1086.35
|
|
|
145
|
227,2
|
51,1
|
|
|
D0=
|
7167,9
|
1086,35
|
4520,05
|
= ‑1023328516
|
|
1600
|
4520,05
|
1086,35
|
|
|
7,00
|
145
|
51,1
|
|
|
D1=
|
227,2
|
7167,9
|
4520,05
|
=622693,521
|
|
51,1
|
1600
|
1086,35
|
|
|
7,00
|
227,2
|
145
|
|
|
D2=
|
227,2
|
1086,35
|
7167,9
|
= ‑ 63755801,64
|
|
51,1
|
4520,05
|
1600
|
|
Визначимо
коефіцієнти квадратичної моделі:
а0= -1023328516
/ -70598524,46 = 14,49
а1=
622693,521 / -70598524,46 = -0,01
а2 =
-63755801,64 / -70598524,46 = 0,90
Отримали наступну
залежність рентабельності від сумарних активів та вартості обігових коштів:
у = 14,49 - 0,01x1 + 0,90x2.
При збільшенні
сумарних активів на 1 млн. грн. рентабельність знизиться на 0,01% при незмінній
вартості обігових коштів, а при збільшенні вартості обігових коштів на 1 млн.
грн. рентабельність збільшиться на 0,90%.
Підставимо в
отримане рівняння вихідні дані про сумарні активи та обігові кошти і отримаємо
прогнозне значення рентабельності (таблиця 2.3).
Таблиця 2.3 –
Прогнозне значення рентабельності по різним підприємствам
|
Номер підприємства
|
Сумарні активи млн. грн.
|
Середньорічна вартість
обертових засобів, млн. грн.
|
Прогнозована рентабельність, %
|
|
1
|
3,8
|
0,7
|
15,08
|
|
2
|
9,8
|
1,7
|
15,92
|
|
3
|
19,4
|
8,9
|
22,31
|
|
4
|
32,2
|
17,1
|
29,56
|
|
5
|
100,4
|
20,8
|
32,21
|
б) визначити
множинні коефіцієнти детермінації та кореляції:
|
номер
|
у
|
уі
|
Е
|
у-усер.
|
(у-усер.) в квадраті
|
|
1
|
18
|
18,456
|
-0,456
|
-2,714
|
7,37
|
|
2
|
27
|
17,572
|
12,428
|
9,286
|
86,22
|
|
3
|
10
|
15,762
|
-5,762
|
-10,714
|
114,80
|
|
4
|
45
|
38,242
|
-0,242
|
17,286
|
298,80
|
|
5
|
25
|
21,712
|
-0,712
|
0,286
|
0,08
|
|
6
|
11
|
16,202
|
-5,202
|
-9,714
|
94,37
|
|
7
|
19
|
15,952
|
1,048
|
-3,714
|
13,80
|
|
Сума
|
|
143,898
|
1,102
|
0,000
|
615,43
|
|
Середнє значення
|
22,14
|
|
|
|
|
R = 1- (1,102/615,43) = 0,998.
Детермінація – D = R2
D = 0,9982 = 0,996
Висновок: рівень
рентабельності повністю залежить від сумарних активів та вартості обігових
коштів, так як коефіцієнт кореляції склав 1. Таким чином, рівень
рентабельності, як результативної ознаки, залежить від факторних ознак (сумарні
активи та вартість обігових коштів) на 99,8 відсотка.
в) побудувати
точковий та інтервальний прогнози для знайденої моделі.
Вираховується
методом підстановки в криву роста величини часу t, тобто в
у = 15,22 - 0,02 x1 + 0,82 x2
Завдання 3
0 х 13 (00 х
00001101)
Визначити,
використовуючи алгоритм МГОА з послідовним виділенням трендів, часткові описи
для другого ряду селекції при наступних даних:
Таблиця 3.1 –
Дані про діяльність фірми за минулі роки
|
Показники
|
1 рік
|
2 рік
|
3 рік
|
4 рік
|
5 рік
|
6 рік
|
7 рік
|
8 рік
|
|
Попит на продукцію,
млн. грн.
|
18,2
|
17,6
|
14,2
|
13,8
|
11,5
|
10,1
|
8,1
|
7,2
|
|
Ціна, грн.
|
24
|
31
|
41
|
51
|
49
|
68
|
77
|
85
|
В якості залежної
змінної прийміть попит на продукцію, а незалежних змінних – час, ціну. В якості
апроксимуючої функції – лінійну залежність.
Розділимо усю
кількість даних (N=8) на
дві частини за часом. Перші шість будемо використовувати для розрахунків, а
двома останніми (n=2)
будемо перевіряти.
Визначимо, який
вид залежності найбільш точно описує залежність попиту на продукцію (Y) від незалежних змінних: часу (X1) та попиту (X2):
y=a0+a1x1;
y=a0+a1x2;
y=a0+a1x1+a2x2;
Визначимо лінійну
залежність попиту на продукцію від часу. Лінійна залежність має вигляд :
y=a0+a1x1.
Для визначення
коефіцієнтів рівняння складемо і розв’яжемо систему :

Таблиця 3.2 - Результати
проміжних розрахунків
|
Рік
|
х1 (час)
|
у (попит)
|
х12
|
х1у
|
|
1
|
1
|
18,2
|
1,00
|
18,20
|
|
2
|
2
|
17,6
|
4,00
|
35,20
|
|
3
|
3
|
14,2
|
9,00
|
42,60
|
|
4
|
4
|
13,8
|
16,00
|
55,20
|
|
5
|
5
|
11,5
|
25,00
|
57,50
|
|
6
|
6
|
10,1
|
36,00
|
|
Сума
|
21
|
85,4
|
91
|
269,30
|
Маємо систему:

Розв'язавши систему
методом підстановки невідомих отримали:
b1= -1,69
b0= 20,15
Залежність попиту
на продукцію від часу має вигляд:
У= 20,15 – 1,69х1,
тобто, щороку
попит знижується в середньому на 1,69 млн.грн.
Визначимо
прогнозні дані на 7 та 8 роки :
У7=20,15
– 1,69*7 = 8,32;
У8=20,15
– 1,69*8 = 6,63.
Знайдемо
середньоквадратичну похибку :
∆7=(8,1+8,32)2/8,12=
4,11,
∆28=(7,2+6,63)2/7,22=
3,69.
Аналогічно
визначимо лінійну залежність попиту на продукцію від ціни:
y=a0+a1x2;
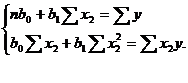
|
Рік
|
х2 (ціна)
|
у (попит)
|
х22
|
х2у
|
|
1
|
24
|
18,2
|
576
|
436,8
|
|
2
|
31
|
17,6
|
961
|
545,60
|
|
3
|
41
|
14,2
|
1681
|
582,2
|
|
4
|
51
|
13,8
|
2601
|
703,8
|
|
5
|
49
|
11,5
|
2401
|
563,50
|
|
6
|
68
|
10,1
|
4624
|
686,8
|
|
Сума
|
264
|
85,4
|
12844
|
3518,7
|
6b0+264b1=85,4 b0 =22,6
264b0+12844b1
= 3518,7, b1 =-0,19
Розв’язавши
методом зрівняння невідомих отримуємо :
y=22,6-0,19x2,
тобто при
зростанні ціни на одну гривню попит знижується в середньому на 0,19 млн. грн..
Визначимо
прогнозні дані на 7 та 8 років:
y7=23,6-0,22*77=6,66;
y8=23,6-0,22*85=4,9.
Знайдемо
середньоквадратичну похибку:
∆7=(77+6,66)2/6,662=
157,8,
∆8=(85+4,9)2/4,92=
336,6.
Визначаємо
лінійну залежність попиту від двох факторів: часу та ціни на продукцію.
Рівняння, що описує залежність матиме вигляд:
y=a0+a1x1+a2x2;
Для визначення
параметрів рівняння складемо і розв’яжемо систему нормальних лінійних рівнянь:

Таблиця 3.4 –
результати проміжних розрахунків (незалежні фактори: час, ціна)
|
Рік
|
Х1
|
Х2
|
У
|
Х12
|
Х22
|
Х1Х2
|
УХ1
|
УХ2
|
|
1
|
1
|
24
|
18,2
|
1
|
576
|
24
|
18,2
|
436,8
|
|
2
|
2
|
31
|
17,6
|
4
|
961
|
62
|
35,2
|
545,6
|
|
3
|
3
|
41
|
14,2
|
9
|
1681
|
123
|
42,6
|
582,2
|
|
4
|
4
|
51
|
13,8
|
16
|
2601
|
204
|
55,2
|
703,8
|
|
5
|
5
|
49
|
11,5
|
25
|
2401
|
245
|
57,5
|
563,5
|
|
6
|
6
|
68
|
10,1
|
36
|
4624
|
408
|
60,6
|
686,8
|
|
Сума
|
21
|
264
|
85,4
|
91
|
12844
|
1066
|
269,3
|
3518,7
|

Коефіцієнти
системи знайдемо за методом Крамера. Запишемо матриці А та С.


а0= , а1=
, а1=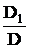 ,
а2=
,
а2=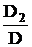 .
.
|
6
|
21
|
264
|
|
|
D=detA=
|
21
|
91
|
1066
|
= 7956
|
|
264
|
1066
|
12844
|
|
|
85,4
|
21
|
264
|
|
|
D0=
|
269,3
|
91
|
1066
|
= 158238,6
|
|
3518,7
|
1066
|
12844
|
|
|
6
|
85,4
|
|
293
|
|
|
D1=
|
21
|
269,3
|
|
1144
|
= ‑ 224946,9
|
|
264
|
3518,7
|
|
15115
|
|
|
6
|
21
|
85,4
|
|
|
D2=
|
21
|
91
|
269,3
|
=134,7
|
|
264
|
1066
|
3518,7
|
|
Визначимо
коефіцієнти квадратичної моделі:
а0 = 19,89
а1= -
28,27
а2= 0,02
Лінійна
залежність попиту на продукцію від часу та ціни має вигляд: y=19,89 - 28,27x1 + 0,02x2.
Коефіцієнти
лінійної багатофакторної моделі показують, що при незмінних цінах щороку попит
на продукцію збільшується в середньому на 28,27 млн. грн.. В середині року при
зростанні цін на одну гривню, попит на продукцію скорочується в середньому на 0,02
млн. грн..
Визначаємо
прогнозні значення та середньоквадратичну похибку:
y7=19,89-28,27*7+0,02*77= - 176,46;
y8=19,89-28,27*8+0,02*85= - 204,57;
∆7=(8,1+176,46)2/8,12=
519,2
∆8=(7,2+204,57)2/7,22=
865,1
Висновок:
залежність попиту на продукцію від часу має найменшу середньоквадратичну
похибку, тому слід віддати їй перевагу над іншими. Тому для прогнозування
приймаємо наступну модель: y=22,6-0,19x2.
СПИСОК
ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Горлова В.Л., Мельникова Е.Н.
Основы прогнозирования
систем - М.: Высш. Шк., 1986.- 287 с.
2. Индуктивный метод самоорганизации
моделей сложных систем/ Ивахненко А.Г. – Киев: Наук. Думка, 1981 – 296 с.
3. Лугінін О.Є., Білоусова С.В., Білоусов
О.М. Економетрія: Навч. посіб. – К. : Центр навчальної літератури, 2005. – 252
с.
4. Прогнозування фінансової
діяльності. Методичні вказівки до самостійної роботи студентів економічних
спеціальностей всіх форм навчання / Укл.: Коробко В.І. - Чернігів: ЧДТУ, 2007.-
9 с.