Анализ режимов работы электрических сетей ОАО "ММК им. Ильича" и разработка адаптивной системы управления режимами электропотребления
Министерство
образования и науки Украины
Приазовский
государственный технический университет
Факультет
информационных технологий
Кафедра
автоматизации энергетических систем и электропривода
Специальность
“Системы управления производством и распределением электроэнергии”
МАГИСТЕРСКАЯ
РАБОТА
по
специальности 8.090615 “Системы управления производством и распределением
электроэнергии”
на
тему: Анализ режимов работы электрических сетей ОАО "ММК им. Ильича"
и разработка адаптивной системы управления режимами электропотребления
Студент Трубчанинова Анна Васильевна
Руководитель
Нормоконтроль
Рецензент
Проект рассмотрен на заседании кафедры
и допущен к защите в ГЭК
Зав. кафедрой АЭС и ЭП
В.Н. Кравченко
Мариуполь
2006 г
"УТВЕРЖДАЮ"
Зав.
кафедрой АЭС и ЭП
_____________
В.Н. Кравченко
ЗАДАНИЕ
на
аттестационную работу магистра Трубчанинова Анна Васильевна
1. Тема работы Исследование режимов работы
электрических сетей ОАО "ММК им. Ильича" и разработка адаптивной
системы управления режимами электропотребления
Тема утверждена приказом по ПГТУ №12-05 от 1
февраля 2006 г.
2. Цель исследования Определение оптимальных
режимов работы электрических сетей. Разработка программного обеспечения для
расчета оптимальных режимов работы электрических сетей.
3. Исходные данные (характеристика объекта,
условий исследования и др.)
Однолинейные схемы замещения электрических
сетей. Графики нагрузок подстанций.
4. Основные задачи исследования:
Определить диапазон изменения параметров
электрических сетей и нагрузок в рабочих и типовых аварийных режимах.
Исследовать и выбрать наиболее эффективные
методы оптимизации режимов сетей.
5. Срок представления работы к защите - 1 июня
2006 г.
6. Дата выдачи задания - 1 сентября 2005 г.
Научный руководитель
_______________________
Задание принял к выполнению _________________
Календарный план
|
№
п/п
|
Название
этапа работы
|
Срок
выполнения этапа
|
Примечание
|
|
1.
|
Получение
задания на дипломную работу.
|
02.10.2005
|
|
|
2.
|
Обзор
технической литературы по теме работы.
|
30.10.2005
|
|
|
3.
|
Изучение
и описание системы электроснабжения ММК им. Ильича
|
30.11.2005
|
|
|
4.
|
Исследование
режимов работы системы электроснабжения ММК им. Ильича
|
15.01.2006
|
|
|
5.
|
Разработка
программного обеспечения для решения задачи оптимизации режимов
электроснабжения
|
15.02.2006
|
|
|
6.
|
Составление
полной схемы замещения системы электроснабжения ММК им. Ильича
|
10.03.2006
|
|
|
7.
|
Расчет
и оптимизация режимов электроснабжения ММК им. Ильича
|
20.03.2006
|
|
|
8.
|
Разработка
структурной схемы автоматизированной системы оптимального управления режимами
электроснабжения ММК им. Ильича
|
1.04.2003
|
|
|
9.
|
Выбор
элементной базы для реализации автоматизированной системы оптимального
управления
|
15.04.2006
|
|
|
10.
|
Написание
пояснительной записки. Создание слайдов для доклада
|
25.04.2006
|
|
|
11.
|
Предварительная
защита
|
28.05.2006
|
|
|
12.
|
Коррекция
работы по результатам предзащиты
|
01.06.2006
|
|
|
13.
|
Окончательное
оформление пояснительной записки и слайдов.
|
12.06.2006
|
|
|
14.
|
Защита
дипломной работы
|
19.06.2006
|
|
Студент _____________________________
Руководитель проекта _________________
Реферат
Пояснительная записка: 96 страниц, 25 рисунков,
21 таблица, 3 приложения, 14 источников.
Объект исследования: электрическая сеть ОАО ММК
им. Ильича
Рассмотрены вопросы оптимизации текущего режима
электропотребления по реактивной мощности и разработки адаптивной системы
управления режимами электропотребления.
Разработано программное обеспечение по
определению оптимальных режимов работы электрических сетей.
Предложена система автоматизации процесса
распределения реактивной мощности, реализованная на оборудовании фирмы
Allen-Bradley.
Разработанная система автоматизации производит
сбор необходимых параметров, рассчитывает текущий режим, определяет оптимальные
мощности компенсирующих устройств и передает управляющие воздействия на устройства,
регулирующие мощности компенсирующих устройств.
ОПТИМИЗАЦИЯ, ЭЛЕКТРОПОТРЕБЛЕНИЕ, РЕАКТИВНАЯ
МОЩНОСТЬ, АКТИВНАЯ МОЩНОСТЬ, ПОТЕРИ МОЩНОСТИ, АВТОМАТИЗАЦИЯ
Abstract
Explanatory note: 96 page, 25
drawings, 21 tables, 3 exhibits, 14 sources.
Object of research: electric network
OAO MMK im. Iliicha
Considereded questions of
optimization current mode electroconsumptions on reactive power and development
adaptive managerial system by modes of electroconsumption.
Designeded software on determination
of optimum states of working electric networks.
Offereded system to automation of
process of distribution reactive power marketed on equipping the company
Allen-Bradley.
Designeded system to automations
produces the collection of necessary parameters, calculates the current mode,
defines the optimum power compensating device and will send (pass) controlling
influences on device, regulative power compensating device.
OPTIMIZATION, ELECTROCONSUMPTION,
REACTIVE POWER, ACTIVE POWER, LOSS a POWER, AUTOMATION
Содержание
Введение........................................................................................................... 9
1
Исследование методов оптимизации 17
1.1
Основные понятия и определения оптимизации 17
1.2
Математическая модель 17
1.3
Методы решения оптимизационных задач 19
1.3.1
Общая характеристика методов решения задач нелинейного программирования 19
1.4
Методы прямого поиска 21
1.4.1
Метод Хука-Дживса 22
1.4.1.1
Исследующий поиск. 23
1.4.1.2
Поиск по образцу. 23
1.4.1.3
Описание алгоритма метода 24
1.4.2
Метод комплексов 25
1.4.3
Методы случайного поиска 27
1.4.4
Метод покоординатного спуска 29
1.5
Градиентные методы 30
1.5.1
Градиентный метод с постоянным шагом 31
1.5.2
Метод скорейшего спуска 32
1.5.3
Метод проектирования градиента 35
1.6
Метод штрафных функций 38
1.7
Методы полиномиальной аппроксимации 39
1.7.1
Квадратичная аппроксимация 40
1.7.1.1
Метод Пауэлла 41
1.7.2
Кубическая интерполяция 43
1.7.3
Квадратичные функции 46
1.8
Метод Нелдера-Мида 48
1.9
Метод неопределенных множителей Лагранжа 54
1.10
Выбор метода оптимизации 56
2
Разработка метода оптимизации по реактивной мощности 58
3
Разработка программного обеспечения метода оптимизации 66
4.
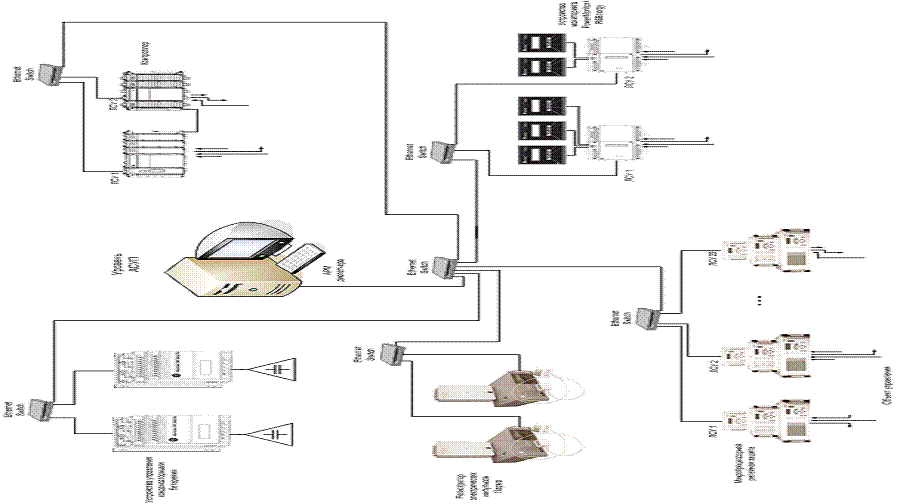
Разработка адаптивной системы управления режимами электропотребления 73
4.1
Функции автоматизированной системы 73
4.2
Описание работы системы 73
4.2.1
Ввод системы в работу 73
4.2.2
Работа системы в нормальном режиме 74
4.2.3
Работа системы в случае изменения конфигурации сети 75
4.3
Требования к оборудованию и программному обеспечению 77
4.4
Выбор оборудование для адаптивной системы 78
4.4.1
Учет электроэнергии 78
4.4.1.1
Устройства мониторинга PowerMonitor 79
4.4.1.2
Программное обеспечение RSEnergy для контроля электропотребления 80
4.4.2
Процессор для диспетчерского пункта 80
4.4.3
Сервер связи 81
4.4.3.1
Основные преимущества 83
4.4.3.2
Минимальные требования RSLinx: 84
4.4.3.3
Различия между разными версиями программного обеспечения RSLinx 84
4.4.3.4
Версия программного обеспечения RSLinx Lite 84
4.4.3.5
Версия программного обеспечения RSLinx OEM 85
4.4.3.6
Версия программного обеспечения RSLinx Professional 86
4.4.3.7
Версия программного обеспечения RSLinx Gateway 87
4.4.3.8
Версия программного обеспечения RSLinx SDK 88
4.4.3.9
Графические функции SuperWho и RSWho 89
5
Исследование и получение оптимальных режимов для ОАО "ММК им. Ильича" 90
5.1
Расчет параметров схемы замещения 90
5.1.1
Теоретические положения 90
5.1.2
Расчет параметров схем замещения линий 93
5.1.3
Расчет параметров схем замещения трансформаторов 93
5.2
Расчет сети при различных нагрузках 100
Выводы 103
Перечень
ссылок 104
Приложение
А 106
Приложение
Б 118
Введение
При исследовании режимов электрических сетей
необходимо обратить особое внимание на явления, связанные с передачей
реактивной мощности по сети, а также на способы ее компенсации.
В отличие от активной мощности реактивная
мощность, потребляется элементами сети и электроприемниками в соизмеримых
количествах. При этом она может генерироваться не только на электрических
станциях, но и в сети. В частности, генерация реактивной мощности емкостью
линий является вынужденной.
Реактивная мощность является практически удачной
формой учета условий протекания периодических процессов в цепи переменного
тока. Поскольку для обеспечения условий их протекания при допустимых параметра
режима приходится применять специальные компенсирующие устройства, то возникает
задача их наивыгоднейшего использования в условиях эксплуатации сети.
При решении этой задачи целесообразно прежде
всего выяснить, с какими дополнительными явлениями связана передача реактивной
мощности по элементам сети и какое влияние эти явления оказывают на
технико-экономические показатели работы систем электроснабжения.
Как известно, передача реактивной мощности
приводит к увеличению потерь напряжения в сети. С передачей реактивной мощности
непосредственно связано увеличение нагрузки в соответствующих элементах сети.
Отсюда следует также и увеличение потерь
активной мощности в элементах системы электроснабжения, которое должно
учитываться в балансе по системе, т. е. компенсироваться соответствующей
дополнительной установленной мощностью оборудования электрических станций.
Одновременно увеличиваются потери энергии за
любой промежуток времени. Дополнительный расход электроэнергии означает
дополнительный расход энергоносителей, практически - топлива, что связано с
дополнительными денежными и материальными расходами.
Это означает, что для выполнения поставленной
вначале задачи в действительности требуется генерация соответственно большей
реактивной мощности, т. е. практически установка дополнительных компенсирующих
устройств.
Следует обратить внимание и на вторичное
явление. Указанное выше увеличение потерь напряжения при неограниченной
величине высшего допустимого напряжения приводит к снижению его низшего
значения у приемного конца сети. А это приводит к увеличению значений токов при
тех же значениях передаваемой мощности и к дополнительной потере активной и
реактивной мощности, а также к дополнительной потере энергии.
При наличии соответствующих компенсирующих
устройств целесообразно компенсировать реактивную мощность на месте, по
возможности устраняя передачу ее по элементам сети на большие расстояния.
Однако надо иметь в виду, что включение в работу новых устройств или увеличение
нагрузки уже работающих иногда приводит к увеличению потерь активной мощности в
них. Наивыгоднейшее решение заранее может быть неизвестно и получается путем
расчета.
В распределительных сетях, особенно в
промышленности, обычно имеет место потребление реактивной мощности в больших
количествах. Основными потребителями реактивной мощности являются асинхронные
двигатели, только намагничивающий ток которых составляет от 40 до 60%
номинального.
Компенсирующие устройства (батареи
конденсаторов), устанавливаемые в распределительных сетях, могут быть
использованы для регулирования напряжения. Это сокращает потребность в местных
регулирующих устройствах. Поэтому экономичность работы компенсирующих устройств
в распределительных сетях следует рассматривать с учетом воздействия на режим
напряжений.
При этом потери энергии в сети не обязательно
получаются наименьшими, так же как и в случае распределения активной мощности
между электрическими станциями в энергетической системе. Наибольшим должен быть
результирующий экономический эффект.
Другое положение получается при использовании
реактивной мощности, генерируемой синхронными двигателями, которые могут быть
установлены в промышленной распределительной сети. Генерация реактивной
мощности синхронными двигателями приводит к аналогичном эффекту регулирования
напряжения, но связана со значительными потерями активной мощности, а
следовательно, и энергии в самих двигателях. Поэтому регулирование напряжения
автоматическим изменением тока возбуждения синхронных двигателей не всегда
экономически обосновано. Обычно использование для этого синхронных двигателей
малой мощности экономически не оправдывается.
В питающей сети, на всех приемных подстанциях
которой имеются регулирующие устройства с достаточным регулировочным
диапазоном, распределение реактивной мощности можно осуществлять по условиям
экономичности работы самой питающей сети. Определяющими здесь являются условия
минимума потерь активной мощности в сети при заданных ограничениях по
наибольшему допустимому напряжению и рабочей реактивной мощности источников
питания.
В послеаварийных режимах перераспределением
реактивной мощности в сети часто удается улучшить параметры режима. При этом
экономичность режима приходится рассматривать как факт второстепенный.
Комплексная проблема определения оптимальных
условий эксплуатации энергосистем или энергообъединений должна решаться на
основе использования экономического критерия минимизации приведенных
народнохозяйственных затрат на производство и распределение электрической и
тепловой энергии. Решение этой проблемы в настоящее время осуществляется на
основе рассмотрения ряда взаимосвязанных задач, условно представленных на
рисунке ниже.
Каждая из перечисленных задач характеризуется
своими частичным экономическим критерием и математической моделью поведения
энергосистемы, которым отвечают определенные алгоритмы, наиболее полно
учитывающие специфику задачи. В процессе решения используются различные
исходные данные, в значительной мере вероятностные и неравноточные.
Под задачей оптимизации текущего режима
энергосистемы или энергообъединения понимают наивыгоднейшее распределение
генерируемых активных и реактивных мощностей между электростанциями, а также
другими регулируемыми источниками реактивной мощности - синхронными
компенсаторами, управляемыми реакторами и батареями статических конденсаторов,
которому отвечает минимум эксплуатационных издержек И на производство и
распределение электрической и тепловой энергии в топливном или стоимостном
выражениях: И(Z)=min. Целевая функция И зависит от вектора переменных Z,
включающего в себя всю совокупность параметров режима.
В зависимости от принятой математической модели
оптимизации, определяемой частичной задачей оптимизации и допущениями при
составлении модели, в состав Z могут входить активные и реактивные мощности
электростанций 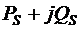 , коэффициенты
трансформации (в общем случае комплексные)
, коэффициенты
трансформации (в общем случае комплексные) 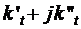 ,
модули напряжений
,
модули напряжений  в некоторых или во
всех узлах расчетной схемы, а при необходимости и другие параметры режима и
оборудования.
в некоторых или во
всех узлах расчетной схемы, а при необходимости и другие параметры режима и
оборудования.

Рис. Взаимосвязь различных задач оптимизации режимов
Составляющие вектора Z связаны между собой рядом
конкретных условий, накладываемых свойствами электрической сети, техническими
характеристиками и условиями надежной работы оборудования. Сюда относятся
обеспечение баланса мощностей, ограничение напряжений в узлах, ограничение тока
и передаваемой мощности по линиям электропередачи, допустимость режимов по
устойчивости параллельной работы электростанций, ограничение мощности
электростанций по характеристикам оборудования и т. п.
В такой общей постановке задача оптимизации
текущего режима является многоэкстремальной задачей нелинейного математического
программирования и для произвольного вида функции И(Z) строгие методы ее
решения не разработаны.
Из изложенного следует, что определения
оптимального рабочего режима электрической сети в процессе ее текущей
эксплуатации нужно значительное количество информации о параметрах режима и
требуется выполнение достаточно сложных расчетов по ее обработке и получению
ответа. В некоторых случаях задача должна решаться одновременно для всей
энергетической системы. Для этого требуется достаточно сложное программное и
аппаратное обеспечение, осуществляющее получение и обработку информации, а
также управление всеми автоматизированными устройствами, имеющимися в системе.
В своем дипломном проекте я оптимизирую текущий
режим энергосистемы, а именно, минимизирую целевую функцию путем решения задачи
нелинейного программирования на языке программирования С++.
Задача безусловной минимизации (минимизации без
ограничений) состоит в поиске минимума min f(х) , где функция f: R"®R
- является по крайней мере непрерывной. Процедуры безусловной минимизации
подразделяются на 3 категории:
оперирующие функцией одной переменной;
работающие с функцией нескольких переменных;
использующие нелинейный метод наименьших
квадратов.
В случае функции одной переменной
предполагается, что на исследуемом отрезке она имеет один экстремум. В
противном случае осуществляется поиск локального минимума.
Поиск минимума функции нескольких переменных
можно выполнить квазиньютоновским методом, модифицированным алгоритмом Ньютона,
методом сопряженных градиентов и методом деформируемого многогранника.
Перечисленные процедуры обеспечивают поиск
локального минимума. Если же функция имеет несколько локальных минимумов и необходимо
найти наилучший, то следует испытать разные начальные точки и интервалы поиска.
С процедурами, использующими только значения функции, следует употреблять
двойную точность. Также полезно использовать процедуры контроля производной,
обеспечивающие проверку работы пользовательских процедур, оценивающих
производные. Как уже указывалось, в настоящее время не существует
единообразного подхода к задаче оптимизации мгновенного режима энергосистемы.
Все многообразие практических методов использования ЦВМ можно классифицировать
по некоторым главным направлениям. Основными задачами расчетов могут являться:
а) комплексная оптимизация распределения
активных и реактивных генерируемых мощностей и коэффициентов трансформации по
условию минимума суммарного расхода или стоимости топлива в системе;
б) оптимальное распределение активных мощностей
между электростанциями с приближенным учетом потерь в сети по условию минимума
суммарного расхода или стоимости топлива;
в) оптимальное распределение реактивных
мощностей между электростанциями и синхронными компенсаторами и выбор
оптимальных коэффициентов трансформации регулируемых трансформаторов по
минимуму потерь в сети.
В расчетах в качестве математической модели
установившегося режима используются либо полные уравнения установившегося
режима, обычно уравнения узловых напряжений в форме баланса мощностей в узлах,
либо упрощенные уравнения баланса активной мощности в целом по системе

1. Исследование методов оптимизации
1.1 Основные понятия и определения оптимизации
Показатель, по величине которого оценивают,
является ли решение оптимальным, называется критерием оптимальности.[1] В
качестве критерия оптимальности наиболее часто принимается экономический
критерий, представляющий собой минимум затрат (финансовых, сырьевых,
энергетических, трудовых) на реализацию поставленной задачи. При заданной или
ограниченной величине указанных затрат экономический критерий выражается в
получении максимальной прибыли.
В электроэнергетике в зависимости от требований
поставленной задачи могут применяться и другие критерии оптимальности, в
частности:
критерий надежности электроснабжения;
критерий качества электроэнергии;
критерий наименьшего отрицательного воздействия
на окружающую среду (экологический критерий).
Решение оптимизационной задачи включает в себя
следующие этапы:
сбор исходной информации (исходных данных);
составление математической модели, под которой
понимается формализованное математическое описание решаемой задачи;
выбор метода решения, определяемого видом
математической модели;
выполнение математических вычислений,
поручаемое, как правило, компьютеру;
анализ решения задачи.
Математическая модель
Математическая модель - формализованное
математическое описание оптимизационной задачи.[1,2] Математическая модель
включает в себя:
целевую функцию;
ограничения;
граничные условия.
Целевая функция представляет собой
математическую запись критерия оптимальности. При решении оптимизационной
задачи ищется экстремум целевой функции, например минимальные затраты или
максимальная прибыль. Обобщенная запись целевой функции имеет следующий вид:
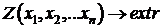 (1.1)
(1.1)
где 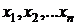 -
искомые переменные, значения которых вычисляются в процессе решения задачи;
-
искомые переменные, значения которых вычисляются в процессе решения задачи;
n - общее количество переменных.
Зависимость между переменными в целевой функции
(1.1) может быть линейной или нелинейной.
Ограничения представляют собой различные
технические, экономические, экологические условия, учитываемые при решении
задачи[1,2]. Ограничения представляют собой зависимости между переменными 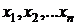 ,
задаваемые в форме неравенств или равенств
,
задаваемые в форме неравенств или равенств
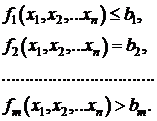 (1.2)
(1.2)
Общее
количество ограничений равно m.
Граничные
условия устанавливают диапазон изменения искомых переменных

 (1.3)
(1.3)
где
di и Di - соответственно нижняя и верхняя границы диапазона изменения
переменной хi.
Методы
решения оптимизационных задач
Для
решения подавляющего большинства оптимизационных задач используются методы
математического программирования, позволяющие найти экстремальное значение
целевой функции (1.1) при соотношениях между переменными, устанавливаемых
ограничениями (1.2), в диапазоне изменения переменных, определяемом граничными
условиями (1.3).
Математическое
программирование представляет собой, как правило, многократно повторяющуюся
вычислительную процедуру, приводящую к искомому оптимальному решению.[2,3]
Выбор
метода математического программирования для решения оптимизационной задачи
определяется видом зависимостей в математической модели, характером искомых
переменных, категорией исходных данных и количеством критериев оптимальности.
Общая
характеристика методов решения задач нелинейного программирования
Когда
целевая функция (1.1) и ограничения (1.2) нелинейны и для поиска точки
экстремума нельзя или очень сложно использовать аналитические методы решения,
тогда для решения задач оптимизации применяются методы нелинейного
программирования. Как правило, при решении задач методами нелинейного
программирования используются численные методы с применением ЭВМ[3,4,5,6].
В
основном методы нелинейного программирования могут быть охарактеризованы как
многошаговые методы или методы последующего улучшения исходного решения. В этих
задачах обычно заранее нельзя сказать, какое число шагов гарантирует нахождение
оптимального значения с заданной степенью точности. Кроме того, в задачах
нелинейного программирования выбор величины шага представляет серьезную
проблему, от успешного решения которой во многом зависит эффективность
применения того или иного метода. Разнообразие методов решения задач
нелинейного программирования как раз и объясняется стремлением найти
оптимальное решение за наименьшее число шагов.
Большинство
методов нелинейного программирования используют идею движения в n-мерном
пространстве в направлении оптимума. При этом из некоторого исходного или
промежуточного состояния Uk осуществляется переход в следующее состояние Uk+1
изменением вектора Uk на величину DUk, называемую шагом , т.е.
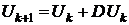 (1.4)
(1.4)
В
ряде методов шаг ,т.е. его величина и направление определяется как некоторая
функция состояния Uk
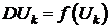 (1.5)
(1.5)
Следовательно,
согласно (1.4) новое состояние Uk, получаемое в результате выполнения шага
(1.5) может рассматриваться как функция исходного состояния Uk
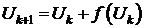 (1.6)
(1.6)
В
некоторых методах DUk обусловлен не только состоянием Uk, но и рядом
предшествующих состояний
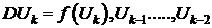 (1.7)
(1.7)
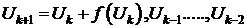 (1.8)
(1.8)
Естественно,
что алгоритмы поиска типа (1.8) являются более общими и принципиально могут
обеспечить более высокую сходимость к оптимуму, т.к. используют больший объем
информации о характере поведения оптимальной функции.
В
настоящее время для решения подобных задач разработано значительное число
методов, однако нельзя отдать предпочтение какому- либо одному. Выбор метода
определяется сложностью объекта и решаемой задачей оптимизации.
Методы
решения задач нелинейного программирования (условной многопараметрической
оптимизации) подразделяют следующим образом:
методы
прямого поиска;
градиентные
методы;
методы
штрафных функций;
методы
полиномиальной аппроксимации.
Методы
прямого поиска
Одними
из методов нахождения минимума функции n-переменных являются методы прямого
поиска. Методы прямого поиска являются методами, в которых используются только
значения функции[1,7].
В
методах прямого поиска ограничения учитываются в явном виде. Необходимость
разработки этих методов связана с тем, что в инженерных приложениях часто
приходится сталкиваться с случаями, когда целевые функции не заданы в явном
виде. Эти методы строятся на интуитивных соображениях, не подкреплены строгой
теорией и, следовательно, не гарантируется их сходимость. Несмотря на это, в
силу своей логической простоты эти методы легко реализуются.
Перед
непосредственным применением методов прямого поиска необходимо провести ряд
мероприятий по подготовке задачи к решению, а именно
исключить
ограничения в виде равенств;
определить
начальную допустимую точку.
Простейший
способ исключения ограничений в виде равенств заключается в решении его
относительно одной из переменных с последующим исключением этой переменной
путем подстановки полученного выражения в соотношения, описывающие задачу. При
этом следует учитывать, что границы значений исключаемых переменных сохраняются
в задаче в виде ограничений - неравенств.
Несмотря
на то, что подстановка является самым простым способом исключения ограничений -
равенств, не всегда оказывается возможным ее осуществить. В этом случае
проблема решается путем численного решения уравнения относительно зависимых
переменных при заданных значениях независимых оптимизирующих переменных.
Для
определения начальной допустимой точки целесообразно использовать процедуру
случайного поиска, основная идея которого будет рассмотрена ниже.
После
проведения процедуры подготовки задачи к решению следует приметить один из
методов условной оптимизации[5,6]. Рассмотрим методы прямого поиска:
модифицированный
метод Хука-Дживса; <#"478342.files/image016.gif"> b1, то
производится поиск по образцу.
Шаг
3. При поиске по образцу используется информация, полученная в процессе
исследования, и минимизация функции завершается поиском в направлении, заданном
образцом. Эта процедура производится следующим образом:
Разумно
двигаться из базисной точки b2 в направлении b2-b1, поскольку поиск в этом
направлении уже привел к уменьшению значения функции. Поэтому вычислим функцию
в точке образца
P1=b1+2*(b2-b1).
(1.10)
В
общем случае
Pi=bi+2*(b(i+1)-bi).
(1.11)
Затем
исследование следует продолжать вокруг точки P1(Pi).
Если
наименьшее значение на шаге B,2 меньше значения в базисной точке b2(в общем
случае b(i+1)), то получают новую базисную точку b3 (b(i+2)), после чего
следует повторить шаг B,1 . В противном случае не производить поиск по образцу
из точки b2(b(i+1)), а продолжить исследования в точке b2(b(i+1)).
Шаг
4. Завершить этот процесс, когда длина шага (длины шагов) будет уменьшена до
заданного малого значения.
1.4.2
Метод комплексов
Алгоритм
[7]:
Заданы
границы значений всех переменных xiL, xiU, i=1,2,..., N (размерность задачи),
допустимая точка xo, параметр отображения a (рекомендуется a =1,3) и параметры
окончания вычислений и d .
Шаг
1. Построение начального комплекса, состоящего из P допустимых точек
(рекомендуется P=2N). Для каждой точки p = 1, 2,...,P-1
случайным
образом определить координаты xp;
если
xp - недопустимая точка, то найти центр тяжести xцт уже найденных точек и
положить xp = xp + (xцт - xp); повторять процедуру до тех пор, пока xp не
станет допустимой;
если
xp - допустимая точка, повторять до тех пор, пока p=P;
вычислить
W(xp) для p=0,1,...,P-1.
Шаг
2. Отражение комплекса:
выбрать
точку xR, для которой W(xR) = max W(xp) = Wmax (решается задача минимизации);
найти
центр тяжести xцт и новую точку xm = xцт + a (xцт - xR);
если
xm - допустимая точка и W(xm)< Wmax, уменьшить в два раза расстояние между
xm и центром тяжести xцт, продолжать поиск, пока W(xm)<Wmax;
если
xm - допустимая точка и W(xm)<Wmax, то перейти к шагу 4;
если
xm - недопустимая точка, то перейти к шагу 3.
Шаг
3. Корректировка для обеспечения допустимости:
если
xim<xiL(нижняя граница допускаемой области), то положить xim = xiL;
если
xim>xiU(верхняя граница допускаемой области), то положить xim = xiU;
если
xm - недопустимая точка, то уменьшить в два раза расстояние до центра тяжести;
продолжать до тех пор, пока xm не станет допустимой точкой.
Шаг
4. Проверка условий окончания вычислений:
положить
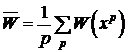
и
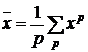 ;
;
если

и
 ,
,
то
вычисления прекратить; в противном случае перейти к шагу 2a.
1.4.3
Методы случайного поиска
Наиболее
простой процедурой случайного поиска [3,5] является прямая выборочная процедура,
заключающаяся в разыгрывании на ЭВМ последовательности точек с координатами
xi
= xiL +ri (xiU - xiL), i=1,2,...,N, (1.12)
где ri - случайная величина, равномерно
распределенная на интервале [0,1].
После проверки каждой точки на допустимость
вычисляются значения целевой функции, которые сравниваются с наилучшим
значением, полученным к данному моменту. Если текущая точка дает лучшее
значение, то она запоминается, в противном - отбрасывается. Процесс
прекращается после заданного числа итераций N или по исчерпанию заданного
машинного времени. Для получения 90% доверительного интервала величиной
i (xiU - xiL), где 0< <1, для переменной xi совместный случайный
поиск требует 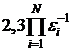 испытаний. При
N=5, i=0,01 число испытаний оценивается в 2,3 1010, что исключает
возможность непосредственного использования метода.
испытаний. При
N=5, i=0,01 число испытаний оценивается в 2,3 1010, что исключает
возможность непосредственного использования метода.
Значительного увеличения эффективности процедуры
случайного поиска можно достигнуть путем группировки выборок в серии. При этом
наилучшая точка в каждой серии используется как начальная точка следующей
серии, точки которой уже выбираются из интервала меньшей величины. Данная
процедура получила название выборки со сжатием пространства поиска. Рассмотрим
более подробно ее алгоритм.
Заданы границы значений всех переменных xiL,
xiU, i=1,2,..., N (размерность задачи), начальные допустимая точка xo и
интервал поиска D xo = xiU - xiL, количество серий Q, количество точек в серии
P и параметр окончания вычислений . Для каждой из серий, начиная с q =
1, необходимо выполнить следующие действия.
Шаг 1. Для i = 1,2,...,N вычислить
xip = xiq-1 +ri D
xq-1, (1.13)
где ri - случайная величина, равномерно
распределенная на интервале [-0,5;0,5].
Шаг 2.
если xp - недопустимая точка и p < P, то
повторить шаг 1;
если xp - допустимая точка, то запомнить xp и
W(xp) и
если p < P, то повторить шаг 1;
если p = P, то найти среди всех допустимых точек
xp точку с наименьшим значением W(xp) и положить ее равной xq.
Шаг 3. Уменьшить интервал поиска, полагая D∙xiq
= i∙D∙xiq-1.
Шаг 4.
Если q > Q, то закончить вычисления.
В противном случае увеличить q=q+1 и продолжить
вычисления, начиная с шага 1.
1.4.4 Метод покоординатного спуска
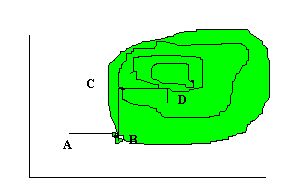
Рисунок
1.1 - Метод покоординатного спуска
Рассмотрим
функцию двух переменных. Ее линии уровня представлены на рис. 1.1, а минимум
лежит в точке (x1*,x2*). Простейшим методом поиска является метод
покоординатного спуска[3,4]. Из точки А произведем поиск минимума вдоль
направления оси х1 и, таким образом, находим точку В, в которой касательная к
линии постоянного уровня параллельна оси х1. Затем, производя поиск из точки В
в направлении оси х2, получаем точку С, производя поиск параллельно оси х2,
получаем точку D, и т.д. Таким образом, мы приходим к оптимальной точке.
Очевидным образом эту идею можно применить для функции n переменных.
Теоретически
данный метод эффективен в случае единственного минимума функции. Но на практике
он оказывается слишком медленным. Поэтому были разработаны более сложные
методы, использующие больше информации на основании уже полученных значений
функции.
1.5
Градиентные методы
Как
следует из названия, эти методы решения нелинейных оптимизационных задач
используют понятие градиента функции[3,5,7]. Градиентом функции  называется
вектор
называется
вектор
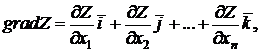 (1.14)
(1.14)
где  -
единичные вектора (орты).
-
единичные вектора (орты).
Величина этого вектора определяется по выражению
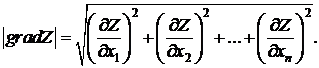 (1.15)
(1.15)
Из (1.14) и (1.15) видно, что функция, градиент
которой определяется, должна быть дифференцируемой по всем n переменным.
Физический смысл градиента функции в том, что он
показывает направление (1.14) и скорость (1.15) наибольшего изменения функции в
рассматриваемой точке. Если в некоторой точке  ,
функция в этой очке не изменяется (не возрастает и не убывает). Эта точка
соответствует экстремуму функции.
,
функция в этой очке не изменяется (не возрастает и не убывает). Эта точка
соответствует экстремуму функции.
1.5.1 Градиентный метод с постоянным шагом
Сущность градиентных методов решения нелинейных
оптимизационных задач [1,5,7] поясним для случая отыскания абсолютного минимума
функции двух переменных 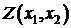 , иллюстрируемого
рис. 1.2. этот минимум находится в точке с координатами х10 и х20.
, иллюстрируемого
рис. 1.2. этот минимум находится в точке с координатами х10 и х20.

Рисунок 1.2 - Иллюстрация градиентного метода с
постоянным шагом 
В соответствии с граничными условиями (1.3), в
большинстве практических оптимизационных задач они принимают только
положительные или нулевые значения, областью 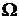 допустимых
значений переменных будет первый квадрант системы координат х1 и х2. в этой
области произвольно выберем исходное (нулевое) приближение - точку с
координатами х10, х20. значение целевой функции в этой точке составляет Z0. В
соответствии с выражением (1.15) вычислим в этой точке величину градиента
функции Z.
допустимых
значений переменных будет первый квадрант системы координат х1 и х2. в этой
области произвольно выберем исходное (нулевое) приближение - точку с
координатами х10, х20. значение целевой функции в этой точке составляет Z0. В
соответствии с выражением (1.15) вычислим в этой точке величину градиента
функции Z.
Выполним шаг единичной длины (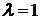 )
в направлении убывание функции Z. В результате выполненного шага получим первое
приближение - точки с координатами х11, х21. Значение целевой функции в этой
точке составляет Z1.
)
в направлении убывание функции Z. В результате выполненного шага получим первое
приближение - точки с координатами х11, х21. Значение целевой функции в этой
точке составляет Z1.
Далее вычислительная процедура повторяется:
последовательно получаем 2-е, 3-е и 4-е приближения - точки с координатами х12,
х22; х13, х23 и х14, х24. Значения целевой функции в этих точках соответственно
составляют Z2, Z3 и Z4.
Из рис. 1.2 видно, что в результате
вычиcлительного процесса последовательно осуществляется "спуск" к
минимуму функции Z. Вычислительная процедура заканчивается, когда относительное
изменение целевой функции на предыдущем i-м и последующем (i+1)-м шагах оказывается
меньше заданной точности вычислений 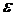 :
:
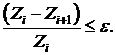 (1.16)
(1.16)
Рассмотренная вычислительная процедура носит
название градиентного метода с постоянным шагом. В этом методе все шаги
выполнялись одинаковой длины 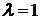 . Метод достаточно
прост. Основной его недостаток - большая вероятность зацикливания
вычислительного процесса в окрестности минимума функции Z. В соответствии с
рис. 1.2 вычислительный процесс зациклится между точками с координатами х13,
х23 и х14, х24. При этом в качестве искомого решения следует принять одну из
этих точек.
. Метод достаточно
прост. Основной его недостаток - большая вероятность зацикливания
вычислительного процесса в окрестности минимума функции Z. В соответствии с
рис. 1.2 вычислительный процесс зациклится между точками с координатами х13,
х23 и х14, х24. При этом в качестве искомого решения следует принять одну из
этих точек.
Для получения более точного результата
необходимо выбрать шаг меньшей длины. При этом объем вычислений (количество
шагов) увеличится.
Таким образом, точность и объем вычислений в
градиентном методе с постоянным шагом определяются величиной этого шага.
1.5.2 Метод скорейшего спуска
Как было отмечено выше, при увеличении длины
шага объем вычислений (количество шагов) уменьшается, однако уменьшается и
точность определения минимума целевой функции. При уменьшении длины шага
точность увеличивается, однако объем вычислений (количество шагов) возрастает.
Поэтому вопрос о выборе рациональной длины шага
в градиентных методах является своего рода оптимизационной задачей. Один из
способов определения оптимальной длины шага 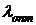 иллюстрируется
на рис. 1.3 и носит название метода скорейшего спуска [1,7].
иллюстрируется
на рис. 1.3 и носит название метода скорейшего спуска [1,7].

Рисунок 1.3 - Иллюстрация метода скорейшего
спуска (а) и параболическая аппроксимация целевой функции для выбора
оптимального шага (б)
В методе наискорейшего спуска желательно
использовать рассмотренное свойство направления градиента. Поэтому, если мы
находимся в точке хi на некотором шаге процесса оптимизации, то поиск минимума
функции осуществляется вдоль направления - .
Данный метод является итерационным. На шаге i точка минимума аппроксимируется
точкой хi . Следующей аппроксимацией является точка
.
Данный метод является итерационным. На шаге i точка минимума аппроксимируется
точкой хi . Следующей аппроксимацией является точка
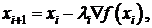 (1.17)
(1.17)
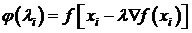 .
(1.18)
.
(1.18)
Значение λi
может быть найдено с помощью одного из методов одномерного поиска (например,
методом квадратичной интерполяции).
В приложении приведена программа, позволяющая
реализовать метод наискорейшего спуска. В ней множитель Лагранжа обозначен
через h. Вектор di является единичным.
Для поиска минимума функции
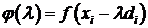 (1.19)
(1.19)
в направлении di из точки xi используется метод
квадратичной интерполяции.
В точке  ,
и мы выбираем длину шага λ такой,
чтобы шаг "перекрыл " минимум функции φ(λ).
Производная
,
и мы выбираем длину шага λ такой,
чтобы шаг "перекрыл " минимум функции φ(λ).
Производная
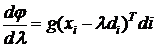 .
(1.20)
.
(1.20)
Данный оператор for(i=0;i<n;i++)
g2+=g[i]*d[i]; - вычисляет выражение
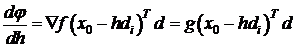 .
(1.21)
.
(1.21)
Оператор if (ff[2]>=ff[0] || g2>=0)
проверяет условие "перекрытия" минимума, которое выполняется при
выполнении либо одного, либо другого условия. Если минимум не попал в отрезок
(0,λ),
то λ
удваивается, и это повторяется столько раз, сколько необходимо для выполнения
условия "перекрытия".
Удостоверившись, что отрезок (0,λ)
содержит минимум, в качестве третьей точки возьмем точку λ/
2. Минимальную точку сглаживающего квадратичного полинома находим в
соответствии с соотношением
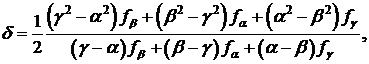 (1.22)
(1.22)
что отражено следующими операторами
l[3]=h*(ff[1]-.75*ff[0]-.25*ff[2]);
l[3]/=2*ff[1]-ff[0]-ff[2];
Оператор
for(i=0;i<n;i++)
{ x[i]=y[i]+l[0]*d[i]; y[i]=x[i]; }
производит присваивание xi+1=xi, и если
|g(xi+1)| достаточно мало, то процесс заканчивается. В процессе поиска
предполагается сходимость к экстремуму, поэтому для эффективности процедуры
разумно уменьшить длину шага. При этом деление шага пополам выбрано
произвольно.
В методе скорейшего спуска, по сравнению с
градиентным методом с постоянным шагом, количество шагов меньше, точность
получаемого результата выше, отсутствует зацикливание вычислительного процесса,
однако объем вычислений на одном шаге больше.
1.5.3 Метод проектирования градиента
Рассмотренные выше градиентные методы
предполагали отыскание абсолютного минимума целевой функции Z. При наличии в
математической модели нелинейных ограничений ищется уже не абсолютный, а
относительный минимум целевой функции Z [1].
Рассмотрим один из методов отыскания
относительного минимума целевой функции, получивший название метода
проектирования градиента.
Для упрощения алгоритма допустим, что имеется
одно ограничение в виде линейного неравенства
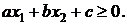 (1.23)
(1.23)
При наличии указанного ограничения минимум
целевой функции следует искать в области 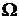 ,
расположенной по одну сторону от прямой
,
расположенной по одну сторону от прямой 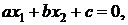 например
выше этой прямой (рис. 1.4).
например
выше этой прямой (рис. 1.4).
Начало вычислительной процедуры такое же, как и
в предыдущих методах:
в области 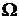 принимается
исходное (нулевое) приближение х10, х20;
принимается
исходное (нулевое) приближение х10, х20;
вычисляется значение целевой функции в этой
точке Z0;
в соответствии с выражением (1.15) в этой точке
вычисляется градиент целевой функции grad Z;
из исходной точки в направлении убывания целевой
функции выполняется шаг.

Рисунок 1.4 - Иллюстрация метода проектирования
градиента
Выбор величины шага может осуществляться
различным образом. Выберем шаг в соответствии с алгоритмом метода скорейшего
спуска и получим первое приближение - точку с координатами х11, х21.
Вычисляется значение целевой функции в этой точке Z1.
Необходимо проверить, принадлежит ли точка с
координатами х11, х21 области 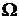 допустимых
значений переменных. Для этого проверяется неравенство (1.23), в которое
подставляются координаты х11, х21:
допустимых
значений переменных. Для этого проверяется неравенство (1.23), в которое
подставляются координаты х11, х21:
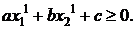 (1.23)
(1.23)
Если это неравенство выполняется, вычислительный
процесс продолжается.
Из точки с координатами х11, х21 выполняется
следующий шаг. В результате этого шага имеем второе приближение - точку с
координатами х12, х22. значение целевой функции в этой точке Z2.
Пусть для этой точки неравенство 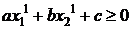 не
выполняется. Следовательно, точка с координатами х12, х22 вышла из области
не
выполняется. Следовательно, точка с координатами х12, х22 вышла из области 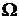 и
необходимо выполнить возврат в эту область.
и
необходимо выполнить возврат в эту область.
Возврат в область 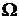 выполняется
следующим образом. Из точки с координатами х12, х22 опускается перпендикуляр на
прямую
выполняется
следующим образом. Из точки с координатами х12, х22 опускается перпендикуляр на
прямую 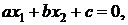 т.е.
конец вектора (х11, х21; х12, х22) проектируется на эту прямую. В результате
получается новое приближение - точка с координатами х13, х23, которая
принадлежит области
т.е.
конец вектора (х11, х21; х12, х22) проектируется на эту прямую. В результате
получается новое приближение - точка с координатами х13, х23, которая
принадлежит области 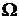 . В этой точке
вычисляется значение целевой функции Z3.
. В этой точке
вычисляется значение целевой функции Z3.
Дальнейший спуск к относительному минимуму
целевой функции продолжается из точки х13, х23. на каждом шаге вычисляется
значение целевой функции и проверяется принадлежность нового приближения к
области 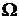 .
Вычислительный процесс заканчивается при выполнении условия (1.16).
.
Вычислительный процесс заканчивается при выполнении условия (1.16).
1.6 Метод штрафных функций
Рассмотрим задачу поиска локального минимума
критерия оптимальности W в области, ограниченной системой неравенств
(3.16)-(3.17). Введение обобщенного критерия оптимальности по методу штрафных
функций [3,5] производится с помощью непрерывной функции
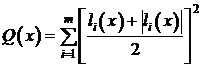 .
(1.24)
.
(1.24)
Обобщенным критерием оптимальности согласно
методу штрафных функций является выражение
T=W+RQ(x),
где R - некоторое положительное число,
называемое коэффициентом штрафа.
Рассматривается некоторая неограниченная,
монотонно возрастающая последовательность {Rk}, k=1,2,... положительных чисел.
Для первого элемента этой последовательности с помощью метода покоординатного
спуска отыскивается локальный минимум функции T. Пусть этот минимум достигается
при значениях (b*,R1).
Вектор (b*,R1) используется как начальное
приближение для решения задачи поиска минимума функции T где R2>R1 и т.д.
Таким образом, решается последовательность задач минимизации функций T(b*,Rk),
k=1,2 ..., причем результат предыдущей оптимизации используется в качестве
начального приближения для поиска последующей.
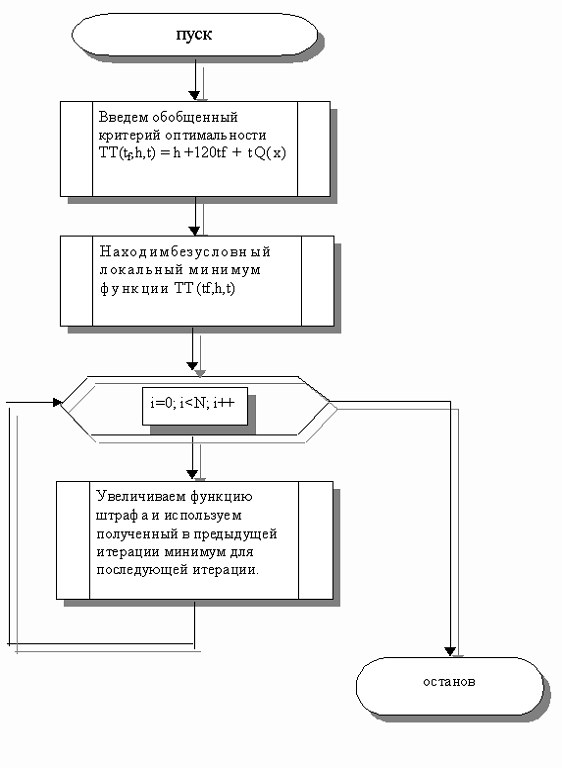
Рисунок 1.5 - Блок-схема метода штрафных функций
1.7 Методы полиномиальной аппроксимации
Согласно теореме Вейерштрасса об аппроксимации,
непрерывную функцию в некотором интервале можно аппроксимировать полиномом
достаточно высокого порядка [6]. Следовательно, если функция унимодальна и
найден полином, который достаточно точно ее аппроксимирует, то координаты точки
оптимума функции можно оценить путем вычисления координаты точки оптимума
полинома.
Рассмотрим следующие вопросы:
квадратичная
аппроксимация <#"478342.files/image051.gif">

|
|
|

|
|
|
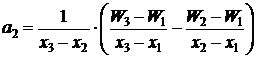
|
|

|

|
1.7.1.1Метод Пауэлла
Если известны значения функции f(x) в трех
разных точках α, β,
γ
равные соответственно fα,
fβ,
fγ,
то функция f(x) может быть аппроксимирована квадратичной функцией
ö(x)=Ax2+Bx+C, (1.26)
где А, В и С определяются из уравнений
Aá2+Bá+C=fá,
Aâ2+Bâ+C=fâ,
Aã2+Bã+C=fã.
(1.27)
После преобразований этих уравнений получаем
A=[(ã-â)fá+(á-ã)fâ+(â-á)fã] / D,
B=[(â2-ã2)fá+(ã2-á2)fâ+(á2-â2)fã] / D,
C=[âã(ã-â)fá+ãá(á-ã)fâ+áâ(â-ã)fã] / D,
(1.28)
где D=(á-â)(â-ã)(ã-á)
Ясно, что φ(x)
будет иметь минимум в точке
x=-B/2A,
если А>0. Следовательно, можно
аппроксимировать точку минимума функции f(x) значением
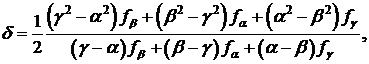 (1.29)
(1.29)
Этот метод может непосредственно применяться к
функциям одной переменной. Он может быть очень полезен для выполнения линейного
поиска в процедурах, описанных в теме №3. В этих процедурах требуется найти
минимум функции f(x) в точках прямой x0+λd,
где x0- заданная точка, а d определяет заданное направление. Значение функции
f(x0+λd)
на этой прямой является значениями функции одной переменной λ:
φλ
= f(x0+λd).
(1.30)
Идеи и результаты, изложенные выше, преобразуются
в вычислительные процедуры, описанные далее. Предположим, что заданы
унимодальная функция одной переменной f(x), начальная аппроксимация положения
минимума и длинна шага D, является величиной того же порядка, что и расстояние
от точки А до точки истинного минимума x*(условие, которое не всегда просто
удовлетворить). Вычислительная процедура имеет следующие шаги:
Шаг 1. x2 = x1 + D x.
Шаг 2. Вычислить W(x1) и W(x2).
Шаг 3.
если W(x1) > W(x2), то x3 = x1 + 2 D x;
если W(x1)< W(x2), то x3 = x1 - D x;
W(x1) > W(x2),
Шаг 4. Вычислить W(x3) и найти
Wmin = min{ W(x1),W(x2), W(x3)},
Xmin = xi, соответствующая Wmin.
Шаг 5. По x1, x2, x3 вычислить x*, используя
формулу для оценивания с помощью квадратической аппроксимации.
Шаг 6. Проверка окончания
если | Wmin - W(x*)| < W, то закончить поиск.
В противном случае к шагу 7;
если | Xmin - x*| < x, то закончить поиск. В
противном случае к шагу 7.
Шаг 7. Выбрать Xmin или x* и две точки по обе
стороны от нее. Обозначить в естественном порядке и перейти к шагу 4.
Заметим, что если точка Е задана
слишком малой, то á, â, ã, а также fá, fâ,
fã будут очень близко
друг к другу и значение d (1.29)
может стать вообще недостижимыми. Чтобы преодолеть эту трудность, перепишем
(1.29) для второй и последней интерполяции:
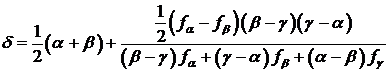 (1.31)
(1.31)
1.7.2 Кубическая интерполяция
Квадратичная интерполяция, которая
рассматривалась в предыдущем разделе, называется методом Пауэлла и
аппроксимирует функцию квадратным трехчленом. В этом разделе рассматривается
метод Давидона [6,7], который гарантирует большую точность и аппроксимирует
функцию кубическим полиномом.
Для кубической интерполяции в этом методе
используются значения функции и ее производной, вычисленных в двух точках.
Рассмотрим задачу минимизации функции f(x) на
прямой x0 + hd , то есть минимизацию функции
 (1.32)
(1.32)
Предположим, что известные следующие значения:
 (1.33)
(1.33)
Эту информацию можно использовать для построения
кубического полинома a+bh+ch2+dh3, который будет аппроксимировать функцию φ(h)
Если p=0 , то уравнения, которые определяют a, b, c, d имеют вид :
 (1.34)
(1.34)
Следовательно, если r является точкой минимума
кубического полинома,
 (1.35)
(1.35)
где
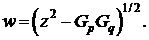
Одно из значений этого выражения является
минимумом. Друга производная равна 2c +6dh.
Если мы выберем положительный знак, то при
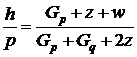
другая производная будет
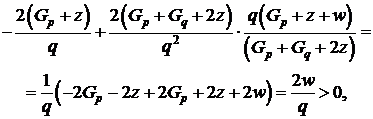 (1.36)
(1.36)
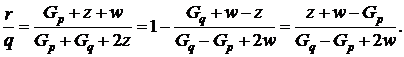 (1.37)
(1.37)
Выбор точки q зависит от нас. Если Gp >0 , то
надо выбрать значение q положительным, то есть сделать шаг в направлении
уменьшения функции φ(h)
, в другом случае значения q надо выбирать отрицательным. Значение должно быть
таким, чтобы интервал (0, ) включал в себя минимум. Это будет верным, если φq
> φ
p или Gp >0.
Если ни одно из этих условий не исполняется, то
мы удваиваем значения q , повторяя это в случае необходимости, пока указанный
интервал не будет содержать в себе минимум.
Давидон, Флетчер и Пауэлл предложили выбирать q
следующим путем:
 (1.38)
(1.38)
где φm
- оценка самого малого значения истинного минимума φ(h),
h-
константа, значение которой обычно берут 2 или 1.
1.7.3 Квадратичные функции
Квадратичная функция [7,8]
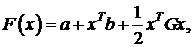 (1.39)
(1.39)
где a - константа;
b - постоянный вектор;
G - положительно определенная симметричная
матрица - имеет минимум в точке x* , где x* определяется следующим путем:
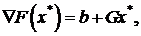 (1.40)
(1.40)
откуда

Любую функцию можно аппроксимировать в
окрестности точки x0 функцией
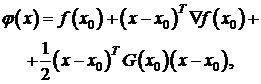 (1.41)
(1.41)
где G(x0) - матрица Гессе, вычисленная в точке
x0.
Аппроксимацией минимума функции f(x) может быть
минимум функции φ(x). Если
последний находится в точке xm, то
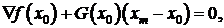 (1.42)
(1.42)
откуда
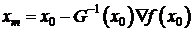
или
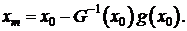 (1.43)
(1.43)
Таким образом точкой xи следующей аппроксимации
минимума будет:
 (1.44)
(1.44)
или
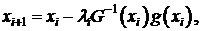 (1.45)
(1.45)
где λи
- длина шага, определяется одномерным поиском в направлении G-1(xи)g(xи).
1.8 Метод Нелдера-Мида
Метод Нелдера-Мида (поиск по деформируемому
многограннику) является развитием симплексного метода Спендли, Хекста и
Химсворта [7,8]. Множество (n+1)-й равноудаленной точки в n-мерном пространстве
называется регулярным симплексом. Эта конфигурация рассматривается в методе
Спендли, Хекста и Химсворта. Следовательно, в двумерном пространстве симплексом
является равносторонний треугольник, а в трехмерном пространстве правильный
тетраэдр. Идея метода состоит в сравнении значений функции в (n+1) вершинах
симплекса и перемещении в направлении оптимальной точки с помощью итерационной
процедуры. В симплексном методе, предложенном первоначально, регулярный
симплекс использовался на каждом этапе. Нелдер и Мид предложили несколько
модификаций этого метода, допускающих, чтобы симплексы были неправильными. В
результате получился очень надежный метод прямого поиска, являющийся одним из
самых эффективных, если n<=6.
В методе Спендли, Хекста и Химсворта симплекс
перемещается с помощью трех основных операций: отражения, растяжения и сжатия.
Смысл этих операций станет понятным при рассмотрении шагов процедуры.
Шаг 1. Найдем значения функции в вершинах
симплекса:
f1=f(
x1), f2=f(x2) ... fn+1=f(xn+1) (1.46)
Шаг 2. Найдем наибольшее значение функции fh,
следующее за наибольшим значением функции fg , наименьшее значение функции fl и
соответствующие им точки xh, xg и xl.
Шаг 3. Найдем центр тяжести всех точек, за
исключением точки xh. Пусть центром тяжести будет
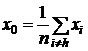 (1.47)
(1.47)
и вычислим f(x0)=f0.
Шаг 4. Удобнее всего начать перемещение от точки
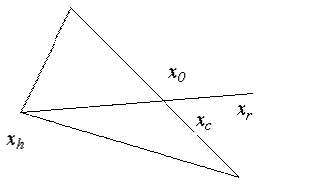
xh. Отразив точку xh относительно точки x0, получим точку xr и найдем f(xr) =
fr.
Операция отражения иллюстрируется рис. 1.6.

Рисунок
1.6 - Операция отражения
Если α>0
- коэффициент отражения, то положение точки xr определяется следующим образом:
xr-x0=α
(x0-xh), т.е.
xr=(1+α)x0
-αxh.
(1.48)
Замечание.
α= |xr-x0| / |x0
-xh|.
Шаг 5. Сравним значения функций fr и fl.
Если fr<fl, то мы получили наименьшее
значение функции. Направление из точки x0 в точку xr наиболее удобно для
перемещения. Таким образом, мы производим растяжение в этом направлении и
находим точку xe и значение функции fe=f(xe). Рисунок 1.7. иллюстрирует
операцию растяжения симплекса. Коэффициент растяжения γ1
можно найти из следующих соотношений: xe-x0=γ
(xr-x0), т.е.
xe=γxr+
(1-γ)x0.
(1.49)
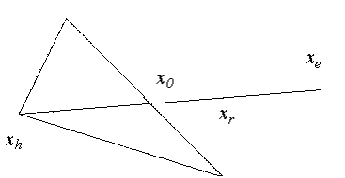
Рисунок
1.7 - Операция растяжения
Замечание
γ=|xe-x0|
/ |xr-x0|
Если
fe<fl, то заменяем точку xh на точку xe и проверяем (n+1)-ую точку симплекса
на сходимость к минимуму (см. шаг 8). Если сходимость достигнута, то процесс
останавливается; в противном случае возвращаемся на шаг 2.
Если
fe=fl , то отбрасываем точку xe. Очевидно, мы переместились слишком далеко от
точки x0 к точке xr. Поэтому следует заменить точку xh на точку xr, в которой
было получено улучшение (шаг 5, 1) проверить сходимость и, если она достигнута,
вернуться на шаг 2.
Если
fr>fl, но fr <=fgто xr является лучшей точкой по сравнению с другими
двумя точками симплекса и мы заменяем точку xh на точку xr и, если сходимость
не достигнута, возвращаемся на шаг 2, т.е. выполняем пункт 1,б, описанный выше.
Если
fr>fl и fr>fgто перейдем на шаг 6.
Шаг
6. Сравним значения функций fr и fh.
Если
fr>f h, то переходим непосредственно к шагу сжатия 6,2.
Если
fr<fh, то заменяем точку xh на точку xr и значение функции fh на значение
функции fr. Запоминаем значение fr>f g из шага 5,2, приведенного выше. Затем
переходим на шаг 6,2.
В
этом случае fr>f h, поэтому ясно, что мы переместились слишком далеко от
точки xh к точке x0. Пытаемся исправить это, найдя точку xc (а затем fс) с
помощью шага сжатия, показанного на рис. 1.8.
Если
fr>f h, то сразу переходим к шагу сжатия и находим точку xc из соотношения
xc-x0=β(xh-x0),
(1.50)
где β(0<b<1)-
коэффициент сжатия. Тогда
xc=βxh+(1-β)x0.
(1.51)
Если fr<f h, то сначала заменим точку xh на
точку xr, а затем произведем сжатие. Тогда точку xc найдем из соотношения
xc-x0=β(xr-x0),
т.е.
xc=βxr+(1-β)x0.
(1.52)
Шаг 7. Сравниваем значения функций fc и fh.
Если fc<f h, то заменяем точку xh на точку
xc, и если сходимость не достигнута ,то возвращаемся на шаг 2.
Если fc>f h, то очевидно, что все наши
попытки найти значение меньшее fh закончились неудачей, поэтому мы переходим на
шаг 8.
На этом шаге мы уменьшаем размерность симплекса
делением пополам расстояния от каждой точки симплекса до xl-точки, определяющей
наименьшее значение функции.

Рисунок
1.8 - Шаг сжатия для fr>fh
Рисунок
1.9 - Шаг сжатия для fr<fh
Таким
образом, точка xi заменяется на точку
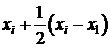 ,
,
т.е.
заменяем точку xi точкой 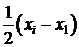 .
.
Затем
вычисляем fi для i=1,2,...,(n+1), проверяем сходимость и, если она достигнута,
возвращаемся на шаг 2.
Шаг
9. Проверка сходимости основана на том, чтобы стандартное отклонение (n+1) -го
значения функции было меньше некоторого заданного малого значения. В этом
случае вычисляется
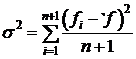 ,
(1.53)
,
(1.53)
где  .
.
Если σ<ε,
то все значения функции очень близки друг к другу, и поэтому они, возможно,
лежат вблизи точки минимума функции xl. Исходя из этого, такой критерий
сходимости является разумным, хотя Бокс, Дэвис и Свенн предлагают то, что они
считают более "безопасной" проверкой.
Коэффициенты αβγ
в вышеприведенной процедуре являются соответственно коэффициентами отражения,
сжатия и растяжения. Нелдер и Мид рекомендуют брать α=1,
β=0.5
и γ=2.
Рекомендация основана на результатах экспериментов с различными комбинациями
значений. Эти значения параметров позволяют методу быть эффективным, но
работать в различных сложных ситуациях.
Начальный симплекс выбирается на наше
усмотрение. В данной программе точка x1 является начальной точкой, затем в
программе формируются точки
x2=x1+ke1,
x3=x1+ke2,
xn+1=x1+ken,
(1.54)
где k - произвольная длина шага,
ej - единичный вектор.
1.9 Метод неопределенных множителей Лагранжа
Естественно, что решение задач условной
оптимизации значительно сложнее решения задач безусловной оптимизации [3].
Естественно стремление сведения задачи условной оптимизации (поиска
относительного экстремума) к более простой задаче безусловной оптимизации
(поиска абсолютного экстремума). Такая процедура осуществляется в методе
Лагранжа. Рассмотрим сущность этого метода.
Необходимо найти условный экстремум нелинейной
функции
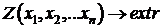 (1.55)
(1.55)
n переменных, при m ограничениях
 (1.56)
(1.56)
Ограничения-неравенства преобразуются в
равенства, а свободные члены переносятся в левые части ограничений, т.е.
система (1.56) приводится к виду
 (1.57)
(1.57)
В соответствии с методом Лагранжа вместо
относительного экстремума функции (1.55) при ограничениях (1.57) ищется
абсолютный экстремум функции Лагранжа, которая имеет следующий вид:
 (1.58)
(1.58)
где 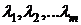 -
неопределенные множители Лагранжа, являющиеся, как и переменные
-
неопределенные множители Лагранжа, являющиеся, как и переменные 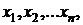 искомыми
переменными.
искомыми
переменными.
Видно, что в функцию Лагранжа входит целевая
функция плюс каждое ограничение, умноженное на множитель Лагранжа.
Доказано, что относительный экстремум целевой
функции (1.55) при ограничениях (1.57) совпадает с абсолютным экстремумом
функции Лагранжа (1.58).
Поиск абсолютного экстремума функции (1.58)
выполняется известными методами. В частности, определяются и приравниваются к
нулю частные производные функции Лагранжа:

 (1.59)
(1.59)
Последние m уравнений представляют собой
ограничения (1.57) оптимизационной задачи.
Система (1.59) содержит (m+n) уравнений и такое
же количество неизвестных.
Решение системы (1.59) даст координаты
абсолютного минимума функции Лагранжа (1.58) или относительного минимума
целевой функции (1.55) при ограничениях (1.57).
Решение системы (1.59) выполняется известными
методами вычислительной математики. Если система (1.59) линейная, используется,
как правило, метод Гаусса. Если система (1.59) нелинейная - метод Ньютона.
1.10 Выбор метода оптимизации
Перед выбором метода оптимизации, проведем
краткий анализ задач, которые должно решать разрабатываемое программное
обеспечение:
программа должна решать задачу условной
минимизации, т.е. находить относительный экстремум, так как в математической
модели кроме линейных ограничений будут иметь место и нелинейные;
так как целевая функция - функция нескольких
переменных, то она может иметь несколько экстремумов, и в этом случае программа
должна осуществлять поиск локального минимума.
Проведя анализ наиболее часто использующихся
методов оптимизации, для реализации поставленной цели был выбран градиентный
метод квадратичного программирования, который представляет собой наиболее
эффективный из вышеперечисленных градиентных методов, модифицированный с
методами полиномиальной аппроксимации.
Предполагается, что целевая функция и граничные
условия аппроксимируются квадратичными зависимостями или полиномами второго
порядка. Более подробно этот метод будет рассмотрен далее в разделе
"Разработка программного обеспечения метода оптимизации".
Данный метод позволяет создать надежную программу,
соответствующую всем вышеперечисленным требованиям.
2. Разработка метода оптимизации по реактивной
мощности
Требуемая в электроэнергетической системе (ЭЭС)
суммарная мощность компенсирующих устройств определяется из уравнения баланса
реактивной мощности (6.1). Эту мощность необходимо разместить в узлах
электрической сети с минимальными затратами.
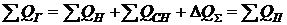 , (2.1)
, (2.1)
где
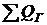 - суммарная
реактивная мощность, генерируемая в ЭЭС, включая реактивную мощность,
поступающую из соседних ЭЭС;
- суммарная
реактивная мощность, генерируемая в ЭЭС, включая реактивную мощность,
поступающую из соседних ЭЭС;
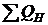 - суммарная
реактивная мощность потребителей ЭЭС, включая реактивную мощность, отдавая в
соседние ЭЭС;
- суммарная
реактивная мощность потребителей ЭЭС, включая реактивную мощность, отдавая в
соседние ЭЭС;
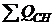 - суммарная
реактивная мощность собственных нужд электростанций;
- суммарная
реактивная мощность собственных нужд электростанций;
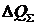 - суммарные
потери реактивной мощности;
- суммарные
потери реактивной мощности;
 - суммарное
потребление реактивной мощности в ЭЭС.
- суммарное
потребление реактивной мощности в ЭЭС.
Рассмотрим
простейшую схему существующей сети (рис.2.1). от источника питания с
напряжением U через сопротивление сети R получает питание нагрузка мощностью
S=P+jQ [9]. На шинах нагрузки установлено компенсирующее устройство мощностью
Qк.
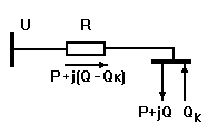
Рисунок
2.1 - Простейшая схема компенсации реактивной мощности
Потери
активной мощности в линии при отсутствии у потребителя компенсирующего
устройства (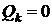 ) составляют
) составляют
 . (2.2)
. (2.2)
При
установке у потребителя компенсирующего устройства (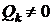 ) эти потери
уменьшатся до величины
) эти потери
уменьшатся до величины
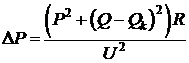 . (2.3)
. (2.3)
Таким образом, компенсация реактивной мощности
позволяет уменьшить потери активной мощности в схеме электроснабжения и,
следовательно, улучшить технико-экономические показатели этой схемы.
Оценим влияние КУ на затраты в сети.
Выражение для суммарных затрат на передачу
мощности к нагрузке при установке КУ будет иметь вид:
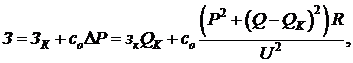 (2.4)
(2.4)
где ЗК - затраты на КУ;
соΔР
- затраты на покрытие потерь активной мощности в сети;
со - стоимость единицы потерянной активной
мощности;
зк - удельные затраты на КУ.
Для определения минимума функции З приравняем к
нулю ее производную от переменной QK:
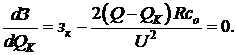 (2.5)
(2.5)
Из (2.5) определяется экономически
целесообразная реактивная мощность, передача которой от источника к потребителю
отвечает минимуму затрат З
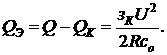 (2.6)
(2.6)
Величина QЭ не зависит от активной мощности Р, а
зависит лишь от соотношения стоимостных показателей зк и со и параметров сети U
и R, по которой передается мощность.
Вопрос о размещении компенсирующих устройств в
электрической сети реальной ЭЭС представляет собой сложную оптимизационную
задачу. Сложность заключается в том, что электроэнергетические системы являются
большими системами, состоящими из взаимосвязанных подсистем. Рассматривать
изолированно каждую отдельную подсистему нельзя, поскольку свойства больших
систем определяются характером взаимосвязей отдельных подсистем.
При анализе больших систем используется
системный подход [9,10,11], согласно которому анализ большой системы
выполняется при разделении ее на подсистемы, непосредственно не связанные между
собой, но влияющие друг на друга через систему более высокого уровня.
Применительно к рассматриваемому вопросу
электрическая сеть представляется разными уровнями, как это показано на рис.
2.2. верхний уровень - это электрическая сеть напряжением 110 кВ и выше. Эта
сложнозамкнутая электрическая сеть, представляемая полной схемой замещения,
показана на рис.2.2 условно, как ЭС1. Реактивные мощности, вырабатываемые
генераторами электростанций QЭС, компенсирующими устройствами QК, линиями
электропередачи QС, а также реактивные мощности, протекающие по связям с
соседними ЭС2 и ЭС3 (Q12, Q21, Q13, Q31) обеспечивают в ЭС1 располагаемую
реактивную мощность Qр1.

Рисунок 2.2 - Схема размещения КУ в
электрической сети
Второй уровень - это множество n разомкнутых
местных распределительных сетей напряжением 35 кВ и ниже, присоединенных к n
узлам электрической сети верхнего уровня через трансформаторы Т. Эти местные
распределительные сети непосредственно не связаны между собой, но влияют друг
на друга через сеть верхнего уровня. Синхронные генераторы, компенсаторы и
двигатели в каждой такой распределительной сети представлены одной
эквивалентной синхронной машиной G. От местных электрических сетей через
распределительные трансформаторы Т1 питаются низковольтные потребители P+jQ.
Компенсирующие устройства могут устанавливаться
на шинах высшего (jQкв) и низшего (jQкс) напряжения трансформаторов Т, а также
на шинах 0,4 кВ распределительных трансформаторов Т1 и в самой сети 0,4 кВ
(jQкн). Значение мощностей этих КУ и подлежит определению.
В общем виде задача оптимизации размещения КУ
формулируется следующим образом: определить реактивные мощности имеющихся в
узлах 6…35 кВ синхронных машин G, мощности КУ в сетях всех напряжений Qкв, Qкс,
Qкн, а также значения реактивных мощностей Qэi (i=1, 2, …n), передаваемых в
сети потребителей, при которых обеспечивается минимум суммарных затрат.
Расчеты компенсации реактивной мощности для
сетей всех видов выполняются как при проектировании развития электрических
сетей, так и в условиях их эксплуатации. При проектировании определяются
мощности КУ и решается задача их распределения в электрической сети. В условиях
эксплуатации определяют оптимальные режимы имеющихся КУ в течение суток.
Критериями оптимальности в этом случае служат минимум потерь мощности и энергии
и соответствие отклонений напряжений допустимым значениям.
При проектировании схемы электроснабжения, как
правило, минимизируются денежные затраты на эту схему. Снижение потерь мощности
за счет установки КУ уменьшает затраты на схему, по следующим причинам:
каждый потерянный кВт мощности необходимо
выработать на электростанциях и, следовательно, затратить на это денежные
средства;
генерация недополученной реактивной мощности на
электростанциях обходится гораздо дороже, чем потребление (в 3 раза!).
Однако и компенсирующие устройства требуют
денежных затрат.
В связи с этим возникает задача определения
оптимальной мощности компенсирующих устройств, отвечающей минимуму суммарных
затрат. Такая задача относится к задаче безусловной оптимизации и может быть
решена, например, градиентными методами.
Рассмотрим такую задачу для магистральной схемы
электроснабжения (рис. 2.3). Необходимо определить мощности компенсирующих
устройств QК1 и QК2 в узлах 1 и 2 исходя из условия минимума суммарных затрат
на установку этих устройств и покрытие потерь активной мощности в схеме.
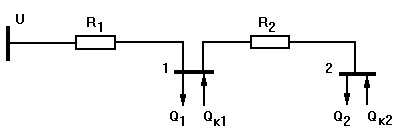
Рисунок 2.3 - Схема электроснабжения
Исходные данные:
напряжение схемы U;
сопротивления линий R1 и R2;
реактивные нагрузки узлов 1 и 2 Q1 и Q2;
удельные затраты на установку компенсирующих
устройств zo;
удельные затраты на покрытие потерь активной
мощности со.
Целевая функция, представляющая собой суммарные
затраты на установку компенсирующих устройств и покрытие потерь активной
мощности в схеме, имеет следующий вид
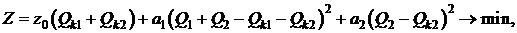 (2.7)
(2.7)
где а1=R1∙co∙10-3/U2=0,0006;
а2=R2∙co∙10-3/U2=0,0004.
Введение числового коэффициента 10-3 необходимо
для приведения всех составляющих целевой функции к одной размерности (у.е.).
Для решения задачи выберем метод покоординатного
спуска. Определим частные производные целевой функции Z по переменным Q1 и Q2:
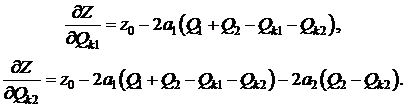 (2.8)
(2.8)
Примем исходное приближение:
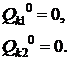 (2.9)
(2.9)
Для этих значений вычислим значения целевой
функции и ее частных производных.
Примем, что в направлении переменной Qk2 целевая
функция Z убывает сильнее, чем в направлении переменной Qk1, т.е.
 (2.10)
(2.10)
В направлении переменной Qk2 и начнем спуск.
Примем
величину шага  =400 квар.
Первое приближение (первый шаг) будет Qk11=0, Qk21=400 квар. Рассчитываем
значение целевой функции Z1.
=400 квар.
Первое приближение (первый шаг) будет Qk11=0, Qk21=400 квар. Рассчитываем
значение целевой функции Z1.
Второй
шаг: Qk12=0, Qk22=400 квар. Рассчитываем значение целевой функции Z2.
Спуск
по координате Qk2 следует продолжать до тех пор, пока Zn<Zn-1. Как только Zn
становится больше предыдущего значения Zn-1, следует спуск координате Qk2 прекратить
и вернуться к значениям переменных Qk1n-1 и Qk2n-1, полученным на n-1 шаге.
Выполним
новый шаг в направлении другой переменной Qk1. Находится новое значение целевой
функции Z. Спуск по этой переменной продолжается так же, как и в направлении
Qk2 - до тех пор, пока Zm<Zm-1.
Точка
с полученными координатами Qk1m-1, Qk2n-1 находится в окрестности минимума
целевой функции Z. При принятой длине шага  =400квар более точное решение
получено быть не может. Для получения более точного решения необходимо
уменьшить шаг и продолжить спуск. Абсолютно точно что, чем меньше шаг, тем
точнее будет результат. Посредством ручного расчета мы не можем добиться такой
точности. Для решения этой задачи целесообразно будет использовать программное
обеспечение, предназначенное для решения задачи нелинейного программирования с
нелинейными ограничениями. Одним из таких языков программирования является язык
С++.
=400квар более точное решение
получено быть не может. Для получения более точного решения необходимо
уменьшить шаг и продолжить спуск. Абсолютно точно что, чем меньше шаг, тем
точнее будет результат. Посредством ручного расчета мы не можем добиться такой
точности. Для решения этой задачи целесообразно будет использовать программное
обеспечение, предназначенное для решения задачи нелинейного программирования с
нелинейными ограничениями. Одним из таких языков программирования является язык
С++.
Это
была рассмотрена задача безусловной оптимизации, т.е. нахождения абсолютного
минимума. При решении поставленной задачи для нахождения оптимального режима
работы сети ОАО "ММК им. Ильича" требуется найти относительный
минимум, так как система ограничений будет иметь нелинейный вид (см. далее
"Разработка программного обеспечения"). Таким образом, перед нами
ставится задача условной оптимизации по реактивной мощности, для которой мы
применяем выбранный ранее градиентный метод квадратичного программирования.
3.
Разработка программного обеспечения метода оптимизации
Для
оптимизации режимов по реактивной мощности разработан комплекс программ (см.
рис. 3.1). Его условно можно разделить на две части:
интерфейсная
часть, разработанная в удобном, понятном виде, предназначенная для работы с
пользователем любого уровня;
расчетная
часть, которая непосредственно выполняет необходимые расчеты для получения
оптимальных режимов.
В
интерфейсную часть комплекса входят программы ввода следующих параметров:
линий;
трансформаторов;
компенсирующих
устройств;
реакторов;
нагрузок.
В
расчетную часть входят следующие программы:
формирования
узловой матрицы;
формирования
векторов узловых токов без оптимизации мощностей компенсирующих устройств;
расчета
узловых напряжений;
формирования
векторов ограничений узловых токов;
расчета
оптимальных значений узловых напряжений;
расчета
оптимальных значений мощностей компенсирующих устройств.
Для
расчета установившегося неоптимального режима разработаны программы:
формирования
матриц узловых проводимостей,
формирования
узловых токов источников,
ЛУ
разложения матрицы,
решение
систем уравнений узловых напряжений.
Рисунок 3.1 - Блок-схема разработанного
программного обеспечения
Для расчета оптимального режима разработана
программа условной оптимизации с нелинейными ограничениями. В качестве исходных
данных для этой программы используется узловые напряжения, рассчитанные для
неоптимального режима. Оптимизация производится градиентным методом
квадратичного программирования.
Программа расчета неоптимального установившегося
режима включает в себя алгоритм треугольного разложения матрицы и итерационный
алгоритм решения системы нелинейных уравнений подобный методу Гаусса-Зейделя,
модифицированный для решения сетевых нелинейных задач.[2,4,8] Особенностью
итерационного алгоритма является то, что на каждой последующей итерации для
определения узловых токов источников используется значения узловых напряжений,
полученное на предыдущей итерации (см. 3.1).
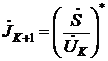 . (3.1)
. (3.1)
Для решения задачи нелинейного программирования
и определения оптимальных узловых напряжений был разработана программа NCONF
CPP, которая реализует последовательный алгоритм квадратичного программирования
и конечноразностный градиент. [12]
NCONF CPP (m, me, n, xguess, ibtype,
xlb, xub, xscale, iprint, maxitn; x, fvalue).
Параметры программы
NCONF CPP:
входные: m, me, n,
xguess, ibtype, xscale, iprint, maxitn;
входной/выходной: xlb, xub;
выходные: x, fvalue.
m - общее число ограничений.
me - число ограничений равенства.
n - число переменных.
x - вектор начальных значений напряжений
(активных и реактивных составляющих).
xguess - вектор размена n, содержащий начальное
предположение о значениях напряжений;
ibtype - скаляр, задающий вид ограничений на
переменные:
ibtype=3 - задаем ограничение на напряжение
первого узла, все остальные будут иметь те же ограничения.
xlb - вектор размера n, содержащий нижние
границы переменных:
входная, если ibtype=0;
выходная, если ibtype=1 или 2;
входная/выходная, если ibtype=3.
xub - вектор размера n, содержащий верхние
границы переменных:
входная, если ibtype=0;
входная/выходная, если ibtype=3.
xscale - вектор размера n, содержащий
диагональную матрицу масштабирования переменных. Все элементы вектора xscale
равны 1.0.
iprint - параметр, задающий желаемый уровень
печати; принимает следующие значения:
0 - нет печати;
1 - выводится итоговый анализ о работе
программы;
2 - дополнительно на каждой итерации выводится
одна строка с промежуточными результатами;
3 - о каждой итерации выводится детальная
информация.
maxitn - максимально допустимое число итераций.
х - вектор размера n, содержащий вычисленное
решение.
fvalue - скаляр, содержащий значение целевой
функции в полученном решении.
Общая задача нелинейного программирования,
решаемая данной программой NCONF CPP, состоит в поиске минимума целевой функции
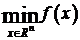 (3.2)
(3.2)
с ограничениями
 (3.3)
(3.3)
где все функции задачи являются непрерывно
дифференцируемыми.
При решении поставленной задачи целевая функция
представляет собой потери мощности и имеет вид:
 , (3.4)
, (3.4)
где
 -
соответственно активная и реактивная составляющие векторов узловых напряжений;
-
соответственно активная и реактивная составляющие векторов узловых напряжений;
 -
соответственно активная и реактивная составляющие векторов узловых
проводимостей.
-
соответственно активная и реактивная составляющие векторов узловых
проводимостей.
Роль
нелинейных ограничений выполняет система узловых уравнений с источниками
реактивной мощности.
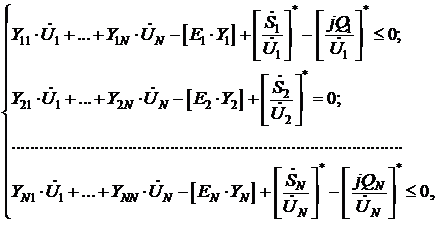 (3.5)
(3.5)
где Y11, …,Y1N - собственные и взаимные
проводимости,
U1,…,U2 - узловые напряжения.
Некоторые
уравнения системы (3.5) могут не содержать составляющую  в том
случае, если в узлах, для которых составляются данные уравнения, не установлены
компенсирующие устройства. Такое уравнение вместо знака ≤ будет содержать
знак равенства и считаться линейным.
в том
случае, если в узлах, для которых составляются данные уравнения, не установлены
компенсирующие устройства. Такое уравнение вместо знака ≤ будет содержать
знак равенства и считаться линейным.
Кроме
целевой функции и ограничений любая задача минимизации должна иметь и граничные
условия:
 , (3.6)
, (3.6)
т.е. значения напряжений в любом, даже самом
удаленном от источника узле не должны выйти за рамки, нормируемые ПУЭ.
Метод, используемый данной программой NCONF CPP,
основан на последовательном выделении и решении подзадач квадратичного
программирования, которые получаются в результате применения квадратичной
аппроксимации лангранжиана и линеаризации ограничений[8,12]. Таким образом, на
каждой итерации решается подзадача
 (3.7)
(3.7)
с ограничениями
 (3.8)
(3.8)
где Bk - положительно определенная аппроксимация
гессиана;
xk - текущая точка.
Пусть dk - решение подзадачи. Тогда новая точка
xk+1 определяется в результате линейного поиска:
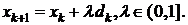 (3.9)
(3.9)
Новая точка такова, что в ней функция качества
имеет наименьшее значение. В качестве функции качества употребляется функция
Лагранжа. Если оптимум не достигнут, то матрица Bk пересчитывается по
положительно определенной формуле секущих.
Главная программа NCONF CPP содержит несколько
подпрограмм:
foryzc - программа формирования матрицы узловых
проводимостей;
luc - программа используется для разложения
матрицы на треугольные сомножители;
rluc - программа, которая отвечает за решение
системы уравнений.
4. Разработка адаптивной системы управления
режимами электропотребления
4.1 Функции автоматизированной системы
Сбор, накопление и передача информации,
характеризующей режим электропотребления комбината (информация о нагрузках).
Сбор, накопление и передача информации,
характеризующей состояние электрической сети (информация об обрывах линий и
переводах в ремонт оборудования)
Передача информации с контрольных точек на
диспетчерский пункт и обратно.
Обработка полученной информации, расчет режима
электропотребления
Автоматическое изменение параметров устройств,
регулирующих реактивную мощность, в местах, где это возможно.
4.2 Описание работы системы
4.2.1 Ввод системы в работу
При первоначальном запуске системы в эксплуатацию
собирается информация о конфигурации электрической сети.
Собираются следующие параметры:
схема сети;
информация о линиях: длина, марка проводов или
кабеля, которыми выполнено питание между подстанциями.
После предварительного расчета, для упрощения
работы программного обеспечения в базу данных диспетчерского пункта заносятся
следующие параметры:
узловая топологическая матрица согласно схеме
замещения электрической сети;
матрица узловых проводимостей схемы;
зарядные мощности линий.
Эти данные хранятся в сервере диспетчерской и
используются в качестве исходных данных для последующего расчета режима работы
сети. Изменяться эти данные могут в случае изменения конфигурации сети при
плановых или аварийных выводах оборудования из работы.
4.2.2 Работа системы в нормальном режиме
На первом этапе в условиях нормальной работы в
определенный момент времени (например, раз в неделю) происходит сбор
информации, характеризующей режим электропотребления.
Собираются следующие параметры:
нагрузки подстанций;
мощности питающих систем (в данном случае,
подстанций "Ильич", "Заря" и "Азовская").
На большинстве подстанций установлено
оборудование, которое может быть использовано для учета электроэнергии,
например, микропроцессорная релейная защита.
Вторым этапом работы автоматизированной системы
является передача по линиям связи собранной информации с подстанций на
диспетчерский пункт.
Третьим этапом является расчет текущего режима
работы электрической сети, нахождение оптимального режима работы электрической
сети, описанный в предыдущих главах пояснительной записки.
Получаем результаты расчета, необходимые для
автоматического внедрения оптимального режима работы сети на практике: мощности
компенсирующих устройств.
Следующим этапом является передача результатов
расчета по линиям связи обратно на подстанцию.
Заключительным этапом можно считать
регулирование компенсирующих устройств в соответствии с данными расчета.
Желательно исключить человеческий фактор, для этого на каждой подстанции помимо
современной релейной защиты, отвечающей за сбор информации, желательно
установить контроллеры, которые будут автоматически регулировать мощность
компенсирующих устройств в местах, где это возможно.
Для более точной работы автоматической системы
необходимо также предусмотреть обратную связь: после всех регулировок
происходит новый сбор информации и перепроверка, что новые установленные
параметры соответствуют оптимальному электропотреблению. В случае если что-либо
было сделано неправильно, вносится коррекция в исходные данные, и весь алгоритм
работы автоматической системы повторяется заново.
4.2.3 Работа системы в случае изменения
конфигурации сети
В случае изменения конфигурации сети: обрыв
линий, вывод в ремонт трансформаторов какой-либо подстанции, поломка
какого-либо электрооборудования, которое влияет на процесс энергопотребления, -
сбор информации происходит вне рабочего графика, т.е. непосредственно после
изменения.
В этом случае собираемые данные:
схема сети;
информация о линиях: длина, марка проводов или
кабеля, которыми выполнено питание между подстанциями;
нагрузки подстанций;
мощности питающих систем (в данном случае,
подстанций "Ильич", "Заря" и "Азовская").
Вторым предварительным этапом пересчитывается
матрица узловых проводимостей, зарядные мощности линий, формируется новая схема
замещения сети.
Далее система работает аналогично работе при
нормальном режиме.
В случае если данные изменения конфигурации сети
планируются на длительный или постоянный срок, результаты предварительного
расчета считаются новыми исходными данными и заносятся в базу данных сервера
диспетчерской.
Таблица 4.1 - Сводная таблица собираемой и
рассчитываемой информации
|
№
п/п
|
Этап
работы автоматизиро-ванной системы
|
Входные
данные
|
Полученные
результаты
|
Дальнейшее
использование результатов
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
Предварительный
расчет
|
Схема
сети; информация о линиях: длина, марка проводов или кабеля, которыми
выполнено питание между подстанциями.
|
узловая
топо-логическая матрица согласно схеме замещения эл. сети; матрица узловых
прово-димостей зарядные мощ-ности линий.
|
Заносятся
в базу данных сервера диспетчеризации, изменяются при изменении конфигурации
сети
|
|
2
|
Первый
этап - сбор информации
|
|
нагрузки
подстанций; мощности питающих систем (в данном случае, подстанций
"Ильич", "Заря" и "Азовская").
|
Второй
этап - передача на диспетчерский пункт
|
|
3
|
Третий
этап - оптимизация текущего режима на языке программирова-ния С++
|
Результаты
предваритель-ного расчета + результаты первого этапа (подробнее см. выше)
|
Оптимальные
потери активной и реактивной мощностей; мощности комп. устройств
|
|
|
4
|
Четвертый
этап - передача с диспетчерского пункта
|
Мощности
компенсирующих устройств
|
|
|
|
5
|
Обратная
связь - проверка соответствия между рассчитанными мощностями КУ и
отрегулирован-ными
|
Входные
данные предваритель-ного расчета + первого этапа + мощности КУ
|
Подтверждение
о соответствии или об сообщение об изменении режима
|
В
случае несоответствия - рекомендации к пересчету режима
|
4.3 Требования к оборудованию и программному
обеспечению
Технический уровень автоматизации должен
соответствовать передовому уровню, достигнутому в мировой практике ко времени
изготовления нестандартного оборудования и поставки серийно производимой
техники.
При внедрении автоматизированной системы на
комбинате должны быть предусмотрены средства эффективного контроля работоспособности
оборудования, диагностики датчиков, подсистем всех уровней и системы в целом,
как в автоматическом режиме, так и по инициативе обслуживающего персонала.
Вывод параметров должен производиться
автоматически на дисплеи и, по требованию, на печать.
Все оборудование вычислительных комплексов,
устанавливаемое на участках производства, должно быть промышленного исполнения
и отвечать требованиям условий работы на металлургическом производстве.
Оборудование должно работать надежно, ритмично и
безаварийно в течение всего годового фонда времени работы стана. Оно должно
быть рассчитано на проведение профилактики без нарушения функционирования
автоматизированной системы.
Работа нового оборудования должна быть
согласована с действующим оборудованием других систем автоматизации.
Связь между подстанциями и диспетчерским пунктом
должна осуществляться с использованием стандартных устройств и протоколов. В
качестве инструмента для создания систем сбора, обработки и представления
информации в графическом виде должны применяться инструментальные оболочки,
соответствующие стандартам МЭК с применением языка, используемого в
документообороте комбината.
Каких-либо особых требований к оборудованию,
устанавливаемому или уже установленному на подстанциях, не имеется, так как
данная система универсальна в отношении источников входных данных. Единственным
требованием, предъявляемым к приборам учета электроэнергии, является получение
данных в аналоговой или дискретной форме. Таким образом, сбор информации для
адаптивной системы может происходить любым из перечисленных далее способов:
с помощью специально предусмотренного
оборудования фирмы Allen-Bradley Power Monitor посредством программного
обеспечения RSEnergy;
с помощью современных микропроцессорных релейных
защит, способных не только защищать силовые цепи, но и измерять необходимые
параметры;
с помощью контроллера автоматически регулируемых
конденсаторных батарей (см. выбор оборудования);
с помощью специально устанавливаемых
измерительных контроллеров.
4.4 Выбор оборудование для адаптивной системы
4.4.1 Учет электроэнергии
Как уже говорилось ранее, адаптивная система
универсальна в отношении способа учета электроэнергии. Если на подстанции
имеется уже установленная, например, микропроцессорная защита, то установки
никакого дополнительного оборудования не требуется. Если же на подстанции нет
ничего, что может производить сбор информации в дискретном либо аналоговом
виде, то мной предлагается установка оборудования фирмы Allen-Bradley семейства
PowerMonitor и программного обеспечения RSEnergy.
4.4.1.1Устройство мониторинга PowerMonitor
PowerMonitor - автономное высокотехнологическое
устройство управления и мониторинга электроснабжения со встроенными функциями
мониторинга, анализа, архивирования и управления[14].
Функции данного устройства:
а) функция отображения:
напряжения по фазам;
токи по фазам;
коэффициент мощности cos  ;
;
коэффициент искажений;
активная, реактивная, полная мощность;
активная, реактивная энергия;
частота;
пиковое значение всех перечисленных параметров;
активная, реактивная энергия: потребленная и
сгенерированная;
коэффициент несимметрии;
последовательность чередования фаз;
б) функция архивирования:
регистрация событий во времени;
регистрация минимальных, максимальных значений;
более подробная регистрация отдельных событий;
счетчик активной и реактивной энергии:
потребляемой и генерируемой;
в) функция анализа:
спектральный анализ и осциллографирование;
коэффициент линейных искажений тока и
напряжения;
г) функция управления:
два управляемых однополюсных резервированных
контакта, конфигурируемых пользователем;
четыре конфигурируемых дискретных входа;
коммутационный интерфейс.
Программное обеспечение RSEnergy для контроля
электропотребления
Самым оптимальным соотношением цены и качества является
установка на каждую подстанцию программного обеспечения фирмы Rockwell
Automation RSEnergy [14]. С помощью RSEnergy можно получить все необходимые
данные по энергопотреблению на предприятии из любого места сети, в данном
случае из диспетчерского пункта. Можно контролировать все энергопотребление по
объединенной в сеть корпорации и управлять им (см. рис. 4.1). Для каждого
измеряемого параметра предоставляются как данные реального времени, так и
накопленные данные.
Имея прямой доступ к оборудованию Allen-Bradley
по контролю за электропитанием и PLC посредством RSLinx, можно:
измерять пиковую нагрузку;
рассчитывать затраты на электроэнергию;
определять режим нагрузок;
измерять качество энергии;
суммировать нагрузку по нескольким зданиям
предприятия или по всей стране.
Достоинства RSEnergy:
получение оперативной информации;
оперативный контроль в режиме реального времени;
разносторонний анализ полученных данных;
регистрирование событий.
4.4.2 Процессор для диспетчерского пункта
Модуль PLC представляет собой модуль
процессоров, которые обеспечивают проверенный подход для промышленного
управления. Процессоры PLC доступны в разном функциональном исполнении и могут
соединяться в различные сети при распределенных процессах и для обеспечения
удаленного расположения ввода-вывода.
Модульность ввода-вывода и коммуникационных
интерфейсов обеспечивает перестраиваемую и расширяемую систему. Изначально
конфигурируется система на число входов/выходов и сетевых связей, которое
необходимо. Если в последствии возникнет необходимость в расширении системы,
можно добавить модули ввода-вывода или коммуникационные интерфейсы.
Процессоры
PLC-5 доступны в диапазоне форсируемых входов-выходов от максимум 512 до
максимум 3072 и в диапазоне памяти пользователя от максимум 6K до максимум 100K
слов. Все процессоры - способны управлять удаленно расположенными модулями
ввода-вывода. Максимальное число удаленных от процессора модулей ввода-вывода
колеблется от 5 до 125. Процессор может контролировать/управлять этими модулями
ввода-вывода через сети ControlNet
<#"478342.files/image129.gif">
Рисунок
5.1 - Схема замещения линии 110-220 кВ
Активное,
реактивное сопротивления линии и емкостная проводимость соответственно
рассчитываются по формулам[9,13]:
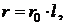 (5.1)
(5.1)
 (5.2)
(5.2)
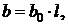 (5.3)
(5.3)
где
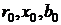 -
соответственно погонные параметры линий,
-
соответственно погонные параметры линий,
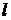 - длина
линии (кабеля).
- длина
линии (кабеля).
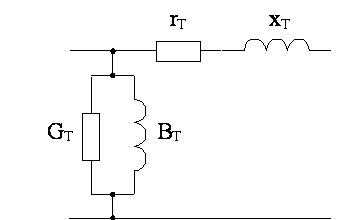
Рисунок
5.2 - Схема замещения двухобмоточного трансформатора
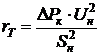 , (5.4)
, (5.4)
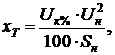 (5.5)
(5.5)
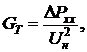 (5.6)
(5.6)
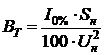 . (5.7)
. (5.7)
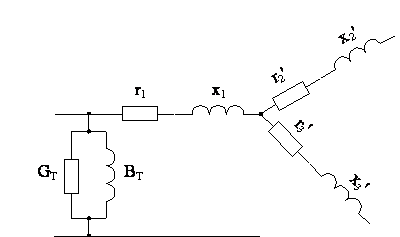
Рисунок
5.3 - Схема замещения трехобмоточного трансформатора
Расчет активных сопротивлений:

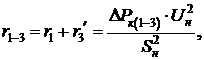
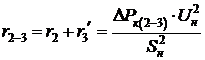 . (5.8)
. (5.8)
Отсюда
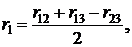

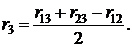 (5.9)
(5.9)
Расчет реактивных сопротивлений:
 (5.10)
(5.10)
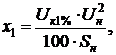

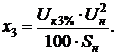 (5.11)
(5.11)
Опыт холостого хода проводится аналогично опыту
для двухобмоточного трансформатора, поэтому активные и реактивные проводимости
в трехобмоточном трансформаторе рассчитываются по тем же формулам (5.7) и
(5.8).
5.1.2 Расчет параметров схем замещения линий
Кабель АСБГ 4(3*240) длина 540 м: r=70.2 Ом.
АС-240 длина 604 м: r=78,52 Ом, x=241.6 Ом;
В=1721,4*10-6 См.
АС-400 длина 634 м: r =50,72 Ом, x=240,9 Ом;
В=1902*10-6 См.
АС-240 длина 686 м: r =89,18 Ом, x=274,4 Ом;
В=1955*10-6 См.
5.1.3 Расчет параметров схем замещения
трансформаторов
Таблица 5.1 - Номинальные параметры
трехобмоточного трансформатора п/ст Ильич
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
I
х.х, %
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
|
|
|
В-С
|
В-Н
|
С-Н
|
|
|
|
ТДТН-25000/110
|
115/38,5/6,6
|
0,7
|
10,5
|
17,5
|
6,5
|
140
|
31
|
Согласно формулам (5.9), (5.11) имеем:
rT=1,5 Ом,
х1=56,9 Ом,
х2=0,
х3=35,7 Ом.
Согласно (5.6)-(5.7):
GT=0.0023,
BT=0.013.
Таблица 5.2 - Номинальные параметры
двухобмоточного трансформатора п/ст Ильич
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
I
х.х, %
|
|
ТРДН-40000/110
|
115/6,3
|
10,5
|
172
|
36
|
0,65
|
Согласно формулам (5.4) - (5.7) имеем:
rT=1,42 Ом,
хТ=34,7 Ом,
GT=0.0027,
BT=0.02.
Таблица 5.3 - Номинальные параметры
двухобмоточного трансформатора Т1 п/ст 28, Т2 п/ст 37
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
I
х.х, %
|
|
ТДНГ-60000/110
|
115/6,3
|
10,5
|
250
|
50
|
0,6
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=0.92 Ом,
хТ=23 Ом,
GT=0.0038,
BT=0.0272.
Таблица 5.4 - Номинальные параметры
двухобмоточного трансформатора Т2 п/ст 28, Т1 и Т2 п/ст 20.
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
I
х.х, %
|
|
ТРДН-63000/110
|
115/6,3
|
10,5
|
260
|
59
|
0,6
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=0.87 Ом,
хТ=22 Ом,
GT=0.0045,
BT=0.0286.
Таблица 5.5 - Номинальные параметры
двухобмоточного трансформатора п/ст 32
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
I
х.х, %
|
|
ТДНГУ-40500/110
|
115/10,5
|
10,5
|
172
|
36
|
0,65
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=1,42 Ом,
хТ=34,7 Ом,
GT=0.0027,
BT=0.0197.
Таблица 5.6 - Номинальные параметры
двухобмоточного трансформатора Т1 п/ст 33
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
I
х.х, %
|
|
Ларкинсон-40500/110
|
115/10,5
|
10,5
|
172
|
36
|
0,65
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=1,42 Ом,
хТ=34,7 Ом,
GT=0.0027,
BT=0.0197.
Таблица 5.7 - Номинальные параметры
двухобмоточного трансформатора Т2 п/ст 33
|
ТрансформаторСреднее
номинальное напряжение, кВUкз, %Ркз, кВтРх.х, кВтI х.х, %
|
|
|
|
|
|
|
ТДНГ-31500/110
|
115/10,5
|
10,5
|
140
|
60
|
0,7
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=1,9 Ом,
хТ=44 Ом,
GT=0.0045,
BT=0.0167.
Таблица 5.8 - Номинальные параметры
трехобмоточного трансформатора п/ст 6, п/ст 42, Т1 - Т2 п/ст 41
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
I
х.х, %
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
|
|
|
В-С
|
В-Н
|
С-Н
|
|
|
|
ТДТН-40000/110
|
115/11/6,6
|
0,6
|
10,5
|
17
|
6
|
200
|
Согласно формулам (5.9), (5.11) имеем:
rT=0,8 Ом,
х1=35,5 Ом,
х2=0,
х3=22,3 Ом.
Согласно (5.6)-(5.7):
GT=0.0033,
BT=0.0181.
Таблица 5.9 - Номинальные параметры
двухобмоточного трансформатора Т1 п/ст 44
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
I
х.х, %
|
|
ТРДН-40000/110
|
115/6,6
|
10,5
|
172
|
36
|
0,65
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=1,42 Ом,
хТ=34,7 Ом,
GT=0.0027,
BT=0.0197.
Таблица 5.10 - Номинальные параметры
двухобмоточного трансформатора Т2 п/ст 44, п/ст 43
|
ТрансформаторСреднее
номинальное напряжение, кВUкз, %Ркз, кВтРх.х, кВтI х.х, %
|
|
|
|
|
|
|
ТРДН-32000/110
|
115/6,6
|
10,5
|
140
|
60
|
0,7
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=1,9 Ом, хТ=44 Ом,
GT=0.0045,BT=0.0167.
Таблица 5.11 - Номинальные параметры
двухобмоточного трансформатора Т1 п/ст 34, п/ст 46
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
I
х.х, %
|
|
ТДН-16000/110
|
115/6,6
|
10,5
|
85
|
19
|
0,7
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=4,38 Ом,
хТ=86,7 Ом,
GT=0.0014,
BT=0.0085.
Таблица 5.12 - Номинальные параметры
двухобмоточного трансформатора Т2 п/ст 34, п/ст 2
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
I
х.х, %
|
|
ТДНГ-31500/110
|
115/6,6
|
10,5
|
140
|
60
|
0,7
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=1,9 Ом,
хТ=44 Ом,
GT=0.0045,
BT=0.0167.
Таблица 5.13 - Номинальные параметры
двухобмоточного трансформатора п/ст 38
|
ТрансформаторСреднее
номинальное напряжение, кВUкз, %Ркз, кВтРх.х, кВтI х.х, %
|
|
|
|
|
|
|
ТДНГ-40500/110
|
115/6,6
|
10,5
|
172
|
36
|
0,65
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=1,42 Ом,
хТ=34,7 Ом,
GT=0.0027,
BT=0.0197.
Таблица 5.14 - Номинальные параметры
двухобмоточного трансформатора Т1 п/ст 37
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
I
х.х, %
|
|
ТДНГУ-40500/110
|
115/6,6
|
10,5
|
172
|
36
|
0,65
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=1,42 Ом,
хТ=34,7 Ом,
GT=0.0027,
BT=0.0197.
Таблица 5.15 - Номинальные параметры двухобмоточного
трансформатора п/ст 40
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
I
х.х, %
|
|
ТДН-31500/110
|
115/6,6
|
10,5
|
140
|
60
|
0,7
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=1,9 Ом,
хТ=44 Ом,
GT=0.0045,
BT=0.0167.
Таблица 5.16 - Номинальные параметры
двухобмоточного трансформатора п/ст 31: ТДНГ-40500/110/10
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
I
х.х, %
|
|
ТДНГУ-40500/110
|
115/11
|
10,5
|
172
|
36
|
0,65
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=1,42 Ом,
хТ=34,7 Ом,
GT=0.0027,
BT=0.0197.
Таблица 5.17 - Номинальные параметры
двухобмоточного трансформатора Т3, Т4 п/ст 41
|
Трансформатор
|
Среднее
номинальное напряжение, кВ
|
Uкз,
%
|
Ркз,
кВт
|
Рх.х,
кВт
|
I
х.х, %
|
|
ТРДЦН-63000/110
|
115/10
|
10,5
|
260
|
59
|
0,6
|
Подставив номинальные параметры в (5.4) - (5.7)
получим:
rT=0,87 Ом,
хТ=22 Ом,
GT=0.0045,
BT=0.0286.
5.2 Расчет сети при различных нагрузках
На
первом этапе (см. рис. 3.1) с помощью разработанного программного обеспечения
были рассчитаны неоптимальные режимы работы сети ОАО "ММК им. Ильича"
с компенсацией реактивной мощности при коэффициенте реактивной мощности 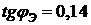 . При
номинальных нагрузках потери активной мощности составили
. При
номинальных нагрузках потери активной мощности составили 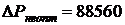 кВт. При
максимальных нагрузках -
кВт. При
максимальных нагрузках - 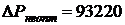 кВт.
кВт.
Таблица
5.18 - Оптимальный режим сети при номинальных нагрузках
|
№
п/ст
|
Приведенные
напряжения к ступени 110 кВ
|
Генерируемые
мощности
|
|
|
активная,
кВА
|
реактивная,
кВА
|
|
28
|
114,2
|
-
|
42351
|
|
2
|
113,8
|
-
|
38136
|
|
6
|
114,5
|
-
|
14233
|
|
32
|
113,7
|
-
|
9541
|
|
38
|
113,9
|
-
|
14919
|
|
46
|
114,1
|
-
|
5351
|
|
37
|
114,3
|
-
|
3780
|
|
40
|
113,8
|
-
|
10280
|
|
44
|
114,2
|
-
|
25306
|
|
34
|
114,5
|
-
|
15570
|
|
33
|
114,6
|
-
|
24905
|
|
20
|
113,8
|
-
|
45693
|
|
31
|
114,2
|
-
|
13560
|
|
43
|
114,1
|
-
|
10751
|
|
42
|
114,3
|
-
|
13341
|
|
41
|
114,2
|
-
|
65340
|
|
ТЭЦ-1
|
114,8
|
15210
|
6800
|
|
ТЭЦ-2
|
115,1
|
32155
|
12751
|
Проведя
расчет оптимального режима сети ОАО "ММК им. Ильича" при номинальных
нагрузках, было получено минимальное значение потерь активной мощности в сети ΔРопт=84500
кВт. Эффект разработанного программного обеспечения оценивается по снижению
потерь активной мощности на величину  кВт.
кВт.
Таблица
5.19 - Оптимальный режим сети при максимальных нагрузках
|
№
п/ст
|
Приведенные
напряжения к ступени 110 кВ
|
Генерируемые
мощности
|
|
|
активная,
кВА
|
реактивная,
кВА
|
|
28
|
113,8
|
-
|
46283
|
|
2
|
113,3
|
-
|
40563
|
|
6
|
114,1
|
-
|
15621
|
|
32
|
113,1
|
-
|
10159
|
|
38
|
113,2
|
-
|
16105
|
|
46
|
113,8
|
-
|
6258
|
|
37
|
113,9
|
-
|
4106
|
|
40
|
113,5
|
-
|
12223
|
|
44
|
113,9
|
-
|
28412
|
|
34
|
114,0
|
-
|
16933
|
|
33
|
114,1
|
-
|
26122
|
|
20
|
113,4
|
-
|
47731
|
|
31
|
113,8
|
-
|
15303
|
|
43
|
113,7
|
-
|
116697
|
|
42
|
113,9
|
-
|
15105
|
|
41
|
113,9
|
-
|
68251
|
|
ТЭЦ-1
|
114,7
|
16250
|
7200
|
|
ТЭЦ-2
|
115,0
|
34120
|
14105
|
Проведя
расчет оптимального режима сети ОАО "ММК им. Ильича" при максимальных
нагрузках, было получено минимальное значение потерь активной мощности в сети ΔРопт=89320
кВт. Эффект разработанного программного обеспечения оценивается по снижению
потерь активной мощности на величину 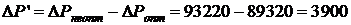 кВт.
кВт.
Выводы
Разработанное
программное обеспечение позволяет решить комплекс проблем, связанных с
оптимальным распределением реактивной мощности по сети.
Разработанная
адаптивная система управления позволяет осуществлять постоянный контроль над
нагрузками подстанций и конфигурацией сети, оперативно реагировать на
какие-либо изменения и производить точный расчет для нового режима.
Внедрение
представленного комплекса, состоящего из программного обеспечения и адаптивной
системы управления, на любое предприятие с любой сложно замкнутой сетью, в данном
случае, на ОАО "ММК им. Ильича" позволяют:
значительно
уменьшить потери энергии;
поддерживать
постоянный уровень напряжения у приемного конца сети;
значительно
уменьшить денежные затраты на потребление и генерацию реактивной мощности.
Минимум
аппаратного обеспечения, необходимого для информационного режима работы
адаптивной системы управления, и совместимость системы с любым оборудованием,
уже установленного на подстанциях, позволяет сделать вывод о целесообразности
применения разработанного программного обеспечения на ОАО "ММК им.
Ильича" и других крупных промышленных предприятий.
Перечень
ссылок
1. В.Н. Костин.:
Оптимизационные задачи электроэнергетики: Учеб. пособие. - СПб.: СЗТУ, 2003 -
120с.
2. В.Г. Карманов.
Математическое программирование. - М.: Наука, 1980 - 256с.
3. Дж. Деннис, Р. Шнабель.
Численные методы безусловной оптимизации и решения нелинейных уравнений. - М.:
Мир, 1988 - 440с.
4. З.Н. Бененсон, М.Р.
Елистратов, Л.К. Ильин и др. Моделирование и оптимизация на ЭВМ
радиоэлектронных устройств. - М.: Радиосвязь, 1981 - 272с.
5. С. Гилл, У. Мюррей.
Численные методы условной оптимизации. - М.: Мир, 1977 - 339с.
6. Васильев С.П. Численные
методы решения экстремальных задач. - М.: Наука, 1980 - 518с.
7. И.Т. Черноруцкий. Методы
оптимизации в теории управления, С.-П.: Питер, 2004 - 226с.
8. В.Е. Болконин, П.И. Чинаев.
Анализ и синтез систем автоматического управления на ЭВМ. Алгоритмы и
программы. - М.: Радио и связь, 1986 - 248с.
9. В.Н. Костин, Е.В. Распопов,
Е.А. Родченко. Передача и распределение электроэнергии: Учеб. пособие. - СПб.:
СЗТУ, 2003 - 147с.
10. Барзам А.Б. Системная
автоматика. - М.: Энергоатомиздат, 1989. - 446с.
11. Баркан Я.Д., Орехов Л.А.
Автоматизация энергосистем: учебное пособие для студентов вузов. - М.: Высш.
школа, 1981. - 271с.
12. А. А. Черносвитов. Курс MCSD
Visual C++ 6.0 и MFC, С.-П.: Питер, 2000 - 554с.
13. Веников В.А. Управление
переходными режимами в электрических системах. - М.: Высшая школа, - 1972. -
352с.
Приложение А
Программа расчета оптимальных режимов
#include <stdio.h>
#include <complex.h>
#include <iostream.h>
#include <conio.h>
#include <math.h>
int luc ( int, complex [][31], int
[], double );
void rluc ( int, complex [][31], int
[], complex [] );
void gauss ( int n, complex [][31],
complex [], complex * );
void start ( int, int, int, complex
[][31], complex [],
complex [], int [], int [], int [],
int );
void vard ( int, int, int, complex
[][31], complex [],
complex [], int [], int [], int []
);
void varm ( int, int, int, complex
[][31], complex [],
complex [], int [], int [], int []
);
void prejc ( int, int, int, complex
[], complex [] );
void rasis ( int, int, complex [], complex
[], complex [], int [], int [] );
void pryzc ( int, complex [], int
[], int [], int );
void foryzc ( int, int, complex
[][31], complex [], int [], int [] );
double w;
void main ( void )
{
complex a[30][31], b[30], yz[90],
tok[90], s;
int imax[90], imin[90], irow[30];
int n, nyz, nej, istop, i, j;
double f;
do
{
clrscr ( );
scanf ( "%i4 %i4 %i4 %i4",
&f, &n, &nyz, &nej, &istop );
w = 2 * M_PI * f;
start ( n, nyz, nej, a, b, yz, imax,
imin, irow, 0 );
for ( i = 0; i < nyz; i++ )
{
yz[i] = 1.0 / yz[i];
cout << yz[i];
if ( ! ( i % 4 ) ) cout <<
'\n';
}
for ( i = 0; i < nyz; i++ )
cin >> imax[i] >>
imin[i];
cin >> n;
vard ( n, nyz, nej, a, b, yz, imax,
imin, irow );
rasis ( n, nyz, b, yz, tok, imax,
imin );
}
while ( istop );
//for ( i = 0; i < n; i++ )
//for ( j = 0; j <= n; j++ )
//cin >> a[i][j];
//for ( i = 0; i < n; i++ )
//b[i] = a[i][n];
//for ( i = 0; i < n; i++ )
//{
//for ( j = 0; j <= n; j++ )
//cout << a[i][j];
//cout << '\n';
//}
//for ( i = 0; i < n; i++ )
//cout << b[i];
//luc ( n, a, irow, 0.00001 );
//rluc ( n, a, irow, b );
//cout << '\n';
//gauss ( n, a, b, &s );
//for ( i = 0; i < n; i++ )
//cout << b[i];
}
int luc ( int n, complex a[][31],
int irow[], double eps )
{
int i, i1, j, k, l, n1;
complex prom;
for ( i = 0; i < n; i++ )
irow[i] = i;
n1 = n - 1;
for ( i = 0; i < n1; i++ )
{
i1 = i + 1;
l = i;
for ( k = i1; k < n; k++ )
if ( abs ( a[k][i] ) > abs (
a[l][i] ) ) l = k;
if ( abs ( a[l][i] ) < eps )
return 0;
if ( l > i )
{
for ( j = 0; j < n; j++ )
{
prom = a[i][j];
a[i][j] = a[l][j];
a[l][j] = prom;
}
irow[i] = l;
}
for ( j = i1; j < n; j++ )
a[i][j] = a[i][j] / a[i][i];
for ( k = i1; k < n; k++ )
for ( j = i1; j < n; j++ )
a[k][j] -= a[k][i] * a[i][j];
}
return 1;
}
void rluc ( int n, complex a[][31],
int irow[], complex b[] )
{
int i, j;
complex sum;
for ( i = 0; i < n; i++ )
if ( i != irow[i] )
{
sum = b[i];
b[i] = b[irow[i]];
b[irow[i]] = sum;
}
for ( i = 0; i < n; i++ )
{
sum = b[i];
for ( j = 0; j < i; j++ )
sum -= a[i][j] * b[j];
b[i] = sum / a[i][i];
}
for ( i = n - 2; i >= 0; i-- )
{
sum = b[i];
for ( j = i+1; j < n; j++ )
sum -= a[i][j] * b[j];
b[i] = sum;
}
}
void gauss ( int n, complex a[][31],
complex x[], complex *s )
{
int i, j, k, l, k1, n1;
complex r;
n1 = n + 1;
for ( k = 0; k < n; k++ )
{
k1 = k + 1;
*s = a[k][k];
j = k;
for ( i = k1; i < n; i++ )
{
r = a[i][k];
if ( abs ( r ) > abs ( *s ) )
{
*s = r;
j = i;
}
}
if ( *s == complex ( 0.0, 0.0 ) )
break;
if ( j != k )
for ( i = k; i < n1; i++ )
{
r = a[k][i];
a[k][i] = a[j][i];
a[j][i] = r;
}
for ( j = k1; j < n1; j++ )
a[k][j] /= *s;
for ( i = k1; i < n; i++ )
{
r = a[i][k];
for ( j = k1; j < n1; j++ )
a[i][j] -= a[k][j] * r;
}
}
if ( *s != complex ( 0.0, 0.0 ) )
for ( i = n - 1; i >= 0; i-- )
{
*s = a[i][n];
for ( j = i + 1; j < n; j++ )
*s -= a[i][j] * x[j];
x[i] = *s;
}
return;
}
void start ( int n, int nyz, int
nej, complex a[][31], complex b[],
complex yz[], int imax[], int
imin[], int irow[], int iy )
{
int i;
pryzc ( nyz, yz, imax, imin, iy );
for ( i = 0; i < nyz; i++ )
{
cout << yz[i];
if ( ! ( i % 4 ) ) cout <<
'\n';
}
vard ( n, nyz, nej, a, b, yz, imax,
imin, irow );
}
void vard ( int n, int nyz, int nej,
complex a[][31], complex b[],
complex yz[], int imax[], int
imin[], int irow[] )
{
int i, j;
foryzc ( n, nyz, a, yz, imax, imin
);
//for ( i = 0; i < n; i++ )
//{
//for ( j = 0; j < n; j++ )
//cout << a[i][j];
//cout << '\n';
//}
if ( luc ( n, a, irow, 1.0e-5 ) )
varm ( n, nyz, nej, a, b, yz, imax,
imin, irow );
else
printf ( "\nв®з®Ґ
аҐиҐЁҐ
Ґ
ў®§¬®¦®"
);
return;
}
void varm ( int n, int nyz, int nej,
complex a[][31], complex b[],
complex yz[], int imax[], int
imin[], int irow[] )
{
int i;
prejc ( n, nej, nyz, b, yz );
for ( i = 0; i < n; i++ )
{
cout << b[i];
if ( ! ( i % 4 ) ) cout <<
'\n';
}
rluc ( n, a, irow, b );
for ( i = 0; i < n; i++ )
{
cout << b[i];
if ( ! ( i % 4 ) ) cout <<
'\n';
}
return;
}
void pryzc ( int nyz, complex yz[],
int imax[], int imin[], int iy )
{
int i, indrlc;
complex rlc;
for ( i = 0; i < nyz; i++ )
{
cin >> rlc >> indrlc
>> imax[i] >> imin[i];
yz[i] = rlc;
if ( indrlc == 2 )
yz[i] = complex ( 0.0, -1000000 / (
w * imag ( rlc ) ) );
if ( indrlc == 1 )
yz[i] = complex ( 0.0, w * imag (
rlc ) * 0.001 );
if ( indrlc == 3 ) yz[i] = polar (
real ( rlc ), imag ( rlc ) );
cout << "YZ["
<< i+1 << "]= " << yz[i];
}
}
void foryzc ( int n, int nyz,
complex a[][31], complex yz[],
int imax[], int imin[] )
{
int i, j, k, kolstr;
for ( i = 0; i < n; i++ )
{
for ( j = 0; j < n; j++ )
a[i][j] = complex ( 0.0, 0.0 );
//cout << '\n';
}
for ( k = 0; k < nyz; k++ )
{
i = imax[k];
j = imin[k];
a[i-1][i-1] += yz[k];
if ( j )
{
a[j-1][j-1] += yz[k];
a[i-1][j-1] -= yz[k];
a[j-1][i-1] = a[i-1][j-1];
}
}
clrscr();
cout << "YZ[i][j]=";
kolstr = 0;
for ( i = 0; i < n; i++ )
{
for ( j = 0; j < n; j++ )
{
cout << "\nYZ["
<< i+1 << "][" << j+1 << "]= "
<< a[i][j];
kolstr++;
if ( kolstr == 22 )
{
kolstr = 0;
getchar ( );
clrscr();
cout << "YZ[i][j]=";
}
}
}
return;
}
void prejc ( int n, int nej, int
nyz, complex b[], complex yz[] )
{
int i, ind1, ind2, imin, imax, iyz;
complex ej;
for ( i = 0; i < n; i++ )
b[i] = complex ( 0.0, 0.0 );
for ( i = 0; i < nej; i++ )
{
cin >> ej >> iyz
>> imax >> imin >> ind1 >> ind2;
if ( ind1 )
ej = polar ( real ( ej ), imag ( ej
) );
if ( ind2 ) ej *= yz[iyz-1];
cout << "ei= "
<< ej;
b[imax-1] += ej;
if ( imin ) b[imin-1] -= ej;
}
return;
}
void rasis ( int n, int nyz, complex
b[], complex yz[],
complex tok[], int imax[], int
imin[] )
{
int i, j, k;
for ( k = 0; k < nyz; k++ )
{
i = imax[k];
j = imin[k];
if ( j )
tok[k] = ( b[i-1] - b[j-1] ) *
yz[k];
else
tok[k] = b[i-1] * yz[k];
}
for ( k = 0; k < nyz; k++ )
cout << "I["<<
k+1 << "]=" << tok[k];
return;
}
Приложение Б
Структурная схема системы управления