Практическое применение методов прогноза валютных курсов

Контрольная работа

Тема:

Практическое применение методов прогноза валютных курсов

Содержание

1. Выбор факторов

. Визуализация данных

. Описание эксперимента

. Результаты эксперимента

. Гибридный метод

Список литературы

1. Выбор факторов

Обозначим P(t) - значение курса USD/RUB в момент времени t. Пусть Δ(t) обозначает относительное изменение курса за 1 день в процентах:

.

Нетрудно понять, что  может принимать как положительные, так и отрицательные значения (в случае, когда курс вырос и упал соответственно). В качестве предсказываемой величины Y(t) (или, иначе, отклика) будем рассмотреть

При прогнозировании валютных курсов многие исследователи сталкивались с проблемой низкой точности предсказаний. Однако низкая точность наблюдалась лишь в работах, где исследователи пытались предсказать вырастет курс или упадет или в работах, где ученые прогнозировали точный курс. В тех же работах, где исследовались кризисные явления (что курс упадет более чем на какую-то величину, например, 2.5%), точность прогнозирования была довольна высока. Однако при прогнозировании экстремумов зачастую есть шанс столкнуться с нехваткой данных для обучения: экстремумы сами по себе достаточно редко возникают в выборке. Для решения данной проблемы мы будем прогнозировать помимо снижения или роста курса на следующий день рост курса не менее чем на 1% или падения более чем на 1%. В нашей выборке из полутора тысяч значений таких скачков свыше трехсот - это достаточно для обучения модели. Вместе с тем это изменение достаточно, чтобы отличаться от ежедневных колебаний курса. Однако в выборке из трехсот значений таких колебаний свыше 150, что, скорее всего, сделает обучение по отрезку времени после перехода на систему свободно плавающего рубля менее эффективным, чем, если мы будем обучать по всей выборке с 2010 года.

В экономической теории для прогнозирования дневных колебаний валютных курсов обычно используются изменения цен основных экспортных товаров и процентных ставок..Согласно Федеральной таможенной службе Российской Федерации основные экспортные товары:

Таблица 1

Основные статьи экспорта Российской Федерации

Среди данных товаров выберем те, биржевые котировки которых мы можем получить. Так, например, для учета изменения цены нефти и нефтепродуктов (включая бензин и дизель) мы будем использовать колебания котировки нефти Brent. Также мы будем использовать котировки газа, алюминия, меди. Стоит учитывать, что по таким продуктам, как автомобили или смешанные удобрения биржевые котировки найти невозможно в силу разнородности товара. Также мы не будем учитывать цену стали в силу того, что сейчас продукция черной металлургии при внешней торговле продается по фьючерсам волатильность которых крайне низка и поэтому не может оказывать влияние на дневные изменения курса валюты. Например, последнее изменение котировки стали на Лондонской бирже произошло второго марта 2016 года - более месяца назад.

Также из экономической теории следует то, что необходимо учитывать процентные ставки по рассматриваемым валютам. С целью охарактеризовать российский рынок была взята индикативная взвешенная ставка рублевых кредитов овернайт RUONIA. Эта ставка, по которым крупнейшие российские банки предоставляют друг другу ликвидность без обеспечения ценными бумагами. Также немаловажно учесть интенсивность работы российского межбанковского рынка, для чего были взяты данные по объему контрактов по RUONIA. Для характеристики процентных ставок по доллару США были взяты изменения в стоимости десятилетних казначейских облигаций (US Treasuries). Также для того, чтобы учесть обесценивание (удорожание) доллара США были взяты данные по колебанию цены золота.

Межбанковская ставка RUONIA рассчитывается с начала 2010 года, поэтому это самый ранний срок, с которого мы будем рассматривать наши факторы. Однако в конце 2014 года в связи переходом на плавающий валютный курс и последовавшим за этим валютным кризисом коренным образом изменилась дневная волатильность рубля. Поэтому помимо основных данных с начала 2010 года (большой выборки) мы будем рассматривать дополнительно выборку с января 2015 года (малую).

. Визуализация данных

Для начала рассмотрим, как меняются значения извлеченных данных на выбранных промежутках времени, и попробуем извлечь какую-нибудь полезную информацию из этих графиков.

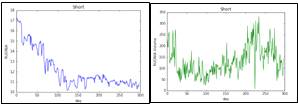
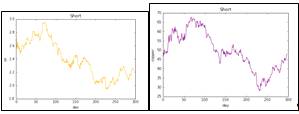
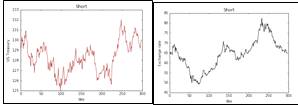
Рис. 1: Графики факторов с января 2015 года по 30 апреля 2016 года: RUONIA, объем сделок по RUONIA, цена алюминия, газа, нефти Brent, меди, 10-летних облигаций федерального займа США, обменного курса USD/RUB

На графике, отображающем динамику факторов за период с января 2015 года мы видим нисходящий тренд по процентной ставке российского межбанковского рынка вызванный постепенным понижением ключевой ставки Центральным Банком после валютного кризиса. Цены на остальные факторы, так же как и объем сделок по RUONIA, крайне волатильны, что вызвано первоначальным обрушением после поднятия ключевой ставки Федеральным Резервом США и восстановлением в начале года. Однако в итоге цены находятся почти на том же уровне (немного меньшем), что и в январе 2015 года.

Рис 2: Графики факторов с января 2010 года по 30 апреля 2016 года: RUONIA, объем сделок по RUONIA, цена алюминия, газа, нефти Brent, меди, 10-летних облигаций федерального займа США, обменного курса USD/RUB

Как мы видим из графиков, ставка межбанковского рынка RUONIA постепенно возрастала после 2010 года, однако резкий её скачок пришелся на поднятие Центральным Банком ключевой ставки с 11 до 17% как меры борьбы с валютным кризисом конца 2014 года. Что интересно, объем сделок по RUONIA после наступления валютного кризиса также увеличился, хотя в целом из-за увеличения денежной массы объем рублевых кредитных операций имел тренд на повышение.

Цены на нефть, также как и цены на остальное сырье включая алюминий, медь и газ в течение выбранного времени имели ярко выраженный тренд на понижение вследствие удорожания доллара и замедления мирового экономического роста. Одна из причин к этому - повышение ключевой ставки Федеральным резервом США (около 1200-ого значения), что привело к обвалу нефтяных и медных котировок, цен на алюминий, газ и валюты развивающихся стран.

Напомним, что в рассматриваемой задаче нас, прежде всего, интересует, зависимость относительных приращений курса от RUONIA и приращений остальных факторов. Попробуем понять “на глаз” есть ли хоть какая-то корреляция между этими величинами. Например, линейную зависимость можно было бы распознать по вытянутости данных вдоль какой-нибудь прямой. Более того, по протяженности достаточно легко понять, положительная или отрицательная корреляция между фактором и откликом: если коэффициент наклона прямой, вдоль которой распределились данные, положителен, то и корреляция должна быть положительна.

Изобразим графики вида фактор-отклик, где на i-й график будут наноситься все точки вида (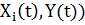 при разных t. Получим облака точек и изобразим их каждое на своем графике (см. Рис. 3).

Рис. 3. Графики зависимостей отклика от факторов

Построим оценки коэффициентов корреляций и убедимся, что их значения соответствуют тому, что сказано выше:

В рассматриваемой нами задаче присутствует 7 факторов, это значит, что соответствующие элементы выборки будут являться точками в семимерном пространстве. Напомним, что мы хотим решать задачу классификации, это значит, что нам надо разбить значения отклика на 2 группы, соответствующие первому и второму классу. Разбиения мы будет делать одним из четырех способов:

•Присвоить всем значениям, большим нуля, один класс, остальным - другой;

•Присвоить всем значениям, большим единицы, один класс, остальным - другой;

•Присвоить всем значениям, меньшим минус единицы, один класс, остальным - другой;

•Присвоить всем значениям, по модулю большим единицы, один класс, остальным - другой;

Каждая точка (элемент выборки - семимерный вектор, состоящий из значений факторов), в зависимости от разбиения на классы, присваивается цвет - в нашем случае красный или синий. Задача заключается в построении поверхности, наилучшим образом отделяющей красные точки от синих. Так как изобразить график в семимерном пространстве не представляется возможным, приведем лишь его проекции на двумерные плоскости.

Чтобы получить эти проекции, нужно рассмотреть все возможные пары факторов  и взять у каждого элемента выборки 2 из 7 координат с номерами i и j. В результате получаем пары () где  Каждому значению t соответствует свой цвет (красный или синий) в зависимости от класса, в который попало значение соответствующего . Красим () в цвет, соответствующий t и изображаем полученные облака точек на графике.

Для наглядности изобразим точки на графиках 2 оттенками каждого цвета. Ярко-синие точки будут соответствовать тем  у которых соответствующие . Бледно-синими будут те элементы выборки, для которых выполнено  Бледно-красные будут значения, соответствующие , и, наконец, красный цвет будет отвечать тем t, у которых отклик  Тогда каждому из четырех способов разбиения точек на 2 класса будут соответствовать свои комбинации цветов:

·  первое разбиение присваивает первому классу все красные точки (яркие и бледные);

·        второе разбиение присваивает первому классу только ярко красные точки, а второму - все точки синего или любого бледного оттенка;

·        третье разбиение присваивает первому классу все точки ярко синего цвета, остальные - второму классу;

·        четвертое разбиение делит точки на группы яркого и бледного оттенков.

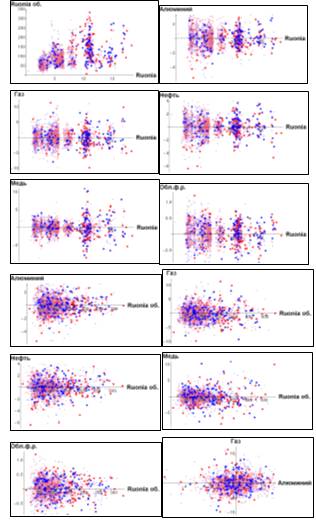
Рис. 4. Проекции конфигурационного пространства и разбиение выборки на классы

Из графиков видно, что данные достаточно сильно “перемешаны”, это означает, что, оптимальная разделяющая поверхность не может быть линейной (в противном случае на одной из проекций была бы видна линейная отделимость классов). Кроме того, по этим данным можно понять, какие из факторов между собой взаимодействуют: например, видно, что нефть и медь положительно коррелируют.

3. Описание эксперимента

Для проведения эксперимента воспользуемся пакетом Wolfram Mathematica для обработки и визуализации данных, а также библиотекой sklern языка python для обучения и сравнения моделей.

Первая часть обработки данных включает в себя построение выборки: основная проблема заключается в том, что для разных факторов могут быть даны данные по разным дням. Для двух рассматриваемых промежутков времени выкидываем все дни, для которых нет значения хотя бы одного из факторов. Таким образом, мы получаем 2 релевантные выборки длиной 297 и 1346 соответственно. Далее для каждого из временных интервалов мы рассматриваем 4 возможных разбиения откликов на классы. В итоге мы получаем 8 различных выборок: четыре длиной 297 и столько же длиной 1346.

Приступим к машинному обучению и начнем с классификации. Мы рассматриваем следующие алгоритмы: SVM, KNN, Binary Model и Decision Tree. Для каждого из рассматриваемых алгоритмов мы будем перебирать различные параметры, и оценивать точность построенной модели. Оценка точности производится двумя способами:

·  с помощью кросс-валидации K-fold. Как было отмечено выше, для короткой выборки, в качестве K стоит брать большее значение, чем для длинной выборки. Поэтому для выборки из 297 значений используем К, равное 60. Для выборки из 1346 значений количество частей, на которые она делится при кросс-валидации, будет равно 10.

·        с помощью кросс-валидации Hold-Out. Для обеих выборок обучение происходит на первых 80% выборки, а оценка точности - на оставшихся 20%.

Для каждой модели мы строим графики, отражающие изменение точности модели при изменении рассматриваемых параметров. Таким образом, мы оцениваем максимальную точность метода и определяем, на каких параметрах может быть достигнута данная точность.

Следующим анализируемым алгоритмом является регрессия. Мы хотим научиться прогнозировать уже не одно из четырех событий (положительное изменение, изменение более чем на 1, менее чем на -1 и изменение по модулю больше чем на 1), а значение относительного изменения курса. Для данного подхода мы будем обучать регуляризованную версию регрессии, и оценивать качество прогноза с помощью  метрики.

Результатом эксперимента является определение наиболее точного алгоритма прогнозирования и использования его для гибридного метода, описываемого далее.

. Результаты эксперимента

Первым тестируемым методом является метод ближайших соседей. Основным параметром метода является количество соседей. Дополнительным параметром является также нормировка данных с помощью метода вычитания математического ожидания и деления на среднеквадратическое отклонение.

Для каждой из 8 рассматриваемых выборок построим следующие графики: для кросс-валидации построим график зависимости точности метода (ось ординат), посчитанной с помощью K-fold, от количества соседей (ось абсцисс).

Количество соседей пробегает значение от 2 до 50. На графике отображаются два различных подхода: c нормировкой данных (Scaled) и без нее (Not scaled). Кроме того, для каждого из подходов найдем максимальное достигаемое значение качества прогноза (горизонтальная пунктирная линия).

Далее для каждого k (параметр, отвечающий количеству соседей) вычислим 95% доверительный интервал (пунктирные ломаные) и нанесем его так же на график.

Результаты приведены на рисунках 15-22.

Рис. 5. Точность метода KNN при прогнозировании роста/падения курса, модель обучена на короткой выборке. Оптимальными параметрами являются: отсутствие нормировки, 4 соседа. Максимальная точность: 59,5%

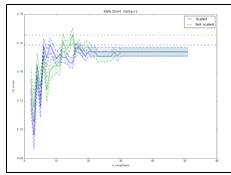
Рис. 6. Точность метода KNN при прогнозировании роста курса свыше 1% за день, модель обучена на короткой выборке. Оптимальными параметрами являются: отсутствие нормировки, 18 соседей. Максимальная точность: 76,7%

экспортный процентный валютный прогнозирование

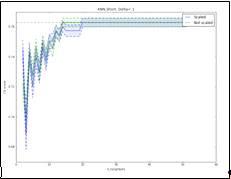
Рис. 7. Точность метода KNN при прогнозировании падение курса более чем на -1% за день, модель обучена на короткой выборке. Оптимальными параметрами являются: отсутствие нормировки, 16 соседей. Максимальная точность: 76,2%

Рис. 8. Точность метода KNN при прогнозировании роста или падения курса свыше 1% за день, модель обучена на короткой выборке. Оптимальными параметрами являются: отсутствие нормировки, 48 соседей. Максимальная точность: 57,5%

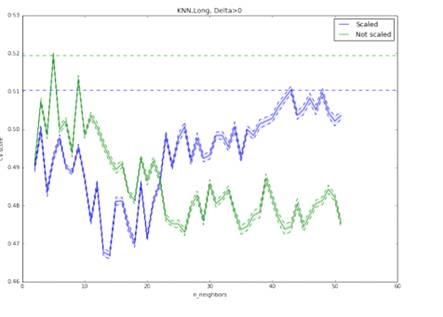
Рис. 9. Результативность метода KNN при прогнозировании роста/падения курса, модель обучена на полной выборке. Оптимальными параметрами являются: отсутствие нормировки, 6 соседей. Максимальная точность: 51,97%

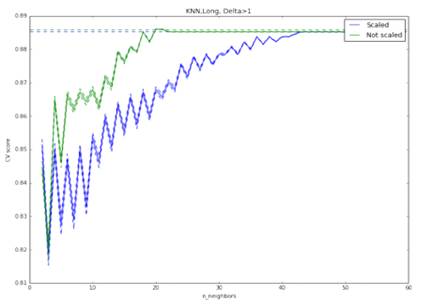
Рис. 10. Результативность метода KNN при прогнозировании роста курса более 1% за день, модель обучена на полной выборке. Оптимальными параметрами являются: отсутствие нормировки, 23 соседа. Максимальная точность: 88,6%

Рис 11. Точность метода KNN при прогнозировании падения курса свыше -1% за день, модель обучена на полной выборке. Оптимальными параметрами являются: отсутствие нормировки, 23 соседа. Максимальная точность: 90,4%

Рис. 12. Результативность метода KNN при прогнозировании роста/падения курса более чем на 1% за день, модель обучена на полной выборке. Оптимальными параметрами являются: нормировка, 48 соседей. Максимальная точность: 77,5%

Из графиков видно, что лучше всего метод работает на полной выборке, при предсказании роста на 1% и падения на -1%. С остальными двумя разбиениями метод справляется чуть хуже. Самые большие проблемы возникают при предсказании роста/падения курса. Стоит также заметить, что доверительные интервалы при предсказании по полной выборке получились достаточно узкими, что позволяет нам говорить о точность оценки качества.

Следующей группой графиков (Рис. 13-20) являются графики, аналогичные тем, что построены выше, но в данном случае проверка точности производится с помощью метода Hold-Out. В этом случае невозможно построить доверительный интервал, поэтому график немного отличается. Мы решили отдельно проверить точность таким методом, потому что кросс-валидация усредняет точность, как бы, перемешивая данные и не учитывая порядок следования событий друг за другом. Проверка Hold-Out позволяет проверить, насколько хорошо метод предсказывает новые данные (последние 20%) по старым (80%).

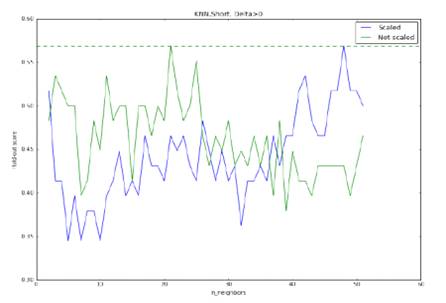
Рис. 13. Точность метода KNN при прогнозировании роста/падения курса, модель обучена на короткой выборке. Оптимальными параметрами являются: отсутствие нормировки, 24 соседа. Максимальная точность: 57,3%

Рис. 14. Точность метода KNN при прогнозировании роста курса свыше 1%, модель обучена на короткой выборке. Оптимальными параметрами являются: отсутствие нормировки, 4 соседа. Максимальная точность: 76%

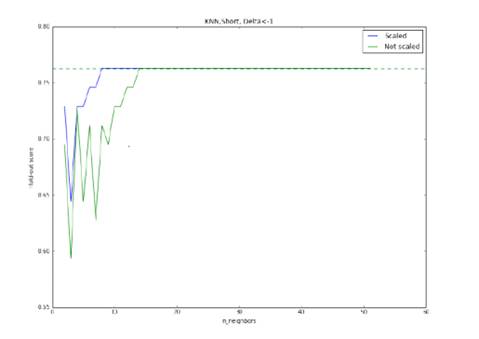
Рис 15. Точность метода KNN при прогнозировании падения курса более чем на -1%, модель обучена на короткой выборке. Оптимальными параметрами являются: нормировка, 8 соседей. Максимальная точность: 76,5%

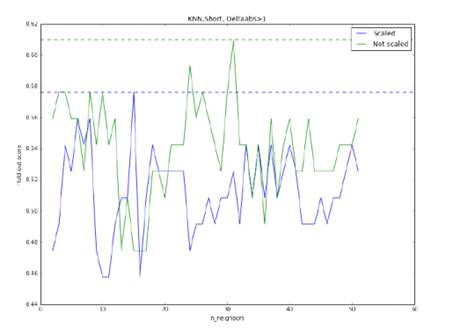
Рис 16. Точность метода KNN при прогнозировании роста или падения курса свыше 1%, модель обучена на короткой выборке. Оптимальными параметрами являются: отсутствие нормировки, 32 соседа. Максимальная точность: 61%

Рис 17. Точность метода KNN при прогнозировании роста/падения курса, модель обучена на полной выборке. Оптимальными параметрами являются: нормировка, 22 соседа. Максимальная точность: 56,5%

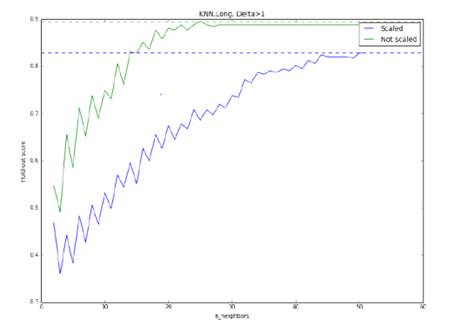
Рис 18. Точность метода KNN при прогнозировании роста курса свыше 1%, модель обучена на полной выборке. Оптимальными параметрами являются: отсутствие нормировки, 32 соседа. Максимальная точность: 90%

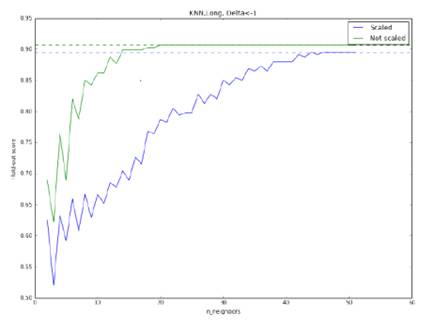
Рис 19. Точность метода KNN при прогнозировании падения курса более чем на -1%, модель обучена на полной выборке. Оптимальными параметрами являются: отсутствие нормировки, 21 сосед. Максимальная точность: 91%

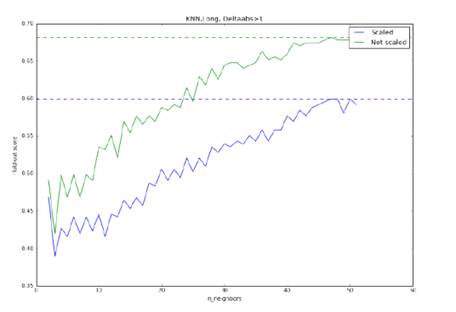
Рис 20. Точность метода KNN при прогнозировании роста или падения курса свыше 1%, модель обучена на полной выборке. Оптимальными параметрами являются: отсутствие нормировки, 46 соседей. Максимальная точность: 68,3%

Из графиков видно, что на полной выборке метод по-прежнему успешно справляется с предсказанием. Максимальная точность получилась для предсказания роста более чем на 1% и падения более чем на -1%. Хочется отметить, что полученная точность в 90% и 91% является очень хорошим результатом при предсказании.

Следующий метод, который, мы будем анализировать - метод опорных векторов. Мы рассматриваем 3 вида ядра:

·  Линейное ядро

·        Полиномиальное ядро: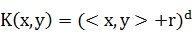

·        Радиальное ядро: ,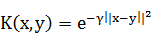

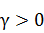
Каждое ядро является функцией с несколькими неизвестными параметрами, которые мы будем подбирать (d, r и ). Аналогично тем графикам, которые построены, выше проанализируем точность полученных методов. Наиболее удачным ядром оказалось полиномальное ядро, параметром которого является коэффициент . Приведем графики только для полной выборки (Рис. 21-24).

Рис. 21. Точность метода SVM метода(полиномиальное ядро) при прогнозировании роста/падения курса, модель обучена на полной выборке. Оптимальными параметрами являются: отсутствие нормировки, 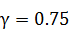. Максимальная точность: 53,1%

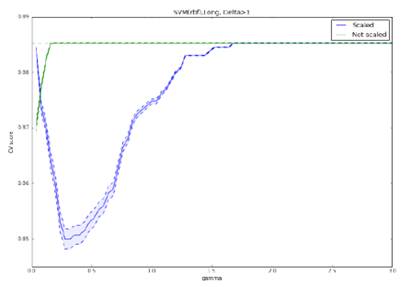
Рис. 22: Точность метода SVM метода (полиномиальное ядро) при прогнозировании роста курса более чем на 1%, модель обучена на полной выборке. Оптимальными параметрами являются: отсутствие нормировки, 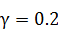. Максимальная точность: 87,1%.

Рис. 23. Точность метода SVM метода (полиномиальное ядро) при прогнозировании падении курса более чем на -1%, модель обучена на полной выборке. Оптимальными параметрами являются: отсутствие нормировки, 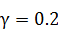. Максимальная точность: 90,2%

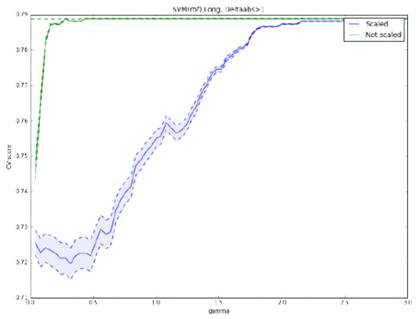
Рис. 24. Точность метода SVM метода (полиномиальное ядро) при прогнозировании роста или падении курса более чем на -1%, модель обучена на полной выборке. Оптимальными параметрами являются: отсутствие нормировки, . Максимальная точность: 78,9%

Из графиков видно, что для разбиений “>1” и “<-1” точность SVM метода получилась меньше, чем у метода ближайших соседей, хотя доверительные интервалы по-прежнему оказались небольшими. Для остальных двух разбиений точность удалось увеличить на 1-2% по сравнению с точностью KNN. Максимальная точность рассматриваемого метода достигает значения 90.2%. Для сравнения, модель бинарного выбора, которая изучалась мной в курсовой работе 2015 года, смогла добиться только 75% точности.

Теперь попробуем обучить дерево принятия решения. У дерева принятия решения нет никаких параметров, кроме того, при использовании данного подхода можно не нормировать данные, потому что алгоритм никаким образом не зависит от расстояния между элементами выборки. Приведем данные по количеству атрибутов в дереве и данные по точности для каждой из 8 выборок:

Несмотря на длительный процесс обучения и большое количество атрибутов нам не удалось достигнуть точности более 71%, что является худшим результатом среди всех методов классификации. Так как основная идея дерева принятия решения, заложенная авторами метода, заключалась в наглядности результата и возможности его интерпретировать приведем пример полученного дерева принятия решения для короткой выборки и разбиения “>0” (Рис. 34). На каждом атрибуте графа приведены следующие данные: атрибут, индекс Джинни (gini), количество элементов выборки (samples), которое анализируется с помощью атрибута, количество элементов в первом и втором классах (value).

Рис. 25. Пример полученного дерева принятия решений. Красный цвет - класс 1, синий - класс 2, чем ярче цвет - тем c с большей вероятностью элемент, подходящий подкритерии данного атрибута может быть отнесет к данному классу

Изначально индекс Джинни равен 0.375, количество элементов в выборке 296, соотношения элементов 1 и 2 класса равно 222:74. На первом дерево принятия решения анализирует изменение по параметру “газ”, если у элемента выборки, который мы хотим классифицировать, относительное изменение котировок газа составило более чем -5,587%, то мы переходим в левую ветвь дерева, в противном случае - в правую. В далее мы анализируем изменение котировок по меди или объем контрактов по Ruonia, в зависимости от того, в какую ветвь мы перешли и так далее до тех пор, пока мы не попадем в лист дерева. Когда мы нашли лист дерева, который бы соответствовал классифицируемому элементу выборки, мы можем дать ответна вопрос произойдет ли рост курса более чем на 1 процент или нет в зависимости от цвета листа (красный - не произойдет, синий - произойдет). Например, если котировки газа упали более чем на -5,587% и при этом медь упала менее, чем на -1,815%, то мы переходим из корня в левого потомка, из левого потомка в правого потомка. Такой элемент выборки попадает в синий лист дерева, а значит, произойдет рост курса более чем на 1% (Рис 26).

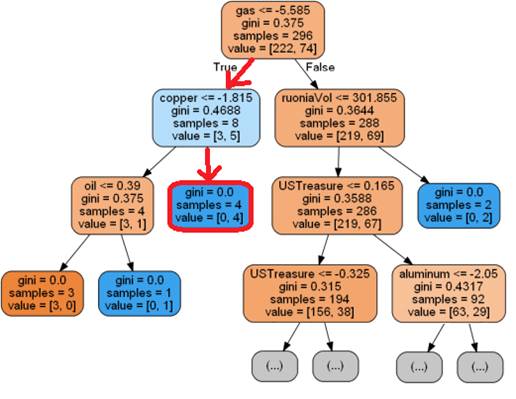
Рис. 26. Иллюстрация примера классификации нового элемента выборки

Переходим к методам регрессии. Здесь мы будем аппроксимировать значения относительных изменений курса с помощью значений факторов. Напомним, как выглядит регуляризованный функционал ошибки, используемый для обучения:

Мы будем рассматривать несколько видов регрессии. Отличаются они, как и в SVM методе, прежде всего, видом ядра. Протестируем три вида ядра: линейное(linear), полиномиальное(poly) и радиальное(rbf).Последние два ядра зависят от параметров: полиномиальное ядро 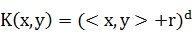 имеет 2 параметра r и d, радиальное ядро:  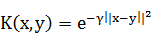зависит от . Кроме того, в формуле функционала ошибки присутствует дополнительный параметр , характеризующий величину штрафа за переобучение. Поэтому у каждого метода, помимо параметров, используемых в функции ядра, будет еще один дополнительный параметр

В задачах регрессии для того, чтобы избавиться от зависимости между факторами, перед построением регрессии принято использовать метод главных компонент(PCA), поэтому протестируем линейную регрессию с нормировкой (With PCA) и без нее (Without PCA). Точность регрессии будем оценивать с помощью коэффициента детерминации , чем ближе его величина к 1, чем лучше считается приближение. Результаты приведены на графиках (Рис. 26-27).

Рис. 27. Точность метода регрессии с линейным ядром, построенная по полной выборке. Оптимальные параметры: отсутствие PCA. Максимальное значение коэффициента детерминации: 0.0075

Рис. 28. Точность метода регрессии с полиномиальным ядром, построенная по полной выборке. Максимальное значение коэффициента детерминации: 0.0075

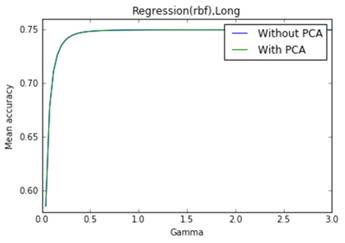
Рис. 29. Точность метода регрессии с радиальным ядром, построенная по полной выборке. Оптимальные параметры: . Максимальное значение коэффициента детерминации: 0.75

Как видно из графиков, линейное и полиномиальное ядро демонстрируют очень плохую точность, радиальное ядро работает гораздо лучше. Максимальное значение коэффициента детерминации равно 0.75. Стоит отметить пару особенностей, выявленных во время эксперимента:

·  Точность регрессии с линейным ядром не зависит от коэффициента детерминации;

·        Метод главных компонент не влияет на точность регрессии с радиальным ядром.

Применение регрессии для предсказания относительного изменения курса оказалось менее успешным, чем методы классификации. Вспомним графики, отвечающие зависимости отклика от фактора (Рис. 13). Облако точек на каждом из графиков не имеет никакой конкретной формы: оно достаточно плотное в центре и очень c сильно размыто по краям. Заметная “бесформенность” зависимости между фактором и откликом свидетельствует о том, что построить конкретную функцию, аппроксимирующую величину изменения курса, будет достаточно сложно. Эти интуитивные соображения были подтверждены в ходе эксперимента с регрессией.

Подведем итоги: несомненным лидером среди всех рассматриваемых методов является метод ближайших соседей. Помимо большого количества преимуществ в виде быстроты обучения и простоты модель оказалась достаточно гибкой и позволила нам получить прогноз с точностью 91%. С небольшим отставанием за методом ближайших соседей следует метод опорных векторов с радиальным ядром. Минусом данного метода является долгая работа кода, что делает его менее привлекательным для практического применения.

5. Гибридный метод

Методы классификации и регрессии, рассматриваемые выше, стоили предсказание отклика на основе значений факторов. Существует и другой подход для анализа относительного изменения курса: для прогноза можно использовать значение курса за предыдущие дни. Данный подход является основной идеей модели временных рядов. Идея гибридного метода заключалась в объединении зависимости этих двух подходов.

Для начала мы хотим установить степень зависимости новых значений данных от старых. Для этого мы использовали модель временных рядов. Для каждого из факторов мы обучили модель временного ряда и определили порядок соответствующих моделей (p и q у ARMA модели). Порядок р для каждой модели оказался не выше 1, откуда мы сделали вывод, что зависимость 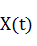от  присутствует, а зависимостью от  уже можно пренебрегать. Аналогичный вывод мы получили и для отклика. Далее помимо  мы стали рассматривать в качестве факторов, соответствующих отклику Y(t), еще и , то есть мы добавили в качестве факторов значения факторов и отклика за предыдущий день. Зависимостью от более ранних данных мы решили пренебречь, основываясь на порядке моделей ARMA. Новое количество факторов стало равно 7+7+1=15.

Протестировав самый метод классификации, полученный ранее, мы пришли к выводу, что существенного вклада в точность прогноза не произошло. Единственным достижением гибридного метода оказалось повышение точности на 2% для разбиений ‘abs>1’(Рис. 30).

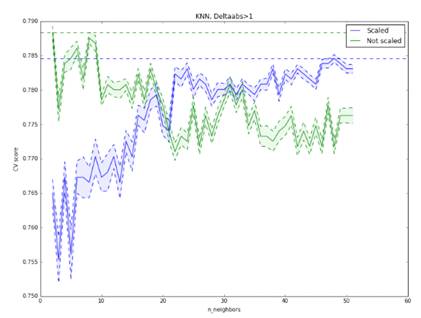
Рис 30. Точность гибридного KNN метода при прогнозировании роста или падении курса более чем на 1%, модель обучена на полной выборке. Оптимальными параметрами являются: отсутствие нормировки, 9 соседей. Максимальная точность: 78,9%

Список литературы

1. Акулов, В.Б. Финансовый менеджмент: Учебное пособие / В.Б. Акулов. - М.: Флинта, МПСУ, 2010. - 264 c.

. Архипов, А.П. Финансовый менеджмент в страховании: учебник / А.П. Архипов. - М.: ФиС, ИНФРА-М, 2010. - 320 c.

. Басовский, Л.Е. Финансовый менеджмент: Учебник / Л.Е. Басовский. - М.: НИЦ ИНФРА-М, 2013. - 240 c.

. Басовский, Л.Е. Финансовый менеджмент: Учебное пособие / Л.Е. Басовский. - М.: ИЦ РИОР, ИНФРА-М, 2011. - 88 c.

. Бахрамов, Ю.М. Финансовый менеджмент: Учебник для вузов. Стандарт третьего поколения / Ю.М. Бахрамов, В.В. Глухов. - СПб.: Питер, 2011. 496 c.

. Боголюбов, В.С. Финансовый менеджмент в туризме и гостиничном хозяйстве: Учебное пособие для студентов высших учебных заведений / В.С. Боголюбов, С.А. Быстров. - М.: ИЦ Академия, 2008. - 400 c.

. Бригхэм, Ю.Ф. Финансовый менеджмент: Экспресс-курс / Ю.Ф. Бригхэм. - СПб.: Питер, 2013. - 592 c.

. Брусов, П.Н. Финансовый менеджмент. Математические основы. Краткосрочная финансовая политика: Учебное пособие / П.Н. Брусов, Т.В. Филатова. - М.: КноРус, 2013. - 304 c.

. Брусов, П.Н. Финансовый менеджмент. Финансовое планирование: Учебное пособие / П.Н. Брусов, Т.В. Филатова. - М.: КноРус, 2013. - 232 c.

. Варламова, Т.П. Финансовый менеджмент: Учебное пособие / Т.П. Варламова, М.А. Варламова. - М.: Дашков и К, 2012. - 304 c.

. Гаврилова, А.Н. Финансовый менеджмент: Учебное пособие / А.Н. Гаврилова, Е.Ф. Сысоева, А.И. Барабанов. - М.: КноРус, 2013. - 432 c.

. Герасименко, А. Финансовый менеджмент - это просто: Базовый курс для руководителей и начинающих специалистов / А. Герасименко. - М.: Альпина Пабл., 2013. - 531 c.

. Гинзбург, М.Ю. Финансовый менеджмент на предприятиях нефтяной и газовой промышленности: Учебное пособие / М.Ю. Гинзбург, Л.Н. Краснова, Р.Р. Садыкова. - М.: НИЦ ИНФРА-М, 2013. - 287 c.

. Ермасова, Н.Б. Финансовый менеджмент: Учебное пособие / Н.Б. Ермасова, С.В. Ермасов. - М.: Юрайт, ИД Юрайт, 2010. - 621 c.

. Зайков, В.П. Финансовый менеджмент: теория, стратегия, организация: Учебное пособие / В.П. Зайков, Е.Д. Селезнева, А.В. Харсеева. - М.: Вуз. книга, 2012. - 340 c.

. Зайцева, Н.А. Финансовый менеджмент в туризме и гостиничном бизнесе: Учебное пособие / Н.А. Зайцева, А.А. Ларионова. - М.: Альфа-М, НИЦ ИНФРА-М, 2013. - 320 c.

. Кандрашина, Е.А. Финансовый менеджмент: Учебник / Е.А. Кандрашина. - М.: Дашков и К, 2013. - 220 c.

. Ковалев, В.В. Финансовый менеджмент в вопросах и ответах: Учебное пособие / В.В. Ковалев, В.В. Ковалев. - М.: Проспект, 2013. - 304 c.

. Ковалев, В.В. Финансовый менеджмент: теория и практика / В.В. Ковалев. - М.: Проспект, 2013. - 1104 c.