|
Вид сырья
|
Запас сырья
|
Расход сырья на
единицу продукции вида
|
|
|
 
|
|
|
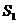 1923 1923
|
|
|
|
|
 1321 1321
|
|
|
|
|
 1503 1503
|
|
|
|
|
 1830 1830
|
|
|
|
Прибыль производства от единицы продукции вида  равна 7 денежным единицам, а от единицы
продукции вида
равна 7 денежным единицам, а от единицы
продукции вида  - 5 денежным единицам. Как следует
спланировать выпуск продукции, чтобы прибыль предприятия была наибольшей.
- 5 денежным единицам. Как следует
спланировать выпуск продукции, чтобы прибыль предприятия была наибольшей.
Для этой задачи целевая функция будет записана в следующем виде:
F(x) = 7П1 + 5П2 → max,
а ограничения:
П1 + 3П2 ≤ 19;
П1 + П2 ≤ 13;
П2 ≤ 15;
П1 ≤ 18;
П1 ≥ 0, П2 ≥ 0
.2
Основные сведения о симплекс-методе
Симплексный метод, в основу которого легла идея
последовательного улучшения решения, универсален. В настоящее время он
используется для компьютерных расчетов, однако несложные примеры с применением
симплексного метода можно решать вручную.
Для реализации симплексного метода - последовательного
улучшения решения - необходимо освоить три основных элемента:
· способ определения какого-либо
первоначального допустимого базисного решения задачи;
· правило перехода к лучшему (точнее, не
худшему) решению;
· критерий проверки оптимальности найденного
решения.
Симплекс-метод включает два этапа:
) определение начального решения, удовлетворяющего
ограничениям;
) последовательное улучшение начального решения и
получение оптимального решения задачи.
.3
Геометрическая интерпретация симплексного метода
Если задача линейного программирования имеет оптимальное
решение, то оно соответствует хотя бы одной угловой точке многогранника решений
и совпадает, по крайней мере, с одним из допустимых базисных решений системы
ограничений. Путь решения задачи линейного программирования: перебрать конечное
число допустимых базисных решений системы ограничений и выбрать среди них то,
на котором целевая функция принимает оптимальное решение. Геометрически это
соответствует перебору всех угловых точек многогранника решений. Такой перебор,
в конце концов, приведет к оптимальному решению (если оно существует), однако
его практическое осуществление связано с огромными трудностями, т.к. для
реальных задач число допустимых базисных решений хотя и конечно, но может быть
чрезвычайно велико.
Число перебираемых допустимых базисных решений можно
сократить, если производить перебор не беспорядочно, а с учетом изменений
линейной функции, т.е., добиваясь того, чтобы каждое следующее решение было
«лучше» (или, по крайней мере, «не хуже»), чем предыдущие, по значениям линейной
функции (увеличение ее при отыскании максимума F→max, уменьшение - при
отыскании минимума F→min).

Рис. 1. Последовательный переход к вершинам
многогранника
Такой перебор позволяет сократить число шагов при отыскании
оптимума. Поясним это на графическом примере.
Пример:
F = 2x1 + 3x2 → max
при ограничениях:
x1 + 3x2 ≤ 15, L1: 2x1 + 3x2 = 15;
x1 + 2x2 ≤ 8, L2: x1 + 2x2 = 8;
x1 ≤ 16, L3: 4x1 = 16;
x2 ≤ 12, L4: 4x2 = 12;
x1 ≥ 0, x2 ≥ 0. L5: x1 = 0; L6: x2 = 0.

Рис. 2. Графическое решение примера
В данном случае вместо пяти перебрали только четыре вершины,
последовательно улучшая значение целевой функции.
.4
Алгебраический смысл симплексного метода
Переход от геометрического способа решения задачи линейного
программирования к симплекс-методу лежит через алгебраическое описание крайних
точек пространства решений. Для реализации этого перехода сначала надо привести
задачу линейного программирования к стандартной форме, преобразовав неравенства
ограничений в равенства путем введения дополнительных переменных.
Стандартная форма задачи линейного программирования
необходима, потому что она позволяет получить базисное решение, используя
систему уравнений, порожденную ограничениями.
Стандартная форма задачи линейного программирования
предполагает выполнение следующих требований.
1. Все ограничения (включая ограничения
неотрицательности переменных) преобразуются в равенства с неотрицательной
правой частью.
2. Все переменные неотрицательные.
. Целевую функцию следует максимизировать, или
минимизировать.
f = c1x1 + c2x2
+ … + cnxn → max1 + a1m+1xm+1
+ … + a1nxn = b1,2 + a2m+1xm+1
+ … + a2nxn = b2,
…m + amm+1xm+1 +
… + amnxn = bm.
xj ≥ 0, j = 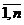
Переход к канонической форме записи производится с помощью
следующих простых действий.
1. Если требуется найти минимум целевой функции f то, умножая f на (-1), переходят к
задаче максимизации; т.к. min f = - max (-f).
2. Если ограничение содержит неравенство со знаком ≤,
то от него переходя к равенству, добавляя в левую часть ограничения
дополнительную неотрицательную переменную.
. Если ограничение содержит неравенство со знаком ≥,
то от него переходят к равенству, вычитая из левой части дополнительную
неотрицательную переменную.
. Если в задаче какая-либо из переменных произвольна,
то от нее избавляются, заменяя ее разностью двух других неотрицательных
переменных.
1.5
Отыскание максимума линейной функции
Отыскание максимума линейной функции рассмотрим на примере с
помощью аналитического симплекс-метода.
Решить симплекс-методом задачу:
F = 2x1 + 3x2 → max
при ограничениях:
x1 + 3x2 ≤ 18,
x1 + x2 ≤ 16,
x2 ≤ 5,
x1 ≤ 21,
x1 ≥ 0, x2 ≥ 0.
Прейдем к канонической форме задач ЛП, с помощью ввода
дополнительных неотрицательных переменных. Все дополнительные переменные
вводятся со знаком «+», т.к. все неравенства имеют вид «≤». Получим
систему ограничений:
x1 + 3x2 + х3 = 18,
x1 + x2 + x4 = 16,
x2 + x5 = 5,
x1 + x6 = 21.
Для нахождения первоначального базисного решения разобьем
переменные на 2 группы - основные и неосновные (свободные).
В качестве основных переменных на первом шаге нужно выбрать
такие переменные, каждая из которых входит в одно уравнение системы ограничений
и при этом нет таких уравнений, в которые не входит ни одна из этих переменных.
Количество основных переменных равно m.
Дополнительные переменные удовлетворяют этому правилу. Если
выбранные по этому правилу переменные имеют те же знаки, что и соответствующие
им свободные члены в правых частях уравнений, то полученное таким образом
базисное решение будет допустимым.
Шаг 1.
1. Определим состав основных и неосновных переменных:
основные переменные (по правилу): х3, x4, x5, x6,
неосновные переменные: x1, x2.
2. Выразим основные переменные через неосновные:
x3 = 18 - x1 - 3x2,
x4 = 16 - 2x1 - x2, (1)
x5 = 5 - x2,
x6 = 21 - 3x1.
Положив неосновные переменные равными нулю, т.е. x1 = 0, x2 = 0, получим первое
базисное решение X1 = (0; 0; 18; 16; 5; 21), которое является допустимым (т.к. нет
отрицательных чисел).
Шаг 2. Выразим F через неосновные переменные и определим ее
значение при выбранном базисном решении:
F = 2x1 + 3x2
F(X1) = 2 ∙ 0 + 3 ∙ 0 = 0.
Легко понять, что F можно увеличить за счет увеличения любой из
неосновных переменных, входящих в выражение для F с положительным
коэффициентом.
Шаг 3. Проверим, доставляет ли выбранное базисное
решение оптимум целевой функции F.
Критерий оптимальности решения при нахождении максимума: если
в выражении F
отсутствуют положительные коэффициенты при неосновных переменных, то решение
является оптимальным.
В соответствии с этим критерием данное базисное решение не
оптимальное. Необходимо перейти к новому базисному решению.
Шаг 4. Переход к новому решению.
1. Определить вводимую переменную.
В новый состав основных переменных вводится та из неосновных
переменных, которая имеет наибольший положительный коэффициент в целевой
функции. В данном случае это коэффициент при x2.
Чтобы новое опорное решение, с одной стороны, улучшая (не
ухудшало) F,
а с другой - было бы опорным, необходимо учитывать ограничения на рост
переменной x2 (из системы ограничений). Ведь нужно сохранять допустимость
решений, т.е. все переменные должны оставаться неотрицательными. Т.е.
дополнительно выполняться следующие неравенства:
x3 = 18 - x1 - 3x2 ≥ 0, x1 = 0 x3 = 18 - 3x2 ≥ 0,
x4 = 16 - 2x1 - x2 ≥ 0,  x4 = 16 - x2 ≥
0,
x4 = 16 - x2 ≥
0,
x5 = 5 - x2 ≥ 0, x5
= 5 - x2 ≥ 0,
x6 = 21 - 3x1 ≥ 0, x6 = 21,
x2 ≤ 18/3
x2 ≤ 16
x2 ≤ 5
Каждое уравнение системы (1), кроме последнего, определяет
оценочное отношение - границу роста переменной x2, сохраняющую
неотрицательность соответствующей переменной. Эта граница определяется
абсолютной величиной отношения свободного члена к коэффициенту при x2 при условии, что эти
числа имеют разные знаки.
При оценке переменной, переводимой в основные, возможны
случаи:
1) xi = 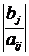 , если bj и aij имеют разные знаки и bj ≠ 0, aij ≠
0;
, если bj и aij имеют разные знаки и bj ≠ 0, aij ≠
0;
если bj и aij одного знака и bj ≠ 0, aij ≠ 0;
2) xi = ∞, если aij = 0;
если bj = 0 и aij > 0;
3) xi = 0, если bj = 0 и aij < 0.
Так, последнее уравнение системы не ограничивает рост
переменной x2, т.к. данная переменная в него не входит (или входит с нулевым
коэффициентом, т.е. aij = 0).
2. Определить выводимую переменную.
Очевидно, что сохранение неотрицательности всех переменных
(допустимость решения) будет возможно, если не нарушается ни одна из полученных
во всех уравнениях границ.
В данном примере наибольшее возможное значение для x2 определяется как
минимум.
x2 = min {18/3; 16; 5; ∞} = 5.
При x2 = 5 переменная x5 - обращается в нуль и
переходит в неосновные.
Уравнение, где достигается наибольшее возможное значение
переменной x2, называется разрешающим.
В данном случае это третье уравнение. Выделим его рамкой.
После проделанных преобразований вновь возвращаемся к первому
шагу.
Шаг 1.
1. Определим состав основных переменных:
основные: x2, x3, x4, x6;
неосновные: x1, x5.
2. Выразим основные переменные через новые
неосновные, начиная с разрешающего уравнения (его используем при записи
выражения для x2):
3. 2 = 5 - x5, x2
= 5 - x5, 3 = 18 - x1 - 3 (5 - x5),  x3
= 3 - x1 - 3x5,4 = 16 - 2x1 - (5 -
x5), x4 = 11 - 2x1
+ x5,6 = 21 - 3x1 x6
= 21 - 3x1.
x3
= 3 - x1 - 3x5,4 = 16 - 2x1 - (5 -
x5), x4 = 11 - 2x1
+ x5,6 = 21 - 3x1 x6
= 21 - 3x1.
4. Получим второе базисное решение (положив
неосновные переменные равными нулю): Х2 = (0; 5; 3; 11; 0; 21),
которое является допустимым.
Шаг 2. Выразим F через неосновные переменные.
F = 2x1 + 3x2 = 2x1 + 3 (5 - x5) = 15 + 2x1 - 3x5. (2)
Определим ее значение при выбранном решении:
F2 = F(X2) = 15.
Изменение значения целевой функции (т.е. ∆F) можно определить как
произведение наибольшего возможного значения переменной, переводимой в основные
(в этом случае это х2), на ее коэффициент в выражении для F (это число 3).
В данном случае ∆F1 = 5 ∙ 3 = 15.
F2 = F1 + ∆F1 = 0 + 15 = 15.
Шаг 3. Проверка оптимальности решения.
Т.к. в выражении для F присутствуют
положительные коэффициенты (в (2) перед х1), то данное решение не
оптимальное, т.е. F2 не максимальное.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
В (2) положительный коэффициент перед х1, т.е. х1
вводим в новый состав основных переменных. Определим допустимое значение х1.
x2 = 5 - x5 ≥ 0 т.к. х5 =0 x2 = 5 ≥ 0 x1 ≤ ∞3
= 3 - x1 + 3x5 ≥ 0  x3 = 3 - x1 ≥ 0 x1 ≤ 3
x3 = 3 - x1 ≥ 0 x1 ≤ 3
x4 = 11 - 2x1 + x5 ≥ 0 x4 = 11 - 2x1 ≥ 0 x1 ≤ 11/2
x6 = 21 - 3x1 ≥ 0 x6 = 21 - 3x1 ≥ 0 x1 ≤ 7
2. Определим выводимую переменную.
x1 = min {∞; 3; 11/2; 7} = 3
При x1 = 3 переменная х3 обращается в
0. Второе уравнение - разрешающее. х3 - переходит в неосновные.
Найдем ∆F2: ∆F2 = 3 ∙ 2 = 6.
Шаг 1.
1. Определим состав основных и неосновных
переменных:
основные: х1, х2, х4, х6;
неосновные: х3, х5.
2. Выразим основные переменные через неосновные,
начиная с разрешающего уравнения:
х1 = 3 - x3 + 3x5 х1
= 3 - x3 + 3x5
x2 = 5 - x5  x2 = 5 - x5 (3)
x2 = 5 - x5 (3)
x4 = 11 - 2 (3 - x3 + 3x5) + x5 x4 = 5 + 2х3 -
5х5
x6 = 21 - 3 (3 - x3 + 3x5) x6 = 12 + 3х3 -
9х5
3.
Получим третье базисное решение (неосновные переменные равны 0): Х3
= (3; 5; 0; 5; 0; 12), которое является допустимым.
Шаг 2. Выразим F через неосновные
переменные.
F = 2x1 + 3x2 = 2 (3 - x3 + 3x5) + 3 (5
- x5) = 21 - 2х3 +
3х5 (4)
F3 = F(X3) = 21.
Действительно, F3 = F2 + ∆F2 = 15 + 6 = 21.
Шаг 3. Проверка решения на оптимальность.
Критерий оптимальности не выполняется, т.к. коэффициент при х5
в (4) положителен. Т.е. F3 не максимальное.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
В (9) положительный коэффициент перед х5, т.е. х5
вводим в новый состав основных переменных. Определим допустимое значение х5.
х1 = 3 - x3 + 3x5 ≥ 0 х3
= 0 х1 = 3 + 3x5 ≥ 0 x5 ≤ ∞
x2 = 5 - x5 ≥ 0  x2 = 5 - x5 ≥ 0 x5 ≤ 54 =
5 + 2х3 - 5х5 ≥ 0 x4 = 5 - 5х5 ≥
0 x5 ≤ 1
x2 = 5 - x5 ≥ 0 x5 ≤ 54 =
5 + 2х3 - 5х5 ≥ 0 x4 = 5 - 5х5 ≥
0 x5 ≤ 1
x6 = 12 + 3х3 - 9х5 ≥ 0 x6 = 12 - 9х5 ≥
0 x5 ≤ 4
2. Определим выводимую переменную.
х5 = min {∞; 5; 1; 4/3} = 1
При x5 = 1 переменная х4 обращается в
0. Третье уравнение - разрешающее. х4 - переходит в неосновные.
Найдем ∆F3: ∆F3 = 1 ∙ 3 = 3.
Шаг 1.
1. Определим состав основных и неосновных
переменных:
основные: х1, х2, х5, х6;
неосновные: х3, х4.
2. Выразим основные переменные через неосновные,
начиная с разрешающего уравнения:





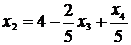
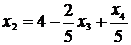
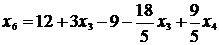
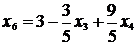
3. Получим четвертое базисное решение (положим
неосновные переменные равными 0): Х4 = (6; 4; 0; 0; 1; 3), которое
является допустимым.
Шаг 2. Выразим F через неосновные
переменные.
F = 2x1 + 3x2 = 2 (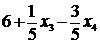 ) + 3 (
) + 3 (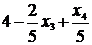 ) = 24 -
) = 24 -  (5)
(5)
F4 = F(X4) = 24.
Действительно, F4 = F3 + ∆F3 = 21 + 3 = 24.
Шаг 3. Проверка решения на оптимальность.
Критерий оптимальности выполнен, т.к. коэффициенты при х3
и х4 в (5) отрицательные и удовлетворяют условию. Т.е. F3 является максимальным.
Ответ: Fmax = 24, х* = 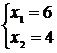
1.5
Отыскание минимума линейной функции
При отыскании минимума линейной функции Z возможны два пути:
1) отыскать максимум функции F, полагая F = - Z и учитывая, что Zmin = - Fmax;
2) модифицировать симплексный метод: на каждом шаге
уменьшать линейную функцию за счет той неосновной переменной, которая входит в
выражение линейной функции с отрицательным коэффициентом.
Рассмотрим это на следующем примере.
Z = 18y1 + 16y2 + 5y3 + 21y4 → min
при ограничениях:
у1 + 2у2 + 3у4 ≥ 2,
у1 + у2 + у3 ≥ 3
yi ≥ 0, i = 1, 2, 3, 4.
Введем дополнительные неотрицательные переменные у5
и у6 со знаком «-», т.к. неравенства имеют вид «≥». Получим
систему уравнений:
у1 + 2у2 + 3у4 - у5 =
2,
у1 + у2 + у3 - у6
= 3.
Если на первом шаге в качестве основных взять дополнительные
переменные, то получим недопустимое базисное решение: (0; 0; 0; 0; -2; -3). В
данном случае в качестве основных удобно взять переменные у3 и у4,
коэффициенты при у3 и у4 положительны, поэтому в качестве
первоначального получим допустимое базисное решение.
Шаг 1.
1. Определим состав основных и неосновных переменных:
основные: у3, у4
неосновные: у1, у2, у5, у6.
. Выразим основные переменные через неосновные:
у1 + 2у2 + 3у4 - у5 =
2,  у3 = 3 - 3у1
- у2 + у6,
у3 = 3 - 3у1
- у2 + у6,
у1 + у2 + у3 - у6 = 3. у4
= 
3. Получим первое базисное решение Y1 = (0; 0; 3; 2/3; 0; 0),
которое является допустимым.
Шаг 2. Выразим Z через неосновные переменные и определим ее
значение при выбранном базисном решении.
Z1 = 18y1 + 16y2 + 5y3 + 21y4 = 18y1 + 16y2 + 5 (3 - 3у1 - у2 + у6) +
21 ( )= = 29 - 4y1 - 3y2 + 7y5 + 5у6.
)= = 29 - 4y1 - 3y2 + 7y5 + 5у6.
Z1 = Z(Y1) = 29.
Это значение не является минимальным, т.к. значение Z можно уменьшить за счет
перевода в основные любой из переменных у1 или у2,
имеющих в выражении для Z отрицательные коэффициенты.
Шаг 3. Проверим, доставляет ли выбранное базисное
решение оптимум целевой функции Z.
Критерий оптимальности решения при нахождении минимума: если
в выражении Z
отсутствуют отрицательные коэффициенты при неосновных переменных, то решение
является оптимальным.
В соответствии с этим критерием данное базисное решение не
оптимальное. Необходимо перейти к новому базисному решению.
Шаг 4. Переход к новому решению.
1. Определить вводимую переменную.
В новый состав основных переменных вводится та из неосновных
переменных, которая имеет наибольший отрицательный коэффициент в целевой
функции. В данном случае это коэффициент при у1.
Чтобы новое опорное решение, с одной стороны, улучшая (не
ухудшало) Z,
а с другой - было бы опорным, необходимо учитывать ограничения на рост
переменной у1 (из системы ограничений). Ведь нужно сохранять
допустимость решений, т.е. все переменные должны оставаться неотрицательными.
Т.е. дополнительно выполняться следующие неравенства:
у3 = 3 - 3у1 - у2 + у6
≥ 0 у2=0, у5=0,
у6=0 у3 = 3 - 3у1 ≥ 0(1)
у4 =  ≥ 0
≥ 0  у4 =
у4 =  ≥ 0,
≥ 0,
у1 ≤ 1
у1 ≤ 2
Каждое уравнение системы (1), кроме последнего, определяет
оценочное отношение - границу роста переменной у1, сохраняющую
неотрицательность соответствующей переменной. Эта граница определяется
абсолютной величиной отношения свободного члена к коэффициенту при у1
при условии, что эти числа имеют разные знаки.
При оценке переменной, переводимой в основные, возможны такие
же случаи, как и при отыскании максимума.
2. Определить выводимую переменную.
Очевидно, что сохранение неотрицательности всех переменных
(допустимость решения) будет возможно, если не нарушается ни одна из полученных
во всех уравнениях границ.
В данном примере наибольшее возможное значение для у1
определяется как минимум.
у1 = min {1; 2} = 1.
При у1 = 1 переменная у3 - обращается в
нуль и переходит в неосновные. Первое уравнение является разрешающим.
Шаг 1.
1. Определим состав основных и неосновных
переменных:
основные: у1, у4
неосновные: у2, у3, у5, у6.
2. Выразим основные переменные через неосновные,
начиная с разрешающего уравнения:
у1 = 
у4 = 
3. Получим второе базисное решение (положив
неосновные переменные равными 0): Y2 = (1; 0; 0; 1/3; 0; 0), которое является
допустимым.
Шаг 2. Выразим Z через новые неосновные переменные и определим ее
значение при выбранном базисном решении.
Z2 = 18y1 + 16y2
+ 5y3 + 21y4 = 18 ( ) + 16y2 + 5y3 + +21 (
) + 16y2 + 5y3 + +21 ( ) =
) =  . (2)2 = Z(Y2) = 25.
. (2)2 = Z(Y2) = 25.
Изменение значения целевой функции (т.е. ∆Z) можно определить как
произведение наибольшего возможного значения переменной, переводимой в основные
(в этом случае это y1), на ее коэффициент в выражении для Z (это число (- 4)).
В данном случае ∆Z1 = 1 ∙ (- 4) = - 4.
Z2 = Z1 + ∆Z1 = 29 - 4 = 25.
Шаг 3. Проверка решения на оптимальность.
Критерий оптимальности не выполняется, т.к. коэффициент при у2
в (2) отрицателен. Т.е. Z2 не минимальное.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
В (2) отрицательный коэффициент перед у2, т.е. у2
вводим в новый состав основных переменных. Определим допустимое значение у2.
у1 =  ≥ 0 у3=0, у5=0, у6=0 у1
=
≥ 0 у3=0, у5=0, у6=0 у1
=  ≥ 0
≥ 0
у4 =  ≥ 0
≥ 0  у4
=
у4
= 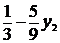 ≥ 0,
≥ 0,
у2 ≤ 3
у2 ≤ 3/5
2. Определим выводимую переменную.
у2 = min {3; 3/5} = 3/5
При у2 = 3/5 переменная у4 обращается в
0. Второе уравнение - разрешающее. у4 - переходит в неосновные.
Найдем ∆Z2: ∆Z2 = 3/5 ∙ (- 5/3) = -1
Шаг 1.
1. Определим состав основных и неосновных переменных:
основные: у1, у2
неосновные: у3, у4, у5, у6.
2. Выразим основные переменные через неосновные, начиная с
разрешающего уравнения:
у1 = 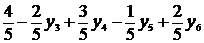
у2 = 
3. Получим третье базисное решение (положив
неосновные переменные равными нулю): Y3 = (4/5; 3/5; 0; 0; 0; 0), которое является
допустимым.
Шаг 2. Выразим Z через новые неосновные переменные и определим ее
значение при выбранном базисном решении.
Z3 = 18y1 + 16y2 + 5y3 + 21y4 = 18 (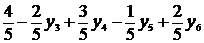 ) + +16 (
) + +16 ( ) + 5y3 + 21y4 = 24 + у3 + 3у4 + 6у5 + 4у6. (3)
) + 5y3 + 21y4 = 24 + у3 + 3у4 + 6у5 + 4у6. (3)
Z3 = Z(Y3) = 24.
Действительно, Z3 = Z2 + ∆Z2 = 25 - 1 = 24.
Шаг 3. Проверка решения на оптимальность.
Критерий оптимальности выполнен, т.к. коэффициенты при у3,
у4, у5 и у6 в (3) положительные и
удовлетворяют условию. Т.е. Z3 является минимальным.
Ответ: Zmin = 24, х* = 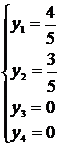
1.6
Особые случаи симплексного метода
Рассмотрим особые случаи, которые могут возникнуть при
решении задачи ЛП симплексным методом.
Неединственность
оптимального решения (альтернативный оптимум)
Рассмотрим этот случай на примере:
F = 3x1 + 3x2 → max
при ограничениях:
х1 + x2 ≤ 8,
x1 - x2 ≥ 1,
x1 - 2x2 ≤ 2,
x1 ≥ 0, x2 ≥ 0.
Приведем задачу к каноническому виду, путем ввода
дополнительных неотрицательных переменных. Получим систему равенств:
х1 + x2 + х3 = 8,
x1 - x2 - х4 = 1,
x1 - 2x2 + х5 = 2,
Шаг 1.
1. Определим состав основных и неосновных переменных:
основные переменные: х3, x4, x5,
неосновные переменные: x1, x2.
2. Выразим основные переменные через неосновные:
x3 = 8 - x1 - x2,
x4 = 1 - 2x1 + x2,
x5 = 2 - x1 + 2x2
Положив неосновные переменные равными нулю, т.е. x1 = 0, x2 = 0, получим первое
базисное решение X1 = (0; 0; 8; 1; 2), которое является допустимым (т.к. нет
отрицательных чисел).
Шаг 2. Выразим F через неосновные переменные и определим ее
значение при выбранном базисном решении:
F = 3x1 + 3x2
F(X1) = 3 ∙ 0 + 3 ∙ 0 = 0.
Легко понять, что F можно увеличить за счет увеличения любой из
неосновных переменных, входящих в выражение для F с положительным
коэффициентом.
Критерий оптимальности решения при нахождении максимума: если
в выражении F
отсутствуют положительные коэффициенты при неосновных переменных, то решение
является оптимальным.
В соответствии с этим критерием данное базисное решение не
оптимальное. Необходимо перейти к новому базисному решению.
Шаг 4. Переход к новому решению.
1. Определить вводимую переменную.
В новый состав основных переменных вводится та из неосновных
переменных, которая имеет наибольший положительный коэффициент в целевой
функции. В данном случае коэффициенты при переменных равны, поэтому выбираем
любой из них. Пусть это будет коэффициент при переменной x1.
Чтобы новое опорное решение, с одной стороны, улучшая (не
ухудшало) F,
а с другой - было бы опорным, необходимо учитывать ограничения на рост
переменной x1 (из системы ограничений). Ведь нужно сохранять допустимость
решений, т.е. все переменные должны оставаться неотрицательными. Т.е.
дополнительно выполняться следующие неравенства:
x3 = 8 - x1 - x2 ≥ 0, х2 =0 x3 = 8 - x1 ≥ 0 x1 ≤ 8
x4 = 1 - 2x1 + x2 ≥ 0,  x4 = 1 - 2x1 ≥ 0
x4 = 1 - 2x1 ≥ 0  x1 ≤ 1/2
x1 ≤ 1/2
x5 = 2 - x1 + 2x2 ≥ 0 x5 = 2 - x1 ≥ 0 x1 ≤
2
2. Определим выводимую переменную.
x1 = min {8; 1/2; 2} = 1/2
При x1=1/2 переменная х4 обращается в
0. Второе уравнение - разрешающее. x4 - переходит в неосновные.
Шаг 1.
1. Определим состав основных и неосновных переменных:
основные: х1, х3, х5,
неосновные: х2, х4.
2. Выразим основные переменные через неосновные,
начиная с разрешающего уравнения:
x1 =  , x1 =
, x1 =  ,
,
x3 = 8 - 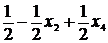 - x2,
- x2,  x3 =
x3 = 
x5 = 2 - 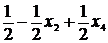 + 2x2 x5 =
+ 2x2 x5 = 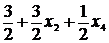
Положив неосновные переменные равными нулю, получим второе
базисное решение X2 = (1/2; 0; 15/2; 0; 3/2), которое является допустимым (т.к. нет
отрицательных чисел).
Шаг 2. Выразим
F через неосновные переменные и определим
ее значение при выбранном базисном решении:
F = 3x1 + 3x2 = 3 ( ) + 3x2 =
) + 3x2 =  . (1)
. (1)
F2 = F(X2) = 3/2.
Найдем ∆F1 = 1/2 ∙ 3 = 3/2.
F2 = F1 + ∆F1 = 0 + 3/2 = 3/2.
Шаг 3. Проверка оптимальности решения.
Т.к. в выражении для F присутствуют
положительные коэффициенты (в (1) перед х2), то данное решение не
оптимальное, т.е. F2 не максимальное.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
В (1) положительный коэффициент перед х2, т.е. х2
вводим в новый состав основных переменных. Определим допустимое значение х2.
x1 = 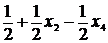 ≥ 0, х4 = 0 x1 =
≥ 0, х4 = 0 x1 =  ≥ 0 х2
= ∞
≥ 0 х2
= ∞
x3 =  ≥ 0,
≥ 0,  x3 =
x3 = 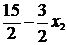 ≥ 0
≥ 0  х2 = 5
х2 = 5
x5 =  ≥ 0 x5 =
≥ 0 x5 =  ≥ 0 х2 = ∞
≥ 0 х2 = ∞
2.
Определим выводимую переменную.
х2 = min {∞; 5; ∞} = 5
При x2=5 переменная х3 обращается в 0.
Второе уравнение - разрешающее. х3 - переходит в неосновные.
Шаг 1.
1. Определим состав основных и неосновных переменных:
основные: х1, х2, х5,
неосновные: х3, х4.
2. Выразим основные переменные через неосновные, начиная
с разрешающего уравнения:
3.
x1 = 
x2 = 
x5 = 9 - x3 - x4.
Положив неосновные переменные равными нулю, получим третье
базисное решение X3 = (5; 3; 0; 0; 9), которое является допустимым (т.к. нет
отрицательных чисел).
Шаг 2. Выразим F через неосновные переменные и определим ее
значение при выбранном базисном решении:
F = 3x1 + 3x2 = 3 ( ) + 3 (
) + 3 ( ) = 24 - х3. (2)
) = 24 - х3. (2)
F3 = F(X3) = 24.
Найдем ∆F2 = 5 ∙ 9/2 = 45/2.
F3 = F2 + ∆F2 = 3/2 + 45/2 = 48/2 =
24.
Шаг 3. Проверка оптимальности решения.
Т.к. в выражении для F отсутствуют
положительные коэффициенты при неосновных переменных, то критерий оптимальности
выполнен. Х3 - оптимальное базисное решение, Fmax = F(X3) = 24.
Однако в выражении (2) для F отсутствует неосновная
переменная х4 (формально она входит с нулевым коэффициентом),
поэтому изменение этой переменной не повлечет за собой изменение линейной
функции. Например, можно перевести в основные переменную х4; х4
= min {15; ∞; 9} = 9.
Переменная х5 перейдет в неосновные, однако изменения линейной
функции не произойдет: ∆F3 = 9 ∙ 0 = 0. Действительно на следующем
шаге получим новое базисное решение Х4 = (6; 2; 0; 9; 0), Fmax = F(X3) = 24. Учитывая, что
переменная х3 = 0 (в базисном решении Х4 она осталась
неосновной), а переменная х4 удовлетворяет неравенству 0 ≤ х4
≤ 9, из системы уравнений можно получить все множество оптимальных
решений задачи.
Появление
вырожденного базисного решения
Рассмотрим появление вырожденного базисного решения на
примере:
F = 2x1 - x2 → max
при ограничениях:
х1 - х2 ≤ 2,
х1 - 2х2 ≤ 6,
х1 - 4х2 ≤ 14,
х1 ≥ 0, х2 ≥ 0
Приведем систему неравенств к каноническому виду, путем ввода
дополнительных неотрицательных переменных.
х1 - х2 + x3 = 2,
х1 - 2х2 + x4 = 6,
х1 - 4х2 + x5 = 14,
Шаг 1.
1. Определим состав основных и неосновных переменных:
основные переменные: х3, x4, x5,
неосновные переменные: x1, x2.
2. Выразим основные переменные через неосновные:
x3 = 2 - x1 + x2,
x4 = 6 - 3x1 + 2x2,
x5 = 14 - 6x1 + 4x2.
Положив неосновные переменные равными нулю получим первое
базисное решение: Х1 = (0; 0; 2; 6; 14), которое является
допустимым.
Шаг 2. Выразим F через неосновные переменные и определим ее
значение при выбранном базисном решении:
F = 2x1 - x2
F1 = F(X1) = 2 ∙ 0 + 0 = 0.
Шаг 3. Проверка оптимальности решения.
Т.к. в выражении для F присутствуют
положительные коэффициенты, то данное решение не оптимальное, т.е. F1 не максимальное.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
Положительный коэффициент в F перед х1,
т.е. х1 вводим в новый состав основных переменных. Определим
допустимое значение х1.
x3 = 2 - x1 + x2 ≥ 0, x2 = 0 x3 = 2 - x1 ≥ 0, x1 ≤ 2,
x4 = 6 - 3x1 + 2x2 ≥ 0,  x4 = 6 - 3x1 ≥
0,
x4 = 6 - 3x1 ≥
0,  x1 ≤
2,
x1 ≤
2,
x5 = 14 - 6x1 + 4x2 ≥ 0 x5 = 14 - 6x1 ≥ 0 x1 ≤ 14/6.
2. Определим выводимую переменную.
х1 = min {2, 2, 14/6} = 2.
Оценочное отношение в двух первых уравнениях совпадают,
поэтому в качестве разрешающего можно взять любое из них, например первое.
Шаг 1.
1. Определим состав основных и неосновных переменных:
основные: х1, х4, х5,
неосновные: х2, х3.
2. Выразим основные переменные через неосновные,
начиная с разрешающего уравнения:
x1 = 2 + x2 - x3, x1 = 2 + x2 - x3,
x4 = 6 - 3
(2 + x2 - x3) + 2x2,  x4 = - x2 + 3x3,
x4 = - x2 + 3x3,
x5 = 14 - 6
(2 + x2 - x3) + 4x2, x5 = 2 - 2x2 + 6x3.
Положив неосновные переменные равными нулю, получим второе
базисное решение: Х2 = (2; 0; 0; 0; 2), которое является допустимым,
но вырожденным, т.к. основная компонента x4 = 0.
Шаг 2. Выразим
F через неосновные переменные и определим
ее значение при выбранном базисном решении:
F = 2x1 - x2 = 2 (2 + x2 - x3) - x2 = 4 + х2 - 2х3
F2 = F(X2) = 4.
Шаг 3. Проверка оптимальности решения.
Т.к. в выражении для F присутствуют
положительные коэффициенты, то данное решение не оптимальное, т.е. F2 не максимальное.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
Положительный коэффициент в F перед х2,
т.е. х2 вводим в новый состав основных переменных. Определим
допустимое значение х2.
x1 = 2 + x2 - x3 ≥ 0, x3 = 0 x1 = 2 + x2 ≥ 0 x2 ≤ ∞
x4 = - x2 + 3x3 ≥ 0,
 x4 = - x2 ≥ 0
x4 = - x2 ≥ 0  x2 ≤ 0
x2 ≤ 0
x5 = 2 - 2x2 + 6x3 ≥ 0, x5 = 2 - 2x2 ≥ 0 x2 ≤ 1
2. Определим выводимую переменную.
х2 = min {∞, 0, 1} = 0.
При x2=0 переменная х4 обращается в 0.
Второе уравнение - разрешающее; х4 - переходит в неосновные.
Шаг 1.
1. Определим состав основных и неосновных переменных:
основные: х1, х2, х5,
неосновные: х3, х4.
2. Выразим основные переменные через неосновные,
начиная с разрешающего уравнения:
х2 = 3х3 - х4, х2
= 3х3 - х4,
x1 = 2 + 2х3
- х4,  x1 = 2 + 2х3 - х4,
x1 = 2 + 2х3 - х4,
x5 = 2 - 2
(3х3 - х4) + 6x3, x5 = 2 - 2х4.
Положив неосновные переменные равными нулю, получим третье
базисное решение: Х3 = (2; 0; 0; 0; 2), которое является допустимым,
но вырожденным.
Шаг 2. Выразим
F через неосновные переменные и определим
ее значение при выбранном базисном решении:
F = 2x1 - x2 = 2 (2 + 2х3 - х4) - (3х3
- х4) = 4 + х3 - х4.
F3 = F(X3) = 4.
Шаг 3. Проверка оптимальности решения.
Изменение целевой функции на этом шаге не произошло. Это
нарушение принципа улучшения решения, который должен выполняться при
использовании симплексного метода, в связи с чем уточним данный принцип: каждый
следующий шаг должен улучшить или, в крайнем случае, не ухудшить значение
целевой функции.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
Положительный коэффициент в F перед х3,
т.е. х3 вводим в новый состав основных переменных. Определим
допустимое значение х3.
х2 = 3х3 - х4 ≥ 0, х4
= 0 х2 = 3х3 ≥ 0 х3
≤ 0
x1 = 2 + 2х3
- х4 ≥ 0,  x1 = 2 + 2х3 ≥ 0 х3
≤ 2
x1 = 2 + 2х3 ≥ 0 х3
≤ 2
x5 = 2 - 2х4
≥ 0 x5 = 2
≥ 0 х3 ≤ ∞
2. Определим выводимую переменную.
х3 = min {0, 2, ∞} = 0.
При x3=0 переменная х2 обращается в 0.
Второе уравнение - разрешающее; х2 - переходит в неосновные.
Шаг 1.
1. Определим состав основных и неосновных переменных:
основные: х1, х3, х5,
неосновные: х2, х4.
2. Выразим основные переменные через неосновные,
начиная с разрешающего уравнения:
х3 =  , х3 =
, х3 =  ,
,
x1 = 2 + 2
( ) - х4,
) - х4,  x1 = 2 +
x1 = 2 + 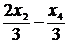 ,
,
x5 = 2 - 2х4
x5 = 2 - 2х4.
Положив неосновные переменные равными нулю, получим четвертое
базисное решение: Х4 = (2; 0; 0; 0; 2), которое является допустимым,
но вырожденным.
Шаг 2. Выразим
F через неосновные переменные и определим
ее значение при выбранном базисном решении:
F = 2x1 - x2 = 2 (2 + 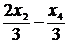 ) - x2 = 4 +
) - x2 = 4 +  .
.
F4 = F(X4) = 4.
Шаг 3. Проверка оптимальности решения.
Изменение целевой функции на этом шаге не произошло.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
Положительный коэффициент в F перед х2,
т.е. х2 вводим в новый состав основных переменных. Определим
допустимое значение х2.
х3 =  ≥ 0, х4 = 0 х3
=
≥ 0, х4 = 0 х3
=  , х2 ≤
0,
, х2 ≤
0,
x1 = 2 + 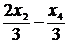 ≥ 0,
≥ 0,  x1 = 2 +
x1 = 2 +  ,
,  х2 ≤ 2,
х2 ≤ 2,
x5 = 2 - 2х4
≥ 0 x5 = 2 х2
≤ ∞
2. Определим выводимую переменную.
х2 = min {0, 2, ∞} = 0.
При x2=0 переменная х3 обращается в 0.
Первое уравнение - разрешающее; х3 - переходит в неосновные.
Шаг 1.
1. Определим состав основных и неосновных переменных:
основные: х1, х2, х5,
неосновные: х3, х4.
2. Выразим основные переменные через неосновные,
начиная с разрешающего уравнения:
х2 = 3х3 - х4, х2
= 3х3 - х4,
x1 = 2 + 
 x1 = 2 + 2х3
- х4,
x1 = 2 + 2х3
- х4,
x5 = 2 - 2х4
x5 = 2 - 2х4
Положив неосновные переменные равными нулю, получим пятое базисное
решение: Х5 = (2; 0; 0; 0; 2), которое является допустимым, но вырожденным.
Шаг 2. Выразим
F через неосновные переменные и определим
ее значение при выбранном базисном решении:
F = 2x1 - x2 = 2 (2 + 2х3 - х4) - (3х3
- х4) = 4 + х3 - х4.
F4 = F(X4) = 4.
Шаг 3. Проверка оптимальности решения.
Изменение целевой функции на этом шаге не произошло.
Выполненный шаг хотя и не вызвал увеличения значения линейной
функции, не является лишним, т.к. привел к новому базисному решению. Наличие
«пустых» шагов (∆F = 0) может привести к так называемому «зацикливанию», т.е.
возвращение к ранее найденному допустимому базисному решению (с тем же набором
основных и неосновных переменных), и в этом случае процесс бесконечен.
Вывод. Если на каком-либо шаге наибольшее возможное
значение переменной достигается в нескольких уравнениях одновременно (совпадают
их оценочные отношения), то разрешающим является любое из них. На следующем
шаге получаем вырожденное базисное решение, переход к очередному базисному
решению может не изменить целевую функцию (∆F = 0).
Замечание. Вырождение, полученное при оптимальном
решении, может привести к альтернативному оптимуму даже при ненулевых
коэффициентах при всех неосновных переменных в линейной функции.
Отсутствие
конечного оптимума (Fmax = ∞ или Fmin = -∞)
Рассмотрим отсутствие конечного оптимума на примере:
F = 2x1 - 3x2 + 1 → min
при ограничениях:
х1 + х2 ≥ 4,
х1 - х2 ≥ 1,
х1 - 2х2 ≤ 1,
х1 ≥ 0, х2 ≥ 0.
После приведения системы неравенств к каноническому виду и
решения нескольких итераций, на очередном шаге решения этой задачи симплексным
методом получаем:
Шаг 1.
1. Определим состав основных и неосновных переменных:
основные: х1, х2, х5,
неосновные: х3, х4.
2. Выразим основные переменные через неосновные, начиная с
разрешающего уравнения:
х1 =  ,
,
х2 =  ,
,
х5 = 4 + х3 - х4.
Положив неосновные переменные равными нулю, получим новое
базисное решение: Х = (5/3; 7/3; 0; 0; 4), которое является допустимым.
Шаг 2. Выразим F через неосновные переменные и определим ее
значение при выбранном базисном решении:
F = 2x1 - 3x2 + 1 = 2 ( ) - 3 (
) - 3 ( ) + 1 =
) + 1 = 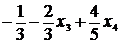 .
.
F = F(X) = -
1/3.
Шаг 3. Проверка оптимальности решения.
Т.к. в выражении для F присутствуют
отрицательные коэффициенты при неосновных переменных, то данное решение не
оптимальное, т.е. F не минимальное.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
Отрицательный коэффициент в F перед х3,
т.е. х3 вводим в новый состав основных переменных. Определим
допустимое значение х3.
х1 =  ≥ 0, х4=0 х1 =
≥ 0, х4=0 х1 =  ≥ 0 х3 ≤
∞
≥ 0 х3 ≤
∞
х2 =  ≥ 0,
≥ 0,  х2 =
х2 = 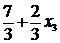 ≥ 0
≥ 0  х3 ≤ ∞
х3 ≤ ∞
х5 = 4 + х3 - х4 ≥ 0 х5
= 4 + х3 ≥ 0 х3 ≤ ∞
2. Определим выводимую переменную.
х3 = min {∞; ∞; ∞} = ∞.
Уравнения не ограничивают рост переменной х3,
поэтому и значение функции F неограниченно и отрицательно, т.е. Fmin = - ∞.
Вывод. Если на каком-либо шаге получаем, что во всех
уравнениях системы бесконечные оценочные отношения той переменной, которая
переводится в основные, то задача не имеет конечного оптимума (Fmax = ∞, если задача
на отыскание максимума, и Fmin = - ∞, если задача
на отыскание минимума).
1.7
Алгоритм табличного симплекс-метода
Пусть система приведена к каноническому виду.
f = c1x1 + c2x2
+ … + cnxn → max1 + a1m+1xm+1
+ … + a1nxn = b1,2 + a2m+1xm+1
+ … + a2nxn = b2,
…m + amm+1xm+1 +
… + amnxn = bm.
xj ≥ 0, j = 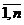
Запишем расширенную систему.
x1 + a1m+1xm+1 +
… + a1nxn = b1,2 + a2m+1xm+1
+ … + a2nxn = b2,
…m + amm+1xm+1 +
… + amnxn = bm,- c1x1 -
c2x2 - … - cnxn = 0.
Шаг 1. Получение начального
решения.
Выбираются m переменных, называемых базисными и обладающих следующим
свойством: они входят с коэффициентом 1 только в одно уравнение и коэффициентом
0 в остальные уравнения системы.
Остальные n - m переменных называют свободными. Все свободные переменные
полагаются равными 0, а базисные переменные - равные правым частям
соответствующих ограничений системы.
Пусть m базисных переменных - это переменные x1, x2, …, xm. Тогда начальное решение
имеет X0 имеет следующий вид:
X0 = {x1=b1, x2=b2, …, xm=bm, xm+1=0, …, xn=0}
Если все bi ≥ 0,  , то начальное решение является
допустимым. Переход к шагу 2. В противном случае используют алгоритмы
нахождения начального решения (Алгоритмы нахождения начального решения будут
описаны в подпунктах 1.8.1. и 1.8.2.).
, то начальное решение является
допустимым. Переход к шагу 2. В противном случае используют алгоритмы
нахождения начального решения (Алгоритмы нахождения начального решения будут
описаны в подпунктах 1.8.1. и 1.8.2.).
Шаг 2.
Выражение функции f только через свободные переменные.
f =  .
.
Переход к шагу 3.
Шаг 3. Проверка
решения на оптимальность.
Составляется симплекс-таблица.
|
Основные
(базисные) переменные
|
Коэффициенты
при переменных
|
Свободные члены
|
Оценочное
отношение
|
|
X1
|
X2
|
…
|
Xm
|
…
|
Xp
|
…
|
Xn
|
|
|
|
X1
|
a11
|
a12
|
…
|
a1m
|
…
|
a1p
|
…
|
a1n
|
b1
|
|
|
X2
|
a21
|
a22
|
…
|
a2m
|
…
|
a2p
|
…
|
a2n
|
b2
|
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
|
Xq
|
aq1
|
aq2
|
…
|
aqm
|
…
|
aqp
|
…
|
aqn
|
bq
|
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
|
Xm
|
am1
|
am2
|
…
|
amm
|
…
|
amp
|
…
|
amn
|
bm
|
|
|
F
|
-c1
|
-c2
|
…
|
-cm
|
…
|
-cp
|
…
|
-cn
|
0
|
|
В левой колонке симплекс-таблицы находятся базисные
переменные, в колонке свободных членов - правые части соответствующих
ограничений. В i-ой строке, j-м столбце стоит коэффициент при j-ой переменной в i-ом ограничении, i = 1,…, m, j = 1,…, n. В последней строке (f-строке) стоит
коэффициент при j-ой переменной в целевой функции из расширенной системы. В
предпоследнем столбце стоит значение свободного члена, входящего в целевую
функцию.
Для проверки решения на оптимальность просматривается
последняя f-строка:
· если коэффициенты, стоящие при свободных
переменных неотрицательны, то полученное решение оптимально;
· полученное решение единственно, если все
эти коэффициенты положительны;
· если среди неотрицательных коэффициентов
встречается хотя бы один нулевой, то задача имеет бесконечное множество
решений;
· если в последней строке есть хотя бы один
отрицательный коэффициент, а в соответствующем этому коэффициенту столбце нет
ни одного положительного элемента, то целевая функция f не ограничена на области
допустимых решений;
· если хотя бы один из коэффициентов,
стоящих при свободных переменных, отрицательный и в соответствующем ему столбце
есть хотя бы один положительный элемент, то полученное решение может быть
улучшено.
Переход к шагу 4.
Шаг 4. Получение нового решения.
1. Выбор переменной, вводимой в список базисных
переменных. Просматривается последняя строка симплекс-таблицы. Среди элементов
этой строки выбирается максимальный по абсолютной величине (по модулю)
отрицательный элемент. Столбец, в котором стоит этот элемент, называется
разрешающим. Пусть, например, это p-й столбец. Переменная xp стоящая в этом столбце,
вводится в список базисных переменных.
2. Выбор переменной, выводимой из списка базисных
переменных. Находят отношение элементов столбца свободных членов к элементам
разрешающего столбца. При делении на противоположный по знаку элемент и на 0
результат полагают равным +∞. Эти значения записываются в последний
столбец симплекс-таблицы. Среди этих отношений находят минимальное. Строка,
соответствующая минимальному отношению, называется разрешающей. Пусть,
например, это q-я
строка. Базисная переменная xq, стоящая в этой строке, выводится из списка
базисных переменных. Элемент симплекс-таблицы aqp, стоящий на пересечении
разрешающего столбца, называется разрешающим элементом.
. Выполнение симплекс-преобразования и переход к новой
симплекс-таблице. Элемент aij новой симплекс-таблицы вычисляется с помощью
следующего симплекс-преобразования (в алгебре это преобразование известно как прямой
ход метода Гаусса для решения систем линейных алгебраических уравнений):

Таким образом, при переходе к новой симплекс-таблице все элементы
разрешающей строки делятся на разрешающий элемент 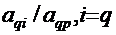 , а все остальные элементы
симплекс-таблицы, включая коэффициенты целевой функции и свободные члены,
пересчитываются по формуле
, а все остальные элементы
симплекс-таблицы, включая коэффициенты целевой функции и свободные члены,
пересчитываются по формуле
 .
.
Новое решение имеет следующий вид: все свободные переменные в нем
полагаются равными 0, а все базисные переменные - свободным членам, стоящим в
одной строке с ними.
После построения новой симплекс-таблицы следует перейти к шагу 3.
Определение
первоначального допустимого базисного решения
Изложенные выше вычисления проводились для случая, когда,
начальное решение является допустимым. Если в начальном решении существуют bi < 0, то допустимое
начальное решение можно найти по следующему алгоритму.
Шаг 1. Выражение функции через свободные переменные,
Шаг 2. Составление симплекс-таблицы.
Шаг 3. Выбор переменной, вводимой в список базисных
переменных.
Просматривается строка, содержащая максимальный по абсолютной
величине отрицательный свободный член, и по максимальному по абсолютной
величине отрицательному элементу этой строки выбирается разрешающий столбец,
например столбец с номером р. Переменная, стоящая в этом столбце, вводится в
список базисных переменных. Если просматриваемая строка не содержит
отрицательных элементов, то система ограничений несовместна, исходная задача
решений не имеет.
Шаг 4. Выбор переменной,
выводимой из списка базисных переменных.
Находят отношения элементов столбца
свободных членов к элементам разрешающего столбца. Рассматривают отношения, в
которых числитель и знаменатель отрицательные, и среди них выбирают минимальное.
Строка, соответствующая выбранному отношению, например q-я, является разрешающей,
и переменная, стоящая в этой строке, выводится из списка базисных переменных.
Элемент аqp, стоящий на пересечении разрешающей строки и разрешающего
столбца, является разрешающие элементом.
Шаг 5. По
формулам 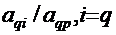 и
и  проводят симплекс-преобразование и переходят к новой
симплекс-таблице. Если в новой таблице все свободные члены неотрицательны, то
найденное решение является допустимым и следует перейти к шагу 3 алгоритма
симплекс-метода, в противном случае - к шагу 2 рассматриваемого алгоритма.
проводят симплекс-преобразование и переходят к новой
симплекс-таблице. Если в новой таблице все свободные члены неотрицательны, то
найденное решение является допустимым и следует перейти к шагу 3 алгоритма
симплекс-метода, в противном случае - к шагу 2 рассматриваемого алгоритма.
Понятие
об М-методе (методе искусственного базиса)
М-метод или метод искусственного базиса используется для
определения первоначального базисного решения, когда оно не является
допустимым, т.е. в начальном решении существуют bi < 0.
При расчете с помощью симплексных таблиц удобнее пользоваться
М-методом. Он заключается в следующем.
В каждое уравнение, дающее отрицательную компоненту в
базисном решении, вводим свою новую неотрицательную искусственную переменную y1, y2, …, yk, которая имеет тот же
знак, что и свободный член в правой части уравнения. В первой таблице включаем
в число основных все искусственные переменные и те обычные добавочные
переменные, которые определяют неотрицательные компоненты базисного решения.
Составляем новую линейную функцию T = F - M(y1 + y2 + … + yk), где М - произвольно большое число, и ищем ее максимум
(Т-задача). Выражение M(y1 + y2 + … + yk) назовем М-функцией. Справедлива теорема:
1. Если в оптимальном решении Т-задачи искусственные
переменные равны 0, то соответствующие значения остальных переменных дают
оптимальное решение исходное задачи (т.е. Tmax = Fmax, если y1 = y2 = … = yk = 0, т.е. минимум
М-функции равен 0).
2. Если имеется оптимальное решение Т-задачи, в
котором хотя бы одна из искусственных переменных отлична от 0, то система
ограничений исходной задачи несовместна.
3. Если Тmax= ∞, то исходная
система также неразрешим, причем либо Fmax= ∞, либо условия
задачи противоречивы.
Из теоремы следует, что вначале следует найти минимум
М-функции. Если он равен 0 и все искусственные переменные обращаются в 0, то
далее можно отбросить эти переменные и решать исходную задачу, исходя из
полученного допустимого базисного решения. На практике находят не минимум
М-функции, а максимум (-М) - функции.
Рассмотрим работу М-метода, используя симплексные таблицы, на
примере.
Найти максимум целевой функции:
F(x) = x1 + 2x2 → max
при наложенных ограничениях:
x1 - x2 ≤ - 1,
x1 - x2 ≥ - 3,
x1 ≤ 3.
Введем необходимое число искусственных переменных и столько
же дополнительных строк в симплексной таблице.
Имеем F(x) = x1 + 2x2 → max
x1 - x2 + x3 = - 1,
x1 - x2 - x4 = - 3,
x1 + x5 = 3.
X1 = (0; 0; -1; 3; 5) - недопустимое базисное
решение с одной отрицательной компонентой, поэтому в первое уравнение введем
искусственную переменную y1 с тем же знаком, что и свободный член:
x1 - x2 + x3 - у1 = - 1,
x1 - x2 - x4 = - 3,
x1 + x5 = 3
x1 + x2 - x3 + у1 = 1,
- x1 + x2 + x4 =
3,1 + x5 = 3.= x1 + 2x2 - My1
→ max.
Составляем первую симплексную таблицу.
|
Основные
переменные
|
Коэффициенты
при переменных
|
Свободные члены
|
Оценочное
отношение
|
|
х1
|
x2
|
x3
|
х4
|
x5
|
у1
|
|
|
|
у1
|
-1
|
1
|
-1
|
0
|
0
|
1
|
1
|
1
|
|
х4
|
-1
|
1
|
0
|
1
|
0
|
0
|
3
|
3
|
|
х5
|
1
|
0
|
0
|
0
|
1
|
0
|
3
|
∞
|
|
F
|
-1
|
-2
|
0
|
0
|
0
|
0
|
0
|
|
|
Mф
|
М
|
-М
|
М
|
0
|
0
|
М
|
М
|
|
Последняя строка - это (-М) - функция, т.е. (-Мф)
у1. Заполняем ее, умножая строку у1 на коэффициент (-М).
Проверяя выполнение критерия оптимальности при отыскании максимума (-М) -
функции, определяем, что в последней строке имеется отрицательный элемент во
втором столбце; значит он является разрешающим, переменная x2 переходит в основные.
Минимальное оценочное отношение в первой строке, она является разрешающей.
Переменная у1 переходит в состав неосновных переменных, обращается в
нуль на следующем базисном решении и далее исключается из рассмотрения.
В соответствии с общим алгоритмом получаем таблицу:
|
Основные
переменные
|
Коэффициенты
при переменных
|
Свободные члены
|
Оценочное
отношение
|
|
х1
|
x2
|
x3
|
х4
|
х5
|
|
|
|
x2
|
-1
|
1
|
-1
|
0
|
0
|
1
|
|
|
х4
|
0
|
0
|
1
|
1
|
0
|
2
|
|
|
х5
|
1
|
0
|
0
|
0
|
1
|
3
|
|
|
F
|
-3
|
0
|
-2
|
0
|
0
|
2
|
|
|
Mф
|
0
|
0
|
0
|
0
|
0
|
0
|
|
Последняя строка показывает, что критерий оптимальности
выполнен; max (-Mф) = 0, значит min Mф = 0, далее эту строку можно не рассматривать.
Получено допустимое базисное решение (0; 1; 0; 2; 3), начиная с которого решаем
исходную задачу в соответствии с обычным алгоритмом.
Замечание. При решении задачи на отыскание минимума
линейной целевой функции рекомендуется вместо Zmin находить (-Z)max.
.8
Алгоритм матричного симплекс-метода
Поставленная описательная задача переводится в математическую
форму. Полученное математическое описание приводят к матричному виду. Затем
матричное описание задачи приводят к канонической форме. После того как система
линейных уравнений приведена к канонической форме, приступают к решению задачи
линейного программирования. Алгоритм решения этой задачи состоит из
последовательности построения матриц.
Алгоритм решения следующий:
1) определить ведущий столбец;
2) определить ведущий элемент;
) определить ведущую строку;
) составить уравнения пересчета матрицы;
) выполнить пересчет матрицы;
) проверить результаты пересчета матрицы на
оптимальность;
) если найденное решение оптимально, то вычисления
прекратить и сформулировать ответ. Если найденное решение не оптимально, то
перейти к п. 1.
Признаком оптимальности является наличие в векторе решений
только отрицательных или нулевых значений коэффициентов, как для фактических
переменных, так и для фиктивных переменных (при решении задачи на поиск
максимума). Столбец в канонической задаче ЛП называется правильным, если все
его элементы равны нулю, кроме единственного положительного и равного единице.
Вся матрица в канонической задаче ЛП называется правильной,
если она содержит m правильных столбцов (где m равно числу строк в
матрице).
Все правильные столбцы должны содержать единицы в разных
строках матрицы.
Ответ записывается следующим образом: каждому отрицательному
коэффициенту в векторе решений ставится в соответствие нулевой коэффициент для
соответствующей переменной в ответе; для каждого нулевого коэффициента в
векторе решений (т.е. для правильного столбца) ставится в соответствие значение
свободного члена (из вектора b) из строки, содержащей единицу в столбце данной
переменной. Фиктивные переменные в ответе не учитываются.
Ведущим столбцом может быть назначен любой столбец t матрицы, удовлетворяющий
одному из условий:
· первый элемент, содержащий положительный
элемент (кроме нуля) в строке (векторе) решений;
· столбец, содержащий наибольший
положительный элемент в строке (векторе) решений;
· если столбец t удовлетворяет условию:
 при решении задач на max;
при решении задач на max;
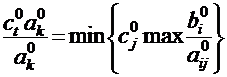 при решении задач на min,
при решении задач на min,
причем 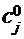 - коэффициент целевой функции в столбце j и
- коэффициент целевой функции в столбце j и  - коэффициент в столбце j выбранной строки i матрицы
А.
- коэффициент в столбце j выбранной строки i матрицы
А.
Третий способ определения ведущего элемента матрицы А
приводит к самому короткому решению задачи, т.к. первые два способа носят
формальный (произвольный) характер.
Критерием останова алгоритма поиска решений будет:
· для поиска max целевой функции - все
коэффициенты вектора решений или равны нулю, или отрицательны;
· для поиска min целевой функции - все
коэффициенты вектора решений или равны нулю, или положительны.
Критерий останова алгоритма сформулирован для задач, целевая
функция которых содержит только положительные коэффициенты. Для решения задач в
общем виде используются два подхода, которые будут расписаны в подпункте 2.5.1.
Рассмотрим работу симплексного метода на примере.
Найти максимум целевой функции:
F = x1 + 2x2 + x3 + 2x4 → max
при наложенных ограничениях:
x1 + x2 + 3x4 ≤ 8;
x1 + 3x2 + x3 ≥ 14;
x2 + 2x3 + 4x4 = 9.
Для решения поставленной задачи необходимо привести систему
ограничений к канонической форме и добавить нулевые члены в каждое уравнение.
x1 + x2 + 0x2 + 3x4 + x5 0x6 = 8;
x1 + 3x2 + x3 + 0x4 + 0x5 - x6 = 14;
0x1 + x2 + 2x3 +
4x4 + 0x5 + 0x6 = 9.(x) = x1 + 2x2
+ x3 + 2x4 + 0x5 + 0x6 → max.
Оставим коэффициенты и получим условия задачи в матричном
виде:

Таким образом, каноническая задача ЛП определена матрицей А,
вектором свободных членов b = {8; 14; 9} и вектором решений c = {1; 2; 1; 2; 0; 0}.
Воспользуемся для расчета третьим способом. Четырем столбцам
матрицы А соответствуют коэффициенты вектора решения больше нуля. Любой
столбец может быть назначен ведущим.
По третьему правилу  определим минимальные элементы в каждом столбце.
определим минимальные элементы в каждом столбце.
Для первого столбца: 8/1 14/2 → 1 ∙ 14/2 = 7.
Для второго столбца: 8/1 14/3 9/1 → 2 ∙ 14/3 = 28/3.
Для третьего столбца: 14/1 9/2 → 1 ∙ 9/2 = 9/2.
Для четвертого столбца: 8/3 9/4 → 2 ∙ 9/4 = 18/4.
Сначала внутри каждого столбца выбираем минимальный элемент и
умножаем его на соответствующее значение из вектора решения. Затем из четырех
величин выбираем максимальное.
Таким образом, ведущим элементом будет элемент a22, ведущий столбец - второй, ведущая строка - вторая.
Во втором столбце будем исключать вторую переменную. Для этого
надо, чтобы в ведущей строке коэффициент при второй переменной был равен 1.
Ведущая строка (ее элементы обозначим буквой φ)
будет пересчитываться по
формуле:
 ,
,
где 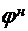 - новое значение элемента ведущей строки;
- новое значение элемента ведущей строки;
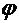 - текущее значение элемента ведущей строки;
- текущее значение элемента ведущей строки;
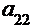 - значение
ведущего элемента
- значение
ведущего элемента

В остальных строках матрицы коэффициент при второй переменной
должен быть равен 0. Для первой строки (элементы, которых обозначим буквой Ψ) получим формулу для пересчета:

где  - новое значение элемента первой строки;
- новое значение элемента первой строки;
 - новое значение элемента второй (ведущей) строки.
- новое значение элемента второй (ведущей) строки.
Такое преобразование строк матрицы носит название преобразования
Жордана-Гаусса.
Для третьей строки:

Для четвертой строки (строки вектора решений):


Значение целевой функции f определим по формуле:
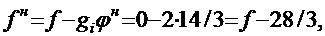
где  - коэффициент целевой функции.
- коэффициент целевой функции.
Т.к. третий, четвертый и шестой элементы вектора решения
положительные, то необходимо вычислить аналогичные вычисления для этих
столбцов.
Для третьего столбца: 14 13/5 → 1/3 ∙ 13/5 = 13/15.
Для четвертого столбца: 10/9 13/12 → 2 ∙ 13/12
= 13/6.
Для шестого столбца: 10 13 → 2/3
∙ 10 = 20/3.
Ведущим элементом будет a16.
Определим формулы для пересчета строк матрицы.
Для ведущей (первой) строки:

Для второй, третьей и четвертой строк соответственно:


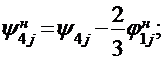

Т.к. третий элемент вектора решений больше нуля, то
вычисления необходимо повторить. В третьем столбце единственный элемент a33 положительный и больший
нуля, поэтому он и будет ведущим элементом.
Для ведущей (третьей) строки:
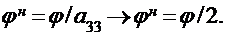
Для первой, второй и четвертой строк соответственно:


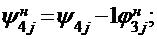

Т.к. вектор решения (фактические и фиктивные переменные)
содержит нулевые и отрицательные значения, то найдено оптимальное решение.
Найденное решение записывается следующим образом: отрицательным
коэффициентам в векторе решений соответствуют нулевые значения, а нулевым
значениям - значения свободных членов (b) в строках, содержащих
единицу.
Ответ: X {0; 8; 1/2; 0}.
Т.к. пятая и шестая переменные - фиктивные, то в решении они
не учитываются. Максимальное значение, равное 33/2, целевая функция принимает
при следующих значениях аргументов: x1 = 0; x2 = 8; x3 = 1/2; x4 = 0.
Проверка:
F(x) = x1 + 2x2 + x3 + 2x4 = 1 ∙ 0 + 2 ∙ 8 + 1 ∙ 1/2 + 2 ∙ 0 = 0 +
16 + 0,5 + 0 = 16,5;
x1 + x2 + 3x4 ≤ 8; 1 ∙ 0 + 1 ∙ 8 + 0 ∙
0,5 + 3 ∙ 0 ≤ 8; 0 + 8 + 0 + 0 ≤ 8; 8 ≤ 8;
x1 + 3x2 + x3 ≥ 14; 2 ∙ 0 + 3 ∙ 8 + 1 ∙
0,5 + 0 ∙ 0 ≥ 14; 24,5 ≥ 14;
x2 + 2x3 + 4x4 = 9; 0 ∙ 0 + 1 ∙ 8 + 2 ∙ 0,5 +
4 ∙ 0 = 9; 0 + 8 + 1 + 0 = 9; 9 = 9.
Общие
случаи решения задач ЛП матричным симплекс-методом
На практике встречаются случаи, когда коэффициенты целевой
функции принимают как положительные, так и отрицательные значения. Для решения
таких задач используют два подхода.
Первый подход. Поставленную задачу решают по правилам,
изложенным в пункте 1.9, добавив новые условия.
Если выполнены условия пункта 1.9 (все элементы последней
строки или отрицательные, или нулевые при поиске максимума и, наоборот, - при
поиске минимума), но количество правильных столбцов матричной модели меньше,
чем количество условий ограничений, то определяют ведущий элемент по правилам
пункта 1.9, но только в строках, которые не были ведущими.
Второй подход. Математическую модель приводят к
правильному виду по правилам, изложенным в пункте 1.9, но в начало процедуры добавляют
один шаг - применяют процедуру Жордана - Гаусса поочередно к тем столбцам,
которые в последней строке матрицы содержат отрицательные коэффициенты,
добиваясь при этом замены отрицательных значений коэффициентов на нулевые
значения.
Рассмотрим пример, решив его вторым подходом.
Найти максимум целевой функции F(x) = - 2x1 + 3x2 → max
при ограничениях:
x1 - x2 ≤ 6;
x1 + 3x2 ≤ 6;
x1 + 2x2 ≤ 8;
xj ≥ 0, 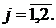
Выполнив необходимые преобразования, получим матричную модель

Первый элемент последней строки - отрицательный. Выполнив
преобразование Жордана - Гаусса относительно элемента а31, т.к. он
имеет коэффициент, равный единице. Формула для пересчета последней строки:


Теперь для определения максимума целевой функции переходим к
алгоритму, описанному в пункте 2.5.
Ведущим элементом будет а22. Пересчитаем
коэффициенты торой строки

Формула для пересчета первой строки:  .
.
Формула для пересчета третьей строки: 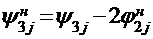 .
.
Формула для пересчета четвертой строки:  .
.

Ведущий элемент - а35. Формула для пересчета
четвертой строки:
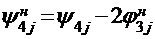 .
.

Все коэффициенты последней строки отрицательные. Целевая
функция достигает своего максимума, равного 6, в точке Х (0; 2).
Проверка:
F(x) = - 2 ∙ 0 + 3 ∙ 2 = 6.
Первое ограничение: 2 ∙ 0 - 1 ∙ 2 ≤ 6, - 2 ≤
6.
Второе ограничение: - 1 ∙ 0 + 3 ∙ 2 ≤ 6, 6 ≤
6.
Третье ограничение: 1 ∙ 0 + 2 ∙ 2 ≤ 8, 4 ≤
8.
2.
Решение задач симплекс-методом
Предприятию требуется составить план выпуска двух видов
изделий четырьмя цехами так, чтобы от продаж изготовленной продукции
предприятие получило наибольшую прибыль. Оба вида изделий последовательно
обрабатываются в этих четырех цехах (таблица 1). В плане должно быть
предусмотрено, что I цех может обрабатывать эту продукцию в течении 15 ч, II
цех - 8 ч, III цех - 16 ч, IV цех - 12 ч.
Таблица 1. Обработка изделий в цехах
|
Изделия
|
Цех
|
|
1
|
2
|
3
|
4
|
|
I
|
2
|
1
|
4
|
0
|
|
II
|
3
|
2
|
0
|
4
|
Предприятие от продажи изделия первого вида получило 2 руб.
прибыли, от второго вида - 3 руб. прибыли.
.1
Решение задачи с помощью симплекс-таблиц
Обозначим первый вид изделия за х1, а второй - х2.
Составим математическую модель этой задачи:
F = 2x1 + 3x2 → max
при ограничениях:
х1 + 3х2 ≤ 15,
х1 + 2х2 ≤ 8,
х1 ≤ 16,
х2 ≤ 12,
х1 ≥ 0, х2 ≥ 0.
Приведем систему ограничений к каноническому виду, введя
дополнительные неотрицательные переменные со знаком «+», т.к. неравенства имеют
вид «≤».
х1 + 3х2 + х3 = 15,
х1 + 2х2 + х4 = 8,
х1 + х5 = 16,
х2 + х6 = 12.
После введения добавочных переменных систему уравнений и
целевую функцию запишем в виде расширенной системы:
х1 + 3х2 + х3 = 15,
х1 + 2х2 + х4 = 8,
х1 + х5 = 16,
х2 + х6 = 12,
F - 2x1 - 3x2 = 0.
Шаг 1.
1. Определим основные и неосновные переменные:
основные: х3, х4, х5, х6;
неосновные: х1, х2.
2. Выразим основные переменные через неосновные:
х3 = 15 - 2х1 - 3х2,
х4 = 8 - х1 - 2х2,
х5 = 16 - 4х1,
х6 = 12 - 4х2.
3.
Запишем первое базисное решение, положив неосновные переменные равными нулю: Х1
= (0; 0; 15; 8; 16; 12).
Шаг 2.
Выразим F через неосновные переменные и вычислим ее значение:
F = 2x1 + 3x2.
F1 = F(X1) = 2 ∙ 0 + 3 ∙ 0 = 0.
Шаг 3. Заполним симплекс-таблицу.
|
Основные
переменные
|
Коэффициенты
при переменных
|
Свободные члены
|
Оценочное
отношение
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
|
|
|
х3
|
2
|
3
|
1
|
0
|
0
|
0
|
15
|
5
|
|
х4
|
1
|
2
|
0
|
1
|
0
|
0
|
8
|
4
|
|
х5
|
4
|
0
|
0
|
0
|
1
|
0
|
16
|
∞
|
|
х6
|
0
|
4
|
0
|
0
|
0
|
1
|
12
|
3
|
|
F
|
-2
|
-3
|
0
|
0
|
0
|
0
|
0
|
|
Т.к. существует отрицательный коэффициент в последней
(оценочной) строке, то решение не оптимально.
Шаг 4. Переход к новому решению.
Выбираем максимальный по модулю коэффициент в оценочной
строке. В данном случае - это коэффициент (- 3). Второй столбец - разрешающий.
Переменная х2 вводится в состав основных.
Чтобы определить выводимую переменную, найдем оценочное
отношение и выберем минимальное. В данном случае минимальное оценочное
отношение равно 3. Четвертая строка является разрешающей. Переменная х5
выводится из состава основных переменных.
Шаг 3. Выполним симплекс-преобразования и перейдем к
новой симплекс-таблице.
|
Основные
переменные
|
Коэффициенты
при переменных
|
Свободные члены
|
Оценочное
отношение
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
|
|
|
х3
|
2
|
0
|
1
|
0
|
0
|
-3/4
|
6
|
3
|
|
х4
|
1
|
0
|
0
|
1
|
0
|
-1/2
|
2
|
2
|
|
х5
|
4
|
0
|
0
|
0
|
1
|
0
|
16
|
4
|
|
х2
|
0
|
1
|
0
|
0
|
0
|
1/4
|
3
|
∞
|
|
F
|
-2
|
0
|
0
|
0
|
0
|
3/4
|
9
|
|
Т.к. существует отрицательный коэффициент в оценочной строке,
то решение не оптимально.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
Отрицательный коэффициент а51 = -2. Первый столбец
- разрешающий. Переменная х1 вводится в состав основных.
2. Определим выводимую переменную.
Найдем оценочное отношение. Минимальное оценочное отношение
равно 2. Вторая строка является разрешающей. Переменная х4 выводится
из состава основных переменных.
Шаг 3. Выполним симплекс-преобразования и перейдем к
новой симплекс-таблице.
|
Основные
переменные
|
Коэффициенты
при переменных
|
Свободные члены
|
Оценочное
отношение
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
|
|
|
х3
|
0
|
0
|
1
|
-2
|
0
|
1/4
|
2
|
8
|
|
х1
|
1
|
0
|
0
|
1
|
0
|
-1/2
|
2
|
∞
|
|
х5
|
0
|
0
|
0
|
-4
|
1
|
2
|
8
|
4
|
|
х2
|
0
|
1
|
0
|
0
|
0
|
1/4
|
3
|
12
|
|
F
|
0
|
0
|
0
|
2
|
0
|
-1/4
|
13
|
|
Т.к. существует отрицательный коэффициент в оценочной строке,
то решение не оптимально.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
Отрицательный коэффициент а56 = -1/4. Шестой
столбец - разрешающий. Переменная х6 вводится в состав основных.
2. Определим выводимую переменную.
Найдем оценочное отношение. Минимальное оценочное отношение
равно 4. Третья строка является разрешающей. Переменная х5 выводится
из состава основных переменных.
Шаг 3. Выполним симплекс-преобразования и перейдем к
новой симплекс-таблице.
|
Основные
переменные
|
Коэффициенты
при переменных
|
Свободные члены
|
Оценочное
отношение
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
|
|
|
х3
|
0
|
0
|
1
|
3/2
|
-1/8
|
0
|
1
|
|
|
х1
|
1
|
0
|
0
|
0
|
1/4
|
0
|
4
|
|
|
х6
|
0
|
0
|
0
|
-2
|
1/2
|
1
|
4
|
|
|
х2
|
0
|
1
|
0
|
1/2
|
-1/8
|
0
|
2
|
|
|
F
|
0
|
0
|
0
|
3/2
|
1/8
|
0
|
14
|
|
Критерий оптимальности выполнен, т.к. в последней строке нет
отрицательных значений. Fmax = 14, оптимальное базисное решение: Х =
(4; 2; 1; 0; 0; 4).
В результате решения получаем ответ:
Для того чтобы предприятие получило максимальную прибыль,
необходимо выпустить 4 изделия первого вида и 2 изделия второго вида, учитывая
последовательную обработку в четырех цехах. В результате этого максимальная
прибыль составит 14 руб.
.2
Решение задачи матричным симплекс-методом
Составим математическую модель данной задачи:
F = 2x1 + 3x2 → max
при ограничениях:
х1 + 3х2 ≤ 15,
х1 + 2х2 ≤ 8,
х1 ≤ 16,
х2 ≤ 12,
х1 ≥ 0, х2 ≥ 0.
Для решения поставленной задачи необходимо привести систему
ограничений к канонической форме и добавить нулевые члены в каждое уравнение.
х1 + 3х2 + х3 + 0х4
+ 0х5 + 0х6 = 15,
х1 + 2х2 + 0х3 + х4
+ 0х5 + 0х6 = 8,
х1 + 0х2 + 0х3 + 0х4
+ х5 + 0х6 = 16,
х1 + 4х2 + 0х3 + 0х4
+ 0х5 + х6 = 12.
F(x) = 2x1 + 3x2 + 0х3 + 0х4 + 0x5 + 0x6 → max.
Оставим коэффициенты и получим условия задачи в матричном
виде:
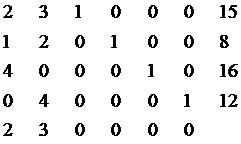
Воспользуемся для расчета третьим способом. Двум столбцам
матрицы А соответствуют коэффициенты вектора решения больше нуля. Любой
столбец может быть назначен ведущим.
Определим минимальные элементы в каждом столбце.
Для первого столбца: 15/2 8/1 16/4 → 2 ∙ 4 = 8.
Для второго столбца: 15/3 8/2 12/4 → 3 ∙ 3 = 9.
Из двух величин выберем максимальное. В данном случае это 9.
Таким образом, ведущим элементом будет элемент a42, ведущий столбец -
второй, ведущая строка - четвертая.
Во втором столбце будем исключать четвертую переменную. Для
этого надо, чтобы в ведущей строке коэффициент при второй переменной был равен
1.
Пересчитаем элементы ведущей строки по формуле и получим
матрицу в виде:
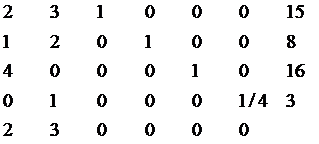
В остальных строках матрицы коэффициент при второй переменной
должен быть равен 0. В итоге получим:
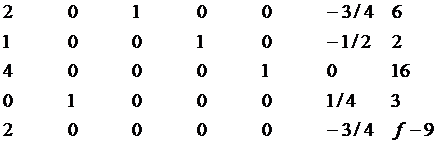
Т.к. первый элемент вектора решений положительный, то
необходимо вычислить аналогичные вычисления для этого столбца.
Для первого столбца: 3 2 4 → 2 ∙ 2 = 4.
Ведущим элементом будет a21.
Пересчитаем строки матрицы.

Т.к. шестой элемент вектора решений больше нуля, то
вычисления необходимо повторить.
Для шестого столбца: 8 4 12 → 1/4 ∙ 4 = 1.
Ведущий элемент - а36.
Пересчитаем строки матрицы.

Т.к. вектор решения содержит нулевые и отрицательные
значения, то найдено оптимальное решение. Fmax = 14, оптимальное
базисное решение: X {4; 2; 1; 0; 0; 4}.
В результате решения получаем ответ:
Для того чтобы предприятие получило максимальную прибыль,
необходимо выпустить 4 изделия первого вида и 2 изделия второго вида, учитывая
последовательную обработку в четырех цехах. В результате этого максимальная
прибыль составит 14 руб.
Сравнение матричного симплекс-метода с табличным.
По моему мнению, матричный симплекс-метод более трудоемкий,
чем табличный, т.к. для пересчета матрицы матричным методом необходимо
постоянно составлять формулы для ведущего столбца, а затем по этой формуле
пересчитывать всю строку. Для каждой строки составляется своя формула. В
табличном симплексе для облегчения заполнения таблицы можно использовать
несколько правил:
1) в последней (оценочной) строке против всех основных
переменных ставим нуль;
2) предыдущая разрешающая строка пересчитывается
делением на разрешающий элемент;
) расставляем нули и единицы в столбцах
соответствующим основным переменным:
· 1 - против «своей основной переменой»,
· 0 - против «чужой переменной»;
4) для заполнения других коэффициентов пользоваться
формулой:

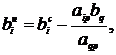
где p - номер разрешающего столбца,
q - номер разрешающей строки.
В матричном симплексе нет понятия основных и свободных
переменных и на первой итерации на конкретном шаге не нужно выражать основные
переменные через свободные.
.3
Решение задачи М-методом (методом искусственного базиса)
Найти максимум целевой функции:
F(x) = x1 + 2x2 → max
при наложенных ограничениях:
x1 - x2 ≤ - 1,
x1 - x2 ≥ - 3,
x1 ≤ 3.
Введем необходимое число искусственных переменных и столько
же дополнительных строк в симплексной таблице.
Имеем: F(x) = x1 + 2x2 → max
при ограничениях:
x1 - x2 + x3 = - 1,
x1 - x2 - x4 = - 3,
x1 + x5 = 3.
Выразим основные переменные через неосновные.
х3 = - 1 - х1 + х2,
х4 = - 3 - х1 + х2,
х5 = 3 - х1.
Положив неосновные переменные равными нулю, получим базисное
решение: X1 = (0; 0; -1; 3; 5), которое является недопустимым, т.к. базисное
решение имеет одну отрицательную компоненту. Поэтому в первое уравнение введем
искусственную переменную y1 с тем же знаком, что и свободный член:
x1 - x2 + x3 - у1 = - 1,
x1 - x2 - x4 = - 3,
x1 + x5 = 3
x1 + x2 - x3 + у1 = 1,
- x1 + x2 + x4 =
3,1 + x5 = 3.= x1 + 2x2 - My1
→ max.
Составляем первую симплексную таблицу.
|
Основные
переменные
|
Коэффициенты
при переменных
|
Свободные члены
|
Оценочное отношение
|
|
х1
|
x2
|
x3
|
х4
|
x5
|
у1
|
|
|
|
у1
|
-1
|
1
|
-1
|
0
|
0
|
1
|
1
|
1
|
|
х4
|
-1
|
1
|
0
|
1
|
0
|
0
|
3
|
3
|
|
х5
|
1
|
0
|
0
|
0
|
1
|
0
|
3
|
∞
|
|
F
|
-1
|
-2
|
0
|
0
|
0
|
0
|
0
|
|
|
Mф
|
М
|
-М
|
М
|
0
|
0
|
М
|
М
|
|
Проверяя выполнение критерия оптимальности при отыскании
максимума (-М) - функции, определяем, что в последней строке имеется
отрицательный элемент во втором столбце. Второй столбец разрешающий, переменная
x2 переходит в состав
основных переменных.
Найдем оценочное отношение. Минимальное оценочное отношение в
первой строке. Первая строка является разрешающей, переменная у1 переходит
в состав неосновных переменных. Обращается в нуль на следующем базисном решении
и далее исключается из рассмотрения.
В соответствии с общим алгоритмом получаем таблицу:
|
Основные
переменные
|
Коэффициенты
при переменных
|
Свободные члены
|
Оценочное отношение
|
|
х1
|
x2
|
x3
|
х4
|
х5
|
|
|
|
x2
|
-1
|
1
|
-1
|
0
|
0
|
1
|
∞
|
|
х4
|
0
|
0
|
1
|
1
|
0
|
2
|
∞
|
|
х5
|
1
|
0
|
0
|
0
|
1
|
3
|
3
|
|
F
|
-3
|
0
|
-2
|
0
|
0
|
2
|
|
|
Mф
|
0
|
0
|
0
|
0
|
0
|
|
Последняя строка показывает, что критерий оптимальности
выполнен; max (-Mф) = 0, значит min Mф = 0, далее эту строку можно не рассматривать.
Получено допустимое базисное решение: Х1 = (0; 1; 0; 2; 3), начиная
с которого решаем исходную задачу в соответствии с обычным алгоритмом.
Т.к. существует отрицательный коэффициент в оценочной строке,
то решение не оптимально.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
Максимальный отрицательный коэффициент а41 = -3.
Первый столбец - разрешающий. Переменная х1 вводится в состав
основных.
2. Определим выводимую переменную.
Найдем оценочное отношение. Минимальное оценочное отношение равно
3. Третья строка является разрешающей. Переменная х5 выводится из
состава основных переменных.
3. Выполним симплекс-преобразования и перейдем к новой
симплекс-таблице.
|
Основные
переменные
|
Коэффициенты
при переменных
|
Свободные члены
|
Оценочное
отношение
|
|
х1
|
x2
|
x3
|
х4
|
х5
|
|
|
|
x2
|
0
|
1
|
-1
|
0
|
1
|
4
|
∞
|
|
х4
|
0
|
0
|
1
|
1
|
0
|
2
|
2
|
|
х1
|
1
|
0
|
0
|
0
|
1
|
3
|
∞
|
|
F
|
0
|
0
|
-2
|
0
|
3
|
11
|
|
Т.к. существует отрицательный коэффициент в оценочной строке,
то решение не оптимально.
Шаг 4. Переход к новому решению.
1. Определим вводимую переменную.
Отрицательный коэффициент а43 = -2. Третий столбец
- разрешающий. Переменная х3 вводится в состав основных.
2. Определим выводимую переменную.
Найдем оценочное отношение. Минимальное оценочное отношение
равно 2. Вторая строка является разрешающей. Переменная х4 выводится
из состава основных переменных.
3. Выполним симплекс-преобразования и перейдем к новой
симплекс-таблице.
|
Основные
переменные
|
Коэффициенты
при переменных
|
Свободные члены
|
Оценочное
отношение
|
|
х1
|
x2
|
x3
|
х4
|
х5
|
|
|
|
x2
|
0
|
1
|
0
|
1
|
1
|
6
|
|
|
х3
|
0
|
0
|
1
|
1
|
0
|
2
|
|
|
х1
|
1
|
0
|
0
|
0
|
1
|
3
|
|
|
F
|
0
|
0
|
0
|
2
|
3
|
15
|
|
Критерий оптимальности выполнен, т.к. в последней строке нет
отрицательных значений. Fmax = 15, оптимальное базисное решение: Х =
(3; 6; 2; 0; 0).
Заключение
В данном курсовом проекте были изучены теоретические основы
задач линейного программирования, история происхождения универсального метода
последовательного улучшения решения, теоретические сведения о применении
разновидностей симплекс-метода в жизни. Работа симплексного метода и его
разновидностей была применена при решении экономической задачи нахождения
оптимального плана производства.
Для упрощения нахождения оптимального плана (решения) был
написан модуль, реализующий работу симплексного метода.
В результате выполнения проекта пришли к следующим выводам:
1. Роль симплексного метода достаточно велика, т.к.
симплекс-метод находит применение для решения широкого круга задач линейного
программирования в экономической сфере, сфере планирования и других сферах,
связанных с производством, и до настоящего времени является одним из основных
методов.
2. Матричный симплекс-метод более трудоемкий, чем
табличный, т.к. для решения задачи матричным симплекс-методом для каждой строки
составляется соответствующая формула пересчета.
. Задачи линейного программирования могут иметь
большое количество вершин (опорных решений), что вызывает вычислительные
трудности. Для упрощения нахождения оптимального плана (решения) был написан
модуль, реализующий работу симплексного метода. Однако несложные примеры с
применением симплексного метода можно решать вручную.
. Симплексный метод и его разновидности в настоящее
время достаточно востребованы во всех сферах производства.
Список литературы
1. Введение в исследование операций. 6-е
издание.: Пер. с англ. - М.: Издательский дом «Вильямс», 2001. - 912 с.: ил. -
Парал. тит. англ.
2. Исследование операций в экономике:
Учебное пособие для вузов/ Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман;
Под ред. проф. Н.Ш. Кремера. - М.: ЮНИТИ, 2001. - 407 с.
. Линейное программирование. Ашманов С.А.
- М.: Наука. Главная редакция физико-математической литературы, 1981. - 340 с.
4. Малеко Е.М. Математические методы и модели
исследования операций: Учеб. пособие. - Магнитогорск: МаГУ, 2003. - 100 с.
5. Математические методы в программировании:
Учебник. - М.: ИД «ФОРУМ»: ИНФРА-М, 2006. - 224 с.: ил. - (Профессиональное
образование). - (Учимся программировать).
6. Математическое программирование: Учебное
пособие. - 2-е издание, переработанное и дополненное / Кузнецов Ю.Н., Кузубов
В.И., Волощенко А.Б. - М.: Высшая школа, 1980. - 300 с.
. Справочник по математике для инженеров и
учащихся втузов. Бронштейн И.Н., Семендяев К.А. - М.: Наука. Главная редакция
физико-математической литературы, 1981.
Приложение
Dim KolBazPer, KolPer, nomerMinus, numStroki,
numStolbca As Integerflag As Boolean
delay(zaderjka)= zaderjka ' Установка задержки= Timer 'Старт таймера While Timer < Start + PauseTime' Позволяет выполнять
действия в процессе задержки
LoopSub
Sub Clear_Click()
'Гасим кнопку вычисление. Enabled =
False
'Форматирование(«A:Z»).Clear(«A:Z»).Select. ColumnWidth =
8.63(«A1»).SelectSub
ПоискРазрешающейСтроки()i = 3 To KolBazPer +
2Worksheets («Лист1»).Cells (i,
nomerMinus).Value * Worksheets («Лист1»).Cells (i, KolPer + 2).Value > 0
Then= Cells (i, KolPer + 2).Value / Cells (i, nomerMinus).Value(i, KolPer + 3)
= OcOtnIf
(Worksheets («Лист1»).Cells (i, nomerMinus).Value *
Worksheets («Лист1»).Cells (i,
KolPer + 2).Value < 0) _(Worksheets («Лист1»).Cells (i, nomerMinus).Value = 0)
_((Worksheets («Лист1»).Cells (i, KolPer + 2).Value = 0) _(Worksheets («Лист1»).Cells (i,
nomerMinus).Value > 0)) Then= «Бесконечность»(i, KolPer + 3) =
OcOtnIf
((Worksheets («Лист1»).Cells (i, KolPer +
2).Value = 0) _(Worksheets («Лист1»).Cells (i, nomerMinus).Value < 0)) Then=
0(i, KolPer + 3) = OcOtnIfi
Worksheets («Лист1»).Cells (3, KolPer + 3) = «Бесконечность» Then= 10000=
Worksheets («Лист1»).Cells (3,
KolPer + 3) 'минимальный элемент - первый
End If= 3 'строка минимального элемента третьяi = 3 To
KolBazPer + 2
'проверка следующего элемента на минимальность
If (Worksheets («Лист1»).Cells (i, KolPer + 3)
< min) And _
(Worksheets («Лист1»).Cells (i, KolPer + 3) <> «Бесконечность») Then=
Worksheets («Лист1»).Cells (i,
KolPer + 3)= iIfi
= nomerMinus(Cells(nomerMinus, 1), Cells
(nomerMinus, KolPer + 3)).Select. Interior. Color = vbGreenSub
ПоискРазрешающегоСтолбца()s, i, j, min As
Integer= 0j = 2 To KolPer + 1Worksheets («Лист1»).Cells (KolBazPer + 3, j) < 0 Then 'Проверка строки на отрицательный элемент
s = s + 1 'сумма отрицательных элементовs = 1 Then 'если
отриц. элемент =1, запомнить номер столбца
nomerMinus = jIfIf
Next j
s = 1 Then 'если отриц. элемент =1, окрасить столбец в
зеленый
numStolbca = nomerMinus(Cells(2, nomerMinus),
Cells (KolBazPer + 3, nomerMinus)).Select. Interior. Color = vbGreens = 0 Then«Найдено оптимальное решение. F =» &
Worksheets («Лист1»).Cells
(KolBazPer + 3, KolPer + 2), vbOK, «Ответ»
flag = True
'Нахождение максимального отрицательного элемента, если в
индексной строке их несколько= Worksheets («Лист1»).Cells (KolBazPer + 3, 2)
'минимальный элемент - первый= 2 'столбец минимального элемента второйi = 2 To
KolPer + 1
'проверка следующего элемента на минимальностьWorksheets
(«Лист1»).Cells (KolBazPer + 3, i) < min Then
min = Worksheets («Лист1»).Cells (KolBazPer + 3,
i)= iIfi= nomerMinus(Cells(2, nomerMinus), Cells (KolBazPer + 3,
nomerMinus)).Select. Interior. Color = vbGreenIfSubНоваяСТ()RazRelem
i = 3 To KolBazPer + 3j = 2 To KolPer + 2(«Лист2»).Cells (i,
j).Value = Worksheets («Лист1»).Cells (i, j).Valueji
= Cells (numStroki, numStolbca).Valuei = 3 To
KolBazPer + 3j = 2 To KolPer + 2Worksheets («Лист2»)numStroki = i Then(i,
j).Value =.Cells (i, j).Value / RazRelem 'вычисление разрешающей строки(i, j).Value =.Cells (i, j).Value - ((.Cells (i,
numStolbca).Value *.Cells (numStroki, j).Value) / RazRelem) 'пересчет таблицыIfWithjiSub
НахождениеМаксимума()
'Снятие окраски(Cells(1, 1),
Cells (KolBazPer + 3, KolPer + 3)).Select. Interior. Color = vbWhite
ПоискРазрешающегоСтолбца(1)Not flag Then ПоискРазрешающейСтроки(1)Not flag
Then НоваяСТ(1)While flag
= FalseSub
Sub Vichislenie_Click()
НахождениеМаксимума
'Гасим кнопку вычисление. Enabled =
FalseSub
Sub VvodParam_Click()= False
'Зажигаем кнопку вычисление. Enabled = True
' Ввод параметров таблицы= CInt (InputBox(«Введите количество
базисных переменных:», «Ввод параметров»))= CInt (InputBox(«Введите количество
переменных:», «Ввод параметров»))
'Оформление шапки(«A1:A2»).Select. FormulaR1C1 = «»Selection= xlCenter=
xlCenter= True= TrueWith(«A:A»).ColumnWidth = 14
(Cells(1, 2), Cells (1, KolPer + 1)).Select.
Merge(«B1»).Value
= «Коэффициенты при переменных»
With Selection= xlCenter= xlCenter= True=
TrueWith
(Cells(1, KolPer + 2), Cells (2, KolPer +
2)).Select. FormulaR1C1 = «Свободные члены»Selection= xlCenter= xlCenter= True= TrueWith(KolPer +
2).ColumnWidth = 14
(Cells(1, KolPer + 3), Cells (2, KolPer +
3)).Select. FormulaR1C1 = «Оценочное отношение»Selection= xlCenter= xlCenter= True=
TrueWith(KolPer + 3).ColumnWidth = 14
(Cells(KolBazPer + 3, 1), Cells (KolBazPer + 3,
1)).Select. Value = «F»Selection= xlCenter= xlCenter= TrueWith
j As Integerj = 2 To KolPer + 1(2, j) = «Х» & j - 1j
'Начертание границ таблицы(Cells(1, 1),
Cells (KolBazPer + 3, KolPer + 3)).Select. Borders(xlDiagonalDown).LineStyle =
xlNone. Borders(xlDiagonalUp).LineStyle = xlNoneSelection. Borders(xlEdgeLeft)=
xlContinuous= xlThin= xlAutomaticWithSelection. Borders(xlEdgeTop)=
xlContinuous= xlThin= xlAutomaticWithSelection. Borders(xlEdgeBottom)=
xlContinuous= xlThin= xlAutomaticWithSelection. Borders(xlEdgeRight)=
xlContinuous= xlThin= xlAutomaticWithSelection. Borders(xlInsideVertical)=
xlContinuous= xlThin= xlAutomaticWithSelection. Borders(xlInsideHorizontal)=
xlContinuous= xlThin= xlAutomaticWith(«A1»).Select
End Sub