|
10
|
3,28
|
2,92
|
2,73
|
2,61
|
2,52
|
2,46
|
2,41
|
2,38
|
2,35
|
2,32
|
f2
|
f1
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
161,4
|
199,5
|
215,7
|
224,6
|
230,2
|
234,0
|
236,8
|
238,9
|
240,5
|
241,9
|
|
2
|
18,51
|
19,0
|
19,16
|
19,25
|
19,30
|
19,33
|
19,35
|
19,37
|
19,39
|
19,40
|
|
3
|
10,13
|
9,55
|
9,28
|
9,12
|
9,01
|
8,94
|
8,89
|
8,85
|
8,81
|
8,79
|
|
4
|
7,71
|
6,94
|
6,59
|
6,39
|
6,26
|
6,16
|
6,09
|
6,04
|
6,00
|
5,96
|
|
5
|
6,61
|
5,79
|
5,41
|
5,19
|
5,05
|
4,95
|
4,88
|
4,82
|
4,77
|
4,74
|
|
6
|
5,99
|
5,14
|
4,76
|
4,53
|
4,39
|
4,28
|
4,21
|
4,15
|
4,10
|
4,06
|
|
7
|
5,59
|
4,74
|
4,35
|
4,12
|
3,97
|
3,87
|
3,79
|
3,73
|
3,68
|
3,64
|
|
8
|
5,32
|
4,46
|
4,07
|
3,84
|
3,69
|
3,58
|
3,50
|
3,44
|
3,39
|
3,35
|
|
9
|
5,12
|
4,26
|
3,86
|
3,63
|
3,48
|
3,37
|
3,29
|
3,23
|
3,18
|
3,14
|
|
10
|
4,46
|
4,10
|
3,71
|
3,48
|
3,33
|
3,22
|
3,14
|
3,07
|
3,02
|
2,98
|
Таблица 4. Значение F для уровня значимости α=0,025
|
f2
|
f1
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
647,8
|
799,5
|
846,2
|
899,6
|
921,8
|
937,1
|
948,2
|
956,7
|
963,3
|
968,6
|
|
2
|
38,51
|
39,00
|
39,16
|
39,25
|
39,30
|
39,33
|
39,36
|
39,37
|
39,39
|
39,40
|
|
3
|
17,44
|
16,04
|
15,44
|
15,10
|
14,88
|
14,74
|
14,62
|
14,54
|
14,47
|
14,42
|
|
4
|
12,22
|
10,65
|
9,98
|
9,60
|
9,36
|
9,20
|
9,07
|
8,98
|
8,90
|
8,84
|
|
5
|
10,01
|
8,43
|
7,76
|
7,39
|
7,15
|
6,98
|
6,85
|
6,76
|
6,68
|
6,62
|
|
6
|
8,81
|
7,26
|
6,60
|
6,23
|
5,99
|
5,82
|
5,70
|
5,60
|
5,52
|
5,46
|
|
7
|
8,07
|
6,54
|
5,89
|
5,52
|
5,29
|
5,12
|
4,99
|
4,90
|
4,82
|
4,76
|
|
8
|
7,57
|
6,06
|
5,42
|
5,05
|
4,82
|
4,65
|
4,53
|
4,43
|
4,36
|
4,30
|
|
9
|
7,21
|
5,71
|
5,08
|
4,72
|
4,48
|
4,32
|
4,20
|
4,10
|
4,03
|
3,96
|
|
10
|
6,94
|
5,46
|
4,83
|
4,47
|
4,24
|
4,07
|
3,95
|
3,85
|
3,78
|
3,72
|
Χ2- распределение

Рис.
5 График плотности вероятности Χ2-
распределение
Пусть имеем выборочную совокупность х1, х2, …
хn, которая подчиняется нормальному закону распределения с генеральными
параметрами μ и σ2.
Если в нормальном законе распределения переменную 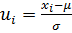 возвести
в квадрат и просуммировать возвести
в квадрат и просуммировать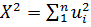 , то величина χ2
подчиняется χ2-распределению с
числом степеней свободы f=n-1. Величина χ2
изменяется в пределах , то величина χ2
подчиняется χ2-распределению с
числом степеней свободы f=n-1. Величина χ2
изменяется в пределах 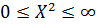 . Функция плотности
вероятностей ассиметрична, но асимметрия уменьшается с увеличением f. . Функция плотности
вероятностей ассиметрична, но асимметрия уменьшается с увеличением f.
Таблица 5. Значения 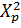 в
зависимости от вероятности P ( в
зависимости от вероятности P (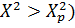 и числа степеней
свободы и числа степеней
свободы
|
Число
степеней cвободыf
|
Вероятность
P (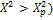
|
|
0,99
|
0,95
|
0,90
|
0,80
|
0,50
|
0,20
|
0,10
|
0,05
|
0,01
|
|
1
|
0,0002
|
0,0039
|
0,016
|
0,0642
|
0,455
|
1,64
|
2,71
|
3,84
|
6,64
|
|
2
|
0,0201
|
0,103
|
0,211
|
0,446
|
1,39
|
3,22
|
4,61
|
5,99
|
9,21
|
|
3
|
0,115
|
0,352
|
0,548
|
1,005
|
2,37
|
4,61
|
6,25
|
7,82
|
11,3
|
|
4
|
0,297
|
0,711
|
1,06
|
1,65
|
3,36
|
6,25
|
7,77
|
9,49
|
13,3
|
|
5
|
0,554
|
1,14
|
1,61
|
2,34
|
4,35
|
7,77
|
9,24
|
11,1
|
15,1
|
|
6
|
0,872
|
1,63
|
2,20
|
3,07
|
5,35
|
9,24
|
10,6
|
12,6
|
16,8
|
|
7
|
1,24
|
2,17
|
2,83
|
3,82
|
6,35
|
10,6
|
12,0
|
14,1
|
18,5
|
|
8
|
1,65
|
2,73
|
3,49
|
4,59
|
7,34
|
12,0
|
13,4
|
15,5
|
20,1
|
|
9
|
2,09
|
3,32
|
4,17
|
5,38
|
8,34
|
17,3
|
14,7
|
16,9
|
|
10
|
2,56
|
3,94
|
4,86
|
6,18
|
9,34
|
18,5
|
16,0
|
18,3
|
23,2
|
r-распределение
Ели в переменной 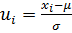 номинированного
нормального закона заменить генеральные параметры на их выборочные оценки номинированного
нормального закона заменить генеральные параметры на их выборочные оценки
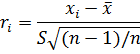
то получим распределение относительно отклонения
или r-распределение. Функция φ(r)
плотности вероятностей зависит от значения riи числа степеней свободы f=n-2.
При больших значениях nr-распределение переходит в нормальное распределение.
Таблица 6. Значение r для различных уровней
значимости
|
Число
степеней свободы f
|
Уровень
значимости α
|
|
0,01
|
0,05
|
0,01
|
0,001
|
|
1
|
1,397
|
1,409
|
1,414
|
1,414
|
|
2
|
1,559
|
1,645
|
1,715
|
1,730
|
|
3
|
1,611
|
1,757
|
1,918
|
1,982
|
|
4
|
1,631
|
1,814
|
2,051
|
2,178
|
|
5
|
1,640
|
1,848
|
2,142
|
2,329
|
|
6
|
1,644
|
1,870
|
2,208
|
2,447
|
|
7
|
1,647
|
1,885
|
2,256
|
2,540
|
|
8
|
1,648
|
1,895
|
2,294
|
2,616
|
|
9
|
1,649
|
1,903
|
2,324
|
2,678
|
|
10
|
1,649
|
1,910
|
2,398
|
2,730
|
Глава 3. Статистическое оценивание результатов
измерений
3.1 Методы исключения грубых ошибок
При проведении любого измерения встречаются
результаты, которые резко отличаются от остальных. Вполне естественно, что в
подобных случаях возникают подозрения о наличии грубых ошибок (промахов),
допущенных исследователем при получении результатов. Единственным надежным
методом выявления грубых ошибок является детальный анализ условий эксперимента.
Если было установлено, что были нарушены стандартные условия, то сомнительный
результат следует отбросить вне зависимости от его величины.
Если в ходе проведения эксперимента был получен
результат, который резко отличается от предыдущих, и условия оставались
прежними, то этот сомнительный результат надо исключить, но заменить тремя
новыми, подряд проведенными измерениями.
На практике далеко не всегда удается
воспользоваться приведенными выше рекомендациями для исключения выбросов,
поэтому для их обнаружения обычно обращаются статистическим критериям. Стоит
отметить, что данные критерии являются условными, поскольку они базируются на
нормальном законе распределения случайных величин, допускающем изменение xот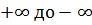 . .
Метод исключения выбросов при известном σ
Если оценка S стандартного отклонения σ
надежно
установлена (оценка при 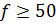 ), то на практике
для исключения промахов допустимо применять «правило трех σ»:
одно,
по меньшей мере, из 10, отдельных измерений может быть квалифицированно как
содержащее грубую погрешность, если его значение лежит вне области ), то на практике
для исключения промахов допустимо применять «правило трех σ»:
одно,
по меньшей мере, из 10, отдельных измерений может быть квалифицированно как
содержащее грубую погрешность, если его значение лежит вне области  ,
где 3σ
рассчитывается по формуле: ,
где 3σ
рассчитывается по формуле:

где V - коэффициент вариации.
Метод исключения выбросов при неизвестном σ
Пусть имеется n изменений x1, x2, x3, … xb … xnи
среди них значение xi вызывает сомнение, так как существенно отличается от
остальных значений. Выдвигается нуль-гипотеза, которая заключается в том, что
сомнительное значение xi принадлежит данной совокупности, то есть не является
выбросом. Для принятия или отклонения ее можно используют r-критерий, значение
которого рассчитывается по формуле:

где 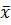 и
S - соответственно среднее значение и стандартное отклонение, подсчитанное по
всем n измерениям, включая и сомнительный результат. и
S - соответственно среднее значение и стандартное отклонение, подсчитанное по
всем n измерениям, включая и сомнительный результат.
Полученное значение ri подчиняется
r-распределению с числом степеней свободы f=n-2; его сопоставляют с табличным
значением rmax(min), значения которых приведены в таблице 7. Если рассчитанное
значение 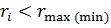 (0,05;f=n-2),
то принимают нуль-гипотезу: результат xi принадлежит данной совокупности. При (0,05;f=n-2),
то принимают нуль-гипотезу: результат xi принадлежит данной совокупности. При  (0,01,
f=n-2) нуль гипотезу отвергают, то есть считают, что сомнительный результат
является выбросом и исключают его из совокупности измерений. (0,01,
f=n-2) нуль гипотезу отвергают, то есть считают, что сомнительный результат
является выбросом и исключают его из совокупности измерений.
Таблица 7. Значения  для
различных уровней значимости для
различных уровней значимости
|
Число
степеней свободы f
|
Уровень
значимости α
|
|
0,10
|
0,05
|
0,025
|
0,01
|
|
1
|
1,406
|
1,412
|
1,414
|
1,414
|
|
2
|
1,645
|
1,689
|
1,710
|
1,723
|
|
3
|
1,791
|
1,869
|
1,917
|
1,955
|
|
4
|
1,894
|
1,996
|
2,067
|
2,130
|
|
5
|
2,041
|
2,093
|
2,182
|
2,265
|
|
6
|
2,097
|
2,172
|
2,273
|
2,374
|
|
7
|
2,146
|
2,238
|
2,349
|
2,464
|
|
8
|
2,190
|
2,294
|
2,470
|
2,540
|
|
9
|
2,229
|
2,343
|
2,519
|
2,606
|
|
10
|
2,264
|
2,387
|
2,563
|
2,663
|
Можно дать следующие рекомендации для выявления
выбросов:
. Если среди n измерений имеются два результата,
из которых один выказывает сомнения в силу того, что он значительно больше
остальных, а другой из-за того, что он значительно меньше, то следует по всем n
результатам рассчитать 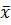 и S и сначала
проверить гипотезу о том, можно ли отбросить, как грубое то значение, которое
больше отличается от среднего. Если окажется, что данное значение не является
выбросом, то принимают нуль-гипотезу: оба результата принадлежат одной
совокупности. Если окажется, что максимально отклоняющееся измерение является
выбросом, то его отбрасывают, по оставшимся (n-1) результатам подсчитывают и S и сначала
проверить гипотезу о том, можно ли отбросить, как грубое то значение, которое
больше отличается от среднего. Если окажется, что данное значение не является
выбросом, то принимают нуль-гипотезу: оба результата принадлежат одной
совокупности. Если окажется, что максимально отклоняющееся измерение является
выбросом, то его отбрасывают, по оставшимся (n-1) результатам подсчитывают 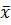 и
Sи проверяют гипотезу о наличии грубой ошибки во втором сомнительном
результате. и
Sи проверяют гипотезу о наличии грубой ошибки во втором сомнительном
результате.
. Если среди измерений имеются два результата,
которые высказывают сомнения, потому что они значительно меньше (или больше)
остальных, то сначала произвольно отбрасывают худший из значительных
результатов. По оставшимся (n-1) измерениям подсчитывают 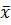 и
S и проверяют гипотезу о наличии грубой ошибки в лучшем из сомнительных
результатов. Если окажется, что это измерение можно квалифицировать как выброс,
то нужно отбросить оба сомнительных результата. Если окажется, что второе
измерение не содержит грубой ошибки, то проверяют гипотезу о наличии промаха в
худшем из сомнительных результатов. При этом и
S и проверяют гипотезу о наличии грубой ошибки в лучшем из сомнительных
результатов. Если окажется, что это измерение можно квалифицировать как выброс,
то нужно отбросить оба сомнительных результата. Если окажется, что второе
измерение не содержит грубой ошибки, то проверяют гипотезу о наличии промаха в
худшем из сомнительных результатов. При этом 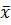 и
Sрассчитывают по всем n измерениям. и
Sрассчитывают по всем n измерениям.
2.2 Сравнение двух дисперсий
В любой экспериментальной работе, включая
решение задач по аналитической химии, нередко требуется сравнить точность
результата измерений.
Если мы имеем две серии измерений: x1, x2, x3 …,
xb … xn1иy1, y2, y3 … yb… yn2. По результатам измерений рассчитаны выборочные
дисперсии 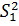 при числе степеней
свободыf1=n1-1 и при числе степеней
свободыf1=n1-1 и  при числе степеней
свободы f2=n2-1. Значение при числе степеней
свободы f2=n2-1. Значение 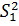 больше значения больше значения  .
Величина .
Величина 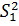 служит
оценкой генеральной дисперсии служит
оценкой генеральной дисперсии 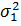 , а , а  -
генеральной дисперсии -
генеральной дисперсии 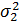 . Нужно сравнить
генеральные дисперсии по известным выборочным. Несмотря на то, что . Нужно сравнить
генеральные дисперсии по известным выборочным. Несмотря на то, что  выдвигается
нуль-гипотеза, которая заключается в том, что генеральные дисперсии равны: выдвигается
нуль-гипотеза, которая заключается в том, что генеральные дисперсии равны: 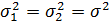 .
Выборочные дисперсии .
Выборочные дисперсии 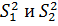 характеризуют одну
и ту же генеральную дисперсию характеризуют одну
и ту же генеральную дисперсию  и называются
однородными. Следовательно необходимо проверить однородность выборочных
дисперсий. и называются
однородными. Следовательно необходимо проверить однородность выборочных
дисперсий.
Принятие или подтверждение выдвинутой
нуль-гипотезы проводят с помощью F-критерия. Для этого находят отношение  при
условии, что в числитель обязательно ставится большая по величине выборочная
дисперсия. При поверке гипотезе о равенстве при
условии, что в числитель обязательно ставится большая по величине выборочная
дисперсия. При поверке гипотезе о равенстве 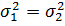 следует
различать два случая. следует
различать два случая.
В первом случае заранее известно, что 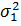 не
может быть меньше не
может быть меньше 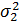 , поэтому проверяют
справедливость одного из двух положений: , поэтому проверяют
справедливость одного из двух положений: 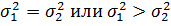 .
В этих условиях рассчитанное значение F сравнивают с табличным с использованием
одностороннего F-критерия. Обычно таблицы для критерия F составлены для
односторонней функции φ(F), поэтому
для принятия нуль-гипотезы находят табличное значение находят табличное
значение при уровне значимости α=0,05
и числе степеней свободы для большей дисперсии .
В этих условиях рассчитанное значение F сравнивают с табличным с использованием
одностороннего F-критерия. Обычно таблицы для критерия F составлены для
односторонней функции φ(F), поэтому
для принятия нуль-гипотезы находят табличное значение находят табличное
значение при уровне значимости α=0,05
и числе степеней свободы для большей дисперсии 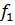 ,
которое откладывается по горизонтали, и меньшей дисперсии ,
которое откладывается по горизонтали, и меньшей дисперсии 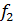 ,
которое откладывается по вертикали соответственно. Если справедливо неравенство ,
которое откладывается по вертикали соответственно. Если справедливо неравенство
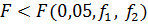 ,
принимают нуль-гипотезу: выборочные дисперсии ,
принимают нуль-гипотезу: выборочные дисперсии 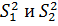 однородны,
то есть они характеризуют одну и ту же генеральную дисперсию. Это позволяет
усреднить выборочные дисперсии. При этом больший статистический вес имеет та
дисперсия, которая определена более надежно, то есть рассчитана по большему
числу измерений, поэтому усредненная дисперсия рассчитывается по формуле: однородны,
то есть они характеризуют одну и ту же генеральную дисперсию. Это позволяет
усреднить выборочные дисперсии. При этом больший статистический вес имеет та
дисперсия, которая определена более надежно, то есть рассчитана по большему
числу измерений, поэтому усредненная дисперсия рассчитывается по формуле:
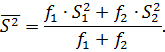
Если 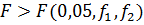 ,то
принять нуль-гипотезу нельзя, но и недостаточно оснований для ее отбрасывания.
Чтобы принять решение, необходимо сравнить значение F сравнить с табличным
F(0,01, ,то
принять нуль-гипотезу нельзя, но и недостаточно оснований для ее отбрасывания.
Чтобы принять решение, необходимо сравнить значение F сравнить с табличным
F(0,01,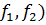 .
Если .
Если 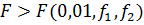 ,
нуль-гипотезу отбрасывают: дисперсии ,
нуль-гипотезу отбрасывают: дисперсии 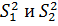 неоднородны. неоднородны.
Во втором случае сравнивают дисперсии 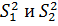 ,
когда из условий постановки эксперимента нельзя определить, какая генеральная
дисперсия больше, то есть справедливо может быть любое из трех положений: ,
когда из условий постановки эксперимента нельзя определить, какая генеральная
дисперсия больше, то есть справедливо может быть любое из трех положений:  .
В этом случае пользуются двухсторонним критерием F: критическая область в
функции плотности вероятностей φ(F)
состоит из двух частей, то есть α=2α1,
где α1
и α
- уровень
значимости соответственно для одностороннего и двухстороннего F-критерия. Чтобы
найти значение двухстороннего F-критерия для уровня значимости α=0,05
по
таблицам, составленным для одностороннего F-критерия, следует использовать α1=0,025
и т.д. В остальном нуль-гипотезу проверяют по тем же правилам, что и в первом
случае. .
В этом случае пользуются двухсторонним критерием F: критическая область в
функции плотности вероятностей φ(F)
состоит из двух частей, то есть α=2α1,
где α1
и α
- уровень
значимости соответственно для одностороннего и двухстороннего F-критерия. Чтобы
найти значение двухстороннего F-критерия для уровня значимости α=0,05
по
таблицам, составленным для одностороннего F-критерия, следует использовать α1=0,025
и т.д. В остальном нуль-гипотезу проверяют по тем же правилам, что и в первом
случае.
2.3 Сравнение нескольких дисперсий
При создании стандартных образцов, проверке
качества работа нескольких однотипных приборов и т.п. возникает задача оценить
однородность нескольких (m) дисперсий 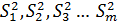 ,
каждая из которых определена с числом степеней свободы ,
каждая из которых определена с числом степеней свободы 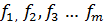 соответственно.
При решении этих вопросов формируется нуль-гипотеза: сравнимые дисперсии
однородны. Принять или отвергнуть ее можно с помощью критериев Бартлетта или
Кохрена. соответственно.
При решении этих вопросов формируется нуль-гипотеза: сравнимые дисперсии
однородны. Принять или отвергнуть ее можно с помощью критериев Бартлетта или
Кохрена.
При сравнении дисперсий с помощью критерия
Бартлетта рассчитывают величину В:
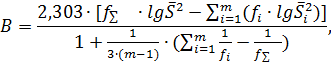
где 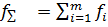 ; ;
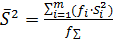 . .
Бартлетт показал, что величина В распределена
приближённо как критерий χ2 с числом
степеней свободы  при условии, что
для всех сравнимых дисперсий спреведливо условие: при условии, что
для всех сравнимых дисперсий спреведливо условие: 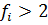 . .
Если  ,
то отбрасывают гипотезу об однородности дисперсий, то есть одна или нескольких
выборочных дисперсий из рассматриваемой совокупности характеризуют другие
генеральные дисперсии. Если ,
то отбрасывают гипотезу об однородности дисперсий, то есть одна или нескольких
выборочных дисперсий из рассматриваемой совокупности характеризуют другие
генеральные дисперсии. Если 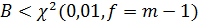 , то нуль-гипотезу
принимают: сравнивание дисперсии однородны и их можно усреднить с учетом числа
степеней свободы каждой дисперсии. , то нуль-гипотезу
принимают: сравнивание дисперсии однородны и их можно усреднить с учетом числа
степеней свободы каждой дисперсии.
Если число степеней свободы для всех выборок
одинаково, то есть 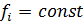 , то для сравнения
дисперсий вместо приближенного критерия Бартлетта используется критерий
Кохрена. Этот критерий основан на законе распределения отношения максимальной
выборочной дисперсии , то для сравнения
дисперсий вместо приближенного критерия Бартлетта используется критерий
Кохрена. Этот критерий основан на законе распределения отношения максимальной
выборочной дисперсии 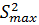 к сумме всех
сравнительных дисперсий: к сумме всех
сравнительных дисперсий:

Для установления однородности/неоднородности
дисперсий используют табличные значения 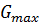 .
При .
При 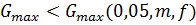 принимают,
что сравнимые дисперсии однородны. Если принимают,
что сравнимые дисперсии однородны. Если 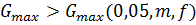 ,
то дисперсия ,
то дисперсия 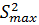 характеризует
другую генеральную дисперсию. Ее исключают из рассмотрения и проверяют по
критерию Кохрена большую из оставшихся дисперсий. характеризует
другую генеральную дисперсию. Ее исключают из рассмотрения и проверяют по
критерию Кохрена большую из оставшихся дисперсий.
2.3 Сравнение двух средних результатов
В экспериментальной работе часто возникает
ситуация, когда требуется сравнить между собой два результата измерения: сопоставление
результатов одной пробы, полученные разными методиками; сравниваются измерения,
сделанные разными приборами и т.д. С позиции статистически данные задачи
решаются одинаково.
Пусть в разных условиях получены две выборки:
х1, х2, х3, …, хn1 (проведено n1измерений),
у1, у2, у3, …, уn2 (проведено n2измерений),
и требуется сравнить их средние результаты 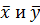 .
Для каждой выборки рассчитывается дисперсии .
Для каждой выборки рассчитывается дисперсии 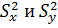 ,
характеризующие воспроизводимость этих измерений. Значения ,
характеризующие воспроизводимость этих измерений. Значения 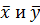 можно
сравнить с помощью t-критерия, если есть основания полагать, что имеем дело с
нормально распределенными наблюдениями. можно
сравнить с помощью t-критерия, если есть основания полагать, что имеем дело с
нормально распределенными наблюдениями.
Однако прежде чем оценивать значимость различия
между х и у, следует проверить однородность дисперсий 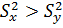 с
помощью F-критерия. При этом можно наблюдать два случая: результаты анализа
равноточные и неравноточные. с
помощью F-критерия. При этом можно наблюдать два случая: результаты анализа
равноточные и неравноточные.
Сравнение равноточных результатов
При  дисперсии дисперсии
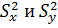 однородны
и, следовательно, сравнивают равноточные результаты измерения,
воспроизводимость которых характеризуется средней дисперсией S2,рассчитывается
по формуле однородны
и, следовательно, сравнивают равноточные результаты измерения,
воспроизводимость которых характеризуется средней дисперсией S2,рассчитывается
по формуле 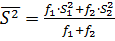 . Дисперсия
S2определена при числе степеней свободы . Дисперсия
S2определена при числе степеней свободы 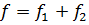 .
Значимость расхождения средних результатов оценивают по формуле: .
Значимость расхождения средних результатов оценивают по формуле:
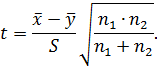
Рассчитанное значение t сравнивают с табличным
значением t-критерием, установленным для уровня значимости α
и
числа степеней свободы 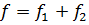 , по которым
определенаS2. Если , по которым
определенаS2. Если 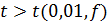 , то различие между , то различие между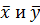 носит систематический характер. При
носит систематический характер. При 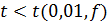 принимают
нуль-гипотезу различие между принимают
нуль-гипотезу различие между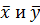 случайно. Оба
результата характеризуют одно и то же математическое ожидание, оценка которого
равна: случайно. Оба
результата характеризуют одно и то же математическое ожидание, оценка которого
равна:

Сравнение неравноточных результатов
Если при оценке однородности дисперсий 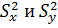 получили,
что получили,
что 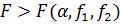 дисперсии
являются неоднородными. В этом случае можно рассчитывать значения t-критерия по
формуле: дисперсии
являются неоднородными. В этом случае можно рассчитывать значения t-критерия по
формуле:
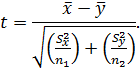
Величину fв общем случае рассчитывают по
формуле:
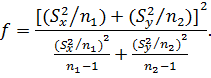
Следует отметить, что в зависимости от того,
насколько различаются по величине дисперсии 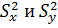 ,
число степеней свободы f изменится в пределах ,
число степеней свободы f изменится в пределах  . .
После определения величины f находят табличное
значение t(α, f) для принятия
или опровержения нуль-гипотезы применяют алгоритм, который был описан выше для
равноточных результатов.
Заключение
Исходя из вышеперечисленного, можно сделать
вывод, что методы математической статистики обработки результатов находят
широкое применение на практике. Они не только позволяют оценить вклад случайной
погрешности, но и помогают определить промахи (грубые погрешности) и исключить
их без проведения дополнительных измерений; сравнить две или несколько
дисперсий, что, например, применимо в случаях, когда нужно сравнить
воспроизводилось двух методик анализа или при установке нового оборудования
возник вопрос: не изменилось ли воспроизводилось результатов измерения.
Сравнение нескольких дисперсий находит свое применение при изготовлении
стандартных образцов, проверке качества однотипных приборов, установленных в
лаборатории и т.д.
Таки образом, математическая статистика является
одним из ключевых компонентов при проведении анализа.
Список литературы
1.
ГармашA.B. Метрологические основы аналитической химии / А.В. Гармаш,
А.М.Сорокина - Москва 2012 г.
.
Дёрффель К. Статистика в аналитической химии / К. Дёрффель - М.: Мир 1994 г.
.
Классификация погрешностей измерений [Электронный ресурс] Режим
доступа:http://metrob.ru/HTML/pogreshnost/klassifikacia-pogreshnosti.htmlДата
доступа: 27.11.2015 погрешность
химия случайный дисперсия
.
Краткие сведения о статической обработке эксперементальных данных [Электронный
ресурс] Режим доступа:http://alnam.ru/book_a_chem2.php?id=26Дата доступа:
1.12.2015
.
Сергеев А.Г. Метрология, стандартизация, сертефикация / А.Г. Сергеев, М.В.
Латышев, В.В. Терегеря - Москва 2005 г.
.
Смагунова А.Н. Методы математической статистики в аналитической химии / А.Н.
Смагунова, О.Р. Карпукова - Феникс, 2012.
.
Теория вероятностей и статистика в аналитической химии [Электронный ресурс]
Режим доступа:http://chemstat.com.ru/lections Дата доступа: 1.12.2015
Похожие работы на - Элементы статистики в аналитической химии
|