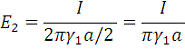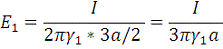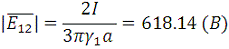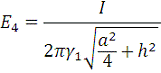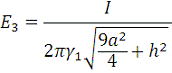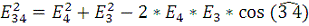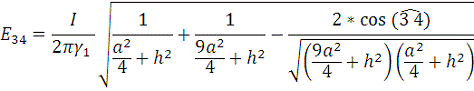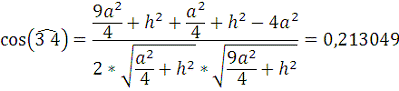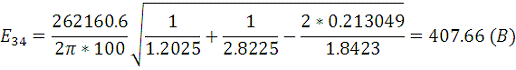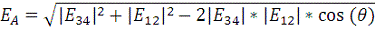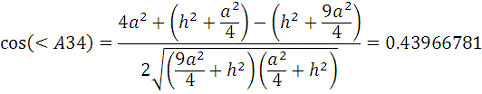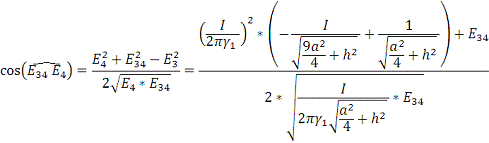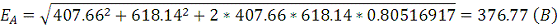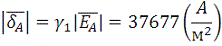Электромагнитные поля и волны

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Пермский национальный исследовательский политехнический университет Кафедра Автоматики и Телемеханики

Расчетная работа

Электромагнитные поля и волны

Выполнил: студент группы АТ-13 Арисов И.А.

Проверил: Щербинин А.Г.

Пермь, 2015 г.

Постановка задачи

Металлический цилиндрический стержень находился в среде с проводимостью γ1 (рис. 1. табл. 1).

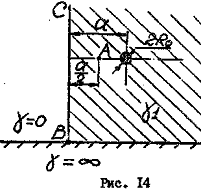
Рис. 1. Условие задачи.

Задание:

I. Найти ток утечки на единицу длины между стержнем и металлической поверхностью проводящего полупространства (γ = ∞), если потенциал стержня относительно этой поверхности φ₀.

. Найти проводимость на единицу длины между стержнем и металлической поверхностью без учета влияния непроводящей стенки, т.е. когда γ₁ = γ₂.

. Построить график изменения потенциала вдоль линии ВС.

. Определить плотность тока в точках А и B.

Таблица 1.

Задание 1.

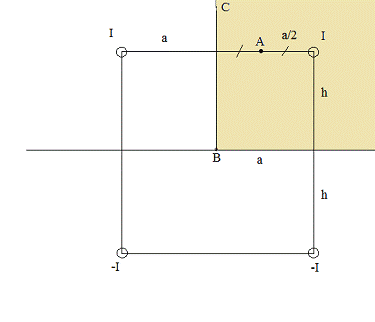
Рис. 2. Применение метода зеркальных изображений для 1-го пункта.

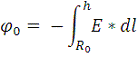
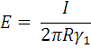
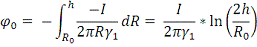
Аналогично:

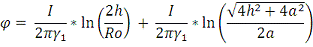
Тогда ток утечки равен:

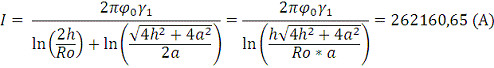
Задание 2

Картина линий напряженности в случае отсутствия непроводящей стенки будет выглядеть так (Рис. 2.):

Рис. 3. Применение метода зеркальных изображений для 2-го пункта.

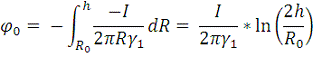
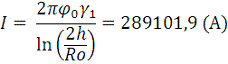
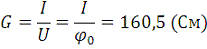
ток металлический стержень проводимость

Задание 3

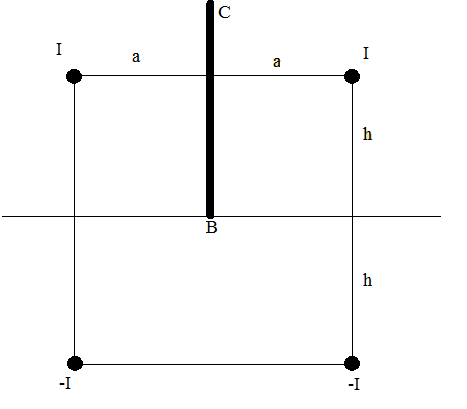
Рис. 4. Условие 3-го пункта.

Потенциал - величина аддитивная.

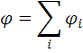
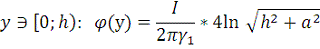
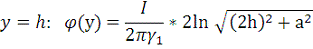
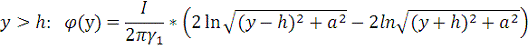
Полученный график:

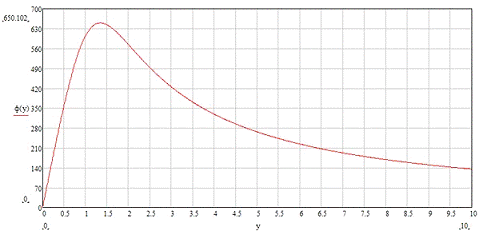
Рис. 5. График зависимости потенциала от координаты на оси, совпадающей с прямой ВС.

Задание 4

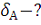
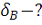
Закон Ома в дифференциальной форме:

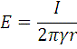
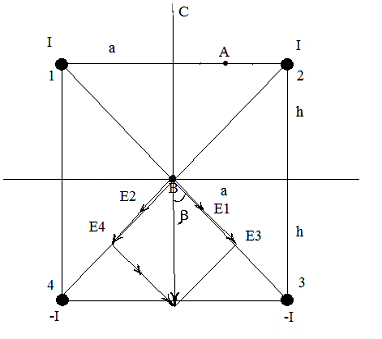
Рис. 6. Сложение векторов для вычисления плотности тока в точке В.

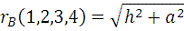
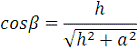
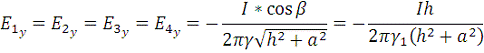
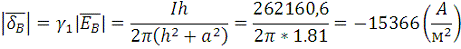
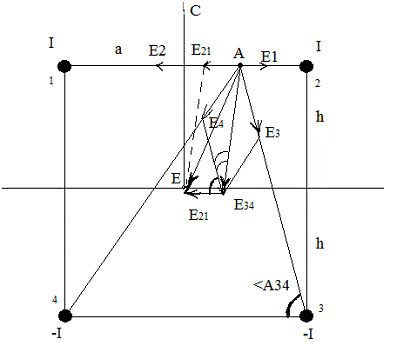
Рис. 8. Сложение векторов для вычисления плотности тока в точке А.