Определение реакций опор одно- и многопролетной балки

Содержание:

Введение

Часть I. Определение реакций опор

Часть II. Расчёт балки на прочность и жёсткость

Часть III. Динамический расчет движения автомобиля

Часть IV. Расчет цилиндрических зубчатых передач

Заключение

Список литературы

Введение

опора прочность цилиндрический зубчатый

Курсовая работа является важным этапом подготовки студентов к решению задач применительно к практике по обработке исходной информации и по обучению оформления технической и нормативной документации в соответствии с ГОСТ и ЕСКД.

Часть I. Определение реакций опор

Наименование темы: «Определение реакций опор одно- и многопролетной балки под действием системы сил, произвольно расположенных на плоскости».

Цель работы: закрепление теоретических знаний студентов и привитие им навыков в самостоятельном решении практических задач по расчету опорных реакций типовых конструкций.

Исходные данные:

расчетная схема - согласно варианту в приложении А;

вариант численных значений параметров согласно варианту в табл.1;

Все размеры на расчетных схемах указаны в метрах.

Таблица 1 - Номера вариантов и исходные данные

Определение опорных реакций однопролетных балок, нагруженных системой сил произвольно расположенных на плоскости, следует выполнять в следующей последовательности:

-       выделить твердое тело, находящееся в равновесии;

-       изобразить все задаваемые силы, приложенные к данному телу;

-       используя принцип освобождаемости от связей, заменить связи реакциями связей;

-       выбрать систему координат;

-       составить уравнения равновесия для плоской системы сил:

, (а)

или

, (б)

или

 (в)

решить уравнения равновесия и определить искомые величины.

Задание. Требуется определить реакции, действующие на балку АВ (рис. 1.1, а) в точках А и С: G =10 кH, Р=5 кН, М=20 кНм, q=1 кН/м, а=30^о, размеры указаны в м.

Решение. Решение задачи начинается с (выделения твердого тела) составления расчетной схемы (рис. 1.1, б), на которой изображаются выбранные оси координат, заданные силы и предполагаемые направления неизвестных сил. Действия, связей на балку заменяются их реакциями (). Реакции  и  по модулю неизвестны, реакция  по модулю равна P.

Рисунок 1.1 Расчетная схема однопролетных балок

Равномерно распределенную нагрузку интенсивностью q заменяют сосредоточенной (равнодействующей) силой , равной по модулю и приложенной в центре тяжести эпюры этой нагрузки.

Для плоской системы сил приложенных к балке, составляем три уравнения равновесия:        

Решая эти уравнения, находим:

R_С = 4 кН, Y_A = 1.5 кН, X_A = 4.65 кН.

Так как значения всех этих величин получились положительными, то принятые направления реакций совпадают с их действительными направлениями.

В рассмотренном примере определялись реакции, действующие на балку от двух шарнирных опор. При этом использовались уравнения равновесия плоской системы сил во второй форме (б), что позволило получить три уравнения, каждое из которых содержало только одно неизвестное.

В задачах, где балка защемлена одним концом, удобнее использовать уравнения плоской системы сил в первой форме (а):

.

Определение опорных реакций для не горизонтальных стержней производится точно так же, как и для балки.

Часть II. Расчёт балки на прочность и жёсткость

Наименование темы: «Расчет балки на прочность и жесткость».

Цель работы: освоение студентами основных методов расчета балок (стержней) на прочность и жесткость.

Исходные данные:

Условие задачи, расчетные схемы балок приведены в приложении Б, значение параметров - в таблице 2 согласно заданию.

Таблица 2 - Номера вариантов и исходные данные

2.1 Основные расчётные формулы

При изгибе стержней в сечениях возникают изгибающие моменты М и поперечные силы Q. Они определяются методом сечений. Величина поперечной силы в произвольном сечении балки равна алгебраической сумме всех внешних поперечных сил, действующих на балку по одну сторону от рассматриваемого сечения.

Величина изгибающего момента М в сечении равна алгебраической сумме моментов всех внешних сил по одну сторону от сечения. Между этими внутренними силовыми факторами имеется следующая связь:

поперечная сила равна первой производной от изгибающего момента по координате, направленной вдоль оси балки

. (2.1)

В свою очередь, между поперечной силой Q и распределённой внешней нагрузкой q имеется аналогичная взаимосвязь

.   (2.2)

Чтобы изучить работу балки от внешних сил и реакции, необходимо построить эпюры (графики) распределения внутренних силовых факторов - поперечной силы и изгибающего момента по её длине.

Сечение, в котором действует наибольший изгибающий момент, называют опасным. В каждой точке балки возникает нормальное напряжение σ, которое линейно изменяется по высоте сечения.

    (2.3)

где у - координата слоя балки, в котором определяются напряжения;

I_х - осевой момент инерции сечения относительно главной оси.

Наибольшее напряжение возникает в нижнем и верхнем слоях сечения

 (2.4)

где  - момент сопротивления изгибу относительно оси х.

Прочность балки оценивается по максимальному нормальному напряжению в опасном сечении. Условия прочности балки имеют вид неравенства:

 (2.5)

где σ_П - предельное напряжение материала, из которого изготовлена балка; [n] - коэффициент запаса прочности.

В сечениях балки возникает касательное напряжение, которое определяется по высоте не линейно (2.6)

 (2.6)

где b - ширина слоя сечения;

 - статический момент площади над слоем.

Касательные напряжения равны нулю в верхнем и нижнем слоях балки и имеют наибольшее значение в слое, проходящем через центр тяжести сечения. Они учитываются при оценке балки на межслойный сдвиг. Касательное напряжение между слоями балки не должны превышать допускаемого

           (2.7)

где  - предельное напряжение (или - предел текучести, или - предел прочности при сдвиге).

При изгибе балки её сечения имеют поперечные перемещения у, которые называют прогибами, и угловые перемещения .

Между прогибом, углом поворота и изгибающим моментом в этом сечении имеются следующие дифференциальные связи:

 (2.8)

где E·I_х - параметр, характеризующий жесткость балки на изгиб.

Для дифференциальных уравнений (2.8) получены универсальные решения, пригодные для любой балки с прямой осью и постоянной жесткостью:

 (2.9)

, (2.10)

где  и у₀ - начальные параметры - угол поворота и прогиб сечения, расположенного в начале координат;

а, b, c, d- координаты приложения соответственно сосредоточенного момента m, силы F и распределенной нагрузки q.

В практических расчетах часто после расчета на прочность производится проверка выполнения условий жесткости.

 (2.11)

где [у] и [] - допускаемый прогиб и угол поворота сечения, которые устанавливаются на основании опыта эксплуатации аналогичных конструкций.

2.2 Правила знаков внутренних силовых факторов при построении эпюр сил и моментов

Правила знаков для внутренних усилий, применяемые в машиностроении:

1. Продольная сила  считается положительной, если она вызывает растяжение отсеченной части и отрицательной, если вызывает ее сжатие.

. Поперечная сила  считается положительной, если она вращает отсеченную часть по ходу часовой стрелки и отрицатель­ ной, если вращение происходит против хода часовой стрелки.

. Изгибающий момент положителен, если сжаты верхние волокна отсеченной части, и отрицателен, если сжаты нижние волокна. Эпюра изгибающих моментов строится на сжатых волокнах.

. Правило знаков для крутящего момента удобно принимать произвольным.

Задание: Для балки, изображенной на рисунке 2.1, а, построить эпюры поперечных сил и изгибающих моментов. Из расчета на прочность по нормальным напряжениям подобрать номер двутавра. Проверить прочность выбранного двутавра по главным напряжениям, используя третью теорию прочности. Построить изогнутую ось балки.

Исходные данные: F₁=10 кН; M₁=15 кНм ;q=5 кН/м; а=3 м; b=1.5 м; с=1.5 м; [σ]=160 МПа.

Рисунок 2.1 - Схема балки, эпюр поперечных сил и изгибающих моментов

Решение:

1. Определим реакции опор  и , составив для этого условия равновесия:

;

;

.

. Сделаем проверку:

Реакции найдены правильно.

3.  Построение эпюр.

Для построения эпюр разобьём балку на три участка и составим уравнение для Q и М.

I участок:

При z=0

При z=a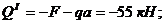

II участок: .

При z=a

При z=a+b

III участок: .

.

При z₁=0

.

При z₁=с

.

На этом участке график поперечной силы пересекает ось эпюры (рис. 2.1, б). Следовательно, в точке, где , изгибающий момент имеет экстремум. Найдём его. Из условия  получаем:

Изгибающий момент при z₁=2,75:

.

По этим данным строим эпюру поперечных сил (рис. 2.1, б) и изгибающих моментов (рис. 2.1, в).

4.  Подберём сечение балки. Наибольший изгибающий момент (рисунок 2.1, в) равен 60,6 кН∙м. Необходимый момент сопротивления:

По таблицам сортамента (приложение В) ближайшими к этому значению являются W_х=467 cм³ (двутавр №30а) и W_х=597cм³ (двутавр №30).

. Проверим, годится ли двутавр №30. Напряжения в нём будут равны:

То есть перенапряжение составляет:

что допустимо.

Рисунок 2.2 Схема сечения двутавра.

Таким образом, в соответствии с расчётом по нормальным напряжениям следует принять двутавр №30а. Обратим, однако, внимание на то, что сечении над левой опорой балки действуют одновременно значительный изгибающий момент М=20 кН∙м и большая поперечная (перерезывающая) сила Q=55 кН (рис. 2.1). Поэтому в этом сечении надо сделать проверку по главным напряжениям.

6. Проверим условие прочности по третьей теории прочности. Из таблиц сортамента выпишем для двутавра №30а: I_х=7780 см⁴; h=300 мм; t= 10,7 мм; d=6,5 мм.

Тогда в точке К сечения (рис. 2.2)

.

Согласно третьей теории прочности должно выполняться условие:

В нашем случае:

.

7.  Определим перенапряжение в точке К.

Перенапряжение составляет:

что допустимо велико (не более 5%).

Таким образом, надо использовать двутавр того же размера. Окончательно принимаем двутавр №30.

Часть III. Динамический расчет движения автомобиля

Цель работы: освоение студентами основных методов динамического расчета механических систем; определение целесообразных областей использования каждого из этих методов.

Основные вопросы, подлежащие разработке:

Задачу решить двумя способами:

с помощью теоремы об изменении кинетической энергии механической системы;

с помощью с помощью дифференциальных уравнений движения механической системы.

В результате выполнения работы должны быть определены все основные параметры динамики движения автомобиля.

Исходные данные:

Условие задачи, схема движения автомобиля, значение параметров в таблице 3 согласно заданию.

Таблица 3 - Номера вариантов и исходные данные

3.1 Определение динамических характеристик автомобиля с помощью теоремы об изменении кинетической энергии

Задание. Какой путь s прошел по прямой до остановки автомобиль, если в момент выключения мотора он двигался со скоростью v =75 км/ч=9,7 м/с. Вес кузова автомобиля с водителем и пассажирами равен =2 кН, вес каждого из четырех колес = 21 Н. Радиус инерции колеса относительно оси, проходящей через его центр инерции перпендикулярно к плоскости материальной симметрии, равен = 25 см, радиус колеса r =30 см. Коэффициент трения качения колес о шоссе =0.11 см.

За какое время и на каком расстоянии может быть остановлен тормозом автомобиль, идущий по горизонтальному пути со скоростью v=75 км/ч, если сопротивление движению, развиваемое при торможении, составляет  (п - коэффициент пропорциональности, Р - вес автомобиля, С - центр тяжести автомобиля).

Колеса автомобиля катятся без скольжения. Силой сопротивления воздуха пренебречь (рис. 3.1).

Рисунок 3.1

Решение 1. При движении автомобиля направо направление положительного отсчета угла поворота φ колес выбираем по часовой стрелке.

Запишем теорему об изменении кинетической энергии системы материальных точек:

. (3.1)

где - кинетическая энергия автомобиля в первом положении;  - кинетическая энергия во втором положении автомобиля; - работа внешних сил, приложенных к автомобилю; - работа внутренних сил, приложенных к автомобилю.

Рисунок 3.2

Изобразим внешние силы, приложенные к автомобилю (рис. 3.2):  и  - силы тяжести колес;  и 2 - нормальные силы реакций, смещенные относительно центра тяжести колес в сторону движения на величину коэффициента трения качения ; 2 и 2 - силы трения колес о шоссе, направленные в сторону, противоположную движению (после выключения двигателя все колеса автомобиля оказываются ведомыми). Внутренние силы не изображаем, считая автомобиль неизменяемой системой и пренебрегая силами внутреннего трения. Следовательно, сумма работ всех внутренних сил автомобиля равна нулю. Теперь уравнение (3.1) принимает вид

. (3.2)

Сумма работ всех внешних сил системы на искомом перемещении s равна

 (3.3)

(коэффициенты «4» соответствуют числу колес автомобиля).

Так как разность высот Δh при перемещениях точек приложения сил  и 4 равна нулю, то

. (3.4)

При качении колес без скольжения их мгновенные центры скоростей К находятся в точках касания. Силы трения всегда приложены к колесам в точках, совпадающих с мгновенными центрами скоростей К и перемещаются вместе с ними. Мощность этих сил трения, вычисляемая по формуле

где  - скорость мгновенного центра скоростей равна .

Следовательно, работа сил трения на конечном перемещении, равная интегралу от мощности по времени, тоже равна нулю:

. (3.5)

Учитывая, что радиусы колес и коэффициенты трения качения для всех четырех колес одинаковы, приводим вычисленные суммы работ пар качения к одному колесу, считая нормальное давление равным . Так как коэффициент трения качения  является плечом пары трения качения, то момент пары трения качения  будет

.

Элементарная работа пары трения качения равна

 (3.6)

(работа отрицательна, так как направление момента пары трения качения противоположно направлению угла поворота φ колес), где dφ - элементарное угловое перемещение колеса вокруг мгновенного центра скоростей К. Учитывая, что dφ связано с элементарным перемещением ds центра тяжести С колеса зависимостью , получим

. (3.7)

Подставляя значение dφ из формулы (3.7) в (3.6), находим:

. (3.8)

Для вычисления суммарной работы пары трения качения на конечном перемещении центра тяжести С колеса остается взять от выражения δA по формуле (3.8) определенный интеграл в пределах от 0 до s. После вычислений получим:

. (3.9)

Подставляя значения A(P₁), 4A(P₂), 4A(F_тр), 4A(M_тк) из формул (3.4), (3.5) и (3.9) в (3.3), находим сумму работ всех внешних сил, приложенных к автомобилю на его перемещении, равном s:

. (3.10)

Переходим к вычислению кинетических энергий автомобиля в его начальном и конечном положениях. Так как в конечном положении, т.е. в момент остановки, скорости всех точек равны нулю, то

. (3.11)

Запишем кинетическую энергию  автомобиля, состоящего из кузова с водителем и пассажирами и четырех колес, в виде

. (3.12)

Кузов с водителем и пассажирами совершает поступательно движение, поэтому

. (3.13)

Колеса совершают плоское движение, поэтому

; (3.14)

так как , то формула (3.14) принимает вид

. (3.15)

Внося значения  и 4 из формул (3.13) и (3.15) в (3.12), находим кинетическую энергию автомобиля в ее начальном положении:

. (3.16)

Подставляя значения ,  и  из формул (3.10), (3.11) и (3.16) в уравнение (3.2) и решив это уравнение относительно s, получим:

 м.

3.2 Определение динамических характеристик движения автомобиля с помощью дифференциальных уравнений

Решение 2. За ось координат примем ось х, направленную вдоль пути торможения автомобиля. Начальными условиями будут: , , . Задаваемые силы - вес автомобиля  и сила сопротивления движению при , . Дифференциальное уравнение движения автомобиля будет иметь вид (рис. 3.2):

.

Интегрируем это уравнение дважды и получаем:

.

По начальным условиям находим постоянные интегрирования  и :

, тогда .

По условию задачи требуется найти время остановки автомобиля, т.е. при v=0 (). Из первого уравнения находим это время:

с.

Подставляя во второе уравнение движения автомобиля, находим путь пройденный автомобилем до полной остановки:

 м.

Часть IV. Расчет цилиндрических зубчатых передач

.1 Основные расчетные зависимости для стальных цилиндрических зубчатых колес

Расчет на контактную прочность рабочих поверхностей зубьев

А. Межосевое расстояние (проектный расчет):

.

Б. Расчетное (рабочее) контактное напряжение (проектный расчет):

) Задан момент на шестерне:

.

) Задано окружное усилие:

;

.

Во всех случаях . Знак плюс в выражении  при внешнем зацеплении, знак минус - при внутреннем.

Обозначения:

i - передаточное число;

 - расчетный момент на шестерне: , где К - коэффициент нагрузки;

- расчетное окружное усилие, ;

В - ширина зубчатого колеса:

 - коэффициент ширины колеса;

- допускаемое контактное напряжение;

 - коэффициент, учитывающий повышение нагрузочной способности за счет увеличения суммарной длины контактных линий; для прямозубых колес =1; для косозубых при угле наклона на делительном цилиндре  =1,35 (при твердости рабочих поверхностей зубьев не более НВ350); =1,5 (при твердости выше НВ350) ; для косозубых и шевронных колес при  не зависимо от твердости =1,15.

Расчет зубьев на изгиб

А. Проверочный расчет.

. По заданному моменту:

.

. По заданному окружному усилию:

Б. Проектный расчет.

.

Примечание: 1. Модуль следует определять для того из сцепляющихся колес, для которого произведение  меньше.

. При расчете по заданному моменту расчетный момент и число зубьев должны относиться к одному и тому же зубчатому колесу ( и  либо  и ).

Обозначения:

 - расчетное и допускаемое напряжение изгиба для зуба шестерни или зубчатого колеса;  - при одностороннем действии нагрузки; - при переменном направлении изгиба зубьев;

 - коэффициент, учитывающий уменьшение момента сопротивления опасного сечения зуба вследствие износа. Для закрытых передач =1; для открытых передач =1,25÷1,5, большие значения при ожидаемом интенсивном износе;

у - коэффициент формы зуба. Принимается по таблице П20 в зависимости от числа зубьев, действительного z для прямозубых и фиктивного для косозубых и шевронных  или конических  рассчитываемого колеса;

 - угол наклона зуба на делительном цилиндре;

 - угол делительного конуса;

 - нормальный модуль зацепления; для прямозубых колес = т;

- коэффициент, учитывающий повышение изгибной прочности зубьев косозубых и шевронных колес по сравнению с прямозубыми; для прямозубых колес =1,0, для косозубых и шевронных =1,4;

z - число зубьев шестерни или колеса;

 - коэффициент ширины колеса (для конических колес - длины зуба).

Таблица 4.1 - Размерность величин, входящих в расчетные зависимости

.2 Методические указания к выполнению задания

Таблица 4.2 - Исходные данные

Задание. Рассчитать зубчатую передачу (зубчатые колеса подъемного механизма z₁ и z₂) одноступенчатого цилиндрического редуктора с косозубыми колесами (рис. 4.1) при  = 4,0 квт;  = 44 рад/с; i = 4. Расчетный срок службы зубчатых колес Т = 6 000 ч. Передача нереверсивная.

Решение.

. Угловая скорость тихоходного вала

.

Рисунок 4.1

. Материалы шестерни и колеса в целях получения наименьших габаритов передачи выбираем с повышенными механическими свойствами. Для шестерни принимаем сталь 40ХН, улучшенную с механическими характеристиками (см. табл. П21): σ_в = 883 Мн/м²; σ_Т = 686 Мн/м² ; НВ 265 (считаем, что диаметр заготовки будет не более 150 мм). Для колеса принимаем сталь 40×11, нормализованную с механическими характеристиками: σ_в = 736 Мн/м²; σ_Т = 550 Мн/м²; НВ 220 (считаем, что диаметр заготовки будет не более 500 мм).

При выборе материалов учтено, что твердость зубьев колеса должна быть на 25 ÷ 50 единиц Бриннеля ниже твердости зубьев шестерни.

. Допускаемое контактное напряжение, так как перепад твердостей материалов шестерни и зубчатого колеса незначителен, определяем для материала зубчатого колеса* .

Коэффициент режима

.

Число циклов нагружения каждого зуба колеса за весь срок службы

Где .

Так как N_ц > 10⁷ то k_pк = 1 и

. Допускаемые напряжения изгиба

так как N_ц > 5∙10⁴ (см. п. 3 расчета).

Для шестерни

принимаем σ_-1 = 400 МН/м²; [п] = 1,5 - коэффициент запаса по табл. П23; для поковок стальных, подвергнутых улучшению, k_σ = 1,6 - коэффициент концентрации напряжений у корня зуба - по табл. П24; при этих значениях для шестерни

.

Для зубчатого колеса

принимаем σ_-1 = 350 МН/м².

При тех же значениях [п] и k_σ

.

. Вращающий момент на ведущем валу

то же на ведомом валу

. Межосевое расстояние из условия контактной прочности

.

а) Расчетный момент на валу шестерни

где К = 1,3 - коэффициент нагрузки при симметричном расположении колес.

б) Коэффициент ширины колеса  принимаем равным 0,3.

* При большом перепаде твердости (НВ_шест - НВ_колеса ≥ 100) принимают для косозубых колес расчетное значение

.

в) Коэффициент повышения нагрузочной способности для непрямозубых колес k_n = 1,35.

Подставив числовые значения, получим

,

принимаем A = 170 мм.

. Нормальный модуль зацепления

.

В соответствии с ГОСТом 9563-60 принимаем т_п = 2,5 мм (см. табл. П19).

. Число зубьев и угол наклона зубьев.

Примем предварительно угол наклона зубьев β = 10°, тогда суммарное число зубьев

Число зубьев шестерни

,

тогда

.

Фактическое передаточное отношение

.

Угол наклона зубьев (уточненное значение)

.

. Диаметры делительных окружностей

.

Значения d_д1 и d_д2 следует вычислять с точностью до сотых долен миллиметра и проверять точное соблюдение равенства

.

В нашем случае это равенство соблюдается

В нашем случае это равенство соблюдается

. Ширина шестерни и колеса

;

.

. Уточненное значение коэффициента нагрузки найдем, предварительно определив окружную скорость

.

При такой окружной скорости можно принять 9-ю степень точности зубчатого зацепления. Так как для косозубых колес обычно не применяют степень точности ниже восьмой, примем 8-ю степень точности. При этом по табл. П26 динамический коэффициент К_дин = 1,1. При постоянной нагрузке передачи коэффициент концентрации нагрузки К_ц= 1,0 и общий коэффициент нагрузки К = К_дин ∙K_кц = 1,1, т. е. меньше принятого предварительно и поэтому проверка рабочих контактных напряжений не нужна.

. Проверка прочности зубьев на изгиб

.

а) Коэффициент формы зуба (табл. П20) выбираем по фиктивному числу зубьев

б) Ширина колеса В₂= 51 мм; шестерни В₁ = 55 мм.

в) Нормальный модуль т_п = 2,5 мм.

г) k_nu = 1,4.

д) Окружное усилие (номинальное и расчетное)

где К = 1,1 (см. п. 11 расчета)

е) Сравнительная оценка прочности зубьев шестерни и колеса на изгиб

;

Расчет ведем для зубьев шестерни, как менее прочных.

Расчетные напряжения изгиба

Сводная таблица основных параметров редуктора

Заключение

Таким образом, в данном курсовом проекте были выполнены задания по определению реакций опор, расчёт балки на прочность и жёсткость, динамический расчет движения автомобиля и расчет цилиндрических зубчатых передач. Данные задания позволили усвоить материалы учебной дисциплины, а также получить практические навыки при решении конкретных задач, которые могут встретиться в практической деятельности.     

Список литературы:

1.      Пономарев А.И. Основы функционирования систем сервиса: методические указания для выполнения курсовой работы. - Калуга: Издательство СПбГЭУ, 2014. - 64 с.

2.      Е.Росляков, И.Кравчук, В.Гладкевич, А.Дружинин. «Энергосиловое оборудование систем жизнеобеспечения». Учебник - СПб: Политехника, 2012. - 350 с.: ил.

.        «Многоцелевые гусеничные и колесные машины.» Под ред. Акад., докт. техн. наук,проф. Г.И.Гладкова - М: Транспорт, 2011. - 214 с.

.        Скойбеда А.Т. и др. «Детали машин и основы конструирования.» Учебник М:, Высшая школа, 2010. - 584 с.

.        Яблонский А.А., Никифорова В.М. Курс теоретической механики. - СПб: Изд. «Лань», 2009. - 788 с.

.        Костенко Н.А. и др. Сопротивление материалов: Учеб. пособие.- М..: Высш. шк., 2007.- 430 с.

.        Фролов К.В. и др. Теория механизмов и машин: Учеб. для втузов. - М.: Высш. шк.,2011. - 496 с.

.        Иванов М.Н. Детали машин: Учеб. для втузов. - М.: Высш. шк., 2010.- 383 с.