Солнечный ветер
Солнечный
ветер
Михаил Иванович Пудовкин,
Санкт-Петербургский государственный университет
Введение
Как показывают наблюдения, выполненные на борту
спутников Земли и других космических аппаратов с высоким апогеем орбиты,
межпланетное пространство заполнено чрезвычайно активной средой - плазмой
солнечного ветра. Солнечный ветер зарождается в верхних слоях атмосферы Солнца,
и его основные параметры определяются соответствующими параметрами солнечной
атмосферы. Однако связь между физическими характеристиками солнечного ветра
вблизи орбиты Земли и физическими явлениями в атмосфере Солнца оказывается
чрезвычайно сложной и, кроме того, меняется в зависимости от уровня солнечной
активности и конкретной ситуации на Солнце. Поэтому для простоты описания
предполагается, что наблюдаемый вблизи орбиты Земли солнечный ветер состоит из
трех в первом приближении независимых компонент [1]:
спокойный солнечный ветер - постоянно существующий
поток солнечной плазмы, заполняющий все межпланетное пространство вплоть до
границ гелиосферы (50-200 а.е.);
квазистационарные высокоскоростные потоки солнечной
плазмы, ответственные за рекуррентные геомагнитные возмущения;
спорадические высокоскоростные потоки - относительно
кратковременные, чрезвычайно неоднородные и сложные по структуре образования,
ответственные за спорадические магнитосферные возмущения.
Следуя этой схеме, рассмотрим морфологические
характеристики и механизм формирования указанных компонент солнечного ветра.
Спокойный
солнечный ветер
Согласно современным представлениям, энергия в недрах
Солнца вырабатывается в ходе процессов ядерного синтеза:
1H + 1H  2D + e+ +
2D + e+ +  + 1,44 MeV,
+ 1,44 MeV,
|
2D + 1H  3He + 3He +  + 5,49 MeV, + 5,49 MeV,
|
(1)
|
3He + 3He  4He + 1H +
1H + 12,85 MeV,
4He + 1H +
1H + 12,85 MeV,
где e+ обозначает позитрон,  - нейтрино и
- нейтрино и 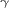 -
- 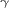 -квант. В результате
перечисленных процессов 1,0078 г водорода переходит в 1,0000 г гелия, а
оставшаяся масса превращается в кинетическую энергию частиц и энергию радиации.
Скорость выделения энергии в ходе реакций протон-протонного цикла определяется
выражением
-квант. В результате
перечисленных процессов 1,0078 г водорода переходит в 1,0000 г гелия, а
оставшаяся масса превращается в кинетическую энергию частиц и энергию радиации.
Скорость выделения энергии в ходе реакций протон-протонного цикла определяется
выражением
|
![$$\varepsilon_{pp}=2,5\cdot 10^{6}\rho X^{2}(\frac{10^{6}}{T})^{2/3}\exp[-33,8(\frac{10^{6}}{T})^{1/3}]~\mbox{эрг/(г}\cdot\mbox{с)}\,,$$](/wimg/1/85284.files/image004.gif)
|
(2)
|
где 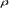 - плотность солнечного вещества, X
- относительное содержание в нем ядер водорода и T - температура. Принимая во
внимание, что как плотность вещества, так и его температура возрастают к центру
Солнца, можно показать, что около 99% солнечной энергии генерируется в ядре
Солнца с радиусом
- плотность солнечного вещества, X
- относительное содержание в нем ядер водорода и T - температура. Принимая во
внимание, что как плотность вещества, так и его температура возрастают к центру
Солнца, можно показать, что около 99% солнечной энергии генерируется в ядре
Солнца с радиусом 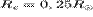 .
.
Известно, что в звездах типа Солнца теплопроводность
играет незначительную роль, так что произведенная в недрах Солнца энергия
передается к его поверхности в основном путем радиационного переноса, то есть в
результате ее поглощения и последующего переизлучения[2].
Однако радиационный перенос солнечной энергии
становится малоэффективным в верхних слоях Солнца. Дело в том, что по мере
уменьшения температуры солнечного вещества степень его ионизации уменьшается и
присутствие в нем нейтральных атомов водорода заметно снижает его прозрачность.
Это, в свою очередь, приводит к еще более быстрому уменьшению температуры
Солнца с расстоянием от центра, вследствие чего любой элементарный объем
солнечного вещества, всплывающий из недр Солнца, обладает большей температурой
и меньшей плотностью, чем окружающая плазма, что приводит к развитию так
называемой конвективной неустойчивости. Условия ее возбуждения уверенно
выполняются в поверхностных слоях Солнца 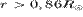 [2], где энергия
переносится главным образом в форме тепловой энергии плазмы, заключенной в
элементах вещества, поднимающихся из недр Солнца.
[2], где энергия
переносится главным образом в форме тепловой энергии плазмы, заключенной в
элементах вещества, поднимающихся из недр Солнца.
Развитие интенсивной турбулентности в поверхностных
слоях Солнца не только обеспечивает перенос энергии к его поверхности, но и
приводит к развитию явлений, играющих ключевую роль в солнечно-земной физике.
Прежде всего развитие конвективной турбулентности в плазме сопровождается
генерацией интенсивных магнитозвуковых волн. Распространяясь в атмосфере
Солнца, где плотность плазмы быстро уменьшается с высотой, звуковые волны
трансформируются в ударные. Они эффективно поглощаются веществом, в результате
чего температура последнего увеличивается, достигая величины (1) - (3)  106 К в солнечной
короне. При этом значительная часть протонов в короне Солнца не может
удерживаться его гравитационным полем, что приводит к непрерывному расширению
короны в космическое пространство, то есть к генерации солнечного ветра.
106 К в солнечной
короне. При этом значительная часть протонов в короне Солнца не может
удерживаться его гравитационным полем, что приводит к непрерывному расширению
короны в космическое пространство, то есть к генерации солнечного ветра.
В современной форме модель солнечного ветра была
разработана Е. Паркером [3]. Краткое изложение этой модели представлено ниже.
В стационарном сферически-симметричном случае
уравнения газодинамики могут быть записаны в следующей форме:
Уравнение движения
|
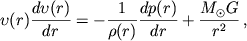
|
(3)
|
где 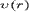 - скорость солнечного
ветра,
- скорость солнечного
ветра, 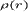 и
и
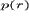 - его
плотность и давление;
- его
плотность и давление; 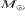 - масса Солнца и G - гравитационная постоянная;
- масса Солнца и G - гравитационная постоянная;
Уравнение
неразрывности потока вещества
|
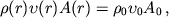
|
(4)
|
где A(r) = A0(r / r0)2 - площадь поперечного сечения
потоковой трубки, индексом 0 отмечены значения переменных на некотором исходном
расстоянии r0 от центра Солнца;
Уравнение
газового состояния
|
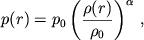
|
(5)
|
где 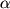 - показатель политропы,
- показатель политропы, 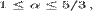 отличный от 5/3 (показатель адиабаты) при
наличии дополнительных источников энергии в солнечном ветре, о них речь пойдет
ниже.
отличный от 5/3 (показатель адиабаты) при
наличии дополнительных источников энергии в солнечном ветре, о них речь пойдет
ниже.
Подставляя равенства (4) и (5) в уравнение (3) и
интегрируя последнее по r, получаем уравнение Бернулли (при 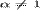 ) в форме
) в форме
|
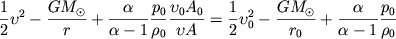
|
(6)
|
Переходя к безразмерным переменным
|
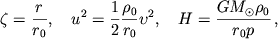
|
(7)
|
перепишем уравнение (6) в виде
|
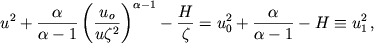
|
(8)
|
где 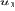 - константа интегрирования,
зависящая от граничных условий на поверхности
- константа интегрирования,
зависящая от граничных условий на поверхности 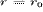 .
.
Уравнения (6) или (8) определяют изменение скорости
солнечного ветра с расстоянием от Солнца. Решение этих уравнений неоднократно
рассматривалось в литературе [1],[3],[4], и мы лишь кратко обсудим полученные
результаты. Уравнения (6) или (8) не имеют точного аналитического решения,
поэтому Паркер исследует асимптотику решения на больших (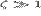 ) и малых (
) и малых (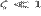 )
расстояниях от Солнца.
)
расстояниях от Солнца.
Большие расстояния
Очевидно, что при 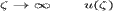 может
либо неограниченно возрастать, либо стремиться к какой-либо постоянной величине
или к нулю. Нетрудно видеть, что
может
либо неограниченно возрастать, либо стремиться к какой-либо постоянной величине
или к нулю. Нетрудно видеть, что 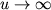 не удовлетворяет
уравнению (8). Действительно, первый член в левой части уравнения неограниченно
возрастает, второй и третий члены стремятся к нулю, тогда как в правой части
(8)
не удовлетворяет
уравнению (8). Действительно, первый член в левой части уравнения неограниченно
возрастает, второй и третий члены стремятся к нулю, тогда как в правой части
(8) 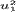 =
const.
=
const.
Вариант 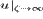 = const
оказывается возможным. В этом случае
= const
оказывается возможным. В этом случае
|
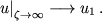
|
(9а)
|
Решение 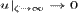 также удовлетворяет
уравнению (8). В этом случае первый и третий члены в левой части уравнения (9)
стремятся к нулю и
также удовлетворяет
уравнению (8). В этом случае первый и третий члены в левой части уравнения (9)
стремятся к нулю и
|
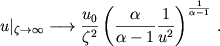
|
(9б)
|
Таким образом, решение уравнения (8) на больших
расстояниях имеет две ветви: верхнюю (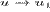 ) и нижнюю (
) и нижнюю (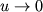 ).
Для того чтобы выбрать решение, приемлемое с физической точки зрения, вычислим
плотность плазмы, соответствующую этим решениям.
).
Для того чтобы выбрать решение, приемлемое с физической точки зрения, вычислим
плотность плазмы, соответствующую этим решениям.
Из равенства (4) следует
|
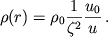
|
(10)
|
Подставляя в (10) величину  из (9а), (9б), находим
из (9а), (9б), находим
|
![$$
\left.u\right|_{\zeta \rightarrow \infty} \rightarrow \left\{
%
\begin{array}{ll} 0 & \mbox{--- верхняя ветвь,} \\
\rho_0\left[\frac{(\alpha-1)u^2_1}{\alpha}\right]^{\frac{1}{\alpha-1}} & \mbox{--- нижняя ветвь.} \\
\end{array}
%
\right.
$$](/wimg/1/85284.files/image037.gif)
|
(11)
|
Из равенств (11) видно, что в случае, когда 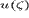 соответствует
нижней ветви решения, плотность плазмы при
соответствует
нижней ветви решения, плотность плазмы при 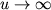 стремится к конечной
и относительно большой величине, что противоречит экспериментальным данным. В
то же время верхняя ветвь решения соответствует
стремится к конечной
и относительно большой величине, что противоречит экспериментальным данным. В
то же время верхняя ветвь решения соответствует 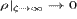 , что удовлетворяет
условиям модели. Таким образом, на больших расстояниях от Солнца физический
смысл имеет лишь верхняя ветвь решения уравнения Паркера.
, что удовлетворяет
условиям модели. Таким образом, на больших расстояниях от Солнца физический
смысл имеет лишь верхняя ветвь решения уравнения Паркера.
Малые расстояния
( )
)
При  третий член в левой
части равенства (8) неограниченно возрастает. Поскольку в правой части
уравнения постоянная величина, это означает, что неограниченное возрастание
третий член в левой
части равенства (8) неограниченно возрастает. Поскольку в правой части
уравнения постоянная величина, это означает, что неограниченное возрастание 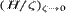 должно быть скомпенсировано одним из
первых двух членов в левой части (8), то есть опять имеют место две ветви решения:
должно быть скомпенсировано одним из
первых двух членов в левой части (8), то есть опять имеют место две ветви решения:
|
![$$
\left.u\right|_{\zeta \rightarrow 0} \rightarrow \left\{
%
\begin{array}{ll} \left(\frac{H}{\zeta}\right)^{1/2} \rightarrow \infty & \mbox{--- верхняя ветвь,} \\
u_0\left[\frac{\alpha}{\alpha-1}\,\frac{1}{H}\right]^{\frac{1}{\alpha-1}} \zeta^{\frac{1}{\alpha-1}-2} & \mbox{--- нижняя ветвь.} \\
\end{array}
%
\right.
$$](/wimg/1/85284.files/image042.gif)
|
(12)
|
Первое решение, соответствующее неограниченному
возрастанию скорости солнечного ветра при  , физически
неприемлемо. Второе решение дает разумный результат
, физически
неприемлемо. Второе решение дает разумный результат 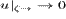 при
значениях показателя политропы, определяемых неравенством
при
значениях показателя политропы, определяемых неравенством 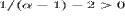 , то
есть
, то
есть 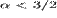 .
.
Таким образом, стационарное решение короны оказывается
возможным лишь в том случае, если показатель политропы a меньше адиабатического
(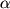 = 5/3),
то есть если имеет место непрерывный приток энергии в корону и солнечный ветер.
В первоначальной модели Паркера предполагалось, что необходимый приток энергии
обеспечивается высокой теплопроводностью солнечной плазмы. Однако, как будет
показано ниже, одного лишь потока тепловой энергии недостаточно для ускорения
солнечного ветра, и требуются дополнительные источники энергии.
= 5/3),
то есть если имеет место непрерывный приток энергии в корону и солнечный ветер.
В первоначальной модели Паркера предполагалось, что необходимый приток энергии
обеспечивается высокой теплопроводностью солнечной плазмы. Однако, как будет
показано ниже, одного лишь потока тепловой энергии недостаточно для ускорения
солнечного ветра, и требуются дополнительные источники энергии.
Итак, мы видим, что физически разумным граничным
условиям при больших 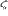 удовлетворяет верхняя ветвь решения уравнения Паркера, а при
малых
удовлетворяет верхняя ветвь решения уравнения Паркера, а при
малых 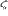 -
нижняя. Сращивание этих двух ветвей решения зависит от поведения решения в
окрестностях некоторой критической точки, положение которой на плоскости
-
нижняя. Сращивание этих двух ветвей решения зависит от поведения решения в
окрестностях некоторой критической точки, положение которой на плоскости 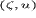 определяется
следующим образом.
определяется
следующим образом.
Продифференцируем уравнение (8) по 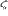 :
:
(13)
|
Определим критическую точку (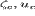 ) как точку, где правая
часть уравнения (13) и коэффициент при
) как точку, где правая
часть уравнения (13) и коэффициент при 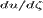 в левой части уравнения
одновременно равны нулю. Тогда
в левой части уравнения
одновременно равны нулю. Тогда
|
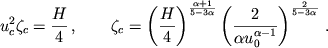
|
(14)
|
Топология решения уравнения (8) в окрестностях
критической точки показана на рис. 1. Решение представляет собой семейство
гипербол. При этом существует лишь одно решение, удовлетворяющее граничным
условиям как на больших, так и на малых расстояниях от Солнца. Этому решению
соответствует кривая, проходящая через критическую точку (критическое решение).
|

|
|
Рис. 1. Семейство кривых решения уравнения
Паркера в окрестности критической точки.
|
Радиальные профили скорости солнечного ветра в случае
изотермической (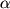 = 1) короны при различной температуре последней представлены на
рис. 2. Из приведенных кривых видно, что решение достаточно чувствительно к
граничным условиям. Так, например, при Т0 = 0,5 106 К скорость солнечного ветра
на орбите Земли оказывается равной 260 км/с, а при T = 4 106 К - около 1150
км/с, что в целом не противоречит экспериментальным данным (см. табл. 1 из
[4]). В то же время рассчитанная плотность плазмы на орбите Земли 25-40 см- 3
вместо реальных 5-10 см- 3.
= 1) короны при различной температуре последней представлены на
рис. 2. Из приведенных кривых видно, что решение достаточно чувствительно к
граничным условиям. Так, например, при Т0 = 0,5 106 К скорость солнечного ветра
на орбите Земли оказывается равной 260 км/с, а при T = 4 106 К - около 1150
км/с, что в целом не противоречит экспериментальным данным (см. табл. 1 из
[4]). В то же время рассчитанная плотность плазмы на орбите Земли 25-40 см- 3
вместо реальных 5-10 см- 3.
|

|
|
Рис. 2.Радиальные профили скорости
солнечного ветра в модели Паркера при различных температурах T короны.
|
Как видно из таблицы, скорость солнечного ветра
меняется в достаточно широком диапазоне - от ~ 300 до ~ 700 км/с. Казалось бы,
эти вариации легко объяснимы в рамках модели Паркера соответствующими
вариациями температуры короны (см. рис. 2). Однако непосредственные наблюдения
свидетельствуют, что источником рекуррентных высокоскоростных потоков являются
корональные дыры (см. ниже), в которых температура короны существенно ниже
средней. В связи с этим обратим внимание на то, что, согласно модели, скорость
солнечного ветра помимо температуры короны зависит также от величины показателя
политропы 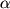 :
чем больше
:
чем больше 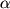 ,
тем меньше скорость солнечного ветра на орбите Земли. Наилучшее соответствие
между модельными расчетами и экспериментальными данными получено Паркером при
,
тем меньше скорость солнечного ветра на орбите Земли. Наилучшее соответствие
между модельными расчетами и экспериментальными данными получено Паркером при 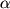 = 1,1 вблизи
Солнца и
= 1,1 вблизи
Солнца и 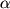 =
5/3 на больших расстояниях от него.
=
5/3 на больших расстояниях от него.
Однако в связи с малой величиной показателя 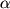 возникает
затруднение следующего рода: при
возникает
затруднение следующего рода: при 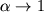 градиент температуры
градиент температуры
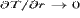 . При этом поток тепла,
обусловленный теплопроводностью, также стремится к нулю. Таким образом, для
поддержания достаточно высокой температуры солнечного ветра требуются
дополнительные нетепловые источники энергии, связанные, скорее всего, с
диссипацией энергии альфвеновских волн [3].
. При этом поток тепла,
обусловленный теплопроводностью, также стремится к нулю. Таким образом, для
поддержания достаточно высокой температуры солнечного ветра требуются
дополнительные нетепловые источники энергии, связанные, скорее всего, с
диссипацией энергии альфвеновских волн [3].
Вклад МГД-волн в тепловую энергию и импульс солнечного
ветра обсуждаются в ряде публикаций. Обзор этих исследований и их дальнейшее
развитие даны И. Чашеем и В. Шишовым (1987 год). Выбрав соответствующим образом
интенсивность и спектр МГД-волн в основании короны, можно получить не только
соответствующую экспериментальным данным скорость солнечного ветра на орбите
Земли, но и необходимую плотность плазмы.
Вместе с тем модель, развиваемая в рамках
одножидкостной гидродинамики, не в состоянии объяснить наблюдаемую разность
электронной и ионной температур в солнечном ветре (см. табл. 1).
Таблица 1. Параметры солнечного ветра на орбите Земли
|
Параметр, размерность
|
Средняя величина
|
Солнечный ветер
|
|
|
|
медленный
|
высоко скоростной
|
|
n, см-3
|
8,7
|
11,9
|
3,9
|
|
 , км/с , км/с
|
468
|
327
|
702
|
|
n , см-2 с-1 , см-2 с-1
|
3,8  108 108
|
3,9  108 108
|
2,7  108 108
|
|
Tp , К
|
7  104 104
|
3,4  104 104
|
2,3  105 105
|
|
Te , К
|
1,4  105 105
|
1,3  105 105
|
1,0  105 105
|
|
Te / Tp
|
1,9
|
4,4
|
0,45
|
Следует заметить, что одножидкостные модели
гидродинамики применимы в физике плазмы лишь в том случае, когда частота
столкновений электронов с ионами достаточно велика, что обеспечивает
эффективный обмен импульсом между электронной и ионной компонентами плазмы и
соответственно равенство их температур. P.A. Sturrock и R.E. Hartle (1966 год)
обратили внимание на то, что в солнечном ветре вследствие быстрого убывания
плотности плазмы с расстоянием от Солнца последнее условие может не выполняться
и температура ионов может существенно отличаться от температуры электронов. При
этом, поскольку ионная теплопроводность относительно мала, протонная компонента
короны Солнца расширяется почти адиабатически и соответственно быстро
охлаждается. В то же время теплопроводность электронной компоненты плазмы
относительно велика, в связи с чем температура последней падает с расстоянием
достаточно медленно, что в целом не противоречит экспериментальным данным (см.
табл. 1).
Такое относительно независимое существование
электронной и ионной компонент плазмы описывается в рамках двухжидкостной
гидродинамики. При этом в уравнении движения (3) газовое давление следует
заменить суммой давлений электронного и ионного газов P = Pe + Pi = nk(Te + Ti
). Кроме того, в случае двухжидкостной гидродинамики уравнение газового
состояния обычно заменяют уравнением сохранения энергии, записанным отдельно
для электронной и ионной компонент, так что система уравнений (2) - (4)
принимает вид [1]
|
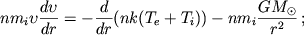
|
(15)
|
|
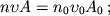
|
(16)
|
|
![$$\frac{1}{r^2}\frac{d}{dr}\left[nm_{i}\upsilon r^{2}\left( \frac{1}{2}\upsilon^{2}+\frac{3}{2}\frac {P_{i}}{nm_{i}} \right) \right]=-\frac{1}{r^{2}}\frac{d}{dr}(P_{i}\upsilon r^{2})-$$](/wimg/1/85284.files/image059.gif)
|
(17)
|
|
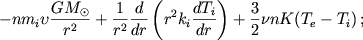
|
|
![$$\frac{1}{r^2} \frac{d}{dr} \left[ nm_{e} \upsilon r^{2} \left( \frac{1}{2} \upsilon^{2}+ \frac{3}{2}\frac {P_{e}}{nm_{e}} \right) \right]=-\frac{1}{r^{2}}\frac{d}{dr}(P_{e} \upsilon r^{2})-$$](/wimg/1/85284.files/image061.gif)
|
(18)
|
|
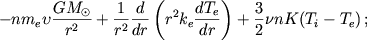
|
здесь 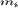 и
и 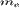 - масса иона и электрона
соответственно,
- масса иона и электрона
соответственно, 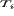 и
и 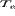 -
ионная и электронная температура;
-
ионная и электронная температура; 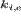 - коэффициент ионной
(электронной) теплопроводности,
- коэффициент ионной
(электронной) теплопроводности, 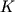 - постоянная Больцмана и
- постоянная Больцмана и  - частота столкновений
ионов с электронами.
- частота столкновений
ионов с электронами.
Результаты численного интегрирования системы уравнений
(15)- (18) представлены на рис. 3 из [1] . Кривая 1 соответствует
одножидкостной модели, кривые 2 и 3 показывают изменение с расстоянием
электронной и ионной температуры солнечного ветра в двухжидкостной модели. Как
видно из рисунка, на орбите Земли (r = 215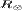 Tp = 4,4 103 K и Te = 3,4 105
K.
Tp = 4,4 103 K и Te = 3,4 105
K.
|

|
|
Рис. 3. Изменение с расстоянием от
Солнца 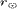 температуры T солнечного ветра в одножидкостной модели (1
), электронной (2 ) и ионной (3 ) температур в двухжидкостной модели. температуры T солнечного ветра в одножидкостной модели (1
), электронной (2 ) и ионной (3 ) температур в двухжидкостной модели.
|
Таким образом, предсказываемая моделью температура
электронов оказывается вдвое больше, а температура протонов - на порядок меньше
реальной температуры частиц в солнечном ветре (см. табл. 1). Такое
несоответствие теоретических и экспериментальных данных можно устранить,
предположив существование дополнительных источников нагрева плазмы, причем
преимущественно ее ионной компоненты. Этому требованию удовлетворяют упомянутые
выше альфвеновские волны. Дело в том, что, хотя сами альфвеновские волны в
солнечном ветре почти не поглощаются, они эффективно трансформируются в ходе
четырехволнового взаимодействия в магнитозвуковые волны. Последние же в
условиях, характерных для солнечного ветра, диссипируют в результате
резонансного взаимодействия с протонами, которые при этом заметно нагреваются.
Параметры солнечного ветра на орбите Земли, полученные
A. Barnes и др. в 1971 году в рамках двухжидкостной модели с учетом
дополнительного источника энергии в виде МГД-волн, представлены в табл. 2.
Таблица 2. Параметры солнечного ветра на орбите Земли в
двухжидкостной модели Барнеса
|
Плотность плазмы n, см-3
|
15
|
|
Скорость  , км/с , км/с
|
330
|
0,46
|
|
Протонная температура Tp ,
K
|
3,2  104 104
|
|
Электронная температура Te
, K
|
2,2  105 105
|
|
Отношение Te / Tp
|
6,9
|
Рассчитанные параметры солнечного ветра на орбите
Земли оказываются близкими к наблюдаемым параметрам медленного солнечного ветра
(см. табл. 1). В то же время параметры высокоскоростных потоков в солнечном
ветре заметно отличаются от предсказываемых моделью. В частности, температура
протонов в этих потоках оказывается выше температуры электронов, что,
по-видимому, свидетельствует о повышенной интенсивности альфвеновских волн в
области их источника на Солнце.
Рассмотрим подробнее высокоскоростной солнечный ветер
и обсудим его возможные источники.
Высокоскоростной
солнечный ветер
Как видно из данных, представленных в табл. 1,
высокоскоростной солнечный ветер характеризуется повышенной скоростью (около
700 км/с), пониженной плотностью плазмы (n = 4 см-3) и повышенной ионной
температурой. Однако, прежде чем обсуждать возможные источники этих потоков,
напомним, что существуют по меньшей мере два рода таких потоков: рекуррентные и
спорадические.
Рекуррентные потоки высокоскоростного солнечного ветра
отличаются прежде всего тем, что существуют в течение многих месяцев, регулярно
появляясь в окрестностях Земли примерно через 27 дней (период оборота Солнца),
что свидетельствует об относительно большом времени жизни их источников. В
течение многих лет происхождение этих потоков оставалось загадкой, поскольку им
не соответствовали какие-либо видимые особенности на поверхности Солнца. Однако
в настоящее время можно считать доказанным, что обсуждаемые потоки зарождаются
на Солнце в области так называемых корональных дыр.
Корональные дыры отчетливо видны на получаемых на
космических аппаратах фотографиях Солнца в рентгеновском и крайнем
ультрафиолетовом диапазонах спектра солнечного излучения (см. рис. 4), где они
фиксируются как обширные области пониженной (в несколько раз) интенсивности
излучения, простирающиеся от полярных широт до экватора или даже в
противоположное полушарие.
|

|
|
Рис. 4. Фотография Солнца в
рентгеновском излучении 21 августа 1973 года.
|
Протяженность корональных дыр по долготе составляет
30° - 90°. Соответственно время прохождения корональной дыры через центральный
меридиан Солнца (вследствие вращения последнего) составляет 3-6 суток, что
вполне согласуется с длительностью существования соответствующих
высокоскоростных потоков в окрестностях Земли [1]. Пониженная интенсивность
рентгеновского излучения в области корональных дыр может определяться как
пониженной плотностью плазмы в этих областях, так и ее пониженной температурой.
Действительно, наземные наблюдения короны во время солнечных затмений
показывают, что в короне существуют, в особенности в высоких широтах, области с
относительно низкой плотностью плазмы. В то же время и температура плазмы в
области корональных дыр оказывается существенно пониженной. Так, например, при
наблюдениях излучения Солнца в радиодиапазоне яркостная температура в области
корональных дыр составляет около 0,8 106 К, что существенно ниже температуры
спокойной короны, и плотность плазмы в корональной дыре составляет 0,25
плотности спокойной короны.
Таким образом, корональные дыры действительно представляют
собой области пониженной плотности плазмы и ее относительно низкой температуры.
Чем вызываются указанные особенности короны в этих областях, не совсем ясно. В
связи с этим обращает на себя внимание то, что корональные дыры, как правило,
совпадают с областями униполярного магнитного поля с квазирадиальными или
слегка расходящимися силовыми линиями [4]. Открытые силовые линии магнитного
поля не препятствуют радиальному расширению корональной плазмы, что может
объяснить пониженную плотность последней в области дыр и увеличение скорости
генерируемого в них солнечного ветра. Вместе с тем увеличение скорости ветра,
обусловленное благоприятной конфигурацией силовых линий магнитного поля, не
может компенсировать ее уменьшения, связанного с низкой температурой плазмы в
рассматриваемых областях, и для объяснения появления высокоскоростных потоков
опять приходится предположить наличие в корональных дырах мощного источника
МГД-волн. К сожалению, прямых подтверждений существования таких волн в области
корональных дыр пока не получено.
Спорадические высокоскоростные потоки. Второй тип
высокоскоростных потоков в солнечном ветре - это кратковременные (время пробега
мимо Земли  =
1-2 суток), часто чрезвычайно интенсивные (скорость солнечного ветра до 1200
км/с) потоки, имеющие весьма большую долготную протяженность. Двигаясь в
межпланетном пространстве, заполненном плазмой относительно медленного
спокойного солнечного ветра, высокоскоростной поток как бы сгребает эту плазму,
в результате чего перед его фронтом образуется движущаяся вместе с ним
отошедшая ударная волна. Пространство между фронтом потока и фронтом отошедшей
ударной волны заполнено относительно плотной (несколько десятков частиц в 1
см3) и горячей плазмой.
=
1-2 суток), часто чрезвычайно интенсивные (скорость солнечного ветра до 1200
км/с) потоки, имеющие весьма большую долготную протяженность. Двигаясь в
межпланетном пространстве, заполненном плазмой относительно медленного
спокойного солнечного ветра, высокоскоростной поток как бы сгребает эту плазму,
в результате чего перед его фронтом образуется движущаяся вместе с ним
отошедшая ударная волна. Пространство между фронтом потока и фронтом отошедшей
ударной волны заполнено относительно плотной (несколько десятков частиц в 1
см3) и горячей плазмой.
Ранее предполагалось, что спорадические потоки в
солнечном ветре обусловлены солнечными вспышками [1] и им подобными явлениями.
Однако в последнее время общественное мнение на этот счет изменилось, и
большинство исследователей, в особенности зарубежных, придерживаются точки
зрения, согласно которой спорадические высокоскоростные потоки в солнечном
ветре обусловлены так называемыми корональными выбросами.
Корональные выбросы, наиболее отчетливо наблюдаемые
вблизи лимба Солнца, представляют собой некоторые относительно протяженные
плазменные образования, движущиеся в короне Солнца вверх от ее основания. Вывод
о том, что спорадические потоки в солнечном ветре связаны именно с корональными
выбросами (или CME), а не со вспышками, основан на следующих экспериментальных
фактах: 1) несмотря на статистически значимую связь между спорадическими
потоками и солнечными вспышками, однозначная связь между ними отсутствует, то
есть, с одной стороны, наблюдаются вспышки, не вызывающие межпланетных ударных
волн, и, с другой - наблюдаются высокоскоростные потоки, не предваряемые
вспышками, и 2) солнечные вспышки непосредственно не связаны с корональными
выбросами. Связь между межпланетными ударными волнами, корональными выбросами и
солнечными вспышками детально исследовалась N. Sheeley и др. (1985 год),
которые, в частности, показали, что 72% ударных волн, наблюдавшихся на борту
космического аппарата "Helios-1", были связаны с большими
низкоширотными корональными выбросами. В то же время лишь 52% тех же ударных
волн были связаны с солнечными вспышками.
В результате подробного анализа этих данных удалось
показать [5],[6], что если исключить из списка ударные волны, наблюдаемые за
лимбом Солнца, то число волн, связанных со вспышками, возрастает до 85%, то
есть связь ударных волн со вспышками оказывается ничуть не хуже, чем с
корональными выбросами. Кроме того, как показали Harrison и др. (1990 год),
корональные выбросы и вспышки связаны с одними и теми же активными областями на
Солнце, и быстрые выбросы (со скоростью порядка 1000 км/с), с которыми обычно
связана межпланетная ударная волна, начинают свое движение в короне
одновременно с началом вспышки.
Таким образом, вывод о непричастности солнечных
вспышек к межпланетным ударным волнам представляется не вполне убедительным, и
мы по-прежнему будем считать солнечные вспышки одним из основных источников
высокоскоростных спорадических потоков в солнечном ветре.
Что касается механизма генерации самих вспышек (и,
естественно, связанных с ними потоков), то наиболее популярной в настоящее
время является предложенная в 1964 году Петчеком модель вспышки, основанная на
гипотезе о магнитном пересоединении (см. [7]). Развитие солнечной вспышки в
рамках модели Петчека представлено на рис. 5.
|

|
|
Рис. 5. Развитие вспышки в модели
Старрока: 1 - линия пересоединения, 2 - формирующаяся ударная волна, 3 -
эжектируемая плазма, 4 - высокоэнергичные частицы, 5 - ударная волна, 6 -
быстрые электроны.
|
В этой модели силовые линии магнитного поля активной
области оказываются, начиная с некоторого уровня, разорванными и образуют две
силовые трубки с антипараллельными полями, разделенными токовым слоем. В
некоторый момент из-за развития ионно-звуковой или ионно-циклотронной
неустойчивости проводимость плазмы в некоторой точке 1 (рис. 5а) в плазменном
слое резко падает, в результате чего токовый слой разрывается и силовые линии
магнитного поля пересоединяются. Магнитная энергия быстро переходит в
кинетическую и тепловую энергию плазмы и происходят интенсивный разогрев и
ускорение плазмы (рис. 5б). Ускоренные частицы, двигаясь вдоль открытых силовых
линий магнитного поля, покидают хромосферу и выбрасываются в межпланетное
пространство (рис. 5в). При этом движущиеся вверх энергичные электроны, проходя
через корону и взаимодействуя с ней, могут вызывать всплески радиоизлучения.
Частота радиоизлучения вследствие уменьшения концентрации фоновой плазмы быстро
уменьшается по мере движения электронов вверх (что соответствует так называемым
всплескам радиоизлучения III типа).
Частицы, движущиеся вдоль силовых линий магнитного
поля к Солнцу, нагревают плазму в нижней хромосфере и фотосфере, вызывая
увеличение яркости водородных эмиссий и образование высокотемпературного
коронального облака. Плазма, ускоряемая в направлении от Солнца, формирует
высокоскоростной поток и связанную с ним ударную волну.
Заключение
Суперпозиция описанных выше потоков солнечной плазмы и
их взаимодействие и создают ту сложную и непрерывно изменяющуюся систему,
которая называется солнечным ветром.
В кратком обзоре современных представлений о
морфологии и механизмах генерации солнечного ветра мы смогли обсудить лишь
самые общие и наиболее полно исследованные характеристики этих процессов, что
может создать несколько ложное представление о действительном состоянии
проблемы. В связи с этим следует еще раз подчеркнуть, что нами опущены многие,
в том числе и весьма существенные, детали рассматриваемых процессов (например,
механизм формирования межпланетного магнитного поля), без отчетливого понимания
которых представленная выше модель солнечного ветра остается не более чем
гипотезой, хотя и весьма вероятной.
Более подробное изложение обсуждаемых вопросов
представлено в упомянутых выше книгах [1]-[4] и обзорах [6], [7].
Список литературы
Хундхаузен А. Расширение короны и солнечный ветер. М.:
Мир, 1976. 302 с.
Гибсон Э. Спокойное Солнце. М.: Мир, 1977. 408 с.
Паркер Е.Н. Динамические процессы в межпланетной
среде. М.: Мир, 1965. 362 с.
Коваленко В.А. Солнечный ветер. М.: Наука, 1983. 272
с.
Pudovkin M.I. // J. Geophys. Res. 1995. V.
100. No A5. P. 7917.
Pudovkin M.I. // Rept. Progr. in Phys.
1995. V. 58. No 9. P. 929.
Пудовкин М.И., Семенов В.С. Теория пересоединения и
взаимодействие солнечного ветра с магнитосферой Земли. М.: Наука, 1985. 126 с.
Для подготовки данной работы были использованы
материалы с сайта http://www.kosmofizika.ru