Решение задач линейного программирования

сОДЕРЖАНИЕ

Введение

.Общая задача линейного программирования (ЛП)

.1 Постановка задачи

.2 Графический метод решения задач ЛП

.3 Симплекс-метод решения задач ЛП

. Примеры решения задач ЛП

Заключение

Список использованных источников

Введение

В последние годы в прикладной математике большое внимание уделяется новому классу задач оптимизации, заключающихся в нахождении в заданной области точек наибольшего или наименьшего значения некоторой функции, зависящей от большого числа переменных. Это так называемые задачи математического программирования, возникающие в самых разнообразных областях человеческой деятельности и прежде всего в экономических исследованиях, в практике планирования и организации производства. Изучение этого круга задач и методов их решения привело к созданию новой научной дисциплины, получившей позднее название линейного программирования.

В данном курсовом проекте будет рассмотрено два метода решения задач линейного программирования: графический и симплекс-метод.

Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трехмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трех изобразить графически вообще невозможно. Поэтому для решения, в том числе этой проблемы, в конце 40-х годов американским математиком Дж. Данцигом был разработан эффективный метод решения данного класса задач - симплекс-метод. К задачам, решаемых этим методом в рамках математического программирования относятся такие типичные экономические задачи как «Задача об оптимальном плане выпуска продукции», «Оптимизация межотраслевых потоков», « Задача о выборе производственной программы», «Транспортная задача», «Задача размещения», «Модель Неймана расширяющейся экономики» и другие. Решение таких задач дает большие выгоды как народному хозяйству в целом, так и отдельным его отраслям.

Таким образом, цель курсовой работы: применение методов линейного программирования к экстремальным задачам экономики.

Для достижения поставленной цели решаются задачи: постановки задачи линейного программирования, графического метода решения задач ЛП, симплекс-метода решения задач ЛП.

1. Общая задача линейного программирования

.1 Постановка задачи

Задача линейного программирования (ЛП) ассоциируется с задачей распределительного типа, в которой требуется распределить ограниченные ресурсы по нескольким видам деятельности. Интерпретация задачи ЛП в этом случае состоит в следующем. Моделируемая ЭИС характеризуется наличием нескольких видов деятельности j (j = 1, …, n), для осуществления которых требуются имеющиеся в ограниченном количестве различные ресурсы bi, (i = 1, …, m). Интенсивность расходования каждого из ресурсов на каждый из видов деятельности ЭИС известна и равна aij. Результативность или ценность каждого j-го вида деятельности ЭИС характеризуется величиной cj. Цель построения модели заключается в определении уровней каждого вида деятельности ЭИС xj, при которых оптимизируется общий результат деятельности ЭИС в целом при выполнении ограничений, накладываемых на использование ресурсов, т. е. cj xj ≤ bi, i = 1, …, m. Структура целевой функции y(u) отражает вклад каждого вида деятельности ЭИС в общий результат. При максимизации сj представляет собой “полезность” j-го вида деятельности (ущерб, наносимый конкуренту по бизнесу, предотвращенный ущерб), а в случае минимизации характеризует затраты (потери собственные, расход материальных средств). Линейность модели выявляется или принимается в качестве допущения на этапе формализации задачи. Линейность предполагает наличие двух свойств - пропорциональности и аддитивности, присущих как целевой функции, так и ограничениям. Пропорциональность целевой функции означает, что вклад каждой управляемой переменной в целевую функцию пропорционален величине этой переменной. Аддитивность же целевой функции заключается в том, что целевая функция представляет собой сумму вкладов от различных управляемых переменных. Пропорциональность ограничений проявляется в том, что общий объем потребляемых ресурсов прямо пропорционален величинам управляемых переменных. Аддитивность ограничений состоит в том, что величина ресурса должна представлять собой сумму расходов по видам деятельности, каждое слагаемое которой пропорционально величине соответствующей управляемой переменной. В формализованном виде задачу ЛП можно представить следующим образом:

Определить

где ,   (1.1)

Условие неотрицательности, накладываемое на переменные xj, означает, что ни одному виду деятельности ЭИС не может быть приписан отрицательный уровень. Ограничение типа ≥ нельзя рассматривать как ограничение в буквальном смысле этого слова. Наличие такого неравенства предполагает необходимость обязательного выполнения каких-либо планов, заданий, нормативов.

Математическая формулировка задачи ЛП выглядит следующим образом: необходимо определить значения управляемых переменных xj, доставляющих экстремум целевой функции y(u) на всем множестве стратегий U = {u} и удовлетворяющих всем имеющимся в задаче ограничениям. Этой формулировкой задача ЛП считается поставленной математически, что позволяет осуществлять поиск ее оптимального решения известными математическими методами.

Формальную постановку задачи ЛП (1.1) для удобства можно представить в упрощенном виде:

определить max (или min) W(x) = при ограничениях:

cj xj (≤, = или ≥) bi, i = 1, …, m; xj ≥ 0,

где W(x) - новое обозначение ЦФ, т. е. W(x) = y(u) = f(x).

Для решения задач ЛП разработано множество методов, но наиболее популярными из них являются графический и симплексный методы, позволяющие получить гораздо больше информации, нежели просто найденное оптимальное решение.

1.2 Графический метод решения задач ЛП

Графический метод, несмотря на свою очевидность и применимость лишь в случае малой размерности задачи, позволяет понять качественные особенности задачи линейного программирования, характерные для любой размерности пространства переменных и лежащие в основе численных методов ее решения. Поясним графический метод на примере задачи ЛП в основной форме для n = 2

(c, x) → max≤ b,

где x = (x1, x2), c = (c1, c2), b = (b1, b2, ..., bm), A - матрица размера (m × 2).

Очевидно, что при данной постановке задачи допустимое множество X в плоскости (x1, x2) представляет собой многоугольник (не обязательно замкнутый), образованный пересечением полуплоскостей H+aibi (где ai - i-я строка матрицы A, i = 1, ..., m), соответствующих ограничениям вида ai1x1 + ai2x2 ≤ bi в исходной задаче. Линии уровня функции f(x) = (c, x) (линией уровня называется множество {xR: f(x)= α, α  R}) образуют семейство параллельных прямых Hcα. При этом grad f(x) = c, т.е. градиент целевой функции всюду одинаков и является нормалью каждой из данных полуплоскостей. В соответствии с предыдущим, поиск решения задачи сводится к нахождению максимального числа α* среди всех таких α, что полуплоскость Hcα имеет непустое пересечение с X. При этом X - множество решений задачи. При неограниченном решений может и не быть, т.е. HcαX Ø при всех α→ .

Из графического представления ясна характерная особенность задачи ЛП (при c ≠ 0): если ее решение существует, то оно достигается обязательно на границе. Отметим, что в рассмотренной задаче ЛП на максимум при поиске α* происходит как бы перемещение прямой Hcα в направлении вектора c. Если же решается задача ЛП на минимум, и, следовательно, ищется минимальное α*, удовлетворяющее указанным требованиям, то Hcα перемещается в направлении, противоположном вектору c.

Пример 1.2.1 Пусть дана задача ЛП

x + y → max

x + y ≤ 2,+ 2y ≤ 7,

x - 3y ≤ 6,≥ 0, y ≥ 0.

Геометрическая интерпретация задачи приведена на рисунке 1.

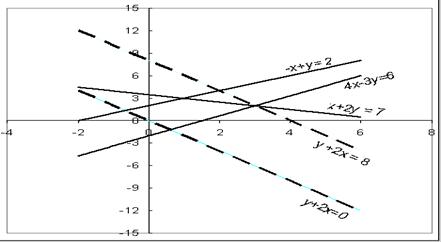
Рисунок 1

Ясно, что решением является точка пересечения прямых

+ 2y = 7 и 4x - 3y = 6, т.е. (x*, y*) = (3, 2).

Очевидно, что графический метод решения задач ЛП применим лишь в случае малой размерности пространства. В общем случае для решения задач линейного программирования в пространстве произвольной размерности широко используется симплекс-метод.

задача линейный программирование симплекс

1.3 Симплекс-метод решения задач ЛП

Симплекс метод - метод линейного программирования <#"827026.files/image008.jpg">

Рисунок 2 - Область допустимых значений-

Для определения направления движения к оптимуму построим вектор-градиент Ñ, координаты которого являются частными производными целевой функции, т.е.

=(16,60)

Что бы построить этот вектор, нужно соединить точку (16;60) с началом координат. При максимизации целевой функции необходимо двигаться в направлении вектора-градиента.

в крайней, угловой точке достигается максимум целевой функции. Для нахождения координат этой точки достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума:

x1+x2=80,

x2=10

Отсюда легко записать решение исходной ЗЛП: max f(x) = 800 и достигается при x1=14 и x2=10.

Рисунок 3. Максимум целевой функции достигается в точке (14,10).

Таким образом, для оптимального плана производства предприятию необходимо изготовить 10 м3 пиломатериалов и 14 м2 фанеры.

Задача 2

Завод производит два вида продукции: велосипеды и мотоциклы. При этом цех по сборке велосипедов имеет мощность 100 тыс. штук в год, цех по сборке мотоциклов 30 тыс. Одна группа механических цехов завода может производить детали либо для 120 тыс. велосипедов, либо для 40 тыс. мотоциклов, либо другую комбинацию деталей, ограниченную этими данными.Другая группа механических цехов может выпускать детали либо для 80 тыс. велосипедов, либо для 60 тыс. мотоциклов, либо любую допустимую их комбинацию. В результате реализации каждой тысячи велосипедов завод получает прибыль в 2 тыс. рублей, а с каждой тыс. мотоциклов- 3 тыс. рублей.

Найти такое сочетание выпусков продукции, которое дает наибольшую сумму прибыли.

Решение

В качестве переменных задачи возьмем количество велосипедов и мотоциклов, выпускаемых заводом в год (в тыс. штук): x1 и x2.

Учитывая возможности сборочных цехов, необходимо потребовать, чтобы

1≤100, (1)

x2≤30 (2)

Проанализируем возможности цехов. При этом необходимо учитывать, что при выпуске обоих видов продукции должно выполняться условие пропорциональности количества продукции данного вида доле производственной мощности , занятой ее выпуском. Если предусматривается производство 1000 велосипедов, то доля занятых производственных мощностей механических цехов первой группы составит 1/120 суммы всех мощностей, принимаемых в данном случае за единицу; на выпуск же x1 тыс. велосипедов потребуется занять (1/120) x1 всей мощности. Аналогично для производства x2 тыс. мотоциклов необходимо выделить (1/40) x2 всей мощности. Так что для реализации плана (x1,x2) потребуется предусмотреть

((1/120)x1+(1/40)x2) мощности механических цехов первой группы. Но в производственном процессе может быть использована не более чем вся наличная производственная мощность рассматриваемых цехов, следовательно

(1/120)x1+(1/40)x2≤1, (3)

Точно также получаем ограничения по производственной мощности механических цехов второй группы:

(1/80)x1+(1/60)x2≤1. (4)

По смыслу задачи:

x2≥0 (6)

Любой план (x1,x2), удовлетворяющий ограничениям (1)-(6), будет допустимым и дает предприятию прибыль (в тыс. руб): f(x1,x2)=2x1+3x2

Соотношения образуют математическую модель задачи:

f(x1,x2)=2x1+3x2→max

x1≤100, (1)

x2≤30, (2)

(1/120)x1+(1/40)x2≤1, (3)

(1/80)x1+(1/60)x2≤1. (4)

x1≥0, x2≥0

Решим данную задачу графическим методом. Для этого на графике отметим координаты прямой (1/120)x1+(1/40)x2=1, она проходит через точки (0,120) и (40,0) и координаты прямой (1/80)x1+(1/60)x2=1, которая проходит через точки (0,80) и (60,0).Также отметим на графике x1=100 и x2=30 (рисунок 3).

Рисунок 3

Для определения направления движения к оптимуму построим вектор-градиент Ñ, координаты которого являются частными производными целевой функции, т.е. =(2;3)

Что бы построить этот вектор, нужно соединить точку (2;3) с началом координат. При максимизации целевой функции необходимо двигаться в направлении вектора-градиента.

в крайней, угловой точке достигается максимум целевой функции. Для нахождения координат этой точки достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума:

(1/120)x1+(1/40)x2=1

(1/80)x1+(1/60)x2=1.

Из первого уравнения выразим x1 и подставим его во второе уравнение:

1+3 x2=120,

x1=120-3 x2.

Таким образом, при выпуске 24 тыс. мотоциклов и 48 тыс. велосипе -дов будет получена наибольшая сумма прибыли.

Задача 3

Решить задачу линейного программирования симплекс-методом.

Дано:

(x)=-2x1+x2→max,

x1+x2≥4,

x1+2x2≤2,

x1+2x2≤10

Приведем задачу к каноническому виду путем добавления искусственных переменных:

(x)=-2x1+x2→max,+x2-x3=4,

-x1+2x2+x4= 2,

x1+2x2+x5= 10

1)Построим симплекс-таблицу:

)По F-строке выбираем наибольший по величине отрицательный элемент у нас он равен -1, соответствующий этому элементу столбец является разрешающим.

)Находим отношения членов к соответствующим элементам разрешающего столбца.

)Среди отношений выбираем минимальное т.е. в данном случае оно равно 1. Строка, которая соответствует минимальному отношению является разрешающей.

Следовательно, элемент находящийся на пересечении разрешающей строки и разрешающего столбца является разрешающим т.е. равен 2.

После выполнения симплекс преобразования переходим к новой таблице.

)Элементы разрешающей строки предыдущей таблицы делим на разрешающий элемент и записываем на прежнее место.

Остальные элементы таблицы записываем по формуле:

Таким образом, оптимальное решение найдено, следовательно, x2=1, а все остальные элементы равны 0.

Задача 4

Компания производит полки для ванных комнат двух размеров - А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, а для полки типа В - 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а для изготовления одной полки типа В - 30 мин; машину можно использовать 160 час в неделю. Если прибыль от продажи полок типа А составляет 3 денежных единицы, а от полок типа В - 4 ден. ед., то сколько полок каждого типа следует выпускать в неделю?

Решение

Составим математическую модель задачи. Пусть x1 - количество полок вида А, x2- количество полок вида В, которые производятся в неделю. Прибыль от продажи такого количества полок составит 3x1+4x2, прибыль требуется максимизировать. Выпишем ограничения задачи .x1+x2≤550- в неделю на рынке может быть реализовано до 550 полок.

Затраты материала: 2x1+3x2≤1200

Затраты машинного времени:12x1+30x2≤9600

Таким образом, приходим к задаче линейного программирования.

=3x1+4x2→max,

x1+x2≤550,

x1+3x2≤1200,

x1+30x2≤9600,

x1≥0,x2≥0.

Решим ее симплекс-методом. Приведем задачу к каноническому виду путем добавления искусственных переменных

x1+3x2+x4=1200,

12x1+30x2+x5=9600,

xi≥0,i=1,2,3,4,5

Составим симплекс-таблицу

В последней оценочной строке есть отрицательные оценки, поэтому нужно делать шаг симплекс метода. Выбираем столбец с наименьшей оценкой, а затем разрешающий элемент по наименьшему отношению свободных членов. Результат шага запишем в таблицу. Аналогично будем повторять шаги, пока не придем к таблице с неотрицательными оценками.

В последнем плане строка F не содержит отрицательных значений, план x1=450,x2=100 оптимален, целевая функция принимает значение 1750.

Таким образом, чтобы получить максимальную прибыль предприятию необходимо производить 450 полок вида A и 100 полок вида В, при этом прибыль составит 1750 ден. ед., а останется неиспользованными 1200 минут машинного времени.

Заключение

В курсовой работе было рассмотрено два метода решения задач линейного программирования: графический и симплекс-метод. Они являются наиболее популярными из всех методов линейного программирования и позволяют получить гораздо большее количество информации, нежели просто найденное оптимальное решение.

Однако, симплекс-метод в отличие от графического можно использовать в задаче пространства с размерностью больше трех и это его значительное преимущество. Тогда как графический метод можно применять только в задачах двумерного пространства.

Таким образом, использование симплекс-метода в задачах линейного программирования является наиболее оптимальным.

Список использованных источников

1)       Солодовников, А.С. Математика в экономике. Часть 1. Линейная алгебра, аналитическая геометрия и линейное программирование / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандра.-М.: Издательство «Финансы и статистика»,2011.

2)      Струченков В.И. Методы оптимизации в прикладных задачах / В.И.Струченков.-М.: Издательство «Солон-Пресс»,2009.

3)      Юденков, А.В. математическое программирование в экономике : Учебное пособие / А.В.Юденков, М.И.Дли, В.В. Круглов.- М.: издательство «Финансы и статистика»,2010.

)        Агишева Д.К., Зотова С.А., Матвеева Т.А., Светличная В.Б. Линейное программирование (учебное пособие) // Успехи современного естествознания. - 2010.

)        Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике(учебное пособие): Издательство «Финансы и статистика», 2012.

)        Карасёв А.Н. Математические методы в экономике/ А.Н. Карасёв, Н.Ш. Кремер, Т.Н. Савельева, 2009

)        Минько Э.В. Методы прогонозирования и исследования операций: Учебное пособие/ Э.В. Минько, А.Э. Минько.-М.:Издптнльство «Инфа-м», 2014

)        Балдин К.В. Математическое программирование/ К.В. Балдин.-М.: Издательство «Дашков и К», 2009

)        Корнев В.В. Прикладные методы оптимизации/ В.В. Корнев, В.В. Курдюмов, В.С. Рыхлов, 2004.