Теорія ймовірностей та математична статистика
НАЦІОНАЛЬНА
АКАДЕМІЯ СТАТИСТИКИ, ОБЛІКУ ТА АУДИТУ
БІЛОЦЕРКІВСЬКИЙ
КОЛЕДЖ ФІНАНСІВ, ОБЛІКУ ТА АУДИТУ
Кафедра
інформаційних систем та технологій
КОНТРОЛЬНА
РОБОТА
З
ПРЕДМЕТУ Математика для економістів
Теорія
ймовірностей та математична статистика
Студентки заочної форми
навчання
Гребень Олени
Геннадіївни
Викладач Дядченко
Людмила Вікторівна
м.
Біла Церква
р.
Завдання 1
Із 20 банків 10 розташовані за
межами міста. Для дослідження випадково обрано 5 банків. Яка ймовірність того,
що серед обраних у межах міста виявиться 3 банки?
Розв’язок. Для розв’язку
скористаємося формулою визначення кількості сполучень:
 ,
,
де n - кількість
елементів множини,- кількість елементів сполучення.
Усього наслідків тут  -
кількість сполучень із 20 банків по 5. Тих, що сприяють події -
-
кількість сполучень із 20 банків по 5. Тих, що сприяють події - 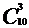 наслідків
обрання трьох банків у межах міста і одночасно
наслідків
обрання трьох банків у межах міста і одночасно 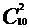 наслідків обрання двох
банків за межами міста. Тоді шукана ймовірність є:
наслідків обрання двох
банків за межами міста. Тоді шукана ймовірність є:

Відповідь. Ймовірність
того, що серед п’яти обраних банків у межах міста виявляться три становить
34,83%.
Завдання 2
|
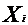 267911 267911
|
|
|
|
|
|
|
 0,0020,0070,0120,0220,001(2+?) 0,0020,0070,0120,0220,001(2+?)
|
|
|
|
|
|
1. Знайти та зобразити графічно
функцію розподілу.
2. Знайти М(х), середнє
квадратичне відхилення.
Розв’язок. Знайдемо  .
Оскільки
.
Оскільки
 , то
0,002+0,007+0,012+0,022+0,001(2+у)=1,
, то
0,002+0,007+0,012+0,022+0,001(2+у)=1,
,001(2+у)=1-0,043,
+у=0,957/0,001,
у=955.
Отже,  .
.
. Знайдемо  :
:
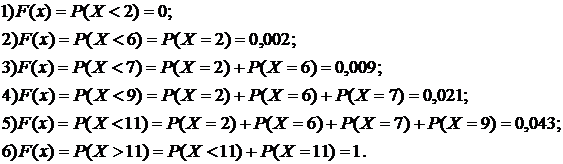
Компактно 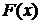 матиме
запис:
матиме
запис:

Графік функції розподілу
F(x) зображено на мал..1.
. Знайдемо математичне
сподівання:
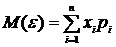
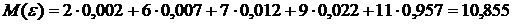
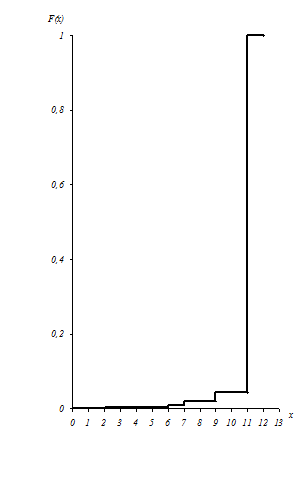
Мал.1. Графік функції
розподілу F(x)
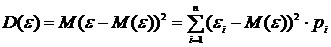

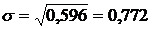
Відповідь: математичне
сподівання рівне 10,855, середнє квадратичне відхилення - 0,772.
Завдання 3
Дано функцію розподілу
величини Х
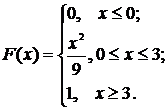
Знайти щільність
розподілу ймовірностей f(x), обчислити М(х), D(x), побудувати графіки функцій
f(x), F(x).
Розв’язок. 1. Знайдемо
щільність розподілу ймовірностей
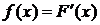 ,
, 

. Обчислимо М(х):
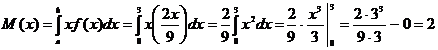
Обчислимо D(x):

Проінтегруємо почленно:
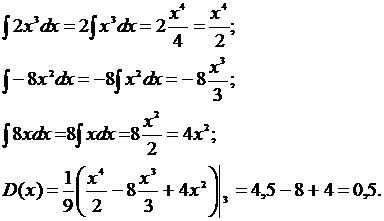
. Побудуємо графіки
функцій f(x), F(x).

Мал.2. Графік функції
розподілу F(x)
Мал.3. Графік щільності
розподілу f(x)
Відповідь. Математичне
сподівання М(х) рівне 2,0, дисперсія D(x)=0,5, щільність розподілу ймовірностей

Завдання 4
ймовірність випадкова
величина відхилення
Закон неперервної випадкової
величини Х задано щільністю ймовірностей

Знайти а. Побудувати
графіки функцій f(x), F(x).
Розв’язок. 1. Значення сталої а
визначаємо з умови нормування:
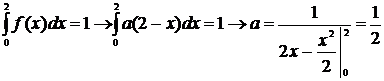
При знайденому значенні
а щільність ймовірностей буде мати вигляд:
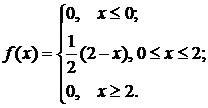
. Функція розподілу
ймовірностей визначається інтегруванням:
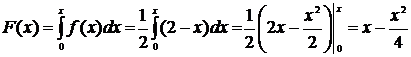
Записуємо загальний
вигляд функції F(x):
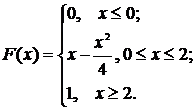
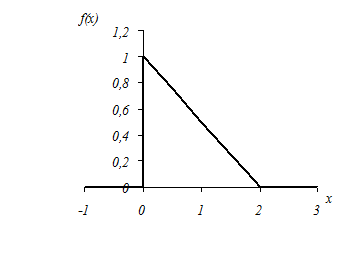
Графіки функцій
розподілу ймовірностей та її щільності показані на малюнках 4 та 5.

Мал.4. Графік функції розподілу F(x)
Відповідь. а = 0,5.