Дослідження характеристик біполярного крокового двигуна

Дослідження характеристик біполярного крокового двигуна

Зміст

Вступ

. Дослідження моделі крокового двигуна, опис машини

. Діалогове вікно і його параметри

. Аналіз і розрахунок моделі крокового двигуна

. Інтерпретація роботи електроприводу гібридного двофазного крокового двигуна за допомогою програми Mathlab

. Приводи і драйвери

Висновок

Перелік використаної літератури

Вступ

Кроковий двигун - електричний двигун, в якому імпульсне живлення електричним струмом призводить до того, що його ротор не обертається неперервно, а виконує щоразу обертальний рух на заданий кут. Завдяки цьому, кут повороту ротора залежить від числа поданих імпульсів струму, а кутова швидкість ротора точно рівна частоті імпульсів помноженій на кут повороту ротора за один цикл роботи двигуна.

Кут повороту двигуна під впливом одного імпульсу може мати різні значення, залежні від конструкції двигуна, - як правило це значення в діапазоні від декількох градусів до декілька десятків градусів. Крокові двигуни, залежно від призначення пристосовані до виконання від частки обороту в секунду до декількох тисяч оборотів в секунду.

Конструктивно крокові електродвигуни складаються із статора, на якому розташовані обмотки збудження, і ротора, виконаного з магніто-м'якого (феромагнітного) матеріалу або з магніто-твердого (магнітного) матеріалу. Крокові двигуни з магнітним ротором дозволяють отримувати більший крутний момент і забезпечують фіксацію ротора при знеструмлених обмотках.

Гібридні двигуни поєднують у собі найкращі риси двигунів зі змінним магнітним опором і двигунів з постійними магнітами.

Статор гібридного двигуна також має зубці, забезпечуючи велику кількість еквівалентних полюсів, на відміну від основних полюсів, на яких розташовані обмотки. Зазвичай використовуються 4 основні полюси для 3,6 градусних двигунів і 8 основних полюсів для 1,8-0,9 градусних двигунів. Зубці ротора забезпечують менший опір магнітного ланцюга у певних положеннях ротора, що покращує статичний і динамічний момент. Це забезпечується відповідним розташуванням зубців, коли частина зубців ротора знаходиться строго навпроти зубців статора, а частина між ними.

Ротор гібридного двигуна має зубці, розташовані в осьовому напрямку. Ротор розділений на дві частини, між якими розташований циліндричний постійний магніт. Таким чином, зубці верхньої половинки ротора є північними полюсами, а зубці нижньої половинки - південними. Крім того, верхня і нижня половинки ротора повернуті один відносно одного на половину кута кроку зубців. Число пар полюсів ротора дорівнює кількості зубців на одній з його половинок. Зубчасті полюсні наконечники ротора, як і статор, набрані з окремих пластин для зменшення втрат на вихрові струми.

Рисунок - полюсний кроковий двигун

Цикл роботи електродвигуна можна розбити на 4 кадри.

Кадр 1: верхній електромагніт (1) включений, відбувається притягання найближчого зуба ротора шестеренної форми. Зуби вирівнюються по електромагніту (1), вони будуть трохи зміщені відносно електромагніта (2).

Кадр 2: верхній електромагніт (1) відключений, а правий електромагніт (2) знаходиться під напругою, потягнувши найближчі зуби прокрутивши ротор вправо. У результаті відбудеться повертання на 3,6° для цього прикладу.

Кадр 3: нижній електромагніт (3) знаходиться під напругою, спричинивши наступне повертання ротора на 3,6°.

Кадр 4: лівий електромагніт (4) включений, що знову проверне ротор на 3,6°. Коли верхній знову увімкнеться, ротор у кінцевому підсумку за 4 кроки повернеться на один зуб, а оскільки у ротора є 25 зубів, то повний оберт займе 100 кроків для даного прикладу.

Переваги:

1.      Кут повороту двигуна пропорційний кількості вхідних імпульсів.

2.      Двигун працює з повним моментом у стані спокою (якщо обмотки підключені до живлення).

.        Прецезійне позиціонування і повторюваність кроку - хороші крокові двигуни мають точність близько 3 - 5% кроку і ці помилки не накопичується від кроку до кроку.

.        Можливість швидкого розгону, гальмування і зміни напряму руху.

.        Безвідмовність - у зв'язку з відсутністю щіток. Довговічність двигуна залежить тільки від довговічності підшипників.

.        Залежність оборотів двигуна від дискретних імпульсів дозволяє керувати двигуном без зворотного зв'язку, завдяки чому кроковий двигун простіший і дешевший в керуванні.

.        Можливість досягнення дуже низьких швидкостей обертання з навантаженням закріпленим безпосередньо на осі двигуна.

.        Широкий діапазон швидкостей обертання отримуваний завдяки тому, що швидкість пропорційна частоті вхідних імпульсів.

Недоліки:

1.    Механічний резонанс з'являється при неправильному керуванні.

2.      Складнощі при роботі з дуже високими швидкостями.

.        Можлива втрата контролю положення у зв'язку з роботою без зворотного зв'язку.

.        Споживання електроенергії не зменшується навіть без навантаження.

.        Невисока питома потужність.

.        Відносно складна схема управління.

1. Дослідження моделі крокового двигуна, опис машини

Рисунок 1 - модель крокового двигуна.

Блок крокового двигуна реалізує загальну модель, яка представляє два найпопулярніших сімейства крокових двигунів:

• крокові двигуни із змінною небажання;

• від постійних магнітів або гібридні крокові двигуни;

Модель крокового двигуна складається з електричних і механічних частин. Верхня частина представлена еквівалентною схемою, конфігурація якого залежить від типу двигуна. Еквівалентні схеми були побудовані з припущенням про те, що магнітний ланцюг лінійний (без насичення) і взаємною індуктивністю між фазами можна знехтувати. Механічний розділ представлений в просторі станом моделі, заснованої на момент інерції і коефіцієнта в'язкого тертя.

Для крокового двигуна зі змінним магнітним опором є еквівалентна схема для однієї фази яка зображена на рисунку 1.

Слід зазначити, що в опорній позиції (Θ = 0), зуб ротора повністю відповідає осі полюса, так що фаза індуктивності обмотки максимальна.

Загальний електромагнітний крутний момент двигуна є сума моментів, вироблених фаз двигуна:

де М-число фаз, IX є обмотки струм у фазі х і Lx є функція індуктивністі фази х обмотки.

Для двигуна з постійними магнітами (PM) або гібридний кроковий двигун, еквівалентна така схема для однієї фази, яку показано на малюнку.

Рисунок 2 - схема однієї фази крокового двигуна зі змінним опором

У цій моделі, Ra і La представляють, відповідно, опір і індуктивність фази обмотки. Індуктивність обмотки змінюється залежно від положення ротора:

У зв'язку з великим значенням повітряного зазору, введених магнітів, індуктивність обмотки з постійними магнітами або гібридний кроковий двигун залежить від положення ротора. Джерело напруги ea(Θ) являє собою двигун зворотньої ЕРС (електрорушійна сила), який є синусоїдальною функцією положення ротора:

де р - число пар полюсів і ψm максимальний магнітний потік двигуна.

В опорній позиції (Θ = 0), Північний полюс на роторі повністю відповідає осі полюса так, щоб фаза ЕРС тоді нулю.

Електромагнітний момент, що обертає двухфазний PM або гібридний кроковий двигун дорівнює сумі крутного моменту в результаті взаємодії фазних струмів і магнітних потоків, що створюються магнітами і фіксуючого крутного моменту, що призводить від положення ротора:

Для з постійними магнітами (PM) або гібридний кроковий двигун, еквівалентна схема для однієї фази показано на малюнку.

Рисунок 3 - схема однієї фази крокового двигуна з постійними магнітами

2. Діалогове вікно і його параметри

Рисунок 4 - діалогове вікно налаштувань гібридного крокового двигуна

Рисунок 5 - діалогове вікно для налаштування необхідних параметрів гібридного крокового двигуна

вихід блоку є вектор, що містить 5 сигналів. Також можна демультіплексувати ці сигнали за допомогою селектора блок Bus, який знаходиться в бібліотеці Simulink.

Параметри, які використовуються в моделі крокового двигуна зазвичай отримують з технічних паспортів виробника. У разі, коли параметри не доступні, вони можуть бути визначені за допомогою проведення експериментальних вимірювань.

Параметри крокового двигуна зі змінним магнітаопором.

Параметри двигуна з постійними магнітами.

Параметри, що надаються паспортах виробника, як правило,: число фаз, утримує момент, крок кут, напруга на фазу, струм на фазу, опір обмотки (Ra), індуктивність обмотки (La), і ротор інерції (J).

Максимальний крутний момент фіксатор (TDM) не завжди вказано. Цей параметр можна припустити, рівним 1-10% від максимального крутного моменту.

Максимальне потокозчеплення (ψm) не завжди вказано. Цей параметр може бути отриманий експериментально, приведенням в дію електродвигуна до постійної швидкості N (оборотів в хвилину) і шляхом вимірювання максимальної холостого ходу обмотки напруги Em (V).

Параметр ψm обчислюється за таким співвідношенням:

ψm = (30/pπ)(Em/N),

де р-число пар полюсів, заданих р = 360 / (2m · крок). Тут m = номер фази, крок = крок кут в градусах.

. Аналіз і розрахунок моделі крокового двигуна

Для аналізу електромеханічних процесів у двофазному КД застосовується структурна модель [1], представлена на рис. 6. Ротор такого двигуна є постійним магнітом і має 2р магнітних полюсів. Статор складається з ідентичних полюсів і обмоток, розташованих через рівні інтервали λ.

Рисунок 6 - Структурна модель крокового двигуна

Раптові стрибкоподібні зміни кутових положень складають основу всіх режимів роботи КД і по суті є єдиною, але дуже важливою його особливістю. Тому всі параметри, які підлягають вимірюванню, також змінюються відповідним чином. Це стає очевидним після розв'язку математичної моделі КД, яка являє собою систему нелінійних диференціальних рівнянь [1]:

де: V_gA, V_gB - напруга живлення, відповідно фази А та В;

L - власна індуктивність кожної фази;

М - взаємна індуктивність;- опір кола обмотки статора;_r - кількість зубців ротора;- момент інерції; - коефіцієнт в’язкого тертя;

q - кут повороту ротора КД відносно статора;

р - число пар полюсів; - кількість витків обмоток;

F_m - взаємоіндукція; _A, i_B - струм в обмотках фаз, відповідно A та В;

l - крок зубців статора КД.

Одним з методів розв'язку системи (1) є приведення нелінійних диференціальних рівнянь до лінійних, таким чином фактично виводиться лінеаризована математична модель КД. Проте тоді стає неможливим знайти похибку і попередньо оцінити адекватність отриманої моделі. Тому розв’яжемо систему (1) для двофазного КД типу M35SP-6 чисельними методами за допомогою сучасних комп’ютерних засобів, які забезпечують похибку не більшу .

Особливу увагу варто звернути на кут пороту q, відповідно кутову швидкість ω = dθ / dt та обертовий момент .

Рисунок 7 - Графік зміни кута повороту вала КД

Рисунок 8 - Графік зміни кутової швидкості вала КД

Рисунок 9 - Графік зміни обертового моменту КД

На рис. 7 показано зміну кута повороту КД та коливання навколо стійких положень, що також спостерігається на графіку зміни кутової швидкості (рис. 8). Різка зміна напряму обертання супроводжується і зміною обертового моменту (рис. 9).

При лінеаризації системи (1) припускається, що L та М не залежать від q, а відхилення δq від положення рівноваги λ/2 достатньо мале, при цьому струм в обох фазах змінюється на [1]. Таким чином припускається, що:

де I₀ - усталене значення струму в обмотках.

Тоді з врахуванням (2), лінеаризована система (1) матиме вигляд:

Розв’язком спрощеної системи лінійних диференціальних рівнянь (3) є аналітичні залежності:

.

де: r - кут моменту;

 - корегувальний коефіцієнт;

 - коефіцієнт, який залежить від типу КД;

 - коефіцієнт, який також залежить від типу КД;

 - коефіцієнт, залежний від типу КД.

Представимо результати розв'язку лінеаризованої математичної моделі (4) у вигляді графічних залежностей кута повороту, кутової швидкості та моменту від часу.

Рисунок 10 - Графік зміни кута повороту вала КД (лінеаризована модель)

Рисунок 11 - Графік зміни кутової швидкості вала КД

Рисунок 12 - Графік зміни обертового моменту КД (лінеаризована модель)

Для визначення відносної похибки лінеаризованої моделі КД відносно нелінійної використовуємо таку розрахункову формулу (5):

,

де:  - кут повороту нелінійної моделі КД;

 - кут повороту лінеаризованої моделі.

Рисунок 13 - Графік зміни відносної похибки лінеаризованої математичної моделі КД відносно нелінійної.

Таким чином максимальне значення похибки лінеаризованої моделі для першого кутового положення становить 12,5%, в подальшому зменшується за експоненціальним законом. Звідси можна судити про адекватність спрощеної моделі, та можливість її застосування замість нелінійної моделі (1). Для опису фізичних процесів у чотирифазному КД використовуємо структурну модель, наведену на рис. 8.

. Інтерпретація роботи електроприводу гібридного двофазного крокового двигуна за допомогою програми Mathlab

Рисунок 14 - блок-схема гібридного двохфазного крокового двигуна.

Фази двигуна подаються на два Н-моста MOSFET ШІМ перетворювачів, підключених до джерела напруги 28 В постійного струму. Фазові двигун струми незалежно під контролем двох контролерів гістерезису на основі яких генерують сигнали порушення MOSFET шляхом порівняння виміряних струмів з їх посилань. Поточні посилання Прямокутний генеруються з використанням амплітуди струму і параметри крок частоти, перелічені в діалоговому вікні. Рух крокової приводу контролюється STEP і сигналів DIR отриманої із зовнішніх джерел.

Наступні сигнали отримують з моделювання 0,25 сек. роботи крокового приводу двигуна, протягом якого крокової повертається впродовж 0,1 сек. в позитивному напрямку, зупиняється на 0,05 сек., обертається в зворотному напрямку за 0,05 сек. і зупиняється.

Рисунок 15 - графіки проведеного дослідження (1 - зміна напруги живлення; 2 - зміна струму; 3 - зміна крутного моменту; 4 - зміна швидкості обертання ротора; 5 - зміна положення ротора;)

Рисунок 16 - графік залежності зміни напруги, струму, крутного моменту, швидкості ротора, положення ротора з часом відповідно.

Блок сигнал Builder

Створює і генерує змінні групи сигналів, чиї хвилі є кусочно-лінійна. Блок сигналу Builder дозволяє створювати взаємозамінні групи джерел кусочно-лінійних сигналів і використовувати їх в моделі.

Блок сигналу Builder виводить скаляр або масив реальних сигналів типу Double.

Блок сигналу Builder має той же діалогове вікно, що і підсистеми блоку. Щоб відкрити діалогове вікно потрібно вибрати Subsystem параметри з контекстного меню блоку.

Характеристика Блок сигналу Builder

Безперервний

Скалярні розширення

Так, переметрів

Вимірювання

Так

Перетин нуля

Так

. Приводи і Драйвери

Блок крокового двигуна являє собою кроковий двигун. Він використовує вхідні імпульси, А і В, щоб контролювати механічну потужність у відповідності з наступними рівняннями:

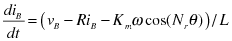
де:

• іА, іB є А і В є фази обмотки струмів.

• Va. та Vb A і В фази в обмотці напруги.

• Км постійна моменту двигуна.

• Nr це кількість зубів на кожному з двох полюсів ротора. Повний розмір кроку (π / 2) / Nr.

• R є опір обмотки.

• L є індуктивність обмотки.

• B є обертальний демпфірування.

• J є інерція.

Якщо початкове положення ротора дорівнює нулю або кратна (π / 2) / NR, то ротор суміщений з фазою обмотки А. Це відбувається, коли є позитивний струм, що протікає від А + до А-портами і є немає струму, що протікає від B + до В-портів.

Для створення імпульсів для блоку крокової двигуна потрібно використовувати драйвер крокового двигуна.

Блок крокового двигуна дає позитивний крутний момент, що діє від механічного С до R портів, коли фаза імпульсу А веде фазу імпульсу B.

Основні припущення та обмеження

Модель заснована на наступних припущеннях:

• Ця модель не враховує магнітні ефекти насичення, що фіксує моменту і будь магнітного зв'язку між фазами.

• При виборі Моделювання Почати сталого прапорець державної в блоці Simscape Рішення Configuration від, цей блок не буде ініціалізувати Початкове значення кута ротора між-π і π.

Блок крокового двигуна

Блок крокового двигуна являє собою драйвер крокової двигуна. Створення імпульсів, А і В, потрібно для керування двигуном. Цей блок ініціює крок кожен раз, коли напруга на ШІМ порту підноситься над Включення порогового напруги.

Якщо напруга на REV порту менше або дорівнює порогові напрузі зворотної, імпульс призводить імпульсу B на 90 градусів. Якщо напруга на REV порту більше, ніж порогова напруга зворотного, імпульс B призводить імпульсом на 90 градусів і напрямок двигуна змінюється на протилежний. У нульовий момент часу, пульс є позитивною, і імпульс В негативний.

Щоб створити напругу на ШІМ-порт потрібно використовувати контрольований блок ШІМ напруги,. Цей блок створює мережу двигуна кожного разу, коли сигнал ШІМ йде високими. Коли запустити тригери починається моделювання з точку, коли сигнал ШІМ стає високим, що забезпечує хорошу точність моделювання. Якщо замість цього використовувати контрольовану напругу джерела блоку з бібліотеки Foundation, який контролюється Simulink, необхідно встановити відповідним невеликий часовий крок для моделювання. Відомості про зазначення в Simulink розмір кроку.

Висновок

В результаті проведених досліджень математичних моделей двофазного КД, було отримано графічні залежності кута повороту, кутової швидкості та обертового моменту. Аналіз результатів розв’язків моделей підтвердив важливість проведених досліджень та виявив необхідність врахування напрямку обертання вала КД при вимірюванні інформативних параметрів.

машина електропривод mathlab

Перелік використаної літератури

1. T. Kenjo, A. Sugawara, Stepping Motors and Their Microprocessor Controls, 2nd Edition, Oxford University Press, Oxford, 2003.

. P. Acarnley, Stepping Motors - A guide to theory and practice, 4th Edition, The Institution of Electrical Engineers, London, 2002.

. Кенио Т. Шаговые двигатели и их микропроцессорные системы управления: Пер. с анг. - М.: Энергоатомиздат, 1987. - 200 с.

. Дискретный электропривод с шаговыми двигателями: под общ. ред. М.Г. Чиликина. - М.: "Энергия", 1971. - 624 с.

. Deb A., Sarcar G., Sen S.K. Linearly pulse-width modulated block pulse functions and their application to linear SISO feedback control system identification // IEE Proc. - Control Theory Appl. - 1995. - 142, №1. - P.44-50.

. Козловський А.В., Кухарчук В.В., Поджаренко В.О. Мікропроцесорні засоби вимірювання контролю обертового моменту: Монографія. - Вінниця: УНІВЕРСУМ, 2005. - 125 с.