Разработка компьютерной программы моделирования дисперсных систем
Оглавление
Введение
. Теоретическая часть
.1 Законы распределения
.2 Характеристики распределения
порошков по размерам
.3 Алгоритм метода Моте-Карло
.4 Метод линейных итераций
.5 Алгоритм метода вязкой суспензии
. Практическая часть
.1 Разработка программы
.2 Первая вкладка
.3 Вторая вкладка
Выводы
Список литературы
Введение
Дисперсные системы - это системы, состоящие из
двух или более фаз, которые имеют четкую границу раздела и не вступают в
химическое взаимодействие друг с другом [1].
фаза - называется дисперсной фазой, частицы.
фаза - среда, в которой размещены частицы первой
фазы (непрерывная). Называется дисперсионной фазой.
Дисперсные системы могут иметь и более сложное
строение, например, представлять собой двухфазное образование, каждая из фаз
которого, будучи непрерывной, проникает в объем другой фазы. К таким системам
относятся твердые тела, пронизанные разветвленной системой каналов-пор,
заполненных газом или жидкостью, некоторые микрогетерогенные полимерные
композиции и другие. Нередки случаи, когда дисперсионная среда
"вырождается" до тончайших слоев (пленок), разделяющих частицы
дисперсной фазы [1].
Для исследования дисперсных систем удобно
использовать компьютерное моделирование, оно позволяет рассчитать параметры
таких систем, а также визуально отобразить полученные данные.
1. Теоретическая часть
.1 Законы распределения
Гамма распределение - это двухпараметрическое
семейство абсолютно непрерывных распределений. Если параметр принимает целое
значение, то такое гамма-распределение также называется распределением Эрланга.
Пусть распределение случайной
величины 
 задаётся плотностью вероятности,
имеющей вид:
задаётся плотностью вероятности,
имеющей вид:

где - гамма-функция Эйлера.
Тогда говорят, что случайная
величина 
 имеет гамма-распределение с
параметрами
имеет гамма-распределение с
параметрами 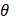
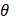 и
и 
 . Пишут
. Пишут 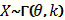
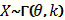 [2].
[2].
Математическое ожидание - 
Дисперсия - 
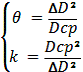
Экспоненциальное или показательное распределение
- абсолютно непрерывное распределение, моделирующее время между двумя
последовательными свершениями одного и того же события
Случайная величина
<#"784205.files/image009.gif"> имеет
экспоненциальное распределение с параметром  , если её плотность
<#"784205.files/image011.gif">.
, если её плотность
<#"784205.files/image011.gif">.
Математическое ожидание - 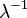
Дисперсия - 
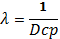
Усеченное нормальное
распределение.
Нормальное распределение, также
называемое распределением Гаусса
<#"784205.files/image015.gif">
Математическое ожидание -  .
.
Дисперсия -  .
.
Нормальное распределение зависит от двух
параметров - смещения и масштаба, то есть является с математической точки
зрения не одним распределением, а целым их семейством. Значения параметров
соответствуют значениям среднего (математического ожидания) и разброса
(стандартного отклонения).
Стандартным нормальным
распределением называется нормальное распределение с математическим ожиданием 0
и стандартным отклонением 1.[2]
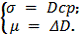
Логнормальное распределение в теории
вероятностей - это двухпараметрическое семейство абсолютно непрерывных
распределений. Если случайная величина имеет логнормальное распределение, то её
логарифм имеет нормальное распределение [2].
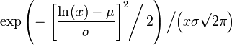
Математическое ожидание - 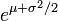
Дисперсия - 

.2 Характеристики распределения
порошков по размерам
Допустим, в порошке содержится N частиц, их
диаметры Di. i=1,2,…,N.

 - плотность распределения частиц по
размерам.(D) - математическая плотность распределения частиц по размерам.(D)dD
- относительное число частиц, которые имеют размер [D,D+dD].
- плотность распределения частиц по
размерам.(D) - математическая плотность распределения частиц по размерам.(D)dD
- относительное число частиц, которые имеют размер [D,D+dD].

 - относительное число частиц, у
которых величина меньше, чем заданное число D[1].
- относительное число частиц, у
которых величина меньше, чем заданное число D[1].
.3 Алгоритм метода Монте-Карло
1) С помощью генератора случайных чисел
задается случайное число R∈[0,1].
) Записывается уравнение F(D)=R, где F(D)
- заданная функция распределения по размерам. Уравнение решается, находится
значение D.
) Пункты 1 и 2 повторяются для каждой
частицы. В результате получается набор N частиц, имеющих заданное распределение
f(D).
В случаях, когда F(D) имеет простое
аналитическое выражение (экспоненциальная функция), то уравнение F(D)=R может
быть решено аналитически и используется зависимость D(R).
.4 Метод линейных итераций
Метод трапеций - метод численного интегрирования
функции одной переменной, заключающийся в замене на каждом элементарном отрезке
подынтегральной функции на многочлен первой степени, то есть линейную функцию.
1. Генерируется число R и в массиве
находится ячейка F=R. Если такой ячейки нет, то находятся значения двух ячеек,
между которыми находится R. С помощью метода линейной интерполяции находится
значение D равное соответствующему R[1].
.5 Алгоритм метода вязкой суспензии
Для заданной объемной концентрации частиц ц и
заданной плотности распределения f(D) происходит генерирование частиц.
Определяется суммарный объем частиц:
= ц*Lx*Ly.
В цикле i=1,..,N методом Монте-Карло
генерируются частицы.
Для вновь генерированной степени
определяем их объем 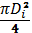
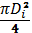 и объем уже существующих частиц
и объем уже существующих частиц 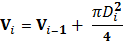
 .
.
Если 
 , процесс продолжается; если
, процесс продолжается; если 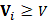
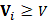 , процесс прекращается. В результате
имеем набор частиц, имеющих заданный закон распределения по размерам и заданную
объемную концентрацию ц.
, процесс прекращается. В результате
имеем набор частиц, имеющих заданный закон распределения по размерам и заданную
объемную концентрацию ц.
1. Все связанные частицы размещаются в
заданном объеме LxLyLz с помощью метода Монте-Карло, т.е. для каждой созданной
частицы создаются координаты:
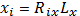


Эти координаты частиц используются в качестве
начальных условий для метода вязкой суспензии [1].
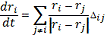
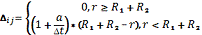
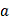
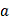 - некий параметр, меняющийся от 0
до 1.
- некий параметр, меняющийся от 0
до 1.
Организуется цикл и вычисляется 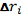
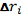 для i=1,..,N.
для i=1,..,N.
После этого во втором цикле
происходит корректировка:
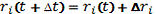
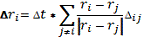
3.
Расчет заканчивается, когда в системе не останется ни одной пары пересекающихся
частиц, то есть, когда все 

Существуют граничные условия: границы расчетной
области - твердая непроницаемая поверхность. Это означает, что частицы не могут
выходить за пределы области, а могут только соприкасаться с ней.
2. Практическая часть
2.1 Разработка программы
В качестве языка
программирования был выбран язык C#. C# - объектно-ориентированный язык
программирования. C# относится к семье языков с C-подобным синтаксисом, из них
его синтаксис наиболее близок к C++ и Java. Язык имеет статическую типизацию,
поддерживает полиморфизм, перегрузку операторов (в том числе операторов явного
и неявного приведения типа), делегаты, атрибуты, события, свойства, обобщённые
типы и методы, итераторы [2].
Лучшей средой разработки для данного языка
является Microsoft Visual Studio 2013. Visual Studio включает в себя редактор
исходного кода с поддержкой технологии IntelliSense и возможностью простейшего
рефакторинга кода. Встроенный отладчик может работать как отладчик уровня
исходного кода, так и как отладчик машинного уровня. Остальные встраиваемые
инструменты включают в себя редактор форм для упрощения создания графического
интерфейса приложения, веб-редактор, дизайнер классов и дизайнер схемы базы
данных. Visual Studio позволяет создавать и подключать сторонние дополнения
(плагины) для расширения функциональности практически на каждом уровне, включая
добавление поддержки систем контроля версий новых наборов инструментов
(например, для редактирования и визуального проектирования кода на
предметно-ориентированных языках программирования или инструментов для прочих
аспектов процесса разработки программного обеспечения (например, клиент Team
Explorer для работы с Team Foundation Server).исходного кода (как например,
Subversion и Visual SourceSafe) [2].
Программа состоит из 3 вкладок: «Состав порошковой
смеси», «Распределение частиц» и «Справка».

Рисунок 1. Вкладки приложения
дисперсный программа
итерация суспензия
Каждая вкладка представляет собой окно с полями
для ввода и отображением информации - результатов работы программы.

Рисунок 2. Поле первой вкладки «Состав
порошковой смеси»
Начальные условия:
Ø N - число частиц;
Ø M - число отрезков;
Ø L - число отрезков для метода
трапеций;
Ø Dmax - максимальный размер
частиц(мат.ожидание);
Ø Dcp - средний размер частиц;
Ø Dis - дисперсия;
Поле для выбора вида распределения:
Ø Логнормальное распределение;
Ø Экспоненциальное распределение;
Ø Гамма распределение;
Ø Усечено нормальное распределение;

Рисунок 3. Поле второй вкладки «Распределение
частиц»
Размер области:
Ø Lx,Ly - размеры области для
генерации частиц;
Ø 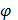
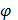 - концентрация частиц;
- концентрация частиц;
Ø а - скорость размещения;
Значения параметров:
Ø Dcp - средний размер
частиц(мат.ожидание);
Ø 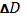
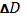 - дисперсия;
- дисперсия;
Ø Dmax - максимальный размер частиц;
Ø 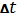
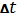 - шаг по времени;
- шаг по времени;
Ø 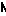
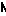 - число отрезков;
- число отрезков;
Ø L - число отрезков для метода
трапеций;
Ø Количество созданных частиц;
Ø Количество тактов;

Рисунок 4. Поле третьей вкладки «Справка»
2.2 Первая вкладка
Первая вкладка - «Состав порошковой смеси».
Здесь содержатся поля для ввода начальных условий, выбор распределения, по
которому будет производиться расчет, график данного распределения и данные,
полученные в результате генерации. Выбор распределения осуществляется с помощью
компонента ComboBox, в котором содержатся названия распределений. Для каждого
распределения необходимо задать начальные условия.

Рисунок 5. Первая вкладка «Состав порошковой
смеси»
После ввода начальных условий необходимо нажать
кнопку «Построить гистограмму» для построения графика и вывода на экран.
Программа создает L диаметров D, высчитывает
соответствующие им значения F. Значения F нормируются, т.е. каждое значение делится
на последний элемент массива. Далее с помощью генератора случайных чисел
генерируется число от 0 до 1 и сравнивается со значениями F. Берутся значения
двух ближайших точек к данному случайному числу, и с помощью метода линейной
интерполяции высчитывается диаметр частицы.
После этого строится график плотности
распределения. Для вывода графика распределений используется модуль ZedGraph -
компонент для рисования графиков под.NET Framework. Преимуществом данного
модуля является возможность изменения масштаба графика одной кнопкой. Так же, в
ZedGraph можно строить различные графики на одной панели (в данном случае нам
необходимы гистограмма и кривая) [2]. Гистограмма показывает плотность
созданных частиц, согласно указанному закону, а кривая - теоретически
определенная плотность распределения.
Для построения гистограммы использовался
следующий алгоритм:
1. Пользователь задает
число М - число отрезков для построения гистограммы;
2. Рассчитывается шаг
a,a1 для построения диаграммы;
3. Диаметр частицы,
полученный методом Монте-Карло делится на шаг a,a1;
4. От полученного
значения берется целая часть встроенным методом Math.Truncate(x). Составляем
массив, смотрим, в какую ячейку попала частица, и увеличиваем счетчик на
единицу в этой ячейке;
5. Шаги 4-5 повторяются
N раз;
6. По полученным
данным строится гистограмма.
.3 Вторая вкладка
Вторая вкладка «Распределение частиц» см.
рисунок 3.
В качестве начальных условий здесь указываются:
После ввода всех условий, необходимо нажать
кнопку «Создать частицы», тогда программа создаст случайным образом частицы,
которые будут отражены в элементе panel.
Частицы на панели отрисовываются с помощью
встроенного метода DrawEllipse, принадлежащего библиотеке
System.Drawing.Graphics. Диаметр частиц и их положение определяются с помощью
генератора случайных чисел.
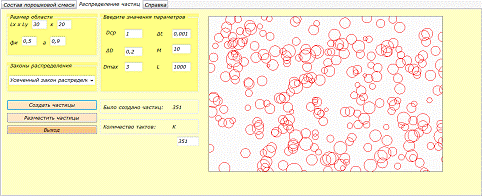
Рисунок 6. Создание частиц

Рисунок 7.