Система регулирования глубины рабочего оборудования мобильной машины с центробежным регулятором

Система регулирования глубины рабочего оборудования мобильной машины с центробежным регулятором

Содержание

Введение

1.      Описание работы и функциональная схема системы

.        Исходные данные

.        Математическая модель

.        Построение частотных характеристик

4.1 Логарифмическая амплитудно-частотная характеристика

.2 Логарифмическая фазо-частотная характеристика

.        Исследование устойчивости разомкнутой системы

.1 Критерий устойчивости по Найквисту

5.2 По критерию Рауса

. Построение желаемой амплитудной характеристики по показателям переходного процесса

6.1 Желаемая ЛАЧХ

.2      Желаемая ЛФЧХ

. Построение графика вещественного процесса

. Построение графика переходного процесса

. Построение корректирующего устройства

Вывод

Список литературы

Введение

Современная теория автоматического регулирования является основной частью теории управления. Система автоматического регулирования состоит из регулируемого объекта и элементов управления, которые воздействуют на объект при изменении одной или нескольких регулируемых переменных. Под влиянием входных сигналов (управления или возмущения), изменяются регулируемые переменные. Цель же регулирования заключается в формировании таких законов, при которых выходные регулируемые переменные мало отличались бы от требуемых значений. Решение данной задачи во многих случаях осложняется наличием случайных возмущений (помех). При этом необходимо выбирать такой закон регулирования, при котором сигналы управления проходили бы через систему с малыми искажениями, а сигналы шума практически не пропускались.

Проектирование систем автоматического регулирования можно вести двумя путями: методом анализа, когда при заранее выбранной структуре системы (расчетным путем или моделированием) определяют ее параметры; методом синтеза, когда по требованиям, к системе сразу же выбирают наилучшую ее структуру и параметры.

Определение параметров системы, когда известна ее структура и требования на всю систему в целом, относится к задаче синтеза. Решение этой задачи при линейном объекте регулирования можно найти, используя, например, частотные методы, способ корневого годографа или изучая траектории корней характеристического уравнения замкнутой системы. Выбор корректирующего устройства методом синтеза в классе дробно-рациональных функций комплексного переменного можно выполнить с помощью графоаналитических методов. Эти же методы позволяют синтезировать корректирующие устройства, подавляющие автоколебательные и неустойчивые периодические режимы в нелинейных системах.

Дальнейшее развитие методы синтеза получили на основе принципов максимума и динамического программирования, когда определяется оптимальный с точки зрения заданного критерия качества закон регулирования, обеспечивающий верхний предел качества системы, к которому необходимо стремиться при ее проектировании. Однако решение этой задачи практически не всегда возможно из-за сложности математического описания физических процессов в системе, невозможности решения самой задачи оптимизации и трудностей технической реализации найденного нелинейного закона регулирования. Необходимо отметить, что реализация сложных законов регулирования возможна лишь при включении цифровой вычислительной машины в контур системы.

Формирование систем автоматического регулирования, как правило, выполняют на основе аналитических методов анализа или синтеза. На этом этапе проектирования систем регулирования на основе принятые допущений составляют математическую модель системы и выбирают предварительную ее структуру. В зависимости от типа модели (линейная или нелинейная) выбирают метод расчета для определения параметров, обеспечивающих заданные показатели устойчивости, точности и качества. После этого уточняют математическую модель и с использованием средств математического моделирования определяют динамические процессы в системе. При действии различных входных сигналов снимают частотные характеристики и сравнивают с расчетными. Затем окончательно устанавливают запасы устойчивости системы по фазе и модулю и находят основные показатели качества.

Далее, задавая на модель типовые управляющие воздействия; снимают характеристики точности. На основании математического моделирования составляют технические требования на аппаратуру системы. Из изготовленной аппаратуры собирают регулятор и передают его на полунатурное моделирование, при котором объект регулирования набирают в виде математической модели.

По полученным в результате полунатурного моделирования характеристикам принимают решение о пригодности работы регулятора с реальным объектом регулирования. Окончательный выбор параметров регулятора и его настройка выполняют в натурных условиях при опытной отработке системы регулирования.

Развитие теории автоматического регулирования на основе уравнений состояния и z-преобразований, принципа максимума и метода динамического программирования совершенствует методику проектирования систем регулирования и позволяет создавать высокоэффективные автоматические системы для самых различных отраслей народного хозяйства. Полученные таким образом системы автоматического регулирования обеспечивают высокое качество выпускаемой продукции, снижают ее себестоимость и увеличивают производительность труда.

1.      Описание работы и функциональная схема системы

Рис.1 Схема привода стола станка с фазовой системой числового управления.

Объект управления - стол станка с закрепленной деталью - перемещается по направляющим с помощью силового цилиндра Ц. Инструмент производит обработку детали, которая должна двигаться с подачей, запрограммированной, например на магнитной ленте.

Система управления подачей стола работает следующим образом. С помощью магнитной головки считывания ЬГС снимается сигнал с магнитной ленты и поступает на вращающийся трансформатор ВТ и фазовый дискриминатор ФД. Ротор ВТ через шестерню входит в зацепление с рейкой стола. На выходе трансформатора формируется сигнал напряжения U по сдвигу фазы пропорциональный перемещению стока. Этот сигнал поступает на вход ФД. На выходе дискриминатора получает сигнал напряжения или тока, который является функцией разности фаз на магнитном передачи k. Увеличенный в усилителе-сумматоре постоянного тока УПТ управляющий сигнал поступает в электромеханический преобразователь ЭМП. Последний в зависимости от полярности и величины сигнала U, J осуществляет управление электрогидравлическим усилителем ГУ, который осуществляет перемещение цилиндра Ц с помощью рабочей жидкости. Для повышения динамических свойств привода в цепь управления могут вводиться КУ, которые работают от датчика скорости ДС или датчика ускорения ДУ объекта. В простых системах может вместо ВТ применяться датчик перемещения, сигнал от которого поступает непосредственно на УПТ. Объект управления непосредственно связан со штоком цилиндра Ц.

Рис.2 Структурная схема системы регулирования глубины рабочего оборудования мобильной машины с центробежным регулятором.

УПТ - усилитель-сумматор постоянного тока

ЭМП - электромеханический преобразователь

С-З - сопло-заслонка

ГУ - электрогидравлический усилитель

ВТ - вращающийся трансформатор

Ц - цилиндр

2.      Исходные данные

Данные для синтеза:

3.      Математическая модель

Сигнал от датчика Uoc поступает на усилитель - сумматор, который определяет ошибку регулирования

где Uo - управляющее напряжение и усиливает сигнал ошибки.

Усилители постоянного тока (УПТ) преобразовывают входной сигнал от датчика или другого элемента. УПТ выполняет функцию и сравнивающего устройства, т.е. алгебраического суммирования можно получить величину отклонения сигнала датчика U от сигнала задающего устройства Uo. Уравнение УПТ с коэффициентом усиления  запишется:

Электромеханический преобразователь (ЭМП) предназначен для преобразования электрического сигнала, поступающего от усилителя в механическое перемещение регулирующего органа (сопла-заслонка, золотникового или клапанного распределителя). ЭМП относится к звену второго порядка и описывается дифференциальным уравнением:

где m - масса подвижных элементов ЭМП;

h - перемещение рабочего органа ЭМП (заслонки, якоря);

Lk и Rk - соответственно индуктивность и сопротивление обмотки электромагнитной катушки ЭМП;

C - жесткость возвратной пружины ЭМП;

 - коэффициент передачи ЭМП;

Гидроусилитель «сопло-заслонка» с учетом ряда допущений.

Уравнение расхода в диагонали гидравлического мостика:

Уравнение сил, действующих на золотник:

где  - расход, поступающий на перемещение золотника при смещении заслонки;

где  - перепад давления на выходе «сопло-заслонки», равный перепаду давления на торцах золотника;

 - площадь торца золотника;  - жесткость центрующих золотник пружин;  - перемещение золотника;  - перемещение заслонки по оси сопел. Передаточная функция гидроцилиндра и объекта управления:

где  - коэффициент передачи зависит от крутизны расходной характеристики, золотника и эффективной площади поршня;

 - коэффициент относительного демпфирования.

ОС:

Сведем исходные уравнения в систему с учетом оператора Лапласа s = d/dt

 (

Рис.3 Структурная схема системы.

4.      Построение частотных характеристик

Логарифмическая амплитудно-фазовая частотная характеристика (ЛАФЧХ) - представление частотного отклика линейной стационарной системы в логарифмическом масштабе. ЛАФЧХ строится в виде двух графиков: логарифмической амплитудно-частотной характеристики и фазо-частотной характеристики, которые обычно располагаются друг под другом.

Анализ систем с помощью ЛАФЧХ весьма прост и удобен, поэтому находит широкое применение в различных отраслях техники, таких как цифровая обработка сигналов, электротехника и теория управления.

привод станок частотный разомкнутый

4.1 Логарифмическая амплитудно-частотная характеристика

Передаточная функция системы имеет вид:

Построение логарифмической амплитудно-частотной характеристики разомкнутой САУ:

 - общий коэффициент усиления разомкнутой системы;

 - степень астатизма системы.

Построение низкочастотной асимптоты

Наклон низкочастотной асимптоты определяется степенью астатизма и равен 0 дб/дек на ординате L(w) = 20 lg(k) при частоте w = 1 c^-1

 = 20lg(45.5) =33

Определение сопрягающей частоты:

Низкочастотная асимптота проводится до первой сопрягающей частоты. Если сопрягающая частота создана полиномом знаменателя передаточной функции, то изменение характеристики отрицательное с наклоном -20 дб/дек.

.2 Логарифмическая фазо-частотная характеристика

Формула для фазовой характеристики будет иметь вид:

Табл.1 Расчет ЛФЧХ

Амплитудной частотной характеристикой элемента или системы называется зависимость отношения амплитуд установившихся колебаний выходной и входной величин от частоты. Фазовой частотной характеристикой называется зависимость сдвига по фазе в колебаниях выходной и входной величин от частоты.

В условиях эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах (старение, температурные колебания и т.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать САУ так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости.

Запас устойчивости по модулю характеризует удаление годографа АФЧХ разомкнутой САУ от критической точки в направлении вещественной оси и определяется расстоянием h от критической точки до точки пересечения годографом оси абсцисс

5.      Исследование устойчивости разомкнутой системы

5.1 Критерий устойчивости по Найквисту

Он позволяет судить об устойчивости замкнутой системы, по частотным характеристикам разомкнутой системы. Если разомкнутая система устойчива, в этом случае для устойчивости замкнутой системы необходимо и достаточно чтобы число переходов ЛФЧХ через линию -180⁰ на участках где ЛАЧХ положительна было четным, в частном случае равным нулю.

Вывод: фазовая характеристика пересекает линию -180⁰ один раз, следовательно замкнутая система не устойчива.

5.2 По критерию Рауса

Этот критерий представляет собой систему неравенств, составленных по особым правилам из коэффициентов характеристического уравнения замкнутой САУ.

Критерий Рауса требует несколько меньшего объема вычислений, чем критерий Гурвица и более удобен для программирования на ЭВМ. Для суждения об устойчивости системы по этому критерию необходимо составить таблицу Рауса.

Табл.2. метод Рауса.

В первой строке таблицы записывают коэффициенты характеристического уравнения, имеющие четные индексы в порядке их возрастания. Во второй строке таблицы записывают коэффициенты с нечетными индексами в порядке их возрастания. В последующие строки вписывают коэффициенты, определяемые как:

Условия устойчивости Рауса: чтобы САУ была устойчивой необходимо и достаточно, чтобы все коэффициенты первого столбца таблицы Рауса имели один и тот же знак, то есть были положительными. Если не все коэффициенты первого столбца таблицы Рауса положительны, то есть САУ неустойчива, число правых корней характеристического уравнения равно числу перемен знака в первом столбце таблицы Рауса.

Характеристическое уравнение системы имеет вид:

Табл.3. таблица Рауса.

Табл.4. Расчет по методу Рауса

Вывод: разомкнутая система не устойчива, т.к. не все коэффициенты первого столбца таблицы РАУСА положительны и меняют свой знак, число правых корней 1.

6.      Построение желаемой амплитудной характеристики по показателям переходного процесса

.1 Желаемая ЛАЧХ

Желаемая логарифмическая амплитудно-частотная характеристика формируется исходя из заданных требований к системе по точности и качеству переходного процесса. Точность задается значениями установившихся ошибок, а качество переходного процесса - величиной перерегулирования и временем регулирования. Построение ведется по методу В.В Солодовникова и начинается с выбора одного из 4 вариантов ЛАЧХ. Исходные данные:  - величина перерегулирования

 - время регулирования переходного процесса

Наиболее близким к исходной ЛАЧХ является тип 4. По номограммам определяем w_ср при

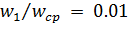
Графически определяем частоту w₂:

На частоте w = 1 c^-1 определяем ординату, cравниваем коэффициент усиления желаемой ЛАЧХ с исходной ЛАЧХ:

Вывод: построенная ЛАЧХ удовлетворяет требованиям: коэффициент усиления увеличился.

.2 Желаемая ЛФЧХ

Передаточная функция системы, имеющей построенную желаемую ЛАЧХ имеет вид:

Логарифмическая фазочастотная характеристика для желаемой ЛАЧХ:

Построение желаемой ЛФЧХ будем проводить для отдельных звеньев, входящих в передаточную функцию, затем суммировать и получать итоговую ЛФЧХ системы. Формула для фазовой характеристики будет иметь вид:

w

Табл.5. Расчет желаемой ЛФЧХ

7.      Построение графика вещественного процесса

Устойчивость является необходимым, но не достаточным условием технической пригодности системы. Помимо устойчивости к переходному процессу представляют требования, обуславливающие его так называемые качественные показатели. Для определения качественных показателей выбранной САУ необходимо построить график переходного процесса

Все многообразие переходных процессов в САУ можно разделить на:

1.      Колебательный процесс, характеризуемый несколькими значениями перерегулирований (кривая 1)

.        Малоколебательный процесс (апериодический), т.е. переходной процесс с одним перерегулированием (кривая 2)

.        Монотонный процесс (кривая 3), когда скорость изменения регулируемой величины не меняет знака в течение всего времени

Передаточная функция имеет вид:

Табл.6. Точки выбранные на ЛАЧХ и спроектированные на ЛФЧХ.

Затем используем монограмму Солодовникова, Лист 3. Находим все необходимые данные.

8.      Построение графика переходного процесса

Табл.8. Данные подобранные с таблицы Иващенко, а также расчет переходного процесса.

Табл.9. Данные подобранные с таблицы Иващенко, а также расчет переходного процесса.

Табл.10. Сумма данных подобранных с таблицы Иващенко, а также расчет переходного процесса.

9.      Построение корректирующего устройства

Все реальные системы содержат нелинейные и инерционные звенья. Это приводит к запаздыванию или искажению сигнала. С целью устранения этих недостатков используются корректирующие устройства. Они обычно выполняют математические операции: сложение, умножение, дифференцирование и т.д., - или их комбинации. Устанавливаются они последовательно, параллельно и в виде дополнительных обратных связей.

Дифференцирующие звенья используются для введения производных от сигнала в закон управления и регулирования.

Пассивные дифференцирующие звенья» осуществляют коррекцию путем подавления низких частот. Недостатком звена является уменьшение коэффициента усиления системы в 1/9 раза; звено (изодромное) также может служить целям дифференцирования. Пассивное интегрирующее звено» подавляет верхние частоты, что уменьшает быстродействие системы.

Интегрирующее - дифференцирующее звено позволяет компенсировать недостатки, присущие другим звеньям.

Мы выбрали желаемое и ЛАЧХ и с помощью него подбираем корректирующее устройство.

Для нашей системы применяем данные корректирующие устройства:

Наносим корректирующее устройство на график. Находим усилительное звено.

Подключены 4 устройства, для того, что нейтрализовать предыдущий наклон. В 1 устройстве наклон +20 Дб/дек от 0.01 Гц до 0.7 Гц. Затем подключаем 2 устройство, оно работает от 1.8 до 10Гц. 3 подключаем, работает от 10 до 240 Гц. Подключаем 4 устройство, оно работает от 240 до 1000 Гц.

Вывод

В данной курсовой работе мы исследовали систему регулирования глубины рабочего оборудования мобильной машины с центробежным регулятором. Исследовали на устойчивость, затем изучили с помощью желаемых ЛФЧХ и ЛАЧХ. Подобрали корректирующее устройство, с помощью которого система должна работать без перебоев.

Список литературы

1. И.Ю. Топчев «Атлас для проектирования CAP»

. «Динамика гидропневмосистем» Методическое указание. Каляшина А.В., Наб.Челны 2001г.

. « Управление техническими системами» Методическое указание. Каляшина А.В. Наб. Челны 2003г.

. Н.Н.Иващенко «Автоматическое регулирование»

. «Синтез корректирующих устройств по логарифмическим амплитудно-частотным характеристикам»