Франк-Кондонский принцип формирования полос люминесценции примесных центров

Франк-Кондонский принцип формирования полос люминесценции примесных центров

Франк-Кондонский принцип формирования полос люминесценции примесных центров

Принцип Франка-Кондона

Структура электронно-колебательного спектра определяется вероятностями соответствующих электронно-колебательных переходов. Колебательная структура участка спектра, соответствующая данному электронному переходу, определяется распределением вероятностей переходов между колебательными подуровнями рассматриваемых электронных состояний. Первостепенную роль играет принцип Франка-Кондона, который в теории колебательной структуры электронно-колебательных спектров кристаллов и молекул в некотором смысле заменяет обычные в спектроскопии правила отбора. Начнем с краткого рассмотрения классического и полуклассического вариантов этого принципа, которые в сочетании с диаграммами потенциальных кривых полезны для качественной интерпретации электронно-колебательных процессов. Затем мы подробно изложим основы квантово-механического вычисления колебательной структуры.

а) Классический принцип Франка-Кондона

Принцип Франка-Кондона в его простейшей формулировке получается из чисто классических представлений. Он состоит в утверждении, что электронное состояние (состояние «быстрой» подсистемы) молекулы (кристалла) изменяется настолько быстро, что за время электронного перехода ядра не успевают ни сместиться (условие 1), ни изменить своих импульсов (условие 2) («медленная подсистема не успевает среагировать»). Если электронно-колебательный переход на диаграмме потенциальных кривых (рис. 1) изображать стрелкой, начало которой показывает энергию и координату колебания в момент начала электронного перехода, а конец фиксирует энергию и координату в момент времени, непосредственно следующий за электронным переходом, то первое условие (R = const) означает, что стрелка должна быть вертикальной. Второе условие (P = const или E_Кин= const) означает, что конец стрелки должен находиться на таком же расстоянии (по энергиям) от потенциальной кривой конечного электронного состояния, на каком находилось начало стрелки от исходной потенциальной кривой (на рисунке АА'=ВВ'). К названным двум условиям, довольно естественно следующим из основной идеи адиабатического приближения, присоединяется еще одно условие.

Рис. 1. Диаграмма потенциальных кривых и принцип Франка-Кондона

Согласно классическому закону движения осциллятор проводит наибольшее время в поворотных точках (точки A и С). Принимается, что в момент электронного перехода осциллятор находится только в этих поворотных точках (условие 3). На диаграмме потенциальных кривых это условие сводится к тому, что изображающие стрелки следует начинать только с потенциальных кривых. Для колебательного состояния с энергией Е₁ (рис. 1) допускаются как начальные для стрелок только точки A и С, точка С - «запрещена». Для уровня энергии Е₂ точка А' «запрещена», изображающие стрелки можно начинать с точек G и F. Согласно условию 2 концы стрелок должны теперь тоже лежать на потенциальной кривой, так как E_кин = 0 до и после перехода (стрелки АВ и CD). Таким образом, классический принцип Франка - Кондона сформулирован в трех пунктах:

) R = const;

) Р=const;

) стрелки начинаются из поворотных точек классического движения осциллятора.

Простые рисунки типа рис. 1 позволяют уже в общих чертах разобраться в распределении интенсивностей в электронно-колебательных полосах поглощения двухатомных молекул.

б) Полуклассический вариант принципа Франка-Кондона

Пункты 1 и 2 в классическом принципе Франка-Кондона, как уже отмечалось, тесно связаны с адиабатическим приближением. Можно думать, что эти условия хорошо выражают истинную ситуацию при электронно-колебательном переходе. Конечно, с точки зрения квантовой механики нельзя одновременно фиксировать координаты и импульсы частиц, но следует ожидать, что для столь массивных частиц, как ядра, квантовые эффекты далеко не всегда сильно выражены. Слабым звеном в классической формулировке является пункт 3, который введен сверх адиабатического приближения как довольно плохо обоснованное дополнительное ограничение. Полуклассическая формулировка сохраняет пункты 1 и 2, но заменяет условие 3 новым: электронные переходы могут иметь место при любых значениях колебательной координаты R с вероятностями w(R), где w(R) - квантовомеханическое распределение координаты. Если мы интересуемся переходами из одного определенного исходного колебательного состояния, то вероятность распределения координаты является просто квадратом модуля волновой функции в координатном представлении: w_i(R) =φ_i(R)². Если исходное состояние представляет собой набор одинаковых систем в состоянии теплового равновесия, мы имеем (для колебания двухатомной молекулы в гармоническом приближении или для одного нормального колебания)

'

где E_i-энергия i-го колебательного уровня,

(T) -нормированный множитель распределения Больцмана.

Первый случай реализуется часто для легких двухатомных молекул, имеющих крупные колебательные кванты (hν~0,l эв). В этих молекулах еще при комнатных температурах (kT~0,025 эв) высшие колебательные уровни (i=1,2,...) почти не возбуждены (в состоянии i=0 находится более 90% молекул). Сказанное относится также к локальным колебаниям высокой частоты в кристаллах. Для кристаллических колебаний, среди которых всегда имеются колебания с малыми частотами, следует даже при температуре жидкого гелия пользоваться функцией

На диаграмме потенциальных кривых (рис. 1) полуклассический принцип разрешает для колебательного состояния E_i (E_i должна теперь совпадать с одним из уровней энергии осциллятора) как стрелки АВ, CD, так и C'D', причем первой стрелке следует приписать вероятность |φ_i(R₁)|² второй - |φ_i(R₂)|² , третьей - |φ_i(R₃)|². Если i=0, то наибольший «вес» приобретает именно стрелка, запрещенная по классическому варианту принципа Франка - Кондона. Это и понятно: в области малых квантовых чисел, особенно при i=0 (нулевые колебания осциллятора!), классическое распределение координаты коренным образом отличается от действительного - квантового - распределения. Естественно возникает сомнение, не приводят ли требования R=const, P=const также к существенным погрешностям, когда речь идет о переходах, начинающихся с нулевого колебательного уровня. Специальное сравнение с точными квантовомеханическими расчетами, проведенными по методу, рассматриваемому ниже, приводит к заключению, что точность полуклассического принципа Франка - Кондона зависит в основном от номера f конечного колебательного уровня. Если актуальная для электронно-колебательного перехода область лежит при больших f (f>10-20), то полуклассический принцип Франка - Кондона дает результаты, весьма близкие к квантово- механическим.

Рис. 2 - Потенциальные кривые для электронного перехода с большими (а) и малыми (б) стоксовыми потерями Р

В центрах люминесценции типа КС1 - Т1+ минимум потенциальной кривой R₀₁₁ сильно смещен относительно точки R₀₁ (стоксовы потери велики), наиболее интенсивная часть электронно-колебательной полосы соответствует уровням f~15-50, и полуклассический принцип Франка - Кондона хорошо воспроизводит действительное распределение интенсивностей (рис. 2, а). Если же потенциальная кривая конечного электронного состояния мало смещена (стоксовы потери малы) и актуальны низкие колебательные уровни f, то полуклассическое рассмотрение приводит к значительным погрешностям, хотя оно и сохраняет смысл для качественного толкования явления (рис. 2, б).

в) Квантово-механический принцип Франка-Кондона

Речь идет просто о вычислении вероятностей электронно-колебательных переходов по правилам квантовой механики. Получаемые результаты, как мы увидим в конце параграфа, допускают наглядное сопоставление с приведенными выше вариантами принципа Франка-Кондона. Поэтому (и, строго говоря, только поэтому) имеет смысл говорить о рассматриваемом квантово-механическом решении задачи как о варианте принципа Франка-Кондона. Как известно, процессы поглощения и люминесценции света достаточно хорошо описываются нестационарной теорией возмущений первого порядка. Согласно этой теории вероятность перехода W_{nn`</sub> системы из состояния с квантовым числом (набором квантовых чисел) n в состояние n' пропорциональна квадрату модуля соответствующего матричного элемента оператора возмущения, вызывающего переход. Пусть оператором возмущения Р служит оператор дипольного момента молекулы. Тогда W<sub>nn`}~|P_{n`n</sub>|<sup>2</sup> и для вычисления вероятности переходу нужно построить матричный элемент оператора Р на волновых функциях системы, соответствующих состояниям n' и n. В дальнейшем нас будет интересовать только функция |P<sub>n`n}|² как функция от частоты перехода. Эта функция описывает как полосу поглощения, так и сопряженную с ней полосу излучения. Коэффициент пропорциональности, связывающий эту функцию с вероятностью перехода (и распределением интенсивностей в спектре), существенно слабее, чем |P_n`n|², зависит от частоты, и мы им в дальнейшем интересоваться не будем.

Рассмотрим вероятность перехода на основе адиабатического приближения. Пусть состояние n характеризуется электронным квантовым числом l и колебательным квантовым числом i, а состояние n'- электронным квантовым числом m и колебательным квантовым числом f. Тогда волновые функции этих состояний запишутся в виде

молекулярный спектр франк кондон

Оператор дипольного момента Р для зарядов электро- нов и ядер имеет вид

где n и Rα представляют собой операторы умножения на координаты электрона номера i и ядра номера α. Матричный элемент оператора Р имеет вид

Так как Ф_m и Ф_l суть две из собственных функций уравнения Шредингера, образующих систему ортогональных и нормированных функций, то член во втором слагаемом, заключенный в квадратную скобку, равен нулю при l≠m и равен единице при l=m. Значит, дипольный момент, связанный с ядрами, вызывает лишь чисто колебательные переходы внутри одного электронного состояния. С этими переходами связано инфракрасное поглощение молекул и кристаллов. Их мы здесь рассматривать не будем. Первое слагаемое дает вероятность электронно-колебательных переходов. Так как электронные волновые функции системы неизвестны, то обозначим

и объявим D_ml(R) параметром теории, который в случае необходимости следует находить из опытных данных. Далее, будем считать электронный матричный элемент D_ml(R), слабо зависящим от ядерных координат и разложим его в ряд возле равновесного положения ядер.

Если ядерных координат много, то ряд (4.2б) является соответствующим многомерным рядом Тейлора.

Приближением Кондона называется замена функции D_ml(R) нулевым членом ряда D⁰_ml, который не зависит от координат ядер. Приближение Кондона более точно, чем предположение Ф(r, R)=Ф(r, R₀), так как, проинтегрировав электронные волновые функции по электронным координатам, мы провели уже некоторое усреднение и для D_ml(R) зависимость от координат ядер уже ослаблена. Пренебрежение последующими членами в выражении (4.2 б) необязательно; никаких особых математических трудностей их учет не представляет. Если их учесть, появляются новые коэффициенты D_ml где r=1,2..., которые также объявляются параметрами теории и подлежат определению из опыта. Мы увидим в дальнейшем, что отклонения от приближения Кондона существенны при электронно-колебательных переходах, запрещенных по соображениям симметрии для равновесной конфигурации молекулы. Таким образом, вероятность электронно-колебательного перехода определяется в основном (в приближении Кондона) следующим выражением:

φ_ml и φ_li являясь решениями разных уравнений Шредингера (1.7) (потенциальные энергии не равны:(R) ≠Wf (R), принадлежат разным ортонормированным системам. Поэтому интеграл перекрывания в (4.3) не обязательно равен нулю при f≠i, если только m≠l

Покажем, что в зависимости интеграла перекрывания от i и f содержатся пункты 1 и 2 классической формулировки принципа Франка - Кондона (R= const, Р= = const) как приближенная оценка величины интеграла. Сравним между собой вероятности электронно-колебательных переходов, изображенных на рис. 3 стрелками

, 2, 3. Это переходы из электронного состояния l с колебательного уровня i=0 в электронное состояние m с колебательными квантовыми числами f. Взят случай заметного сдвига минимума верхней потенциальной кривой. Вероятности таких переходов пропорциональны квантово-механическим вероятностям электронно-колебательного перехода 3 функции φ_lo и φ_mo просто не перекрываются, в случае 1 функция φ_lo перекрывается с сильно осциллирующим участком функции φ_mf.

Рис. 3 - Соответствие принципа Франка-Кондона квантово-механическим вероятностям электронно-колебательного перехода

г) Принцип Франка-Кондона как правило отбора

Выше уже говорилось, что принцип Франка - Кондона в некотором смысле заменяет правила отбора электронно-колебательных переходов. В то же время принцип Франка - Кондона не является правилом отбора в обычном смысле: он не накладывает никаких строгих запретов на переходы. Он говорит лишь о том, что переходы на одни колебательные состояния весьма вероятны (стрелка 2 на рис. 3), на другие - несколько менее вероятны (на уровни, классические точки поворота для которых близки к 5), а на уровни с заметным нарушением принципа Франка - Кондона - весьма маловероятны. Эта особенность принципа Франка - Кондона как правила отбора связана с адиабатическим приближением. Использование адиабатических волновых функций в предыдущем разделе параграфа привело к тому, что матричный элемент (см. формулу (4.3))

определяющий распределение вероятностей по колебательным уровням, строится на колебательных волновых функциях, принадлежащих к разным наборам ортонормированных собственных функций (φ_li являются собственными функциями одного уравнения Шредингера) с оператором потенциальной энергии Wl(R),

φ_mf - собственные функции другого уравнения Шредингера с потенциалом Wm(R). При квантовомеханическом вычислении вероятностей переходов мы имеем обычно дело с одним набором ортонормированных собственных функций. Именно свойства ортогональности волновых функций, фигурирующих в матричных элементах, в сочетании со свойствами симметрии системы (свойствами симметрии одного гамильтониана) лежат в основе обычных правил отбора спектроскопии. Эти правила отбора сформулированы в виде «решительного» утверждения («линия есть или ее нет») и носят, поэтому зачастую также название правил запрета.

Например, для дипольных переходов гармонического осциллятора известное правило отбора утверждает, что колебательное квантовое число i может измениться только на единицу

Все другие переходы в дипольном приближении запрещены. В случае электронно-колебательных переходов (относящихся также, прежде всего к гармоническим осцилляторам!) это правило отбора полностью теряет силу. Заменяющий его принцип Франка - Кондона не может обычно быть сформулирован в виде правила запрета. Однако имеется исключение - случай равенства потенциалов движения ядер в обоих электронных состояниях Wl (R)= Wm(R) (стоксовы потери отсутствуют). В этом случае наборы колебательных волновых функций φ_li(R) и φ_mf(R) совпадают. В формуле (4.3) мы можем опустить индексы электронного состояния и воспользоваться обычным условием ортонормированности для колебательных функций двух разных электронных состояний l и m

Итак, мы пришли к строгому правилу отбора. Его можно сформулировать как правило: «При одинаковых адиабатических потенциалах в приближении Кондона запрещены все переходы с изменением колебательного состояния решетки». Для сравнения с правилом отбора для чисто колебательных переходов (4.5) можно (4.6) записать в виде

Правило отбора (4.6) или (4.7) точно никогда не реализуется, но оно приближенно верно для систем с весьма малыми стоксовыми потерями (например, f-f переходы в редкоземельных ионах в кристаллах). Кроме того, оно реализуется точно в пределе (по N^-1, где N - число кристаллических колебаний) в исключительно актуальном случае взаимодействия электронного перехода в примесном центре с кристаллическими колебаниями. Мы увидим ниже, как это приводит к возникновению квазилинейчатых электронно-колебательных спектров. На основе этого особого случая справедливости в пределе правила отбора (4.6) или (4.7) может быть понято также возникновение эффекта Мёссбауэра. К рассмотрению этого эффекта, природа которого родственна квазилинейчатым электронно-колебательным спектрам, мы обратимся в дальнейшем. Отметим, что принцип Франка-Кондона применим (в несколько ином толковании в пространстве импульсов) также в случае эффекта Мёссбауэра.

Заметим еще, что правило отбора (4.6) или (4.7), очевидно, существенно связано с приближением Кондона и не зависит непосредственно (зависит «неявно» через точность приближения Кондона) от характера взаимодействия со светом, т. е. от того, какие - дипольные, квадрупольные и другие - переходы принимаются во внимание. Нетрудно модифицировать правило отбора (4.6) с учетом отклонения от приближения Кондона. Например, учет линейного члена в разложении электронного матричного элемента (4.2) приводит к любопытному результату - к правилу 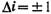, т. е. к обычному правилу отбора (4.5) гармонического осциллятора.