Анализ метрологических характеристик вторичного измерительного преобразователя

Анализ метрологических характеристик вторичного измерительного преобразователя

ВВЕДЕНИЕ

Средство измерений - это техническое средство, используемое при измерениях и имеющее нормированные метрологические свойства. Измерительный преобразователь - СИ, предназначенное для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и хранения, но не поддающейся непосредственному восприятию наблюдателем. Измерительные преобразователи могут как входить в состав измерительных приборов, так и применяться самостоятельно. Поэтому категория СИ, охватывающая измерительные приборы и преобразователи, называется также измерительными устройствами.

Для оценки свойств СИ и определения возможности их применения в тех или иных условиях служат характеристики СИ, весь комплекс которых можно разбить на технические, позволяющие, как и для других технических средств, установить назначение СИ и область применения, а также оценить его эксплуатационные возможности, и метрологические, оказывающие влияние на результаты и погрешности измерений. Характеристики погрешности СИ позволяют количественно оценить инструментальную погрешность измерения .

Погрешность СИ может быть представлена в форме абсолютной, относительной или приведенной погрешности.

В данной работе проведен анализ метрологических характеристик электрического преобразователя. Проведена обработка двух серий прямых многократных измерений. Осуществлена проверка полученных измерений на равнорассеянность, однородность и наличие корреляционной связи.

Проведено объединение двух серий с целью увеличения количества исходных значений, а, следовательно, увеличения достоверности полученных оценок.

Произведен анализ всех расчетов, на основании которых сделан вывод о классе точности прибора.

Область применения методики расчета: метрологическая проверка измерительных приборов.

Это позволило определить суммарную погрешность исследуемого устройства и получить данные о возможностях его дальнейшего использования с целью определения тех или иных электрических параметров.

Метрологическим назначением большинства СИ является использование их для получения результатов измерений при научных исследованиях, в производственных и технологических процессах и в целом в народном хозяйстве. К метрологическим характеристикам СИ будем относить такие характеристики, которые позволяют судить о пригодности СИ для использования в заданном диапазоне с известной точностью (погрешностью).

Основные метрологические характеристики СИ в целях установления единого подхода регламентируются ГОСТ 8.009-72 «Нормируемые метрологические характеристики средств измерения». Для любого СИ устанавливается диапазон измерения, определяемый как область значений измеряемой величины, для которой нормированы допускаемые погрешности СИ.

В данной работе осуществляется анализ метрологических характеристик. Согласно ГОСТ 16263-70 измерительным преобразователем называется средство измерений, служащее «для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и (или) хранения, но не поддающейся непосредственному восприятию наблюдателем». Измерительные преобразователи чаще всего являются лишь составными частями более или менее сложных измерительных комплексов и систем автоматического контроля, управления и регулирования. Целю данной работы является анализ метрологических характеристик электрического преобразователя.

Функциональная схема измерительной установки показана на рисунке 1.

Рисунок 1- Функциональная схема измерительной установки

где:

Г - генератор;

ИП - измерительный преобразователь;

В1, В2 - вольтметры;

Н - магазин сопротивлений (нагрузка).

1. ПОЛУЧЕНИЕ ИСХОДНОЙ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ И ПЕРВИЧНАЯ ОБРАБОТКА ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

В данном разделе мы снимаем экспериментальные данные и рассчитываем среднеарифметическое значение выходного напряжения в каждой точке входного для каждой таблицы данных отдельно, также вычисляем среднеквадратическое отклонение, дисперсии и проверку на промахи. Так как среднеарифметическое значение является более близким к математическому ожиданию, дисперсию (Дисперсия случайной погрешности равна дисперсии результатов наблюдения и является характеристикой их рассеиваний относительно математического ожидания), среднеквадратическое отклонение (что является корнем из дисперсии).

САЗ рассчитывается по формуле (1.1):

   (1.1)

СКО рассчитывается по формуле (1.1.2):

 (1.2)

Дисперсия рассчитывается по формуле (1.3):

 (1.3),

где n - количество измерений в каждой точке;

vi - отклонение от среднего значения в каждой точке входного напряжения;- количество измеренных значений в каждой точке.

В таблице 1.1 отражены результаты первой группы измерений, а также посчитаны средние арифметические значения для ряда в целом, по возрастанию и по убыванию:

Таблица 1.1-Результаты первой группы измерений

В таблице 1.2 отражены результаты второй группы измерений, проведенные через 30 минут после первых:

Таблица 1.2-Результаты второй группы измерений

Теперь строим два СХП на одном графике, что отражено на Рисунке1.1:

Рисунок 1.1-СХП первой и второй группы наблюдений

Вычислив значения случайных отклонений по формуле (1.4)

  (1.4),

воспользуемся ими для расчета СКО результатов измерений (таблица.1.5) :

 (1.5),

где n - число измерений в ряду.

 Таблица 1.3-Нахождение СКО результатов измерений

Зная значения СКО, по известной зависимости  найдем значения дисперсий значений выходных напряжений в каждой точке (Таблица 1.4) :

Таблица 1.4-Нахождение дисперсий результатов измерений

Для исключения случайных (грубых) погрешностей проведем проверку на промахи по критерию 3-х σ по формуле (1.6):

(1.6) .

Проверка на промахи первой группы измерений отражена в таблице 1.5:

Таблица 1.5-Проверка на промахи первой группы измерений.

Проверка на промахи второй группы измерений отражена в таблице 1.6:

Таблица 1.6-Проверка на промахи второй группы измерений.

Затем определяем неопределенность гистерезиса. Для повышения достоверности полученных результатов обработка группы измерений производится отдельно для возрастающих и убывающих значений входного сигнала. Таким образом получим гистерезис СХП средства измерения в i-й точке диапазона измерения. Для этого для двух таблиц исходных данных определим зависимость среднего значения каждого ряда от входного.

Графически данные зависимости будут иметь следующий вид :

Для первой группы измерений (Рисунок-1.2) :

Рисунок 1.2-Неопределенность гистерезиса для первой таблицы

Неопределенность гистерезиса для второй таблицы будет иметь такой вид (Рисунок 1.3):

Рисунок 1.3-Неопределенность гистерезиса второй таблицы

2. ОБЪЕДИНЕНИЕ ГРУПП РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

.1 Выполнение проверки на однородность в каждой контрольной точке, используя Т-критерий

Проверка на однородность по Т-критерию проводится для того, чтобы определить, содержат ли средние значения систематические составляющие погрешности измерения напряжения. Для этого сравнивают экспериментальное значение Тэксп, которое определяется по формуле 2.1, и теоретическое Тдоп, соответствующее равенству 2.2 :

  (2.1)

где  и  - коэффициенты Стьюдента, которые выбираются из таблицы статистики Стьюдента в зависимости от значений доверительной вероятности Рдов и числа степеней свободы k1 и k2.

В данном случае значения Рдов = 0,95, = 2,02. В таблице 2.1 приведены значения Тэксп и Тдоп для каждой контрольной точки результатов измерений:

 Таблица 2.1-Проверка результатов измерения по Т-критерию

Если Тэксп < Тдоп, то максимальное расхождение средних значений признаётся случайным, систематическую составляющую погрешности несущественной и результаты измерений, полученные для одной отметки шкалы объединить. Следовательно, для этих данных условие однородности выполняется, и результаты двух групп измерений можно объединить.

.2 Выполнение проверки на равноточность в каждой точке, используя критерий Фишера

Проверка производится путем сравнения экспериментального значения Fэксп, определяемого по формуле (2.2.1), с допустимым значением Fдоп, выбираемым по статистике F-распределения Фишера с учетом выбранного Рдов и числа степеней свободы k.

 (2.1),

 (2.2).

Если неравенство 2.2 выполняется, то результаты измерений признаются равноточными. В обратном случае для объединения результатов необходимо ввести весовые коэффициенты для точек, в которых условия критерия Фишера не выполняются, а также средневзвешенные значения выходных величин в этих точках. В таблице 2.1 приведены значения Fдоп и Fэксп для каждой контрольной точки и их соответствие условиям критерия для Рдов= 0,95.

Таблица 2.1-Проверка результатов измерения по F-критерию.

допустимое выбирается из таблицы распределения Фишера при Рдов=0,95 и к1=к2=9. Fэкспериментальное вычисляется по формуле:

 (2.3).

При Fэксп<FДоп дисперсии признаются равнорассеяными (если они являются независимыми, однако распределенными случайными величинами), а результаты - равноточными.

Результаты измерений, кроме точки U=0.98, считаются неравноточными и их можно объединить в одну групп в каждой точке диапазона входных напряжений, при этом в качестве средних использовать средневзвешенные значения.

напряжение метрологический среднеарифметический

2.3 Объединение результатов измерений в одну таблицу

Объединенные результаты наблюдений показаны в таблице 2.1:

Таблица 2.1-Оъединенные результаты наблюдений.

Новая СХП(СХП объединенных результатов наблюдений) изображена на рисунке 2.1:

Рисунок 2.1-Новая СХП.

3. НАХОЖДЕНИЕ ТЕОРЕТИЧЕСКОЙ СХП И ОЦЕНКИ СТЕПЕНИ ЕЕ ДОСТОВЕРНОСТИ

Для нахождения теоретической СХП будем использовать метод наименьших квадратов (МНК). Согласно этому методу оценки Uj выбираются так, чтобы минимизировать сумму квадратов остаточных погрешностей условных уравнений.

Итак, в таблице 3.1 запишем полученные средние и входные значения напряжения:

Таблица 3.1-Средние и входные значения напряжения

Запишем систему условных уравнений в соответствии с количеством точек измерений по диапазону:

Условные уравнения имеют избыточность, так как число уравнений превышает число неизвестных. Для получения системы нормальных уравнений, т.е. такой, для которой число неизвестных равно числу уравнений, пользуются постулатом Лежандра: решение условных уравнений должно быть таким, чтобы сумма квадратов невязок была минимальной. Следовательно, нормальные уравнения (НУ) для линейной аппроксимирующей зависимости имеют вид:

A[xx]+B[xy]=[xl], (3.2)[xy]+B[yy]=[yl],

Где

Итак, учитывая эти коэффициенты, НУ будут такими:

*A+9.9*B=11.487753; (3.4)

9.9*A+8.954*B=10.373472.

Выполним решение НУ методом определителей:

  (3.5)

 (3.6)

 (3.7)

Таким образом, получаем решение: = 0.3387;=0.7839.

Тогда расчетное напряжения выхода преобразователя аппроксимируем следующей линейной зависимостью:

Uвых=0,3387+0,7839*Uвх (3.8)

Проводим расчет теоретических значений согласно полученному уравнению будет таким(Таблица 3.2):

Таблица 3.2-Расчет теоретических значений напряжения.

Оценку дисперсий S2 условных уравнений определяем из соотношения:

  (3.9),

где vi - невязка в i-той точке диапазона;

n - число точек диапазона;

β =2 - число искомых неизвестных.

Оценки СКО значений коэффициентов a и b будут такими:

 (3.10),

 (3.11).

Теоретическая СХП с аппроксимирующей прямой изображена на Рисунке 3.1:

Рисунок 3.1-Теоретическая СХП с апроксимирующей прямой.

4. ОПРЕДЕЛЕНИЕ КЛАССА ТОЧНОСТИ ИЗМЕРИТЕЛЬНОГО ПРЕОБРАЗОВАТЕЛЯ

.1 Нахождение отклонений экспериментальной и теоретической СХП в каждой точке

Найдем отклонения экспериментальной СХП в каждой точке. Для удобства введем все необходимые результаты в таблицу 4.1.1:

Таблица 4.1-Отклонения теоретической и экспериментальной гистограмм

.2 Введение аппроксимирующего полинома и расчет его коэффициентов

Введем аппроксимирующий полином и рассчитаем его коэффициенты (будем использовать полином только первого порядка). При нахождении этого полинома будем снова использовать метод наименьших квадратов.

Объединим в таблицу 4.2.1 полученные отклонения и входные значения напряжения:

Таблица 4.1 - Отклонения и входные значения напряжения

Теперь запишем систему условных уравнений :

Нормальные уравнения (НУ) для линейной аппроксимирующей зависимости будут иметь вид:

[xx]a+[xy]b=[xl]

[xy]a+[yy]b=[yl] (4.2).

где:

[xx] = 11;

[xy] =[yx]= 9.9;

[yy] =8.954;

[xl] =0.0322468;

[yl]=0.029027968.

Итак, НУ будут такими:

11a+9.9b=0.032247

9.9a+8.954b=0.029028 (4.3).

Выполним решение НУ метом определителей:

 (4.4),

 (4.5),

 (4.6).

Таким образом, получаем решение:

а= 0.002812= 0,000133

Таким образом, зависимость отклонений экспериментальной и теоретической СХП от входного значения напряжения аппроксимируется следующей линейной зависимостью:

Δi=0.002812+0.000133*Uвх (4.7)

Расчет значений согласно полученному уравнению:

Δ1=0.0029184;

Δ2=0.00292106;

Δ3=0.00292372;

Δ4=0.00292638;

Δ5=0.00292904;

Δ6=0.0029317;

Δ7=0.00293436;

Δ8=0.00293702;

Δ9=0.00293968;

Δ10=0.00294234;

Δ11=0.002945.

 Представим зависимость погрешности преобразователя от значений контрольных точек(Рисунок4.2.1):

Рисунок 4.1- Зависимость разности экспериментальной и теоретической СХП

Оценку дисперсий S2 условных уравнений определяем из соотношения:

  (4.8)

где vi - невязка в i-той точке диапазона;

n - число точек диапазона;

β =2 - число искомых неизвестных.

Оценки СКО значений коэффициентов a и b будут такими:

 (4.9),

 (4.10).

Исходя из коэффициентов степень полинома не превышает границы, следовательно, полином первой степени.

.3 Определение класса точности измерительного преобразователя

Определение класса точности производится по формуле 4.1:

 (4.1).

Таким образом получаем Δосн=0,00282.

4.4 Оценка неопределенности результатов преобразователя

Подставив данные в выражение(4.1)получим ΔUвх=0,00212.

5.ОПРЕДЕЛЕНИЕ СПОСОБА РАСПРЕДЕЛЕНИЯ ОБЪЕДИНЕННЫХ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ

.1 Построение экспериментальной гистограммы

Построим гистограмму экспериментального распределения по отклонениям каждого значения объединенных результатов от среднего в каждой контрольной точке. Отклонения объединенных результатов от среднего в каждой контрольной точке отражены в таблице 5.1:

Таблица 5.1- Отклонения объединенных результатов от среднего в каждой контрольной точке.

После этого строим экспериментальную гистограмму. Для этого выстраиваем все отклонения в вариационный ряд, то есть рассматриваем полученные случайные отклонения в порядке возрастания, потом найдем количество интервалов, на которое необходимо разбить данный ряд. Так как полученный ряд имеет 220 значений, значит L=10. Далее определим СКО полученного ряда:

Рассчитаем шаг интервалов:

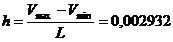 (5.2)

Теперь рассчитаем средние значения полученных интервалов, а также количество значений ряда, которое попало в каждый интервал. Для удобства сведем результаты в Таблицу 5.1.2:

Таблица 5.2-Количество значений в каждом интервале и средние значения полученных интервалов.

Экспериментальная гистограмма будет иметь вид(Рисунок 5.1):

Рисунок 5.1-Экспериментальная гистограмма

.2 Построение теоретической гистограммы

Найдем среднеарифметическое значение (САЗ) вариационного ряда:

 (5.1).

Следующим шагом будет нахождение нормированных отклонений середины каждого интервала гистограммы от САЗ, далее определить по таблице нормированной функции нормального распределения плотность вероятности y(t ) для каждого интервала гистограммы, и в конце необходимо вычислить теоретические частоты Nт (теоретическое число результатов измерений - количество результатов измерений, которые должны попасть в каждый интервал), соответствующие каждому интервалу.

Для удобства полученные результаты сведем в таблицу 5.1:

Параметры t , y(tj ), Nт вычисляются по формулам (5.1) - (5.3) соответственно:

  (5.1),

 (5.2),

 (5.3).

Теоретическая гистограмма будет иметь вид(Рисунок 5.1):

Рисунок 5.1-Теоретическая гистограмма

5.3 Проверка соответствия теоретической и экспериментальной гистограммы по критерию Пирсона

Проверка соответствия экспериментальной и теоретической гистограмм выполняется с использованием критерия согласия χ2 - Пирсона, обеспечивающего минимальную ошибку принятия гипотезы по сравнению с другими критериями. Показатель разности частот экспериментального и теоретического распределений можно вычислить по формуле:

  (5.1).

По уровню значимости q (0,02≤q≤0,1) и числу степеней свободы k=r-3 из таблицы χ2 - распределения находим границу критической области критерия χq2 .

Возьмем q=0,02 (к=6), тогда χq2 =14,067

Итак, можно сделать вывод: так как χq2<χЭ2, то это означает что гипотеза о нормальности распределения не принимается.

 5.4 Расчет общей неопределенности преобразователя

Общая погрешность преобразователя рассчитывается по формуле(5.1):

Δ=0,06+0,00268+0,00282+0,002120,0019=0,06952

ЗАКЛЮЧЕНИЕ

В ходе данной работы были обработаны две группы прямых многократных измерений, проделано три основных этапа:

получение результатов измерений;

обработка полученных данных эксперимента;

определение метрологических характеристик преобразователя.

Условия получения результатов измерений указаны в задании на курсовую работу.

Обработка данных эксперимента дала следующее: проверка по Т-критерию показала, что максимальное расхождение средних значений двух таблиц носит случайный характер, а следовательно случайная составляющая погрешности является несущественной. Результаты двух таблиц оказались равноточными и не равнорассеяными, следовательно нам не пришлось вводить весовые коэффициенты. Гипотеза о нормальности закона распределения не подтвердилась.

Что касается метрологических характеристик преобразователя, то, во-первых, удалось получить его функцию преобразования Uвых=f(Uвх) данного средства измерения (аппроксимирующий полином первого порядка).Также была рассчитана неопределенность преобразователя.

ПЕРЕЧЕНЬ ССЫЛОК

1.      Бурдун Г.Д., Б.Н. Марков. Основы метрологии: учеб.пособ. - М: издательство стандартов, 1975. - 335 с.

.        Науменко А.М., Чебыкина Т.В. Методы обработки результатов экспериментов: метод. пособ. - Х: «ХАИ», 2003. - 28 с.

.        Науменко А.М., Улитенко В.П. Определение погрешностей технических измерений: учеб.пособ. - Х: «ХАИ», 1992. - 131 с.