Статистический анализ уголовных преступлений в г. Нерюнгри
Технический
институт (филиал) федерального государственного автономного образовательного
учреждения высшего профессионального образования
«Северо-Восточный
федеральный университет имени М.К. Аммосова»
в
г. Нерюнгри
Кафедра
Математики и Информатики
КУРСОВАЯ
РАБОТА
По
дисциплине «Теория вероятностей и математическая статистика»
На
тему: «Статистический анализ уголовных преступлений в г. Нерюнгри»
Выполнила: ст.гр.ПИ-11
Кучеренко О.В.
Научный руководитель:
доцент, зав. кафедрой МиИ
Самохина В.М.
Нерюнгри,
2013 г.
Содержание
Введение
Теоретическая часть
Теоретические основы юридической статистики
Числовые характеристики
Практическая часть
Задание № 1. Построение гистограммы выборки
Задание № 2. Оценка среднего значения, дисперсии и эксцесса
Задание № 3. Подгонка кривых функций плотности и функций
распределения нормального закона.
Задание № 4. Проверка гипотезы о распределение генеральной
совокупности по критерию хи квадрат
Задание № 5. Интервальная оценка среднего значения нормального
распределения
Задание № 6. Найти выборочное уравнение прямой линии регрессии Y
на X по данным приведенным в корреляционных таблицах
Задание № 7. Метод наименьших квадратов
Список использованной литературы
Введение
Статистика России охватывает стороны
культурной и правовой жизни, экономики и политики нашего государства, а также
разделяется на ряд отраслей.
Одна из таких отраслей - правовая
(юридическая) статистика.
Сферы человеческой деятельности,
регулируемые правом очень разнообразны. В реальной жизни нет таких областей,
которые бы не имели правового обеспечения. Они различаются по уровням
регулирования. Различные аспекты человеческой деятельности, регулируемые правом
и имеющие статистическое отражение, являются предметом юридической статистики.
Юридическая статистика имеет
несколько отраслей. Одна из них - уголовно - правовая статистика. Она изучает
количественную сторону преступности, судимости и деятельности государственных
органов по борьбе с преступностью.
Преступность - это одно из
социальных явлений, угрожающих безопасности человека. Влияние преступности на
уверенность людей в безопасности является неконтролируемым, поскольку оно
складывается из представлений населения о распространенности преступлений, о
способности государственных органов защитить их от преступных посягательств, а
также от ряда иных моментов.
Представления людей о социальных
явлениях формируются под воздействием личного опыта, и на основе информации,
поступающей из официальных и неофициальных источников. Поэтому будет актуально
рассмотреть, как обстоит дело с преступностью в городе, в котором живем - в г.
Нерюнгри.
Цель работы: провести анализ и
статистику уголовных дел против жизни и здоровья, на примере УВД г. Нерюнгри за
2010-2012гг.
Для достижения цели были поставлены
следующие задачи:
Проработка специальной литературы.
Сбор необходимой информации.
Проведение первичной обработки
данных.
Статистический анализ уголовных дел.
Теоретическая часть
Теоретические основы юридической
статистики
Объектом юридической статистики
является количество совершенных преступлений и деятельность государственных
органов по борьбе с преступностью.
Юридическая статистика
подразделяется на следующие разделы:
а) статистику предварительного
расследования - деятельность органов предварительного расследования (количество
возбужденных уголовных дел, зарегистрированных преступлений, арестованных,
сроки расследования, раскрываемость, возвращенных на дополнительное
расследование дел и другие показатели);
б) статистику уголовного
судопроизводства - учет судимости и деятельности судов (количество
рассмотренных уголовных дел, осужденных, освобожденных от уголовной
ответственности, оправданных, меры наказания, работу надзорной инстанций,
мировых судей и т.п.);
в) статистику исполнения
приговоров - учет деятельности прокуратуры по надзору за местами лишения
свободы, работу судов по условно-досрочному освобождению (учет подследственных
заключенных, по срокам наказания, срокам содержания под стражей, видам
преступления и другим показателям).
В последние годы в виде самостоятельной
отрасли выделяется криминологическая статистика - изучает количественные
характеристики преступности, ее причины и личности преступника.
Жизнь в любом городе часто вынуждает
людей пользоваться услугами юристов и адвокатов. Оснований для этого может быть
много: семейные споры, право получения наследства и много других трудностей в
понимании различных областей юриспруденции.
На данный момент, юридическая помощь
- это перспективное направление в правоохранительной деятельности, закрепленное
в Конституции РФ.
Статистический анализ позволяет
наглядно увидеть структуру судебных дел и дает возможность судить об
эффективности деятельности правоохранительных органов по борьбе с
правонарушениями.
Статистическое наблюдение - это учет
интересующих фактов о правовых и юридически значимых явлениях и процессах и
сбор полученных на основе этого учета массовых первичных данных в какую-то
совокупность.
Любое юридическо-статистическое
исследование начинается с:
получения исходной
социально-статистической информации (учет преступлений, правонарушений,
гражданских споров, приговоров, судебных решений, видов наказания и других
юридически значимых фактов).
обобщения учтенных фактов в
соответствующую совокупность.
На практике эти два аспекта
статистического наблюдения составляют единый процесс учета и отчетности:
вначале учитываются уголовные или гражданские дела, обвиняемые или ответчики по
каким-тo необходимым нам признакам, а затем полученные сведения представляются
в различных формах отчетности.
Числовые характеристики.
Для проведения статистического
анализа, воспользуемся следующими формулами и понятиями:
Средняя арифметическая:
Мода - значение
случайной величины, имеющее наибольшую вероятность. На многоугольнике
распределения мода - это абсцисса самой высокой точки. Обозначается символом
«Мо».
Дисперсия - это средний
квадрат отклонения изучаемого признака от теоретического (среднего) показателя.
Она характеризует уровень однородности исследуемой совокупности и обозначается
символом «s2».
где 
- условный момент
первого порядка
- - условный момент
второго порядка
Среднеквадратическое
отклонение «s»:
Коэффициент вариации -
это относительная мера вариации. 
Эксцесс (коэффициент
островершинности) - мера остроты пика распределения случайной величины.
Практическая часть
Задание № 1. Построение
гистограммы выборки
а) Возраст задержанных и
кол-во совершаемых ими преступлений за 2011 год
Таблица 1
|
возраст
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
|
количество задержанных
|
6
|
12
|
9
|
18
|
21
|
24
|
27
|
36
|
42
|
Постановка задачи. По выборкам
составить вариационных ряд; вычислить относительные частоты и накопленные
частоты; построить график вариационного ряда (гистограмму и полигон).
Порядок выполнения
задания. Находим: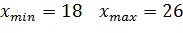 
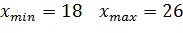. Составим вариационный
ряд:
Таблица 2
|
|
ni (2011)
|
Xi(2011)
|
ni/n
|
Накопленные частности
|
|
|
6
|
18
|
0,029411765
|
0,0294
|
|
|
12
|
19
|
0,058823529
|
0,0882
|
|
|
9
|
20
|
0,044117647
|
0,1324
|
|
|
18
|
21
|
0,088235294
|
0,2206
|
|
|
21
|
22
|
0,102941176
|
0,3235
|
|
|
24
|
23
|
0,117647059
|
0,4412
|
|
|
27
|
24
|
0,132352941
|
0,5735
|
|
|
36
|
25
|
0,176470588
|
0,7500
|
|
|
42
|
26
|
0,205882353
|
0,9559
|
|
n=
|
9
|
|
|
|
|
|
195
|
|
0,044117647
|
|
Для наглядности построим гистограмму
Рис.1. Гистограмма вариационного
ряда
б) Возраст задержанных и кол-во
совершаемых ими преступлений за 2012 год
Таблица 3
|
возраст
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
|
Количество задержанных
|
3
|
6
|
9
|
12
|
18
|
21
|
24
|
36
|
24
|
Находим: 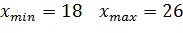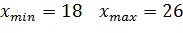. Cоставим вариационный
ряд:
Таблица 4
|
|
ni (2011)
|
Xi(2011)
|
ni/n
|
Накопленные частности
|
|
|
3
|
18
|
0,014705882
|
0,0147
|
|
|
6
|
19
|
0,029411765
|
0,0441
|
|
|
9
|
20
|
0,044117647
|
0,0882
|
|
|
12
|
21
|
0,058823529
|
0,1471
|
|
|
18
|
22
|
0,088235294
|
0,2353
|
|
|
21
|
23
|
0,102941176
|
0,3382
|
|
|
24
|
24
|
0,117647059
|
0,4559
|
|
|
36
|
25
|
0,176470588
|
0,6324
|
|
|
24
|
26
|
0,117647059
|
0,7500
|
|
n=
|
9
|
|
|
|
|
|
153
|
|
0,044117647
|
|
Составим гистрограмму:
Рис.2. Гистограмма вариационного
ряда
Полигон распределения - ломаная
кривая, которая показывает распределение полученных данных.
Полигоны представлены на рисунках:
Рис.3. Полигон вариационного ряда
Рис.4. Полигон вариационного ряда
Задание № 2. Оценка среднего
значения, дисперсии, ассиметрии и эксцесса
Постановка задачи: по выборкам
вычислить числовые характеристики µ, σ,
γ1 и γ2 вариационного ряда.
Порядок выполнения задания: найдем
числовые характеристики. Вычисление сумм для выборочного среднего, выборочной
дисперсии, выборочных коэффициентов асимметрии и эксцесса по формулам и по
вариационному ряду.
а) Данные за 2011 год
Таблица 5
|
xi
|
ni
|
|
|
|
|
|
|
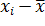
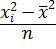
18
|
6
|
-4,000
|
-160,000
|
-17,778
|
-535,111
|
-14364,444
|
|
19
|
12
|
-3,000
|
-123,000
|
-13,667
|
-25266,333
|
14473,444
|
|
20
|
9
|
-2,000
|
-84,000
|
-9,333
|
882,222
|
17777,637
|
|
21
|
18
|
-1,000
|
-43,000
|
-4,778
|
1028,859
|
21608,867
|
|
22
|
21
|
0,000
|
0,000
|
0,000
|
1182,979
|
26028,319
|
|
23
|
24
|
1,000
|
45,000
|
5,000
|
1351,764
|
31093,327
|
|
24
|
27
|
2,000
|
92,000
|
10,222
|
1535,882
|
36864,000
|
|
25
|
36
|
3,000
|
141,000
|
15,667
|
1736,111
|
43391,715
|
|
26
|
42
|
4,000
|
192,000
|
21,333
|
1941,826
|
50775,111
|
|
198
|
195
|
0,000
|
60,000
|
6,667
|
11088,000
|
253692,222
|
Вычисляем:
Выборочное среднее
Дисперсию
Вычисление несмещенных оценок
параметров
Выборочный коэффициент асимметрии
Выборочный коэффициент эксцесса
б) Данные за 2012 год
Таблица 6
|
xini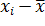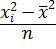
|
|
|
|
|
|
|
|
18
|
3
|
-4,000
|
-160,000
|
-17,778
|
-14364,444
|
|
19
|
6
|
-3,000
|
-123,000
|
-13,667
|
-25266,333
|
14473,444
|
|
20
|
9
|
-2,000
|
-84,000
|
-9,333
|
882,222
|
17777,637
|
|
21
|
12
|
-1,000
|
-43,000
|
-4,778
|
1028,859
|
21608,867
|
|
22
|
18
|
0,000
|
0,000
|
0,000
|
1182,979
|
26028,319
|
|
23
|
21
|
1,000
|
45,000
|
5,000
|
1351,764
|
31093,327
|
|
24
|
24
|
2,000
|
92,000
|
10,222
|
1535,882
|
36864,000
|
|
25
|
36
|
3,000
|
141,000
|
15,667
|
1736,111
|
43391,715
|
|
26
|
24
|
4,000
|
192,000
|
21,333
|
1941,826
|
50775,111
|
|
198
|
153
|
0,000
|
60,000
|
6,667
|
11088,000
|
253692,222
|
Вычисляем:
Выборочное среднее
Дисперсию
Вычисление несмещенных оценок
параметров
Выборочный коэффициент асимметрии
Выборочный коэффициент
эксцесса
Задание № 3. Подгонка
кривых функций плотности и функций распределения нормального закона
Задача: Вычислить
значения функции Ф(х), Fn(x) и построить их графики. По выборкам Найти ∆=max|
Ф(х) - Fn(x) |.
Порядок выполнения
задания.
Вычисляются значения
функции Ф(х) (по функции распределения нормального распределения) и Fn(x).
Вычерчивается график эмпирической функции распределения Fn(X). Для сравнения
функций распределения график функции Ф(х) наносится на чертеж эмпирической
функции распределения Fn(х).
Вычисляется величина
наибольшего уклонения между «теоретической» и эмпирической функциями
распределения по формуле: ∆=max | Ф(x) - Fn(x) |.
а) данные за 2011год
юридическая статистика
гистограмма корреляционный
Таблица 7
|
|
|
|
|
|
|
18
|
-3,77123617
|
0,030769231
|
0,0000812204
|
0,03068801
|
|
19
|
-2,82842712
|
0,092307692
|
0,0023388675
|
0,089968825
|
|
20
|
-1,88561808
|
0,138461538
|
0,0296732194
|
0,108788319
|
|
21
|
-0,94280904
|
0,230769231
|
0,1728892931
|
0,057879938
|
|
22
|
0
|
0,338461538
|
0,5000000000
|
0,161538462
|
|
23
|
0,942809042
|
0,461538462
|
0,8271107069
|
0,365572245
|
|
24
|
1,885618083
|
0,6
|
0,9703267806
|
0,370326781
|
|
25
|
2,828427125
|
0,784615385
|
0,9976611325
|
0,213045748
|
|
26
|
3,771236166
|
1
|
0,9999187796
|
8,12204E-05
|
|
|
|
|
|
|
|
|
|
|
0,370326781
|
.
Рис.5 График эмпирической функции
распределения и оценки функции выборки за 2011 год
б) данные за 2012 год
Таблица 8
|
|
|
|
|
|
|
18
|
-1,46059349
|
0,015384615
|
0,072063517
|
0,056678902
|
|
19
|
-1,09544512
|
0,046153846
|
0,136660839
|
0,090506993
|
|
20
|
-0,73029674
|
0,092307692
|
0,232604409
|
0,140296717
|
|
21
|
-0,36514837
|
0,153846154
|
0,357500327
|
0,203654173
|
|
22
|
0
|
0,246153846
|
0,5
|
0,253846154
|
|
23
|
0,365148372
|
0,353846154
|
0,642499673
|
0,288653519
|
|
24
|
0,730296743
|
0,476923077
|
0,767395591
|
0,290472514
|
|
25
|
1,095445115
|
0,661538462
|
0,863339161
|
0,201800699
|
|
26
|
1,460593487
|
0,784615385
|
0,927936483
|
0,143321098
|
|
|
|
|
|
|
|
|
max(Ф(x)-Fn(x))
|
0,290472514
|
Рис.6 График эмпирической функции
распределения и оценки функции распределения выборки за 2012 год
Задание № 4. Проверка гипотезы о
распределение генеральной совокупности по критерию хи квадрат
Постановка задачи: a) По выборке при
уровне значимости α проверить гипотезу о распределении Пуассона соответствующей
генеральной совокупности. б) По выборке при уровне значимости α = 0,05 проверить
гипотезу о нормальном распределении соответствующей генеральной совокупности.
Порядок выполнения задания для
выборки за 2011 год.
a) При решении задания №
3 был получен вариационный ряд (см. табл. 1) и значения (из задания № 2).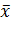 
Вычислим теоретические
частоты, учитывая что n=195, h=1, Dв=5.3571 по формуле:
Составим расчетную
таблицу (значения функции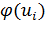 
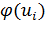помещены в приложении
1).
Таблица 9
|
|
|
|
|
|
|
|
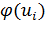
1
|
18
|
-0,313024653
|
0,3814
|
6
|
0,640749978
|
|
2
|
19
|
-0,126358576
|
0,1942
|
12
|
0,32625497
|
|
3
|
20
|
0,060307502
|
0,3982
|
9
|
0,668973889
|
|
4
|
21
|
0,24697358
|
0,3876
|
18
|
0,651165945
|
|
5
|
22
|
0,433639657
|
0,3637
|
21
|
0,611014072
|
|
6
|
23
|
0,620305735
|
0,3292
|
24
|
0,553054255
|
|
7
|
24
|
0,806971812
|
0,2897
|
27
|
0,486694464
|
|
8
|
25
|
0,99363789
|
0,2444
|
36
|
0,410590704
|
|
9
|
26
|
1,180303967
|
0,1989
|
42
|
0,334150945
|
|
|
|
|
|
195
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравним эмпирические и теоретические
частоты.
Составим расчетную таблицу из
которой найдем наблюдаемое значение критерия
Таблица 10
|
|
|
|
|
|
|
|
1
|
6
|
13,88291619
|
-7,882916188
|
62,14036763
|
4,476031317
|
|
2
|
12
|
7,068857692
|
4,931142308
|
24,31616446
|
3,439900126
|
|
3
|
9
|
14,49443426
|
-5,494434258
|
30,18880782
|
2,082786212
|
|
4
|
18
|
14,10859548
|
3,891404524
|
15,14302917
|
1,073319396
|
|
5
|
21
|
13,23863822
|
7,761361779
|
60,23873666
|
4,55022153
|
|
6
|
24
|
11,98284218
|
12,01715782
|
144,412082
|
12,05157172
|
|
7
|
27
|
10,54504672
|
16,45495328
|
270,7654874
|
25,6770306
|
|
8
|
36
|
8,896131925
|
27,10386807
|
734,6196646
|
82,57742475
|
|
9
|
42
|
7,239937152
|
34,76006285
|
1208,261969
|
166,888461
|
|
|
195
|
|
|
|
|
Из таблицы находим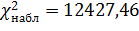 
.
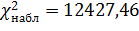
б) По таблице
критических точек распределения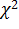 
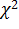(см. приложение 5), по
уровню значимости α = 0,05 и числу степеней свободы k=s-3=9-3=6
находим критическую точку правосторонней критической области:
Вывод: так как 
- гипотезу о нормальном
распределении генеральной совокупности отвергаем. Эмпирические и теоретические
частоты различаются значимо
Порядок выполнения
задания для выборки за 2012 год. a) При решении задания № 3 был получен
вариационный ряд (см. табл. 1) и значения (из задания № 2).
Вычислим теоретические
частоты, учитывая что n=153, h=1, Dв=4,4344 по формуле:
Составим расчетную
таблицу (значения функции 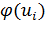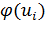помещены в приложении
1).
Таблица 11
|
|
|
|
|
|
|
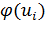
1
|
18
|
0,31394191
|
0,3814
|
3
|
0,774076001
|
|
2
|
19
|
0,539448587
|
0,3467
|
6
|
0,703650104
|
|
3
|
20
|
0,764955783
|
0,2989
|
9
|
0,606636908
|
|
4
|
21
|
0,990462979
|
0,2444
|
12
|
0,496025629
|
|
5
|
22
|
1,215970175
|
0,1919
|
18
|
0,389473478
|
|
6
|
23
|
1,441477371
|
0,1415
|
21
|
0,287183414
|
|
7
|
24
|
1,666984567
|
0,1006
|
24
|
0,204174215
|
|
8
|
25
|
1,892491763
|
0,0669
|
36
|
0,135777883
|
|
9
|
26
|
2,11799896
|
0,0422
|
24
|
0,085647633
|
|
å
|
|
|
|
153
|
|
Сравним эмпирические и теоретические
частоты. Составим расчетную таблицу из которой найдем наблюдаемое значение
критерия
Таблица 12
|
|
|
|
|
|
|
|
1
|
3
|
0,774076001
|
2,225923999
|
4,954737648
|
6,400841311
|
|
2
|
6
|
0,703650104
|
5,296349896
|
28,05132222
|
39,86544173
|
|
3
|
9
|
0,606636908
|
8,393363092
|
70,44854399
|
116,12967
|
|
4
|
12
|
0,496025629
|
11,50397437
|
132,3414263
|
266,8036059
|
|
5
|
18
|
0,389473478
|
17,61052652
|
310,1306444
|
796,2818049
|
|
6
|
21
|
0,287183414
|
20,71281659
|
429,0207709
|
1493,891185
|
|
7
|
24
|
0,204174215
|
23,79582578
|
566,2413248
|
2773,324358
|
|
8
|
36
|
0,135777883
|
35,86422212
|
1286,242428
|
9473,13658
|
|
9
|
24
|
0,085647633
|
23,91435237
|
571,8962491
|
6677,31528
|
|
å
|
153
|
|
|
|
|
Из таблицы находим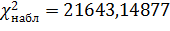 
.
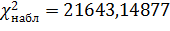
б) По таблице
критических точек распределения 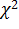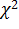(см. приложение 5), по
уровню значимости α = 0,05 и числу степеней свободы k=s-3=9-3=6
находим критическую точку правосторонней критической области:
Вывод:
Так как - гипотезу о нормальном
распределении генеральной совокупности отвергаем. Эмпирические и теоретические
частоты различаются значимо
Задание № 5.
Интервальная оценка среднего значения нормального распределения
Постановка задачи. Найти
доверительные интервалы для среднего µ генеральных совокупностей при
доверительной вероятности γ.
Порядок выполнения
задания. а) Столбцы выборки 2011 имеют объем n = 9, k=n-1=8. Так как V=16, γ=0,95
α= 1−γ=0,05. Из таблицы распределения Стьюдента
найдем ty:ty=2,31.
По выборке получаем
следующие доверительные интервалы:
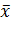
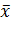=22; 
=1,125; S=1,061. 
=0,35.
-0,35 ≤ µ ≤
22+0,35 или 21,65 ≤ µ ≤ 22,35
б) Вторая выборка за
2012 год имеет объем n=9, k=n-1=8. Так как V=16, γ=0,95 α=1−γ=0,05.
Из таблицы распределения Стьюдента найдем ty: ty=2,31.
По второй выборке
получаем следующие доверительные интервалы:
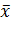
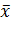=22; =7,5; S=2,74.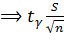 
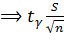=0,91.
-0,91 ≤ µ ≤
22+0,91 или 21,09 ≤ µ ≤ 22,91.
Задание № 6. Найти
выборочное уравнение прямой линии регрессии Y на X по данным приведенным в
корреляционных таблицах
Постановка задачи: по
выборке составить корреляционную таблицу для двумерной выборки XY. Вычислить
условные средние арифметические и построить графики эмпирической регрессии.
Найти линейные функции регрессии и построить их графики.
Порядок выполнения
заданий: найдем минимальное и максимальные значения случайных величин X, Y: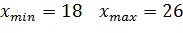
а) Данные за 2011 год
Таблица 13
|
Y1
|
X1
|
ny
|
|
3
|
6
|
9
|
12
|
15
|
18
|
21
|
24
|
27
|
|
|
18
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
|
19
|
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
|
20
|
-
|
-
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
|
21
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
-
|
-
|
1
|
|
22
|
7
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
7
|
|
23
|
-
|
-
|
-
|
2
|
-
|
-
|
-
|
-
|
-
|
2
|
|
24
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
1
|
|
25
|
-
|
-
|
-
|
-
|
-
|
2
|
-
|
-
|
-
|
2
|
|
26
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
-
|
-
|
2
|
|
nx
|
9
|
2
|
1
|
2
|
0
|
3
|
2
|
0
|
1
|
n=20
|
Выборочное уравнение регрессии имеет
вид:
Где 
- условная средняя; ,
- выборочные средние
признаков X на Y, 
и 
- выборочные средние
квадратические отклонения, 
- выборочный
коэффициент корреляции, причем
Составим корреляционную
таблицу в условных вариантах, выбрав в качестве ложных нулей C1=15 и С2=22,
варианты, стоящие в середине соответствующего вариационного ряда.
Таблица 14
|
v1
|
u1
|
nv
|
|
-4
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
4
|
|
|
-4
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
|
-3
|
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
|
-2
|
-
|
-
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
|
-1
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
-
|
-
|
1
|
|
0
|
7
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
7
|
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
1
|
|
3
|
-
|
-
|
-
|
-
|
-
|
2
|
-
|
-
|
-
|
2
|
|
4
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
-
|
-
|
2
|
|
nu
|
9
|
2
|
1
|
2
|
0
|
3
|
2
|
0
|
1
|
n1=20
|
Найдем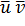 
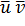
Найдем вспомогательные
величины 
Найдем 
Найдем 
для этого составим
таблицу:
Таблица 15
Найдем искомый
коэффициент корреляции
Найдем шаги h1 и h2
(разности между двумя соседними вариантами)=6-3=3; h2=19-18=1
Найдем 
учитывая, что C1=15 и
С2=22
Найдем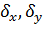 
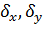
Подставим данные
величины в уравнение регрессии получим:
Или окончательно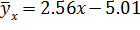 
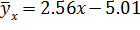
б) Данные за 2012 год
Таблица 16
|
Y2
|
X2
|
ny
|
|
3
|
6
|
9
|
12
|
15
|
18
|
21
|
24
|
27
|
|
|
18
|
-
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
|
19
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
|
20
|
-
|
-
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
|
21
|
-
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
|
22
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
-
|
-
|
1
|
|
23
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
-
|
1
|
|
24
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
1
|
|
25
|
-
|
-
|
-
|
-
|
-
|
2
|
-
|
-
|
-
|
2
|
|
26
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
1
|
|
nx
|
2
|
4
|
1
|
0
|
0
|
3
|
1
|
2
|
0
|
n2=13
|
Составим корреляционную таблицу в
условных вариантах, выбрав в качестве ложных нулей, варианты, стоящие в
середине соответствующего вариационного ряда.
Таблица 17
|
v2
|
u2
|
n2v
|
|
-4
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
4
|
|
|
-4
|
-
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
|
-3
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
|
-2
|
-
|
-
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
|
-1
|
-
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
|
0
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
-
|
-
|
1
|
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
-
|
1
|
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
1
|
|
3
|
-
|
-
|
-
|
-
|
-
|
2
|
-
|
-
|
-
|
2
|
|
4
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
1
|
|
n2u
|
2
|
4
|
1
|
0
|
0
|
3
|
1
|
2
|
0
|
n2=13
|
Найдем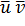
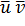
Найдем вспомогательные
величины
Найдем 
Найдем для этого составим
таблицу:
Таблица 18
|
v2
|
u2
|
|
U=nuvu
|
v*U
|
|
-4
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
4
|
|
|
|
-4
|
-
|
-6
|
-
|
-
|
-
|
-
|
-
|
-
|
-6
|
24
|
|
-
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
|
-
|
-8
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
|
-3
|
-8
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-8
|
24
|
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
|
-6
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
|
-2
|
-
|
-
|
-2
|
-
|
-
|
-
|
-
|
-
|
-
|
-2
|
4
|
|
-
|
-
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
|
-
|
-
|
-2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
|
-1
|
-
|
-6
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-6
|
6
|
|
-
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
|
-
|
-2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
|
0
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
-
|
-
|
1
|
0
|
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
-
|
-
|
-
|
|
|
-
|
-
|
-
|
-
|
-
|
0
|
-
|
-
|
-
|
-
|
|
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
-
|
-
|
2
|
2
|
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
-
|
-
|
|
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
-
|
-
|
|
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
3
|
-
|
3
|
6
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
-
|
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
-
|
-
|
|
|
3
|
-
|
-
|
-
|
-
|
-
|
2
|
-
|
-
|
-
|
2
|
6
|
|
-
|
-
|
-
|
-
|
-
|
2
|
-
|
-
|
-
|
-
|
|
|
-
|
-
|
-
|
-
|
-
|
6
|
-
|
-
|
-
|
-
|
|
|
4
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
3
|
-
|
3
|
12
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
1
|
-
|
-
|
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
4
|
-
|
-
|
|
|
V=nuvv
|
-6
|
-10
|
-2
|
0
|
0
|
6
|
1
|
6
|
0
|
|
84
|
|
u*v
|
24
|
30
|
4
|
0
|
0
|
6
|
2
|
18
|
0
|
84
|
|
Найдем искомый коэффициент
корреляции
Найдем шаги h1 и h2 (разности между
двумя соседними вариантами)=6-3=3; h2=19-18=1
Найдем учитывая, что C1=15 и
С2=22
Найдем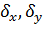
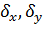
Подставим данные
величины в уравнение регрессии получим:
Или окончательно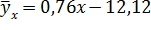 
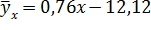
Задание № 8. Метод
наименьших квадратов
а) Возраст задержанных и
кол-во совершаемых ими преступлений за 2011 год
Таблица 19
|
Возраст(x)
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
|
Количество задержанных(y)
|
6
|
12
|
9
|
18
|
21
|
24
|
27
|
36
|
42
|
Находим:
из уравнений
Находим: 
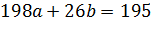
б) Данные за 2012 год.
Возраст задержанных и
кол-во совершаемых ими преступлений за 2012 год
Таблица 20
|
возраст
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
|
Количество задержанных
|
3
|
6
|
9
|
12
|
18
|
21
|
24
|
36
|
24
|
Находим:
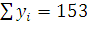
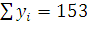
из уравнений
Находим:
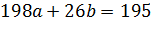
Отсюда:
Список использованной
литературы
1. Соколов Г.А. Справочное пособие по теории вероятностей и
математической статистике (законы распределения): учеб. пособие для студ. вузов
/ Г.А. Соколов, Н. А. Чистяков. - Москва: Высш. школа, 2007. - 248 с.
. Соколов Г.А. Математическая статистика: учеб. для студ.
вузов / Г. А. Соколов, И. М. Гладких. - Москва: Экзамен, 2004. - 431 с.
. Лунеев В.В. Юридическая статистика: Учебник. - 2-е изд.,
псрераб. и доп., с изм. - М.: Юрист, 2007. - 394 с.
. Шмайлова Р.А. Практикум по теории статистики - М.:
“Финансы и статистика” 2000
. Гмурман В.Е. Руководство к решению задач по теории
вероятностей и математической статистике: Учеб. пособие для студентов вузов.
Изд. 5-е, стер. - М.: Высш. шк., 2000-400с.: ил.