Исследование удержания плазмы в модернизированной установке ГДЛ

Исследование удержания плазмы в модернизированной установке ГДЛ

Введение

В данной работе представлены результаты исследования удержания плазмы в установке Газодинамическая ловушка (ГДЛ) [1,2] в Институте ядерной физики имени Г.И. Будкера СО РАН. Программа экспериментов на установке ГДЛ ориентирована с одной стороны на получение фундаментальных знаний по физике удержания плазмы с субтермоядерными параметрами в магнитных ловушках открытого типа, а с другой стороны на экспериментальное обоснование проекта мощного источника 14 МэВ нейтронов для материаловедческих исследований, управления подкритичными ядерными реакторами и других приложений [3,4].

В настоящее время завершена модернизация установки ГДЛ, направленная на увеличение температуры электронов до 200-300 эВ. Для этого была создана новая система атомарной инжекции из 8-ми инжекторов с энергией атомов 23-25 кэВ, суммарной мощностью до 5 МВт и длительностью импульса до 5 мс. Эти инжекторы обладают фокусирующей ионно-оптической системой, что позволяет существенно увеличить плотность тока в пучках. Кроме того, в рамках проводимой модернизации была увеличена емкость конденсаторных накопителей энергии в системе питания катушек магнитного поля установки, что позволило увеличить магнитное поле в центральном сечении ГДЛ с 0.3 T до 0.35 Т и менять пробочное отношение в широких пределах. Благодаря проведенным мероприятиям по модернизации установки, в ГДЛ реализован квазистационарный режим удержания двухкомпонентной плазмы с высоким относительным давлением плотной анизотропной плазмы b (до 60%) и температурой электронов свыше 200 эВ.

Предлагаемая квалификационная работа посвящена изучению удержания плазмы с высокими параметрами в установке ГДЛ в этом режиме. Работа состоит из Введения, трех содержательных разделов и Заключения. В первом содержательном разделе (глава 2) представлен краткий аналитический обзор по теме работы: описана теория продольного и поперечного удержания основной («мишенной») компоненты плазмы, а также затронуты вопросы накопления и удержания быстрых ионов с сильной анизотропией функции распределения. Следующий раздел (глава 3) содержит описание установки ГДЛ, режимов ее работы, сценария экспериментов, а также диагностик, использованных в данной работе. Основной 3 раздел (глава 4) содержит результаты проведенных исследований. Он посвящен подробному изучению параметров плазмы, истекающей через пробки газодинамической ловушки в расширитель.

Целью исследований было сравнение параметров плазмы в расширителе с предсказаниями теории, основанной на модели бесстолкновительного течения плазмы через пробки. Указанный режим течения наиболее интересен, поскольку именно он должен реализоваться при параметрах плазмы, характерных для нейтронного источника. Полученные данные о величинах потоков вещества и энергии в расширитель, а также о перепаде амбиполярного потенциала, позволяют сделать важные выводы о физике продольного удержания вещества и энергии в газодинамической ловушке. Кроме того, полученные в эксперименте данные можно использовать для анализа поперечного удержания частиц и энергии в ГДЛ.

В Заключении приведены основные выводы данной квалификационной работы и список используемой литературы.

1. Краткий обзор работ по удержанию плазмы в ГДЛ

1.1 Продольное удержание плазмы в ГДЛ

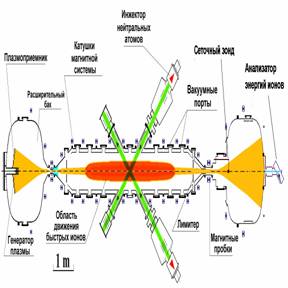
Рисунок 1. Общая схема установки ГДЛ

Газодинамическая ловушка (рисунок 1) представляет собой аксиально-симметричный пробкотрон с большим пробочным отношением (R = B_m/B₀ >> 1) и длиной L, превосходящей среднюю длину пробега ионов относительно рассеяния в конус потерь [1,2].

                                                        (1).

В этих условиях удерживаемая в ловушке плазма является столкновительной, а время продольного удержания пропорционально пробочному отношению R и длине ловушки L. Его можно оценить как время вытекания плазмы из объема S₀×L через узкое отверстие сечения S = S₀/R, где S₀ - сечение плазмы в центре ловушки. (V_Ti - тепловая скорость ионов):

газодинамический ловушка пироэлектрический болометр

                                                      (2).

Плазма в ГДЛ двухкомпонентная. Мишенная плазма представляет собой относительно холодную и плотную столкновительную плазму с температурой несколько электрон-вольт и с изотропной в пространстве скоростей максвелловской функцией распределения частиц. Она создается в начале эксперимента в центральной части ловушки при помощи дугового источника плазмы, расположенного в торцевом баке, и удерживается в газодинамическом режиме. После того, как источник плазмы перестает работать, включаются нагревные инжекторы. Пучки водорода или дейтерия с энергией 23-25 кэВ инжектируются под углом 45° относительно оси симметрии ГДЛ в центр установки и захватываются мишенной плазмой, образуя вторую компоненту - популяцию быстрых ионов. Эти ионы удерживаются адиабатически и постепенно тормозятся на мишенной плазме, нагревая ее до температуры ~ 200 эВ. Длительность работы нагревных инжекторов составляет 5 мс. За это время в ловушке успевает накопиться популяция быстрых ионов со средней энергией около 10 кэВ и плотностью в точках остановки до 5·10¹³ см ^-3.

Как уже было отмечено выше, время жизни плазмы в газодинамической ловушке дается простой газодинамической оценкой. Более точные количественные оценки времени жизни плазмы в ГДЛ требуют аккуратного вычисления потоков частиц и энергии через пробки. Величины этих потоков, выраженные через параметры плазмы внутри ловушки, необходимы при расчетах энергетического и материального баланса плазмы, а также в расчетах устойчивости.

В ГДЛ реализуется бесстолкновительный режим истечения плазмы через пробки. Противоположный случай - случай частых столкновений, когда движение плазмы на участке сужающегося поля вблизи магнитной пробки можно описывать уравнениями магнитной гидродинамики.

Количественная теория продольных потерь для бесстолкновительного течения, когда длина свободного пробега ионов превышает характерные размеры магнитных пробок, изложена в работах [5,6]. Коротко остановимся на обзоре основных результатов этих работ, следуя [7].

Для простоты описания представим, что ГДЛ состоит из длинной центральной части и достаточно коротких пробок с переходным участком. Вытекающая из ловушки плазма расширяется в запробочной области и поглощается условной стенкой, которая в свою очередь считается не эмитирующей, т.е. поглощающей все частицы, попавшие на нее. В центральной части ловушки имеет место максвелловское распределение частиц с заполненным конусом потерь. При выполнении условия бесстолкновительного течения через пробку, вычисление потоков вещества и энергии сводится к интегрированию максвелловской функции распределения по области пространства скоростей, соответствующей вылетающим частицам.

Поддержание в каждой точке ловушки квазинейтральности и выравнивание потоков ионов и электронов из центральной части происходит за счет возникающего в плазме амбиполярного потенциала, который ускоряет ионы и тормозит электроны. Если считать потенциал на стенке равным нулю, то всюду в ловушке он положителен и монотонно спадает от центра к краю. При этом в центральной части, где магнитное поле однородно, потенциал постоянен и испытывает перепад порядка T_e от начала переходного участка до среза пробки. Профиль потенциала в расширителе зависит от режима удержания электронов в этой области.

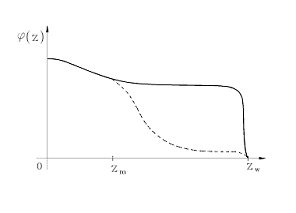
Рисунок 2. Ход амбиполярного потенциала в расширителе в зависимости от степени расширения при бесстолкновительном режиме течения через пробки: сплошная линия - в отсутствии рассеяния электронов; пунктирная линия - при наличии запертых электронов

Если предположить, что столкновения при пролете через расширитель происходят так редко, что за рассматриваемые времена там нет заметного накопления запертых электронов, то в этом случае потенциал за пробкой практически постоянен, вплоть до стенки, и лишь в узком дебаевском слое у стенки испытывает скачек до нуля [6]. Качественный вид потенциала для случая, когда в расширителе нет рассеяния, и запертые электроны не накапливаются, приведен на рисунке 2 (сплошная кривая).

Если стенка эмитирующая, то поток вторичных холодных электронов со стенки может проникнуть в центральную область ловушки, что приведет к быстрому охлаждению плазмы за счет электронной теплопроводности. Однако учет слабых столкновений в почти бесстолкновительной плазме приводит к тому, что в области между выходной пробкой ловушки и стенкой появляются запертые электроны, которые своим пространственным зарядом препятствуют проникновению холодных вторичных электронов в центральную часть, подавляя тем самым теплопроводность. В этом случае ход потенциала в расширителе имеет монотонно спадающий вид, как представлено на рисунке 2 (пунктирная линия). В работе [8] теоретически изучался вопрос об уменьшении электронного потока тепла в открытых ловушках при резком расширении выходящего потока плазмы за пробкой. Анализ уравнений показал, что в случае неограниченной эмитирующей способности стенки, запирающий потенциал связан со степенью расширения плазмы соотношением, из которого следует, что сравнительно небольшого расширения достаточно для существенного уменьшения электронного потока тепла. В работе [9] экспериментально было подтверждено, что в расширителе действительно присутствует популяция запертых электронов, а электронный поток тепла мал.

Функция распределения ионов по продольным энергиям ε_|| в расширителе при наличии амбиполярного потенциала имеет очень сложный вид. Однако можно существенно упростить задачу, предположив, что весь перепад потенциала происходит после пробки, тогда функция распределения ионов по продольным энергиям в расширителе вблизи стенки имеет вид [9]:

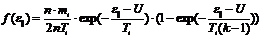              (3),

где U - перепад амбиполярного потенциала между центром и приемником плазмы в расширителе; k = B_m/B_w - степень расширения; n - плотность на расстоянии порядка λ от пробки.

В описываемом случае температура электронов, вылетающих из ловушки, постоянна вдоль силовой линии всюду в расширителе, и для электронов устанавливается больцмановское распределение:

                                           (4),

где - потенциальная энергия электронов, Т_e - электронная температура в энергетических единицах.

Для нахождения распределения потенциала в расширителе удобно ввести эффективную потенциальную энергию продольного движения (так называемый потенциал Юшманова):

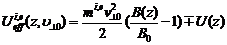                    (5).

Для случая, когда T_e = T_i = T, из решения данной задачи [6,7] получается следующий результат:

полный перепад амбиполярного потенциала между центром и стенкой

                                                       (6),

поток вещества на срезе пробки

                                  (7),

поток энергии, выносимый в пробку

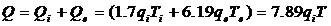                   (8).

В работе [9] экспериментально измеренные потоки вещества и энергии в расширитель при умеренных параметрах плазмы в центральной части ГДЛ очень хорошо совпадали с приведенными теоретическими оценками (6) - (8).

.2 Поперечные потери

В общем случае осесимметричная магнитная ловушка не обладает конфигурацией благоприятной для обеспечения МГД устойчивого удержания плазмы [10]. В описываемых экспериментах для подавления поперечных потерь, связанных с развитием неустойчивых МГД мод в аксиально-симметричном пробкотроне без использования дополнительных стабилизирующих магнитных ячеек, был применен метод вихревого удержания. Этот метод заключается в создании зоны дифференциального вращения вблизи радиальной границы плазменного столба. Метод вихревого удержания был хорошо обоснован ранее экспериментально и теоретически [11,12]. Вихревое удержание реализуется при создании «ступенчатого» вида радиального профиля электрического потенциала в плазме, причем «скачек» потенциала должен располагаться в периферийной по радиусу области плазменного столба. Такой профиль потенциала формировался при помощи специальных электродов: секционированных по радиусу поглотителей плазмы, расположенных за пробками вблизи плоскостей, где величина магнитного поля в 100 раз меньше соответствующей величины в пробках, а также при помощи радиальных лимитеров, установленных внутри ловушки вблизи магнитных пробок. На радиальные лимитеры и наружные радиальные секции поглотителей плазмы, которые проецировались друг на друга по силовым линиям магнитного поля, подавался положительный электрический потенциал величиной 250 - 300 В относительно заземленных внутренних секций поглотителей плазмы. Радиальное распределение электрического потенциала такого вида порождает зону дифференциального вращения в периферийной по радиусу области плазменного столба. При этом оказывается, что сочетание дифференциального вращения плазмы с ее движением в стадии насыщения неустойчивых МГД мод приводит к формированию стационарной вихревой структуры линий потока плазмы.

В рамках работы [11] проведен анализ влияния сдвигового течения на удержание плазмы в пробкотроне. Построены аналитическая и численная модели вихревого удержания, которое реализуется при формировании перепада электрического потенциала в плазме вблизи радиуса лимитера. Модель учитывает наиболее существенные эффекты, которые определяют конвективный поперечный перенос в плазме в условиях дифференциального вращения: электрический контакт с лимитерами и торцевыми поглотителями плазмы, градиент электронной температуры, эффекты конечного ларморовского радиуса, и поэтому способна описать нелинейное развитие различных крупномасштабных неустойчивостей. В частности, описываются неустойчивости Кельвина-Гельмгольца, желобковая и температурно-градиентная.

Вихревое удержание плазмы, описываемое моделью, заключается в том, что горячая центральная часть разряда может удерживаться в застойной зоне вихревого течения. Если это течение генерировать и поддерживать внешними источниками, то можно попасть в режим с малыми конвективными потерями. Хотя плазма остаётся линейно неустойчивой, конвекция насыщается на низком уровне, и, главное, центральная конвективная ячейка не доходит до лимитера. Нелинейное насыщение конвекции, как и генерация вихревого течения, связаны с торцевой токовой диссипацией. Эта диссипация особенно эффективна для крупномасштабных мод типа m=1, преимущественная селекция которых происходит в плазме с горячими ионами за счёт эффектов конечного ларморовского радиуса. Основной вывод из работы [11] заключается в том, что для газодинамической ловушки метод вихревого удержания позволяет достичь мощности поперечных потерь энергии в 10 - 15% от мощности продольных. При этом дополнительные энергетические затраты на поддержание режима вихревого удержания не превышают нескольких процентов от полной мощности нагрева плазмы. Эти выводы справедливы и для проектируемого источника нейтронов на основе ГДЛ.

.3 Удержание быстрых ионов и микронеустойчивости

Для быстрых ионов, образовавшихся в результате наклонной инжекции мощных атомарных пучков, характерен бесстолкновительный адиабатический режим удержания, когда, в силу законов сохранения энергии и магнитного момента быстрых ионов, они отражаются от области сильного магнитного поля. Таким образом, для популяции быстрых ионов пробкотрон ГДЛ является обычной зеркальной ловушкой.

Плотность и температура мишенной плазмы в центральной части ГДЛ, а также энергия инжектируемых атомов находятся в таком соотношении, что характерное время торможения быстрых ионов оказывается много меньшим, чем характерное время рассеяния на угол порядка единицы. Атомарная инжекция ведется под углом 45^o к оси установки. При этом быстрые ионы, совершая продольные баунс-колебания между точками отражения («точками остановки»), сохраняют малый угловой разброс, характерный для инжектированных атомарных пучков. В этих условиях вблизи областей отражения частиц продольный профиль плотности быстрых ионов оказывается пикированным.

Очень важно также, что наклонная инжекция позволяет минимизировать отрицательный вклад быстрых ионов в МГД устойчивость двухкомпонентной плазмы, так как их плотность в центре пробкотрона - в области наиболее неблагоприятной кривизны, минимальна. С другой стороны, наклонная инжекция эффективно уменьшает анизотропию функции распределения быстрых ионов в пространстве скоростей вблизи областей отражения, что, в свою очередь, благоприятно влияет на стабильность плазмы относительно развития микронеустойчивостей. Стоить отметить, что по данным экспериментов на установке ГДЛ [17] на сегодняшний день не обнаружено развитие микронеустойчивостей, приводящих к быстрому рассеянию быстрых частиц в конус потерь и ухудшению их продольного удержания. Релаксация быстрых ионов определяется их взаимодействием с частицами мишенной плазмы, в основном с электронами, и хорошо описывается теорией парных кулоновских столкновений.

Тем не менее, вопрос о развитии микронеустойчивостей в сильно анизотропной плазме остается весьма важным для физики открытых ловушек и для различных термоядерных приложений ГДЛ. Поэтому исследования микронеустойчивостей проводились в специальных экспериментах по формированию и исследованию синтезированного сгустка сильно анизотропных ионов с термоядерными параметрами, создаваемого в дополнительном пробкотроне малого размера, присоединенном к одной из магнитных пробок установки ГДЛ [13] (SHIP-эксперимент). Для создания такого компактного пробкотрона (КП) было произведено изменение конструкции пробочного узла установки ГДЛ, а именно дополнительная вакуумная камера и катушка установлены вблизи имеющегося пробочного узла (рисунок 3). Поле в центральном сечении КП составляло B₀ = 24 кГс, пробочное отношение R = 2 (пробочные отношения для левой и правой пробок отличаются на 5%), расстояние между центрами пробочных катушек ~ 43 см, внутренний диаметр вакуумной камеры ~ 70 см. Для создания компоненты быстрых ионов использовались два сфокусированных пучка атомарного водорода с энергией 21 - 23 кэВ, суммарным эквивалентным током до 45 эквив. А и длительностью 4 мс. Пучки имели небольшой угловой разброс (менее 1°) и инжектировались перпендикулярно оси установки.

Рисунок 3. 1-торцевые баки, 2-центральная секция , 3-компактный пробкотрон, 4 -плазмоприемник, 5-источник плазмы, 6 -катушки основной магнитной системы, 7 - нагревные инжекторы атомов, 8 -инжекторы для SHIP -эксперимента

В работе [14] приведены результаты экспериментального изучения микронеустойчивости, развивающейся в КП ГДЛ. Для определения типа развивающейся в КП ГДЛ микронеустойчивости была использована система из высокочастотных электрических и магнитных зондов. Неустойчивость была идентифицирована как Альфвеновская ионно-циклотронная (AIC), о чем свидетельствовали малые азимутальные волновые числа, частота колебаний ниже ионно-циклотронной частоты и вращение вектора поляризации магнитного поля волны в направлении ларморовского движения ионов.

Исследуемые колебания носили ярко выраженный пороговый характер. На рисунке 4 изображены зависимости диамагнетизма быстрых ионов, амплитуды высокочастотных колебаний на магнитном зонде, а также анизотропии быстрых ионов в компактном пробкотроне от времени. Как видно из рисунка 4, развитая микронеустойчивость не приводит к значительному рассеянию быстрых частиц и уменьшению анизотропии. Анизотропия быстрых ионов увеличилась примерно в 1.5 раза к концу инжекции.

Рисунок 4. Временная зависимость (в КП ГДЛ): a) диамагнетизма быстрых ионов; b) амплитуды высокочастотных колебаний на магнитном зонде; c) анизотропии быстрых ионов

Также в анизотропной плазме может развиваться дрейфово-конусная неустойчивость (DCLC). В экспериментах с КП наличие этой микронеустойчивости не было обнаружено. Это возможно есть следствие наличия теплой плазмы («подпитка» плазмы в центральной части за счет поддува газа), которая может стабилизировать эту неустойчивость. Более подробно об эксперименте в КП ГДЛ и исследовании микронеустойчивостей анизотропной плазмы написано в [15]. Качественная и количественная теория развития Альфвеновской ионно-циклотронной неустойчивости в ГДЛ описана в [16].

2.     
Описание эксперимента и диагностик

2.1 Описание эксперимента

Таблица 1. Основные параметры эксперимента на установке ГДЛ

Типичная временная последовательность работы систем установки ГДЛ была следующей. Сначала создавалось магнитное поле. Затем производилось заполнение ловушки предварительной плазмой с температурой около 10 эВ при помощи плазменного источника, расположенного за пробкой с одной из сторон установки. Выходная апертура источника находится в плоскости, где величина магнитного поля в 100 раз меньше величины магнитного поля в пробках. Время работы генератора плазмы составляло 4 мс. После выключения генератора плазмы начиналась инжекция атомарных пучков из 8 модулей атомарных инжекторов, которая продолжалась в течение 5 мс. Одновременно с началом инжекции пучков включалась система инжекции газообразного водорода или дейтерия, которая производилась в периферийную область плазмы равномерно по азимуту при помощи двух импульсных клапанов, расположенных в областях, близких к магнитным пробкам, где плазма имеет относительно малый диаметр и относительно прозрачна для франк-кондоновских нейтралов, образующихся при диссоциации молекул газа. Длительность работы системы напуска газа была обычно несколько больше 5 мс.

Описанный сценарий эксперимента позволял получать в установке ГДЛ двухкомпонентную плазму с высоким относительным давлением плотной анизотропной плазмы b до 60% и температурой электронов свыше 200 эВ. Время эксперимента, определяемое длительностью атомарной инжекции в 5 мс, было сравнимо или превышало основные характерные времена жизни плазмы: энергетическое время жизни быстрых ионов и время продольного истечения мишенной плазмы. В таких условиях можно утверждать, что в проводимом эксперименте был реализован квазистационарный режим удержания плазмы. Основные параметры установки ГДЛ и двухкомпонентной плазмы приведены в таблице 1.

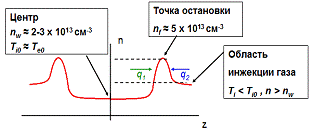
Рисунок 5. Особенности эксперимента

Реализованный квазистационарный режим с высокой плотностью быстрых ионов имеет свои особенности, касаемо продольного удержания. На рисунке 5 представлена качественная зависимость плотности ионов от продольной координаты. Значения температуры и плотности теплой мишенной плазмы, используемые в работе, измерялись в центральном сечении ГДЛ. Плотность быстрых ионов в точках остановки оценивалась из знания их средней энергии и относительного давления:

                                        (9).

Для β ≈ 0.6 и < ε > ≈ 10 кэВ согласно оценке следует, что плотность ионов в точках остановки существенно превышает плотность теплой плазмы в центре и составляет n_f ≈ 5·10¹³ см ^-3. Высокая плотность быстрых ионов достигается за счет обнаруженного в этих режимах формирования узкого радиального профиля быстрых ионов (пинчевания) [17]. В область между точками остановки и пробками инжектируется холодный газ, где он ионизуется и подпитывает плазму в центральном соленоиде. Прямое измерение температуры и плотности мишенной плазмы в этих областях на сегодняшний день не представляется возможным, однако можно сделать следующие оценки. Так как реализуется стационарный режим с высокими параметрами плазмы, то температура ионов T_i в этой области должна быть равна или лишь немного ниже, чем температура ионов в центральном сечении ловушки T_i0. Также из условия постоянства плотности по времени следует равенство потоков из этой области «подпитки» в центр установки и из центра в пробку q₁ = q₂. Поэтому плотность ионов n в этой области должна быть несколько выше, чем плотность теплых ионов в центре n_w. На продольное удержание также оказывает влияние потенциал, вызванный наличием пиков плотности быстрых ионов в точках остановки.

Из-за указанных особенностей, режим продольного удержания может отличаться от режимов, упомянутых в Разделе 2 настоящей работы (например [9]). В этих условиях прямое экспериментальное исследование продольных потерь вещества и энергии представляется весьма важным с точки зрения будущих термоядерных приложений ГДЛ.

2.2 Диагностики

Двухсеточный зонд

Для измерения продольного потока ионов в данной работе использовался двухсеточный зонд (рисунок 6). Диаметр входного отверстия составляет 2 мм, расстояния между первой и второй сеткой (1 и 2 на рисунке 6) d = 0.5 мм, между второй сеткой и коллектором (3) D = 2 мм. Первая сетка находится под потенциалом земли. Между первой и второй сетками создается вытягивающее напряжение U1~ 300…500 В. Для подавления вторичной электронной эмиссии с коллектора на него подавался потенциал U2 на +50 В выше относительно потенциала U1 второй сетки. С резистора сопротивлением R=130 Ом снимается напряжение. Таким образом, можно легко вычислить ток текущий через него, а следовательно, и поток ионов падающих на коллектор. Сеточный зонд размещался на подвижном устройстве в расширителе (рисунок 8).

Пироэлектрический болометр

Рисунок 6. Двухсеточный зонд: 1-плазменная сетка, 2-вытягивающая сетка, 3-коллектор

Для измерения продольного потока энергии плазмы в работе использовался пироэлектрический болометр [18]. Схема болометра приведена на рисунке 7. Датчик пироэлектрического болометра представляет собой диск (диаметр 10 мм, толщина 0,5 мм), из ниобата лития LiNbO₃ с вектором спонтанной поляризации P_s, ориентированным по нормали к торцевым поверхностям, на которые были нанесены электроды из серебра. Для ниобата лития в достаточно широком диапазоне температур коэффициент γ =d P_s/dT. Пироэлектрические болометры использовались на установке ГДЛ ранее для измерения перезарядных, радиационных, а также продольных потерь через магнитные пробки, эти эксперименты и принцип работы пироэлектрического болометра подробно описаны в препринте [19].

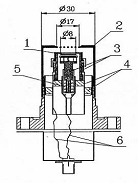
Рисунок 7. Пироэлектрический болометр: 1 - пироэлектрический кристалл, 2 - корпус, 3 - электроды, 4 - изолятор, 5 - пружина, 6 - проводники

Таблица 2. Калибровка болометра

Болометр размещался на подвижном устройстве в расширителе ГДЛ рядом с сеточным зондом (рисунок 8), что позволяло производить одновременные измерения плотности потока ионов и потока тепла в расширитель. Для того чтобы надежно измерять болометром абсолютные значения потока энергии, перед началом измерений его необходимо откалибровать, т.е. определить коэффициент, связывающий амплитуду сигнала с падающей на единицу поверхности болометра мощностью. Калибровка производилась с помощью измерителя мощности, кварцевой лампы накаливания мощностью 500 Вт и фокусирующей линзы. Лампа и линза устанавливались так, чтобы свет фокусировался на измерителе мощности. После того, как были получены данные с измерителя мощности, вместо него на стенд устанавливался болометр и модулятор, который использовался для получения переменного потока энергии на болометре. Поверхность пироэлектрического элемента была зачернена сажей, что гарантировало коэффициент поглощения, близкий к единице. Затем снималось напряжение на болометре. Было произведено несколько измерений при разных расстояниях между лампой и болометром. В таблице 2 приведены результаты шести калибровочных измерений с разной падающей мощностью излучения и посчитанные по ним коэффициенты пропорциональности. Усредненный по серии калибровок коэффициент равен k = 4,7 ± 0,2 Вт/В.

Рисунок 8. Фотография пироэлектрического болометра и двухсеточного зонда на подвижном устройстве

Анализатор энергий ионов

Рисунок 9. Торцевой 45º анализатор энергий ионов

Для получения энергетического спектра теплых ионов, вылетающих вдоль оси установки в расширитель, и определения полного перепада потенциала между точкой остановки быстрых ионов и стенкой, использовался 45º торцевой энергоанализатор. Он состоит их коллиматора, 45º-го плоского конденсатора и 6-канального детектора на основе микроканальной пластины. Его фотография представлена на рисунке 9. Координата канала x и энергия влетевшей в анализатор частицы E_i связаны друг с другом следующей формулой: , где d - расстояние между пластинами, U - напряжение на обкладках конденсатора. На верхнюю обкладку конденсатора подавалось напряжение от 0 до 15 кВ, что позволяло регистрировать ионы с энергиями от 0 до 25 кэВ. Меняя напряжение на конденсаторе, можно было построить полный энергетический спектр ионов.

3.     
Результаты измерений и их интерпретация

Проведено несколько серий экспериментов с различными комбинациями масс горячих ионов и ионов теплой плазмы. Наиболее близким к стационарному оказывается режим с инжекцией водородных пучков в водородную плазму. Наибольшее значение диамагнетизма получено в режимах с инжекцией дейтериевых пучков в водородную или дейтериевую плазму. Эти обстоятельства связаны с различным значением энергетического времени жизни горячих ионов, которое определяется, в основном, торможением на электронах и пропорционально массе ионов:

  (10),

где m_i, z - масса и заряд горячих ионов, m_e, e, n, T_e - масса, заряд, плотность и температура электронов, L - кулоновский логарифм. Для режимов с инжекцией водорода в водородную плазму и дейтерия в дейтериевую плазму времена жизни горячих ионов оцениваются согласно формуле (10) для параметров плазмы в этих экспериментах соответственно как ~1.5 мс и ~4 мс. Поэтому в режиме с инжекцией водорода возможно достижение квазистационарного режима через несколько миллисекунд после начала инжекции, как видно из рисунка 10, на котором приведена временная зависимость температуры электронов в центре на оси ГДЛ.

Рисунок 10. Временная зависимость температуры электронов

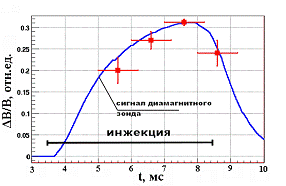
Рисунок 11. Временной ход относительного изменения магнитного поля в центре плазменного столба в области остановки горячих ионов (квадраты). Сигнал диамагнитного зонда, пропорциональный интегральному по сечению плазмы изменению магнитного потока (сплошная линия)

                                              (11),

где B_v - значение вакуумного магнитного поля, DB = B_v - B - изменение магнитного поля за счет диамагнетизма плазмы, B - измеренное значение поля.

Среднему значению DB/B_v = 0.32 соответствует b = 0.54, максимальному значению DB/B_v = 0.37 соответствует b = 0.6. Используя значения b, B_v и средней энергии быстрых ионов <e>, как было уже сказано выше, можно оценить максимальную плотность горячих ионов n_f в области остановки: 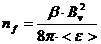. Для режима с b=0.6, < e > » 10 кэВ из оценки следует n_f » 5×10¹³ см ^-3.

Для режима с инжекцией водорода в водородную плазму радиальный профиль локального изменения магнитного поля приведен на рисунке 12.

Рисунок 12. Радиальный профиль локального изменения магнитного поля в области остановки горячих ионов

Как отмечалось выше, радиальный профиль имеет достаточно узкий вид, что является следствием пикировки плотности быстрых ионов на оси.

Дальнейшие результаты и выводы в этой главе приведены для режима с инжекцией водорода в водородную плазму, как наиболее близкого к стационарному режиму.

Чтобы оценить роль поперечных потерь по сравнению с продольными, а также построить скейлинг зависимости электронной температуры от мощности нагрева плазмы была проведена серия измерений ряда параметров в зависимости от мощности атомарных пучков. Система атомарной инжекции включает всего 8 инжекторных модулей. Серии измерений были проведены в режиме с инжекцией пучков водорода в водородную плазму с использованием 2, 4, 6, и 8 атомарных инжекторов. Были проведены измерения плотности плазмы и температуры электронов в центральной плоскости, мощности пучков, захваченной в плазму, а также мощности перезарядных потерь горячих ионов.

Оценка значения температуры электронов в ГДЛ, которое определяется балансом тепловых потоков в плазме, была произведена с учетом следующих предположений:

1.      предполагалось, что реализуется стационарный режим относительно всех процессов, определяющих удержание плазмы в ГДЛ;

2.      стационарный баланс энергии определяется равенством мощности нагрева атомарной инжекцией и мощности продольных потерь тепла при газодинамическом течении плазмы через пробки, поперечные потери отсутствуют;

Как уже было сказано в главе 2, согласно выводам работы [6], которые хорошо согласуются с результатами предыдущих экспериментов [9], плотность потока ионов и электронов на «срезе» пробки в ГДЛ при газодинамическом течение плазмы равна:

,

где m_w - масса ионов теплой компоненты, n_w - плотность теплых ионов в ловушке. Из результатов работ [6,9] также следует, что каждая электрон-ионная пара, покидая газодинамическую ловушку, должна выносить в среднем энергию около 8×T_e, а плотность потока энергии на «срезе» пробки должна быть равна

.

Приравнивая мощность продольных потерь в две пробки к мощности нагрева плазмы, получим:

                    (12),

где S_m=p×a²/R - площадь сечения плазмы на «срезе» пробки, a - радиус плазмы в центральной плоскости, R - пробочное отношение, P_h - мощность нагрева плазмы атомарной инжекцией (равна захваченной мощности атомарных пучков за вычетом перезарядных потерь горячих ионов, предполагается, что другие каналы потерь быстрых ионов несущественны). Подставив в равенство (12) соответствующие выражения и выразив T_e, получим в практических единицах:

Рисунок 13. Зависимость температуры электронов от мощности нагрева плазмы: ромбы - расчет по оценочной формуле (13); квадраты - экспериментально измеренное значение; треугольники - расчет в случае наличия электронной теплопроводности на торец

                                         (13),

где P_h следует выражать в МВт, n_w - в единицах 10¹⁹ м^-3, a - в см, искомое значение T_e - в электрон - вольтах.

На рисунке 13 показаны зависимости температуры электронов, рассчитанной по оценочной формуле (13) и полученной в результате измерения с помощью диагностики на основе томсоновского рассеяния лазерного излучения на электронах [21], от мощности нагрева плазмы, а также для сравнения приведена зависимость температуры электронов в случае наличия спитцеровской электронной теплопроводности на торец. Для расчетов были использованы оценочные значения плотности теплых ионов n_w для участка плазменного столба между пробками и областями остановки горячих ионов, поскольку плотность теплых ионов именно на этих участках определяет продольный поток тепла через пробки. Согласно оценкам, приведенным выше, эта плотность составила величину порядка 2·10¹³ см ^-3. Видно, что при T_e > 150 эВ результаты измерений и расчетов, основанных на самых жестких предположениях относительно удержания плазмы в ГДЛ, близки по абсолютной величине. Отличие при малых значениях T_e, по всей видимости, связано с ростом поперечных потерь в режимах с низкой температурой, что не учитывается в оценке (13). Максимальное значение T_e = 230 эВ было получено в результате измерений в режиме с инжекцией дейтериевых пучков в дейтериевую плазму.

Рисунок 14. Радиальный профиль плотности потока частиц

Для оценки мощности поперечных потерь были проведены измерения радиальных профилей плотности потока частиц и энергии в областях за пробками вблизи торцевых поглотителей плазмы. На рисунке 14 представлены радиальный профиль потока ионов в расширитель - экспериментально измеренные значения с помощью двухсеточного зонда. На рисунке 15 приведен радиальный профиль потока энергии в расширитель, измеренный с помощью пироэлектрического болометра. Полная мощность продольных потерь тепла на стадии окончания атомарной инжекции составляет P_|| = 1.3 ± 0.2 МВт. При этом мощность нагрева за счет атомарной инжекции (захваченная в плазму мощность атомарных пучков за вычетом мощности перезарядных потерь) составила P_h = 1.4 ± 0.1 МВт. Таким образом, согласно результатам измерений, можно сделать оценку значения мощности поперечных потерь тепла P_^ ≈ 0.2 МВт, что не превышает 15% от P_h.

Рисунок 15. Радиальный профиль плотности потока энергии

Рисунок 16. Радиальный профиль энергии, выносимой парой i-e

Важной характеристикой продольного удержания плазмы является энергия, выносимая одной парой электрон-ион. На рисунке 16 представлен радиальный профиль энергии, выносимой одной электрон-ионной парой, полученный из сравнения плотностей продольных потоков энергии и частиц. Видно, что каждая электрон-ионная пара выносит из ловушки в среднем энергию в 5 - 8 T_e, что неплохо согласуется с предсказаниями теории относительно продольных потерь тепла для газодинамического режима течения плазмы через магнитные пробки [6].

Из данных, представленных выше, можно сделать два важных заключения:

.        при вихревом удержании в ГДЛ мощность поперечных потерь энергии мала по сравнению с мощностью продольных, так что оказывается справедливым скейлинг (13), основанный на простом балансе мощности нагрева и продольного потока энергии при газодинамическом течение столкновительной плазмы через магнитные пробки;

.        при увеличении захваченной мощности атомарных пучков до значений более 20 МВт, как этого требует проект источника нейтронов на основе ГДЛ, температура электронов должна быть »1 кэВ, что обеспечивает нужное время жизни горячих ионов и приемлемый уровень эффективности производства нейтронов.

Для определения влияния потенциала горячих ионов в точках остановки были проведены измерения 45º торцевым энергоанализатором в специальном режиме без инжекции газа со стороны измерений. При помощи анализатора производилось измерение энергетического распределения ионов, вылетающих через пробку вдоль оси. Функция распределения ионов представляет собой «половинку максвелла», ускоренного в потенциале между центральной ячейкой и стенкой. При наличии потенциала от быстрых ионов в точках остановки до анализатора доходят лишь ионы, которые смогли преодолеть этот потенциал.

В работе были учтены как погрешности измерений, связанные с измерительной аппаратурой, так и статистические ошибки, связанные с изменением параметров плазмы в одном режиме от выстрела к выстрелу.

Заключение

В заключении приведем основные результаты, полученные в ходе данной работы:

·        Создана диагностика для измерения радиальных профилей плотности потока частиц и энергии вблизи торцевых поглотителей плазмы.

·        Проведены серии экспериментов по удержанию двухкомпонентной плазмы в ГДЛ в различных режимах с высоким значением относительного давления. Подробно изучен режим с инжекцией атомарных пучков водорода в водородную плазму, как наиболее близкий к стационарному.

·        Измерены радиальные профили продольных потоков частиц и энергии через магнитные пробки ГДЛ. Проведено сравнение результатов экспериментов с моделью бесстолкновительного газодинамического истечения плазмы через магнитные пробки. Показано, что продольные потери частиц и энергии хорошо соответствуют этой модели, а роль поперечных потерь несущественна (~15% от мощности нагрева). Продемонстрировано, что справедлив скейлинг:

·        Экспериментально зафиксирован рост амбиполярного потенциала, который связан с накоплением горячих ионов в областях остановки.

·        Полученные результаты в совокупности с рядом предыдущих являются существенным аргументом в пользу реализуемости проекта источника нейтронов на основе ГДЛ с точки зрения ключевых вопросов физики удержания плазмы в магнитных ловушках открытого типа.

Список литературы

[1] В.В. Мирнов, Д.Д. Рютов, Газодинамическая линейная ловушка для удержания плазмы, Письма в ЖТФ, т. 5, 678, (1979)

[2] Д.Д. Рютов, Открытые ловушки, Препринт ИЯФ СО АН СССР 87-105П, Новосибирск, (1987)

[3] P.A. Bagryansky, A.A. Ivanov, E.P. Kruglyakov, et. al., Fusion Engineering and Design 70 (2004) pp.13-33

[4] K. Noack, A. Rogov, A.V. Anikeev, et. al., Annals of Nuclear Energy 35 (2008) pp.1216-1222.

[5] В.В. Мирнов, Д.Д. Рютов, Газодинамическая ловушка. Вопросы Атомной Науки и Техники. Сер. Термоядерный синтез. (1980). вып. 1 (5). С. 57.

[6] В.В. Мирнов, О.А. Ткаченко, Распределение электростатического потенциала в газодинамической ловушке. Новосибирск, 1986. (Препринт ИЯФ СО АН СССР, 86-28.)

[7] В.В. Мирнов, Д.Д. Рютов, Газодинамическая ловушка. Итоги науки и техники. Серия Физика плазмы. 1988. Т.8. С. 77.

[8] И.К. Конкашбаев, И.С. Ландман, Ф.Р. Улинич, О возможности уменьшения электронного потока тепла из открытых ловушек. ЖЭТФ, Т.74, No.3. (1978) С. 956.

[9] А.В. Аникеев, П.А. Багрянский, Г.И. Кузнецов, Н.В. Ступишин, Продольное удержание вещества и энергии в газодинамической ловушке, Физика Плазмы, т. 25, №10 (1999) стр. 842-850

[10] M.N. Rosenbluth, G. Longmire, Ann. Phys., 1957, v. 1, p. 120.

[11] A.D. Beklemishev, Shear Flow Effects in Open Traps, Theory of Fusion Plasmas, AIP Conference Proceedings 1069 (2008) pp.3-14.

[12] Е.И. Солдаткина, П.А. Багрянский, А.Л. Соломахин, Физика плазмы, 2008, т. 34, No. 4, с. 291-296.

[13] A.V. Anikeev, P.A. Bagryansky, A.A. Ivanov, A.A. Lizunov, S.V. Murakhtin, V.V. Prikhodko, A.L. Solomakhin, and K. Noack «Confinement of Strongly Anisotropic Hot-ion Plasma in a Compact Mirror» Journal of Fusion Energy 26, pp.103-107, (2007)

[14] М.С. Коржавина, А.В. Аникеев, П.А. Багрянский «Изучение микронеустойчивостей в анизотропном плазмоиде ионов с термоядерными энергиями» Вестник НГУ, Серия Физика, Том 4, Вып.1, 25-29, (2009)

[15] М.С. Коржавина. Квалификационная работа «Изучение микронеустойчивостей в анизотропном плазмоиде ионов с термоядерными энергиями» (2008)

[16] И.С. Черноштанов, Альфвеновская ионно-циклотронная неустойчивость в плазме с большой анизотропией, Материалы ХLVIII Международной научной студенческой конференции (Новосибирск, 2010).

[17] В.В. Приходько, А.В. Аникеев, П.А. Багрянский, А.А. Лизунов, В.В. Максимов, С.В. Мурахтин, Ю.А. Цидулко, Эффект формирования узкого радиального распределения плотности быстрых ионов в установке ГДЛ, Физика плазмы, т. 31, No.11, с. 969-977.

[18] Л.С. Кременчугский, О.В. Ройцина, Пироэлектрические приемники излучения (обзор). Приборы и техника эксперимента. N.3, (1976), c. 7

[19] П.А. Багрянский, В.Н. Бочаров, П.П. Дейчули, А.А. Иванов, А.Н. Карпушов, В.В. Максимов, А.И. Рогозин, Т.В. Саликова. Диагностический комплекс установки ГДЛ для изучения нагрева плазмы при инжекции мощных атомарных пучков.

[20] P.A. Bagryansky, P.P. Deichuli, A.A. Ivanov, et. al., Review of Scientific Instruments, V. 74, Number 3 (2003), pp. 1592-1595

[21] V.V. Maximov Study of electron temperature profiles in GDT during neutral beam heating by Thomson scattering systems, Transactions of fusion technology, (1999), Vol.35, No.1T p. 362-265