Розрахунок структурної та алгоритмічної надійності комп’ютерного томографа Brilliance iCT

Розрахунок структурної та алгоритмічної надійності комп’ютерного томографа Brilliance iCT

Міністерство освіти і науки, молоді та спорту України

Національний авіаційний університет

Інститут аерокосмічних систем управління

Кафедра біокібернетики та аерокосмічної медицини

Контрольна робота

з навчальної дисципліни

«Конструювання та технології біомедичної апаратури»

Тема

Розрахунок структурної та алгоритмічної надійності комп’ютерного томографа Brilliance iCT

Виконав: ст. групи БМ-513

Колесник В.В.

Перевірила: Іванець О.Б.

Київ 2011

Розрахунок надійності

Завдання 1

виріб, що нормально функціонує, завжди може бути представлено, як певна структура, доцільно складена з ряду взаємопов'язаних елементів. Логіка, структурні схеми розрахунку надійності необов'язково збігаються зі структурною схемою самого виробу. Для розрахунку надійності необхідно знати інтенсивності відмови або безвідмовної роботи елементів, і час роботи.

Рис 26. Структурна схема виробу

Інтенсивності безвідмовної роботи елементів:

;;

;

;

;

;

;

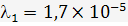
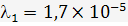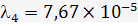
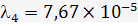Час роботи: t = 1000 годин

Необхідно:

Сформулювати умови безвідмовної роботи при однаковому t;

Розрахувати загальну надійність виробу;

Визначити середній час напрацювання до першої відмови;

Визначити середній час напрацювання на відмову;

Визначити інтенсивність відмови кожного елемента;

Побудувати графіки функцій надійності і ненадійності.

Перед розрахунком сформулюємо умову безвідмовної роботи: влаштування безвідмовно працює, якщо у безвідмовному стані буде перебувати елемент 1 і 2, і 4, або 3 і 5, і 6 або 7, або хоча б елемент 8.

Так як у нашому виробі елементи мають послідовно-паралельні з'єднання, то можна застосувати метод перетворення структурної схеми (метод звірки), об'єднуючи елементи в більші блоки і застосовуючи формули розрахунку для елементарних схем надійності.

Для послідовного з'єднання:

Для паралельного з'єднання:

Зробимо декомпозицію структурної схеми, для чого розіб'ємо її на послідовні і паралельні з'єднання елементів (рис. 2).

Далі необхідно розрахувати ймовірність безвідмовної роботи кожного окремого елемента за формулою:

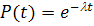
Таким чином, маємо:

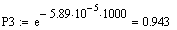
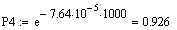
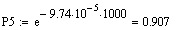
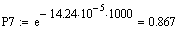
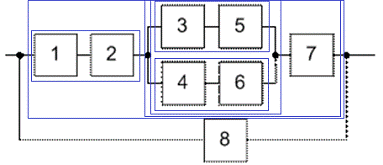
Рис. 27. Структурна схема виробу після декомпозиції

Розрахуємо надійності структурних блоків, представлених на схемі. Паралельне з'єднання рівнозначно функції диз'юнкції, а послідовне - кон'юнкції.

;

;

;

;

;

;

;

.

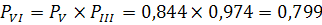
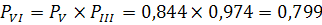Отримана ймовірність безвідмовної роботи всього виробу дає змогу оцінити інтенсивність відмов:

Середній час наробітку до відмови:

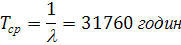
Функції надійності та ненадійності виглядають наступним чином:

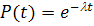
Розрахунок функції надійності для різних значень t

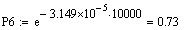
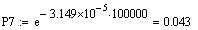
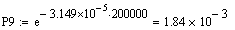
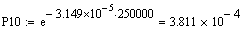
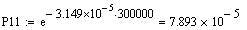
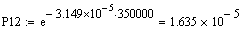
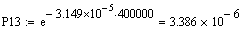
Розрахунок функції ненадійності для різних значень t

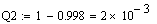
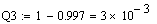
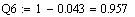
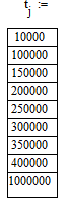
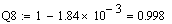
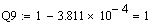
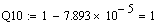
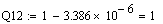
За отриманими таблиць побудуємо функції надійності та ненадійності (рис. 3 і 4). З вищенаведених розрахунків і побудованих графіків, очевидно, що виконується одна з основних положень теорії надійності: при паралельному з'єднанні елементів загальна надійність завжди вище надійності самого надійного елемента, а при послідовному з'єднанні загальна надійність завжди менше надійності самого ненадійного елемента.

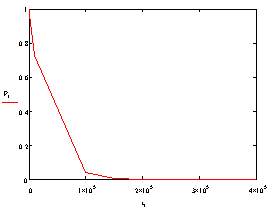
Функція надійності

Завдання 2

Необхідно:

Вибрати в структурній схемі (перше завдання) розрахунку ділянку з п'яти елементів.

Провести розрахунок функції надійності та ненадійності (побудувати графіки) вироби, інтенсивність відмови вироби, середній час напрацювання на відмову табличним методом для вибраної ділянки.

- Порівняти результати, отримані в першому і другому завданнях.

І теоретично, і практично табличний метод обчислення структурної надійності є універсальним, тобто він придатний для розрахунку системи будь-якої складності та конфігурації.

Вибираємо ділянку структурної схеми вироби з першого завдання (рис. 5).

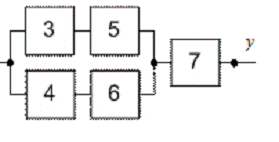
Рис. 30. Ділянка структурної схеми виробу

У будь-якому рядку позначається один з  станів, де n - число елементів. Безліч  станів являє собою повну групу несумісних складних подій.

Вихід у характеризує стан схеми: на виході у буде 1, якщо в безвідмовному стані знаходяться елементи 1 і 2, і 4, або 3 і 5.

Ймовірність безвідмовної роботи визначається як сума ймовірностей безвідмовних несумісних випадкових подій, розрахунок яких представлений в табл. 2.

Стан системи

Розрахунок ймовірності безвідмовної роботи

томограф надійність відмова

;

;

;

;

;

;

.

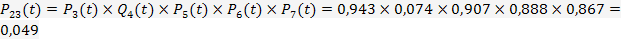
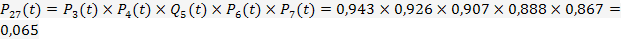
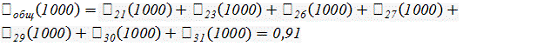
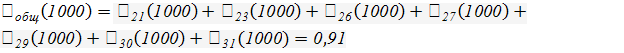Інтенсивність відмови вироби знаходиться як:

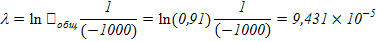
Середній час напрацювання на відмову:

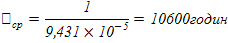
Очевидним є те, що ймовірність безвідмовної роботи виробу, розрахованого в другому завданні, дорівнює ймовірності безвідмовної роботи блоку V вироби, розглянутого в першому завданні.

При порівнянні отриманих результатів видно, що надійність даного вироби менше, ніж вироби, розрахованого в першому завданні, так як у нього відсутня дублюючий елемент. Також у даного вироби на порядок менше середній час напрацювання на відмову і більше інтенсивність відмов.