Применение метода нулевого поля для задач дифракции на включениях в плоскослоистых средах
ДИПЛОМНА
РОБОТА
ЗІ
СПЕЦІАЛЬНОСТІ
«РАДІОФІЗИКА
І ЕЛЕКТРОНІКА»
ДИПЛОМНАЯ
РАБОТА
ПО
СПЕЦИАЛЬНОСТИ
«РАДИОФИЗИКА
И ЭЛЕКТРОНИКА»
ПРИМЕНЕНИЕ
Метода нулевого поля для задач дифракции на вкЛЮЧЕниях в плоскослоистЫХ средах
СОДЕРЖАНИЕ
Введение
1. Аналитический обзор
2. Решение прямой задачи
рассеяния методом нулевого поля
2.1 Постановка задачи
дифракции и вывод исходных дифференциальных уравнений
2.2 Система интегральных
уравнений
2.2.1 Частный случай
включения в плоскослоистой среде
2.2.3 Частный случай
однородного слоя
2.3 Формирование СЛАУ
методу нулевого поля
3. Описание
вычислительного алгоритма и результаты вычислительных экспериментов
3.1 Алгоритм решения
задачи рассеяния
3.2 Результаты
вычислительных экспериментов
3.2.1 Диаграммы рассеяния
для кругового цилиндра в однородном пространстве
3.2.2 Диаграммы рассеяния
для цилиндрического рассеивателя в однородном полупространстве
3.2.3 Зависимость мощности
обратного рассеяния от конфигурации слоистой подложки под слоем с тонким
цилиндрическим включением
3.2.4 Диаграммы рассеяния
при наличии потерь в материале включения
Выводы
Литература
Введение
В последнее время в различных отраслях биологических наук и медицине
широкое распространение получили радиофизические методы воздействия на
биологические объекты и системы с целью физиологической, иммунной и
психомоторной коррекции процессов функционирования живых структур. Особенно
интенсивно развиваются исследования различного рода эффектов, связных с
взаимодействием электромагнитного излучения с биологическими тканями человека и
их анализ. При проведении современных биомедицинских исследований все большее
применение находят радиофизические методы и модели. В первую очередь они
используются для решения задач, связанных с обнаружением, идентификацией и позиционированием
различных неоднородностей, каковыми с электродинамической точки зрения являются
деформированные участки биологической ткани человека. Перспективность такого
подхода определяется тем, что для определенного диапазона длин электромагнитных
волн биологические ткани являются проницаемыми, в то время как
электродинамические свойства больных тканей значительно отличаются по сравнению
со свойствами здоровых тканей. Это означает, что именно электромагнитные волны
являются эффективным инструментом решения поставленных задач, в то время как
рентгеновские лучи и ультразвуковые волны имеют свои оптимальные области
использования и для рассматриваемых задач практически непригодны ввиду низкого
контраста между здоровыми и больными тканями для этих волн.
Отметим также, что область применимости математических и физических
моделей, вычислительных алгоритмов и программного обеспечения для решения
электродинамических задач, отнюдь не ограничивается биомедицинскими
приложениями. Важными также являются задачи дистанционного зондирования
природных сред и неразрушающего контроля промышленных изделий и сооружений.
Таким образом, проблема анализа взаимодействия электромагнитных волн с
биологическими тканями и разработка нового вычислительного алгоритма решения
задач дифракции электромагнитных волн на неоднородных проницаемых включениях
цилиндрической формы в сложных объектах представляется весьма актуальной и
практически значимой.
Исходя из вышеизложенного, цель настоящей работы - произвести анализ
взаимодействия электромагнитных волн с биологическими тканями и разработка
нового вычислительного алгоритма и соответствующего программного обеспечения
для анализа рассеяния монохроматических электромагнитных волн неоднородными
контрастными объектами цилиндрической формы.
Работа построена следующим образом: в аналитическом обзоре приведены
основные сведения, имеющиеся в научной литературе по данной проблематике. Кроме
того, проведен анализ возможных альтернативных подходов к решению поставленных
задач, исследованы их достоинства и недостатки с точки зрения практического
использования. На основании этого осуществлен выбор конкретного направления
исследований и определены методы и средства достижения поставленных целей.
В первом разделе детально рассмотрена постановка соответствующей
электродинамической задачи. Исходя из уравнений Максвелла и волнового
уравнения, записанного в форме, адаптированной к условиям рассматриваемой
задачи выведено исходное интегро-дифференциальное уравнение.
Второй раздел посвящен рассмотрению возможных схем решения полученного
ранее интегро-дифференциального уравнения.
В третьем разделе рассмотрены вычислительные аспекты поставленной
проблемы и приведены результаты экспериментов по численному моделированию.
В заключении подведены итоги проделанной работы и намечены основные
перспективы дальнейшего развития предложенного подхода.
1. Аналитический обзор
Проблема, которая возникает при исследовании взаимодействия
электромагнитной волны с биологическими тканями, требует внедрения новых
методов и соответствующим им вычислительных алгоритмов для обнаружения,
позиционирования и визуализации диэлектрических неоднородностей в сложных
структурах с помощью микроволн, она имеет важное значение, например, в связи с
потенциальной возможностью обнаружения поврежденных (больных) тканей организма
человека, а также для обнаружения и идентификации болезней кровеносных сосудов.
Именно поэтому ее решению было уделено значительное внимание работе [1].
Перспективность такого подхода следует из того факта, что так называемый электрический
контраст (отношение соответствующих диэлектрических проницаемостей) между
тканями раковой опухоли и нормальными (здоровыми) тканями достаточно высок.
Современные микроволновые системы способны отображать биомедицинские объекты
различных размеров, в отдельных случаях даже полностью человеческое тело. В
частности, для диагностики болезней крови, применяются как монохроматические
электромагнитные волны, так и импульсные сигналы. В качестве образца для
моделирования рассеяния электромагнитных волн на включении в тканях организмов
была выбрана проблема обнаружения и идентификации различных болезней
кровеносных сосудов. Однако следует отметить, что используемая методика
применима и для решения других электродинамических задач. В ниже перечисленных
статьях рассмотрено взаимодействие электромагнитных волн со структурами,
которые своими формами моделируют опухоли, сосуды и соответственно полученные
результаты могут быть использованы в данной работе.
Работа [1] посвящена анализу собственных типов волн и постоянных
распространения решетки идентичных диэлектрических стержней. Стержни имеют вид
цилиндров неограниченной длины с поперечным сечением произвольной формы.
Диэлектрическая проницаемость стержней любая комплексная величина. Нахождение
полей соответствующих собственным типам волн указанной структуры необходимо для
решения задачи возбуждения заданными источниками волноводно-стержневой решетки.
|

|
|
Рис. 1.1
|
Собственные типы волн и постоянные распространения стержней (рис. 1.1)
находится как решения уравнений поля, удовлетворяющие граничным условиям на
поверхности стержней и условиям периодичности. Согласно теореме Флоке в
рассматриваемом случае условия периодичности для электрического вектора поля
имеют вид
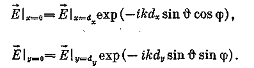
В работе [2] обсуждается проблема собственных волн
компланарной, щелевой, высокодобротной и других полосковых линий с учетом
конечной толщины проводников. Рассматривается применение метода импедансных и
адмитансных интегральных уравнений для исследования собственных волн полосковых
линий различных типов с учетом конечной толщины проводников. Показано, что
метод пригоден для анализа как экранированных, так и открытых систем. Метод
импедансных и адмитансных интегральных уравнений был распространен на системы с
проводящими листами конечной толщины. Таким путем был построен алгоритм,
предназначенный для анализа собственных волн экранированных колосковых линий
различных типов, включая линии с «подвешенной» подложкой. В [2] обсуждались
также результаты реализации алгоритма для случая экранированной несимметричной
полосковой линии.
Кроме перечисленных в [2] типов линий предложенным методом можно
анализировать и так называемую высокодобротную линию. Поскольку эта система
имеет горизонтальную плоскость симметрии, достаточно рассматривать лишь верхнюю
подобласть задачи, заменяя при этом, указанную среднюю плоскость границей с
условием Ех=0 и в другом случае с условием Hх=0. Этим
двум задачам соответствуют волны высокодобротной линии двух типов симметрии;
низшей в первом случае является ее противофазная волна, а во втором -
синфазная.
В работе [3] рассмотрено построение строгой математической модели
рассеяния собственных электрических волн планарного диэлектрического волновода
на конечном числе периодических канавок вырезанных на поверхности идеально
проводящего экрана. Такие структуры широко используются в антеннах
дифракционного излучения использующих эффект преобразования поверхностных волн
в объемные. Отдельно рассмотрены случаи конечного и нулевого зазора между
волноводом и экраном. Изучено влияние степени связи на дифракционные
характеристики антенны. На основании метода сингулярных интегральных уравнений
(СИУ) впервые построена строгая математическая модель рассеяния собственных
электрических волн диэлектрического волновода на конечном числе прямоугольных
канавок, вырезанных на поверхности идеально проводящего экрана. Такие структуры
широко используются в качестве сканирующих антенн. Поле в каждой канавке
учитывается отдельно, что позволяет рассматривать структуры с большим числом
различных канавок. Особый интерес представляет влияние степени связи волновода
с гребенкой.
Построенная модель достаточно эффективна и может быть применима для
оптимизации характеристик рассеяния антенн с достаточно большим числом
различных канавок. Удобными инструментами для этого является генетические
алгоритмы.
Работа [4] посвящена вычислению характеристических типов колебаний
(собственных волн) идеально проводящих тел вращения, анализу их свойств и
применению для решения задач рассеяния в резонансной области. Повышение
скорости и точности предложенного в работе [4] численного метода позволило
выполнить вычисления для конечного цилиндра, конуса и сферы.
Рассмотрена связь свойств собственных волн с электрическими характеристиками
тел. Приведены и обсуждены диаграммы рассеяния тел для случая облучения плоской
линейно-поляризованной волной вдоль оси вращения.
Однако постоянно возрастающее количество численных результатов обострило
ряд проблем стоящих перед исследователями и разработчиками.
Применение ЭВМ для решения задач рассеяния и излучения электромагнитных
волн объектами, соразмерными с длиной волны возбуждающего поля (резонансная
область), позволило в последние годы существенно расширить круг решаемых
вопросов. Однако постоянно возрастающее количество численных результатов
обострило ряд проблем, состоящих перед исследователями и разработчиками. Одна
из проблем заключается в эффективном использовании численного материала, что
настоятельно требует наличия достаточно простой модели рассеяния, физически
описывающей электромагнитные процессы в рассеивающем объекте. Другая важная
проблема - поиск новых принципов воздействия на характеристики излучения
объектов, тесно связанных с их геометрическими электрическими особенностями.
При решении этих проблем полезным является подход к анализу рассеяния в
резонансной области с точки зрения характеристических (собственных) типов
колебаний рассеивающего тела, называемых собственными волнами. В данной работе
при вычислении собственных волн рассматривались идеально проводящие тела
вращения, окруженные средой без потерь ε=1, μ=1,
σ=0.
Для вычисления собственных волн в работе применялся метод коллокации, в
котором граничные условия удовлетворялись в дискретных точках поверхности тела.
При простоте программирования и небольших затратах счетного времени этот метод,
как выяснилось, имеет существенный недостаток: результате вычислений
недопустимо сильно изменяются при изменении положения и количеству граничных
точек.
Основные вычисления собственных волн выполнены с применением метода,
получившего название мультипольного варианта обобщенного метода разделению
переменных. Вычисления обобщенным методом разделения переменных дают устойчивые
и сравнительно быстро сходящиеся результаты для широкого класса тел вращения.
Для контроля точности вычислений собственных волн использовался ряд признаков
ухудшения точности, основанных на свойствах собственных волн и особенностях
вычислительной схемы, а также оптическая теорема
В настоящей работе было вычислено собственные волны сфероида,
сферо-сфероида, конечного цилиндра, конуса и конуса сферы. Были вычислены и
исследованы собственные волны фиксированных азимутальных параметров m=0
(симметричные собственные волны) и m=+1 (несимметричные собственные волны) ряда
тел. При этом рассчитывались и анализировались поведение собственных фазовых
углов отражения, поверхностных токов и электрических полей собственных волн в
зависимости от электрических размеров, пропорций и формы тел. Анализ свойств
собственных волн позволил выделить 3 состояния их, условно названные начальным,
активным и конечным (пассивным). Выяснено, что состояния и свойства отдельной
волны зависят, прежде всего, от электрической длины образующей идеально
проводящего тела вращения.
Если отрезок образующей, приходящийся в среднем на один полупериод
диаграммы поверхностного тока, значительно меньше четверти длины волны, то, как
показывают расчеты, возбуждаемый на поверхности тела ток данной собственной
волны имеет очень малую амплитуду. Подобные собственные волны находятся в
начальном состоянии, а на характеристиках фазовых углов им соответствуют
горизонтальные участки с σ=0 или π.
При помощи собственных волн изучались закономерности формирования полей
рассеяния идеально проводящих тел вращения в зависимости от их электрических
размеров, пропорций и формы.
В работе решался такой вопрос, как влияния на диаграммы рассеяния форм
освещенной и теневой частей тел в частном случае облучения - вдоль оси
вращения. Диаграммы полей рассеяния сферо-сфероида при облучении его в
сфероидальную часть напоминают диаграммы сфероида, а при облучении в
сферическую часть диаграммы этого сферо-сфероида ближе к диаграммам сферы.
Для некоторых тел можно указать участки поверхности, играющие при любом
направлении облучения доминирующую роль в формировании полей рассеяния в
резонансной области. Например, у сильно вытянутого конуса и конуса-сферы
таковой является коническая часть.
В работе [5] рассмотрена проблема поддержки одна из важных проблем при
создании волоконного тракта. Возможное решение этой задачи состоит в
использовании профильного волокна, в котором поле собственных волн отжато от
краев, крепящихся к опорам. Если считать, что опоры делаются от того же (но
менее чистого) материала, что и световедущая нить, то, очевидно, собственные
волны частично высвечиваются через соединение с опорой и поглощаются в ней. Это
равносильно тому, что материал опоры можно считать простирающимся до
бесконечности (рис.1.2), а собственные волны вытекающими.
|

|
|
Рис.1.2
|
Установленная выше аналогия между границей диэлектрик-воздух и
металлической границей сводит задачу о волокне с поддержкой к задаче о
вытекающих Е-волнах в металлическом волноводе того же профиля с продольными
щелями. Для решения же этой задачи разработан и реализован простой аппарат
расчета комплексных постоянных распространения.
В работе [6] рассмотрена проблема о собственных волнах диэлектрических
волноводов сложного сечения. Работа посвящена методам математического анализа
регулярных диэлектрических волноводов произвольного сечения с произвольным
заполнением е(х, у). При
исследовании поверхностных волн целесообразно в качестве двух скалярных
потенциалов принимать поперечные декартовы компоненты магнитного или
электрического поля. Формулируются некоторые общие свойства волн,
устанавливается вычислительный аппарат (в частности, приводятся стационарные
функционалы) и исследуются подробно три асимптотических случая малый перепад
диэлектрической проницаемости, высокая и низкая частоты (т. е. области частот,
соответственно далекие и близкие к критической частоте данной полны). Дли
первых двух случаев магнитное поле в старшем порядке (и в отсутствие
вырождения) линейно поляризовано; для этих случаен приведен ряд дисперсионных
кривых. Исследуются свойства поверхностных (медленных) волн, которые могут
распространяться вдоль таких волноводов», т. е. решений однородных уравнений
Максвелла.
электромагнитный монохроматический волна рассеяние
2. решение прямой задачи рассеяния
методом нулевого поля
.1 Постановка задачи дифракции и вывод исходных
дифференциальных уравнений
Мы начнем с вывода уравнений метода нулевого поля, соответствующих,
неоднородному включению, находящемуся в неоднородной среде (рис.2.1). Для
упрощения выкладок остановимся на двумерном случае, для которого исходная
векторная задача может быть сведена к отысканию решения двух скалярных задач.
Итак, пусть в трехмерном пространстве расположен проницаемый цилиндр
произвольного поперечного сечения Sp, ограниченного контуром L
достаточно регулярным, чтобы выполнялась теорема Грина.
|

|
|
Рис.2.1. Геометрия задачи в
общей постановке
|
Введем
систему координат XYZ (см. рис.2.1) и предположим, что в области Se,
окружающей объект, расположены сторонние источники f и структурные границы
раздела. Образующие цилиндра параллельны оси ОХ. Внутри включения среда
характеризуется материальным параметром 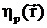 и
локальным волновым числом
и
локальным волновым числом 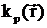 , а вне его
, а вне его  и
и 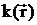 соответственно.
соответственно.
Поля
внутри и снаружи включения удовлетворяют уравнениям (2.1) и (2.2)
соответственно:
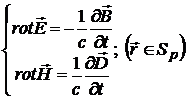 (2.1)
(2.1)
 (2.2)
(2.2)
Пусть
временная зависимость полей  , тогда
дифференцируя по времени (1), и, учитывая, что
, тогда
дифференцируя по времени (1), и, учитывая, что  ,
,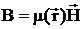 , получаем:
, получаем:
 ,
(2.3)
,
(2.3)
Применяя
оператор ротора к векторам 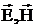 ,
получаем уравнения для компонент полей:
,
получаем уравнения для компонент полей:
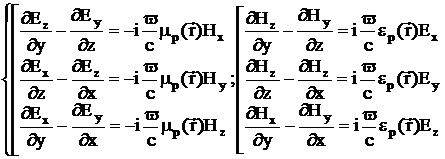 ,
(2.5)
,
(2.5)
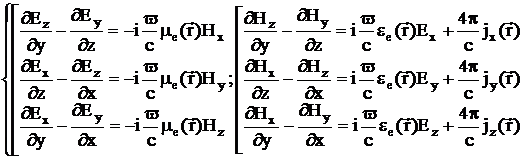 , (2.6)
, (2.6)
Т.к.
 , то:
, то:
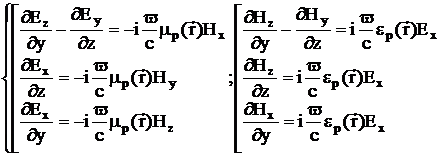 (2.7)
(2.7)
 (2.8)
(2.8)
Теперь
рассмотрим два случая, когда:
.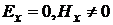 Н-поляризация падающего поля
Н-поляризация падающего поля
. Е-поляризация падающего поля
Е-поляризация падающего поля
Н-поляризация
падающего поля
С
учетом  , соотношения (2.7) и (2.8) принимают вид:
, соотношения (2.7) и (2.8) принимают вид:
 (2.9)
(2.9)
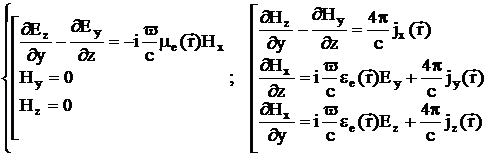 (2.10)
(2.10)
Выражая Ey и Ez ,получаем:
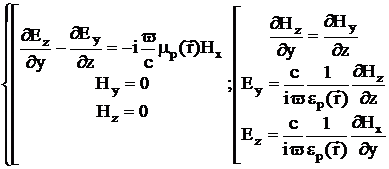 (2.11)
(2.11)
 (2.12)
(2.12)
Подставляя
Ey и Ez , приходим к соотношениям:
 (2.13)
(2.13)
 ;
(2.14)
;
(2.14)
Выпишем уравнения (2.13):
 ,
,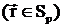 (2.15)
(2.15)
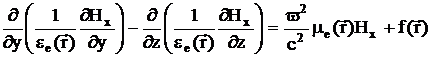 ,
, (2.16)
(2.16)
где введено обозначение:
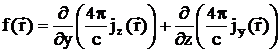 .
.
Домножая
обе части соотношений (2.15,16) на
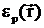 и
и 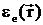 соответственно,
перепишем их в окончательном виде:
соответственно,
перепишем их в окончательном виде:
 ,
, , (2.17)
, (2.17)
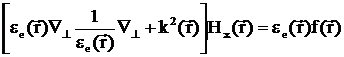 ,
, , (2.18)
, (2.18)
Где
 ,
, 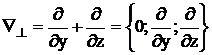
поляризация
падающего поля
Подставляя
 в соотношения (2.7,8) получим уравнения для амплитуд
поля внутри и снаружи включения для случая Е-поляризации падающего поля:
в соотношения (2.7,8) получим уравнения для амплитуд
поля внутри и снаружи включения для случая Е-поляризации падающего поля:
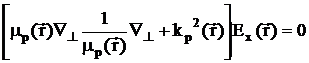 ,
, , (2.19)
, (2.19)
 ,
(2.20)
,
(2.20)
Исходя из всего вышесказанного, можно записать соотношения для амплитуд
полей снаружи и внутри включения в следующем виде:
 ,
, , (2.21)
, (2.21)
 ,
, , (2.22)
, (2.22)
=(0,y.z),
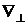 - двумерный оператор Лапласа, и граничным условиям:
- двумерный оператор Лапласа, и граничным условиям:
 ;
;  ; (
; ( )
(2.23)
)
(2.23)
а
также условиям непрерывности величин ue,  ,
,  , up
,
, up
, ,
, 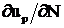 на
структурных границах раздела в Se, Sp и Ue удовлетворяет
условию излучения при
на
структурных границах раздела в Se, Sp и Ue удовлетворяет
условию излучения при  , а источники на бесконечности считаются
отсутствующими. Здесь и далее
, а источники на бесконечности считаются
отсутствующими. Здесь и далее  - нормаль
к контуру L рассеивателя, направленная в сторону Se ,
- нормаль
к контуру L рассеивателя, направленная в сторону Se , 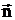 - нормаль к структурной границе раздела в материале
включения или окружающей среде.
- нормаль к структурной границе раздела в материале
включения или окружающей среде.
В
случае возбуждения вертикально (s) поляризованной волной (Hz=Нy=Еx=0
- случай Н-поляризации) в качестве функций ue , uin, usc
удобно выбрать x- компоненту вектора напряженности магнитного поля, а
функции 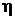 (
(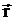 ),
),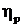 (
(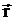 ) при этом описывают диэлектрическую проницаемость.
Компоненты электрического поля тогда связаны с соответствующими потенциалами,
вытекающими из уравнений Максвелла соотношениями:
) при этом описывают диэлектрическую проницаемость.
Компоненты электрического поля тогда связаны с соответствующими потенциалами,
вытекающими из уравнений Максвелла соотношениями:
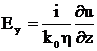 ;
; 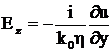 ;
; 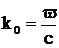
При
возбуждении горизонтально (p) поляризованной волной (Ey=Ez=Hx=0
- случай Е-поляризации) функции ue, uin, usc
имеют смысл х-компоненты электрического поля, а функции 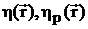 -магнитной проницаемости. Замена Ey
-магнитной проницаемости. Замена Ey  -Hy ; Ez
-Hy ; Ez  - Hz позволяет непосредственно из последних
формул определить компоненты магнитного поля.
- Hz позволяет непосредственно из последних
формул определить компоненты магнитного поля.
2.2 Система интегральных уравнений
Пусть
в отсутствие рассеивателя поле, которое мы будем далее называть первичным, и
обозначать  , удовлетворяет уравнению:
, удовлетворяет уравнению:
 (2.24)
(2.24)
и
условию излучения (УИ) при r +
+ , а также совместно с
, а также совместно с 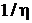
 условию непрерывности. Функция Грина регулярной задачи
условию непрерывности. Функция Грина регулярной задачи
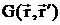 введем как решение уравнения:
введем как решение уравнения:
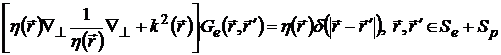 ,
(2.25)
,
(2.25)
удовлетворяющее
УИ при  и совместно с
и совместно с 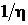 и
и 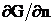 условию непрерывности на структурных границах
раздела.
условию непрерывности на структурных границах
раздела.
Представим
теперь поле ue , существующее в Se как сумму
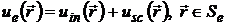 ,
(2.26)
,
(2.26)
при условии, что usc удовлетворяет волновому уравнению внутри
Se и стандартным условиям излучения и непрерывности, а внутри Sp
выполняется уравнение (3.22) и условия:
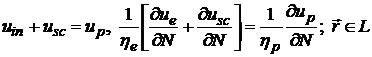 (2.27)
(2.27)
Домножая обе части уравнений, которым удовлетворяют usc и G на
Gsc и u соответственно, вычитая затем одно из другого, интегрируя по
Sp и пользуясь формулой Остроградского-Гаусса, получим в итоге
формулу Гельмгольца-Кирхгофа для рассеянного поля (с участием граничных
значений рассеянного же поля)
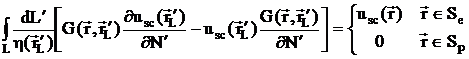 .
(2.28)
.
(2.28)
Аналогичным образом получим формулу Гельмгольца-Кирхгофа для рассеянного
поля (с учетом граничных значений полного поля):

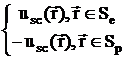 (2.29)
(2.29)
Пусть
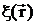 - произвольное решение уравнения:
- произвольное решение уравнения:
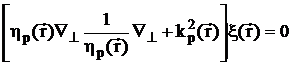 ;
; 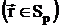 (2.30)
(2.30)
определенное по крайней мере в области Sp. Тогда из уравнений
(2.22) и (2.30) можно получить следующее билинейное соотношение с участием
произвольного решения однородного волнового уравнения внутри включения:
 0.
(2.31)
0.
(2.31)
Пусть
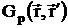 - произвольное решение уравнения (2.22) с правой
частью
- произвольное решение уравнения (2.22) с правой
частью 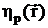
 , определенное в некоторой области
, определенное в некоторой области  , объемлющей Sp (
, объемлющей Sp (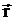 ,
,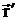
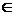 Sp).
Считается, что
Sp).
Считается, что  ,
, 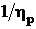 ,
,  непрерывны на структурных границах раздела внутри
непрерывны на структурных границах раздела внутри  .
.
Подчеркнем,
что:
а)
коэффициенты  , kp уравнения для up считаются
изначально заданными в области
, kp уравнения для up считаются
изначально заданными в области 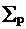 ,
несколько большей, чем Sp ;
,
несколько большей, чем Sp ;
б)Gp
не обязана удовлетворять УИ или быть симметричной относительно перестановок
своих аргументов. Последнее, однако, далее для удобства считается выполненным.
Из
уравнений для Gp и up в Sp с учетом
соотношений симметрии для Gp и условий сопряжения на L получаем
итоговый результат:
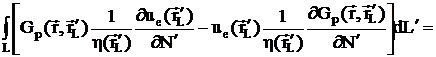 0.
0.
Заменив
в (2.21) up на ue , 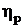 на
на 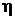 получим билинейное соотношение относительно
предельных значений поля и его нормальной производной вне включения:
получим билинейное соотношение относительно
предельных значений поля и его нормальной производной вне включения:
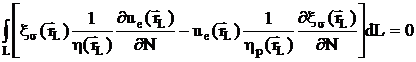 ;(
;(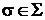 )
)
где
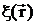 по-прежнему произвольное решение однородного
волнового уравнения в материале включения.
по-прежнему произвольное решение однородного
волнового уравнения в материале включения.
Из рассмотренных соотношений, связывающих амплитуды полного либо
рассеянного поля и их нормальные производные с другими параметрами задачи,
следуют два варианта уравнений метода нулевого поля, первый из которых мы и
будем рассматривать далее.
Первый вариант уравнений метода нулевого поля.
Рассмотрим
уравнение (2.7,8) на контуре L и (2.24) при специально подобранных функциях 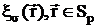 . Поскольку интегралы в левых частях этих соотношений,
также как и
. Поскольку интегралы в левых частях этих соотношений,
также как и 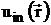 кусочно-аналитические функции переменного
кусочно-аналитические функции переменного 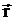 в соответствующей области, для выполнения этих
соотношений необходимо и достаточно, чтобы они выполнялись на некоторых
контурах, лежащих внутри рассматриваемой области Sp :
в соответствующей области, для выполнения этих
соотношений необходимо и достаточно, чтобы они выполнялись на некоторых
контурах, лежащих внутри рассматриваемой области Sp :
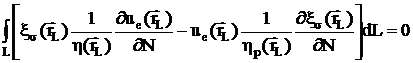 ;
; 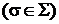 (2.33)
(2.33)
Здесь
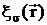 - такие решения однородного уравнения (10), что
- такие решения однородного уравнения (10), что 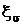 и
и  непрерывны
на структурных границах раздела в Sp, а
непрерывны
на структурных границах раздела в Sp, а 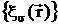 и
и  образуют
порознь полные системы функций.
образуют
порознь полные системы функций. 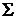 здесь и
далее представляет собой множество значений индекса
здесь и
далее представляет собой множество значений индекса 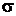 (возможно многомерное). Lp -произвольный
контур, вообще говоря, незамкнутый, целиком лежащий в области Sp.
Пара уравнений (2.26) и (2.27) образует задачу для отыскания функций ue
и
(возможно многомерное). Lp -произвольный
контур, вообще говоря, незамкнутый, целиком лежащий в области Sp.
Пара уравнений (2.26) и (2.27) образует задачу для отыскания функций ue
и  .
.
Зная
ue и  на L из формул (2.17,18) при
на L из формул (2.17,18) при 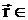 Se и
Se и 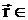 Sp
соответственно получаем:
Sp
соответственно получаем:
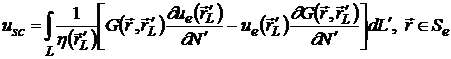 (2.34)
(2.34)
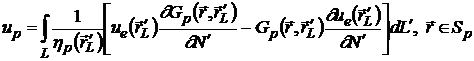 (2.35)
(2.35)
Это - прямые квадратурные формулы для вычисления значений рассеянного
поля и поля внутри включения.
2.2.1 Частный случай включения в плоскослоистой среде
Как следует из общих соотношений, полученных выше, вычислительная
эффективность метода существенным образом зависит от процедуры построения
функции Грина регулярной среды. В некоторых практически важных случаях такое
построение удается выполнить численно-аналитическими методами. Один из таких
случаев - плоскослоистой среды мы рассмотрим подробнее.
Считаем, что материальные параметры объемлющей среды зависят лишь от
координаты z . Тогда уравнение для функции Грина регулярной среды примет вид:
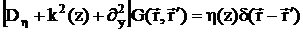 ;
;  (2.36)
(2.36)
Здесь
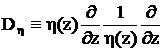 ,
,  . Функция
Грина
. Функция
Грина 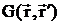 по-прежнему должна удовлетворять условию излучения на
бесконечности и вместе со своей нормальной производной - условиям непрерывности
на границах раздела регулярной среды (они теперь заданы уравнением z=const).
Решение задачи (3.36) можно искать в виде:
по-прежнему должна удовлетворять условию излучения на
бесконечности и вместе со своей нормальной производной - условиям непрерывности
на границах раздела регулярной среды (они теперь заданы уравнением z=const).
Решение задачи (3.36) можно искать в виде:
 (2.37)
(2.37)
Для
спектральных амплитуд  получается задача:
получается задача:
 ,
(2.38)
,
(2.38)
решение
которой, G вместе с  непрерывно на границах раздела, а G удовлетворяет
условию излучения при
непрерывно на границах раздела, а G удовлетворяет
условию излучения при  . В общем виде оно может быть найдено с помощью
представления:
. В общем виде оно может быть найдено с помощью
представления:
 , (2.39)
, (2.39)
где
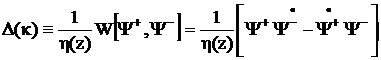 ,
,
> = max(z,z|),
z<= min(z,z|). Здесь  -
решения задачи:
-
решения задачи:
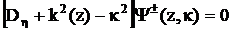 ;
;  , (2.40)
, (2.40)
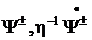 -
непрерывны всюду по z,
-
непрерывны всюду по z,  - удовлетворяет УИ при
- удовлетворяет УИ при 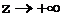 , а
, а  - при
- при 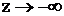 , а
, а  .
.
Особый
интерес представляет случай, когда  задана
на ограниченном интервале d<z,z| <b, что физически
соответствует плоскому слою конечной толщины. В этом случае схема построения
задана
на ограниченном интервале d<z,z| <b, что физически
соответствует плоскому слою конечной толщины. В этом случае схема построения  выглядит следующим образом.
выглядит следующим образом.
Предположим,
что 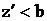 . Тогда при z=b+0 можно записать:
. Тогда при z=b+0 можно записать:
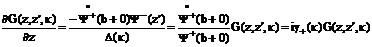 ,
(2.41)
,
(2.41)
где
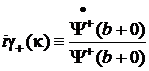 .
.
Ввиду
того, что при z=b должно быть:
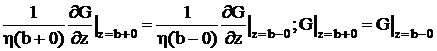 ,
,
получаем
граничное условие при z=b-0 в следующем виде:
 ; (z=b-0,
z| <b). (2.42)
; (z=b-0,
z| <b). (2.42)
При z=d+0, после преобразований, подобных тем, что приведены выше,
получаем следующее ГУ:
 .
(2.43)
.
(2.43)
Таким
образом, граничные условия (42,43) совместно с уравнением (38) образуют
замкнутую задачу для  на интервале [d,b]. Построение алгоритма нахождения
на интервале [d,b]. Построение алгоритма нахождения  позволит далее на основе модифицированного метода
нулевого поля (ММНП) в принципе решить задачу о рассеянии волн неоднородным
включением в такой структуре. Однако, чтобы избежать неоправданного усложнения
формул и продемонстрировать эффективность ММНП мы подробнее остановимся на
более простой модели вмещающей среды.
позволит далее на основе модифицированного метода
нулевого поля (ММНП) в принципе решить задачу о рассеянии волн неоднородным
включением в такой структуре. Однако, чтобы избежать неоправданного усложнения
формул и продемонстрировать эффективность ММНП мы подробнее остановимся на
более простой модели вмещающей среды.
2.2.3 Частный случай однородного слоя
Пусть
при d<z<b параметры  , k(z) принимают постоянные значения
, k(z) принимают постоянные значения  , kS соответственно. Поскольку в исходном
интегральном уравнении (2.32) и квадратурных формулах (2.34, 2.35)
, kS соответственно. Поскольку в исходном
интегральном уравнении (2.32) и квадратурных формулах (2.34, 2.35)  , a
, a 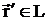 ,
необходимо рассмотреть два случая, соответствующих наблюдению поля внутри и вне
слоя при условии, что источник находится внутри слоя.
,
необходимо рассмотреть два случая, соответствующих наблюдению поля внутри и вне
слоя при условии, что источник находится внутри слоя.
Поле
и источник внутри слоя.
В
этом случае при  задача для
задача для  принимает
вид:
принимает
вид:
 (2.44)
(2.44)
 ;
;
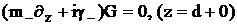 ;
;
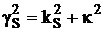 ;
;
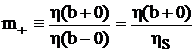 ;
; 
 .
.
Ищем
ее решение в форме:
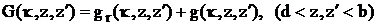 ,
(2.45)
,
(2.45)
где
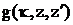 - решение задачи для безграничной среды с
материальными параметрами слоя:
- решение задачи для безграничной среды с
материальными параметрами слоя:
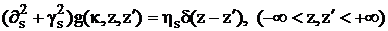 ;
(2.46)
;
(2.46)
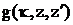 удовлетворяет
УИ при
удовлетворяет
УИ при  . Функция
. Функция 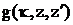 имеет
вид:
имеет
вид:
 (2.47)
(2.47)
а
 учитывает вклад границ при z=b и z=d.
учитывает вклад границ при z=b и z=d.
 (2.48)
(2.48)
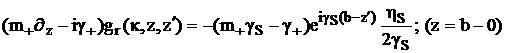
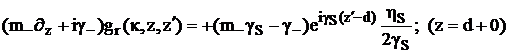
Теперь
построим решение задачи для  которое
будем искать в виде:
которое
будем искать в виде:
 .
(2.49)
.
(2.49)
Неопределенные коэффициенты C+ и C- находятся из
системы уравнений, к которой сводятся в таком случае граничные условия задачи
(2.48):
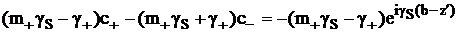 ,
(2.50)
,
(2.50)
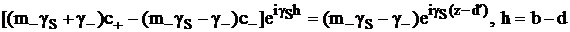 .
.
Подставляя
решение (2.34) в (2.33) получаем:
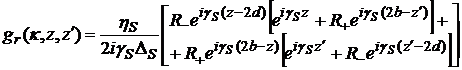 , (2.51)
, (2.51)
где
 , а
, а
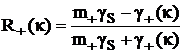 ,
, 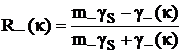 , коэффициенты отражения плоских волн от верхней и
нижней границ однородного слоя. Применение к (2.45) обратного преобразования
Фурье из (2.37) позволяет получить окончательное выражение для
, коэффициенты отражения плоских волн от верхней и
нижней границ однородного слоя. Применение к (2.45) обратного преобразования
Фурье из (2.37) позволяет получить окончательное выражение для  , которое мы приведем ниже.
, которое мы приведем ниже.
Поле
внутри, а источник вне слоя.
Теперь
переменная z изменяется на интервале (d,b), а точка наблюдения z>b либо
z<d. После подстановки в граничное значение  при z=b
выражений (47,51) для
при z=b
выражений (47,51) для 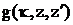 и
и  получаем
следующее представление для
получаем
следующее представление для  при
z>b
при
z>b
 .
(2.52)
.
(2.52)
Аналогичным образом при z<d получаем:
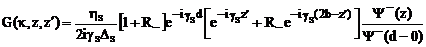 .
(2.53)
.
(2.53)
Однако, для успешного решения задачи о рассеянии поля включением
необходимо иметь универсальный способ представления как функции Грина, так и
полей, фигурирующих в исходных уравнениях (32,33). Весьма эффективным для этих
целей является разложение соответствующих величин по полной системе специальных
функций.
2.3 Формирование СЛАУ методу нулевого поля
Представим неизвестные амплитуды полного поля на контуре и его нормальную
производную, входящие в выражение (2.34), в виде следующих разложений:
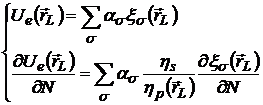

Заметим,
что для определения равенства коэффициентов в разложениях поля и производной мы
воспользовались первым из вышеприведенных уравнений. Следовательно, из
последующих выкладок его нужно исключить:
Для
случая однородного включения воспользуемся следующими базисными функциями  :
:

При
этом мы учли, что для однородного включения  .
.

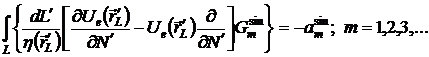
Коэффициенты
разложения первичного поля и функции Грина по цилиндрическим волнам:
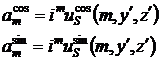

Подставим в данные уравнения разложения поля и производной и поменяем
порядок суммирования и интегрирования:
Верхний левый блок системы:

Верхний
правый блок системы:
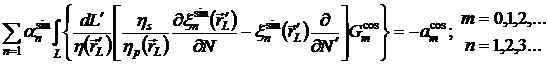
Нижний
левый блок системы:
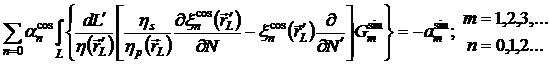
Нижний
правый блок системы:
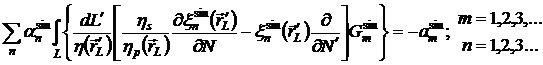
3. Описание вычислительного
алгоритма и результаты вычислительных экспериментов
.1 Алгоритм решения задачи рассеяния
Таким образом, для определения поля, рассеянного плоскослоистой средой с
включением, нам потребуется процедура вычисления интеграла Кирхгофа-Котлера:

 -
комплексная амплитуда поля, рассеянного включением
-
комплексная амплитуда поля, рассеянного включением
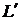 - контур
включения. Штрих указывает на то, что интегрируя по множеству точек контура
- контур
включения. Штрих указывает на то, что интегрируя по множеству точек контура  мы, фактически, производим суммирование полей вторичных
источников, расположенных на этом контуре.
мы, фактически, производим суммирование полей вторичных
источников, расположенных на этом контуре.
 -
координата точки наблюдения (радиус-вектор в точку наблюдения)
-
координата точки наблюдения (радиус-вектор в точку наблюдения)
 - переменная
интегрирования, координата точки источника (радиус-вектор в точку источника). В
данном интегральном представлении под «точкой источника» подразумеваются
вторичные источники, расположенные на границе включения (чтобы подчеркнуть это
вводится индекс
- переменная
интегрирования, координата точки источника (радиус-вектор в точку источника). В
данном интегральном представлении под «точкой источника» подразумеваются
вторичные источники, расположенные на границе включения (чтобы подчеркнуть это
вводится индекс  ).
).
 -
внешняя (по отношению к включению) область пространства
-
внешняя (по отношению к включению) область пространства
 -
материальный параметр среды. В случае Е-поляризации падающего поля, имеет смысл
магнитной проницаемости, а для Н-поляризации - диэлектрической проницаемости.
-
материальный параметр среды. В случае Е-поляризации падающего поля, имеет смысл
магнитной проницаемости, а для Н-поляризации - диэлектрической проницаемости.
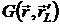 -
функция Грина объемлющей среды.
-
функция Грина объемлющей среды.
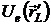 ,
,  - амплитуда полного поля и его нормальная производная
на контуре
- амплитуда полного поля и его нормальная производная
на контуре  .
.
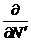 -
нормальная производная относительно внешней нормали к контуру
-
нормальная производная относительно внешней нормали к контуру  .
.
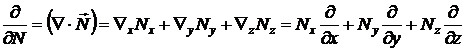
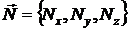 - вектор
внешней нормали к контуру.
- вектор
внешней нормали к контуру.
Алгоритм
решения задачи можно представить в виде набора следующих шагов:
1. Формирование набора исходных данных - физико-геометрических
параметров слоев и включения
2. Формирование элементов матрицы рассеяния Q.

3. Решение системы линейных алгебраических уравнений относительно
неизвестных коэффициентов разложения полей.

Или

где
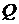 - матрица рассеяния,
- матрица рассеяния,  ,
, 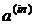 - матрицы-столбцы неизвестных коэффициентов и
первичного поля соответственно.
- матрицы-столбцы неизвестных коэффициентов и
первичного поля соответственно.
4. Нахождение диаграмм распределения поля по формулам:
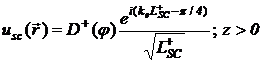

Здесь
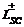 - расстояния от верхней (нижней) границы слоя до
точки наблюдения;
- расстояния от верхней (нижней) границы слоя до
точки наблюдения;  - угол наблюдения;
- угол наблюдения; 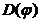 -
диаграммы направленности или амплитуды рассеяния, задаваемые формулами:
-
диаграммы направленности или амплитуды рассеяния, задаваемые формулами:
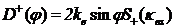 ,
,  ,
,
 ,
,
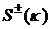 -
спектральные амплитуды рассеяния
-
спектральные амплитуды рассеяния
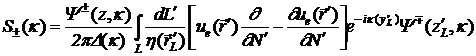
где
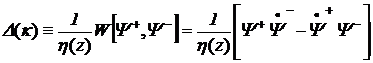 ,
,
а
функции 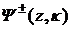 -удовлетворяют уравнению:
-удовлетворяют уравнению:
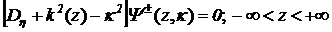
5. Пересчет полученных значений электродинамических величин в
физические либо геометрические параметры исследуемой структуры.
3.2 Результаты вычислительных экспериментов
По описанному выше алгоритму для расчета амплитуды поля рассеянного на
однородном цилиндрическом включении в плоскослоистой среде была написана
программа на языке Фортран. В настоящей работе проводилось исследование
зависимости диаграмм рассеяния от характеристик рассеивающего объекта. При
проведении вычислительных экспериментов в качестве первичного поля рассматривалась
плоская монохроматическая волна. А в качестве объемлющей среды рассматривался
плоский однородный слой, разделяющий два однородных полупространства. Включение
представляло собой однородный эллиптический цилиндр.
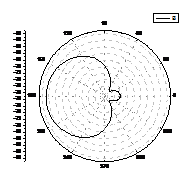
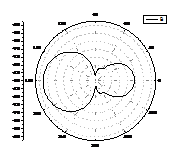
3.2.1 Диаграммы рассеяния для кругового цилиндра в однородном
пространстве
В данной серии вычислительных экспериментов в качестве рассеивателя
рассматривался круговой однородный цилиндр в однородном пространстве. Центр
цилиндра расположен на расстоянии 2λ от точечного источника.
 а)
а)
|
б) 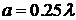
|
|
в)
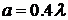

|
г) 
|
|
|
Рис.3.1 Диаграммы рассеяния
для цилиндрического рассеивателя в однородном пространстве (для разных
радиусов цилиндра)
|
3.2.2 Диаграммы рассеяния для цилиндрического рассеивателя в
однородном полупространстве
В данной серии вычислительных экспериментов в качестве рассеивателя
рассматривался тонкий круговой однородный цилиндр (радиус цилиндра 0.1λ)
в однородном
полупространстве.
3.2.3 Зависимость мощности обратного рассеяния от конфигурации
слоистой подложки под слоем с тонким цилиндрическим включением
В данной серии вычислительных экспериментов в качестве рассеивателя
рассматривался тонкий (радиус 0.1λ) круговой однородный цилиндр,
расположенный в первом слое двухслойной среды, разделяющей два однородных
полупространства.
|

|
|
Рис.3.3 Зависимость
мощности обратного рассеяния от глубины тонкого цилиндрического включения,
расположенного в однородном слое, разделяющем два однородных полупространства
|
3.2.4 Диаграммы рассеяния при наличии потерь в материале
включения
|

|
|
Рис.3.4 Диаграммы рассеяния
для цилиндрического включения с потерями, расположенного в однородном слое
|
Выводы
На основании анализа существующих подходов к решению проблемы
взаимодействия электромагнитных волн с биологическими тканями выбрано новое
направление для решения задачи дифракции.
В данной работе реализован теоретический подход к проблеме анализа
взаимодействия электромагнитных волн с биологическими тканями посредством
изучения собственных волн с целью нахождения нового направления для решения
соответствующих электродинамических задач.
Литература
1. Винниченко
Ю.П., Туманская А.Е. Собственные типы волн и постоянные распространения решетки
диэлектрических стержней.-1974. Т 8,-С.1583-1592
2. Карнишин
В.В. Собственные волны и решение задач дифракции // Радиотехника и
электроника.-1973. Т 11,-С.2241-2253
. Кириленко
А.А.,Стешенко С.А. Строгая двумерная модель эффекта преобразования
поверхностных волн в обьемные. // Радиотехника и электроника.-2004. Т
5,-С.32-38
. Ораевский
А.Н.,Щеглов В.А. О собственных колебаниях диэлектрических резонаторов -1965. Т
10,-С.965 -973
. Догадкин
А.Б. Возбуждения собственных волн в круглом волноводе. -1959. Т 5,-С.235 -243
7. Литвиненко
Л.Н., Просвирнин С.Л. Анализ дифракции волн на последовательности идентичных
ленточных решеток // Радиофизика и радиоастрономия. - 1999. - Т.4, № 3. - С.
276-286.
8. Грибовский
А.В., Литвиненко Л.Н., Просвирнин С.Л. Дифракция электромагнитных волн на
многослойной структуре из бесконечных металлических экранов с прямоугольными
отверстиями // Радиофизика и радиоастрономия. - 2000. - Т. 5, № 2. - С.
166-170.
. Бриллюэн
Л., Пароди М. Распространение волн в периодических структурах. - М.: И.Л.,
1959. - 457 с.
10. Финкельштейн
М.И., Мендельсон В.Л., Кутев В.А. Радиолокация слоистых земных покровов. - М.:
Сов. радио, 1977. - 174 с.
11. Зильберман
Г.Е., Макаренко Б.И., Голтвянская Г.Ф., Даржания А.Ю. Некоторые особенности
отражения электромагнитных волн от периодической диэлектрической структуры //
Радиотехника и электроника. - 1988. - Т. 33, № 5. - С. 915-921.
12. Зильберман
Г.Е., Макаренко Б.И., Голтвянская Г.Ф., Голтвянский И.Н. Некоторые особенности
прохождения электромагнитных волн через периодическую диэлектрическую структуру
// Радиотехника и электроника. - 1989. - Т. 34, № 10. - С. 2215.
. Литвиненко
Д.Л., Литвиненко Л.Н., Просвирнин С.Л. Метод анализа дифракции волн на
многослойных периодических структурах // Радиофизика и радиоастрономия. - 1997.
- Т. 2, № 4. - С. 485-491.
. Бреховских
Л.М. Волны в слоистых средах. - М.: Наука, 1973. - 502 с.
. Алимин
Б.Ф., Торгованов В.А. Методы расчета поглотителей электромагнитных волн //
Зарубежная радиоэлектроника. - 1976. Ч. 1. - № 3. - С. 29-57. Ч. 2. - № 8. - С.
60-80.
. Шестопалов
В.П., Кириленко А.А., Рудь Л.А. Резонансное рассеяние волн. Т.1. Дифракционные
решетки. - К.: Наукова думка, 1986. - 232 с.
. Шестопалов
В.П., Кириленко А.А., Рудь Л.А. Резонансное рассеяние волн. Т.2. Волноводные
неоднородности. - К.: Наукова думка, 1986. - 216 с.
. Шестопалов
В.П., Литвиненко Л.Н., Масалов С.А., Сологуб В.Г. Дифракция волн на решетках. -
Харьков: Изд. Харьк. унив., 1973. - 287 с.