Движение механизма перемещения желоба
КУРСОВАЯ
РАБОТА
По
дисциплине: Металлургия
Тема:
Движение механизма перемещения желоба
Содержание
Содержание
Аннотация
.
Исходные данные и задачи проектирования
.
Динамическое исследование движения системы
.
Проектирование маховика как регулятора движения системы
.
Кинетостатический анализ механизма
.1
Расчеты скорости и ускорения начального звена
.2
Кинетостатический расчет реакций в связях и уравновешивающего момента
.2.1
Структурная группа 5-4
.2.2
Структурная группа 3-2
.2.3
Начальный механизм 0-1
.3
Рычаг Жуковского
.
Список используемой литературы
Аннотация
В курсовом проектировании выполнено динамическое исследование движения
механизма перемещения желоба с определением закона движения начального звена,
получен график угловой скорости начального кривошипа в установившемся режиме
работы.
Выполнен синтез маховика как регулятора равномерности движения в заданных
пределах колебания скорости при установившемся режиме работы, рассчитан
необходимый момент инерции и предложены размеры маховика.
Проведен силовой анализ механизма в одном положении в такте рабочего хода
(положение №8), при этом рассчитаны реакции во всех кинематических парах
механизма и уравновешивающий момент на начальном звене, показывающий
необходимый движущий момент для преодоления заданных сил сопротивлений
движению.
Summary
course designing the dynamic research of movement of the
mechanism of moving of a cutter of the machine with definition of the law of
movement of an initial link is executed, the diagram of angular speed initial
in the established mode of operations is received.synthesis as regulator of
uniformity of movement in the given limits of fluctuation of speed is executed
at the established mode of operations, the necessary moment of inertia is
designed and the sizes are offered.power analysis of the mechanism in one rule
in a step of a working course is carried out, thus the reactions in all pairs
of mechanism and equilibrating the moment on an initial part showing necessary
driving moment for overcoming the given forces of resistance to movement are
designed.
1. Исходные
данные и задачи проектирования
Для проведения исследований в курсовом проектировании дана схема
механизма с линейными размерами звеньев, рис. 1. Исходные данные представлены в
таблице № 1.
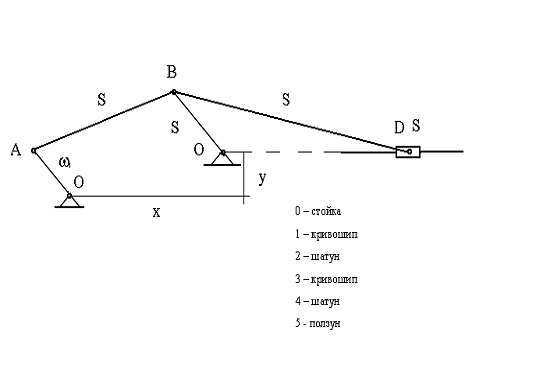
рис.1
Механизм
Таблица 1. Общие исходные данные
|
О1А, м
|
АВ м
|
O3B м
|
BD м
|
x, м
|
y, м
|
w1 с-1
|
m2, кг
|
m3, кг
|
m4, кг
|
m5, кг
|
mM, кг
|
J01, кгм2
|
Js2, кгм2
|
Js3, кгм2
|
Js4, кгм2
|
JDB, кгм2
|
Pc1, кН
|
Pc2, кН
|
wдв, с-1
|
δ
|
|
0,1
|
0,46
|
0,33
|
2
|
0,34
|
0,06
|
8
|
100
|
150
|
200
|
500
|
1000
|
1
|
2
|
1,5
|
100
|
0,15
|
2,5
|
6
|
150
|
0,08
|
Заданы массы mi и моменты инерции JSi звеньев, силы Pc1 и Pc2
сопротивления движению на выходном звене по тактам холостого и рабочего ходов
механизма, коэффициент неравномерности движения . Задан в цикле
движения механизма постоянным движущий момент, величина его подлежит расчету.
Кинематика механизма исследована при постоянной угловой скорости
начального звена ранее в расчетно-графической работе по теории механизмов и
машин. Планы скоростей в 12-ти возможных положениях механизма построены
решением векторных уравнений скоростей звеньев при последовательном
рассмотрении структурных групп механизма. В курсовом проектировании используем
первые передаточные функции механизма в виде отношений отрезков планов
скоростей соответствующих звеньев и точек.
По заданной схеме и исходным данным выполняем динамическое исследование
движения механизма перемещения желоба за один полный цикл работы. В результате
устанавливаем закон скорости начального звена, вычисляем коэффициент неравномерности
движения и определяем потребность в маховике.
Выполняем синтез маховика как регулятора равномерности хода механизма по
заданным условиям работы. Определяем необходимый момент инерции маховика и
размеры поперечного сечения его обода с проверкой на критическую скорость.
В одном положении механизма в такте рабочего хода (положение №8)
определить скорость и ускорение начального звена с учетом момента инерции
маховика, построить планы скоростей и ускорений и выполнить кинетостатический
анализ механизма с расчетом реакций во всех кинематических парах и
уравновешивающего момента. Уравновешивающий момент вычисляем также способом
проф. Н. Е. Жуковского.
Последовательность выполнения проекта определена методическими указаниями
[1, 2].
2.
Динамическое исследование движения системы
Приведенный к начальному звену - кривошипу О1А - момент сил сопротивлений
с отношениями скоростей в виде отрезков планов выражаем формулой [1]
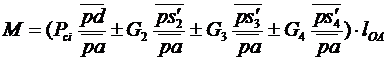 , [1]
, [1]
где
М - приведенный момент сопротивления, Н×м;
Pсi -
сила сопротивления для рабочего и холостого ходов, Н; i - сила тяжести
масс соответствующего звена, Н;
p -полюс плана
скоростей;
 ,
, 

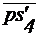 - изображения на планах скоростей механизма проекций
скоростей точек приложения сил на линии действия соответствующих сил, мм;
- изображения на планах скоростей механизма проекций
скоростей точек приложения сил на линии действия соответствующих сил, мм;
 =40 мм -
изображение скорости кривошипной точки A, мм; =OA -
радиус кривошипа, м.
=40 мм -
изображение скорости кривошипной точки A, мм; =OA -
радиус кривошипа, м.
В
составляющих момента от сил тяжести масс звеньев знак «плюс» соответствует
направлению вектора 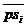 вверх, знак «минус» - направлению вектора вниз.
вверх, знак «минус» - направлению вектора вниз.
В
качестве примера для одного положения выполняем численные расчеты приведенных
моментов сил сопротивлений. Изображения скоростей на планах в миллиметрах
чертежа получены в кинематическом исследовании механизма.
Для
такта холостого хода (расчет в положении 2)

Для
такта рабочего хода (расчет в положении 8)


Результаты
расчетов приведенного момента сил сопротивлений по формуле (1) за цикл движения
механизма представлены в табл. 2.
Таблица 2. Результаты расчёта приведённого момента сопротивлений
|
Положения
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
Fп с
|
Н
|
2500
|
2500
|
2500
|
2500
|
2500
|
2500
|
6000
|
6000
|
6000
|
6000
|
6000
|
6000
|
6000
|
|
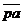 мм50 мм50
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
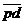 мм053634622171023343745330 мм053634622171023343745330
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 мм0-24-25-13-14-3192825236-90 мм0-24-25-13-14-3192825236-90
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 мм0-4-7-10-8-558992-30 мм0-4-7-10-8-558992-30
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
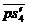 мм0-3,5-6-9-7-34,57,58712,50 мм0-3,5-6-9-7-34,57,58712,50
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Н981 Н981
|
|
|
|
 Н1471,5 Н1471,5
|
|
|
|
 Н1962 Н1962
|
|
|
|
Мсс
|
Нм
|
0
|
240,5
|
277,25
|
174,69
|
39,4
|
80,49
|
247
|
479,88
|
643,7
|
678,85
|
701,9
|
449,6
|
0
|
|
мм
|
0
|
48
|
55
|
35
|
8
|
16
|
47
|
96
|
129
|
136
|
140
|
99
|
Строим график ММ(j) на чертеже (см. л. 1, ТММКП рис.1) с необходимой крупностью
изображений в масштабах моментов сил mМ и углов μφ.
где Мmax - максимальный момент, Н×м;
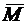 max - его
черчежное изображение на графике, мм;
max - его
черчежное изображение на графике, мм;
 240 мм -
изображение одного оборота кривошипа на графике моментов сил.
240 мм -
изображение одного оборота кривошипа на графике моментов сил.
Интегрированием
[1] приведенного момента сил по углу положения начального звена строим график
работ приведенных сил сопротивлений в масштабе
mАh mМ ,
где
mА в Дж/мм; - полюсное расстояние при интегрировании,
мм.
mА=80×5×0,0262 = 10,48
Дж/мм.
С
учетом постоянного момента движущих сил строим прямолинейный график работ этих
сил, исходя из того, что за цикл установившегося движения системы сумма работ
сил сопротивлений и движущих сил равна нулю. Дифференцированием графика работ
движущих сил по углу положения начального звена получаем в масштабе на графике
момент движущих сил.
Алгебраическим
суммированием ординат графиков работ приведенных сил сопротивлений и движущих
сил строим масштабный график избыточных работ исследуемой системы.
Таблица 3. Результаты расчёта избыточной работы.
|
Положения
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
DА
|
мм
|
0
|
9
|
13
|
18
|
29
|
42
|
50
|
59
|
38
|
23
|
5
|
-6
|
0
|
|
DА
|
Дж
|
0
|
94
|
136
|
189
|
304
|
440
|
524
|
618
|
398
|
241
|
52
|
-63
|
0
|
Составляем расчетную формулу приведенного к начальному звену момента
инерции системы
 [2]
[2]
где
JSi - момент инерции звена относительно оси Si в кг×м; - масса звена, кг.
По
формуле (3) рассчитаем постоянную часть приведенного момента инерции и выделим
переменную часть в функции угла положения начального звена.
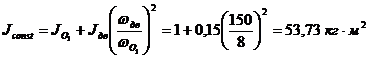 [3]
[3]
 [4]
[4]
где
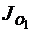 - момент инерции начального кривошипа относительно
оси О, кг×м2;дв - момент инерции ротора двигателя, кг×м;
- момент инерции начального кривошипа относительно
оси О, кг×м2;дв - момент инерции ротора двигателя, кг×м;
wдв - угловая
скорость ротора, рад/с.
w1 - угловая скорость
начального кривошипа, рад/с.
Для
данного механизма формулу (4) представим в удобном для расчетов виде где
отдельные составляющие по звеньям получают выражения

где
m=m5 холостого хода, а для рабочего - m=m5 + mM .
Для
примера расчеты выполняем в положений 2 и 8.
Приведенный момент инерции.

Таблица 4. Результаты приведённого момента инерции
|
Положения
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
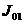 кг м21 кг м21
|
|
|
|
 кг м20,15 кг м20,15
|
|
|
|
 с-1150 с-1150
|
|
|
|
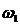 с-18 с-18
|
|
|
|
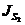 2 2
|
|
|
|
 кг м21,5 кг м21,5
|
|
|
|
 кг м2100 кг м2100
|
|
|
|
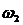 с-11,743,043,000,910,651,521,911,871,520,650,440,441,74 с-11,743,043,000,910,651,521,911,871,520,650,440,441,74
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 с-10,003,394,273,271,700,480,851,822,422,002,731,940,00 с-10,003,394,273,271,700,480,851,822,422,002,731,940,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
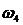 с-10,000,090,130,210,140,050,080,160,170,180,030,050,00 с-10,000,090,130,210,140,050,080,160,170,180,030,050,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2
|
кг
|
100
|
|
m3
|
кг
|
150
|
|
m4
|
кг
|
200
|
|
m5
|
кг
|
500
|
|
mM
|
кг
|
1000
|
|
 м/с0,40,680,900,920,660,460,400,580,720,620,840,720,4 м/с0,40,680,900,920,660,460,400,580,720,620,840,720,4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
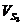 м/с0,000,560,680,560,280,100,140,300,400,440,460,360,00 м/с0,000,560,680,560,280,100,140,300,400,440,460,360,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
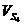 м/с0,001,101,300,980,500,140,220,500,720,780,900,660,00 м/с0,001,101,300,980,500,140,220,500,720,780,900,660,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 м/с01,081,280,920,440,140,20,480,680,740,900,760 м/с01,081,280,920,440,140,20,480,680,740,900,760
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
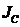 кг м253,7353,7353,7353,7353,7353,7353,7353,7353,7353,7353,7353,7353,73 кг м253,7353,7353,7353,7353,7353,7353,7353,7353,7353,7353,7353,7353,73
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
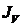 кг м20,3420,1121,1212,093,270,541,537,1413,915,9423,316,110,34 кг м20,3420,1121,1212,093,270,541,537,1413,915,9423,316,110,34
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
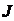 кг м254,0773,8474,8565,8257,0054,2755,2660,8767,6369,6777,0369,8454,07 кг м254,0773,8474,8565,8257,0054,2755,2660,8767,6369,6777,0369,8454,07
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
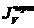 мм2134140812241048931061551072 мм2134140812241048931061551072
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Строим на чертеже график приведенного момента инерции (Jv) системы в функции угла положения
начального звена в масштабе

Учитывая
последующую необходимость исключения углового параметра, оси графика изображаем
повернутыми на 90° по часовой стрелке (см. график моментов инерции на
листе 1 КПР ТММ).
Решением
дифференциального уравнения движения системы в форме квадратуры получена
формула [5] для расчетов угловой скорости начального кривошипа в каждом
положении механизма
 [5]
[5]
где
DТ  T, Дж,
учитывая знак;
T, Дж,
учитывая знак;
 -
изображения избыточной энергии на графике, мм; () и w - соответственно приведенный момент инерции
системы и угловая скорость звена приведения в начале цикла движения (в
положении 0), принимаемая равной заданному среднему ее значению.
-
изображения избыточной энергии на графике, мм; () и w - соответственно приведенный момент инерции
системы и угловая скорость звена приведения в начале цикла движения (в
положении 0), принимаемая равной заданному среднему ее значению.
Для
примера в 2-ом положении угловая скорость кривошипа рассчитывается по формуле
[2]
Результаты
расчетов избыточной энергии и угловой скорости начального звена по формуле [6]
за цикл движения механизма представлены в табл. 5.
Таблица 5. Результаты расчёта угловой скорости
|
Положения
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
12
|
|
DТ, Дж
|
0
|
94,32
|
136,24
|
188,64
|
303,92
|
440,16
|
524,00
|
618,32
|
398,24
|
241,04
|
52,40
|
-62,88
|
0,00
|
|
 ,
кгм254,0754,0754,0754,0754,0754,0754,0754,0754,0754,0754,0754,0754,07 ,
кгм254,0754,0754,0754,0754,0754,0754,0754,0754,0754,0754,0754,0754,07
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w0, рад/с
|
8
|
8
|
8
|
8
|
8
|
8
|
8
|
8
|
8
|
8
|
8
|
8
|
8
|
|
 ,
кгм254,0773,8474,8565,8257,0054,2755,2660,8767,6369,6777,0369,8454,07 ,
кгм254,0773,8474,8565,8257,0054,2755,2660,8767,6369,6777,0369,8454,07
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w, рад/с
|
8
|
7,03
|
7,06
|
7,64
|
8,45
|
8,94
|
9,03
|
8,78
|
7,93
|
7,52
|
6,80
|
6,91
|
8
|
|
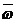 ,
мм400352353382423447452439397376340346400 ,
мм400352353382423447452439397376340346400
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Строим на чертеже график угловой скорости звена приведения в масштабе
(откладывая значения от w =
8 рад/с, т.е. начало координат на чертеже по оси ординат равно w = 8 рад/с, см. лист 1 КПР ТММ)

Определяем
по графику максимальную и минимальную угловые скорости max и min
начального звена и по ним находим среднюю за цикл угловую скорость ср,

рассчитываем
коэффициент ф неравномерности движения механизма, по которому
заключаем - нужен ли маховик в данной системе.

требуется
маховик для регулирования движения системы.
3.
Проектирование маховика как регулятора движения системы
Совместным решением зависимостей DТ=DТ(j) и J=J(j) при исключении углового параметра
(выполнено графически на листе 1 ТММКПР диаграмма Виттенбауэра)
получаем функцию DТ=DТ(J), графически представляемую
диаграммой Ф. Виттенбауэра. Построением к ней внешних касательных с наклонами к
оси моментов инерции под углами Ymax и Ymin
определяем на оси DТ
отрезок t¢t¢¢=12,45 мм, изображающий часть
избыточной энергии, соответствующей постоянной части приведенного момента
инерции системы, включая маховик.
tg Ymax=0,5 (mJ/mT)(1+d)w2=0,15/(2*10,48)×(1+0,08)*82 = 0,4948;
Ymax=26°.
Ymin =0,5 (mJ/mT)(1-d)w2= 0,15/(2*10,48)*(1-0,08)*82 =0,4214;
Ymin=22°.
Момент инерции маховика
м=mT (t¢t¢¢)/(dw2),
где d и w - заданы в качестве исходных величин для проектирования,
Jм=10,48×12,45/[0,08×82] =25,48 кг·м²;
Учитывая, что часть момента инерции приходится на ступицу и спицы
махового колеса, момент инерции обода маховикаоб=0,9*Jм; Jоб=0,9×25,48=22,932 кг·м².
Представляя обод маховика в виде кольца с массой, условно сосредоточенной
на расчетном диаметре маховика Dм, определяем размеры поперечного сечения обода
шириной b и толщиной h. Диаметром обода задаемся как ориентировочным
Dм=10 rA=10×0,1=1 м.
Масса обода на этом диаметре
mоб = 4Jоб/Dм2 = 4×22,93/12 = 91,73 кг
Рассчитываем размеры h и b.
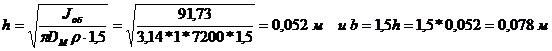
Принимаем
вариант с диаметром обода Dм=1 м, поперечными размерами bxh=78х52 мм и
проверяем маховик на критическую скорость. Окружная скорость на расчетном
диаметре
что меньше критической скорости vкр»36 м/с для маховика из серого чугуна.
4.
Кинетостатический анализ механизма
.1 Расчеты
скорости и ускорения начального звена
Рассчитываем угловую скорость кривошипа в заданном положении 8 (выделено
было на плане положений в кинематическом исследовании) в такте рабочего хода
механизма и при =8 рад/с в начале цикла, как предписано заданием. Формула (5)
в таком случае получает вид
w(8)= ;
;
w(8) = = 7,93 рад/с.
= 7,93 рад/с.
Угловое ускорение e(8) начального звена рассчитываем по дифференциальному
уравнению движения для того же положения механизма
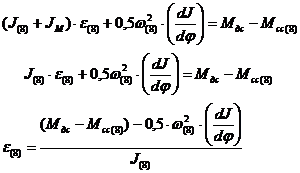
где
 - значение производной в этом же 8-м положении с
учетом знака, полученное по графику дифференцированием приведенного момента
инерции на участке ряда положений, включая расчетное положение механизма.
- значение производной в этом же 8-м положении с
учетом знака, полученное по графику дифференцированием приведенного момента
инерции на участке ряда положений, включая расчетное положение механизма.

где
k - отношение изображений в миллиметрах искомой производной в расчетном
положении к принятому в дифференцировании полюсному расстоянию. По рис.4.

Алгебраическую
сумму моментов приведенных движущих сил и сил сопротивлений в положении 8
определяем по графику моментов сил с учетом масштаба.
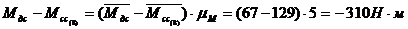
По
формуле (7)
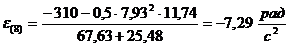
Далее
в данном (8-м) положении механизма с вычисленным ускорением e(8) кривошипа строим масштабный план ускорений (см план
ускорений л.2 ТММ КПР),что позволит определить векторы сил инерций и моменты
сил инерций звеньев для кинетостатического анализа механизма.
.2
Кинетостатический расчет реакций в связях и уравновешивающего момента
Расчет выполняем в одном положении при рабочем ходе механизма. Определим
угловые ускорения, веса, силы инерции и моменты сил инерции всех звеньев:

 ;
; 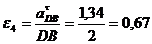
 ;
;  ;
;
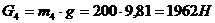 ;
; 
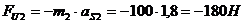 ;
; 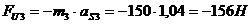
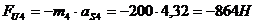
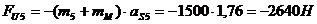
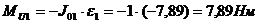 ;
; 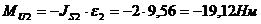


Векторы
сил инерции направлены против ускорений центров масс соответствующих звеньев А
теперь рассмотрим структурные группы Ассура
4.2.1
Структурная группа 5-4
Запишем уравнение равновесия моментов сил звена 4 относительно точки С,
плечи сил при этом выражаем в миллиметрах чертежа:
 ,
,
откуда определим тангенциальную составляющую реакции звена 3 на звено 4:
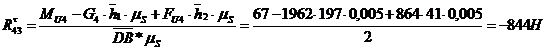
Для
расчетов нормальной составляющей реакции запишем векторное уравнение равновесия
сил структурной группы 4-5 и построим соответствующий план сил в масштабе 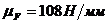 :
:
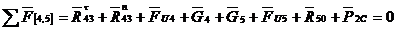
Рассчитав
изображения сил в миллиметрах чертежа по формуле 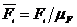 , строим
план сил.
, строим
план сил.
Расчетами
по плану сил группы получаем нормальную составляющую реакции звена 3 на звено
4: 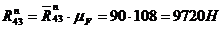 , полное значение реакции звена 3 на звено 4:
, полное значение реакции звена 3 на звено 4: 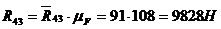 , значение реакции звена 5 на звено 0:
, значение реакции звена 5 на звено 0:  .
.
4.2.2
Структурная группа 3-2
Составим уравнение равновесия моментов сил относительно точки B, действующих на звено 3; плечи сил,
как и ранее, в миллиметрах чертежа:
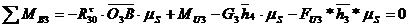
Из
этого уравнения определяем реакцию :
:
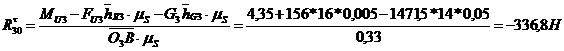
Теперь
составим уравнение равновесия моментов сил относительно точки B,
действующих на звено 2:

Из
этого уравнения определяем реакцию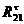 :
:
Направление
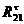 противоположно принятому.
противоположно принятому.
Для
определения реакции  и
и 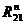 запишем
векторное уравнение равновесия сил структурной группы 2-3 и построим план сил
(см. План сил для структурной группы 2-3 на листе 2 КПР ТММ) с масштабом µF =
54
запишем
векторное уравнение равновесия сил структурной группы 2-3 и построим план сил
(см. План сил для структурной группы 2-3 на листе 2 КПР ТММ) с масштабом µF =
54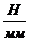 :
:
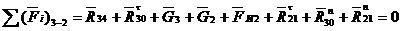 .
.
По
построенному плану сил определяем значения и направления реакций  ,
, 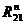 ,
, 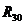 и
и 
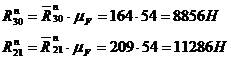

4.2.3
Начальный механизм 0-1
Из уравнения равновесия моментов сил на начальном звене относительно оси
О1 определим уравновешивающую силу, которая прикладывается к кривошипной точке
А перпендикулярно кривошипу и направлена таким образом, чтобы создаваемый ее
момент уравновешивал момент от реакции R12= -R21 (R21 = - R23).
механизм перемещение желоб равновесие
 = 0;
= 0;
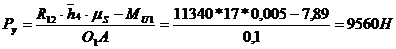
С
помощью определенной уравновешивающей силы можно определить уравновешивающий
момент, который она создает.
Му = Pу·О1А=9800·0,1= 980 Н·м
Из плана сил определяем реакцию

4.3 Рычаг
Жуковского
Уравновешивающий момент рассчитываем еще способом профессора Н.Е.
Жуковского. Строим в масштабе mn=0,024 м/c·мм план
скоростей, повернутым на 90°, и загружаем его всеми внешними силами в соответствующих подобных точках
механизма («рычаг Жуковского»). Решением уравнения равновесия моментов сил
относительно полюса р “рычага” определим уравновешивающий момент Му. Плечи сил
при этом в миллиметрах чертежа:
 ;
;
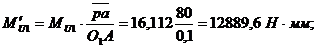
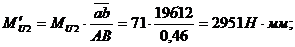
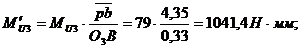
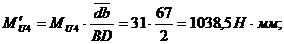

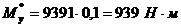
Погрешность
уравновешивающего момента по сравнению с результатом расчета способом “рычага
Жуковского” вычисляется по формуле
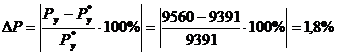
5. Список
используемой литературы
1. Динамическое
исследование механизма машины с расчетом момента инерции маховика: Методические
указания по курсовому проектированию /Санкт-Петербургский горный институт.
Сост. И.П. Иванов.- СПб., 1996.-19 с./
2. Попов
С.А. Курсовое проектирование по теории механизмов и механике машин. М.: Высш.
Школа, 1986.
. Теория
механизмов и машин/Под ред. К.В.Фролова. М.: Высш. Школа, 1987.