Формирование математических способностей (по В.А. Крутецкому) при изучении математики в деятельностном подходе
Введение
Замысел моей дипломной работы состоит в том,
чтобы посмотреть на математический курс, разработанный под задачу формирования
общий способности к исследовательской деятельности как на курс, позволяющий
формировать специальные математические способности.
Цель дипломной работы состоит в оценке
возможности формирования математических способностей при изучении математики в
деятельностном подходе, а именно при изучении темы «Теория делимости» в курсе
«Начала алгебры» для 6 класса.
Для достижения поставленной цели решались
следующие задачи:
а) изучение литературы, в том числе работы В.А.
Крутецкого [8], посвященной понятию математических способностей.
б) реконструкция специфики и содержания курса
«Начала алгебры».
в) анализ задачного материала темы «Теория
делимости» курса «Начала алгебры» с целью ответа на вопрос о возможности
развития математических способностей в рамках данного курса.
Объектом дипломной работы является задачный
материал темы «Теория делимости».
Предметом дипломной работы являются предметные
действия с учебным материалом.
Результат дипломной работы: состоит в том, что в
ходе теоретического анализа получено подтверждение гипотезы о том, что
деятельностное изучение математики формируют следующие математические
способности:
способность к формализованному восприятию
математического материала, схватывания формальной структуры задачи;
способность к логическому рассуждению в сфере
количественных и пространственных отношений, числовой и знаковой символики;
способность к быстрому и широкому обобщению
математических объектов.
Дипломная работа состоит из введения, трех глав,
заключения, списка литературы и содержит 5 таблиц.
Первая глава посвящена понятию способностей,
математической способности и их связь с умениями и навыками, также описана
общая схема математических способностей как три основных этапа решения
математической задачи.
Вторая глава посвящена непосредственному
выяснению возможностей формирования математических способностей при изучении
темы «Теория делимости» в деятельностном подходе.
Единицей обучения в курсе «Начала алгебры»
является учебный цикл, состоящий из шести этапов:
оформление существующих знаний;
постановка проблемы (задачи);
открытие нового понятия (может использовать
рабочий язык);
систематизация новых знаний;
анализ текстов учебников (переход на культурный
язык);
выделение класса типовых задач (на навык);
контроль и оценка.
Можно предположить, что на каждом из этапов
становятся разные математические способности. Например, на этапе оформление
существующих знаний становится способность формализованному восприятию
математического материала, на этапе открытия нового понятия - способность к
логическому рассуждению, на этапе систематизация новых знаний - способность к
быстрому и широкому обобщению.
Для обоснования этого предположения мы
проанализировали и типологизировали задачный материал (около 100 задач) и
выяснили, что предметные действия, способствующие становлению трех из восьми
способностей (по В.А. Крутецкому) с необходимостью требуются при решении целых
классов задач темы «Теория делимости». Это дает основание утверждать, что три
способности действительно формируются при изучении данной темы.
А именно мы показали, что задачный материал темы
«Теория делимости» курса «Начала алгебры» позволяет сформировать способность к
формализованному восприятию математического материала; способность к
логическому рассуждению; способность к быстрому и широкому обобщению, за счет
того, что задачи, содержащиеся в учебном курсе требуют выполнения предметных
действий, обеспечивающих развитие указанных способностей.
Хочется выразить глубокую признательность одному
из разработчику курса «Начала алгебры» О.И. Белоконь за полезные обсуждения и
помощь в подготовке к выступлению защиты дипломной работы.
Глава 1. Анализ представлений о
математических способностях
.1 Способности и их связь с умениями
и навыками
математический способность
восприятие крутецкий
Анализ способностей вызывает необходимость
различить понятия способностей, с одной стороны, и умений и навыков - с другой.
Эти категории взаимосвязаны и взаимозависимы. С.Л. Рубинштейн писал о
«своеобразной диалектике между способностями и умениями».[15] С одной стороны,
в процессе приобретения знаний, умений и навыков развиваются способности. Их
формирование и развитие невозможно вне этого процесса. С другой стороны -
способности позволяют быстрее, легче и глубже овладеть соответствующими
знаниями, умениями и навыками.
Мы считаем, что реальная тесная связь и
взаимозависимость способностей и умений, навыков не «закрывает» возможности
дифференцировать эти категории. Как неверно было бы разрывать их, так
неправильно было бы и отождествлять их.
Как же отличать способности от умений и навыков?
В основе определения понятия «способности» лежит характеристика
индивидуально-психологических особенностей человека. С другой стороны, все
определения навыков, умений основываются из понятия деятельности. А.Н. Леонтьев
говорит об умении как о целесообразном выполнении действий. [9] В этом
различие: когда говорят о способностях, имеют в виду психологическую характеристику
человека в деятельности, когда говорят об умениях (навыках) - психологическую
характеристику деятельности человека.
Все это дает основание следующим образом
дифференцировать указанные понятия. Под способностями понимается
индивидуально-психологические особенности человека, которые благоприятствуют
овладению определенной, например, математической деятельностью, овладению
соответствующими навыками и умениями; под умениями и навыками понимается
конкретные акты деятельности (например, математической), которые осуществляются
человеком на сравнительно высоком уровне (это понятие исходит из анализа данной
конкретной деятельности).
Необходимо подчеркнуть, что при анализе, как
умений, навыков, так и способностей анализируется деятельность. И о наличие
способностей, и о наличие умений и навыков, необходимо судить по особенностям
выполнения человеком соответствующей (например, математической) деятельности.
Классификация способностей человека.
В теории способности в первую очередь различают
природные, или естественные и социальные человеческие способности, имеющие
общественно-историческое происхождение. [11]
К природным способностям относятся такие
элементарные способности как восприятие, память, мышление, способность к
элементарным коммуникациям на уровне экспрессии.
К социальным способностям относятся общие и
специальные высшие интеллектуальные способности.
Общие способности включают в себя те, которыми
определяются успехи человека в самых различных видах деятельности. К ним,
например, относятся умственные способности, тонкость и точность ручных
движений, развитая память, совершенная речь и ряд других. Специальные
способности определяют успехи человека в специфических видах деятельности, для
осуществления которых необходимы задатки особого рода и их развитие. К таким способностям
можно отнести музыкальные, математические, лингвистические, технические,
литературные, художественно-творческие, спортивные и ряд других.
Наличие у человека общих способностей не
исключает развития специальных и наоборот. Нередко общие и специальные
способности сосуществуют, взаимно дополняя и обогащая друг друга.
В зависимости от деятельности, которую
осуществляет человек, специальные способности могут классифицироваться как:
) Теоретические и практические способности. Эти
способности отличаются тем, что первые предопределяют склонность человека к
абстрактно-теоретическим размышлениям, а вторые - к конкретным, практическим
действиям. Такие способности, в отличие от общих и специальных, часто не
сочетаются друг с другом, вместе встречаясь только у одаренных, разносторонне
талантливых людей.
) Способности к общению, взаимодействию с
людьми, а также предметно-деятелъностные, или предметно-познавательные,
способности. Они в наибольшей степени социально обусловлены. В качестве
примеров способностей первого вида можно привести речь человека как средство
общения (речь в ее коммуникативной функции), способности межличностного
восприятия и оценивания людей, способности социально-психологической адаптации
к различным ситуациям, способности входить в контакт с различными людьми,
располагать их к себе, оказывать на них влияние и т.п.
) Учебные и творческие отличаются друг от друга
по мнению Р.С. Немова тем, что первые определяют успешность обучения и
воспитания, усвоения человеком знаний, умений, навыков, формирования качеств
личности, в то время как вторые - создание предметов материальной и духовной
культуры, производство новых идей, открытий и изобретений, словом -
индивидуальное творчество в различных областях человеческой деятельности. [11]
Но нам кажется, различие между двумя способностями не носит абсолютный
характер. Изучая математические способности школьников, мы имеем в виду не
просто обучаемость.
В нашем исследовании будет идти речь хотя и об
учебных способностях школьников, но и о творческих учебных способностях,
связанных с самостоятельным творческим овладением математикой в условиях
школьного обучения, с самостоятельной постановкой несложных математических
проблем и нахождением путей и методов для их решения, изобретением
доказательств, самостоятельным выведением формул. Все это несомненно тоже
проявление математического творчества. Если критерием собственно
математического мышления является наличие творческого начала, то не надо
забывать, что математическое творчество может быть не только объективным, но и
субъективным.
Устанавливая специфические критерии, отличающие
творческий мыслительный процесс от нетворческого, А. Ньюэлл, Д. Шоу и Г. Саймон
отмечают следующие признаки творческого мышления:
) продукт мыслительной деятельности обладает
новизной и ценностью как в субъективном и в объективном смысле;
мыслительный процесс также отличается новизной в
том смысле, что требует преобразования ранее принятых идей или отказа от них.
[13]
Творческий мыслительный процесс характеризуется
наличием сильной мотивацией и устойчивости, протекая либо в течение
значительного периода времени, либо с большой интенсивностью.
Способности и успешное выполнение деятельности
Определяют успешность выполнения какой-либо
деятельности не отдельные способности, а лишь их удачное сочетание, именно
такое, какое для данной деятельности необходимо. Практически нет такой
деятельности, успех в которой определялся бы лишь одной способностью. С другой
стороны, относительная слабость какой-нибудь одной способности не исключает
возможности успешного выполнения той деятельности, с которой она связана, так
как недостающая способность может быть компенсирована другими, входящими в
комплекс, обеспечивающий данную деятельность. К примеру, слабое зрение частично
компенсируется особым развитием слуха и кожной чувствительности.
Способности не только совместно определяют
успешность деятельности, но и взаимодействуют, оказывая влияние друг на друга.
Сочетание различных высокоразвитых способностей называют одаренностью, и эта
характеристика относится к человеку, способному ко многим различным видам
деятельности.
Многоплановость и разнообразие видов
деятельности, в которые одновременно включается человек, выступает как одно из
важнейших условий комплексного и разностороннего развития его способностей. В
этой связи следует обсудить основные требования, которые предъявляются к
деятельности, развивающей способности человека. Р.С. Немов в теории социального
научения выделил следующие требования: творческий характер деятельности,
оптимальный уровень ее трудности для исполнителя, должная мотивация и
обеспечение положительного эмоционального настроя в ходе и по окончании
выполнения деятельности. [11]
Если деятельность ребенка носит творческий,
нерутинный характер, то она постоянно заставляет его думать и сама по себе
становится достаточно привлекательным делом как средство проверки и развития
способностей. Такая деятельность всегда связана с созданием чего-либо нового,
открытием для себя нового знания, обнаружения в самом себе новых возможностей.
Это само по себе становится сильным и действенным стимулом к занятиям ею, к
приложению необходимых усилий, направленных на преодоление возникающих
трудностей. Такая деятельность укрепляет положительную самооценку, повышает
уровень притязаний, порождает уверенность в себе и чувство удовлетворенности от
достигнутых успехов.
Если выполняемая деятельность находится в зоне
оптимальной трудности, т.е. на пределе возможностей ребенка, то она ведет за
собой развитие его способностей, реализуя то, что Л.С.Выготский называл зоной потенциального
развития. [2] Деятельность, не находящаяся в пределах этой зоны, гораздо в
меньшей степени ведет за собой развитие способностей. Если она слишком проста,
то обеспечивает лишь реализацию уже имеющихся способностей; если же она
чрезмерно сложна, то становится невыполнимой и, следовательно, также не
приводит к формированию новых умений и навыков.
Поддержание интереса к деятельности через
стимулирующую мотивацию означает превращение цели соответствующей деятельности
в актуальную потребность человека. В русле теории социального научения особо
подчеркивалось то обстоятельство, что для приобретения и закрепления у человека
новых форм поведения, необходимо научение, а оно без соответствующего
подкрепления не происходит. Становление и развитие способностей - это тоже
результат научения, и чем сильнее подкрепление, тем быстрее будет идти
развитие. Что же касается нужного эмоционального настроя, то он создается таким
чередованием успехов и неудач в деятельности, развивающей способности человека,
при котором за неудачами (они не исключены, если деятельность находится в зоне
потенциального развития) обязательно следует эмоционально подкрепляемые успехи,
причем их количество в целом является большим, чем число неудач.
Математические способности
Исследованием математических способностей
занимались и такие яркие представители определенных направлений в зарубежной
психологии, как А. Бинэ, Э. Трондайк и Г. Ревеш, и такие выдающиеся математики,
как А. Пуанкаре и Ж. Адамар. Большое разнообразие направлений определило и
большое разнообразие в подходе к исследованию математических способностей, в
методических средствах и теоретических обобщениях. Единственное, в чем сходятся
все исследователи, это, пожалуй, мнение о том, что следует различать обычные,
«школьные» способности к усвоению математических знаний, к их репродуцированию
и самостоятельному применению и творческие математические способности,
связанные с самостоятельным созданием оригинального и имеющего общественную
ценность продукта. Большое единство взглядов проявляют зарубежные исследователи
по вопросу о врожденности или приобретенности математических способностей. Если
и здесь различать два разных аспекта этих способностей - «школьные» и
творческие способности, то в отношении вторых существует полное единство -
творческие способности ученого-математика являются врожденным образованием,
благоприятная среда необходима только для их проявления и развития. В отношении
«школьных» (учебных) способностей зарубежные психологи высказываются не столь
единодушно. Здесь, пожалуй, доминирует теория параллельного действия двух
факторов - биологического потенциала и среды. Основным вопросом в исследовании
математических способностей (как учебных, так и творческих) за рубежом был и
остается вопрос о сущности этого сложного психологического образования.
Выделяют три важные проблемы.
Проблема специфичности математических
способностей. Существуют ли собственно математические способности как
специфическое образование, отличное от категории общего интеллекта? Или
математические способности есть качественная специализация общих психических
процессов и свойств личности, то есть общие интеллектуальные способности,
развитые применительно к математической деятельности? Иначе говоря, можно ли
утверждать, что математическая одаренность - это не что иное, как общий
интеллект плюс интерес к математике и склонность заниматься ею?
Проблема структурности математических
способностей. Является ли математическая одаренность унитарным (единым
неразложимым) или интегральным (сложным) свойством? В последнем случае можно
ставить вопрос о структуре математических способностей, о компонентах этого
сложного психического образования.
Проблема типологических различий в
математических способностях. Существуют ли различные типы математической
одаренности или при одной и той же основе имеют место различия только в
интересах и склонностях к тем или иным разделам математики?
Для математика недостаточно иметь хорошую память
и внимание. По мнению Пуанкаре, людей, способных к математике, отличает умение
уловить порядок, в котором должны быть расположены элементы, необходимые для
математического доказательства. [14] Наличие интуиции такого рода - есть
основной элемент математического творчества. Одни люди не владеют этим тонким
чувством и не обладают сильной памятью и вниманием и поэтому не способны
понимать математику. Другие обладают слабой интуицией, но одарены хорошей
памятью и способностью к напряженному вниманию и потому могут понимать и
применять математику. Третьи владеют такой особой интуицией и даже при отсутствии
отличной памяти могут не только понимать математику, но и делать математические
открытия. [1] Здесь речь идет о математическом творчестве, доступном немногим.
Но, как писал Ж. Адамар, «между работой ученика, решающего задачу по алгебре
или геометрии, и творческой работой разница лишь в уровне, в качестве, так как
обе работы аналогичного характера». [1] Для того чтобы понять, какие качества
еще требуются для достижения успехов в математике, исследователями
анализировалась математическая деятельность: процесс решения задач, способы
доказательств, логических рассуждений, особенности математической памяти. Этот
анализ привел к созданию различных вариантов структур математических
способностей, сложных по своему компонентному составу. При этом мнения большинства
исследователей сходились в одном - что нет и не может быть единственной ярко
выраженной математической способности - это совокупная характеристика, в
которой отражаются особенности разных психических процессов: восприятия,
мышления, памяти, воображения.
Основным положением отечественной психологии в
этом вопросе является положение о решающем значении социальных факторов в
развитии способностей, ведущей роли социального опыта человека, условий его
жизни и деятельности. Психические особенности не могут быть врожденными. Это
целиком относится и к способностям. Способности всегда результат развития. Они
формируются и развиваются в жизни, в процессе деятельности, в процессе обучения
и воспитания. В индивидах должны существовать предпосылки, внутренние условия для
развития способностей. А.Н. Леонтьев и А.Р. Лурия также говорят о необходимых
внутренних условиях, делающих возможным возникновение способностей. Способности
не заключены в задатках. В онтогенезе они не проявляются, а формируются.
Задаток не потенциальная способность (а способность не задаток в развитии), так
как анатомо-физиологическая особенность ни при каких условиях не может
развиваться в психическую особенность. [10]
Среди наиболее важных компонентов математических
способностей выделяются специфическая способность к обобщению математического
материала, способность к пространственным представлениям, способность к
отвлеченному мышлению. Некоторые исследователи выделяют также в качестве
самостоятельного компонента математических способностей математическую память
на схемы рассуждений и доказательств, методы решения задач и принципы подхода к
ним. Отечественный психолог, исследовавший математические способности у
школьников, В.А. Крутецкий дает следующее определение математическим
способностям: «Под способностями к изучению математики мы понимаем
индивидуально-психологические особенности (прежде всего особенности умственной
деятельности), отвечающие требованиям учебной математической деятельности и
обусловливающие на прочих равных условиях успешность творческого овладения
математикой как учебным предметом, в частности относительно быстрое, легкое и
глубокое овладение знаниями, умениями и навыками в области математики». [8]
1.2 Общая структура математических
способностей (по В.А. Крутецкому)
В этом параграфе представлена общая структура
математических способностей в школьном возрасте по В.А. Крутецкому. Она
рассматривается исходя из основных этапов решения задач: I. получение
математической информации; II. переработка математической информации; III. хранение
математической информации. Каждому из этапов I - III соответствует одна или
несколько математических способностей. Приведем описание каждой математической
способности с выделением действий, которые присущи каждой способности и
описание протоколов решения задач способными и неспособными учениками,
описанные Вадимом Андреевичем Крутецким в книге [8].
Способности, необходимые для
получения математической информации
Способность к формализованному восприятию
математического материала, схватывания формальной структуры задачи
Действия, представленные за данной способностью.
При наличии данной математической способности школьники выполняют следующие
действия:
выделять различные элементы в математическом
материале задачи;
давать элементам математического материала
задачи различную оценку;
систематизировать элементы математического
материала задачи;
объединять элементы математического материала
задачи в комплексы;
отыскивать отношения и функциональные
зависимости элементов математического материала задачи.
Первые три действия направлены на восприятия
математического материала задачи аналитически, другие же направлены на
синтетическое восприятие математического материала задачи.
Особенности выполнения I этапа решения задач
учащимися, обладающие этой способностью. Для выяснения особенности восприятия
математического материала В.А. Крутецкий используется серия «Системы однотипных
задач». Эта серия рассчитана на учащихся, еще незнакомых с формулами
сокращенного умножения. Исследовалось, как учащиеся могут выделить основное,
главное, существенное с точки зрения типа задачи, отвлечься от несущественного,
второстепенного, от деталей. При помощи этой серии исследуется также процесс
обобщения - подведение объектов под только что, сформировавшееся в своей основе
понятия.
Рассмотрим решение одного из тестов серии
«Системы однотипных задач» направленного на выяснения овладения этой
способностью способными к математике и неспособными к математике учащимися.
Серия представляет собой своеобразную «лестницу задач» одного и того же типа,
от наиболее простой к весьма сложной. Выясняется, как сумеет испытуемый
доказать, что данная задача, несмотря на ее внешнее отличие, принадлежит к тому
же самому типу, и как, учитывая конкретные особенности задачи, он собирается
решать ее по общей схеме решения задач установленного им типа.
Приведем наглядный пример, как справлялись с
одной из задач этой серией способные к математике ученики и неспособные.
Способные ученики при решении задачи на
применение формулу сокращенного умножения (a+b)2. Они легко выделяют
существенные для данного типа моменты (сумма двух алгебраических выражений в
квадрате), равно как и несущественные для данного типа (конкретная величина и
характер алгебраических выражений, составляющие число a и b). Другими словами
имела место своеобразная формализация структуры задачи при ее восприятии, когда
задача (например, 6ах+1/2by)2 «схватывалась в такой форме: (›+›)2=.
Неспособные же учащиеся узкоограниченно
представляли себе «первое» и «второе» число в этой формуле, им было трудно
понять, что a и b обозначают любую величину и любое алгебраическое выражение.
Поэтому они и не улавливали самостоятельно структурного «костяка» задачи.
Способности, необходимые для
переработки математической информации
Способность к логическому рассуждению в сфере
количественных и пространственных отношений, числовой и знаковой символики
Характеристика способности. Одной из особенности
математики является алгоритмичность решения многих задач. Алгоритмом, как
известно, называется определенное указание относительно того, какие операции и
в какой последовательности надо выполнить, чтобы решить любую задачу некоторого
типа. Алгоритм представляет собой обобщение, так как применим ко всем задачам
соответствующего типа. Конечно, очень большое количество задач не
алгоритмизируется и решается с помощью специальных, особых приемов. Поэтому
способность находить пути решения, не подходящие под стандартное правило,
является одной из существенных особенностей математического мышления.
Действия, представленные за данной способностью.
При наличии данной математической способности школьники выполняют следующие
действия:
логически рассуждают (доказывать, обосновывать);
оперируют специальными математическими знаками,
условными символическими обозначениями количественных величин и отношений и
пространственных свойств;
переводят на язык символов.
Особенности выполнения II этапа решения задач
учащимися, обладающими данной способностью. Для выяснения этой способности
применяется серия «Задачи на доказательство». Серия представляет собой систему
однотипных задач, все усложняющихся доказательств.
Для примера возьмем решения задачи способным и
неспособным учеником.
Вот как решал задачу способный ученик:
«Доказать, что сумма любых трех последовательных чисел делится на 3 (при любом
целом значении а)». Последовательные числа - это такие числа, когда каждое из
последующих на единицу больше предыдущего, так кажется? Как же тут доказать? 2,
3 и 4 в сумме действительно делятся на 3; 12, 13, 14 тоже в сумме дают 39.
Можно доказать так: сумма трех одинаковых чисел, разумеется, делится на 3. Да
еще прибавляются 3 единицы (второе число на единицу, а третье - на две единицы
больше первого), которые тоже делятся на 3. Можно и алгебраически доказать:
х+(х+1)+(х+2)=3х+3=3(х+1). Последнее выражение всегда можно разделить на 3,
каково бы ни было исходное число х.
Вот как справляется с подобной задачей
неспособный ученик.
Задача. Задумайте любое число, умножьте его на
число, больше задуманного на 6 и прибавить 9. Доказать, что полученный
результат является квадратом.
Уч.: А что значит «является квадратом? Квадратом
какого числа?
Эксп.: Есть числа, которые не являются квадратом
какого-либо числа, например 13 или 20. А есть числа, которые являются
результатом возведения в квадрат какого-либо числа, например 9 (т.е.3).
Уч.: Понятно. А здесь как доказывать?
Эксп.: Подумай. Примени, способ алгебраического
доказательства. Сказано: «Задумайте любое число». Как в алгебре обозначается
«любое число»?
Уч.: А теперь знаю: х×(х+6)+9=х2+6х+9.
Вот х2 и есть квадрат задуманного числа.
Эксп.: Ты взял только часть результата. А тебе
нужно доказать, что весь полученный результат есть квадрат какого-то числа.
Квадратом какого выражения является полученный тобой результат? Вспомни формулы
сокращенного умножения?
Уч.: Знаю. Получится (х+3)2. (дает ответ не
сразу).
Эксп.: Но всегда ли в результате получится
квадрат?
Уч.: Не знаю.
Лишь после продолжительного разъяснения
экспериментатора ответил: «По-моему, всегда, так как мы брали любое число».
Способность к быстрому и широкому обобщению
математических объектов
Характеристика способности. Способность к
обобщению математического материала рассматривается в двух планах: 1) как
способность человека увидеть в частном, конкретном уже известном ему общее
(подведение частного случая под известное общее понятие) и 2) способность
увидеть в единичном, частном пока еще неизвестное общее (вывести общее из
частных случаев, образовать понятие). Одно дело - увидеть возможность
применение к данному частному случаю уже известной ученику формулы, другое - на
основание частных случаев вывести формулу, еще неизвестную ученику.
Действия, представленные за данной способностью.
При наличии данной математической способности школьники выполняют следующие
действия:
видят сходную ситуацию в сфере числовой и
знаковой символики (где применить);
владеют обобщенным типом решения, обобщенной
схемой доказательства, рассуждения (что применить).
И в том и другом случае необходимо отвлечься от
конкретного содержания и выделить сходное, общее и существенное в структурах
объектов, отношений или действий.
Особенности выполнения II этапа решения задач
учащимися, обладающими данной способностью. На выявление этой способности В.А.
Крутецкий предлагает серию задач, которая уже использовалась для проверки
математической способности - способность к формализованному восприятию математического
материала.
Приведем пример решения одной из задачи этой
серии. После решения примера на применение формулы «квадрат суммы» дается
способному ученику для решения пример: (C+D+E)(E+C+D). Ученик применяет формулу
и пишет (C+D+E)2 и соединяет два члена - (C+(D+E))2 после чего непосредственно
применяет формулу и раскрывает скобки.
Неспособные к математике ученик, усвоив формулу
(a+b)2 и принцип рассуждения приступает к решению примера (1+ а3b2)2.
а3b2)2.
Эксп.: А вот этот пример можно решить по формуле
сокращенного умножения?.
Уч.: Здесь что-то другое - и a и b справа и не
разделяются плюсом… (пишет:  ». Эксп.: «Куда же
делась единица?. Ученик молчит.
». Эксп.: «Куда же
делась единица?. Ученик молчит.
Эксп.: Ну а реши такой пример: (2x+y)2.
Ученик пишет, повторяя вслух формулу: 4x2+2×2x×y+y2=4x2+4x+y2.
Эксп.: Верно. Вот так же решай и предыдущую
задачу.
Уч.: А здесь что-то другое… квадрат первого -
это  .
.
Эксп.: Давай рассуждать вместе. Чтобы применить
формулу, надо убедиться, что мы имеем дело с квадратом суммы двух чисел. Тебе
ясно, что это квадрат?
Уч.: Вот здесь (показывает) цифра 2 показывает,
что-то, что в скобках, надо помножить само на себя.
Эксп.: Верно. А в скобках двучлен? Покажи, где
первый член, первое «число».
Уч.:  …или
нет, что я говорю… между членами должен быть знак плюс. Тут нет первого члена,
только второй.
…или
нет, что я говорю… между членами должен быть знак плюс. Тут нет первого члена,
только второй.
В дальнейшем ученик все же решает данный пример
с помощью экспериментатора.
Способность к свертыванию процесса
математического рассуждения и системы соответствующих действий. Способность
мыслить свернутыми структурами
Характеристика способности. Наряду с
развернутыми умозаключениями в умственной деятельности школьников при решении
задач занимает определенное место и свернутые умозаключения, когда ученик не
осознает правила, общего положения, в соответствии с которыми он фактически действует.
Действия, представленные за данной способностью.
При наличии данной математической способности школьники выполняют действие -
свертывание умозаключений.
То есть в процессе решения задач ученик не
выполняет всей той цепи соображений и умозаключений, которые образуют полную,
развернутую структуру решения.
Особенности выполнения II этапа решения задач
учащимися, обладающими данной способностью. На выявление этой способности
применяется серия «Система разнотипных задач». Приведем пример как способный ученик
решал одну из задач этой серии.
Задача. Автомобиль прошел путь из А в Б со
скоростью 20 км в час, а обратно со скоростью 30 км в час. Какова средняя
скорость автомобиля за весь рейс?
Уч.: Ясно, что со скоростью 30 км в час он шел
меньше времени, чем со скоростью 20 км в час (при одинаковом пути). А раз так,
то средняя скорость не будет равна 25 км в час. Как же решить? (Дальнейший ход
решения разбиваем на отдельные звенья.) Буду решать по рассуждению.
Скорость - это результат от деления пути на
время. Значит, надо знать общий путь и общее время, затраченное на весь путь, и
поделить общий путь на общее время.
Теперь ясно, как решить. Надо узнать весь
пройденный путь. Если путь в один конец обозначим через х, то весь путь - 2х.
Теперь надо узнать время. Оно различно. Чтобы
узнать время, надо поделить путь на скорость.
На путь туда потратили 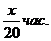
А на путь обратно потрачено 
А всего весь путь занял, значит,  =
=
Делим теперь общий путь на общее количество
часов:
х :  км
в час.
км
в час.
Что касается неспособных, то у них не замечалось
сколько-нибудь заметного свертывания даже в результате многих упражнений. На
первых этапах овладения они постоянно путаются в громоздкой цепи умозаключений,
которая с трудом, с помощью экспериментатора, закрепляется, постепенно
превращается в относительно стройную систему. Ни о каком свертывании на этих
этапах не может быть и речи, так как сам процесс рассуждения еще находится на
стадии становления. Да и в дальнейшем они нуждались лишь в полном составе
рассуждений.
Характеристика способности. Эта математическая
способность выражается в легком и свободном переключении с одной умственной
операции на другую, в многообразие аспектов подходов к решению задач, в
легкости перестройки сложившихся схем мышления и систем действий.
Действия, представленные за данной способностью.
При наличии данной математической способности школьники выполняют следующие
действие - переключаются на новый способ действия, т.е. с одной умственной
операции на другую.
Особенности выполнения II этапа решения задач
учащимися, обладающими данной способностью. На эту способность направлены серия
тестов «Задачи, наталкивающие на «самоограничение»». В эту серию отобраны
задачи на рассуждение, отличающиеся следующими способностями: либо их условие
обычно воспринимается с ограничением, которого в действительности не
существует, либо в процессе решения решающий невольно ограничивает себя
некоторыми возможностями, неправомерно исключая друг друга. В том и другом
случае непроизвольное ограничение приводит к мысли о невозможности решения
задачи.
Способный ученик решает задачу «В прямоугольном
треугольнике один катет 7 см. Определить две другие стороны, если они выражены
целыми числами».
«Построить треугольник по одной стороне? Что-то
странное…Правда, еще угол дан - прямой, но все равно нельзя… (чертит). Ну, вот
же видно - сторона и угол постоянны, а вот сколько разных треугольников. Может
быть, задача не решается? (Эксп.: Нет. Задача решается».) Странно… (чертит) Ну
вот же ясно видно, что бесконечное количество решений (еще чертит). Что-то я не
столько решаю, сколько пытаюсь доказать, что она не решается... Может быть,
вариантов-то много, но все они выражаются дробными числами (еще раз читает
условие). Может быть только один случай, когда выражаются целыми числами?
Наверное, так - в условии об этом не говориться, но можно понять…Но тогда это
надо доказать… Если гипотенуза а, а неизвестный катет b, то a2=49+b2 по
Пифагору, а 49=a2-b2…Ну и что дальше? a+b=49/a-b. Чувствую, что это что-то
даст…Если a и b - целые числа, то и их сумма - целое число…Ну вот, ясно все:
значит, 49 делится на a-b без остатка. А 49 делится только на 7…Но a-b не может
быть равно 7, так как тогда и треугольника не будет (гипотенуза в точности
равна двум катетам - две стороны равны третий)…Где-то тут есть решение, я его
упустил… Но ведь 49 делится не только 7, а и на 1, и на 49. Ну вот теперь
решение в кармане: 49 тоже не может быть - гипотенуза будет больше, чем сумма
катетов. Остается одно: a-b=1, a a+b=49. Получится 25 см. гипотенуза и 24 см
катет».
Неспособных учеников отличает инертность,
косность, скованность мысли в сфере математических отношений и действий,
устойчивый, стереотипный характер действий, навязчивое удерживание в сознании
предшествующего принципа решений, способа действий, оказывающего тормозящее
влияние при необходимости перестроить действие, что определяет ярко выраженную
затрудненность и переключении от одной умственной операции к другой,
качественно иной.
Стремления к ясности, простоте решения,
экономности и рациональности решения
Характеристика способности. Эта особенность
математического мышления способных к математике учащихся тесно связана с
предыдущей. Для способных учеников весьма характерно стремление к наиболее
рациональным решениям задач, поиски наиболее ясного, кратчайшего, а,
следовательно, и наиболее «изящного» пути к цели. Это выглядит как своеобразная
тенденция к экономии мысли, выражающееся в поисках наиболее экономных путей
решения задач.
Действия, представленные за данной способностью.
При наличии данной математической способности школьники выполняют следующие
действие - находят наиболее рациональное решение задачи.
Особенности выполнения II этапа решения задач
учащимися, обладающими данной способностью. Эту способность Вадим Андреевич
выяснял при помощи «Задачи на соображение логическое рассуждение». Для этого он
сопоставлял реальный процесс рассуждения школьника с максимально развернутым.
Сравнивал количество и характер «звеньев» в том и другом случае, они
сопоставляются с характером и количеством звеньев действительно развернутой
структуры.
Например, способный ученик решал задачу: «Найти
наименьшее число, которое при деление на 3 дает остаток 1, при делении на 4
дает остаток 2, при делении на 5 дает в остатке 3 и при делении на 6 дает в
остатке 4» Способный ученик прежде всего нашел наименьшее общее кратное данных
чисел (60) и произнес: «60-2=58. Это число 58». По просьбе экспериментатора
пояснил: «Я представил все числа и остатки столбиком и сразу увидел, что во
всех случаях разница между делителем и остатком - 2. Значит, если добавить к
искомому числу 2, то оно разделится на все числа без остатка. Наименьшее из
таких чисел - 60. Но теперь уберем двойку - будем 58».
Неспособные учащиеся не обращают особого
внимания на качество решения. Они прекращают работу после над задачей и не
задаются вопросом: «А нельзя ли решить проще, яснее?».
Способность к быстрой и свободной перестройке
направленности мыслительного процесса, переключению с прямого на обратный ход
мысли (обратимость мыслительного процесса при математическом рассуждении)
Характеристика способности. Под обратимостью
мыслительного процесса понимается перестройка его направленности в смысле
переключения с прямого на обратный ход мысли. Это понятие объединяет два
разных, хотя и связанных друг с другом процесса.
Во-первых, это установление двухсторонних (или
обратимых) ассоциаций (связей) А«Б в
противоположность односторонним связям типа А®Б,
функционирующим только в одном направлении.
Во-вторых, это обратимость мыслительного
процесса в рассуждении, обратное направление мысли от результата, продукта к
исходным данным, что имеет место, например, при переходе от прямой к обратной
теореме.
Действия, представленные за данной способностью.
При наличии данной математической способности школьники выполняют следующие
действие - перестраивать мыслительный процесс с прямого на обратный ход мыслей.
Особенности выполнения II этапа решения задач
учащимися, обладающими данной способностью. Для выяснения этой способности В.А.
Крутецкий предлагал серию задач «Прямые и обратные задачи». В этой серии
включены парные задачи - прямая и обратная. Обратными задачами условно
называются те, которые по сравнению с исходными (прямыми) задачами при
сохранении сюжета искомое входит в состав условия, а один или несколько
элементов условия становятся искомыми.
Приведем пример как способные, и неспособные
учащиеся решали эти задачи:
Способный ученик овладел типом решения по
формуле «произведения суммы двух чисел на их разность равно разности квадратов
этих чисел».
Ему предлагается разложить на множители
выражение (x-y)2-25y8. Он тут говорит, что эта задача наоборот и тут уже есть
разность квадратов и записывает выражение (x-y+5y4) (x-y-5y4). Свое решение он
объясняет, что нужно подумать из чего получились квадраты и взять сумму этих
чисел и помножить на разность.
Неспособный ученик с трудом, после большого
количества упражнений, овладел способом решения задач по этой формуле.
Эксп.: Реши задачу 5×5=(ученик
дает верный ответ). А теперь реши такую: какие числа надо перемножить, чтобы
получить 25 (ученик дает верный ответ). Теперь смотри 5×5=25,
а 25=5×5.
Вторая задача обратная первой. Реши задачу (2x+y)(2x-y)= (ученик дает верный
ответ). Правильно. Но если (2x+y)(2x-y)=4x2-4y2, то наоборот можно ли сказать,
что 4x2-4y2= (2x+y)(2x-y)? (Ученик дает утвердительный ответ). А 9x2-4y2 чему
равняется?
Уч.: Не знаю. Это какие-то чудные задачи. Мы
такие не решали.
Эксп.: Да, не решали, но учимся решать. Вот ты
подумай: чему равно произведение суммы двух чисел на их разность? Это ты
знаешь.
Уч.: Произведение суммы двух чисел на их
разность равняется квадрату первого минус квадрат второго.
Эксп.: Верно. А обратно можно сказать? Чему
равна разность квадратов? Чему равно a2-b2?.
Уч.: a2-b2=(a+b)(a-b).
Эксп.: А 9x2-4y2 чему равно?
Уч.: (9x+4y)(9x-4y)…
Дальнейший ход беседы опускаем. Лишь после
многократных пояснений и упражнений ученик научился решать задачи этого типа,
да и только простейшие.
Способности, необходимые для
хранения математической информации
Математическая память (обобщенная память на
математические отношения, типовые характеристики, схемы рассуждений и
доказательств, методы решения задач и принципы подхода к ним)
Характеристика способности. Сущность
математической памяти заключается в обобщенном запоминании типовых схем
рассуждений и действий. Что же касается памяти на конкретные данные, числовые
параметры, то она «нейтральна» по отношению к математическим способностям.
Действия, представленные за данной способностью.
При наличии данной математической способности школьники выполняют следующие
действия:
запоминают типовые признаки задач и обобщенные
способы их решения, схемы рассуждений, основные линии доказательств, логические
схемы;
сохраняют в памяти типовые признаки задач и
обобщенные способы их решения, схемы рассуждений, основные линии доказательств,
логические схемы.
Особенности выполнения III этапа решения задач
учащимися, обладающими данной способностью. Способные ученики в большинстве случаев
довольно долго помнят тип решенной ими в свое время задачи, общий характер
действий, но не помнят конкретных данных задачи, чисел. Неспособные, наоборот,
помнят только конкретные числовые данные или конкретные факты, относящиеся к
задаче. Если неспособный помнит, что решал «какую-то задачу с клетками и
кроликами», или «что-то про рыбу, которая весит 2 пуда», то способный обычно
гораздо чаще помнит тип задачи: «Решал задачу на различные сочетания частей
целого - про рыбу, у которой хвост с головой весит столько-то, а голова с
туловищем - столько-то, и хвост с туловищем - еще столько-то».
Выделенные способности тесно связаны, влияют
друг на друга и образуют в своей совокупности единую систему, целостную
структуру, своеобразный синдром математической одаренности, математический
склад ума.
Не входят в структуру математической одаренности
те способности, наличие которых в этой системе не обязательно (хотя и полезно).
В этом смысле они являются нейтральными по отношению к математической
одаренности. Однако их наличие или отсутствие в структуре (точнее, степень их
развития) определяют тип математического склада ума. Не являются обязательными
в структуре математической одаренности следующие компоненты:
Быстрота мыслительных процессов как временная
характеристика.
Вычислительные способности (способности к
быстрым и точным вычислениям, часто в уме).
Память на цифры, числа, формулы.
Способность к пространственным представлениям.
Способность наглядно представить абстрактные
математические отношения и зависимости.
1.3 Формирование математических
способностей
Среди учителей распространены следующие
заблуждения. Во-первых, многие считают, что математические способности
заключаются, прежде всего, в способности к быстрому и точному вычислению (в
частности в уме). На самом деле вычислительные способности далеко не всегда
связаны с формированием подлинно математических способностей. Во-вторых, многие
думают, что способные к математике школьники отличаются хорошей памятью на
формулы, цифры, числа. Однако, как указывает академик А. Н. Колмогоров, успех в
математике меньше всего основан на способности быстро и прочно запоминать
большое количество фактов, цифр, формул. [6] Наконец, считают, что одним из
показателей математических способностей является быстрота мыслительных процессов.
[3] Особенно быстрый темп работы сам по себе не имеет отношения к
математических способностям. Ученик может работать медленно и неторопливо, но в
то же время вдумчиво, творчески, успешно продвигаясь в усвоении математики.
Исследования психологических особенностей
формирования математических способностей у школьников показали, что обычно
учащиеся усваивают содержательную сторону знаний и непосредственно с ней
связанные конкретные приемы решения довольно узкого круга задач. Лишь у
школьников с высокой обучаемостью на основе решения единичных задач формируются
обобщенные приемы, методы решения целого класса задач.[7]
Формирование такого рода обобщенных приемов
умственной деятельности чрезвычайно важно, так как оно означает существенный
сдвиг в интеллектуальном развитии, расширяет возможности переноса знаний в
относительно новые условия. Поскольку основная масса учащихся самостоятельно не
овладевает более обобщенными приемами умственной деятельности, их формирование
является важной задачей обучения.
В практике используется специальное формирование
обобщенных приемов умственной деятельности. Обобщенные приемы умственной
деятельности делятся на две большие группы - приемы алгоритмического типа и
эвристические.
Приемы алгоритмического типа - это приемы рационального,
правильного мышления, полностью соответствующего законам формальной логики.
Точное следование предписаниям, даваемым такими приемами, обеспечивает
безошибочное решение широкого класса задач, на который эти приемы
непосредственно рассчитаны. С помощью этого приема учеников обучают тому, как
определять понятия, классифицировать их, строить умозаключения, решать в
соответствии с данным алгоритмом задачи, оказывает положительное влияние и на
самостоятельное, продуктивное мышление, обеспечивает возможность решения
задач-проблем.
Формирование приемов мыслительной деятельности
алгоритмического типа, ориентирующих на формально-логический анализ задач,
является необходимым, но не достаточным условием формирования математических
способностей. Необходимо оно, во-первых, потому, что содействует
совершенствованию репродуктивного мышления, являющегося важным компонентом
творческой деятельности (особенно на начальном и конечном этапах решения
проблем). Во-вторых, эти приемы служат тем фондом знаний, из которых ученик
может черпать «строительный материал» для создания, конструирования методов
решения новых для него задач.
Недостаточным формирование алгоритмических
приемов является потому, что не соответствует специфике продуктивного мышления,
не стимулирует интенсивное развитие именно этой стороны мыслительной
деятельности. Вот почему формирование таких приемов должно сочетаться со
специальным вооружением учащихся приемами эвристического типа.
Приемы другого типа назвали эвристическими
потому, что они непосредственно стимулируют поиск решения новых проблем,
открытие новых проблем, открытие новых для субъекта знаний и тем самым
соответствуют самой природе, специфике творческого мышления. В отличие от
приемов алгоритмического типа, эвристические приемы ориентируют не на
формально-логический, а на содержательный анализ проблем. Они направляют мысль
решающих на проникновение в суть описываемого в условии предметного содержания,
на то, чтобы за каждым словом они видели его реальное содержание и по нему
судили о роли в решении того или иного данного.
Многие эвристические приемы стимулируют
включение в процесс решения проблем наглядно-образного мышления, что позволяет
использовать его преимущество перед словесно логическим мышлением - возможность
целостного восприятия, видения всей описываемой в условии ситуации.
Часть этих приемов направляет решающего на
использование весьма характерного для творческой деятельности мыслительного
эксперимента, который облегчает постановку и предварительную проверку гипотез и
пути решения проблем. Включая имеющиеся в условии задачи данные в различные
связи, в новые ситуации, решающий тем самым «вычерпывает» их новые признаки,
используя оптимальный для творческого процесса «анализ через синтез».
К эвристическим приемам относится конкретизация,
когда ученик придает абстрактным данным условия более конкретную форму. Этот
прием дополняется приемом графического анализа, вводящего наглядные опоры
различной степени символизации. [7]
Противоположным является прием абстрагирования,
когда решающий отбрасывает конкретные детали, «оголяя» данные и соотношения
между ними. «На 4800 рублей больше и вдвое дороже» - вот и все, что выделено
учеником в одной из задач, и на этом сосредотачивает он внимание.
Наиболее распространенным приемом, облегчающим
выявление функциональных связей между данными, является варьирование. Этот
прием заключается в том, что ученик произвольно отбрасывает или изменяет
величину одного из данных (а иногда и нескольких) и на основе логического
рассуждения выясняет, какие следствия вытекают из такого преобразования, как
отразилась изоляция данного на остальных. По этим изменениям легче судить о
связи выделенного данного с другими.
Широко используются при решении проблем приемы
аналогии, постановка аналитических вопросов. Ю.Н. Кулюткин указывает, что
положительным итогом проведенного обучения явилось изменение самого подхода к
учению. [16] Школьников стала привлекать самостоятельная познавательная
деятельность, т.е. у них изменилась мотивация учения. Очевидно, существенное
влияние оказали положительные эмоции, возникающие при самостоятельном открытии,
которое оценивается решающим, как его интеллектуальная победа.
Итак, алгоритмические приемы обеспечивают
правильное решение задач известных учащимся типов; они учат школьников логике
рассуждений, служат фоном, который возможно использовать при поисках решения
проблем. Эвристические приемы позволяют действовать в условиях
неопределенности, в принципиально новых ситуациях, облегчая поиск решения новых
проблем.
Дискуссионным остается вопрос о том, следует ли
заботиться о знании учениками формул, их всегда можно воспроизвести по
справочникам. Ответ на вопрос, надо ли запоминать формулы, в частности, получен
в исследовании С. И. Шапиро. Результаты экспериментов показали, что в простых
ситуациях, когда зависимости используются всегда одинаково (т. е. когда
требуется репродуктивное мышление), их предварительное специальное запоминание
не обязательно, вполне возможно использование внешних средств (справочников и
т.п.). Напротив, в сложных ситуациях, при решении нестандартных задач, т.е.
тогда, когда должно активизироваться продуктивное мышление, необходимо прочное
закрепление основных формул в памяти. Известный педагог В. Ф. Шаталов на
аналогичный вопрос отвечает: «Ученик, который работает со справочником,
отличается от ученика, который знает все формулы, так же как отличается
начинающий шахматист от гроссмейстера. Он видит только один ход вперед». [12]
Прямая установка на запоминание повышает уровень мыслительной активности при
работе над подлежащим усвоению материалом, степень ее саморегуляции и
самоконтроля, что значительно увеличивает эффект усвоения. Этому же
способствует сознательное применение рациональных приемов мнемической
деятельности (таких как группировка, классификация, составление плана,
выделение смысловых опор и т.д.). Чтобы открывать новое, отвергать уже
известное, необходимо владеть этим старым, иметь достаточно широкий объем
знаний (включая и их операционную сторону), достаточных для движения вперед и
находящихся в состоянии готовности к актуализации в соответствии с поставленной
перед субъектом целью. Чтобы выполнить это чрезвычайно важное требование, нужно
предусмотреть специальную организацию мнемической деятельности, обеспечивающую
прочность усваиваемых знаний и их готовность к актуализации при решении
проблем. Эта специальная организация - один из важнейших принципов формирования
математических способностей младших школьников.
Для обеспечения достаточного уровня знаний
авторы учебных программ и учебников стремятся вводить в них все новые и новые
данные. Однако, чем больше объем подлежащих усвоению знаний, тем труднее
обеспечить прочность их усвоения. Следовательно, необходимо как-то ограничить
тот круг знаний, которые подлежат усвоению, и искать пути организации знаний в
такую систему высокого уровня обобщения, в которой по относительно немногим
прочно закрепленным ее звеньям на основе рассуждений ученик мог бы найти
дополнительные звенья, необходимые для оперирования приобретенными знаниями.
Важно четко ограничить обязательный минимум знаний от второстепенного материала
и ориентировать учащихся на тщательное закрепление именно основных знаний и
способов оперирования ими, что лучше делать сразу же при введении нового
материала.
Ориентация на выделение и обобщение
существенного в материале, классификацию в зависимости от его значимости
содействует формированию одного из важнейших качеств продуктивного мышления -
глубины ума. В связи с большим объемом подлежащих усвоению знаний необходимо по
возможности «сжать», «уплотнить» их, что может быть осуществлено на основе
более раннего введения обобщенных знаний - теорий, законов, общих методов
решения широкого класса задач. Такие знания позволяют учащимся не запоминать
множество отдельных частных закономерностей, способов решения, а самим на
основе логических рассуждений «выводить» их из общих положений.
Нами рассмотрены понятия способностей и
математической способности и их связь с умениями и навыками. Также изучены 8
математических способностей (по В.А. Крутецкому), выделили действия, характеризующие
каждую способность. И изучили формирование математических способностей в
деятельностном подходе.
Глава 2. О возможностях формирования
математических способностей в курсе «Начала алгебры»
.1 Характеристика курса
Проанализируем учебный курс «Начала алгебры»,
разработанный в рамках деятельностного подхода и выполняющий одну из задач
предпрофильной подготовки, т.е. создание условий для получения учащимися
минимального личного опыта в различных видах деятельности. [17]
Курс «Начала алгебры» предназначен для классов,
продолжающих развивающего обучение математике в среднем звене разработан
сотрудниками лаборатории развивающего обучения математике института психологии
и педагогики развития г. Красноярска под руководством О.В. Знаменской. Он предназначен
для классов обучающихся первые 4 года по системе Д.Б. Эльконина - В.В.
Давыдова.
В методическом руководстве курса «Начала
алгебры» отмечается, что единицей обучения в курсе является учебный цикл,
состоящий из шести этапов:
постановка проблемы (задачи);
открытие нового понятия (может использовать
рабочий язык);
систематизация новых знаний;
анализ текстов учебников (переход на культурный
язык);
выделение класса типовых задач (на навык);
контроль и оценка.»[5]
В программу заложен дифференцированный подход к
обучению, по мнению авторов, это позволяет, как сохранить интерес к предмету у
слабых учащихся и, так обеспечивать возможность развития для всех. Это
обеспечивается за счет:
наличия разных уровней проработки материала при
решении учебной задачи и возможности переходить с одного уровня на другой, что
позволяет даже самому слабому учащемуся вносить вклад в решение общей проблемы
и сохранять интерес к предмету;
введения нескольких способов решения одной
задачи, которые могут быть, как открыты самими учащимися, так и найдены в
литературе (в частности, в учебнике). (Более слабый учащийся может выбрать
наиболее понятный ему способ решения задачи, сильный может освоить все и
выбирать наиболее эффективный способ для конкретной ситуации.);
наличия дополнительного образовательного
пространства как места для математического творчества и самостоятельного
инициативного движения, учащихся в предмете математики;
наличия условий для написания разножанровых
творческих работ, связанных как места для математического творчества и
самостоятельного инициативного движения, учащихся в предмете математики;
постепенного усложнения требований (то, что на
пятом году обучения способны делать самостоятельно лидеры и остальные учащиеся
в коллективно-распределенной форме, к шестому - седьмому годам обучения
начинает требоваться как норма от всех учащихся).
Авторами говорится, что одна из основных задач
курса состоит в том, чтобы представить математику не как набор разрозненных
фактов, а как цельную развивающуюся дисциплину общекультурного характера, что
может сделать процесс изучения школьной математики осмысленным как для ученика,
так и для учителя. В качестве основного результата обучения в среднем звене
авторами рассматривается математическая грамотность учащихся как общекультурное
умение. В это умения входит:
владение основными понятиями и методами изучения
математических объектов (такими как общение, спецификация, аналогия,
распространение, систематизация и др.);
умение эффективно использовать математические
способы вычислений, преобразований и др.;
владение языком изложения математических знаний
(письменная математическая речь);
владение терминологией, связанной с
исследованием (гипотеза, утверждение, доказательство).
Основы математической грамотности закладываются
на пятом году обучения. Авторами описаны результаты 5 года обучения следующим
образом: учащиеся должны иметь навыки работы с записью (построения и
преобразования формы записи), уметь формулировать утверждения и проверять их на
правдоподобность, различать способы проверки утверждения для произвольного и
для конкретного случая, понимать разницу между утверждением, теоремой,
гипотезой, оценивать эффективность применения способа.
Попытаемся соотнести компоненты a-d
математической грамотности и типов математических способностей, описанных в
предыдущей главе. По нашему мнению, первые три компонента востребуют
становления следующих математических способностей:
способность к формализованному восприятию
математического материала, схватывания формальной структуры задачи;
способность к быстрому и широкому обобщению
математических объектов;
способность к логическому рассуждению в сфере
количественных и пространственных отношений, числовой и знаковой символики.
Формирование способностей, в том числе и математических
«не могут существовать иначе, как в постоянном процессе развития»[11], это
обеспечивается курсом «Начала алгебры» за счет: различных уровней проработки
материала; введение нескольких способов решения одной задачи; постепенного
усложнения требований и т.д.
Можно предположить, что на каждом из этапов
становятся разные математические способности. Например, на этапе оформление
существующих знаний становится способность формализованному восприятию
математического материала, на этапе открытия нового понятия - способность к
логическому рассуждению, на этапе систематизация новых знаний.
Таким образом, можно выдвинуть следующее
предположение: учебный материал курса «Начала алгебры» способствует
формированию следующих математических способностей:
способность к формализованному восприятию
математического материала, схватывания формальной структуры задачи;
способность к логическому рассуждению в сфере
количественных и пространственных отношений, числовой и знаковой символики;
способность к быстрому и широкому обобщению
математических объектов.
Нашей задачей является проанализировать задачный
материал курса, для того чтобы выявить наличие или отсутствие действий, лежащих
за каждой из перечисленной способности при решении этих задач и тем самым
получить основания для преобразования в гипотезу.
.2 Анализ задачного материала темы
«Теория делимости»
Итак, мы будем искать подтверждение тому, что
учебный материал темы «Теория делимости», а именно здесь, наиболее ярко
прослеживается задумка авторов курса «Начала алгебры», способствует
формированию следующих математических способностей:
способность к формализованному восприятию
математического материала, схватывания формальной структуры задачи;
способность к логическому рассуждению в сфере
количественных и пространственных отношений, числовой и знаковой символики;
способность к быстрому и широкому обобщению
математических объектов.
Для этого проанализируем соответствие действий,
выполнение которых задает те или иные математические способности (по В.А.
Крутецкому) действиям, которые выполняются при решении задач темы «Теория
делимости» курса «Начала алгебры».
Формирование способности к
формализованному восприятию математического материала
Эта математическая способность проявляется в
стремлении к своеобразной формализации структуры математического материала в
процессе его восприятия. Формализованное восприятия - это своего рода
обобщенное восприятия функциональных связей, отдельных от предметной и числовой
формы, когда в конкретном воспринимается его общая структура.
Для примера приведем анализ решения одной из
задач темы «Теория делимости» курса «Начала алгебры».
Задание. «Составьте таблицу умножения для систем
счисления с основаниями 2, 3, 4.
Выведите признаки делимости двухзначных чисел в
этих системах счисления».[4]
Для того чтобы выполнить это задание, необходимо
заполнить таблицу, правильно выполнив умножения. Правильность умножения можно
проверить при помощи сложения или перевода в 10-ичную систему счисления. При
помощи признаков делимости в 10-ичной системы счисления можно определить,
делится ли оно на некоторое заданное число. А в записи всех кратных чисел,
данному в системе счисления по основанию р (р=2, р=3, р=4) можно обнаружить
некоторую закономерность, то есть вывести признак делимости на заданное число.
Если рассматривать действия, выполняемые при
решении данного задания, и перевести их на язык математической способности, то
можно сказать, что задание направлено на формирование способности к
формализованному восприятию математического материала. Так как действие
«заполнения таблицы» можно соотнести с действием «поиска объединения элементов
математического материала в комплексы», а «обнаружения закономерности» с действием
«отыскать отношения и функциональных зависимостей элементов математического
материала задачи», то можно сказать, что данная задача позволяет формировать
математическую способность - формализованное восприятия математического
материала.
Ниже в таблице №1 приведены задания из темы
«Теория делимости» курса «Начала алгебры», которые, по нашей оценке, позволяют
формировать эту математическую способность.
Таблица 1
|
Математическая
способность
|
Действия,
присущие способности
|
Тип
задания
|
Образец
задания
|
|
Способность
к формализованному восприятию математического материала, схватывание
формальной структуры задачи.
|
Выделять
различные элементы в математическом материале задачи; давать элементам
математического материала задачи различную оценку; систематизировать элементы
математического материала задачи; объединять элементы математического
материала задачи в комплексы; отыскивать отношения и функциональные
зависимости элементов математического материала задачи.
|
Выберите
из заданного набора утверждений о делимости нацело конкретных чисел верные.
Доопределите объект, данный в утверждении, достройте запись числа так, чтобы
утверждение стало истинным. Записать формулу числа а, кратного b. Записать
формулу деления числа a на b с остатком. 4. Приведите несколько примеров к
каждому из утверждений о свойствах делимости чисел, записанных в общем виде.
5. Обобщите утверждения о делимости чисел, заменив числа буквами. Какие из
получившихся утверждений не будут верны для всех значений букв. 6.
Правдоподобно ли данное утверждение о делимости чисел. 7. Установите
делимость числа на а, если известны признаки делимости на делители а.
Сформулируйте соответствующее утверждение. 8.Даны некоторые объекты теории
чисел, для которых справедливы некоторые свойства.Сформулируйте утверждение,
которое кажется вам верным. Проверьте, справедливо ли оно для более широкого
класса объектов.
|
1.Выпишите
номера верных утверждений о делимости чисел нацело. 1)Число 355 делится на
5. 2)Число 355 делится на10. 3)Число 355 не делится на 2. 2. Какие цифры
можно поставить вместо * так, чтобы стало верным утверждение: 23* кратно
двум ______; 3. Записать формулу числа, кратного двум:____Запишите формулу
деления на два с остатком. 4. Приведите несколько примеров к каждому из
свойств отношения делимости: (1) 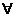 m, n, k m, n, k 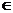  (n (n m и m m и m k) k)  n n k;
5.Замените числа буквами в утверждениях: 8356 k;
5.Замените числа буквами в утверждениях: 8356 2 и 2638 2 и 2638 2 2  (8356+2638) (8356+2638) 2; 6.
Проверьте, правдоподобно ли утверждение «Если число делится на 9, то оно
делится на 3», приведя свои примеры или еще каким-либо способом.
7.Сформулируйте утверждение о делимости чисел 121212, 2424242, 444 на 6. 8.
Постройте примеры, показывающие, что можно (или нельзя) без изменения
распространить признаки делимости для двузначных чисел в произвольной системе
счисления на числа с произвольным количеством цифр в записи. Сформулируйте
утверждение, которое кажется вам верным. 2; 6.
Проверьте, правдоподобно ли утверждение «Если число делится на 9, то оно
делится на 3», приведя свои примеры или еще каким-либо способом.
7.Сформулируйте утверждение о делимости чисел 121212, 2424242, 444 на 6. 8.
Постройте примеры, показывающие, что можно (или нельзя) без изменения
распространить признаки делимости для двузначных чисел в произвольной системе
счисления на числа с произвольным количеством цифр в записи. Сформулируйте
утверждение, которое кажется вам верным.
Формирование способности к
логическому рассуждению в сфере количественных и пространственных отношений,
числовой и знаковой символики
Способность к логическому рассуждению в сфере
количественных и пространственных отношений, числовой и знаковой символики
является одной из существенных особенностей математического мышления и
позволяет находить пути решения, не подходящие под стандартное правило.
Рассмотрим задание из темы «Теория делимости»
курса «Начала алгебры», которое, по нашему мнению, позволяет формировать эту
математическую способность.
Задание. «Выясните, можно ли без изменения
распространить признаки делимости для чисел вида  на
числа с произвольным количеством цифр в записи. Какие утверждения кажутся вам
верными?».[4] на
числа с произвольным количеством цифр в записи. Какие утверждения кажутся вам
верными?».[4]
Для решения этого задания необходимо
сформулировать и записать утверждение о делимости натурального числа  .
Затем найти многозначное число, для которого эти утверждения не верны. Если же
такое число не найдется, то есть сформулированное утверждение ложно, то надо
используется те же идеи, что для случая n=2. .
Затем найти многозначное число, для которого эти утверждения не верны. Если же
такое число не найдется, то есть сформулированное утверждение ложно, то надо
используется те же идеи, что для случая n=2.
Если рассматривать действия, выполняемые при
решении данного задания и перевести их на язык математических способностей, то
можно сказать, что задание способствует формированию способности к логическому
рассуждению в сфере количественных отношений, числовой и знаковой символики.
Так как действие «сформулировать утверждение о
записи натурального ряда» можно соотнести с действием «оперирования
специальными математическими знаками, условными символическими обозначениями
количественных величин и отношений», действие «записать утверждение о делимости
натурального числа» - с действием «перевода на язык символов», а «проверка
утверждения на истинность» с действием «умением логически рассуждать
(доказывать, обосновывать)».
Ниже в таблице №2 приведены задания из темы
«Теория делимости» курса «Начала алгебры», которые, по нашей оценке, позволяют
формировать эту математическую способность.
Таблица 2
|
Математическая
способность
|
Действие,
присущие способности
|
Тип
задания
|
Образец
задания
|
|
Способность
к логическому рассуждению в сфере количественных и пространственных
отношений, числовой и знаковой символики.
|
уметь
логически рассуждать (доказывать, обосновывать); оперировать специальными
математическими знаками, условными символическими обозначениями
количественных величин и отношений и пространственных свойств; переводить на
язык символов.
|
Восстановить
утверждение о делимости чисел, вписав недостающие данные. Записать
утверждение о делимости (данное в готовом виде, либо построенное самими
учащимися) в заданной форме "Если…, то…". 3. Дано утверждение о
числах, привести примеры чисел, обладающих таким же свойством.
|
1.
Заполни пробелы Если число оканчивается цифрами [_] и [_], то оно кратно
пяти. 2. Запишите в форме утверждения «Если…, то…» следующий признак
делимости числа на 3: «Число, у которого сумма цифр делится на 3, кратно 3».
3.Прочитайте утверждения и приведите примеры других чисел, обладающих такими
же свойствами: 8356 2 и 2638 2 и 2638 2 2  (8356+2638) (8356+2638) 2; 2;
|
Вывод: задачи такого же типа рассматриваются в
теме «Теория делимости» курса «Начала алгебры» систематически и условия задач
постепенно усложняются, то можно говорить, что способность к логическому
рассуждению в сфере количественных и пространственных отношений, числовой и
знаковой символики формируется.
Формирование способности к быстрому
и широкому обобщению математических объектов
Перейдем к следующей математической способности
- способность к быстрому и широкому обобщению математических объектов. Проверку
будем осуществлять таким же образом, как и в предыдущем анализе.
Способность к обобщению математического
материала рассматривается в двух планах: 1) как способность человека увидеть в
частном, конкретном уже известном ему общее (подведение частного случая под
известное общее понятие) и 2) способность увидеть в единичном, частном пока еще
неизвестное общее (вывести общее из частных случаев, образовать понятие). Одно
дело - увидеть возможность применение к данному частному случаю уже известной
ученику формулы, другое - на основание частных случаев вывести формулу, еще
неизвестную ученику.
Рассмотрим задание из темы «Теория делимости»
курса «Начала алгебры», которое, по нашему мнению, позволяет формировать эту
математическую способность.
Задание. «Как быстро (не производя вычисления)
определить, кратна ли трем сумма 3798+222?».[4]
Задача решается при помощи использования свойств
отношений делимости.
Так как действие «использование свойств отношений
делимости» можно соотнести с действием «обобщения типа решения», «обобщения
схемы доказательства, рассуждения» (что применить), то можно сказать, что
данная задача позволяет формировать математическую способность - способность к
быстрому и широкому обобщению математических объектов.
Ниже в таблице №3 приведены задания из темы
«Теория делимости» курса «Начала алгебры», которые, по нашей оценке, позволяют
формировать эту математическую способность.
Таблица 3
|
Математическая
способность
|
Действие,
присущие способности
|
Тип
задания
|
Образец
задания
|
|
Способность
к быстрому и широкому обобщению математических объектов.
|
видят
сходную ситуацию в сфере числовой и знаковой символики (где применить);
владеют обобщенным типом решения, обобщенной схемой доказательства,
рассуждения (что применить).
|
1.Даны
некоторые объекты теории чисел, для которых справедливы некоторые свойства.
Сформулируйте утверждение, которое кажется вам верным. Проверьте, справедливо
ли оно для более широкого класса объектов. 2. В данных утверждениях о числах
замените числа буквами. Запишите полученные утверждения. 3.Установите
делимость числа на а, если известны признаки делимости на делители а.
Сформулируйте соответствующее утверждение.
|
1.Постройте
примеры, показывающие, что можно (или нельзя) без изменения распространить
признаки делимости для двузначных чисел в произвольной системе счисления на
числа с произвольным количеством цифр в записи. Сформулируйте утверждение,
которое кажется вам верным. 2. Замените в следующих утверждениях числа буквами:
(а) 8356 2 и 2638 2 и 2638 2 2  (8356+
2638) (8356+
2638) 2;
3.Сформулируйте утверждение о делимости чисел 121212, 2424242, 444 на 6. 2;
3.Сформулируйте утверждение о делимости чисел 121212, 2424242, 444 на 6.
|
Вывод: так как такие задачи в материале темы
«Теория делимости» курса «Начала алгебры» встречаются систематически и условия
задач постепенно усложняются, то можно говорить, что способность к быстрому и
широкому обобщению математических объектов формируется.
Также при анализе задачного материала темы
«Теория делимости» курса «Начала алгебры» были выявлены задачи, которые
направлены на формирование двух других математических способностей: 1) гибкость
мыслительных процессов в математической деятельности, 2) способность к быстрой
и свободной перестройке направленности мыслительного процесса, переключение с
прямого на обратный ход мысли.
Ниже в таблицах №4, 5 приведены задания из курса
«Начала алгебры» темы «Теория делимости», которые, по нашей оценке, направлены
на формирование этих математических способностей.
Таблица 4
|
Математическая
способность
|
Действие,
присущие способности
|
Тип
задания
|
Образец
задания
|
|
Гибкость
мыслительных процессов в математической деятельности.
|
переключаются
на новый способ действия, т.е. с одной умственной операции на другую.
|
Определить
делиться ли на а набор числел Какие из этих чисел делиться на b? 2.
Определить каким числам кратно данное число. 3. Придумать число, которое
делится на а, но не делится на b. 4. Делится ли х на a, если известно, что х
делится на b.
|
Определить,
делится ли на 9 число 2754. Делится ли оно на 3. Найти среди набора числа
кратные 2. Придумать семизначное число, которое делится на 3, но не делится
на 9. Делится ли х на 6, если х делится на 12
|
Таблица 5
|
Математическая
способность
|
Действие,
присущие способности
|
Тип
задания
|
Образец
задания
|
|
Способность
к быстрой и свободной перестройке направленности мыслительного процесса,
переключение с прямого на обратный ход мысли.
|
перестраивать
мыслительный процесс с прямого на обратный ход мыслей.
|
1.
Допишите утверждение о делимости так, чтобы оно стало истинным. 2. Проверить
следующие утверждения.
|
1.
Заполни пробелы: Если число оканчивается цифрами ___, то оно делится на 5.
Если число делится на 10, то ______________. Прочитайте следующие
утверждения. Верны ли они? 8356 2 и 2638 2 и 2638  2 Þ
(8356+2638) 2 Þ
(8356+2638)  2
99999999Þ 12345678 2
99999999Þ 12345678  3 и
87654321 3 и
87654321 3. 3.
|
Вывод: Задания, которые позволяют формировать
эти способности, встречаются не систематически, то есть каждый тип заданий
представлена в теме «Теория делимости» курса «Начала алгебры» лишь одним
заданием. Поэтому мы не можем говорить, что учебный материал темы «Теория
делимости» курса «Начала алгебры» эти направлен на формирования этих
способностей.
Предположение: возможно, что наличие
дополнительного образовательного пространства как места для математического
творчества и самостоятельного инициативного движения, учащихся в предмете
математики и наличие условий для написания разножанровых творческих работ могут
задать системность в формировании способностей к гибкости и обратимости
мыслительного процесса.
Итак, мы обосновали, что учебный материал темы
«Теория делимости» курса «Начала алгебры» способствует формированию
математических способностей: 1) способность к формализованному восприятию
математического материала, схватывания формальной структуры задачи; 2)
способность к логическому рассуждению в сфере количественных и пространственных
отношений, числовой и знаковой символики; 3) способность к быстрому и широкому
обобщению математических объектов.
Заключение
Результаты дипломной работы позволят посмотреть
на курс, разработанный для формирования общих способностей к исследовательской
деятельности как на курс, позволяющий формировать специальные математические
способности.
В дипломной работе представлен анализ задачного
материала темы «Теория делимости» курса «Начала алгебры». Курс ориентирован на
решение задач деятельностного математического образования. В дипломной работе
получено подтверждение, что, задачный материал позволяет формировать три из
восьми математических способностей. В этом и состоит основной результат работы.
А именно мы показали, что задачный материал темы
«Теория делимости» курса «Начала алгебры» позволяет сформировать способность к
формализованному восприятию математического материала; способность к
логическому рассуждению; способность к быстрому и широкому обобщению, за счет
того, что задачи, содержащиеся в учебном курсе требуют выполнения предметных
действий, обеспечивающих развитие указанных способностей.
Нами также выдвинуто предположение, что
способности к гибкости и обратимости мыслительного процесса могут быть
сформированы за счет реализации дополнительного образовательного пространства.
И это требует дополнительного исследования.
Список литературы
1. Адамар
Ж. Исследование психологии процесса изобретения в области математики. - М.,
1970.
2. Выготский
Л.С. Развитие высших психических функций. - М.: АПН РСФСР, 1960.
. Гальперин
П.Я. О методе формирования умственных действий/ Хрестоматия по возрастной и
педагогической психологии. - М., 1981.
. Знаменская
О.В., Юдина Ю.Г. Начала алгебры. 6 класс/ Красноярская университетская гимназия
№1 «Универс», 2004.
. Знаменская
О.В., Юдина Ю.Г. Начала алгебры., 6 класс. Методические материалы./ Красноярск,
ИППР, 2004.
. Кордемский
Б.А. Увлечь школьников математикой. - М: Просвещение, 1981.
. Крутецкий
В.А. Психология математических способностей школьников. - Москва - Воронеж,
1998.
. Леонтьев
А.Н. Избранные психологические произведения. В 2 т. T.I - М, 1983.
. Лурия
А.Р. Мозг человека и психические процессы. М. изд-во АПН РСФСР, 1963.
. Немов
Р.С. Психология: учеб. для студ. высш. пед. учеб. заведений. В кн.3 - 4-е изд.
- М, 1997.
. Новосельцева
З.И. Развернутые планы лекций и учебные задания для студентов по курсу
"Теоретические основы обучения математике"/ СПб.: Образование, РГПУ,
1997.
. Ньюэлл
А., Шоу Дж., Сайсон Г.А. Процессы творческого мышления. (пер. с анг). Сб.
Психология мышления. ред. А.М. Матюшина. М, 1965.
. Пуанкаре
А. О науке (под ред. Л.С. Понтрягина). - М., Наука, 1989. - «Ценность науки.
Математические науки» (пер. с фр. Т.Д. Блохинцева; А.С. Шибанов).
. Рубинштейн
С.Л. Основы общей психологии: В 2-х т. - М., 1989.
. Хутогорский
А.В. Развитие одаренности школьников: Методика продуктивного обучения. - М.:
ВЛАДОС, 2000.
. Рекомендации
об организации предпрофильной подготовки учащихся основной школы (Приложение к
письму МО РФ от 20.08.2003 г.).
Похожие работы на - Формирование математических способностей (по В.А. Крутецкому) при изучении математики в деятельностном подходе
|