Уравнения линейной регрессии, коэффициент регрессии
Федеральное агентство по образованию
Всероссийский заочный финансово-экономический
институт
Контрольная работа
по дисциплине «Эконометрика»
Архангельск
2008
Условие задачи
По предприятиям лёгкой
промышленности региона получена информация, характеризующая зависимость объема
выпуска продукции (Y, млн. руб.) от
объема капиталовложений (X,
млн. руб.).
Требуется:
1. Найти параметры
уравнения линейной регрессии, дать экономическую интерпретацию коэффициента
регрессии.
2. Вычислить остатки;
найти остаточную сумму квадратов; оценить дисперсию остатков  ; построить график остатков.
; построить график остатков.
3. Проверить выполнение
предпосылок МНК.
4. Осуществить проверку
значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).
5. Вычислить коэффициент
детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти
среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
6. Осуществить
прогнозирование среднего значения показателя Y при уровне значимости α=0,1, если прогнозное значение фактора
X составляет 80% от его максимального
значения.
7. Представить графически
фактические и модельные значения Y
точки прогноза.
8. Составить уравнения
нелинейной регрессии:
·
Гиперболической;
·
Степенной;
·
Показательной.
Привести графики
построенных уравнений регрессии.
9. Для указанных моделей
найти коэффициенты детерминации, коэффициенты эластичности и средние
относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и
сделать вывод.
|
Х
|
17
|
22
|
10
|
7
|
12
|
21
|
14
|
7
|
20
|
3
|
|
Y
|
26
|
27
|
22
|
19
|
21
|
26
|
20
|
15
|
30
|
13
|
регрессия
уравнение стьюдент фишер аппроксимация
Решение задачи.
1. Найти параметры
уравнения линейной регрессии, дать экономическую интерпретацию коэффициента
регрессии.
Для нахождения параметров
уравнения линейной регрессии 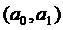 решим систему нормальных уравнений:
решим систему нормальных уравнений:
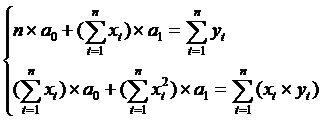
n=10
|
x
|
y
|
x^2
|
xy
|
|
17
|
26
|
289
|
442
|
|
22
|
27
|
484
|
594
|
|
10
|
22
|
100
|
220
|
|
7
|
19
|
49
|
133
|
|
12
|
21
|
144
|
252
|
|
21
|
26
|
441
|
546
|
|
14
|
20
|
196
|
280
|
|
7
|
15
|
49
|
105
|
|
20
|
30
|
400
|
600
|
|
3
|
13
|
9
|
39
|
|
133
|
219
|
2161
|
3211
|




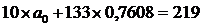
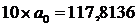

Найдём параметры
уравнения линейной регрессии, используя надстройку «Мастер диаграмм» в Excel, тип диаграммы – точечная, выделяем
столбцы (А1:В11), выбираем команду «Добавить линию тренда», выбираем 2
последние команды:
- показывать уравнение на
диаграмме;
- поместить на диаграмму
величину достоверности аппроксимации.
Общий вид уравнения
регрессии имеет вид:

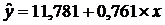


 коэффициент
регрессии.
коэффициент
регрессии.
Величина коэффициента
регрессии (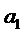 ) показывает, на сколько в среднем
изменяется значение результата с изменением фактора на 1 единицу. Т.о в нашем
случае, с увеличением объема капиталовложений (Х) на 1 млн.руб. объём выпуска
продукции (У) возрастает в среднем на 0,761 млн.руб. (рис. 1).
) показывает, на сколько в среднем
изменяется значение результата с изменением фактора на 1 единицу. Т.о в нашем
случае, с увеличением объема капиталовложений (Х) на 1 млн.руб. объём выпуска
продукции (У) возрастает в среднем на 0,761 млн.руб. (рис. 1).
|
X
|
Y
|
|
17
|
26
|
|
22
|
27
|
|
10
|
22
|
|
7
|
19
|
|
12
|
21
|
|
21
|
26
|
|
14
|
20
|
|
7
|
15
|
|
20
|
30
|
|
3
|
13
|
|
а0=11,781
|
|
|
а1=0,761
|
|

Рис. 1
2. Вычислить остатки;
найти остаточную сумму квадратов; оценить дисперсию остатков  . Построить график остатков.
. Построить график остатков.
Вычислим остатки по
формуле: 

|
x
|
y
|

|

|
m
|
|
|
17
|
26
|
24,718
|
1,282
|
*
|
1,6435
|
|
22
|
27
|
28,523
|
-1,523
|
1
|
2,3195
|
|
10
|
22
|
19,391
|
2,609
|
1
|
6,8069
|
|
7
|
19
|
17,108
|
1,892
|
0
|
3,5797
|
|
12
|
21
|
20,913
|
0,087
|
0
|
0,0076
|
|
21
|
26
|
27,762
|
-1,762
|
0
|
3,1046
|
|
14
|
20
|
22,435
|
-2,435
|
1
|
5,9292
|
|
7
|
15
|
17,108
|
-2,108
|
0
|
44437
|
|
20
|
30
|
27,001
|
2,999
|
1
|
8,9940
|
|
3
|
13
|
14,064
|
-1,064
|
*
|
1,1321
|
|
133
|
219
|
*
|
-0,023
|
4
|
37,9608
|
Оценка дисперсии
остатков:
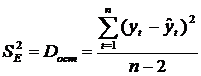

По следующим данным
строим график остатков (рис. 2):
|
Y
|
Е(t)
|
|
26
|
1,282
|
|
27
|
-1,523
|
|
22
|
2,609
|
|
19
|
1,892
|
|
21
|
0,087
|
|
26
|
-1,762
|
|
20
|
-2,435
|
|
15
|
-2,108
|
|
30
|
2,999
|
|
13
|
-1,064
|
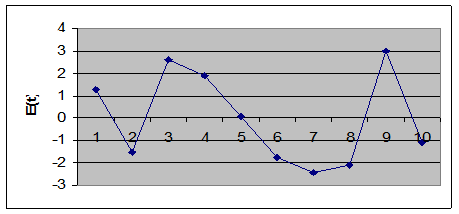
Рис. 2
3. Проверить
выполнение предпосылок МНК.
1. Случайный характер
остатков (критерий поворотных точек, критерий пиков):
 ,
,
где n- количество наблюдений;
m – количество поворотных точек
(пиков).
Точка считается
поворотной, если она больше предшествующей и последующей (или меньше).
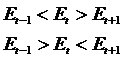
 является
поворотной точкой
является
поворотной точкой
 является
поворотной точкой
является
поворотной точкой
 не
является поворотной точкой
не
является поворотной точкой
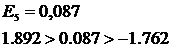 не
является поворотной точкой
не
является поворотной точкой
 не
является поворотной точкой
не
является поворотной точкой
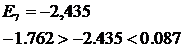 является
поворотной точкой
является
поворотной точкой
 не
является поворотной точкой
не
является поворотной точкой
 является
поворотной точкой.
является
поворотной точкой.
m=4

m=4>2, следовательно неравенство
выполняется, свойство выполняется.
2. Независимость
значений остатков (отсутствие автокорреляции). Критерий Дарбина-Уотсона.

|
x
|
y
|

|

|
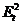
|
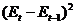
|
|
17
|
26
|
24,718
|
1,282
|
1,6435
|
*
|
|
22
|
27
|
28,523
|
-1,523
|
2,3195
|
7,8680
|
|
10
|
22
|
19,391
|
2,609
|
6,8069
|
17,0734
|
|
7
|
19
|
17,108
|
1,892
|
3,5797
|
0,5141
|
|
12
|
21
|
20,913
|
0,087
|
0,0076
|
3,2580
|
|
21
|
26
|
27,762
|
-1,762
|
3,1046
|
3,4188
|
|
14
|
20
|
22,435
|
-2,435
|
5,9292
|
0,4529
|
|
7
|
15
|
17,108
|
-2,108
|
4,4437
|
0,1069
|
|
20
|
30
|
27,001
|
2,999
|
8,9940
|
26,0814
|
|
3
|
13
|
14,064
|
-1,064
|
1,1321
|
16,5080
|
|
133
|
219
|
*
|
-0,023
|
37,9608
|
75,2816
|

 сравниваем
с двумя табличными:
сравниваем
с двумя табличными: 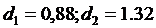
 ,
следовательно, свойство выполняется, остатки независимы.
,
следовательно, свойство выполняется, остатки независимы.
3. Подчинение остатков
нормальному закону (R/S критерий).
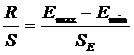

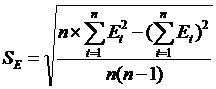
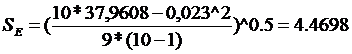

Расчётный критерий
сравниваем с двумя табличными, если расчётный критерий попадает внутрь
табличного интервала, то свойство выполняется.
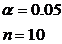 (2,67;3,57)
(2,67;3,57)
1,216 < 2,67,
следовательно, свойство не выполняется, остатки не подчинены нормальному
закону.
4. Проверка равенства
М(Е)=0, средняя величина остатков равна 0 (критерий Стьюдента).
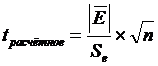

Если 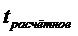 <
<  , то свойство выполняется.
, то свойство выполняется.

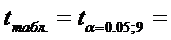 2,2281
2,2281
 ,
следовательно, свойство выполняется.
,
следовательно, свойство выполняется.
5. Гомоскедастичность
остатков, то есть
дисперсия остатков ( ) одинаково для каждого
значения
) одинаково для каждого
значения 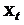 (остатки имеют постоянную дисперсию).
(остатки имеют постоянную дисперсию).
Если дисперсия остатков
неодинакова, то имеет место гетероскедастичность.
Если предпосылки не
выполняются, то модель нужно уточнять. Применяем тест Голдфельд-Квандта:
1)
упорядочить
(ранжировать) наблюдения по мере возрастания фактора «Х».
2) исключить d-средних наблюдений.
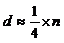 ,
,
где n – количество наблюдений.
2)
разделить
совокупность на две группы: с малыми и большими значениями «Х» и для каждой из
частей найти уравнение регрессии.
3)
найти остаточную
сумму квадратов отклонений ( ) для каждого
уравнения регрессии.
) для каждого
уравнения регрессии.


4)
применяют
критерий Фишера:

Если  , то гетероскедастичность имеет место,
то есть пятая предпосылка не выполняется.
, то гетероскедастичность имеет место,
то есть пятая предпосылка не выполняется.
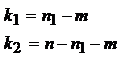
|
X
|
Y
|
|
17
|
22
|
|
22
|
27
|
|
10
|
22
|
|
7
|
19
|
|
12
|
21
|
|
21
|
26
|
|
14
|
20
|
|
7
|
15
|
|
20
|
30
|
|
3
|
13
|
Упорядочим наблюдениям по
мере возрастания переменной Х:
|
X
|
Y
|
|
3
|
13
|
|
7
|
19
|
|
7
|
15
|
|
10
|
22
|
|
12
|
21
|
|
14
|
20
|
|
17
|
22
|
|
20
|
30
|
|
21
|
26
|
|
22
|
27
|
X5=12; Y5=21 и Х6=14; Y6=20
исключаем.
 ;
n=10
;
n=10
|
x
|
y
|
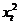
|

|

|
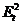
|
|
3
|
13
|
9
|
12,517
|
0,483
|
0,2333
|
|
7
|
19
|
49
|
17,569
|
1,431
|
2,0478
|
|
7
|
15
|
49
|
17,569
|
-2,569
|
6,5998
|
|
10
|
22
|
100
|
21,358
|
0,642
|
0,4122
|
|
27
|
69
|
207
|
*
|
-0,013
|
9,2930
|
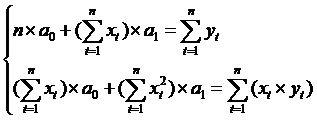
n=4
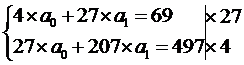
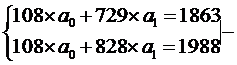
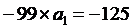


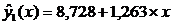

|
x
|
y
|
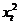
|

|

|
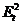
|
|
17
|
22
|
289
|
23,25
|
-1,25
|
1,5625
|
|
20
|
30
|
400
|
26,25
|
3,75
|
14,0625
|
|
21
|
26
|
441
|
27,25
|
-1,25
|
1,5625
|
|
22
|
27
|
484
|
28,25
|
-1,25
|
4,5625
|
|
80
|
105
|
1614
|
*
|
0
|
18,75
|
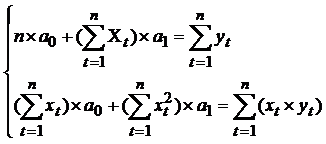
n=4




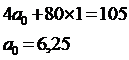


 , так как
, так как 


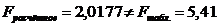 , значит, пятая предпосылка выполняется,
следовательно, модель нужно адекватна.
, значит, пятая предпосылка выполняется,
следовательно, модель нужно адекватна.
4. Осуществить
проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).
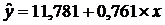
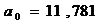

 ;
;
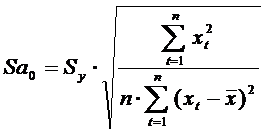

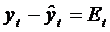
|
x
|
y
|
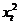
|

|

|
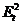
|

|
|
17
|
26
|
289
|
24,718
|
1,282
|
1,6435
|
13,69
|
|
22
|
27
|
484
|
28,523
|
-1,523
|
2,3195
|
75,69
|
|
10
|
22
|
100
|
19,391
|
2,609
|
6,8069
|
1,89
|
|
7
|
19
|
49
|
17,108
|
1,892
|
3,5797
|
39,9
|
|
12
|
21
|
144
|
20,913
|
0,087
|
0,0076
|
1,69
|
|
21
|
26
|
441
|
27,762
|
-1,762
|
3,1046
|
59,29
|
|
14
|
20
|
196
|
22,435
|
-2,435
|
5,9292
|
0,49
|
|
7
|
15
|
49
|
17,108
|
-2,108
|
4,4437
|
39,69
|
|
20
|
30
|
400
|
27,001
|
2,999
|
8,9940
|
44,89
|
|
3
|
13
|
9
|
14,064
|
-1,064
|
1,1321
|
106,09
|
|
133
|
219
|
2161
|
*
|
-0,023
|
37,9608
|
392,1
|

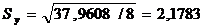





 ,
следовательно, параметр
,
следовательно, параметр  значим.
значим.

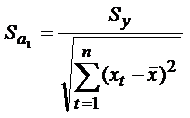

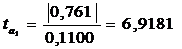


 ,
следовательно, коэффициент регрессии
,
следовательно, коэффициент регрессии  значим.
значим.
Интервальная оценка:



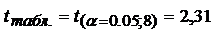
а0: 11,781 2,31*1,617
2,31*1,617
а0: 11,781 3,735
3,735
Нижняя граница: 11,781-3,735=8,046
Верхняя граница: 11,781+3,735=15,516
а0: (8,046 15,516), следовательно, параметр а0
значим, так как в эти границы не попадает 0.
15,516), следовательно, параметр а0
значим, так как в эти границы не попадает 0.
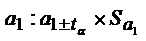
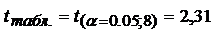
а1: 0,761 2,31*0,11
2,31*0,11
а1: 0,761 0,2541
0,2541
Нижняя граница: 0,761-0,254=0,507
Верхняя граница: 0,761+0,254=1,015
а1: (0,507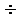 1,015), следовательно, коэффициент
регрессии а1 значим, так как в эти границы не попадает 0.
1,015), следовательно, коэффициент
регрессии а1 значим, так как в эти границы не попадает 0.
5. Вычислить
коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти
среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
Для нахождения
коэффициента детерминации найдём коэффициент парной корреляции:
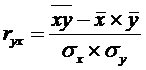






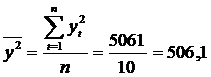
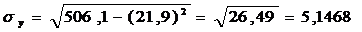

Проверяем значимость 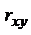 по критерию Стьюдента:
по критерию Стьюдента:
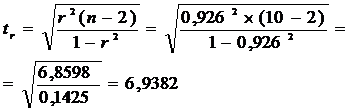


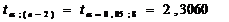
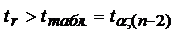 ,
следовательно,
,
следовательно, 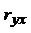 значим.
значим.
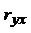 =0,926,
то есть связь между переменными y и x очень тесная (то есть близко к 1) и
прямая (так как больше 0).
=0,926,
то есть связь между переменными y и x очень тесная (то есть близко к 1) и
прямая (так как больше 0).
Находим коэффициент
детерминации:
 ,
то есть 85,8% - изменение объёма выпуска продукции (зависимой переменной «y») происходит под влиянием объёма
капиталовложений (фактора «х», включённого в модель).
,
то есть 85,8% - изменение объёма выпуска продукции (зависимой переменной «y») происходит под влиянием объёма
капиталовложений (фактора «х», включённого в модель).
Значимость уравнения
регрессии по критерию Фишера:
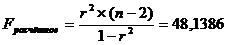



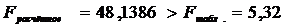 ,
следовательно, уравнение регрессии значимо, модель адекватна.
,
следовательно, уравнение регрессии значимо, модель адекватна.
Средняя относительная
ошибка аппроксимации:

|
x
|
y
|

|

|

|
|
17
|
26
|
24,718
|
1,282
|
0,0493
|
|
22
|
27
|
28,523
|
-1,523
|
0,0564
|
|
10
|
22
|
19,391
|
2,609
|
0,1186
|
|
7
|
19
|
17,108
|
1,892
|
0,0996
|
|
12
|
21
|
20,913
|
0,087
|
0,0041
|
|
21
|
26
|
27,762
|
-1,762
|
0,0678
|
|
14
|
20
|
22,435
|
0,1218
|
|
7
|
15
|
17,108
|
-2,108
|
0,1405
|
|
20
|
30
|
27,001
|
2,999
|
0,1000
|
|
3
|
13
|
14,064
|
-1,064
|
0,0818
|
|
133
|
219
|
*
|
-0,023
|
0,7332
|
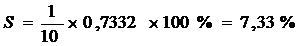
Так как  , значит модель не достаточно точная.
, значит модель не достаточно точная.
F-критерий
намного больше табличного значения, коэффициент детерминации  очень близок к 1, а относительная
ошибка аппроксимации составляет 7,33%. На основании рассчитанных критериев
можно сделать вывод о хорошем качестве модели.
очень близок к 1, а относительная
ошибка аппроксимации составляет 7,33%. На основании рассчитанных критериев
можно сделать вывод о хорошем качестве модели.
6.
Осуществить прогнозирование среднего значения показателя Y при уровне значимости α=0,1, если прогнозное значение
фактора X составляет 80% от его максимального
значения.

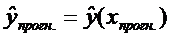

 - прогноз факторного признака (объема капиталовложений).
- прогноз факторного признака (объема капиталовложений).
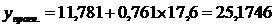 -
точечный прогноз.
-
точечный прогноз.
(17,6; 25,2) – точка
должна лежать на графике модели.
Интервальный прогноз:
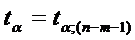

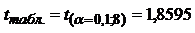
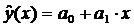



25,2 1,86
1,86 1,81
1,81
25,2 3,37
3,37
Нижняя граница: 25,2-3,37=21,83
Верхняя граница: 25,2+3,37=28,57
То есть при уровне
значимости 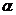 =0,1, если прогнозное значение фактора «Х»
составит 80% от его максимального значения или 17,6, точечный прогноз среднего
значения «Y» по линейной модели составит 25,2.
Доверительный интервал: 21,83
=0,1, если прогнозное значение фактора «Х»
составит 80% от его максимального значения или 17,6, точечный прогноз среднего
значения «Y» по линейной модели составит 25,2.
Доверительный интервал: 21,83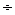 28,57.
28,57.
7. Представить
графически фактические и модельные значения Y точки прогноза рис. 3.

Рис. 3
8. Составить уравнения
нелинейной регрессии:
·
Гиперболической;
·
Степенной;
·
Показательной.
Привести графики
построенных уравнений регрессии.
9. Для указанных
моделей найти коэффициенты детерминации, коэффициенты эластичности и средние
относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и
сделать вывод.
Уравнение степенной
модели парной регрессии:
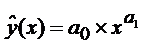
Для построения этой
модели необходимо произвести линеаризацию переменных. Для этого произведём
логарифмирование обеих частей уравнения:
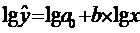
Обозначим  ,
, 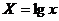 ,
,  . Тогда уравнение примет вид
. Тогда уравнение примет вид  - линейное уравнение регрессии.
- линейное уравнение регрессии.
Рассчитаем его параметры
(см. приложение).


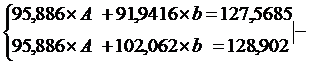


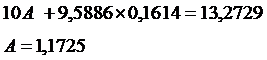
Получим уравнение
степенной модели регрессии:

Построим график (рис. 4):
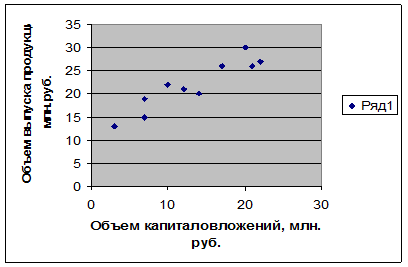
Рис. 4
Определим коэффициент
корреляции:
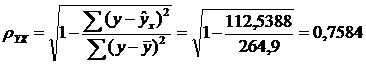
Связь между показателем y и фактором x можно считать достаточно тесной.
Коэффициент детерминации:
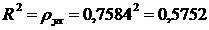
Вариация результата Y (объёма выпуска продукции) на 57,5%
объясняется вариацией фактора X
(объёмом капиталовложений).
Средняя относительная
ошибка аппроксимации:
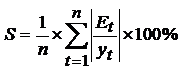

В среднем расчётные
значения  для степенной модели отличаются от
фактических значений на 14,6%.
для степенной модели отличаются от
фактических значений на 14,6%.
Коэффициент эластичности
для степенной модели регрессии:
 ,
значит, если фактор X (объём
капиталовложений) увеличить на 1%, то значение зависимой переменной Y (объём выпуска продукции) увеличится
в среднем на 0,16%.
,
значит, если фактор X (объём
капиталовложений) увеличить на 1%, то значение зависимой переменной Y (объём выпуска продукции) увеличится
в среднем на 0,16%.
Уравнение
показательной модели парной регрессии:
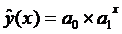
Для построения этой
модели необходимо произвести линеаризацию переменных. Для этого осуществим
логарифмирование обеих частей уравнения:
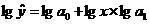
Обозначим  ,
, 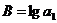 ,
, 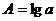 . Тогда уравнение примет вид
. Тогда уравнение примет вид  - линейное уравнение регрессии.
- линейное уравнение регрессии.
Рассчитаем его параметры.



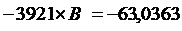
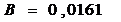
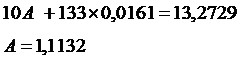


Перейдём к исходным
переменным x и y.

Построим график (рис. 5):
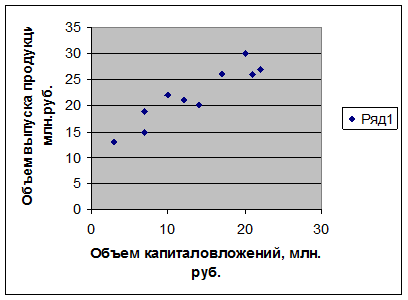
Рис. 5
Определим индекс
корреляции:
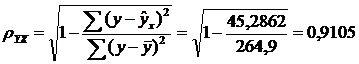
Связь между показателем y и фактором x можно считать достаточно тесной.
Коэффициент детерминации:
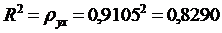
Вариация результата Y (объёма выпуска продукции) на 82,9%
объясняется вариацией фактора X
(объёмом капиталовложений).
Средняя относительная
ошибка аппроксимации:

В среднем расчётные
значения  для степенной модели отличаются от
фактических значений на 9,5%.
для степенной модели отличаются от
фактических значений на 9,5%.
Коэффициент эластичности
для показательной модели регрессии:
 ,
значит, если фактор X (объём
капиталовложений) увеличить на 1%, то значение зависимой переменной Y (объём выпуска продукции) увеличится
в среднем на 0,49%.
,
значит, если фактор X (объём
капиталовложений) увеличить на 1%, то значение зависимой переменной Y (объём выпуска продукции) увеличится
в среднем на 0,49%.
Уравнение
гиперболической модели парной регрессии:

Произведём линеаризацию
модели путём замены  .
.
В результате получим
линейное уравнение:

Рассчитаем его параметры.
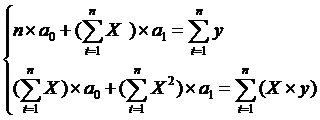

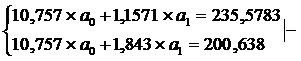



Получим следующее
уравнение гиперболической модели:
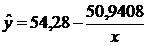
Построим график (рис. 6):

Рис. 6
Определим индекс
корреляции:

Связь между показателем y и фактором x можно достаточно тесной.
Коэффициент детерминации:
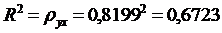
Вариация результата Y (объёма выпуска продукции) на 67,2%
объясняется вариацией фактора X
(объёмом капиталовложений).
Средняя относительная
ошибка аппроксимации:

В среднем расчётные
значения  для степенной модели отличаются от
фактических значений на 12,46%.
для степенной модели отличаются от
фактических значений на 12,46%.
Коэффициент эластичности
для гиперболической модели регрессии:
 %,
значит, если фактор X (объём
капиталовложений) увеличить на 1%, то значение зависимой переменной Y (объём выпуска продукции) увеличится
в среднем на 0,18%.
%,
значит, если фактор X (объём
капиталовложений) увеличить на 1%, то значение зависимой переменной Y (объём выпуска продукции) увеличится
в среднем на 0,18%.
Сравним модели по
коэффициенту детерминации, коэффициенту эластичности и средней относительной
ошибке аппроксимации:
|
Модель парной регрессии
|
Критерий
|
|
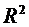
|
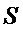
|
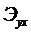
|
|
Степенная
|
0,575
|
14,6%
|
0,16%
|
|
Показательная
|
0,829
|
9,5%
|
0,49%
|
|
Гиперболическая
|
0,672
|
12,5%
|
0,18%
|
Самое хорошее качество
имеет показательная модель. Коэффициент детерминации наиболее близок к 1
(вариация объёма капиталовложений на 82,9% объясняет вариацию объёма выпуска
продукции), наименьшая средняя относительная ошибка аппроксимации S=9,5% и среднее значение коэффициента
эластичности 
 .
.