Кинетика химических и электрохимических процессов
Министерство
образования и науки Российской Федерации
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Федеральное государственное
образовательное учреждение высшего профессионального образования
«Чувашский государственный
университет им. И.Н. Ульянова»
Методические
указания к практическим занятиям по физической химии:
КИНЕТИКА ХИМИЧЕСКИХ И
ЭЛЕКТРОХИМИЧЕСКИХ ПРОЦЕССОВ
Чебоксары 2007
УДК 541.1:541.2:541.6
Составители:
С.М. Верхунов
Р.А. Зимин
Э.В. Андреева
Н.И. Кольцов
Кинетика химических и
электрохимических процессов: Метод. указания к практическим занятиям по
физической химии / Сост. С.М. Верхунов, Р.А. Зимин, Э.В. Андреева, Н.И. Кольцов;
Чуваш. ун-т. Чебоксары, 2007. 61 с.
Содержат задачи по
следующим темам: электрическая проводимость, равновесия в растворах
электролитов, электродвижущие силы, электродные потенциалы, формальная
кинетика, сложные реакции, зависимость скорости реакции от температуры,
фотохимические реакции. К каждой теме приведены необходимые теоретические
сведения, основные уравнения, методики решения задач, предложены задачи для
самостоятельного решения с ответами.
Для студентов III и IV курсов химико-фармацевтического факультета.
Ответственный редактор
д-р хим. наук, профессор Н.И. Кольцов
Утверждено Методическим
советом университета.
1.
Электрическая проводимость. Равновесие в растворах электролитов
1.1 Необходимые
исходные сведения и основные уравнения
Электролитом называется
вещество, которое при взаимодействии с водой способно распадаться на
ионы и тем самым переносить электрический заряд. По способу переноса
электрического заряда все проводники делятся на два рода. К проводникам первого
рода относятся проводники с электронной проводимостью (все металлы, углерод,
графит, некоторые неметаллы). К проводникам второго рода относятся проводники с
ионной проводимостью (растворы кислот, большинства солей и оснований, а также
их расплавы).
Важнейшей характеристикой
электрической проводимости является электрическое сопротивление проводников:
R = r∙l/s,(1.1)
где r - удельное электрическое
сопротивление, Ом.м; l – длина проводника первого рода или расстояние между электродами в
проводнике второго рода, м; s
– площадь поперечного сечения проводника первого рода или площадь электродов
проводника второго рода, м2.
Величина, обратная
сопротивлению, называется электрической проводимостью:
1/r = c,(1.2)
где c - удельная электрическая
проводимость, Ом-1.м-1. Удельной электрической
проводимостью называется электрическая проводимость электролита, заключенного
между электродами площадью 1 м2 и расположенными на расстоянии 1 м
друг от друга.
Для растворов электролитов часто
пользуются понятием «эквивалентная электрическая проводимость» l:
l = c/с (1.3)
где с –
эквивалентная концентрация электролита, моль.м-3.
Эквивалентной электрической проводимостью называется электрическая проводимость
электролита, заключенного между электродами, находящимися на расстоянии 1 м
друг от друга и такой площади, что в пространстве между ними содержится 1 моль
электролита.
Зависимость эквивалентной
электрической проводимости от концентрации описывается уравнением Кольрауша:
l = l¥ - А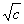 ,(1.4)
,(1.4)
где l¥ - эквивалентная электрическая
проводимость при бесконечном разбавлении, Ом-1.моль-1.м2;
А – постоянная, зависящая от природы электролита.
Так как проводник второго
рода при растворении в воде распадается на два типа ионов, то электрический
заряд переносится совместно катионами и анионами и справедливо уравнение
Кольрауша (закон независимости движения ионов):
l¥ = l+ + l-,(1.5)
где l+ и l- - электрические проводимости соответственно катиона и
аниона, Ом-1.моль-1.м2. Электрическая
проводимость катиона и аниона в большей степени определяется скоростью их
движения:
u+ = u+0U/l и v- = v-0U/l,(1.6)
где u+0 и v-0 – абсолютные скорости движения ионов,
м2.с-1.В-1; U/l – напряженность электрического поля, В.м-1,
l+ = F.v+0 и l- = F.v-0,(1.7)
где F – число Фарадея (F = 96500 Кл).
Абсолютные скорости движения ионов
различны. Так как в проводниках второго рода электрический заряд переносится од-новременно
катионами и анионами, то
Q = Q+ + Q-и I = I+ + I- (1.8)
где Q – перенесенный заряд, Кл; Q+ и Q- - заряд, перенесенный катионами и
анионами, Кл; I, I-, I+ - общая сила
тока и сила тока, определяемая движением анионов и катионов, А.
Количество заряда,
перенесенного ионами, зависит от скорости движения (подвижности), заряда и
размера ионов, а также от некоторых других факторов. В большинстве случаев доли
зарядов, перенесенных разными видами ионов, не совпадают друг с другом. По этой
причине вводится понятие о числах переноса ионов (t+ и t-). Числом
переноса ионов называется доля заряда, перенесенного данным видом иона:
t+ = Q+/(Q+
+ Q-) = I+/(I+ + I-);
(1.9)
t- = Q-/(Q+
+ Q-) = I-/(I+ + I-).
(1.10)
Очевидно, что t+ + t- = 1.
Отсюда:
t+ = 1 – t- и t- = 1 – t+.
(1.11)
Числа переноса можно
выражать через скорости движения и подвижности ионов:
t+ = v+0/(v+0 + v-0) = λ+/(λ+ + λ-)
= λ+/λ∞;
t- = v-0/(v+0 + v-0) = λ-/(λ+ + λ-)
= λ-/λ∞. (1.12)
Так как в ходе переноса
заряда ионы разряжаются на электродах, то концентрации электролита в анодном,
катодном и среднем пространствах различны:
t+ = Δск/Δс
иt- = Δса/Δс (1.13)
где Dск и Dса– изменение концентрации электролита
в катодном и анодном пространствах; Dс
– общая убыль концентрации элек-тролита (изменение концентрации в среднем
пространстве).
Количественно степень распада
электролита на ионы выра-жается через a (степень диссоциации):
a = np/n, (1.14)
где np – количество молекул, распавшихся на
ионы; n – общее количество молекул
электролита, введенных в раствор. По значению a различают сильные и слабые электролиты (a > 0,85 и 0,25 > a > 0,85 соответственно).
При диссоциации слабого
электролита, распадающегося на одновалентные ионы по схеме: АВ ↔ А+
+ В-, константа диссоциации:
Кд = [А+].[В-]/[АВ], (1.15)
где символы в квадратных скобках
указывают на концентрации соответствующих веществ. Если степень диссоциации
a = [А+]/с = [В-]/с
= λ/λ∞, (1.16)
то Кд =
a2.с, или a = 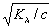 . (1.17)
. (1.17)
Соотношение (1.17)
называется законом разведения Оствальда (в простейшей форме). После подстановки
(1.16) в (1.17) закон разведения Оствальда примет вид
Кд = λ2. с/[(λ∞.(λ∞
- λ)]. (1.18)
Зависимость константы
диссоциации от температуры описывается уравнением
lg (К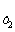 /К
/К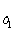 ) = -ΔНдисс(1/Т2
– 1/Т1)/(2,3.R), (1.19)
) = -ΔНдисс(1/Т2
– 1/Т1)/(2,3.R), (1.19)
где DНдисс– теплота диссоциации, Дж.моль-1.
Работу диссоциации можно
определить по уравнению изотермы Вант-Гоффа:
w = -DG0 = RTlnKи w = -DG0 = 2,3RTlgK, (1.20)
где DG0 – стандартное изменение энергии Гиббса
(изобарно-изотермического потенциала) при диссоциации, кДж.моль-1.
Необходимо учесть, что для сильных
электролитов в приведенные выше уравнения вместо концентрации необходимо
подставлять активности, которые связаны с концентрациями через коэффициент
активности:
а = g.c, (1.21)
где а – активность
сильного электролита, моль.м-3; g - коэффициент активности сильного
электролита при данной концентрации, с – молярная концентрация сильного
электролита, моль.м-3;
Активностью сильного
электролита называется активная часть этого вещества в растворе. Коэффициенты
активностей для большинства веществ известны и приведены в справочнике (например,
в [8]). Активность электролитов чаще всего выражают через моляльность m и средние ионные коэффициенты
активности γ±.
Таблица 1 - Соотношения между моляльностью m, средней ионной моляльностью m±, активностью а и средним ионным коэффициентом
активности γ± для некоторых электролитов
|
Тип валентности электролита
|
Пример
|
а = =(m±∙γ±)ν
|
а± =
= ν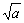
|
|
1-1, 2-2, 3-3
|
KCl (1-1); ZnSO4 (2-2);
AlPO4 (3-3)
|
m2g±2
|
mg±
|
|
2-1, 1-2
|
CaCl2 (2-1);
Na2SO4 (1-2)
|
4m3g±3
|
3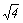 mg± mg±
|
|
3-1, 1-3
|
AlCl3 (3-1),
Na3PO4 (1-3)
|
27m4g±4
|
4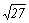 mg± mg±
|
|
3-2, 2-3
|
Al(SO4)3
(3-2); Fe3(PO4)2 (2-3)
|
108m5g±5
|
5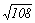 mg± mg±
|
Здесь ν – количество
ионов, на которые распадается данный электролит. Моляльностью называется число
молей вещества (электролита), содержащегося в 1000 г чистого растворителя (для
воды – в 1000 мл).
Зависимость средней
ионной моляльности от моляльности электролита выражается уравнением
m± = m(n+n+.n-n-)1/n, (1.22)
где n+ и n- - соответственно количество катионов и анионов на которые распадается
молекула электролита при диссоциации (n = n+ + n-). Средний
ионный коэффициент активности можно выразить через ионные коэффициенты
активности:
g± = (g+n+.g-n-)1/n, (1.23)
где g+ и g- -
соответственно коэффициенты активности катиона и аниона. Средняя ионная
активность составит
а± = m±..g±. (1.24)
Общая активность
электролита:
а = (а±)n = а+n+.а-n-, (1.25)
где а+
и а- - соответственно активности катионов и анионов:
а+ = g+. m+иa- = g-. m-. (1.26)
Ионные моляльности
связаны с моляльностью электролита соотношениями:
m+ = m × n+ иm- = m × n-.
(1.27)
Зависимость среднего
ионного коэффициента активности от ионной силы раствора (предельное уравнение
Дебая и Гюккеля) имеет вид
lgg± = 0,509. z+. z-. . (1.28)
. (1.28)
где z+ и z- - соответственно заряды катиона и аниона; I – ионная сила раствора:
I = 0,5.åmi.zi2. (1.29)
Cмвол i указывает на тип иона. Для 1-1 - валентного элек-тролита
уравнение (1.29) имеет вид
lgg± = -0,509.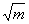 . (1.30)
. (1.30)
Это уравнение применимо
для растворов электролитов, в которых I £ 0,001.
1.2 Задачи с решениями
1. Удельная электрическая
проводимость 0,135 моль/л раствора пропионовой кислоты С2Н5СООН
равна 4,79.10-2 Ом-1.м-1.
Рассчитайте эквивалентную электрическую проводимость раствора, константу
диссоциации кислоты и рН раствора, если предельные подвижности Н+ и
С2Н5СОО- равны 349,8 Ом.см2/моль
и 37,2 Ом.см2/моль соответственно.
Решение: l∞ = 349,8 + 37,2 = 387,0 Ом-1.см2/моль;
l = = c.1000/с = 4,79.10-2 Ом-1.м-1/0,135
моль.л-1 = 3,55. a = l/l∞ = = 3,55/387,0 = 0,009. Кд
= (a2.с)/(1-a) = (0,0092.0,135)/(1–0,009) = = 1,15.105,
[Н+] = a.с = 1,24.10-3
моль/л. рН = – lg [Н+]
= 2,91.
Ответ: l = 3,55 Ом-1.см2/моль;
a = 0,009; Кд =1,15.10-5
моль/л; рН = 2,91.
2. Для раствора
КС1 концентрации 0,01 моль/л удельное сопротивление r = 709,22 Ом.см. Вычислите
удельную (c) и
эквивалентную (l )
электрические проводимости.
Решение. Удельную
электрическую проводимость вычисляем по уравнению (1.2): c = 1/709,22 = 1,41.10-3
= = 0,141. Эквивалентная электрическая проводимость согласно уравнению (1.3)
выражается уравнением l =
0,141/0,0 = 0,0141; l =
0,141.10-1.
Ответ: c = 0,141 Ом-1.м-1;
l = 1,41.10-2 Ом-1.моль-1.м2.
3. Вычислите
эквивалентную электрическую проводимость уксусной кислоты при бесконечном
разведении, при 298 К, если электрические проводимости НС1, NаСООСН3, NaCl равны 0,0426; 0,0091; 0,0126 Ом-1.моль-1.м2
соответственно.
Решение.
Составляем систему уравнений согласно (1.5):
l∞,HCl = l∞,H+ + l∞,Cl- = 0,0426 Ом-1.моль-1.м2
(1), l∞,CH3COOH
= = l∞,Na++l∞,CH3COO- = 0,091 Ом-1.моль-1.м2
(2), l∞,NaCl = l∞,Na+ + + l∞,Cl- = 0,0126 Ом-1.моль-1.м2
(3). Согласно соотношению (1.5) складываем уравнения (1) и (2),
вычитаем из них уравнение (3) и получаем
l∞,НС1 + l∞,СН3СООNа – l∞,NaС1 = lН+ + lСН3СОО- = l0,СН3СООН = = 0,0426 + 0,0091 – 0,0126 =
0,0391.
Ответ: l = 0,0391 Ом-1.моль-1.м2.
4. Для
бесконечно разбавленного раствора NН4С1 при 298,2 К число переноса катиона t+ = 0,491. Вычислите электрическую подвижность и
абсолютную скорость движения аниона С1-; l∞,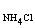 = 0,0150 Ом-1.моль-1.м2.
= 0,0150 Ом-1.моль-1.м2.
Решение. Согласно
уравнениям (1.9 и 1.10) l- = = l∞.(1 – t+) = 0,015.
(1-0,491) = 0,00763 Ом-1.моль-1.м2.
Абсолютную скорость движения v-0 рассчитываем по уравнению (1.7): v-0 = 0,00763 / 9,65.104 = 7,91.10-8.
Ответ: v-0 = 7,91.10-8 м2/(с.В).
5. При электролизе
раствора AgNO3 на катоде выделилось 0,5831 г серебра, убыль AgNO3 в катодном пространстве составила 2,85.10-3
моль. Определите числа переноса t- и t+ для нитрата серебра.
Решение. Убыль
серебра в катодном пространстве Dск и общая
убыль AgNO3 в растворе Dс,
соответствующая количеству серебра, выделившегося на катоде, должны быть
выражены в одних и тех же единицах. Находим число молей серебра, выделившегося
на катоде: Dс = Dn = m/M =0,5831/107,9=5,4.10-3 моль.
Подставим в уравнение (1.13) и получим t- =2,85.10-3/5,4.10-3
= = 0,528; t+ = 1 – t- = 0,472.
Ответ: t- = 0,528; t+
= 0,472.
6. Для 0,1 М раствора Cr2(SO4)3 вычислите среднюю
ионную моляльность, активность, общую активность электролита и активности ионов
SO42- и Cr3+ при 298 К.
Решение. Среднюю ионную
моляльность вычисляем по уравнению
m± = m (n+n+n-n-)1/n = (22.33)1/5.
0,1 = 0,255. Среднюю ионную активность вычисляем по уравнению а± = m±. g±.(g± = 0,0458 = = 0,255.0,0458=0,0177.
Общую активность электролита а вычисляем по уравнению а = (а±)n = (0,0177)5 = 2,17.1010.
Ионные моляльности m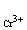 и m
и m рассчитаем
по уравнениям: m
рассчитаем
по уравнениям: m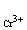 = = m.n
= = m.n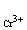 = 0,1.3 = 0,3; m
= 0,1.3 = 0,3; m =
m.n
=
m.n  =
0,1.2 = 0,2; активности аниона и катиона определяем по уравнениям а
=
0,1.2 = 0,2; активности аниона и катиона определяем по уравнениям а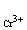 = g
= g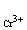 х х m
х х m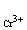 = 0,3.0,0458 = 0,0137; a
= 0,3.0,0458 = 0,0137; a = g
= g . m
. m = = 0,2.0,0458 = 0,0092.
= = 0,2.0,0458 = 0,0092.
Ответ: m±=0,255 моль/1000 г; g±=0,0177; a=2,17.1010 моль/л; m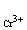 0,3
моль/1000г; m
0,3
моль/1000г; m =0,2 моль/1000 г; a
=0,2 моль/1000 г; a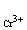 = =0,0137 моль/л; a
= =0,0137 моль/л; a =0,0092 моль/л.
=0,0092 моль/л.
7. Определите ионную силу
I раствора, содержащего 0,001 моль Н2SO4 и 0,002 моль MgSO4 на 1000 г воды при 298 К.
Решение. Согласно
уравнению (1.30):
I = 0,5. (m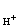 ..z+2 +
+m
..z+2 +
+m ..z-2-
+ m
..z-2-
+ m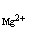 ..z+2 + m
..z+2 + m ..z-2). Моляльности ионов определяем по уравнению (1.30).
Тогда ионная сила I=1/2.(2.0,001.12+0,001.22+0,002.22+0,002.22)
= 0,011.
..z-2). Моляльности ионов определяем по уравнению (1.30).
Тогда ионная сила I=1/2.(2.0,001.12+0,001.22+0,002.22+0,002.22)
= 0,011.
Ответ: I = 0,011.
8. Удельная электрическая
проводимость с = 5%-го раствора нитрата магния при 18 оС
равна 4,38 Ом-1.м-1, а его плотность – 1,038 г.см-3.
Рассчитайте эквивалентную электрическую проводимость раствора λ и
кажущуюся степень диссоциации соли в растворе. Подвижности ионов Mg2+ и NO3-
при 18 оС равны 44,6 и 62,6 Ом-1.см2.моль-1.
Решение. М = с.r/М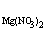 = 0,05.1,038/148.1000 = = 0,70 моль.л-1;
l = c/(с.1000) = 4,38/(0,70.1000)
= = 6,25.10-3; l∞= 44,6 + 62,6 =107,2 Ом-1.см2.моль-1; a = l/l∞ =
62,5/107,2 = 0,583.
= 0,05.1,038/148.1000 = = 0,70 моль.л-1;
l = c/(с.1000) = 4,38/(0,70.1000)
= = 6,25.10-3; l∞= 44,6 + 62,6 =107,2 Ом-1.см2.моль-1; a = l/l∞ =
62,5/107,2 = 0,583.
Ответ: l = 62,510-3 Ом-1.м2.моль-1;
a = 0,583.
1.3 Задачи для
самостоятельного решения
1. Константа диссоциации
масляной кислоты С3Н7СООН равна 1,5.10-5.
Вычислите степень ее диссоциации в 0,005 М растворе.
2. Чему равна
концентрация ионов водорода в водном раст-воре муравьиной кислоты, если α
= 0,03?
3. Вычислите ионную силу
и активность ионов в растворе, содержащем 0,01 моль/л Ca(NO3)2 и 0,01 моль/л CaCl2.
4. Рассчитайте активность
электролита а и среднюю ионную активность а± в
растворе CaCl2 при 25 оC, если средний ионный коэффициент активности γ±
= 0,518, а молярная концентрация m =
0,1.
5. Для реакции
диссоциации муравьиной кислоты: НСООН ↔ Н+ + НСОО-
дана зависимость константы от температуры: lgКД = -1342,85/Т + 5,2743 – 0,0152.T. Вычислите теплоту диссоциации
муравьиной кислоты в разбавленном вод-ном растворе.
6. Определите
температуру, при которой диссоциация му-равьиной кислоты в водном растворе
максимальна. Уравнение зависимости константы диссоциации НСООН от температуры
приведено в предыдущей задаче.
7. Рассчитайте удельную
электрическую проводимость абсолютно чистой воды при 25 оС. Ионное
произведение воды при этой температуре равно 1.10-14.
8. Эквивалентные
электрические проводимости бесконечно разбавленных растворов KCl, KNO3, и AgNO3 при 25 оС
равны соответственно 149,9, 145,0 и 133,4 Ом-1.см2.моль-1.
Какова эквивалентная электрическая проводимость бесконечно разбавленного
раствора AgCl при этой температуре?
9. Удельная электрическая
проводимость 4 % -го водного раствора Н2SO4 при 18 оС равна 0,168 Ом-1.см-1,
плотность раствора равна 1,026 г/см3. Рассчитайте эквивалентную
электри-ческую проводимость этого раствора.
10. Для 0,01 молярного
раствора KCl удельное сопротивление равно 709,22
Ом.см. Вычислите удельную и эквивалентную электрические
проводимости.
11. Какую долю общего
тока переносит ион Li+ в водном растворе LiBr при 25 оС?
12. Эквивалентная
электрическая проводимость раствора уксусной кислоты молярной концентрации 1,59.10-4
моль.л-1 при 25 оС равна 12,77 Ом-1.см2.моль-1.
Рассчитайте константу диссо-циации кислоты и рН раствора.
13. Для бесконечно
разбавленного раствора NH4Cl при 298,2 К число переноса катиона t+ = 0,491. Вычислите электро-литическую подвижность и
абсолютную скорость движения аниона Cl-;
λ∞(NH4Cl) = 0,015 Ом-1.моль-1.м2.
14. При электролизе
раствора AgNO3 на катоде выделилось 0,5831 г серебра, убыль AgNO3 в анодном пространстве соста-вила
2,85.10-3 моль. Определите числа переноса t+ и t-
для AgNO3.
15. При электролизе раствора
AgNO3 c
серебряными электродами увеличение количества соли в анодном про-странстве
составило 0,0625 г. Чему равна убыль соли, г, в катодном пространстве?
2. ЭЛЕКТРОДВИЖУЩИЕ
СИЛЫ. ЭЛЕКТРОДНЫЕ ПОТЕНЦИАЛЫ
2.1 Необходимые
исходные сведения и основные уравнения
ЭДС гальванического
элемента Е равна разности условных электродных потенциалов его
полуэлементов φ1 и φ2. Если значением
диффузионного потенциала можно пренебречь то
Е = φ2 - φ1(2.1)
(индекс 2 относится к
более положительному электродному потенциалу). Электрохимические реакции,
протекающие на электродах, и сами электроды разделяют на следующие типы:
1. Электроды 1-го рода,
обратимые по катиону: Меn+ + ne = = Ме0, где Меn+ и Ме0 ― окисленная
и восстановленная формы вещества; nе
- количество электронов. Потенциал электрода 1-го рода рассчитывается по
уравнению Нернста:
φ = φ0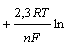 (aOx/aRed),(2.2)
(aOx/aRed),(2.2)
где φ - потенциал
электрода, В; φ0 - стандартный потенциал электрода, В; n - число электронов, участвующих в
элемен-тарной реакции; F
- число Фарадея; aRed и aOx - активности вос-становленной и
окисленной форм вещества, вступающего в реакцию. Множитель  при Т = 298 К и значении R, равном 8,31 Дж/(моль.К), равен 0,059. К
электродам 1-го рода относятся:
при Т = 298 К и значении R, равном 8,31 Дж/(моль.К), равен 0,059. К
электродам 1-го рода относятся:
а) серебряный электрод:
Ag+│Ag; Ag+ + e =
Ag0; n =1;aOx = aAg+; aRed = aAg =1,
φ = φ0Ag+  lgaAg+; (2.3)
lgaAg+; (2.3)
б) амальгамный электрод:
Cd2+ │[Cd] (Hg)Cd2+ + 2e = [Cd]ам;
n = 2; aOx = aCd+
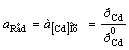 ; φ = φ0AСd2+
; φ = φ0AСd2+ 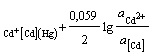 ,(2.4)
,(2.4)
где φ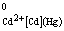 - потенциал амальгамного электрода
при активности кадмия в амальгаме, а[Cd] = 1;
- потенциал амальгамного электрода
при активности кадмия в амальгаме, а[Cd] = 1;
в) газовый электрод:
H+ │Pt,
H2; H+ + e =½ H2; n = 1; aOx
= aH++; aRed = 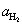 =
= 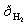 ;
;
φ = φ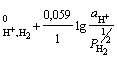 .(2.5)
.(2.5)
2. Электроды 2-го рода, обратимые по аниону, представляют
собой металл, покрытый труднорастворимой солью этого метал-ла, который
находится в равновесии с раствором, содержащим соответствующий анион: AgCl + e = Ag + Cl-; n=1;
aOx = aAgCl = 1; aRed = aCl-;
φ = φ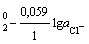 ; (2.6)
; (2.6)
φ02 =
φ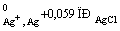 ,(2.7)
,(2.7)
где j 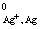 ― стандартный потенциал серебряного
электрода, обратимого по катиону; ПРAgCl ― произведение растворимости
хлорида серебра. К электродам 2-го рода относятся:
― стандартный потенциал серебряного
электрода, обратимого по катиону; ПРAgCl ― произведение растворимости
хлорида серебра. К электродам 2-го рода относятся:
а) газовый электрод:
½ Cl2
+ e = Cl-; n = 1; aOx = 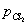 ; aRed =
; aRed = 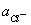 ;
;
φ = φ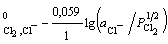 . (2.8)
. (2.8)
б) каломельный электрод Cl-│Hg2Cl2, на котором идет электродная реакция HgCl2 + 2e
= Hg+ + 2Cl- ;
φ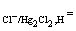 φ
φ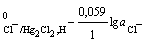 .
.
в) хлорсеребряный
электрод Cl-│AgCl, Ag, на котором идет электродная реакция
AgCl + e = Ag+ + Cl-;
φ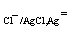 φ
φ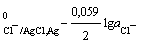 .
.
Окислительно-восстановительные
электроды (редокси – электроды) представляют собой инертный металл, опущенный в
раствор, содержащий окисленную и восстановленную формы. Уравнение Нернста для
данных электродов имеет вид:
φ Red = φ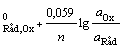 , (2.9)
, (2.9)
где аОх(аО)
― активность окисленного иона; aRed(aВ) - активность восстановленного иона. Они делятся:
а) на простые: Fe3+ + e = Fe2+; n = 1; aRed = 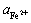 ; aOx =
; aOx = 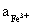 ;
;
φ = φ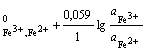 ; (2.10)
; (2.10)
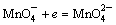 ; n = 1;
; n = 1; 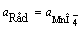 ;
; 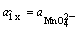 ;
;
φ = φ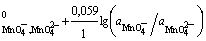 ; (2.11)
; (2.11)
б) на сложные:
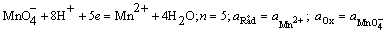 ;
;
φ = φ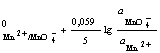 . (2.12)
. (2.12)
Хингидронный электрод: C6H4O2 (хинон) + 2H+ + 2e
= = C6H4(OH)2
(гидрохинон);
n = 2, aRed
= aгх = 1; аОх = ах =
1;
φ = φ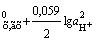 + φ
+ φ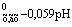 . (2.13)
. (2.13)
Связь константы
равновесия химической реакции и стандартных электродных потенциалов выражается
соотноше-нием
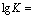 (φ02 – φ01).n/0,0592 (Т = 298 К). (2.14)
(φ02 – φ01).n/0,0592 (Т = 298 К). (2.14)
Для концентрационных
цепей уравнение Нернста (при отсутствии диффузионного потенциала) для электродов
типа
Cu | Cu2+ ║ Cu2+ | Cu ; Ag, AgCl | HCl ║ HCl | Ag, AgCl
a1 a2 (a2 >
a1) a1 a2 (a2
> a1)
имеет вид
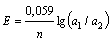 , (2.15)
, (2.15)
где а1
и а2 ─ активности ионов Cu2+ и Cl- соответственно.
Для электродов 2-го рода
типа: Pt, H2 (P1) | HCl | Pt, H2 (P2), уравнение (2.15) преобразуется в уравнение
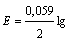 (Р1/Р2), (2.16)
(Р1/Р2), (2.16)
где P1 и P2 - давления
водорода, P1 > P2.
Для амальгамного элемента:
Hg [Cd] (a1) | Cd2+ | Hg [Cd] (a2), (a2 > a1), уравнение Нернста имеет вид
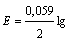 (а1/а2), (2.17)
(а1/а2), (2.17)
где a1 и a2
─ активности металлического кадмия в амальгаме. Для элемента типа: Cd(ж) (a1 = 1) | Cd в расплаве солей | Cd в расплаве Cd – Sn (a2) уравнение (2.17) принимает вид
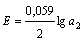 , (2.18)
, (2.18)
где a2 ─ активность кадмия в расплаве Cd – Sn.
Расчет ЭДС
концентрационной цепи (например, серебряной, Ag | AgNO3 (а1)
║ AgNO3 (а2) | Ag,) производится по формуле
Е = 2. 0,059. l∞,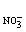 . lg(а1/а2) /(l∞,
. lg(а1/а2) /(l∞,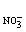 +l∞,
+l∞,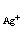 ) (2.19)
) (2.19)
где λ∞,Ag+ и λ∞,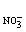 - подвижности аниона и катиона.
- подвижности аниона и катиона.
Термодинамические функции
ΔG, ΔS, ΔH для электрохимических реакций рассчитывают по уравнениям:
ΔG = - nEF, (2.20)
 , (2.21)
, (2.21)
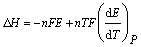 , (2.22)
, (2.22)
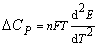 , (2.23)
, (2.23)
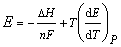 , (2.24)
, (2.24)
где n – число электронов, участвующих в
реакции; F – число Фарадея, Кл; E – ЭДС, В.
2.2 Задачи с решениями
электролит
проводимость потенциал кинетика
1. Гальванический элемент
состоит из металлического цинка, погруженного в 0,1 М раствор нитрата цинка, и
металлического свинца, погруженного в 0,02 М раствор нитрата свинца. Вычислите
ЭДС элемента.
Решение. Чтобы определить
ЭДС элемента, необходимо вычислить электродные потенциалы. Для этого из табл.
[8], берем значения стандартных электродных потенциалов систем Zn2+|Zn (-0,76 В) и Pb2+|Pb (-0,13 В), а затем рассчитываем значение φ по уравнению
Нернста: φZn/Zn2+ = -0,76+(0,059.lg0,1)/2 = =-0,79 В, φPb/Pb2+=-0,13+(0,059.lg0,02)/2=-0,18 В. Находим ЭДС
элемента: Е = φ Pb/Pb2+ – φ Zn/Zn 2+ = -0,18+0,79 = 0,61.
Ответ:0,61 В.
2. Вычислите потенциал
серебряного электрода в насыщенном растворе AgBr (ПР = 6.10-13), содержащем,
кроме того, 0,1 моль/л бромида калия.
Решение. Запишем
уравнение Нернста для системы Ag+|Ag: φ = φ0 + 0,059.lg[Ag+]. Значение φ0 для этой системы составляет
0,8 В (табл. [8]). Поскольку бромид калия полностью диссоциирован, то [Br-]=0,1 моль/л. Отсюда находим концентрацию ионов
серебра: [Ag+] = ПРAgBr /[Br-] = 6.10-13/0,1
= = 6.10-12 моль/л. Теперь подставляем значения φ0
и [Ag+] в уравнение электродного потенциала: φ = 0,8 +
0,059.lg(6∙10-12)
= = 0,14.
Ответ: 0,14 В.
3. Вычислите активность
ионов Н+ в растворе, в котором потенциал водородного электрода равен
82 мВ.
Решение. Из уравнения
φ = -0,059рН находим: рН = = 0,082/0,059 = 1,39. Следовательно, аН+
= 0,041.
Ответ: аН+
= 0,041 моль/л.
4. Рассчитайте
стандартный электродный потенциал пары Cu2+|Cu+ по следующим данным: φ0Cu2+|Cu = 0,337 В, φ0Cu+|Cu = = 0,521 В.
Решение. Для реакции Cu2+ + 2е = Cu, ΔG0 = -nFЕ0 = = −2.96485.0,337
= −65031 Дж.моль-1. Для реакции Cu+ + е = Cu, ΔG0 = −96485.0,521
= −50269 Дж.моль-1. Вычитая из первой реакции
вторую, получим Cu2+ + е = Cu+ и, следовательно, ΔG0 = = −14762 Дж.моль-1,
откуда Е0 = 0,153.
Ответ: Е0
= 0,153 В.
5. ΔН реакции
Pb + Hg2Cl2 = PbCl2 + 2Hg,
протекающей в гальваническом элементе, равно −94,2 кДж/моль при 298,2 К.
ЭДС этого элемента возрастает на 1,45.10-4 В при повышении
температуры на 1 К. Рассчитайте ЭДС элемента и ΔS при 298,2 К.
Решение. 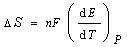 = 2,96485.1,45.10-4 = =
28,0. ΔG
= ΔН – ТΔS = nFE, откуда E =
− (ΔН - ТΔS)/nF =
= 0,5314.
= 2,96485.1,45.10-4 = =
28,0. ΔG
= ΔН – ТΔS = nFE, откуда E =
− (ΔН - ТΔS)/nF =
= 0,5314.
Ответ: ΔS = 28,0 Дж/(моль.К); E = 0,5314 В.
6. Рассчитайте константу
равновесия реакции Cd2+ + Zn = = Zn2+ + Cd, если φ0Cd2+/Cd = -403 В; φ0Zn2+/Zn = -0,763 В.
Р е ш е н и е. Константу
равновесия вычисляем по уравнению: 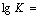 (φ02 – φ01).n/0,0592. После подстановки данных
получим
(φ02 – φ01).n/0,0592. После подстановки данных
получим 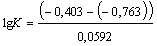 = 12,16.
Откуда К = 1,45.1012.
= 12,16.
Откуда К = 1,45.1012.
Ответ: К = 1,45.1012.
2.3 Задачи для
самостоятельного решения
1. Гальванический элемент
состоит из серебряного электрода, погруженного в 2 М раствор AgNO3, и стандартного водородного электрода. Напишите
уравнения электродных процессов и суммарной реакции, происходящей при работе
элемента. Определите его ЭДС.
2. Рассчитайте
электродные потенциалы магния в растворе его соли при концентрациях иона Mg2+, равной 0,1; 0,01 и 0,001 моль/л.
3. Вычислите потенциал
свинцового электрода в насыщенном растворе PbBr2, если [Br-] = 1 моль/л, а ПРPbBr2+= 9,1.10-6.
4. Гальванический элемент
составлен из стандартного цинкового электрода и хромового электрода,
погруженного в раствор, содержащий ионы Cr3+. При какой концентрации ионов Cr3+ ЭДС этого элемента окажется равной 0?
5. ЭДС гальванического
элемента, составленного из 2 водородных электродов, равна 272 мВ. Чему равен рН
раствора, в который погружен анод, если катод погружен в раствор с рН = 3?
6. Рассчитайте константу
равновесия реакции диспропорционирования 2 Cu+ + Cu2+ + Cu при 25 оC.
7. Рассчитайте константу
равновесия реакции ZnSO4 + Cd = = CdSO4 + Zn при 25 оС по данным о
стандартных электродных потенциалах.
8. Рассчитайте потенциал
водородного электрода в чистой воде при 25 оС.
9. ЭДС элемента, в котором
обратимо протекает реакция 0,5 Hg2Cl2 + Ag = AgCl + Hg, равна 0,456 В при 298 К и 0,439 В при 293 К. Рассчитайте
ΔG, ΔH и ΔS реакции.
10. Значение ΔН
реакции Pb + 2 AgCl = PbCl2 + Ag,
протекающей в гальваническом элементе, - 105,1 кДж/моль. ЭДС этого элемента
равна 0,4901 В при 298,2 К. Рассчитайте ЭДС элемента при 293,2 К.
11. Вычислите полезную
работу реакции Ag + 0,5Cl2 = AgCl,
используя данные о нормальных электродных потенциалах, если Р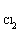 = 101,3 кПа, Т = 298
К.
= 101,3 кПа, Т = 298
К.
12. Температурный
коэффициент элемента, работающего за счет реакции: Pb + Hg2Cl2 = PbCl2 + 2 Hg, 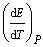 = 1,45.10-4 В/К. Определите количество
теплоты, выделяющейся (поглощающейся) при работе элемента и сопоставьте
полученное значение с тепловым эффектом, рассчитанным по следствию из закона
Гесса.
= 1,45.10-4 В/К. Определите количество
теплоты, выделяющейся (поглощающейся) при работе элемента и сопоставьте
полученное значение с тепловым эффектом, рассчитанным по следствию из закона
Гесса.
13. Для гальванического
элемента, в котором протекает реакция Hg2SO4 + Pb = PbSO4 + 2Hg вычислите ЭДС при 298 К и
температурный коэффициент 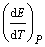 , используя данные таблиц стандартных
термодинамических величин.
, используя данные таблиц стандартных
термодинамических величин.
14. Рассчитайте потенциал
серебряного электрода, опущенного в насыщенный раствор AgI, по данным о произведении растворимости соли и нормальном
электродном потенциале серебра.
15. Определите ЭДС гальванического
элемента, представленного: Ag|AgNO3 (0,001 М)||AgNO3
(0,1 M)|Ag. В каком направлении будут перемещаться электроны во внешней
цепи при работе этого элемента?
3. ФОРМАЛЬНАЯ КИНЕТИКА
3.1 Необходимые
исходные сведения и основные уравнения
Химическая кинетика –
раздел физической химии изучающий закономерности протекания химической реакции
во времени. В задачу этого раздела входит определение скорости и константы
скорости химической реакции, а также изучение закономерностей их изменения в
зависимости от различных факторов (температуры, давления, концентрации
реагирующих веществ и др.).
Под скоростью химической
реакции понимают изменение концентрации веществ в единицу времени. Для реакций,
описываемых стехиометрическим уравнением
n А1 + n
А1 + n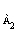 А2
+n
А2
+n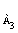 А3 А3 +…. ® n
А3 А3 +…. ® n В1
+ n
В1
+ n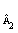 В2 + n
В2 + n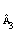 В3 +…,
В3 +…,
истинная скорость
выражается
v = -dc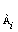 / dt = +dc
/ dt = +dc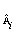 / dt,(3.1)
/ dt,(3.1)
где 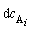 - изменение концентрации одного из
реагирующих веществ, моль/л;
- изменение концентрации одного из
реагирующих веществ, моль/л; 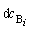 - изменение концентрации одного из продуктов
реакции, моль/л.; dt -
промежуток времени, в течение которого произошло это изменение, с. Знак «+»
относится к продуктам реакции (прибывают во времени), знак «-» относится к
исходным веществам (убывают во времени). Средняя скорость химической реакции в
конечном промежутке времени выражается формулой
- изменение концентрации одного из продуктов
реакции, моль/л.; dt -
промежуток времени, в течение которого произошло это изменение, с. Знак «+»
относится к продуктам реакции (прибывают во времени), знак «-» относится к
исходным веществам (убывают во времени). Средняя скорость химической реакции в
конечном промежутке времени выражается формулой
v = ± Dсi/Dt, (3.2)
где Dсi – изменение концентрации любого
участника химичес-кой реакции за промежуток времени Dt. Зависимость скорости химической
реакции от концентрации исходных веществ выражается законом действия масс
(основной постулат химической кинетики):
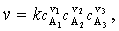 (3.3)
(3.3)
где k – константа скорости химической
реакции. Физический смысл константы скорости химической реакции заключается в
том, что она численно равна скорости химической реакции в случае равенства единице
(в молях на литр) концентрации всех реагирующих веществ. В химической кинетике
различают также понятия «молекулярность» и «порядок реакции».
Молекулярность – это количество
частиц, участвующих в элементарном акте химической реакции. Она может принимать
любое целое положительное число. Однако вследствие малой вероятности
одновременного столкновения большого количества частиц реакции с
молекулярностью, превышающей четыре, практически не встречаются.
Порядок реакции – это сумма
стехиометрических коэффициентов, стоящих перед символами химических веществ,
участвующих в реакции, или сумма показателей степеней, с которыми концентрации
веществ входят в основной постулат химической кинетики:
n = Σ vi, (3.4)
где n – порядок реакции.
Вследствие того, что запись химического
уравнения не от-ражает механизма протекания реакции, в большинстве случаев
порядок реакции не совпадает с суммой стехиометрических коэффициентов. Порядок
реакции может принимать любое положительное значение, включая ноль и дробные числа.
Порядок реакции необходим для правильного выбора кинети-ческого уравнения,
позволяющего рассчитать скорость и константу скорости химической реакции.
Реакции нулевого
порядка. В этих
реакциях Sni = 0,
следо-вательно, после объединения уравнений (3.1), (3.2) и (3.3) получаем
dc/dt = k.(3.5)
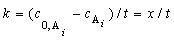 ,(3.6)
,(3.6)
где c0, – начальная концентрация реагирующего вещества,
моль/л, х – число молей исходного вещества А, прореагировавшего к
моменту времени t, с, в
единице объема, моль.
– начальная концентрация реагирующего вещества,
моль/л, х – число молей исходного вещества А, прореагировавшего к
моменту времени t, с, в
единице объема, моль.
Реакции первого
порядка. В этих
реакциях Sn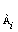 = 1, и кинетическое уравнение имеет
вид
= 1, и кинетическое уравнение имеет
вид
dc/dt = k с, (3.7)
k = (2,3.lgcA/c0,А)/t. (3.8)
Реакции второго
порядка. В этих
реакциях Sn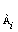 = 2. Следует различать два случая: n
= 2. Следует различать два случая: n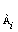 = 2 и n
= 2 и n = 1, n
= 1, n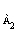 = 1. В первом случае начальные концентрации
реагирующих веществ одинаковы, поэтому− dc/dt = k.с2, (3.9)
= 1. В первом случае начальные концентрации
реагирующих веществ одинаковы, поэтому− dc/dt = k.с2, (3.9)
k = t-1.( cA-1 - c0,А-1). (3.10)
Во втором случае
начальные концентрации реагирующих веществ не одинаковы
k=2,3.t-1(c0, -1- c0,
-1- c0,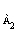 -1).lg[(c
-1).lg[(c .c0,
.c0,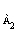 )/(c
)/(c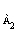 . c0,
. c0, )]. (3.11)
)]. (3.11)
Реакции n-го порядка. В этих реакциях Sn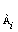 = n. Поэтому
общее кинетическое уравнение имеет вид
= n. Поэтому
общее кинетическое уравнение имеет вид
k = (n-1)-1.t-1. (cA1-n − c0,А1-n). (3.12)
Под периодом
полупревращения вещества t1/2 понимают
промежуток времени, с, в течение которого прореагировала ровно половина
первоначально взятого вещества. Период полураспада для разных реакций может
принимать очень широкое значение: от долей секунды (радиоактивный распад
большинства трансурановых элементов, взрывные реакции и др.) до миллионов лет
(радиоактивный распад урана, окисление горных пород и др.). С учетом
приведенного определения (c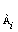 = 1/2 c0,
= 1/2 c0,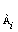 ), для реакций нулевого порядка
), для реакций нулевого порядка
t1/2 = 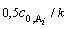 , (3..13)
, (3..13)
для реакций первого
порядка
t1/2 = 0,693/k, (3.14)
для реакций второго
порядка
t1/2 =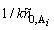 . (3.15)
. (3.15)
Определение порядка
реакции методом Оствальда-Нойеса (интегральный метод):
ni = [(lg(t'1/2/t"1/2)/lg(c0,2/c0,1)] + 1, (3.16)
где t'1/2 – период полураспада,
соответствующий начальной концентрации реагирующего вещества c0,1; t"1/2 – период полураспада этого же вещества
при другой начальной концентрации c0,2.
Определение порядка
реакции методом Вант-Гоффа (дифференциальный метод):
ni = (lgw1
- lgw2)/(lgc0,1/c0,2), (3.17)
где w1, w2 – средние
скорости реакции, соответствующие начальным концентрациям с0,1
и с0,2.
3.2 Задачи с решениями
1. Вычислите константу
скорости бимолекулярной реакции образования фосгена СО + С12 = СОС12,
если при 27оС количество реагирующих веществ изменяется следующим
образом:
|
Время, мин
|
0
|
12
|
24
|
36
|
|
Концентрация СО, моль/л
|
0,01873
|
0,01794
|
0,011734
|
0,01674
|
Определите концентрацию
исходных веществ через три часа после начала реакции.
Решение.
Используем уравнение для расчета констант скоростей второго порядка, когда с1
= с2: k
= t-1.( c0,A-1 -.c0-1). После подстановки в эту формулу
данных из приведенной таблицы (любые три пары) получим: kср = 0,186 мин-1. Рассчитаем
концентрацию исходных веществ через три часа после начала реакции: 1,627.х
= 0,01174; х = 0,0072; а – х = 0,01873 - 0,00720 = = 0,0115.
Ответ: kср = 0,186 мин-1; [С12]
= 0,0072 моль/л; [СО] = = 0,0015 моль/л.
2. Превращение
пероксида бензоила в диэтиловый эфир (реакция 1-го порядка) прошло за 10 минут
на 75,2%. Вычислите константу скорости реакции.
Решение Напишем уравнение для расчета
константы скорости реакции первого порядка и подставим в него соответствующие
значения: k = (2,303/t).lg[a/(a-x)] = (2,303/10) х х lg(100/24,8) = 0,2303/0,606 = 0,140.
Ответ: k = 0,140 мин-1.
3. Для химической реакции
А ® В константа скорости k = = 0,5, исходная концентрация c0,А=1 моль/л. На основании этих данных
определите степень превращения вещества А за время t = 1 ч, если реакция идет: а) по нулевому; б) первому;
в) второму порядку. Как зависит степень превращения от порядка реакции?
Решение. Для реакции,
протекающей по нулевому порядку, согласно уравнению (3.6): 0,5 = х/t; т. е. х = 0,5. Для реакции,
протекающей по первому порядку, согласно уравнению (3.9): 0,5 = 2,3/1.lg[1/(1-х)]; 0,5/2,3 = −lg(1-а); а = 0,39. Для
реакции, протекающей по второму порядку, согласно уравнению (3.11): 0,5 = 1/1.[1/(с0.(1-х)]
– 1/с0); 0,5 = 1/(1-а); а = 0,33.
Ответ: Чем выше порядок,
тем меньше степень превращения, тем медленнее идет реакция.
4. Период полураспада
радиоактивного изотопа 14С составляет 5730 лет. При археологических
раскопках были найдены остатки дерева, содержание изотопа 14С в
котором составляло 72% от нормального. Определите возраст дерева.
Ответ: t = 2720 лет.
5. В некоторой реакции
целого порядка nА ® В концентрация исходного вещества,
равная 0,5 моль/л, была достигнута за 4 мин при начальной концентрации этого
вещества 1 моль/л и за 5 мин при начальной концентрации 2 моль/л. Установите
порядок реакции.
Решение. Из первого опыта
следует, что период полураспада вещества при начальной концентрации 1 моль/л равен
4 мин. Во втором опыте при начальной концентрации 2 моль/л период полураспада
равен 1 мин (переход от 2 до 0,5 моль/л прошел за 5 мин, из них от 1 до 0,5
моль/л – 4 мин, следовательно, переход от 2 до 1 моль/л потребовал 1 мин).
Таким образом, при увеличении начальной концентрации в два раза период
полураспада уменьшился в 4 = 2n-1 раза, следовательно, порядок реакции n=3.
Ответ: Реакция 3-го
порядка.
6. Для изучения
разложения щавелевой кислоты в концентрированной серной кислоте приготовили
1/40 М раствор щавелевой кислоты в 99,5%-й серной кислоте. Через определенные
промежутки времени из смеси отбирали пробы и определяли объем раствора
перманганата калия, необходимый для титрования 10 мл раствора. Результаты
эксперимента приведены ниже.
|
t, мин
|
0
|
120
|
240
|
420
|
600
|
900
|
1440
|
|
V, мл
|
11,45
|
9,63
|
8,11
|
6,22
|
4,79
|
2,97
|
1,44
|
Определите порядок
реакции и ее константу скорости.
Решение. Данную задачу удобнее решить
методом перебора кинетических уравнений для реакций различных порядков.
Предположим,
что реакция имеет первый порядок. Кинетическим уравнением в этом случае
является уравнение (3.8). После подстановки в это уравнение экспериментальных
данных получим ряд констант скоростей: k = 0,00144; 0,00144; 0,00145; 0,00150; 0,00140.
Совпадение этих данных
свидетельствует о правильном нашем предположении. В результате получаем вывод:
эта реакция имеет первый порядок, а среднее значение ее константы скорости k = 0,00145 мин-1.
Любое иное
наше предположение о возможном другом порядке реакции после подстановки
экспериментальных данных в соответствующие кинетические уравнения (3.6),
(3.10), (3.12), (3.15) не приводит к удовлетворительному совпадению констант
скоростей, рассчитанных с использованием полученных экспериментальных данных.
Ответ:
Реакция первого порядка, k
= 0,00145 мин-1.
7. При взаимодействии
брома с этиловым спиртом были получены следующие результаты:
|
t, мин
|
0
|
4
|
|
c1, моль/л
|
0,00814
|
0,00610
|
|
c2, моль/л
|
0,00424
|
0,00314
|
Определите порядок
реакции по этим данным.
Решение. Определяем
порядок реакции по методу Вант-Гоффа (3.17). Бесконечно малые приращения
времени dt и убыли концентраций dс при определении скорости реакции заменяем на конечные
приращения этих функций. В этом случае возможно применение уравнения (3.17) в
виде n = [lg(Dс1/Dt) - - lg(Dс2/t)]/(lgс1 – lgс2).
Подставляем необходимые
данные. Так как Dс/Dt = w, а скорость реакции средняя, то и концентрации с1 и
с2 также необходимо взять средние:
с1 = (0,00814 + 0,00610)/2 = 0,00712;
с2 = (0,00424 + 0,00314)/2 = 0,00369;
n = lg(0,00814-0,00610)/4 – lg(0,00424-0,00314)/4:
(lg0,00712 − 1g0,00369) = 0,91 » 1.
Следовательно,
данная реакция является реакцией первого порядка.
Ответ: Реакция первого
порядка.
3.3 Задачи для
самостоятельного решения
1. В некоторый момент
времени скорость сгорания циклогексана в избытке кислорода равна 0,350 моль/(л.с).
Чему равны скорость образования СО2 и скорость расходования
кислорода в этот момент?
2. В реакции второго
порядка А + В ® 2D начальные концентрации веществ А и В
равны друг другу (по 1,5 моль/л). Скорость реакции равна 2,0.0-4
моль/(л.с) при [А]=1,0 моль/л. Рассчитайте константу скорости и
скорость реакции при [В] = = 0,2 моль/л.
3. Разложение Н2О2
в спиртовом растворе – реакция первого порядка. Начальная скорость реакции при
температуре 40 оС и концентрации Н2О2 0,156 М
равна 1,14.10-5 моль/(л.с). Рассчитайте
константу скорости.
4. Реакция первого
порядка протекает на 30% за 7 мин. Через какое время реакция завершится на 99%?
5. Период полураспада
радиоактивного изотопа 137Cs, который попал в атмосферу в результате Чернобыльской аварии, - 29,7
года. Через какое время количество этого изотопа составит менее 1% исходного?
6. Изотоп иод-131,
который применяют для лечения некоторых опухолей, имеет период полураспада 8,1
суток. Какое время должно пройти, чтобы количество радиоактивного йода в
организме больного уменьшилось в 100 раз?
7. Период полураспада
радиоактивного изотоп 90Sr, который попадает в атмосферу при ядерных испытаниях, − 28,1 года.
Предположим, что организм новорожденного ребенка поглотил 1,00 мг этого
изотопа. Сколько стронция останется в организме через: а) 18 лет, б) 70 лет,
если считать, что он не выводится из организма?
8. Разложение
иодоводорода HI(г) = ½ Н2(г) + ½
I2(г) на поверхности золота – реакция
нулевого порядка. За 100 с концентрация йодоводорода уменьшилась с 0,335 М до
0,285 М. Рассчитайте константу скорости и период полураспада при начальной
молярной концентрации йодоводорода 0,400 М.
9. Реакция второго
порядка А + В ® Р проводится в
растворе с начальными концентрациями [А]0 = 0,050 моль/л и [В]0
= = 0,080 моль/л. Через 1 ч концентрация вещества А уменьшилась до 0,020
моль/л. Рассчитайте константу скорости и периоды полураспада обоих веществ.
10. В некоторой реакции
целого порядка nА ® В молярная концентрация исходного вещества
1,5 моль/л была достигнута за 5,0 мин при начальной концентрации 3,0 моль/л и
за 6,25 мин при начальной концентрации 6,0 моль/л. Установите порядок реакции.
11. Было найдено, что при
изменении начальной молярной концентрации с 0,502 до 1,007 моль/л период
полураспада в некоторой реакции уменьшился с 51 до 26 с. Каков порядок этой
реакции и чему равна константа скорости?
12. В течение часа
подвергается распаду 1/16 часть неко-торого радиоактивного элемента. Определите
период полу-распада этого элемента.
13. Концентрация атомов
трития в воздухе приблизительно 5.10-15 моль/л. Период
полураспада трития около 12 лет. Через сколько лет распадается 90% трития,
содержащегося в воздухе? Пополнение содержания трития в воздухе за счет реакций
синтеза не учитывать.
14. Пероксид водорода в
водном растворе разлагается по уравнению 2 Н2О2
® 2 Н2О
+ О2. Кинетику этой реакции исследовали титрованием проб одинакового
объема (2 мл) 0,015 М раствором перманганата калия. Определите порядок реакции
всеми возможными способами и вычислите среднее значение константы скорости этой
реакции, пользуясь приведенными данными:
|
Время, мин
|
0
|
5
|
10
|
15
|
20
|
30
|
40
|
|
Количество KMnO4, мл
|
23,6
|
18,1
|
14,8
|
12,1
|
9,4
|
5,8
|
3,7
|
15. При нагревании
раствор дибромянтарной кислоты распадается на бромалеиновую кислоту и НВr по уравнению
СООН-СНBr-CHBr-COOH ® CHCOOH-CBrCOOH + HBr
При титровании раствора
стандартным раствором щелочи через t,
мин, титр ее в объеме раствора изменялся следующим образом:
|
t, мин
|
0
|
214
|
380
|
|
Vщ, см3
|
12,11
|
12,44
|
12,68
|
Вычислите константу
скорости реакции. Через сколько времени разложится 1/3 дибромянтарной кислоты?
16. Бимолекулярная
реакция, для которой сА=сВ, протекает за 10
мин на 25%. Сколько потребуется времени, чтобы реакция прошла на 50% при той же
температуре?
17. При определенной
температуре раствор уксусноэтилового эфира концентрации 0,01 моль/л омыляется раствором
NaOH концентрации 0,002 моль/л на 10% за
23 мин. Через сколько минут он будет омылен до такой же степени раствором NaOH концентрации 0,005 моль/л если
реакция омыления эфира – реакция второго порядка, а щелочь диссоциирована
полностью?
18. Фенилдиазохлорид
разлагается по уравнению C6H5N2CI= =C6H5CI + N2. При 323 К и начальной концентрации 10 г/л были
получены следующие результаты:
|
Время, мин
|
6
|
9
|
12
|
14
|
22
|
24
|
26
|
30
|
¥
|
|
Выделено N2, см3
|
19,3
|
26,0
|
32,6
|
36,0
|
45,0
|
46,5
|
48,3
|
50,4
|
58,3
|
Определите порядок и
константу скорости реакции.
19. Реакция разложения
аммиака на горячей вольфрамовой проволоке протекает по стехиометрическому
уравнению 2 NH3 = N2 + 3 H2. Во время реакции в различные
моменты времени давление повышалось следующим образом:
|
Время, с
|
100
|
200
|
400
|
600
|
800
|
1000
|
|
ΔР, Па
|
1466,3
|
2945,9
|
5865,2
|
8837,8
|
11717,0
|
14663,0
|
Определите порядок
реакции.
20. Окисление FeCl2 с помощью КС1О3 в присутствии НС1 –
реакция третьего порядка. Если время выражать в минутах, а концентрации – в
молях на литр, то константа скорости этой реакции равна приблизительно единице.
Вычислите концентрацию FeCl2 через 1,5
ч после начала реакции, если начальные концентрации всех реагирующих веществ
равны 0,2 моль/л.
4.
Зависимость скорости реакции от температуры
4.1 Необходимые исходные сведения и
основные уравнения
Как правило, скорость
химических реакций увеличивается при росте температуры. Этот рост в большинстве
случаев подчиняется эмпирическому правилу Вант-Гоффа: при повышении температуры
на каждые 10 оС скорость большинства реакций увеличивается в 2…4
раза. Температурный коэффициент скорости химической реакции g можно определить из отношения
констант скоростей при двух разных температурах: k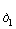 и k
и k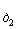 :
:
k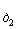 / k
/ k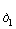 = g(T2-T1)/10. (4.1)
= g(T2-T1)/10. (4.1)
Экспериментальные данные
показывают, что решение этого уравнения для подавляющего большинства химических
реакций дает значение g,
находящееся в интервале значений 2…4. По этой причине g носит название «температурный
коэффициент повышения скорости химической реакции» или «коэффициент
Вант-Гоффа».
Однако сам коэффициент
Вант-Гоффа зависит от температуры и по этой причине уравнение 4.1 оказывается
непригодным при расчете скорости реакций в широком интервале температур. Более
точно зависимость константы скорости химической реакции от температуры
описывается уравнением Аррениуса (в дифференциальной форме):
dlnk/dT = Eоп/RT2, (4.2)
где Еоп (или
Еа) – энергия активации, Дж/моль.
После интегрирования
получаем уравнение, пригодное для практических расчетов:
lgk2/k1 = Eоп.(T2−T1 ) / (2,3R.T1.T2)(4.3)
или k = k0 е-Еоп /RT,(4.4)
где k0 – постоянная (предэкспоненциальный множитель).
Из уравнения (4.3) видно,
что зависимость lgk от обратной
температуры представляет собой прямую. Такая зависимость позволяет определять
энергию активации и предэкспоненциальный множитель графически:
Eоп = 2,3.tga, (4.5)
где a - угол наклона прямой.
4.2 Задачи с решениями
1. При 25 оС
некоторая реакция заканчивается за 3 часа. Принимая температурный коэффициент g равным 2,5, рассчи-тайте значение
температуры, при котором реакция закончится в течение 30 мин.
Р е ш е н и е. Чем
выше константа скорости, тем быстрее заканчивается реакция. Поэтому между этими
величинами будет обратная зависимость: k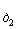 /k
/k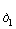 = t1/t2 = g(T2-T1)/10; 180/30=2,5(T2- 25). Т2
= 44,5 оС.
= t1/t2 = g(T2-T1)/10; 180/30=2,5(T2- 25). Т2
= 44,5 оС.
Ответ: Т2
= 44,5 оС.
2. Если проводить
химическую реакцию между фиксированными концентрациями реагентов, период
полураспада веществ зависит от температуры согласно нижеприведенной таблице:
|
Температура, К
|
798
|
813
|
828
|
843
|
858
|
873
|
|
Период полураспада, с
|
1072
|
631
|
380
|
229
|
144,5
|
89,1
|
Определите энергию
активации реакции.
Решение. Допустим,
что исходные вещества взяты в равных концентрациях. Тогда для реакции первого
порядка t1/2 = = 0,693/k, а для реакций второго порядка t1/2 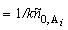 . Для реакций третьего порядка аналогично. Подставив опытные
данные в эти уравнения (независимо от порядка) и приравняв правые части
уравнений, получим, что энергия активации равна 45,5 кДж/моль. Такое же
значение получается и при других температурах.
. Для реакций третьего порядка аналогично. Подставив опытные
данные в эти уравнения (независимо от порядка) и приравняв правые части
уравнений, получим, что энергия активации равна 45,5 кДж/моль. Такое же
значение получается и при других температурах.
Ответ: Еоп
= 45,5 кДж/моль.
3. Скорость
некоторой реакции изучалась в широкой области температур, и были найдены
значения энергии активации при разных температурах:
|
t, оС
|
500
|
1000
|
1500
|
2000
|
2500
|
|
Еа, кДж/моль
|
48,0
|
46,0
|
44,0
|
42,1
|
40,1
|
Покажите, что полученные
результаты согласуются с температурной зависимостью предэкспоненциального
фактора в виде А = Тn и определите n.
Решение. Из данных
видно, что Е = −4∙10-3. Поэтому зависимость
энергии активации от температуры можно представить в виде уравнения (в
интервале 500-2500 оС): Еа,Т = =50+(dE/dT)T. Например, при 1500 оС: Еа,1500
= 50 – 4.10-3.1500 = = 44 кДж/моль.
Учитывая, что после
логарифмирования и применения урав-нения Аррениуса получаем:
∆Т = nRT + T = Tопыт.
Таким образом, имеем два
уравнения: Еоп – Е = nRT и Еоп – 50 = (dE/dT)Т
Следовательно, nR=dE/dT; n.2.10-3= −4.10-3
; n = −2.
Зависимость
предэкспоненциального фактора от температуры вытекает как из теории бинарных
соударений, так и из теории активированного комплекса. В первой теории в
предэкспоненту входит зависимость скорости движения молекул газа от
температуры, во второй теории в этот же фактор входит зависимость
статистических сумм вращательного и колебательного движения от температуры. Но
так как химические реакции обычно проводятся в узком интервале температур, то зависимость
А от Т так резко не выражается, что приводит к настоящему наклону
прямой Аррениуса.
Ответ: n = −2.
4. Гидролиз (CН2)6СС1СН3
в 80 %-м этаноле протекает по первому порядку. В одном из опытов для этой
реакции были получены следующие значения константы скорости:
|
Т, К
|
273
|
298
|
308
|
318
|
|
K,с
|
1,06∙10-5
|
3,19∙10-4
|
9,86∙10-4
|
2,92∙10-3
|
Рассчитайте энергию
активации и предэкспоненциальный множитель.
Решение. По формуле
Аррениуса определяем энергию активации: lgk2/k1 = Eоп(T2-T1)/(2,3.RT1.T2); Еср = 957 кДж/моль. Для
нахождения k0 можно взять любую температуру. lgk = lgk0 - -E/RT; lgko = lgk+E.RT.Т = 298К. lgkо = lg(3,19.104)
+ +957/(2,303 х х 8,314.298) = 13,28. k0= 1,9.1013e-0,5700/RT.
Ответ: k0= 1,9∙1013е-0,5700/RT.
5. Вещество
разлагается двумя параллельными путями с константами скорости k1 и k2. Какова
разность энергий активации этих двух реакций, если при Т = 283 К k1/k2 = 10, а
при Т = 313 К - k1/k2 = 0,1.
Решение. Схема реакции: В
¬ А ® С. Введем обозначения: а – начальная
концентрация А; х – общее число молей вещества А, превратившегося в
продукты В(х1) и С(х2); х = х1
+ х2.
Для параллельных реакций k1+k2 = k. Учитывая, что k = = k0∙е-Еоп /RT, получим для Т1=283
К: А ® В, для Т2 = 313К:
А ® ® С. По уравнению Аррениуса: lgk2/k1=Eоп.(T2 − T1 )/(2,3.R.T1.T2), откуда Е1 = -56,53 кДж/моль и Е2
= 56,53 кДж/моль.
Отрицательная энергия
активации для направления А ® В по сравнению с направлением А ® С в параллельных реакциях говорит о том, что при повышении
температуры константа скорости реакции в первом направлении падает. Значит, при
повышенных температурах вещество А с большей скоростью превращается не в
вещество В, а в вещество С. Одной из реакций подобного типа является
образование нитрозилбромида по схеме: 2 NО + Вr ® 2 NОВr.
Дифференциальное
кинетическое уравнение этой реакции имеет вид d[NOBr]/dt = К[NO]2[Br2] и согласуется со следующими
стадиями процесса:
1) NO+Br2
« NOBr2; 2) NOBr2+NO « 2 NOBr
Опыты показывают, что
энергия активации этой реакции отрицательна. Это может быть в том случае, когда
при повышенных температурах скорость распада NOBr2 на NO и Br2 с константой скорости k2 концентрация NOBr2 уменьшается, что ведет к уменьшению скорости
образования NOBr на второй ста-дии. Следовательно,
из-за уменьшения константы скорости на лимитирующей стадии по мере повышения
температуры энергия активации реакции оказывается величиной отрицательной. По-добные
примеры не единичны. Например,в реакции 2NO + O2 « « 2NO2 константа скорости прямой реакции понижается при повышении
температуры. Как правило, понижение константы скорости реакции при росте
температуры наблюдается для тех реакций, где имеются конкурирующие реакции.
Ответ: Еа1
= -56,53 кД/моль и Еа2 = 23,04 кДж/моль.
4.3 Задачи для
самостоятельного решения
1. Константа
скорости разложения NOCl меняется с
температурой следующим образом:
|
Т, К
|
303
|
313
|
316
|
323
|
|
k, с−1
|
0,0144
|
0,0342
|
0,0530
|
0,0806
|
Определите энергию
активации и константу скорости при 308 К.
2. Энергия
активации разложения N2O5, протекающего по кинетическому уравнению первого
порядка, равна 103,25 кДж/моль. Период полураспада при -25 оС равен
трем годам. Предполагая, что энергия активации от температуры не зависит,
вычислите период полураспада при 125 оС.
3. Для
термического разложения a-оксида этилена энергия активации равна 217 кДж/моль. Определите, как
влияет на рост активных молекул повышение температуры от 417 до 427 оС.
4. Для
термического разложения этана были получены следующие константы скорости:
|
k∙10-5, с-1
|
2,5
|
8,2
|
23,1
|
57,6
|
92,4
|
|
T, K
|
823
|
843
|
863
|
883
|
893
|
Определите энергию
активации и предэкспоненциальный множитель.
5. В парообразном
состоянии изопропенилаллиловый эфир изомеризуется в аллилацетон и скорость
реакции подчиняется уравнению первого порядка. Зависимость константы скорости
от температуры описывается уравнением k=5,4∙1011е−29300/RT. Сколько времени потребуется при 150
оС, чтобы парциальное давление аллилацетона стало равным 300 мм рт.
ст., если реак-ция начинается при давлении изопропенилаллилового эфира, равном
760 мм рт. ст.?
6. Во сколько раз следует увеличить
давление газовой смеси, чтобы скорость тримолекулярной реакции 2 NO(г)+О2(г) = = 2 NO2(г) увеличилась в 1000 раз?
7. Во сколько раз
необходимо увеличить концентрацию вещества А, чтобы при уменьшении концентрации
вещества В в четыре раза скорость реакции 2 А (г) + В (г)
= С (г) не изменилась?
8. Температурный
коэффициент скорости некоторой реакции равен 3. Как изменится скорость этой
реакции при повышении температуры от 80 до 130 оС?
9. На сколько градусов
следует повысить температуру системы, чтобы скорость протекающей в ней реакции
возросла в 50 раз? Коэффициент Вант-Гоффа равен 1,8.
10. Вычислите температурный
коэффициент скорости реакции, если константа скорости ее при 100 оС
составляет 6∙10-4, а при 150 оС – 7,2.10-2.
11. Температурный
коэффициент скорости одной реакции равен 3, второй – 4. При некоторой
температуре константа скорости второй реакции в три раза выше константы
скорости первой. Насколько следует повысить температуру, чтобы константа
скорости второй реакции в пять раз превысила константу скорости первой?
12. При температуре 100 оС
скорость одной реакции в два раза больше скорости второй. Температурный
коэффициент скорости первой реакции равен 2, второй – 4. При какой температуре
скорости обеих реакций выравняются?
13. Для некоторой реакции
первого порядка период полураспада при 378,5 K равен 363 мин. Энергия активации равна 12,381 кДж/моль.
Определите, сколько времени потребуется для разложения 75% исходного вещества
при 450 К.
14. С помощью правила Вант-Гоффа
вычислите, при какой температуре реакция закончится через 15 мин, если при 20оС
на это требуется 2 ч. Температурный коэффициент скорости равен 3.
15. Время полураспада вещества при
323 К равно 100 мин, а при 353 К - 15 мин. Определите температурный коэффициент
скорости реакции распада.
16. Какой должна быть энергия
активации, чтобы скорость реакции увеличивалась в три раза при возрастании
температуры на 10оС: а) при 300 К; б) при 1000 К?
17. Энергия активации реакции,
приводящей к скисанию молока, равна 75 кДж/моль. При температуре 21оС
молоко скисает за 8 ч. Как долго можно хранить молоко в холодильнике при
температуре 5оС? Время скисания можно принять обратно
пропорциональным константе скорости.
18. Две реакции одинакового порядка
имеют равные предэкспоненциальные множители, но их энергии активации
различаются на 41,9 кДж/моль. Рассчитайте соотношения констант скоростей этих
реакций при 600 К.
19. Разложение некоторого вещества
является реакцией первого порядка с энергией активации 231 кДж/моль. При 300 К в
течение 1 ч разлагается 95% этого вещества. Вычислите температуру, при которой в
течение 1 мин разложится 0,1% вещества.
20. Период полупревращения вещества в
реакции первого порядка при 323,2 К составляет 100 мин, а при 353,2 К 15 мин.
При какой температуре константа скорости будет равна 4?
5. ФОТОХИМИЧЕСКИЕ
РЕАКЦИИ
5.1 Необходимые
исходные сведения и основные уравнения
При решении задач по
фотохимическим реакциям необходимо учитывать законы светопоглощения и
фотохимии, то есть, какая часть энергии поглощенного света идет непосредственно
на химическую реакцию. Количественно это характеризуется квантовым выходом
реакции. Квантовый выход фотохимической реакции g определяется как отношение числа прореагировавших
молекул к числу поглощенных квантов. В СИ отсутствует общепринятое обозначение
для указанной величины.
Энергия одного кванта
светового излучения определяется по формуле
Е = h∙n,(5.1)
где h – постоянная Планка, равная 6,626∙10-34
Дж∙с-1; n - частота световой волны, с-1
(Гц).
Квантовый выход
определяется из соотношения
g = n∙h∙n/Q,(5.2)
где n–количество прореагировавших молекул;
Q – количество поглощенной световой
энергии, Дж. Если перейти к числу мо-лей, то
g =N∙NА∙h∙n/ Q,(5.3)
где N – количество прореагировавших молей
вещества; NА – число Авагадро, моль-1.
Это связано с тем, что в
соответствии с законом фотохимической эквивалентности Эйнштейна каждый
поглощенный квант вызывает превращение одной молекулы; g-величина безразмерная. Произведение NА∙h∙n равно
количеству энергии, необходимой для превращения 1 моль вещества, и выражается в
Джоуль моль в минус первой степени (Дж. моль-1). Длина
волны λ, м, и частота светового излучения n, с-1, связаны со
скоростью света с (с = 2,998∙108 м/c) соотношением
с = l.n.(5.4)
В зависимости от длины
волны света, создаваемого источником излучения, одной и той же энергии света
соответствует разное число квантов. Например, для 1 Дж при длине волны 200 нм
число квантов
N = NА.h.n.(5.5)
Поскольку для
фотохимических реакций чаще всего используется излучение в ультрафиолетовой и
видимой областях электромагнитного излучения, то n = NА.h.λ. (λ = = 400…600, где 400…600 –
диапазон электромагнитного ультра-фиолетового излучения, нм).
Аналогичным образом можно
получить таблицу, показывающую соотношение между энергией 1018
квантов и длиной волны электромагнитного излучения в диапазоне 200…700 нм.
|
Длина волны, нм
|
200
|
300
|
400
|
500
|
600
|
700
|
|
Е, Дж
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
При проведении
фотохимических реакций большое значение имеет количество излучения. С этой
целью широко используются приемники излучения различных типов: термоэлемент,
вакуумные фотоэлементы, селеновые фотоэлементы, фотодиоды, квантовые счетчики,
химические приемники (актинометры). В этих приемниках под действием света
происходит химическая реакция, для которой квантовый выход известен из
специальных опытов. Например, ферриоксалатный актинометр представляет собой
раствор K3[Fe(C2O4)3] (0,006- -0,15 моль/л) в разбавленной серной
кислоте. Под действием света в интервале 250…577 нм протекает реакция:
2 [Fe(C2O4)3]3-
® 2 Fe2+
+ 5 C2O42- + 2 CO2.
Для раствора концентрации
0,15 моль/л при длине волны 468 нм поглощается 85% падающего света при толщине
слоя 1,5 см. Квантовый выход реакции при этих условиях равен 0,93. Продукт
реакции Fe2+ колориметрически определяется в виде о-фенантралинового
комплекса при 495 нм. В результате этих опытов определяется интенсивность
облучения, Дж.моль-1.с-1.
В актинометре на основе
уранилоксалата под действием света идет реакция H2C2O4 + UO22+ ® CO + CO2 + H2O + UO22+. Ион уранила выполняет здесь роль носителя энергии и многократно
участвует в реакции разложения. Эта реакция протекает при облучении системы
светом в диапазоне 250…430 нм с квантовым выходом 0,5-0,6.
5.2 Задачи с решениями
1. Образец
газообразного ацетона облучается монохроматическим светом с длиной волны 313
нм. Под действием света протекает реакция (СН3)2СО ® С2Н6 + СО.
Кювета, в которой протекает реакция, имеет вместимость 59.10-6
м3. Пары ацетона поглощают 91,5% падающей энергии. В ходе
эксперимента получены следующие данные: Т=329,85 К; начальное давление Р0
= 1,021.105 Па; время облучения – 7 ч;
конечное давление – 1,044.105 Па; падающая энергия
48,1.10-4 Дж/с. Найти квантовый выход реакции.
Решение. Определяем
количество поглощенной энергии, необходимой для превращения 1 моль вещества
(Эйнштейн).
Е = NA.h.n = NA.h.c.l = (6,022.1023.6,62.10-34.3.108)/313.10-9
= =3,82.105.Дж/моль.
Находим количество
поглощенной ацетоном энергии: (48,1.10-4.0,915.7.60.60)/3,82.105
= 2,9.10-4 Дж/моль. Обозначим через х
давление СО в кювете. Тогда Р0 – х + х + х
= Робщ; Р0 + х = Робщ;
х = (1,044 - 1,021).105 = 0,023.105
Па.
Учитывая, что P.V = n.R.T, находим n: n = P.V/R.T = = (16,9.59.10-3)/(760.0,082.329,85)
= 0,485.10-4 моль. Квантовый выход: 0,485.10-4/2,9.10-4
= 0,17.
Ответ: g = 0,17.
2. Для
фотолитического разложения газообразного азометана квантовый выход по азоту
равен единице. Этот выход от давления не зависит. При фотолизе азоэтана
квантовый выход уменьшается с ростом давления. Подобный же эффект наблюдается
при фотолизе перфторазометана. Объясните эти факты исходя из масс реагирующих
частиц и числа степеней свободы.
Решение. Опыты
показывают, что облучение азосоединений может привести либо к цистранс-изомеризации,
либо к разрыву связи С-N.
Схема распада азометана: СН3 –N=N-CH3 ® ® CH•3 + N2 + CH3• ® C2H6 + N2. Квантовый выход по азоту равен единице при облучении светом
с длиной волны 365 нм. Энергия облучения составит Е=365.10-7.0,022.1023.1,986.10-23
х х 103 кДж/моль = 327 кДж/моль.
По справочным данным
энергии диссоциации связи C - N имеют следующие значения:
|
Исходные вещества
|
Продукты
|
Разрываемая связь
|
Энергия диссоциации, кДж/моль
|
|
CH3NH2
|
CH3×, NH2×
|
C-N
|
337,6
|
|
CH3NO2
|
CH3×, NO2
|
C-N
|
256,5
|
Сравнивая эти данные,
можно сказать, что энергия падающего света сопоставима с энергией диссоциации
связи С-N. Если учитывать участие внутренних
степеней свободы для реакции разложения трех соединений, то получим следующие
результаты:
|
Реакция
|
Число атомов в исходной молекуле
|
Число степеней свободы
|
Число колебательных частот
|
|
CH3NNCH3®N2+C2H6
|
10
|
30
|
24
|
|
CH3CH2NNCH2CH3®N2+C4H10
|
16
|
48
|
42
|
|
CF3NNCF3®N2+C2F6
|
10
|
30
|
24
|
По теории переходного
состояния путь реакции в этих процессах совпадает с валентным симметричным
колебанием связи C-N. Поэтому для термического разложения
азометана значение предэкспоненциального множителя k0 должно
иметь значение 1013…1014 с-1. Множитель k0 входит в выражение для константы скорости k,
поскольку k = k0.е-Еа/RТ,
где Еа - энергия активации реакции, Т -
температура.
Опыты показывают, что
константа скорости при высоких давлениях k¥ описывается уравнением k¥ = = 1016,5.е-52440/RT.с-1. Здесь энергия диссоциации Ед.
дана в калориях. При переходе в СИ получаем Еа = 52440.10-3.4,184
= = 219 кДж/моль. По другим опытным данным Еа = = 55500.10-3.4,184
= 232 кДж/моль при k0=1017,3с-1.
Следовательно k0оп> k0теор. Это можно объяснить тем, что в
переходном состоянии длина связи С-N возрастает из-за уменьшения барьера внутреннего вращения, при этом
энтропия переходного комп-лекса растет, что в конечном счете и приводит к росту
k0.
Что касается
фотохимического разложения, то можно предположить следующую схему реакции (А =
СН3NNCH3):
1. А + hn ® A* активация Va = Iабс (интенсивность поглощения);
2. А* + А ® А + А дезактивация Vd = kd [A*][A],
где kd - константа реакции дезактивации;
3. А* ® продукты реакции. Vp = kр [A*],
где kp - константа скорости реакции.
В теории
мономолекулярных реакций разложения молекула рассматривается как совокупность
гармонических осцилляторов. Для протекания реакции необходимо, чтобы
определенное число квантов за конкретный промежуток времени сосредоточилось на
разрываемой связи и чтобы энергия всех этих квантов была равна или больше
энергии активации реакции. Естественно, что чем больше колебательных частот в
данной молекуле, тем больше требуется времени для накопления поглощенного
кванта света на данной связи. За это время молекула может по стадии 2 отдать
свою энергию другой, неактивной молекуле, что должно привести к падению
скорости по стадии 3. Поскольку скорость реакции по стадии 2 резко возрастает
по мере повышения давления в системе, то константа скорости kp должна падать по мере роста
давления, что и подтверждается опытом. Поэтому влияние давления будет более
резко выражено для азоэтана и перфтор-азометана (число частот равно 42), чем
для азометана (число частот равно 24).
Сравним
собственное время жизни возбужденного состояния t0 и время между столкновениями в газовой фазе.
В теории
соударений длина свободного пробега l рассчитывается по уравнению: 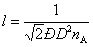 , где D–диаметр
молекулы, nA - число молекул в 1 см3, Р
– давление газа. Допустим, что диаметры молекул азометана, азоэтана,
перфторазометана равны соответственно 460 и 800 и 950 нм. Тогда при Т = 300
К и Р=1,0133.105 Па по данным
соответственно для трех молекул получим l = 5,7.10-8; 2,6.10-8;
1,5.10-8 м. Вычисляем скорость движения молекул V по формуле
, где D–диаметр
молекулы, nA - число молекул в 1 см3, Р
– давление газа. Допустим, что диаметры молекул азометана, азоэтана,
перфторазометана равны соответственно 460 и 800 и 950 нм. Тогда при Т = 300
К и Р=1,0133.105 Па по данным
соответственно для трех молекул получим l = 5,7.10-8; 2,6.10-8;
1,5.10-8 м. Вычисляем скорость движения молекул V по формуле 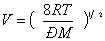 . Для этих же газов получим: V = 3,3.102; 2,7.102
и 1,9.102 м/с. Рассчитаем время между соударениями
для трех газов по формуле t = l/V. Получим 1,7.10–10;
0,9.10-10 и 0,8.10-10
с. Рассчитаем эти параметры для азометана при различных давлениях. Полученные
данные сведены в таблицу. В электронной спектроскопии время жизни возбужденного
состояния t0
. Для этих же газов получим: V = 3,3.102; 2,7.102
и 1,9.102 м/с. Рассчитаем время между соударениями
для трех газов по формуле t = l/V. Получим 1,7.10–10;
0,9.10-10 и 0,8.10-10
с. Рассчитаем эти параметры для азометана при различных давлениях. Полученные
данные сведены в таблицу. В электронной спектроскопии время жизни возбужденного
состояния t0 рассчитывается по формуле
рассчитывается по формуле
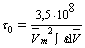 ,(5.6)
,(5.6)
где V-средняя частота полосы поглощения,
см-1,  -интегральная
интенсивность поглощения, ε - коэффициент экстинкции, Vm- частота поглощения максимума.
-интегральная
интенсивность поглощения, ε - коэффициент экстинкции, Vm- частота поглощения максимума.
|
Давление, Па
|
nA,..10-19
|
L,.10-8,м
|
T.1010с
|
|
10
|
0,032
|
437,5
|
3,3
|
132,5
|
|
100
|
0,32
|
43,7
|
3,3
|
13,6
|
|
200
|
0,64
|
21,8
|
3,3
|
6,6
|
|
400
|
1,28
|
10,9
|
3,3
|
3,3
|
|
500
|
1,60
|
8,7
|
3,3
|
2,6
|
|
600
|
1,92
|
7,3
|
3,3
|
2,2
|
|
700
|
2,43
|
5,7
|
3,3
|
1,7
|
Спектральные приборы дают
кривую поглощения в координатах: процент пропускания света – длина волны, нм.
Из полученных данных строится график в координатах e – 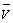 или lge – V.
или lge – V.
Для нахождения  существуют различные
способы, но если полоса поглощения имеет более или менее симметричный вид, то
этот интеграл заменяется произведением emах.Dn1/2. В этом выражении emax – максимальный коэффициент
экстинкции, Dn1/2 - полуширина полосы поглощения, м-1.
Опыты показывают, что азосоединения имеют время жизни порядка 10-12
с, где малоинтенсивные полосы поглощения наблюдаются в видимой части или на
границе ультрафиолетовой части. Обычно lge=1…2 (e<30).
Тогда по формуле (5.6) получим t0 = 3,5.108/(286)2.0,500
= = 4,2.10-5. Примем, что полуширина полосы
поглощения равна 500 см-1, e = 20, тогда можно вычислить максимум волнового числа поглощения
V, см-1, по формуле ώmax = 107 / 350 = 28600.
существуют различные
способы, но если полоса поглощения имеет более или менее симметричный вид, то
этот интеграл заменяется произведением emах.Dn1/2. В этом выражении emax – максимальный коэффициент
экстинкции, Dn1/2 - полуширина полосы поглощения, м-1.
Опыты показывают, что азосоединения имеют время жизни порядка 10-12
с, где малоинтенсивные полосы поглощения наблюдаются в видимой части или на
границе ультрафиолетовой части. Обычно lge=1…2 (e<30).
Тогда по формуле (5.6) получим t0 = 3,5.108/(286)2.0,500
= = 4,2.10-5. Примем, что полуширина полосы
поглощения равна 500 см-1, e = 20, тогда можно вычислить максимум волнового числа поглощения
V, см-1, по формуле ώmax = 107 / 350 = 28600.
Сравним полученные
данные. Время между столкновениями порядка 10-10 с, t0 = 10-5 с. Малый
коэффициент экстинкции указывает на запрещенность излучательного перехода, что
должно привести к удлинению времени жизни возбужденность состояния. Несмотря на
малое время между столкновениями, молекула сохраняет уровни энергии.
При замене атома Н на
атом F увеличивается приведенная масса, что
должно вызвать уменьшение частоты колебания связи С–F по сравнению с подобной частотой для связи С-Н.
Влияние масс на частоту
можно ориентировочно рассчитать по формуле n = Кm*, где n –частота колебания, с-1, К
– силовая постоянная, Н/м; m*- приведенная масса, кг.
Валентное колебание связи
С-F в СF4 равно 1277 см-1, такое же колебание связи С-Н в
СН4 равно 3020 см-1. Уменьшение частоты увеличивает
вероятность возбуждения при соударении и может влиять и на колебания связи С–N, разрыв которой во всех случаях
остается единственным путем реакции. Кроме того, необходимо учитывать, что ядро
фтора имеет 9 протонов и 10 нейтронов, спиновое число ядра равно ½.
Поэтому помимо давления на константу скорости реакции будут оказывать влияние
спин-орбитальное взаимодействие электронов и ядра тяжелого атома.
3. Ртутная лампа среднего
давления мощностью 450 Вт излучает 25,6 Вт при длине волны 366 нм. Предполагая,
что образец поглощает весь падающий свет, рассчитайте, какое время потребуется
для фоторазложения 1 моль вещества, если квантовый выход реакции составляет
0,1.
Решение. Учитывая, что 1
Вт = 1 Дж. с-1, рассчитаем число квантов,
испускаемых лампой в 1 с. Оно равно 47,1.1018.
Энергия одного кванта Е = h.n = 5,4.10-19 Дж. Энергия 1 моля
квантов равна NAE =6,022.1023.5,4.10-19
= 32,5.104 Дж/моль.
Рассчитаем число молей квантов
в секунду. Получим: (47,1.1018)/(6,02.1023)
= 7,8.10-5 молей квантов. Поскольку расчет ведется
на 1 моль вещества, то число молей света должно быть в десять раз меньше.
Поэтому с учетом квантового выхода 7,8.10-5.10-1
= 7,8.10-6.t = 1/7,8.10-6 = 1,3.105
с = 1,3.105/3600 = 36.
Ответ: t = 36 ч.
4. Актинометр на основе уранилоксалата
Н2С2О4(VO22+) облучается в течение трех часов ультрафиолетовым светом. За это время
разложилось 8,6.10-3 моль оксалата. Предполагая,
что квантовый выход равен 0,57, рассчитайте интенсивность света.
Р е ш е н и е. Определяем
число поглощенных квантов Q:
0,57 = (8,6.10-3.6,023.1023)/Q; Q = 90,87.1020.
С учетом времени получаем
интенсивность падающего света I:
I = 90,87.1020/3,60.60
= 8,41.1017.
Ответ: I = 8,41.1017 лк.
5.3 Задачи для
самостоятельного решения
1. Распад N2O на N2 и О2 идет по схеме N2О ® N2 + О. При облучении светом с длиной волны 180 нм
энергия активации Еа не совпадает с энергией
термического распада, которая равна 222 кДж/моль. Сравните две величины энергии
активации и объясните их расхождение.
2. При облучении НI светом с длиной волны 263 нм газо-образный
НI разлагается на I2 и Н2. Энергии диссоциации НI соответствует 24080 Дж/моль.
Рассчитайте энергию, которой обладает 1 молекула продукта реакции. При
поглощении 22,6 кДж разлагается 0,1 моль НI. Рассчитайте квантовый выход.
3. Рассчитайте
длинноволновую границу спектра, где энергия поглощенного кванта света
достаточна для диссоциации молекулы хлора. Примите энергию разрыва связи в
молекуле хлора равной 242,6 кДж/моль.
4. Смесь водорода и хлора
хранится под водой при 10 оС в V = 10 литровом сосуде при Р = 700 мм рт. ст.
Найдите квантовый выход реакции образования НС1, если в результате поглощения
103 Дж лучистой энергии с длиной волны 589 нм давление снизилось на 85 мм рт.
ст.
5. При фотобромировании коричной
кислоты с использованием света с длиной волны 435,8 нм при температуре 30,6 оС
интенсивностью 1,4.10-3 Дж/с скорость уменьшения
количества Вr2 составляет 0,075 моль в течение 1105 с. Раствор
поглощает 80,1% прошедшего через него света. Рассчитать квантовый выход.
6. Предполагается, что
механизм фотохимической реакции водорода с парами йода при 480 К следующий:
I2
+ hn ® 2 I•k1
2 I•
+ I2 ® 2 I2k2
2 I•
+ H2 ® I2 + H2k3
2 I•
+ H2 ® 2 HIk4
При условии, что k4<< k3 и I – интенсивность поглощенного света,
показать, что d[HI] / dτ
= 2.I. k4[H2]/k2. [I2]+ k3.[H2]
7. Определите квантовый
выход фотохимического синтеза фосгена СО + С12 = СОС12,
если количество поглощенной энергии Q = 2.105 Дж, длина волны l = 510 нм, выход фосгена 8,5 кг.
8. Сосуд вместимостью 100
см3, содержащий смесь водорода с хлором, облучен светом с длиной
волны l = 400 нм. Скорость поглощения света
равна 11,0.10-7 Дж/с. После одной минуты облучения
парциальное давление С12 (Р0 = 205 мм рт. ст.)
понизилось на 49 мм рт. ст. (проведено при 0 оС). Каков квантовый
выход НС1?
9 Аммиак разлагается
ультрафиолетовым светом (l=200
нм) с квантовым выходом g =
0,14. Определите количество лучистой энергии, необходимой для разложения 1 г NH3.
6. СЛОЖНЫЕ РЕАКЦИИ
6.1 Необходимые
исходные сведения и основные уравнения
Для мономолекулярных
обратимых реакций типа А « В
дифференциальные формы кинетического уравнения:
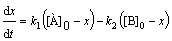 ,(6.1)
,(6.1)
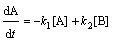 .(6.2)
.(6.2)
При равновесии 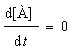 , и если при t = 0 [B] = 0, то
, и если при t = 0 [B] = 0, то
[В]р/[А]р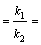 Кр; (6.3)
Кр; (6.3)
[B]р = [А]0 - [А]р;(6.4)
[В]р 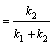 [А]0,(6.5)
[А]0,(6.5)
где [А], [B] – текущие концентрации веществ А и
В; [А]0 – концентрация А при t = 0; k1
и k2 – константы скорости прямой и обратной реакций; [А]р
и [B]р – концентрации А и В
при равновесии; Кр– константа равновесия.
Интегральные формы
кинетического уравнения:
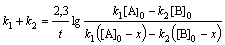 ;(6.6)
;(6.6)
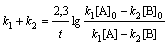 . (6.6а)
. (6.6а)
При условии, что в момент
времени t = 0 [B]0 = 0:
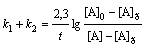 .(6.7)
.(6.7)
Для мономолекулярных
параллельных реакций типа
С ¬ А ® В дифференциальные формы кинетического уравнения:
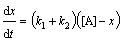 ;(6.8)
;(6.8)
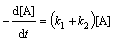 .(6.9)
.(6.9)
Интегральные формы кинетического уравнения:
 ; (6.10)
; (6.10)
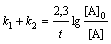 , (6.11)
, (6.11)
где k1 и k2 –
константы скорости первой и второй реакций. Константы скоростей отдельных
стадий для реакций данного типа определяют по соотношению:
х1/х2 = k1/k2, (6.12)
где х1
и х2 – количества молей веществ В и С, образовавшихся к
моменту времени t или
приращение концентраций веществ В и С. Текущая концентрация исходного вещества
имеет вид
[А] = [А]0 – х.
(6.12а)
Для мономолекулярных
последовательных реакций типа
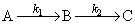 дифференциальные формы кинетического
уравнения:
дифференциальные формы кинетического
уравнения:
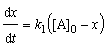 ; (6.13)
; (6.13)
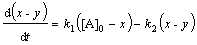 ; (6.14)
; (6.14)
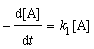 ; (6.15)
; (6.15)
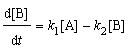 ; (6.16)
; (6.16)
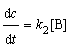 . (6.17)
. (6.17)
Интегральные формы
кинетического уравнения:
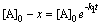 ; (6.18)
; (6.18)
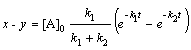 ; (6.19)
; (6.19)
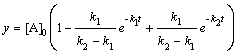 ; (6.20)
; (6.20)
 ; (6.21)
; (6.21)
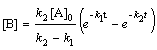 ; (6.22)
; (6.22)
[C] = [А]0 -
[А] - [B], (6.23)
где [А], [В], [С] –
текущие концентрации веществ А, В, С; [А]0 – концентрация вещества А
при t = 0; k1 и k2 –
константы скорости первой и второй реакций: [А] = [А]0 – х; [В]
= x – y; [C] = y.
Точка максимума на кривой
[В] = f(t) характеризуется уравнениями
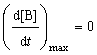 ; (6.24)
; (6.24)
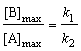 ; (6.25)
; (6.25)
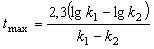 , (6.26)
, (6.26)
где tmax – время соответствующее максимальной
концентрации вещества В.
6.2 Задачи с решениями
1. Для обратимой
реакции первого порядка 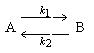
Кр = 8, а k1 = 0,4 c-1. Вычислите время, при котором
концентрации веществ А и В станут равными, если начальная концентрация вещества
В равна 0.
Решение. Из
константы равновесия находим константу скорости обратной реакции: k-1 = k1/К = 0,4/8 = 0,05 с-1. По условию мы
должны найти время, за которое прореагирует ровно половина вещества А. Для
этого надо подставить значение х(t) = а/2 в решение кинетического уравнения для
обратимых реакций:
t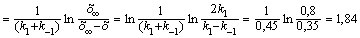 .
.
Ответ: t = 1,84 с.
2. В параллельных
реакциях первого порядка С ¬ А ® В выход
вещества В равен 63%, а время превращения а на 1/3 равно 7 мин. Найдите k1 и k2.
Решение. Кинетическое
уравнение для разложения вещества в параллельных реакциях имеет вид уравнения
первого порядка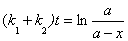 , в
которое вместо одной константы входит сумма констант скорости отдельных стадий.
Следовательно, по аналогии с реакциями первого порядка, по времени превращения
А на 1/3 (х(t)
= a/3) можно определить сумму констант k1 + k2:
, в
которое вместо одной константы входит сумма констант скорости отдельных стадий.
Следовательно, по аналогии с реакциями первого порядка, по времени превращения
А на 1/3 (х(t)
= a/3) можно определить сумму констант k1 + k2:
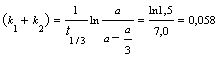 мин-1.
мин-1.
Выход вещества В равен 63%,
а вещества D – 37%. Отношение этих выходов равно
отношению конечных концентраций веществ В и D, следовательно оно равно отношению соответствующих констант
скоростей
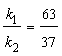 . Решая это уравнение совместно с предыдущим,
находим: k1 = 0,037, k2 = 0,021.
. Решая это уравнение совместно с предыдущим,
находим: k1 = 0,037, k2 = 0,021.
Ответ: k1 = 0,037 мин-1, k2 = 0,021 мин-1.
3. В системе
протекают две параллельные реакции А + 2В→ → продукты (k1) и A +2C → продукты (k2). Отношение k1/ k2 = 5.
Начальные концентрации веществ В и С одинаковы. К моменту времени t прореагировало 50% вещества В. Какая
часть вещества С прореагировала к этому моменту?
Решение. Запишем
кинетические уравнения для первой и второй реакций: 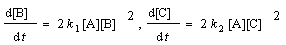 . Поделив одно кинетическое уравнение на
другое, избавимся от временной зависимости и получим дифференциальное
уравнение, описывающее фазовый портрет системы, т. е. зависимость концентрации
одного из веществ от концентрации другого:
. Поделив одно кинетическое уравнение на
другое, избавимся от временной зависимости и получим дифференциальное
уравнение, описывающее фазовый портрет системы, т. е. зависимость концентрации
одного из веществ от концентрации другого: 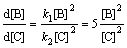 с начальным условием [В]0 = [С]0.
Это уравнение решается методом разделения переменных:
с начальным условием [В]0 = [С]0.
Это уравнение решается методом разделения переменных: 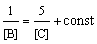 , где константа находится из начального условия
, где константа находится из начального условия
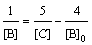 . Подставляя в это
решение [В] = [В]0/2, находим [С] = 5[В]/6 = 5[С]0/6,
т.е. к моменту времени t прореагирует
1/6 вещества С.
. Подставляя в это
решение [В] = [В]0/2, находим [С] = 5[В]/6 = 5[С]0/6,
т.е. к моменту времени t прореагирует
1/6 вещества С.
4. Реакция
разложения изопропилового спирта протекает в присутствии катализатора триоксида
ванадия при 588 К с образованием ацетона, пропилена и пропана. Концентрации
веществ реакции, измеренные через 4,3 с после начала опыта, следующие, ммоль: с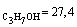 ; с
; с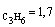 ; с
; с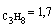 . Определите константу скорости каждой реакции,
если в начальный момент в системе присутствовал только С3Н7ОН.
. Определите константу скорости каждой реакции,
если в начальный момент в системе присутствовал только С3Н7ОН.
Решение: Определим
начальное количество С3Н7ОН: [А]0 = с1
+ с2 + с3 + с4 = 24,7
+ 7,5 + 8,1 + 1,7 = 44,7 ммоль/л. Вычислим сумму констант скоростей реакций:
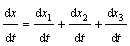
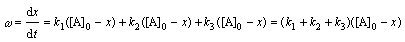
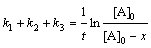 ,
,  c-1.
c-1.
Определим константу
скорости каждой реакции:
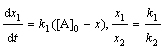 ;
; 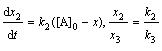 ;
; 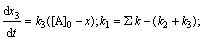
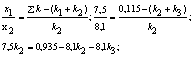
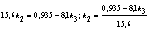 ;
;
Так как х2/х3
= k2/k3, то 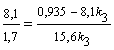 ;
;
 ;
;
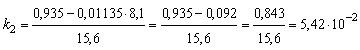 с-1;
с-1;
 .
.
Ответ: 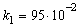 с-1.
с-1.
5. Последовательная
реакция первого порядка протекает по схеме 
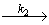 В. При 298 К имеет удельные скорости: k1 = 0,1 ч-1; k2 = 0,05 ч-1; начальная концентрация
исходного вещества [А]0 = 1 моль/л. Вычислите: 1) координаты
максимума кривой [Р] = f(t); 2) время достижения концентрации [А] = 0,001 моль/л,
продолжительность tA
реакции А→Р; 3) концентрации [Р] и [В] в момент окончания реакции А→Р;
4) время, за которое концентрация В достигнет значении 0,01 моль/л и продолжительность
индукционного периода этой реакции, tинд; 5) координаты точки перегиба кривой
[В] = f(t); 6) точку пересечения кривых [А] = f(t) и [Р] = f(t). Решение:
Рассчитаем время, которому будет соответствовать максимальная концентрация
промежуточного продукта, ч:
В. При 298 К имеет удельные скорости: k1 = 0,1 ч-1; k2 = 0,05 ч-1; начальная концентрация
исходного вещества [А]0 = 1 моль/л. Вычислите: 1) координаты
максимума кривой [Р] = f(t); 2) время достижения концентрации [А] = 0,001 моль/л,
продолжительность tA
реакции А→Р; 3) концентрации [Р] и [В] в момент окончания реакции А→Р;
4) время, за которое концентрация В достигнет значении 0,01 моль/л и продолжительность
индукционного периода этой реакции, tинд; 5) координаты точки перегиба кривой
[В] = f(t); 6) точку пересечения кривых [А] = f(t) и [Р] = f(t). Решение:
Рассчитаем время, которому будет соответствовать максимальная концентрация
промежуточного продукта, ч:
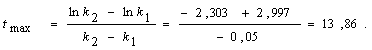
Обозначим концентрацию А
при tmax через [А]max. Тогда [А]max = [А]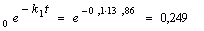 моль/л; максимальная концентрация
промежуточного продукта будет [Р]max = (k1/k2).[А]max = (0,1/0,05).0,249=0,598 моль/л.
Примем [А]0 = = 0,001 моль/л; тогда
моль/л; максимальная концентрация
промежуточного продукта будет [Р]max = (k1/k2).[А]max = (0,1/0,05).0,249=0,598 моль/л.
Примем [А]0 = = 0,001 моль/л; тогда 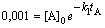 ;
; 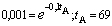 ч. Рассчитаем концентрацию Р при t = 69 ч:
ч. Рассчитаем концентрацию Р при t = 69 ч:
[В]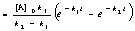 ;
;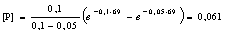 моль/л.
моль/л.
Рассчитаем концентрацию
продукта [В] через 69 ч: [В] = = [А]0 - [Р] - [А] = = 1 – 0,061 –
0,001 = 0,938 моль/л. Вычислим время tинд, за которое устанавливается
концентрация В, равная 0,01 моль/л, по уравнению
[В] = [А]0 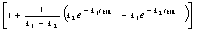 ; [В]
; [В]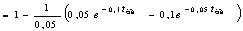 ;
; (1)
(1)
Уравнение (1) решаем
относительно tинд методом подбора на основании
экспериментальных данных:
|
tинд, ч
|
1
|
2
|
2,5
|
3
|
4
|
|
[В], моль/л
|
0
|
0,008
|
0,014
|
0,018
|
0,032
|
Принимаем tинд = 2 ч. Точку перегиба кривой [В] = f(t) находим, используя условие 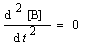 . После дифференцирования и преобразований
уравнения [В]=[А]0•
. После дифференцирования и преобразований
уравнения [В]=[А]0•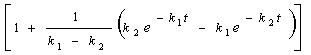 полу-чим точку перегиба:
полу-чим точку перегиба: 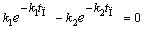 или
или 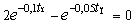 , где tП – координата точки перегиба, которую находим методом
подбора для значений индукционных периодов tинд 5, 15, 10, 20 ч. Строим график
зависимости х = f(t): х = 2е-0,1t – е-0,05t, откуда х = 0,05 при t = 13,6 ч. Концентрацию [В] в точке перегиба
находим по уравнению (2): [В] = = 0,243 моль/л.
, где tП – координата точки перегиба, которую находим методом
подбора для значений индукционных периодов tинд 5, 15, 10, 20 ч. Строим график
зависимости х = f(t): х = 2е-0,1t – е-0,05t, откуда х = 0,05 при t = 13,6 ч. Концентрацию [В] в точке перегиба
находим по уравнению (2): [В] = = 0,243 моль/л.
6.3 Задачи для
самостоятельного решения
1. Для обратимой реакции
первого порядка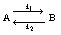 Кр=10,
а k1 = 0,2 с–1. Вычислите время, при котором
концентрации веществ А и В станут равными, если начальная концентрация вещества
В равна 0.
Кр=10,
а k1 = 0,2 с–1. Вычислите время, при котором
концентрации веществ А и В станут равными, если начальная концентрация вещества
В равна 0.
2. Превращение роданида
аммония NH4SCN в тиомочевину (NH2)2CS ─ обратимая
реакция первого порядка. Рассчитайте скорости прямой и обратной реакций,
используя следующие экспериментальные данные:
|
t, мин
|
0
|
19
|
38
|
48
|
60
|
∞
|
|
Доля прореагировавшего NH4SCN, %
|
2.0
|
6,9
|
10,4
|
12,3
|
13,6
|
23,2
|
3. В параллельных
реакциях первого порядка: В ¬ А ® С выход
вещества В равен 53%, а время превращения А на 1/3 равно 40 с. Найдите k1
и k2.
4. Реакция разложения
вещества А может протекать парал-лельно по трем направлениям:
D ¬ А ® В
î® C.
Концентрации продуктов в
смеси через 5 мин после начала реакции составляли, моль/л: [В]=3,2, [С]=1,8, [D]=4,0. Опреде-лите константы скорости
k1…k3, если период полураспада ве-щества
А равен 10 мин.
5. Реакция разложения
вещества А может протекать по трем направлениям:D ¬ А ® В
î® C.
Концентрации продуктов в
смеси через 10 мин после начала реакции составляли, моль/л: [В]=1,6, [С]=3,6, [D]=7,8. Опреде-лите константы скорости
k1…k3, если период полураспада ве-щества
А равен 8 мин.
6. Образец
радиоактивного урана массой 100 г распадается по схеме: 239U ® 239Np ® 239Pu. (периоды полураспада – 20 и 600 мин). Рассчитайте массы
нептуния и плутония: через 20 мин и 20 суток после начала распада. Определите
максимальную массу нептуния, которая может быть получена из данного образца
урана.
7. Кинетика обратимой
реакции А ↔ В измерена при двух значениях температуры. Получены следующие
эксперимен-тальные данные:
1)
Т = 293 К
|
t. мин
|
0
|
10
|
20
|
∞
|
|
Доля В в смеси, %
|
2,0
|
21,5
|
31,0
|
39,7
|
2) Т = 313 К.
|
t. мин
|
0
|
3
|
9
|
∞
|
|
Доля В в смеси, %
|
2,0
|
27,1
|
45,2
|
50,7
|
Рассчитайте; а) энергии
активации прямой и обратной реакций; б) константы равновесия при двух значениях
температуры; в) тепловой эффект прямой реакции.
8. В системе протекают
две параллельные реакции: А + В → → продукты (k1)
и А + С → продукты (k2). Отношение k1/k2
= 7. Начальные концентрации веществ В и С одинаковы. К моменту времени t прореагировало 50% вещества В. Какая
часть вещества С прореагировало к этому моменту?
9. Константа реакции
цис-, трансизомеризации бутена-2 при 417 оС равна 8,52.10-7
с-1, Константа равновесия при этой температуре равна 1,14. В
начальный момент времени присутствует только цисизомер. Определите время, за
которое прореагирует 30% бутена-2.
10. Константа скорости
прямой реакции NH4SCN ↔ ↔ (NH2)2CS при 25 оС равна 7,66.10-7 мин-1.
Константа равновесия при этой температуре равна 1,30. В начальный момент
времени присутствует только роданид аммония. Определите время, за которое
прореагирует 40% исходного вещества.
11. При смешении (273 К)
раствор содержал 73,2% этилового спирта, 0,677 моль HCOOH и 0,0261% HCl (вода не учитывается). Для исследования кинетики реакции образования
формиата при 521 К отбирали в различное время пробы объемом 5 мл и
оттитровывали Ba(OH)2. Результаты титрования представлены в таблице:
|
t, мин
|
0
|
50
|
100
|
160
|
220
|
∞
|
|
V, мл
|
43,52
|
40,40
|
37,75
|
35,10
|
31,09
|
24,28
|
Вычислите константы
образования k1 и разложения k2 этилформиата
в этом растворе и константу равновесия обратимой реакции Кр,
если концентрации воды, этанола и ионов водорода постоянны.
12. Образование
этилового эфира муравьиной кислоты при 303 К протекает по уравнению реакции
первого порядка: HCOOH + C2H6O → HCOOC2H5. Были получены следующие результаты:
|
t, мин
|
0
|
1700
|
1000
|
14000
|
20000
|
40000
|
|
Количество кислоты, см3
|
29,44
|
28,59
|
24,77
|
23,05
|
21,28
|
16,80
|
Концентрацию кислоты
определяли титрованием. Константа обратной реакции k1 = 1,5.10-5 мин-1.
Концентрация продукта прямой реакции в начальный момент равна 0. Определите
константу прямой реакции.
13. Для реакции между
иодистым метилом и раствором диметилпаратолуидина в нитробензоле CH3C6H4N(CH3)2+CH3I® ® H4C6H3CN(CH3)3 получены следующие данные:
|
t, мин
|
10,2
|
26,5
|
36,0
|
78,0
|
|
x/c0
|
0,175
|
0,343
|
0,402
|
0,523
|
Константа равновесия
реакции равна 69,8. Начальные концентрации обоих реагентов равны 0,05 моль/л,
продукт в процессе реакции отводится. Определите, по какому кинетическому
уравнению следует описать кинетическую кривую, и рассчитайте константу скорости
реакции.
14. Реакция термического
крекинга нефти относится к консекутивной реакции, причем бензин является
промежуточным продуктом, распадающимся на газообразные вещества. Определите
максимальную концентрацию бензина и время ее достижения при крекинге 1 т нефти,
если при 673 К константа образования бензина k1 = 0,283 ч-1, а константа
распада бензина k2 = 0,102 ч-1.
15. Покажите, что для
реакций А 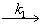 В и А
В и А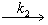 С время, за которое
образуется половина количества В (по сравнению с его количеством при t = ∞) и время, за которое
образуется половина количества С, одинаково, хотя константы k1 и k2 имеют
разные значения.
С время, за которое
образуется половина количества В (по сравнению с его количеством при t = ∞) и время, за которое
образуется половина количества С, одинаково, хотя константы k1 и k2 имеют
разные значения.
16. Определите периоды
полураспада RaB и RaC, связанные генетическим рядом: RaB 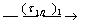 RaC
RaC 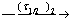 RaC΄, если
существует зависимость изменения концентрации радиоактивных ядер RaB от времени и время, при котором кон-
центрации накопленных RaC, RaC΄ будут максимальны, τmax = = 35 мин. (опыт проводили с
чистыми ядрами RaB).
RaC΄, если
существует зависимость изменения концентрации радиоактивных ядер RaB от времени и время, при котором кон-
центрации накопленных RaC, RaC΄ будут максимальны, τmax = = 35 мин. (опыт проводили с
чистыми ядрами RaB).
|
Число ядер
NRaB
|
100
|
70
|
50
|
34
|
17
|
5
|
4
|
2,5
|
|
τ, мин
|
0
|
10
|
20
|
40
|
50
|
80
|
90
|
100
|
17. Для последовательной
реакции первого порядка
А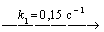 В
В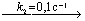 С определите максимальную концентрацию
промежуточного вещества В и время ее достижения.
С определите максимальную концентрацию
промежуточного вещества В и время ее достижения.
18. Для последовательной
реакции первого порядка: А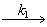 В
В  С начальная концентрация А равна 1 моль/л, k1 = 0,1 мин-1, k2 = 0,05 мин-1. Определите: 1) максимальное
значение концентрации промежуточного вещества В и время ее достижения t; 2) концентрации веществ А и С в
момент времени t.
С начальная концентрация А равна 1 моль/л, k1 = 0,1 мин-1, k2 = 0,05 мин-1. Определите: 1) максимальное
значение концентрации промежуточного вещества В и время ее достижения t; 2) концентрации веществ А и С в
момент времени t.
19. Для последовательной
реакции первого порядка: А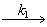 В
В  С начальная концентрация А равна 2 моль/л, k1 = 0,12 мин-1, k2 = 0,05 мин-1. Определите: 1) максимальное
значение концентрации промежуточного вещества В и время ее достижения t; 2) концентрации веществ А и С в
момент времени t.
С начальная концентрация А равна 2 моль/л, k1 = 0,12 мин-1, k2 = 0,05 мин-1. Определите: 1) максимальное
значение концентрации промежуточного вещества В и время ее достижения t; 2) концентрации веществ А и С в
момент времени t.
ОТВЕТЫ К ЗАДАЧАМ
Тема 1
1. 0,055. 2. 6.10-3
моль/л. 3. I
= 0,006; aCa2+ = 6,4.10-3
моль/л; aCl- = а =
1,5.10-2 моль/л. 4. а± =
8,223.10-2; а = 5,56.10-4.
5.-133,15 кДж/моль. 6. 297 К. 7. 5,5.10-6
Ом-1.м-1. 8. 138,3 Ом-1.м2.моль-1.
9. 387,9 Ом-1.см2.моль-1. 10.
0,141 Ом-1.м-1; 0,0141 Ом-1.моль-1.м2.
11. 0,78. 12 К=1,75.10-7 моль/л; рН
= 5,29. 13. λ- = 0,00763 Ом-1.моль-1.м2;
v0- = 7,91.10-8 м2.с-1.В-1.
14. t+ = 0,472; t- = 0,528. 15. 0,0298 г.
=
1,5.10-2 моль/л. 4. а± =
8,223.10-2; а = 5,56.10-4.
5.-133,15 кДж/моль. 6. 297 К. 7. 5,5.10-6
Ом-1.м-1. 8. 138,3 Ом-1.м2.моль-1.
9. 387,9 Ом-1.см2.моль-1. 10.
0,141 Ом-1.м-1; 0,0141 Ом-1.моль-1.м2.
11. 0,78. 12 К=1,75.10-7 моль/л; рН
= 5,29. 13. λ- = 0,00763 Ом-1.моль-1.м2;
v0- = 7,91.10-8 м2.с-1.В-1.
14. t+ = 0,472; t- = 0,528. 15. 0,0298 г.
Тема 2
1. -126 В. 2. -2,39 В; -2,42 В;
-2,45 В. 3. -0,28 В. 4. 0,1 моль/л. 5. 7,6. 6. 1,8.106.
7. 6,5.10-13. 8. -0,4141 В. 9.
ΔG = = -4,400 кДж/моль; DH = 5,348 кДж/моль; ΔS = 32,8 Дж/(моль.К). 10.
0,4910 В. 11. 109,99 кДж/моль. 12. -94,25 кДж/моль. 13. Е
= 0,968 В; (dE/dT)p = 1/85.10-4
В/К. 14. 0,1287 В. 15. 0,12 В.
Тема 3
1. 0,21 л/с и 0,15 л/с. 2. 0,0045 моль/(л.с);
0.0023 моль/(л.с). 3. 0,15 с-1; 4. 144
мин.; 5. 49 лет. 6. 120 суток. 7. 0,091 мг.; 0,003 мг. 8.
0,018 моль/(л.с); 25 с. 9. 0,043 л.с/моль; 45 мин;
34 мин. 10. 2. 11. 1; 0,0095 с-1. 12. 29,4 ч.; 13.
11,6 лет. 14. 2; 0,0012 моль/(л.с). 15. 0,0037 моль/(л.с);
320 с. 16. 38 мин. 17. 34 мин. 18. 1; 0,018 с-1.
19. 2. 20. 0,0075 моль/л.
Тема 4
1. 70,1 кДж/моль; 0,02264 с-1.
2. 0,58 сек. 3. 3,69.10-17;
4,2.1024. 4. 314,9 кДж/моль; 4,2.1024.
5. 1210 сек. 6. В 10 раз. 7. В два
раза. 8. В 43 раза. 9. На 67 0С. 10.
2,6. 11 На 18 0С. 12. При 110 0С. 13.
13,57 мин. 14. 39 0С. 15. 1,9. 16.
85 кДж/моль; 920 кДж/моль. 17. 47 ч. 18. 0,0002. 19.
350 К. 20. 288 К.
Тема 5
1. Е = 663,5 кДж/моль.2.
γ = 2,1. 3. λ = 0,5.10-6м. 4. 2,5.10
Дж/(моль.с). 5. γ = 4,8.105.
6. γ = 16,6. 8. γ = 100. 9. 251 кДж.
Тема 6
1. 3,36 ч. 2. w1 = 0,22 моль/(л.c); w2 = 0,003
моль/(л.c). 3. k1=0,01 c-1; k=0,05 c-1. 4. k1=0,004 c-1; k2= 0,0023 c-1; k3=0,002 c-1. 5. k1=0,024 c-1; k2= 0,021 c-1; k3=0,019 c-1. 6. 21,5 г; 17,6 г; 1,9 г; 0.7
г. 7. Еа,1,2=126,5 и 212,7 кДж; К1,2
= 0,15 и 1,25; -345,4 кДж/моль. 8. 48,1%. 9. 94 с. 10. 220
мин. 11. k1=0,133 c-1; k2 0,096 c-1; K=47,6; 12. k= 1,35 c-1. 13. По уравнению
реакции второго порядка. 14. 1,823 кмоль/м3; 1,6 ч.1 6.
t1 = 12,5 мин; t2=15,8 мин. 17. 23,3 моль/л; 138 c. 18. 1) 0,347 моль/л; 52 мин;
2) 0,625 моль/л; 0,127 моль/л. 19. 1) 0,237 моль/л; 35 мин; 2) 0,165
моль/л; 0,118 моль/л.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Стромберг А.Г., Лельчук Х.А.,
Картушинская А.И. Сборник задач по химической кинетике: учеб. пособие для хим.
техн. спец. вузов / Под ред. А.Г. Стромберга. М.: Высш. шк., 1985. 192 с.
2. Задачи по физической химии: учеб.
пособие / В.В. Еремин, С.И. Каргов, И.А. Успенская, Н.Е. Кузьменко, В.В. Лунин.
М.: Экзамен, 2003. 320 с.
3. Киселева Е.В. и др. Сборник
примеров и задач по физической химии. М.: Химия, 1984. 455 с.
4. Пономарева И.С. Сборник задач по
физической химии. М.: Химия, 1965. 200 с.
5. Баталин Т.И. Сборник примеров и
задач по физической химии / Киев. ун-т. Киев, 1960. 546 с.
6. Карапетьянц М.Х. Примеры и задачи
по электрохимии. М.: Химия, 1974. 301 с.
7. Сборник вопросов и задач по
физической химии для самоконтроля: учеб. пособие для вузов/под ред. С.Ф.
Белевского. М.: Высш. шк., 1979. 118 с.
8. Краткий справочник
физико-химических величин / под ред. А.А. Равделя и А.М. Пономаревой. Л.:
Химия, 1983. 231 с.
11. Зайцев О.С. Химическая кинетика к
курсу общей химии. М.: Изд-во Моск. ун-та, 1973. 294 с.
12. Свиридов В.В., Попкович Г.А.,
Васильева Г.И.. Задачи, вопросы и упражнения по общей и неорганической химии.
Минск: Изд-во Белорус. ун-та, 1978. 352 с.