Расчёт параметров изгиба однопролётной балки со свободно опертым и упруго защемленным концами

Расчёт параметров изгиба однопролётной балки со свободно опертым и упруго защемленным концами

Курсовая работа

Расчёт параметров изгиба однопролётной балки со свободно опёртым и упруго защемленным концами

L = 6.8 м = 680 см.

q₀ = 22.2 кгс/см

E = 210000 МПа

J = 5800 см⁴

æ = 0.93

1. Дифференциальное уравнение изгиба призматической балки имеет следующий вид:

EJW^IV (x) = q (x) (1)

После четырёхкратного интегрирования дифференциального уравнения изгиба балки (1) общий интеграл этого уравнения представляется выражением:

, (2)

в котором величины А, В, С, D являются постоянными интегрирования, определяемые исходя из граничных условий по концам рассматриваемой балки.

2. Граничные условия для параметров изгиба балки на её левом конце при значении х = 0 имеют вид:

W(0) = 0 (3)

W^II (0) = 0 (4)

На правом конце балки при значении х = L граничные условия для параметров изгиба имеют вид:

W(L) = 0 (5)

 (6)

3. В связи с тем, что в конкретном рассматриваемом примере на заданную однопролётную балку действует равномерно распределённая внешняя нагрузка интенсивностью q(x)= q₀ = const, дифференциальное уравнение (1) изгиба призматической балки будет иметь вид:

EJW^IV (x) = q ₀, (7)

а выражение (2) для общего интеграла дифференциального уравнения (7) будет:

 (8)

Для подчинения общего интеграла (8) дифференциального уравнения (7) граничным условиям (3), (4), (5). (6) необходимо предварительно получить выражения для первой и второй производных от общего интеграла (8), которые будут иметь соответственно вид:

 (9)

 (10)

Если подчинить выражение общего интеграла (8) граничному условию (3), то в результате получим, что

W(0) = D,

откуда следует, что величина D будет равна:

 D = 0 (11)

Если воспользоваться граничным условием (4), то подставляя в выражение (10) значение х = 0, в результате получим, что

W^II(0)=В,

откуда следует, что величина В будет равна:

 В = 0 (12)

Подчиняя выражение общего интеграла (8) граничному условию (5), получим, что

 (13)

Воспользовавшись выражениями (9) и (10), из граничного условия (6) получим следующую зависимость:

 (14)

или

,

откуда после преобразований и приведения подобных членов, получается выражение вида

 (15)

Выражения (14) и (15) в окончательном виде преобразуются к уравнениям относительно двух неизвестных величин А и С, которые образуют систему двух алгебраических уравнений:

 (16)

Для решения системы уравнений (16) можно воспользоваться методом миноров.

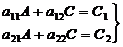
  (17)

значения неизвестных величин А и С будут определяться следующими формулами:

; (18)

, (19)

где:

Δ₀ – определитель системы уравнений (17), составляемый из коэффициентов при неизвестных величинах А и С:

Δ_{А -} определитель системы уравнений (17), составляемый из коэффициентов правой части С₁ и С₂ и коэффициентов при неизвестной величине С:

Δ_С - определитель системы уравнений (17), составляемый из коэффициентов при неизвестной величине А и из коэффициентов правой части С₁ и С₂:

Учитывая вышеприведенные формулы, получим следующие выражения:

,

которые после несложных преобразований примут вид:

Тогда, учитывая выражения (18) и (19), значения величин А и С будут определяться формулами:

 (20)

 (21)

в которых введены обозначения:

 (22)

 (23)

4. Общий интеграл (8) дифференциального уравнения (7), являющийся выражением, описывающим характер изменения прогиба W(x) по длине рассматриваемой однопролётной статически неопределимой балки, после подстановки значений величин А и С, запишется:

5. Общий интеграл приведенный к виду с безразмерными значениями переменного аргумента:

 (24)

6. Значения изгибающих моментов M(x), действующих на балку в любом сечении по её длине, определяются второй производной по прогибу балки, которая учитывая полученную формулу (24) преобразуется к виду:

или к выражению, содержащему «безразмерную» переменную величину, равную отношению «х/L»:

 (25)

На основании формулы (25) может быть построена эпюра значений изгибающих моментов M(x).

Для определения экстремального значения изгибающего момента в пролёте балки M_пр необходимо в первую очередь определить значение координаты (x_пр) расположения этого изгибающего момента M_пр. Для определения значения координаты (x_пр) необходимо получить выражение для первой производной от выражения (25):

 (26)

Тогда значение координаты (x_пр), где изгибающий момент будет иметь экстремальное значение M_пр, определится из условия:

или, учитывая выражение (26), из следующего уравнения:

,

откуда

(x_пр) (27)

Тогда экстремальное значение M_пр будет равно:

 (28)

Наибольшее значение изгибающий момент M(x), исходя из характера его распределения по длине балки, может иметь или в районе упругой заделки при х = L (значение M_оп) или при x = x_пр (значение M_пр).

Значение M_оп определим из выражения (25), подставляя в последнее значение координаты х = L:

 (29)

7. Коэффициент опорной пары æ определяется отношением значения изгибающего момента, действующего в районе упругой заделки M_оп, к значению изгибающего момента в этом районе при условии абсолютно жёсткого защемления M_жз:

æ  (30)

Значение изгибающего момента M_жз в районе упругой заделки в предположении его абсолютно жёсткого защемления определится из формулы (29), если в последней предположить, что коэффициент податливости заделки or равен нулю:

, (31)

тогда на основании формул (29), (30), (31) получим выражение, определяющее значение коэффициента опорной пары æ упруго защемлённого конца рассматриваемой статически неопределимой однопролётной балки:

æ (32)

Из формулы (32) может быть установлена зависимость коэффициента податливости упругой заделки or через значения коэффициента опорной пары æ:

 (33)

Использование формулы (33) позволяет выразить значения коэффициентов А^I и С^I при постоянных интегрирования А и С, определяемых формулами (22) и (23), выражениями, содержащими только значения коэффициентов опорной пары æ:

 (34)

 (35)

Тогда экстремальное значения изгибающего момента в пролёте балки M_пр и значения опорного изгибающего момента в районе упругого защемления M_оп будут определяться соответственно следующими выражениями через значения коэффициентов опорной пары æ:

 (36)

 (37)

А значение координаты (x_пр) расположения экстремального значения изгибающего момента в пролёте балки M_пр в соответствии с формулой (27) определится выражением:

 (38)

8. Значения перерезывающих сил N (x), действующих на балку в любом сечении по её длине, определяются известной зависимостью Журавского:

,

которая, учитывая формулу (25), для рассматриваемой однопролётной статически неопределимой балки преобразуется к виду:

 (39)

Из формулы (39) следует, что перерезывающие силы распределяются по длине балки по линейному закону, то есть по прямой линии, поэтому для построения эпюры перерезывающих сил достаточно определить значения перерезывающей силы в двух крайних точках, а именно в начале координат:

 (40)

и в районе упругой заделки (при x = L):

 (41)

Откуда видно, что выполняется следующее очевидное соотношение

9. Расчет значений параметров изгиба однопролетной балки со свободно опертым и упруго защемленным концами.

В этом случае, исходя из формул (34) и (35)

;

,

а координата (x_пр) расположения экстремального значения изгибающего момента в пролёте балки M_пр в соответствии с формулой (27) будет равна:

или в безразмерном относительном виде:

0.383

Экстремальное значение изгибающего момента в пролёте балки M_пр и значение опорного изгибающего момента в районе упругого защемления M_оп в соответствии с формулами (25) и (29) будут равны:

M_пр =M(260,8)  - 755359 кг*с*см

 1194621 кг*с*см

Определим значение перерезывающей силы в начале координат (на левой опоре) на основании формулы (40):

N(0) = - 5791 H.

На основании формулы (41) определим значение перерезывающей силы в районе упругого защемления балки (на правой опоре):

N(L) = 9305 H.

Отметим, что перерезывающая сила N в районе действия экстремального значения изгибающего момента M_пр в пролёте балки имеет нулевое значение:

,00 Н.