Разработка электропривода для лебедки-подъёмника

Введение

Электропривод является неотъемлемой частью многих агрегатов и комплексов, используемых в различных отраслях народного хозяйства, науки и техники. Наряду с тенденцией автоматизации технологических и производственных процессов на базе вычислительной техники, современный электропривод стал наиболее распространённой разновидностью систем автоматического управления техническими объектами. В которых основными производственными агрегатами являются механизмы циклического действия. Особенностью этих механизмов являются специфические режимы работы, состоящие из ряда повторяющихся циклов. Каждый рабочий цикл включает участки установившейся работы или паузы, участки пуска, торможения и реверса, что усложняет работу электропривода и сказывается на процессе работы.

В связи с этим к электроприводу предъявляется ряд требований. Эти требования продиктованы жёсткими пуско-тормозными режимами работы, характеризующимися числом включений, необходимостью регулирования скоростью в заданном диапазоне, надёжностью и экономичностью.

1. Выбор системы электропривода

Современный регулируемый электропривод содержит, как правило, статический (электронный) преобразователь электроэнергии (регулятор, коммутатор), с помощью которого обеспечивается экономичное и плавное регулирование параметров движения в широком диапазоне, формирование переходных процессов с заданным качеством, автоматизация процессов управления. Тип управляемого преобразователя, тип электродвигателя, а также способ управляющего воздействия на двигатель определяют в целом систему электропривода.

Выбор системы электропривода возможен на основе сравнительного анализа технических данных, приведенных в таблице 1, и исходных данных на проектирование электропривода с учетом изложенных выше особенностей применения наиболее распространенных систем электропривода.

Исходя из условий задания, определяем диапазон регулирования скорости и полезную мощность двигателя:

Диапазон регулирования скорости:

Таблица 1-Технические показатели систем электропривода

– в зоне частотного регулирования 5…20 Гц,

Таблица 2-Удельная стоимость электрооборудования, усл. ед./кВт

Для некоторых электроприводов важнейшим является массогабаритный показатель. Этот показатель можно использовать и для окончательного выбора, если экономические показатели сравниваемых систем оказались достаточно близкими. Ориентировочные показатели массы различных систем электропривода приведены ниже в таблице 3.

Таблица 3 – Удельная масса электроприводов, кг/кВт

Принимая во внимание технические показатели, экономичность и удельную массу электроприводов, и назначение механизма (лебёдка-подъёмник), выбираем систему ПЧИ-АД, так как она позволяет применить асинхронный двигатель с короткозамкнутым ротором получить большой диапазон регулирования и добиться высоких динамических показателей электропривода. Применение систем ПЧИ-АД является единственно возможным для крановых механизмов, работающих в условиях, где не возможен доступ для обслуживания (агрессивные и радиоактивные среды).

Согласно дополнительным требованиям, обеспечение ускорения 0,3 м/с², механизм относится к строительным башенным кранам [3, стр. 428, т. 13,3]

2. Выбор передаточного устройства и приведение механических величин к валу электропривода

Передаточное устройство привода преобразует вращательное движение электродвигателя во вращающееся или поступательное движение исполнительного органа. В современных приводах существует тенденция упрощения передаточного устройства путем исключения промежуточных звеньев в виде редукторов или других механизмов. При этом заметно возрастает точность, быстродействие и надежность привода. Однако для безредукторных приводов часто требуются специальные низкоскоростные двигатели, выпуск которых отечественной промышленностью явно отстает от потребностей современного электропривода.

Значения конструктивных параметров отдельных звеньев передаточного устройства принимаем с учетом следующих требований:

1) диаметр барабанов должен быть в пределах 0,25…1 м с промежуточными значениями по ряду R10;

D=0.32 м

2) передаточные числа зубчатых цилиндрических передач должны находиться в пределах 8…50 при двух ступенях и в пределах 16…125 при трех ступенях.

Выбирая двухступенчатый редуктор принимаем передаточное число j =25

Для электропривода лебёдки-подъемника выбираем передачу двухступенчатый редуктор – барабан – трос (рис. 1).

Рисунок 1 – Кинематическая схема грузоподъёмной лебёдки.

Д – электродвигатель, Р – двухступенчатый редуктор, Б – барабан, Г – груз.

КПД передачи [3, стр. 426, т. 13.1]

где η_бкп –КПД блока канатной передачи, 0,97;

η_ред –КПД редуктора, 0,78 – 0,8;

Скорость барабана:

 (1)

Определим угловые скорости для участков:

1.

2.

4.

5.

Наибольшую скорость примем за номинальную т.е.

ω_2макс= ω_ном=6,25 рад/с

Найдём скорость вращения вала двигателя:

 (2)

1.

2.

4.

5.

1.

2.

4.

5.

Приведение скорости рабочего органа к валу двигателя сведено в таблице 4

Таблица 4 – Скорость рабочего органа и вала двигателя i-того участка

Рисунок 2 – Приведение многомассовой системы к одномассовой при вращательном движении ЭД – электродвигатель; ПМ – передаточный механизм; ИМ – исполнительный механизм;

Момент механизма:

1.

2.

4.

5.

Момент сопротивления приведённый к валу двигателя [1 стр. 30 (1,79) 3]

 (3)

1.

2.

4.

5.

Мощность на каждом участке [1. стр. 9., (1,1)]:

 (4)

1.

2.

4.

5.

Приведение момента к валу двигателя сведено в таблицу 5.

Таблица 5

3. Предварительный выбор мощности электродвигателя и его параметров

Выбор электродвигателя производится из условий эксплуатации и требований, предъявляемых к системе. В крановых приводах используются асинхронные двигатели переменного тока серии 4А. Электродвигатели серии 4А применяют для привода механизмов подъёма и передвижения электрических талей. В связи с тяжёлыми условиями эксплуатации применяют двигатели со степенью защиты IP44.

Та как в данном электроприводе нагрузка на валу двигателя меняется в достаточно широких пределах, произведём выбор электродвигателя по эквивалентному моменту [3. стр. 189 (5,22а; 5,22б)]:

 (5)

Исходя из условия, что

Так как выбранный таким образом двигатель P=55кВт подходит по моменту, но не подходит по условиям нагрева.

Выбираем двигатель [4, стр. 29. таб. 2,1] серии 4А200М4У3 со следующими параметрами:

- номинальная мощность

- номинальный момент

- номинальная частота вращения

- номинальный ток двигателя

- число пар полюсов

- номинальная величина скольжения

- номинальное напряжение сети

- коэффициент полезного действия

- коэффициент активной мощности

- перегрузочная способность

- кратность пускового момента

- кратность пускового тока

- момент инерции ротора:  

– исполнение двигателя: IP44

– класс изоляции: F

C учётом передачи барабан – редуктор J_Σ=0.481

Определим номинальный момент двигателя:

 (6)

4. Разработка схемы и выбор силовой цепи

В качестве системы ПЧИ-АД выберем [3] систему: неуправляемый выпрямитель – автономный инвертор напряжения – асинхронный двигатель (НВ-АИН-АД).

Рисунок 6 – Схема принципиальная ПЧИ-АД

Выбираем в качестве выпрямителя три диодных модуля RM100CA/C1A-XXF с параметрами:

– средний ток в открытом состоянии 100А;

– импульс обратного напряжения 600 В.

Выбор силового модуля на IGBT транзисторах осуществим исходя из условия:

Расчет параметров емкостного фильтра выполним на основе рекомендаций, изложенных в справочнике.

Емкость конденсатора С определим по формуле:

 (7)

где =2;

q-коэффициент пульсаций выпрямленного напряжения (для трехфазного неуправляемого выпрямителя q=0.1);

В качестве  принимаем

Таким образом:

Рабочее напряжение конденсатора определяется как:

Значение емкости, выберем с некоторым запасом, чтобы пропустить значительные токи, возникающие при гашении инвертора.

Исходя из вышеизложенных соображений, выберем необходимый конденсатор К50–12:

– номинальная ёмкость

– номинальное напряжение

На основании литературных источников известно, что в общем случае рекуперативное торможение эффективно при мощности двигателя больше 30 кВт.

При меньшей мощности используется резистивное торможение, где энергия торможения, превышающая потери энергии в двигателе и инверторе, рассеивается в тормозном сопротивлении, включаемом через коммутируемый транзистор на шины промежуточного звена постоянного тока.

С помощью управления тормозным транзистором VT поддерживается заданный уровень напряжения в звене постоянного тока.

При торможении кинетическая энергия, освобождаемая инерционными массами электропривода при снижении скорости, рассеивается в виде потерь в АД, АИН и тормозном сопротивлении Rт:

 (8)

где J, ω – момент инерции электропривода и угловая скорость АД,

Iт – ток в тормозном сопротивлении Rт,

,  – потери мощности в АД и АИН.

Выполним расчет величины тормозного сопротивления без учета потерь мощности в АД и АИН, считая, что вся запасенная кинетическая энергия выделяется в виде тепла на сопротивлении Rт.

Величину тормозного тока Iт определим из соотношения:

 (9)

Интегрируя левую часть уравнения (8), получим:

Интегрируя правую часть уравнения (8) с учетом (9), получим:

 (10)

Подставим уравнения (8) и (10) в уравнение (8):

Аппараты защиты.

Защита необходима для ликвидации аварийных ситуаций (коротких замыканий, перегрузок) недопустимых с точки зрения нормальной работы вентилей и двигателя.

Выбор автоматического выключателя для цепи переменного тока (перед выпрямителем):

По справочнику [7] выбираем автомат А3110 со следующими параметрами:

– номинальный ток

– ток установки расцепителя

– номинальное напряжение

Для защиты полупроводниковых приборов используют быстродействующие предохранители, выбираем их из следующих условий: . Так как  диода больше чем ток , то целесообразно записать: .

По справочнику [7] выбираем предохранители ПР-2–60:

- предельный ток

- номинальный ток

5. Расчет статических характеристик электропривода

Пересчитаем параметры обмоток асинхронного двигателя из относительных единиц в абсолютные:

Электрическая мощность, забираемая из сети в номинальном режиме:

 (11)

Номинальный ток одной фазы:

 (12)

Полное сопротивление одной фазы:

 (13)

Умножим на Zн все параметры схемы замещения:

Для расчета статических механических характеристик воспользуемся уточненной формулой Клосса:

Закон управления будет заключаться в том, чтобы критический момент оставался постоянным М_к=599Н*м

Параметры рабочих режимов сведены в таблицу 6

Таблица 6

Будем считать, что для формирования необходимых нам статических характеристик система управления электроприводом реализует закон управления ,

При этом можно записать:

В двигательном режиме двигатель работает при скоростях  и .

Рассчитаем механические характеристики на участках:

1) при w₁=78,125 с^-1

Напряжение на выходе преобразователя:

Частота тока на выходе преобразователя:

;

;

2) при w₂=7,8125 с^-1

Напряжение на выходе преобразователя:

Частота тока на выходе преобразователя:

В тормозном режиме двигатель работает при скоростях  и .

3) при w₄=-156,25 с^-1

Напряжение на выходе преобразователя:

Частота тока на выходе преобразователя:

4) при w₅=-15,625 с^-1

Напряжение на выходе преобразователя:

Частота тока на выходе преобразователя:

6. Расчёт переходных процессов в электроприводе

Произведем линеаризацию характеристик на рабочем участке.

Так как при малом ускорении динамический момент мал, можно рассматривать переходный процесс как для двигателя постоянного тока с независимым возбуждением (с линейной характеристикой).

Ускорение подъёмника общего применения, согласно [2] ограничивают 0,3 м/с². Приведём его к валу двигателя:

Ускорение обеспечивается при помощи задатчика интенсивности.

Рассчитаем данные для построения переходных процессов:

– процесс колебательный

1) Пуск двигателя:

Для простоты построения колебательный процесс заменяем апериодическим, с постоянной времени

2) Снижение скорости движения до :

3) Торможение двигателя:

4) Пуск двигателя в обратную сторону:

5) Снижение скорости двигателя до :

6) Остановка двигателя:

7. Проверка выбранного двигателя по нагреву

Тепловые процессы в двигателях в нормальных условиях, благодаря, большой тепловой инерции протекают замедленно, поэтому быстрые изменения нагрузки и, соответственно, тепловыделения фильтруются и зависимость превышения температуры τ(t) сглаживается тем в большей степени, чем меньше время цикла, в сравнении с постоянной времени нагрева Тн двигателя.

Для нашего электропривода условие tц =2,91 мин<<Tн=45 мин и, как выше было отмечено, через некоторое время после начала работы наступает установившийся тепловой режим, при котором превышение температуры колеблется относительно среднего значения τср в узких пределах.

Произведём проверку выбранного двигателя по нагреву, с использованием метода средних потерь, суть которого заключается в вычислении средних потерь двигателя за рабочий цикл и сравнения их с потерями двигателя при работе в номинальном режиме:

 (23)

Суммарные потери в асинхронном двигателе:

; (24)

Постоянные потери в номинальном режиме:

 (25)

Номинальные потери двигателя определяются как:

 (26)

Переменные потери в номинальном режиме, с учетом намагничивающих потерь:

 (27)

где

При частотном способе регулирования скорости асинхронного двигателя постоянные потери определяются следующим выражением:

 (28)

Считая, что: , определим постоянные потери в двигателе для каждого интервала рабочего цикла:

Переменные потери:

Ток статора определяется по формуле:

 (29)

Приведенный ток ротора определяем по формуле:

 (30)

Определим токи ротора для каждого интервала рабочего цикла

Подставим уравнение (29) в (30), получим расчетную формулу для определения переменных потерь для каждого интервала рабочего цикла:

 (31)

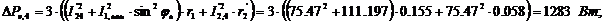
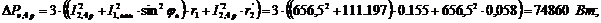
Суммарные потери в асинхронном двигателе для каждого интервала рабочего цикла:

Средние потери двигателя за рабочий цикл равны:

 (32)

-коэффициент, учитывающий ухудшение вентиляции.

=0,5 – коэффициент ухудшения вентиляции при неподвижном роторе.

ti-время i-го интервала.

Сравним средние потери двигателя за рабочий цикл с потерями двигателя при работе в номинальном режиме:

 (33)

Таким образом, перегрузка двигателя составляет менее 10%. Следовательно, двигатель удовлетворяет требованиям по перегрузке.

8. Исследовательская часть

Задание: Исследовать точный останов двигателя.

Рассмотрим задачу точного позиционирования рабочего органа механизма в заданных точках пути по сигналам путевых датчиков, или, как ее называют иначе, задачу автоматического точного останова электропривода. Эта задача сводится к автоматическому отключению двигателя и наложению механического тормоза в такой точке пути, из которой электропривод за время торможения, двигаясь по инерции, перемещается в заданную точку пути с требуемой точностью.

Процесс останова, таким образом, начинается с поступления в схему управления электроприводом импульса путевого командоаппарата на отключение двигателя и наложение механического тормоза. Если принять, что отключение двигателя и наложение механического тормоза происходят одновременно и усилие тормоза возрастает до установленного значения скачком, то весь процесс точного останова можно разделить на два этапа.

Первый этап обусловлен наличием собственного времени срабатывания аппаратуры t_a в схеме управления электроприводом. В схеме моделирования вследствие возникающего запаздывания в течение времени t_a двигатель не отключается от сети, и электропривод продолжает движение со скоростью _нач, с которой он подошел к датчику точного останова, и проходит заданный путь.

По истечении времени срабатывания аппаратуры двигатель отключается от сети, и накладывается механический тормоз. Наступает второй этап процесса останова, во время которого запасенная во всех движущихся массах системы кинетическая энергия расходуется на совершение работы по преодолению сил статического сопротивления движению на проходимом при этом пути φ».

Моделирование точного останова с помощью Matlab 6.1., по системе управления ПЧИ-АД производилось по принципу изменения частоты питающего напряжения. То есть при прохождении заданного пути, происходит снижение скорости вращения ω_нач двигателя и в момент достижения скорости ω_кон, наложение тормозного момента М_т для полного останова двигателя.

Рисунок 13 – Зависимость ω=f(φ) в процессе точного останова

Зависимость =f(φ) при установке датчика точного останова (ДТО) в точке φ=0 и некоторой начальной скорости _нач показана на рис. 13 (кривая 1). Так как все параметры, определяющие путь, проходимый электроприводом в процессе точного останова, при работе электропривода не остаются постоянными, абсолютно точный останов невозможен. Так как после срабатывания ДТО движение системы является неуправляемым, наибольшая неточность останова зависит только от пределов изменения параметров входящих (34).

φ=φ’+φ’’=ω_начt_a+J_Σω²_нач/2 (M_c+M_т) (34)

Рисунок 14 – Схема моделирования в Matlab Simulink6.1.

Пределы перемещения можно представить:

φ=φ_ср±Δ φ_max (35)

где φ_ср-средний путь при точном останове;

Δ φ_max-максимальная ошибка позиционирования или максимальная неточность останова.

Как показано на рис. 13, ДТО должен устанавливаться на расстоянии φ₃=φ_cp, там же кривые 2 и 3 дают представления о зависимостях =f(φ) при сочетаниях параметров, соответствующих наибольшей ошибке позиционирования.

Максимальная неточность останова:

Δ φ_max =(φ_max – φ_min)/2 (36)

Докажем вышеизложенное на основе модели отрабатывающей точный останов двигателя.

Опыт 1:

Рисунок 15 – Зависимость ω=f(φ) в процессе точного останова (модель Matlab 6)

Рисунок 16 – Зависимости ω(t), М(t), φ(t)

Рисунок 17 – Зависимость ω(t), показывающая ошибку позиционирования

Согласно формуле (36) максимальная неточность останова, на основании экспериментальных данных будет равна:

Δ φ_max=(92,55–89)/2=1,775

Рисунок 18 – Зависимости ω=f(φ) в процессе замедления до пониженной скорости и точного останова двигателя

На рис. 18 показаны зависимости =f() при двух нагрузках электропривода М_с=М_с.max и М_с=М_с.min, соответствующие как процессу точного останова, так и предшествующему процессу замедления.

Кривые построены в предположении, что при любой нагрузке процессы замедления протекают при неизменном тормозном моменте двигателя М=М_max=const. Тогда ускорение электропривода в этом процессе будет зависеть от нагрузки:

ε = – (M_max+M_c)/J_Σ (37)

причем наименьшей нагрузке на валу М_с.min соответствует и наименьшее по абсолютному значению ускорение. При М_с=М_с.min начальная рабочая скорость при ограниченной жесткости механических характеристик электропривода максимальна: _р=_р.max, путь, проходимый электроприводом за время снижения скорости от _р.max до _нач.max при минимальном ускорении _min, также имеет максимальное значение φ_зам.max. Датчик импульса замедления (ДИЗ), дающий команду на замедление, устанавливается от ДТО на расстоянии 1,1·φ_зам.max, поэтому, как показано на рис. 18, при М_с=М_с.min электропривод на пониженной скорости _нач.max проходит весьма небольшой отрезок пути и время дотягивания к ДТО невелико. При М=М_с.max, _р=_р.min соответственно φ_зам=φ_зам.min<<1,1φ_зам.max Как следствие большой отрезок пути φ_зам=1,1φ_зам.max-φ_зам.max электропривод проходит на пониженной скорости _нач.min, время дотягивания при _нач.min<<_р.min оказывается значительным и соизмеримым с общим временем, требующимся для перемещения механизма из исходного рабочего положения в заданное.

Рассматривая рис. 18, можно заключить, что время дотягивания при любых нагрузках может быть сведено к минимуму, если устранить статическую ошибку регулирования скорости и сформировать стабильную зависимость =f(t) в процессе замедления.

Докажем вышеизложенное на основе модели отрабатывающей замедление до пониженной скорости и точный останов двигателя:

Опыт 2:

Рисунок 19 – Зависимости ω=f(φ) в процессе замедления до пониженной скорости и точного останова двигателя (модель Matlab 6)

Рисунок 20 – Зависимости ω(t), М(t), φ(t)

Рисунок 21 – Зависимость ω(t), показывающая ошибку позиционирования

Согласно формуле (36) максимальная неточность останова, на основании экспериментальных данных будет равна:

Δ φ_max=(182,8–182,49)/2=0,155

Проанализировав данные полученные с помощью проведённых опытов, можно сделать вывод, что система замедления скорости до пониженной и точный останов, позволяют обеспечить наименьшую ошибку позиционирования, что и позволяет более точно производить остановку.

Литература

1. Фираго Б.И. Теория электропривода: Учебное пособие/ Б.И. Фираго, Л.Б. Павлячик. – Мн.: ЗАО «Техноперспектива», 2004. – 527 с.

2. Лебедев А.М. «Следящие электроприводы станков с ЧПУ» Москва. «Энергоатомиздат» 1988

3. Справочник по автоматизированному электроприводу. Под ред. В.А. Елисеева и А.В. Шинянского. – М.: Энергоатомиздат, 1983. – 616 с. Ил.

4. Асинхронные двигатели серии 4А: Справочник/А.Э. Кравчик, М.М. Шлаф, Е.А. Соболенская. – М.: Энергоатомиздат, 1982. – 504 с., ил.

5. Онищенко Г.Б. Электрический привод. Учебник для вузов – М.:РАСХН, 2003. – 320 с. ил.

6. Абрамович И.И. Грузоподъёмные краны промышленных предприятий: Справочник. – М.: Машиностроение, 1989. – 360 с.: ил.

7. И.И. Алиев, М.Б. Абрамов. Электрические аппараты