Обработка электрического сигнала с помощью фильтрации
ПЕНЗЕНСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра «Медицинские приборы и оборудование»
Курсовой проект
на тему:
«Обработка электрического сигнала с
помощью фильтрации»
по дисциплине «Методы обработки биомедицинских сигналов»
Пенза
2005
Введение
Методы и техника обработки сигналов в
настоящее время составляют основу важнейших разработок во многих областях
научных знаний. В течение последних лет методы цифровой обработки сигналов
приобрели большую важность ввиду того, что теперь они не только заменяют
классические аналоговые методы во многих традиционных областях техники, но и
применяются во многих новых областях, таких как медицинская техника.
В большинстве случаев электрический фильтр представляет
собой частотно-избирательное устройство. Следовательно, он пропускает сигналы определенных
частот и задерживает или ослабляет сигналы других частот. Наиболее общими
типами частотно-избирательных фильтров являются фильтры нижних частот (которые
пропускают низкие частоты и задерживают высокие), фильтры верхних частот
(которые пропускают высокие частоты и задерживают низкие), полосно-пропускающие
фильтры (которые пропускают полосу частот и задерживают те частоты, которые
расположены выше или ниже этой полосы) и полосно-заграждающие фильтры
(которые задерживают полосу частот и пропускают частоты, расположенные выше и
ниже этой полосы).
1. Основы
анализа электрических сигналов
Применение методов цифровой обработки сигналов и, в
частности, цифровой фильтрации широко распространено и используется во многих
важных областях исследовании, например: обработка речевых сигналов, цифровая
телефония и цифровая связь, обработка фототелеграфных и телевизионных
изображений, радио- и гидролокационные системы, биология и медицина,
космические исследовательские и действующие системы, исследование земных
ресурсов и т.д.
В биомедицинской практике используется множество сигналов,
имеющих электрическую природу. При регистрации и оценке таких сигналов
сталкиваются с значительным влиянием на конечные результаты помех различного
рода, поэтому биомедицинские сигналы нуждаются в обработке.
Из всех методов, используемых
при цифровой обработке сигналов, наиболее важным является цифровая фильтрация.
В прошлом интерес ограничивается теоретическими исследованиями, но последнее
время она используется во многих важных практических приложениях для обработки
одномерных и двумерных сигналов.
2. Исследование полосового фильтра
Полосовой (или полосно-пропускающий) фильтр представляет собой устройство, которое пропускает сигналы
в диапазоне частот с шириной полосы BW, расположенной приблизительно вокруг
центральной частоты ω0 (рад/с). На рисунке 1 изображена
идеальная и реальная амплитудно-частотные характеристики полосового фильтра.

Рисунок 1
В реальной характеристике частоты ωL и ωU
представляют собой нижнюю и верхнюю частоты среза и определяют полосу
пропускания ωL≤ω0≤ωU
и ее ширину BW= ωU – ωL.
В полосе пропускания амплитудно-частотная характеристика
никогда не превышает некоторого определенного значения, например А1.
Существует также две полосы задерживания, где значение амплитудно-частотной
характеристики никогда не превышает заранее выбранного значения, наример А2.
Диапазоны частот пежду полосами задерживания и полосой пропускания образуют
нижнюю и верхнюю переходные области, в которых характеристика является
монотонной.
Отношение Q= ω0/BW характеризует качество
самого фильтра и является мерой его избирательности. Высокому значению Q
соответствует относительно узкая, а низкому значению Q – относительно широкая
ширина полосы пропускания. Коэффициент усиления фильтра К определяется как значение
его амплитудно-частотной характеристики на центральной частоте.
Передаточная функция полосно-пропускающего фильтра имеет следующий
вид:

Для исследования полосового фильтра, ввели в
командное окно пакета MATLAB оператор «rlcdemo». Открылось окно,
предназначенное для построения аналогового фильтра. Выбрали полосовой фильтр с
последовательным соединением соединением элементов RLC: R=4,5; L=2,5; C=0,5
(рисунок 2).

Рисунок 2
Исходя из значений системных параметров рассчитали
коэффициенты полиномов числителя и знаменателя:

 G(s)= 1.8s
G(s)= 1.8s
S2+1.8s+0.8
Средствами MATLAB построли прередаточную функцию системы
sys:
>> sys=tf([0 1.8 0], [1 1.8 0.8])
Transfer function:
1.8 s
–
s^2 + 1.8 s + 0.8
Затем мы исследовали характеристики
фильтра.
Во-первых, это диаграмма Боде (ЛАЧХ И ФЧХ) (рисунок 3).
>> bode(sys)

Рисунок 3
Во-вторых, это реакция системы на
единичное воздействие (рисунок 4).
>> step(sys)

Рисунок 4
В-третьих, это диаграмма Найквиста, то
есть представление вещественной и мнимой частей характеристики в зависимости от
частоты (рисунок 5).
>> nyquist(sys)

Рисунок 5
И наконец, это импульсная характеристика
(рисунок 6).
>> impulse(sys)

Рисунок 6
Сравнивая полученные характеристики фильтра с
представленными на рисунке 2, убедились, что они идентичны.
3. Реализация модели фильтра в Simulink
Перевели данные содержащие
электрокардиограмму (приложение 1) из MSExcel в MATLAB и построили график
кардиосигнала (рисунок 7).
>> plot(G)

Рисунок 7
Затем наложили на исходный сигнал помеху
(рисунок 8):
n=length(G);
e=rand(n)*17225
for i=1:n
s(i)=e(i)+G(i)
end
>> plot(s)

Рисунок 8
r=0
for i=1:n;
r=r+1;
t(i)=r;
end
S=s’
В приложении Simulink собрали схему,
реализующую модель данного фильтра (рисунок 9).

Рисунок 9
На вход фильтра подается сигнал с помехой.
Значения коэффициентов полиномов передаточной функции взяты из рабочей области
MATLAB. На рисунке 10 представленны результаты фильтрации и исходный сигнал с помехой.
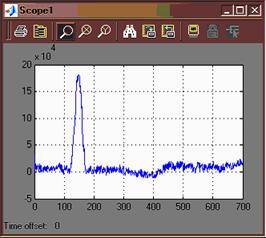

Рисунок 10
Заметим, что результат фильтрации
неудовлетворителен, появляется значительный по амплитуде отрицательный выброс,
в то время как амплитуда R-зубца уменьшается почти в четыре раза.
4. Реализация полосового фильтра в цифровой форме
Итак для фильтрации электрокардиосигнала
аналоговый полосовой фильтр оказался молоэффективен. Однако, MATLAB
предоставляет широкие возможности для проектирования различных фильтров (в том
числе и полосно-пропускающего) в цифровой форме.
В MATLAB существует библиотека (toolbox) Filter Design,
предназначенная для решения задач проектирования, включая процедуры коррекции
полученных результатов с учётом эффектов квантования. Библиотека имеет
интерактивную графическую программу (GUI) fdatool, с помощью которой можно
рассчитывать цифровые фильтры.
Сразу после загрузки программы отображается главное окно
библиотеки. В нем мы задали параметры проектируемого фильтра (рисунок 11) в соотфетствии
с полученными ранее ЛАЧХ И ФЧХ.

Рисунок 11
Воспользовавшись кнопками Import filter,
Filter Coefficient, вывели значения коэффициентов фильтра (рисунок 12).

Рисунок 12
Последовательно выбирая команды Magnitude Recponse, Phase
Recponse, Impulse Recponse, Step Recponse, определили характеристики фильтра.
Амплитудно-частотная характеристика фильтра (рисунок 13)

Рисунок 13
Фазо-частотная характеристика (рисунок 14)

Рисунок 14
Импульсная характеристика (рисунок 15)

Рисунок 15
Отклик на единичное воздействие (рисунок
16)

Рисунок 16
5. Реализация модели фильтра в Simulink
Нажав на кнопку  мы
получаем созданный фильтр в виде блока-элемента библиотеки Simulink. Дважды
щелкнув мышью на изображении этого блока можно получить его внутреннюю
структуру (рисунок 17)
мы
получаем созданный фильтр в виде блока-элемента библиотеки Simulink. Дважды
щелкнув мышью на изображении этого блока можно получить его внутреннюю
структуру (рисунок 17)

Рисунок 17
На рисунке 18 представлена схема, реализующая модельданного
фильтра.

Рисунок 19
На вход фильтра подавали тот же сигнал, что и при исследовании
аналогового фильтра
На рисунке 20 представлены результаты фильтрации и исходный сигнал с помехой.
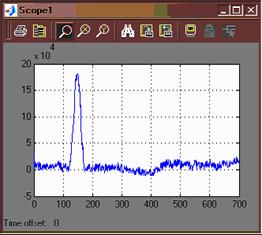

Рисунок 20
При сравнении двух осциллограмм можно говорить об
удовлетворительном результате фильтрации.
6. Исследование
характеристик WAVELET и WAVELET-преобразований одномерных сигналов
Тoolbox Wavelet – набор инструментов, встроенных в
вычислительную среду MATLAB, для решения разнообразных инженерных задач,
связанных с компрессией сигналов, анализом их особенностей, очисткой от шумов и
др. В основе используемых процедур лежит относительно новая теория разложения
сигналов по специальным функциям всплескам (wavelet), главные особенности
которых ограниченность во времени, самоподобие и компактная локализация энергии
по времени и частоте.
Тулбокс Wavelet состоит из набора подпрограмм, которые
позволяют:
·
ознакомиться и исследовать
характеристики индивидуальных wavelet и wavelet-пакетов;
·
вычислять непрерывное wavelet-преобразование
одномерных сигналов;
·
производить анализ и синтез дискретных
одномерных и двумерных сигналов на основе дискретного wavelet-преобразования;
·
раскладывать одно- и двумерные сигналы
по пакету wavelet;
·
исследовать статистические
характеристики сигналов;
·
производить сжатие и очистку от шума
одномерных и двумерных сигналов.
Wavemenu запускается из командной строки MATLAB командой «wavemenu».
В качестве исходного сигнала используем
все тот же сигнал ЭКГ с наложенной на него помехой (рисунок 21):

Рисунок 21
Wavelet-преобразование позволяет разложить
сигнал по компактным, хорошо локализованным по времени и частоте, базисным
функциям, что позволяет, в отличие от преобразования Фурье, описывать
нестационарные сигналы. При этом важно, что такое разложение достаточно
экономно в вычислительном отношении.
В отличие от кратковременного преобразования Фурье (STFT),
непрерывное wavelet-преобразование (CWT) имеет переменное разрешение по времени
и частоте. В области высоких частот оно обеспечивает хорошее разрешение по времени
и плохое по частоте, а в области низких частот хорошее разрешение по частоте и
плохое по времени (рис. 3). Применение wavelet-преобразования дает хорошие
результаты, особенно когда компоненты сигнала с высокой частотой имеют
небольшую длительность, а низкочастотные компоненты достаточно большую.
Практически все биологические сигналы имеют подобную структуру.
Выбрали wavelet Добеши с двумя уровнями
декомпозиции (ортогональный фильтр с конечной маской) (рисунок 22).

Рисунок 22
Дискретное wavelet-преобразование наиболее эффективно в
задачах сжатия сигналов и изображений, задаче очистки сигнала от шумов.
Нажатие на кнопку Stanistics позволяет получить
статистические данные относительно исследуемого сигнала (рисунок 23).
При сжатии сигнала используют следующую
схему: производится wavelet-преобразование исходного сигнала, после чего
запоминаются только значащие коэффициенты, то есть те, которые больше
некоторого заданного порога. Восстановление сигнала производится при помощи
обратного wavelet-преобразования, при этом пропущенные коэффициенты заменяются
нулями.
Результаты сжатия представлены на рисунке 24.

Рисунок 23

Рисунок 24
Графический интерфейс позволяет решать
задачи уменьшения уровня шума в дискретном (цифровом) сигнале (очистки от
шума). Для этого необходимо нажать на кнопку «Denoise» в середине правой
колонки, под кнопкой «Analyze». Параметры и результаты уменьшения шума
представлены на рисунке 25.
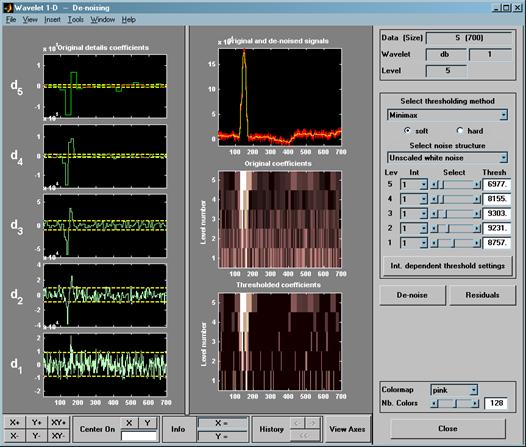
На рисунке 26 подробнее представлен результат очистки
сигнала от шума.

Рисунок 26
Заключение
В ходе курсового проекта быди получены навыки современных методов
обработки биомедицинских сигналов с использованием средств вычислительной
техники. Выполняя курсовой
проект исследовали аналоговый и цифровой полосно-пропускающий фильтр,
реализовали модель фильтра в Simulink, а также познакомились с wavelet-преобразованиями.
Методы цифровой обработки сигналов
приобрели большую важность ввиду того, что теперь они не только заменяют
классические аналоговые методы во многих традиционных областях техники, но и
применяются во многих новых областях, таких как медицинская техника.
Дискретное wavelet-преобразование наиболее эффективно в
задачах сжатия сигналов и изображений, задаче очистки сигнала от шумов.
Список
использованных источников
1. Джонсон Д. Справочник по активным фильтрам. – М.: Энергоатомиздат,
1983
2. Макс Жак Методы и техника обработки сигналов при физических
измерениях. Пер. с фр. Под ред Волкова Н.Г. – М.: Мир, 1983
3. Дьяконов В. Simulink 4. Специальный справочник. –
СПб.: Питер, 2002
4. Андреев И.И., Ланнэ А.А. MATLAB для DSP: SPTool –
инструмент для расчёта цифровых фильтров и спектрального анализа сигналов //
Цифровая обработка сигналов. 2000. №2.
5. Потемкин В.Г. MATLAB 5 для студентов /Диалог-МИФИ.
1999.