Дослідження локальних формацій із заданими властивостями
Курсова робота
Дослідження локальних
формацій із заданими властивостями
Введення
Формації, тобто класи груп, замкнуті відносно фактор - груп і під
прямих добутків, завжди перебували в поле діяльності дослідників по теорії
кінцевих груп. Однак аж до 1963 р. формаційний розвиток теорії кінцевих
груп ішло лише по шляху нагромадження фактів, що ставляться до різних
конкретних формацій, з яких найбільш популярними були формація розв'язних груп
і її подформації, складені з абелевих, нильпотентних груп.
У курсовій роботі розглядається добуток формацій, операції на класах
груп, що приводять до формацій. Розглядаються локальні формації й екрани.
Розглядаються найпростіші властивості локальної формації всіх груп з
нильпотентним компонентом.
Визначення 1.1 Класом груп називають усяка множина груп, що містить
разом з кожною своєю групою  й всі групи, ізоморфні
й всі групи, ізоморфні  .
.
Якщо група (підгрупа) належать класу  , то вона називається
, то вона називається  групою (
групою ( - підгрупою).
- підгрупою).
Визначення 1.2. Клас груп  називається формацією, якщо виконуються
наступні умови:
називається формацією, якщо виконуються
наступні умови:
1) кожна фактор - група будь - якої групи з  також належить
також належить  ;
;
2) із  завжди
треба
завжди
треба  .
.
Якщо формації  й
й
 такі, що
такі, що  , то
, то  називається підформацією формації
називається підформацією формації  .
.
По визначенню, порожня множина є формацією (порожня формація).
Множина  всіх груп є,
звичайно, формацією. Одинична формація
всіх груп є,
звичайно, формацією. Одинична формація  – це непустий клас груп, що складає лише з
одиничних груп. Формаціями є: клас
– це непустий клас груп, що складає лише з
одиничних груп. Формаціями є: клас  усіх
усіх  - груп, клас
- груп, клас  всіх абелевих груп, клас
всіх абелевих груп, клас  всіх нильпотентних груп, клас
всіх нильпотентних груп, клас  усіх
усіх  - груп (
- груп ( – фіксоване простої число), клас
– фіксоване простої число), клас  всіх нильпотентних
всіх нильпотентних  - груп, клас
- груп, клас  всіх розв'язних груп, клас
всіх розв'язних груп, клас  всіх розв'язних
всіх розв'язних  - груп. Ми привели поки
лише приклади тих формацій, за яких закріплені відповідні позначення.
- груп. Ми привели поки
лише приклади тих формацій, за яких закріплені відповідні позначення.
Лема 1.1. Справедливі наступні твердження:
1) перетинання будь - якої множини формацій також є формацією;
2) якщо  –
деяка множина формацій, лінійно впорядковане щодо включення
–
деяка множина формацій, лінійно впорядковане щодо включення  , то об'єднання
, то об'єднання  є формацією.
є формацією.
Доказ здійснюється перевіркою.
Визначення 1.3. Нехай  – непуста формація. Позначимо через
– непуста формація. Позначимо через  і
і  - корадикалом групи
- корадикалом групи  перетинання всіх тих нормальних підгруп
перетинання всіх тих нормальних підгруп  з
з  , для яких
, для яких  .
.
Очевидно,  -
корадикал будь - якої групи є характеристичною підгрупою.
-
корадикал будь - якої групи є характеристичною підгрупою.  - корадикал групи
- корадикал групи  позначають інакше через
позначають інакше через  і називають
і називають  - корадикалом.
- корадикалом.  - корадикал будемо називати нильпотентним
радикалом; зрозумілі також терміни розв'язний корадикал,
- корадикал будемо називати нильпотентним
радикалом; зрозумілі також терміни розв'язний корадикал,  - розв'язний корадикал,
- розв'язний корадикал,  - корадикал і т.д.
- корадикал і т.д.  - корадикал (або абелев
корадикал) – це комутант групи. Так само як і комутант,
- корадикал (або абелев
корадикал) – це комутант групи. Так само як і комутант,  - корадикал зберігається при
гомоморфізмах.
- корадикал зберігається при
гомоморфізмах.
Лема 1.2. Нехай  – непуста формація,
– непуста формація,  . Тоді справедливі наступні твердження:
. Тоді справедливі наступні твердження:
1) 
2) якщо  те
те 
3) якщо  й
й  , те
, те 
Доказ. Нехай  .
Тоді
.
Тоді

Звідси треба, що  . З іншого боку,
. З іншого боку,

звідки одержуємо  . З
. З  і
і  треба рівність
треба рівність  . Твердження 1) доведено.
. Твердження 1) доведено.
Нехай  –
природний гомоморфізм групи
–
природний гомоморфізм групи  на
на  Очевидно,
Очевидно,

звідки треба рівність  . Зокрема, якщо
. Зокрема, якщо  , те
, те  . Лема доведена.
. Лема доведена.
Визначення 1.4. Нехай  і
і  – деякі формації. Якщо
– деякі формації. Якщо  , то покладемо
, то покладемо  Якщо
Якщо  , те позначимо через
, те позначимо через  клас всіх тих груп
клас всіх тих груп  , для яких
, для яких  Клас
Клас  називається добутком формацій
називається добутком формацій  і
і  .
.
З визначення 1.4 треба, що добуток формацій  є порожньою формацією тоді й тільки тоді, коли
принаймні одна з формацій
є порожньою формацією тоді й тільки тоді, коли
принаймні одна з формацій  є порожньою. Можна визначити добуток декількох
формацій як результат послідовного множення. Якщо задано впорядкований набір
формацій
є порожньою. Можна визначити добуток декількох
формацій як результат послідовного множення. Якщо задано впорядкований набір
формацій  причому
добуток
причому
добуток  уже визначений,
то
уже визначений,
то  Зокрема, якщо
Зокрема, якщо  для будь - якого
для будь - якого  те ми приходимо до поняття
ступеня
те ми приходимо до поняття
ступеня 
Поняття добутку формацій становить інтерес із погляду побудови
формацій.
Теорема 1.1. Добуток будь - яких двох формацій також є формацією.
Лема 1.3. Нехай  і
і  – нормальні підгрупи групи
– нормальні підгрупи групи  . Тоді кожний головний фактор групи
. Тоді кожний головний фактор групи 
 - ізоморфний або деякому головному фактору
групи
- ізоморфний або деякому головному фактору
групи  , або деякому
головному фактору групи
, або деякому
головному фактору групи 
Доказ випливає з розгляду  - ізоморфізму
- ізоморфізму 
Теорема 1.2. Нехай  – деяка формація,
– деяка формація,  – клас всіх тих груп, всі головні фактори яких
належать
– клас всіх тих груп, всі головні фактори яких
належать  Нехай
Нехай  – об'єднання формацій
– об'єднання формацій  Тоді
Тоді  – підформація формації
– підформація формації 
Доказ. З леми 1.3 виводимо, що  – формація. З теореми 1.1 і леми 1.1 випливає,
що клас
– формація. З теореми 1.1 і леми 1.1 випливає,
що клас  є формацією.
Якщо
є формацією.
Якщо  – мінімальна
нормальна підгрупа групи
– мінімальна
нормальна підгрупа групи  ,
то по індукції
,
то по індукції  для
деякого натурального
для
деякого натурального  .
Але тоді або
.
Але тоді або  , або
, або  –
–  - корадикал групи
- корадикал групи  . Тому що
. Тому що  , те звідси випливає, що
, те звідси випливає, що  , і теорема доведена.
, і теорема доведена.
Операції на класах груп
Визначення 2.1. Усяке відображення множини всіх класів груп у себе
називається операцією на класах груп.
Операції ми будемо позначати, як правило, прямими більшими
латинськими буквами. Результат операції  , застосованої до класу
, застосованої до класу  позначається через
позначається через  Ступінь операції
Ступінь операції  визначається так:
визначається так:  Добуток операцій визначається
рівностями:
Добуток операцій визначається
рівностями:

Уведемо операції  в такий спосіб:
в такий спосіб:
 тоді й
тільки тоді, коли
тоді й
тільки тоді, коли  вкладається
як підгрупа в якусь
вкладається
як підгрупа в якусь  -
групу;
-
групу;
 тоді й
тільки тоді, коли
тоді й
тільки тоді, коли  вкладається
як нормальна підгрупа в якусь
вкладається
як нормальна підгрупа в якусь  - групу;
- групу;
 тоді й
тільки тоді, коли
тоді й
тільки тоді, коли  є
гомоморфним образом якоїсь
є
гомоморфним образом якоїсь  - групи;
- групи;
 тоді й
тільки тоді, коли
тоді й
тільки тоді, коли  співпадає
з добутком деякого кінцевого числа своїх нормальних
співпадає
з добутком деякого кінцевого числа своїх нормальних  - підгруп;
- підгруп;
 тоді й
тільки тоді, коли
тоді й
тільки тоді, коли  має
нормальні підгрупи
має
нормальні підгрупи  такі,
що
такі,
що

 тоді й
тільки тоді, коли
тоді й
тільки тоді, коли  є
розширенням
є
розширенням  - групи за
допомогою
- групи за
допомогою  - групи;
- групи;
 тоді й
тільки тоді, коли
тоді й
тільки тоді, коли  має
нормальну підгрупу
має
нормальну підгрупу  таку,
що
таку,
що 
Якщо  , то
замість
, то
замість  пишуть
пишуть  Оборотний увага на той
факт, що якщо
Оборотний увага на той
факт, що якщо  –
нормальні підгрупи групи
–
нормальні підгрупи групи  ,
причому
,
причому  для кожного
для кожного  , то
, то  Помітимо ще, що операцію
Помітимо ще, що операцію  можна визначити за
допомогою поняття підпрямого добутку. Нагадаємо (див. Каргаполов і Мерзляков
[1]), що підгрупа
можна визначити за
допомогою поняття підпрямого добутку. Нагадаємо (див. Каргаполов і Мерзляков
[1]), що підгрупа  прямого
добутку
прямого
добутку  називається підпрямим
добутком груп
називається підпрямим
добутком груп  якщо
проекція
якщо
проекція  на
на  збігається з
збігається з  Легко бачити, що
Легко бачити, що  тоді й тільки тоді, коли
тоді й тільки тоді, коли  є добуток деякого кінцевого
числа
є добуток деякого кінцевого
числа  - груп.
- груп.
Визначення 2.2. Клас  називається замкнутим щодо операції
називається замкнутим щодо операції  або, більш коротко,
або, більш коротко,  - замкнутим, якщо
- замкнутим, якщо 
Формацію можна визначити тепер як клас груп, що одночасно  - замкнуть і
- замкнуть і  - замкнуть.
- замкнуть.  - замкнутий клас згідно Гашюцу [3]
називається насиченим.
- замкнутий клас згідно Гашюцу [3]
називається насиченим.  -
замкнутий клас груп називається гомоморфом. Клас груп називається замкнутим
щодо підгруп (нормальних підгруп), якщо він
-
замкнутий клас груп називається гомоморфом. Клас груп називається замкнутим
щодо підгруп (нормальних підгруп), якщо він  - замкнутий (відповідно
- замкнутий (відповідно  - замкнуть).
- замкнуть).
Лема 2.1.  .
Якщо клас груп
.
Якщо клас груп  містить
одиничну групу й
містить
одиничну групу й  - замкнуть,
то
- замкнуть,
то 
Доказ. Щодо операцій  і
і  твердження очевидно. Нехай
твердження очевидно. Нехай  – довільний клас груп. Ясно, що
– довільний клас груп. Ясно, що  Якщо
Якщо  , те в
, те в  найдеться нормальна підгрупа
найдеться нормальна підгрупа  така, що
така, що  . Група
. Група  має нормальну підгрупу
має нормальну підгрупу  таку, що
таку, що  й
й  Але тоді
Але тоді  Тому що
Тому що  , те
, те , а виходить,
, а виходить,  Таким чином,
Таким чином,  , що й потрібно.
, що й потрібно.
Нехай  . Якщо
. Якщо
 , то
, то  має нормальну
має нормальну  - підгрупу
- підгрупу  таку, що
таку, що  Група
Група  має нормальну
має нормальну  - підгрупу
- підгрупу  таку, що
таку, що  . Тому що
. Тому що  й
й  , те з
, те з  - замкнутості класу
- замкнутості класу  треба, що
треба, що  . Виходить,
. Виходить,  , тобто
, тобто  . Зворотне включення очевидно.
. Зворотне включення очевидно.
Лема 2.2. Для будь - якого класу  справедливо наступне твердження:
справедливо наступне твердження: 
Доказ. Якщо  ,
то
,
то  Нехай
Нехай  Якщо
Якщо  , те
, те , а виходить,
, а виходить,  . Таким чином,
. Таким чином,  . Нехай
. Нехай  . Тоді
. Тоді  має такі нормальні підгрупи
має такі нормальні підгрупи  , що
, що  Група
Група  має такі нормальні підгрупи
має такі нормальні підгрупи  , що
, що  Тому що
Тому що  , те
, те , що й доводить рівність
, що й доводить рівність 
Лема 2.3. Для будь - якого класу  має місце включення
має місце включення 
Доказ. Якщо  ,
то
,
то  . Нехай
. Нехай  і група
і група  є підпрямим добутком груп
є підпрямим добутком груп  , де
, де  . Розглянемо функцію
. Розглянемо функцію 
 . Функція
. Функція  є гомоморфізмом групи
є гомоморфізмом групи  в групу
в групу  . Ясно, що
. Ясно, що

є добуток груп  , причому
, причому  . Отже,
. Отже,  , і лема доведена.
, і лема доведена.
Лема 2.4. 
У роботі Фишера, Гашюца й Хартли [1] уведене наступне поняття, у
деякому змісті двоїсте визначенню формації.
Визначення 2.3. Клас груп  називається класом Фиттинга, якщо він
одночасно
називається класом Фиттинга, якщо він
одночасно  - замкнутий
і
- замкнутий
і  - замкнуть.
- замкнуть.
Клас Фиттинга ми будемо надалі називати інакше радикальним класом. Через
подвійність (нормальна підгрупа – фактор - група) формацію можна було б назвати
корадикальним класом.
Визначення 2.4. Нехай  непустий
непустий  - замкнутий клас, що містить 1. Позначимо
через
- замкнутий клас, що містить 1. Позначимо
через  і назвемо
і назвемо  - радикалом групи
- радикалом групи  добуток всіх її нормальних
добуток всіх її нормальних  - підгруп.
- підгруп.
Класи  є
радикальними.
є
радикальними.  - радикал
групи
- радикал
групи  – це її підгрупа
Фиттинга
– це її підгрупа
Фиттинга 
 - радикал позначають інакше
через
- радикал позначають інакше
через  і називають
і називають  - радикалом.
- радикалом.  - радикал називають розв'язним
радикалом; зрозумілі також терміни
- радикал називають розв'язним
радикалом; зрозумілі також терміни  - нильпотентний радикал,
- нильпотентний радикал,  - замкнутий радикал і т.д. Клас усіх
- замкнутий радикал і т.д. Клас усіх
 - нильпотентних груп є
одночасно радикальним і корадикальним;
- нильпотентних груп є
одночасно радикальним і корадикальним;  – це
– це  - нильпотентний радикал групи
- нильпотентний радикал групи  .
.
Надалі ми будемо вивчати формації, замкнуті щодо тих або інших
операцій; зокрема, будуть розглядатися радикальні формації, тобто формації, що
є одночасно й класами Фиттинга. Зараз ми звернемося до задачі побудова формацій
за допомогою операцій 
Визначення 2.5. Нехай  – деяка множина груп. Нехай
– деяка множина груп. Нехай  – перетинання всіх тих формацій, які
містять
– перетинання всіх тих формацій, які
містять  клас
клас  називається формацією,
породженої множиною груп
називається формацією,
породженої множиною груп 
Помітимо, що операцію  часто позначають інакше через
часто позначають інакше через  Якщо
Якщо  те пишуть
те пишуть  замість
замість  , причому в цьому випадку
, причому в цьому випадку  називають формацією, породженою
групою
називають формацією, породженою
групою  .
.
Теорема 2.2. Для будь - якого класу  має місце рівність:
має місце рівність: 
Доказ. Якщо  ,
те
,
те , і твердження
вірно. Нехай
, і твердження
вірно. Нехай  . Тому що
. Тому що  , те клас
, те клас  є
є  - замкнутим.
- замкнутим.  є клас і
є клас і  по лемі 2.2. Використовуючи це й леми 2.3 і
2.4, одержуємо
по лемі 2.2. Використовуючи це й леми 2.3 і
2.4, одержуємо

Останнє означає  - замкнутість класу
- замкнутість класу  . Отже,
. Отже,  – формація, що містить
– формація, що містить  , тому що
, тому що  . Виходить,
. Виходить,  . Зворотне включення очевидно.
. Зворотне включення очевидно.
Лема 2.5. Для будь - яких елементів  групи
групи  виконуються рівності
виконуються рівності  Якщо
Якщо  – підгрупи групи
– підгрупи групи  , то виконуються наступні твердження:
, то виконуються наступні твердження:
1) 
2)  для
будь - якого гомоморфізму
для
будь - якого гомоморфізму  групи
групи  ; зокрема, якщо група
; зокрема, якщо група  з
з  нормалізує
нормалізує  й
й  , те
, те  нормалізує й
нормалізує й 
Лема 2.6 Нехай  – підгрупа нильпотентної групи
– підгрупа нильпотентної групи  , причому
, причому  . Тоді
. Тоді 
Доказ. Для того щоб довести лему, досить установити, що при будь - якому
натуральному  виконується
включення:
виконується
включення:

При  це
вірно, тому що
це
вірно, тому що  , а
виходить,
, а
виходить,  . Припустимо,
що включення (*) справедливо при якімсь
. Припустимо,
що включення (*) справедливо при якімсь  . Тоді, використовуючи лему 2.5, одержуємо
. Тоді, використовуючи лему 2.5, одержуємо



Тим самим (*) доведено.
Теорема 2.3 (Брайант, Брайс, Хартли [1]). Якщо  – така підгрупа групи
– така підгрупа групи  , що
, що  , то
, то 
Доказ. Нехай  –
нильпотентна нормальна підгрупа групи
–
нильпотентна нормальна підгрупа групи  , а
, а  – така підгрупа з
– така підгрупа з  , що
, що  . Доведемо індукцією по
. Доведемо індукцією по  , що
, що  . Це вірно, якщо
. Це вірно, якщо  . Тому будемо вважати, що
. Тому будемо вважати, що  . Розглянемо наступні підгрупи
прямого добутку
. Розглянемо наступні підгрупи
прямого добутку 

Очевидно, підгрупа  нормалізує
нормалізує  й
й  . Позначимо через
. Позначимо через  підгрупу групи
підгрупу групи  , породжену підгрупами
, породжену підгрупами  . Оскільки проекції
. Оскільки проекції  на множники прямого добутку
на множники прямого добутку  рівні
рівні  , те
, те  . Помітимо ще, що
. Помітимо ще, що  , де
, де  нормально в
нормально в  і нильпотентна як добуток з
і нильпотентна як добуток з  .
.
Нехай  –
центр підгрупи
–
центр підгрупи  ,
,  . Легко бачити, що
. Легко бачити, що  , причому
, причому  й
й  ; аналогічно,
; аналогічно,  і
і  . Але тоді
. Але тоді  , абелева й нормальна в.
, абелева й нормальна в.  Якщо
Якщо  , те
, те , де
, де  , і якщо
, і якщо  , те
, те , що тягне
, що тягне  . Отже,
. Отже,  . Якщо
. Якщо  абелева, те
абелева, те , і ми маємо
, і ми маємо

Припустимо тепер, що  . Ясно, що
. Ясно, що  . Тому що
. Тому що

те  нильпотентна
щабля
нильпотентна
щабля  . Тому що
. Тому що  , те
, те  ізоморфна
ізоморфна  й має щабель
й має щабель  , а тому відповідно до леми 2.6 її нормальне
замикання
, а тому відповідно до леми 2.6 її нормальне
замикання  в
в  має щабель
має щабель  . Тому що
. Тому що  нормалізує
нормалізує  й
й  , те
, те  нормальна в.
нормальна в.  Отже,
Отже,  , причому
, причому  . По індукції
. По індукції

Для групи  і
її нильпотентної нормальної підгрупи
і
її нильпотентної нормальної підгрупи  щабля
щабля  теорема також вірна по індукції. Тому
теорема також вірна по індукції. Тому

Теорема доведена.
Теорема 2.4. (Нейман [1]) Формація, породжена розв'язною групою,
містить лише кінцеве число підформацій.
Доказ. Нехай  –
підформація формації
–
підформація формації  .
Якщо
.
Якщо  , то по теоремі
2.3 має місце
, то по теоремі
2.3 має місце  , що й
потрібно.
, що й
потрібно.
Екрани
Недоліком поняття групової функції  є те, що не завжди ущільнення
є те, що не завжди ущільнення  - центрального ряду нормальними
підгрупами є
- центрального ряду нормальними
підгрупами є  - центральним
рядом.
- центральним
рядом.
Визначення 3.1. Відображення  класу
класу  всіх груп у множину класів груп назвемо
екраном, якщо для будь - якої групи
всіх груп у множину класів груп назвемо
екраном, якщо для будь - якої групи  виконуються наступні умови:
виконуються наступні умови:
1)  –
формація;
–
формація;
2)  для
будь - якого гомоморфізму
для
будь - якого гомоморфізму  групи
групи  ;
;
3)  .
.
З умови 2) випливає, що екран  приймає однакове значення на ізоморфних
групах, тобто є груповою функцією в змісті визначення 3.1. Крім того, видно, що
якщо
приймає однакове значення на ізоморфних
групах, тобто є груповою функцією в змісті визначення 3.1. Крім того, видно, що
якщо  – екран, те
кожний f - центральний ряд після видалення повторень може бути ущільнений до f
- центрального головного ряду, а виходить, клас груп, що володіють f - центральними
рядами, співпадає з формацією
– екран, те
кожний f - центральний ряд після видалення повторень може бути ущільнений до f
- центрального головного ряду, а виходить, клас груп, що володіють f - центральними
рядами, співпадає з формацією  .
.
Лема 3.1. Нехай  – екран,
– екран,  – група операторів групи
– група операторів групи  ,
,  – деяка нормальна
– деяка нормальна  - припустима підгрупа з
- припустима підгрупа з  . Якщо
. Якщо  володіє нормальним
володіє нормальним  - припустимим рядом, фактори якого
- припустимим рядом, фактори якого  - центральні відносно
- центральні відносно  , то один з таких рядів
проходить через
, то один з таких рядів
проходить через  .
.
Доказ. Нехай даний ряд, що задовольняє умові леми:

Нехай  .
Тоді ряд
.
Тоді ряд

буде шуканим. У цьому неважко переконатися, використовуючи
визначення екрана й  - ізоморфизми:
- ізоморфизми:

Лема 3.2. Справедливі наступні твердження:
1) перетинання будь - якої непустої множини екранів також є екраном;
2) об'єднання будь - якого непустого ланцюга екранів також є
екраном.
Доказ. Перше твердження очевидно. Нехай непуста множина екранів  є ланцюгом, тобто лінійно
впорядковано (з відношенням часткової впорядкованості
є ланцюгом, тобто лінійно
впорядковано (з відношенням часткової впорядкованості  , уведеним у визначенні 3.5). Тоді для будь - якої
групи
, уведеним у визначенні 3.5). Тоді для будь - якої
групи  множина формацій
множина формацій
 лінійно впорядковано
щодо включення, а отже, через лему 1.1 об'єднання
лінійно впорядковано
щодо включення, а отже, через лему 1.1 об'єднання  є формацією. Тим самим лема доведена.
є формацією. Тим самим лема доведена.
Визначення 3.2. Екран  назвемо:
назвемо:
1) p - однорідним, якщо він p - постійний і для будь - якої групи  і її силовської p –
підгрупи
і її силовської p –
підгрупи  має місце
має місце  ;
;
2) однорідним, якщо він p - однорідний для будь - якого простого p;
3) локальним, якщо він є локальною груповою функцією;
4) композиційним, якщо для будь - якої групи  має місце
має місце  , де
, де  пробігає всі фактори групи
пробігає всі фактори групи 
5) порожнім, якщо  для будь - якої неодиничної групи
для будь - якої неодиничної групи  ;
;
6)  - екраном,
якщо
- екраном,
якщо  для будь - якої
групи
для будь - якої
групи  .
.
 - екран при
- екран при
 будемо називати
одиничним екраном.
будемо називати
одиничним екраном.
Легко бачити, що кожний локальний екран є однорідним, а кожний
композиційний екран є примарно постійним.
Приклад 3.1. Нехай  і
і  – непусті формації, причому
– непусті формації, причому  , а групова функція
, а групова функція  така, що
така, що  для кожної групи
для кожної групи  й
й  для будь - який групи
для будь - який групи  . Тоді
. Тоді  – однорідний екран, що не є ні локальним, ні
композиційним.
– однорідний екран, що не є ні локальним, ні
композиційним.
Приклад 3.2. Нехай  – непуста формація, а групова функція
– непуста формація, а групова функція  така, що для будь - який
групи
така, що для будь - який
групи  виконуються
умови:
виконуються
умови:
1)  , якщо
, якщо  не має абелевих
композиційних факторів;
не має абелевих
композиційних факторів;
2)  , якщо
, якщо  має хоча б один абелев
композиційний фактор.
має хоча б один абелев
композиційний фактор.
Тоді  –
композиційний екран, що не є однорідним.
–
композиційний екран, що не є однорідним.
Зауваження 1. Локальний екран повністю визначається своїми
значеннями на підгрупах. Щоб побудувати локальний екран  , досить кожному простому числу
, досить кожному простому числу  поставити у відповідність
деяку формацію
поставити у відповідність
деяку формацію  , а
потім для будь - якої групи
, а
потім для будь - якої групи  покласти
покласти  , де
, де  пробігає
пробігає  .
.
Зауваження 2. Щоб побудувати композиційний екран  , потрібно кожній простій групі
, потрібно кожній простій групі  поставити у відповідність
деяку формацію
поставити у відповідність
деяку формацію  , а
потім для будь - якої групи
, а
потім для будь - якої групи  покласти
покласти  , де
, де  пробігає всі композиційні фактори групи
пробігає всі композиційні фактори групи  .
.
Лема 3.3. Справедливі наступні твердження: 1) перетинання будь - якої
непустої множини однорідних екранів знову є однорідним екраном;
2) перетинання будь - якої непустої множини локальних екранів знову
є локальним екраном;
3) перетинання будь - якої непустої множини композиційних екранів
знову є композиційним екраном.
Доказ. Нехай екран  є перетинанням множини екранів
є перетинанням множини екранів  . Припустимо, що всі екрани
. Припустимо, що всі екрани  є локальними, тобто для
будь - яких
є локальними, тобто для
будь - яких  і
і  має місце рівність:
має місце рівність:
де  пробігає
всі підгрупи групи
пробігає
всі підгрупи групи  .
Тоді
.
Тоді

а виходить,  –
локальний екран.
–
локальний екран.
Лема 3.4. Об'єднання будь - якого непустого ланцюга примарно
постійних екранів є примарно постійним екраном.
Доказ. Нехай  –
деякий ланцюг екранів,
–
деякий ланцюг екранів,  –
її об'єднання,
–
її об'єднання,  . По
лемі 3.3 функція
. По
лемі 3.3 функція  є
екраном, причому ясно, що постійність
є
екраном, причому ясно, що постійність  тягне постійність екрана
тягне постійність екрана  . Припустимо, що все
. Припустимо, що все  є однорідними екранами. Тоді, якщо
є однорідними екранами. Тоді, якщо  – будь - яка група й
– будь - яка група й  , те
, те  . Отже,
. Отже,

що й доводить однорідність екрана  .
.
Екрани формацій
Кожної групової функції  відповідає формація
відповідає формація  .
.
Лема 3.5.  є
непустою формацією для будь - якої групової функції
є
непустою формацією для будь - якої групової функції  .
.
Визначення 3.3. Нехай  – деяка формація. Якщо
– деяка формація. Якщо  – такий екран, що
– такий екран, що  , то формація
, то формація  називається східчастою формацією,
причому в цьому випадку будемо говорити, що
називається східчастою формацією,
причому в цьому випадку будемо говорити, що
 – екран
формації
– екран
формації  ,
,
 має екран
має екран  ,
,
екран  визначає
формацію
визначає
формацію  ,
,
 визначається
екраном
визначається
екраном  .
.
Формація  має
одиничний екран. Одинична формація
має
одиничний екран. Одинична формація  має порожній екран.
має порожній екран.
Визначення 3.4. Екран  назвемо внутрішнім, якщо
назвемо внутрішнім, якщо  – внутрішня групова функція, тобто
– внутрішня групова функція, тобто  для будь - якої неодиничної
групи
для будь - якої неодиничної
групи  .
.
Лема 3.6. Кожна східчаста формація має принаймні один екран.
Доказ. Нехай  –
екран формації
–
екран формації  .
Визначимо функцію
.
Визначимо функцію  в такий
спосіб:
в такий
спосіб:  для будь - якої
групи
для будь - якої
групи  . Легко бачити,
що
. Легко бачити,
що  – екран, причому
– екран, причому  . Якщо
. Якщо  й
й  – головний фактор групи
– головний фактор групи  , то
, то  . Тому що клас
. Тому що клас 
 - замкнуть, те
- замкнуть, те , а виходить,
, а виходить, 
 - центральний
- центральний  Таким чином,
Таким чином,  . Отже,
. Отже,  , тобто
, тобто  – шуканий внутрішній екран.
– шуканий внутрішній екран.
Лема 3.7. Нехай  – екран формації
– екран формації  . Тоді
. Тоді  є екраном формації
є екраном формації  .
.
Доказ. Нехай  –
довільний головний фактор групи
–
довільний головний фактор групи  . Нехай
. Нехай  . Тому що
. Тому що  , те
, те  . Виходить,
. Виходить,  , тобто
, тобто 
 - в.
- в.  Звідси треба, що
Звідси треба, що  .
.
Обернено, якщо  , те головний ряд групи
, те головний ряд групи  буде
буде  - центральним для будь - якого
- центральним для будь - якого  , тобто
, тобто  . Отже,
. Отже,  .
.
Лема 3.8. Перетинання  будь - якої непустої множини
будь - якої непустої множини  екранів формації
екранів формації  знову є екраном формації
знову є екраном формації  . Крім того, якщо в
. Крім того, якщо в  є хоча б один внутрішній
екран, те
є хоча б один внутрішній
екран, те  – внутрішній
екран.
– внутрішній
екран.
Доказ. Те, що  –
екран формації
–
екран формації  ,
безпосередньо треба з леми 3.7. Нехай у
,
безпосередньо треба з леми 3.7. Нехай у  є внутрішній екран
є внутрішній екран  . Тоді
. Тоді  для будь - якої групи
для будь - якої групи  . Виходить,
. Виходить,  – внутрішній екран.
– внутрішній екран.
Формація з однорідним екраном
Теорема 3.1. (Шеметков) Усяка формація, що має принаймні один
однорідний екран, є локальною формацією.
Доказ. Нехай формація  має однорідний екран. Через лему 3.6 формація
має однорідний екран. Через лему 3.6 формація  має внутрішній однорідний
екран
має внутрішній однорідний
екран  . Побудуємо
локальний екран
. Побудуємо
локальний екран  , що
задовольняє наступній умові:
, що
задовольняє наступній умові:  для будь - якого простого
для будь - якого простого  . Тоді
. Тоді  й, отже,
й, отже,  . Припустимо, що формація
. Припустимо, що формація  має групи, що не входять в
має групи, що не входять в  , і виберемо серед всіх
таких груп групу
, і виберемо серед всіх
таких груп групу  , що
має найменший порядок. Тоді
, що
має найменший порядок. Тоді  є єдиною мінімальною нормальною підгрупою
групи
є єдиною мінімальною нормальною підгрупою
групи  . Тому що
. Тому що  , те для кожного
, те для кожного  має місце
має місце

Якщо  неабелева,
то
неабелева,
то  й
й  . Якщо ж
. Якщо ж  –
–  - група, то виходить, що
- група, то виходить, що 
 - центральна в.
- центральна в.  А це суперечить тому, що
А це суперечить тому, що  . Теорема доведена.
. Теорема доведена.
Локальна формація
Неодинична формація, що має локальний екран, містить деякі
неодиничні групи.
Визначення 4.1. Формація  називається локальної, якщо вона має хоча б
один локальний екран.
називається локальної, якщо вона має хоча б
один локальний екран.
Визначення 4.2. Нехай  – внутрішній локальний екран формації
– внутрішній локальний екран формації  , що є максимальним
елементом множини всіх внутрішніх локальних екранів формації
, що є максимальним
елементом множини всіх внутрішніх локальних екранів формації  . Тоді
. Тоді  називається максимальним внутрішнім локальним
екраном формації
називається максимальним внутрішнім локальним
екраном формації  .
.
Теорема 4.1. (Картер і Хоукс [1], Шмид [5]). Локальна формація  має єдиний максимальний
внутрішній локальний екран
має єдиний максимальний
внутрішній локальний екран  , причому
, причому  задовольняє наступній умові:
задовольняє наступній умові:  для будь - якого простого числа p.
для будь - якого простого числа p.
Визначення 4.3. Нехай  – локальна формація. Мінімальний елемент
множини всіх локальних екранів формації
– локальна формація. Мінімальний елемент
множини всіх локальних екранів формації  назвемо мінімальним локальним екраном формації
назвемо мінімальним локальним екраном формації
 .
.
Теорема 4.2. Локальна формація має єдиний мінімальний локальний
екран, що є до того ж внутрішнім екраном.
Доказ. Нехай  –
множина всіх локальних екранів формації
–
множина всіх локальних екранів формації  , причому
, причому  . Позначимо через
. Позначимо через  перетинання множини екранів
перетинання множини екранів  . У множині
. У множині  є внутрішній екран, тому
є внутрішній екран, тому  – внутрішній екран формації
– внутрішній екран формації  . По лемі 3.4 екран
. По лемі 3.4 екран  є локальним. Через лему 3.8
є локальним. Через лему 3.8
 – шуканий екран.
– шуканий екран.
Побудова локальних формацій
1. Формація всіх груп. Формація  має локальний екран
має локальний екран  таким, що
таким, що  для будь - якого простого
для будь - якого простого  .
.
2. Формація одиничних груп. Формація  має порожній екран, що, мабуть, локальний.
має порожній екран, що, мабуть, локальний.
3. Формація нильпотентних  - груп. Нехай
- груп. Нехай  – формація всіх нильпотентних
– формація всіх нильпотентних  - груп,
- груп,  – такий локальний екран, що
– такий локальний екран, що  для кожного
для кожного  для кожного
для кожного  . Очевидно,
. Очевидно,  – мінімальний локальний екран формації
– мінімальний локальний екран формації  .
.
4. Формація  -
груп. Нехай
-
груп. Нехай  – формація
всіх
– формація
всіх  - груп,
- груп,  – такий локальний екран, що
– такий локальний екран, що
 для кожного
для кожного  для кожного
для кожного  . Очевидно,
. Очевидно,  –локальний екран формації
–локальний екран формації  .
.
5. Формація  -
нильпотентних груп. Нехай
-
нильпотентних груп. Нехай  – формація всіх
– формація всіх  - нильпотентних груп (
- нильпотентних груп ( – фіксоване простої число),
– фіксоване простої число),  – такий локальний екран, що
– такий локальний екран, що  для будь - якого простого
числа
для будь - якого простого
числа  , відмінного від
, відмінного від  . Покажемо, що
. Покажемо, що  – екран формації
– екран формації  . Головний ряд
. Головний ряд  - нильпотентної групи
- нильпотентної групи  - центральний. Нехай
- центральний. Нехай  . Потрібно встановити, що
. Потрібно встановити, що 
 - нильпотентна. Нехай
- нильпотентна. Нехай  – мінімальна нормальна підгрупа групи
– мінімальна нормальна підгрупа групи  . По індукції
. По індукції 
 - нильпотентна. Якщо
- нильпотентна. Якщо  –
–  - група, то звідси треба, що й
- група, то звідси треба, що й 
 - нильпотентна. Якщо ж
- нильпотентна. Якщо ж  - група, те
- група, те , тобто
, тобто  . Якщо тепер
. Якщо тепер  –
–  - підгрупа з
- підгрупа з  , то через
, то через  підгрупа
підгрупа 
 - нильпотентна, а виходить, і
- нильпотентна, а виходить, і 
 - нильпотентна. Тим самим показано, що
- нильпотентна. Тим самим показано, що  .
.
Теорема 5.1. У кожній  - групі
- групі  підгрупа
підгрупа  збігається з перетинанням у
збігається з перетинанням у  всіх головних
всіх головних  - факторів групи
- факторів групи  .
.
Наслідок 5.1.1. У будь - якій групі  підгрупа Фиттинга
підгрупа Фиттинга  збігається з перетинанням у
збігається з перетинанням у  всіх головних факторів групи
всіх головних факторів групи  .
.
Наслідок 5.1.2. Для кожної  - розв'язної групи
- розв'язної групи  має місце включення
має місце включення  .
.
Наслідок 5.1.3. (Фиттинг).  для будь - якої розв'язної групи
для будь - якої розв'язної групи  .
.
Наслідок 5.1.4. (Чунихин [3]). Комутант  - групи
- групи  - нильпотентний.
- нильпотентний.
6. Формація  -
замкнутих груп. Нехай
-
замкнутих груп. Нехай  –
формація всіх
–
формація всіх  - замкнутих
груп (
- замкнутих
груп ( – деяка
фіксована множина простих чисел),
– деяка
фіксована множина простих чисел),  – такий локальний екран, що
– такий локальний екран, що  для кожного
для кожного  для кожного
для кожного  . Покажемо, що
. Покажемо, що  – екран формації
– екран формації  .
.
Очевидно,  .
Припустимо, що клас
.
Припустимо, що клас  не
порожній, і виберемо в ньому групу
не
порожній, і виберемо в ньому групу  найменшого порядку. Тоді
найменшого порядку. Тоді  має єдину мінімальну нормальну
підгрупу
має єдину мінімальну нормальну
підгрупу  , причому
, причому  не є
не є  - групою. Нехай
- групою. Нехай  . Тому що
. Тому що  , те
, те , а виходить,
, а виходить,  . Тому
. Тому  – абелева
– абелева  - група. Тому що
- група. Тому що 
 - замкнута, те й
- замкнута, те й 
 - замкнута, тобто
- замкнута, тобто  має нормальну
має нормальну  - підгрупу
- підгрупу  . Ясно, що
. Ясно, що  . Тому що
. Тому що  , те
, те  . Легко бачити, що
. Легко бачити, що  , а виходить, і група
, а виходить, і група 
 - замкнута. Тим самим показано, що
- замкнута. Тим самим показано, що  .
.
7. Формація  -
дисперсивних груп. Нехай
-
дисперсивних груп. Нехай  –
деяке лінійне впорядкування множини всіх простих чисел,
–
деяке лінійне впорядкування множини всіх простих чисел,  – формація всіх
– формація всіх  - дисперсивних груп. Покажемо, що
- дисперсивних груп. Покажемо, що  локально.
локально.
Розглянемо всілякі множини  простих чисел, що володіють наступною
властивістю:
простих чисел, що володіють наступною
властивістю:  для всіх
для всіх  . Нехай
. Нехай  – формація всіх
– формація всіх  - замкнутих груп. Очевидно,
- замкнутих груп. Очевидно,  . Тому що формації
. Тому що формації  локальні, то по лемі 3.4
формація
локальні, то по лемі 3.4
формація  також є
локальною.
також є
локальною.
8. Формація  -
розв'язних груп. Нехай
-
розв'язних груп. Нехай  –
формація всіх
–
формація всіх  - розв'язних
груп,
- розв'язних
груп,  – такий
локальний екран, що
– такий
локальний екран, що  для
будь - якого простого
для
будь - якого простого  .
Неважко помітити, що
.
Неважко помітити, що  –
максимальний внутрішній локальний екран формації
–
максимальний внутрішній локальний екран формації  . Зокрема, формація
. Зокрема, формація  є локальною.
є локальною.
9. Формація  -
груп. Нехай
-
груп. Нехай  – формація
всіх
– формація
всіх  - груп. Позначимо
через
- груп. Позначимо
через  формацію всіх абелевих
груп експоненти, що ділить
формацію всіх абелевих
груп експоненти, що ділить  . Побудуємо локальний екран
. Побудуємо локальний екран  такий, що
такий, що  для кожного
для кожного  для кожного
для кожного  . Покажемо, що
. Покажемо, що  . Ясно, що
. Ясно, що  . Нехай
. Нехай  ,
,  – мінімальна нормальна підгрупа групи
– мінімальна нормальна підгрупа групи  . По індукції
. По індукції  . Якщо
. Якщо  –
–  - група, то
- група, то 
 - понад розв'язна. Нехай порядок
- понад розв'язна. Нехай порядок  ділиться на деяке число
ділиться на деяке число  . Тоді, якщо
. Тоді, якщо  , те
, те

Звідси треба, що  –
–  - група.
- група.
Лема 5.1. Нехай  – деяка що не приводиться абелева група
автоморфизмів
– деяка що не приводиться абелева група
автоморфизмів  - групи
- групи  й
й  . Тоді
. Тоді  – циклічна група порядку, що ділить
– циклічна група порядку, що ділить  . Крім того,
. Крім того,  – найменше натуральне число, що
задовольняє порівнянню
– найменше натуральне число, що
задовольняє порівнянню  .
.
Доказ. Будемо вважати, що  – аддитивна абелева група. Тоді
– аддитивна абелева група. Тоді  можна розглядати як правий векторний
простір розмірності
можна розглядати як правий векторний
простір розмірності  над
полем
над
полем  з
з  елементів. Нехай
елементів. Нехай  – комутативне підкольцо кільця
– комутативне підкольцо кільця  , породжене елементами
, породжене елементами  й
й  . Через умову
. Через умову  є правим
є правим  - модулем (визначення, пов'язані з
- модулем (визначення, пов'язані з  - модулями, див. у Кертиса
й Райнера [1]). По лемі Шура,
- модулями, див. у Кертиса
й Райнера [1]). По лемі Шура,  – тіло. Тому що
– тіло. Тому що  комутативне, те
комутативне, те  . Легко бачити, що множина всіх ненульових
елементів із
. Легко бачити, що множина всіх ненульових
елементів із  замкнуто
щодо операції множення й, отже, є групою. Тому
замкнуто
щодо операції множення й, отже, є групою. Тому  – поле. Тому що
– поле. Тому що  - модуль не
- модуль не  приводимо, те
приводимо, те  для будь - якого ненульового
для будь - якого ненульового  ; але тоді відображення
; але тоді відображення  , є
, є  - гомоморфізмом
- гомоморфізмом  - модуля
- модуля  на
на  . Тому що ядро
. Тому що ядро  є ідеал поля
є ідеал поля  , те
, те  – ізоморфізм. Отже,
– ізоморфізм. Отже,  . Відомо, що мультиплікативна група кінцевого
поля циклічна. Тому
. Відомо, що мультиплікативна група кінцевого
поля циклічна. Тому  циклічна
й
циклічна
й  ділить
ділить  .
.
Нехай  –
найменше натуральне число, що задовольняє порівнянню
–
найменше натуральне число, що задовольняє порівнянню  . Тоді
. Тоді  ділить
ділить  . Добре відомо, що поле
. Добре відомо, що поле  порядку
порядку  містить
містить  порядку
порядку  . Тому що циклічна група містить точно одну
підгрупу кожного можливого порядку й
. Тому що циклічна група містить точно одну
підгрупу кожного можливого порядку й  ділить
ділить , то
, то  . Але тоді
. Але тоді  й
й  . Лема доведена.
. Лема доведена.
10. Формація  .
Нехай
.
Нехай  – непуста
формація,
– непуста
формація,  – такий
локальний екран, що
– такий
локальний екран, що  для
будь - якого простого
для
будь - якого простого  .
Застосовуючи наслідок 7.1.1 можна побачити, що
.
Застосовуючи наслідок 7.1.1 можна побачити, що  – екран формації
– екран формації  . Зокрема, формації
. Зокрема, формації  і
і  є локальними формаціями.
є локальними формаціями.
Нехай  –
локальний екран деякої підформації
–
локальний екран деякої підформації  з
з  . Застосовуючи леми 3.3 і 4.3, бачимо, що
. Застосовуючи леми 3.3 і 4.3, бачимо, що  є локальним
є локальним  - екраном формації
- екраном формації  . Таким чином, кожна локальна підформація
формації
. Таким чином, кожна локальна підформація
формації  має
внутрішній локальний
має
внутрішній локальний  -
екран. Зокрема, будь - яка локальна підформація формації
-
екран. Зокрема, будь - яка локальна підформація формації  має внутрішній локальний
має внутрішній локальний  - екран.
- екран.
Локальні формації із заданими властивостями
Нехай  –
деяка операція,
–
деяка операція,  –
локальний екран формації
–
локальний екран формації  .
Природно виникають два питання:
.
Природно виникають два питання:
1) чи Буде 
 - замкнутої, якщо
- замкнутої, якщо 
 - замкнута для будь - якого простого
- замкнута для будь - якого простого  ?
?
2) чи Буде 
 - замкнутої для будь - якого
простого
- замкнутої для будь - якого
простого  , якщо
, якщо 
 - замкнута?
- замкнута?
Ми дамо позитивну відповідь на ці питання в деяких конкретних
випадках.
Теорема Слепова 1 Нехай  – деякий клас груп,
– деякий клас груп,  – максимальний внутрішній локальний екран
формації
– максимальний внутрішній локальний екран
формації  ,
,  – фіксоване простої число.
Тоді справедливі наступні твердження:
– фіксоване простої число.
Тоді справедливі наступні твердження:
1) якщо  ,
те
,
те  ;
;
2) якщо  ,
те
,
те  .
.
Доказ. Будемо доводити обоє твердження одночасно. Нехай  – одна з операцій
– одна з операцій  ,
,  . Припустимо, що
. Припустимо, що  . Нехай
. Нехай  – (нормальна) підгрупа групи
– (нормальна) підгрупа групи  й
й  . Розглянемо регулярне сплетення
. Розглянемо регулярне сплетення  , де
, де  ,
,  – елементарна абелева
– елементарна абелева  - група. По лемі 3.11.
- група. По лемі 3.11.  Тому що
Тому що  , те
, те  . Розглянемо головний ряд групи
. Розглянемо головний ряд групи  :
:
Нехай  .
Тому що
.
Тому що  й
й  , те
, те

для кожного  .
Отже,
.
Отже,  , де
, де  . По властивості
регулярного сплетення
. По властивості
регулярного сплетення  .
Отже,
.
Отже,  , і по лемі 3.10
підгрупа
, і по лемі 3.10
підгрупа  є
є  - групою. Тому що
- групою. Тому що  й формація
й формація  є по теоремі 3.3
є по теоремі 3.3  - замкнутої, то ми одержуємо, що
- замкнутої, то ми одержуємо, що  . Теорема доведена.
. Теорема доведена.
Теорема Подуфалова, Слепова 2 Нехай  – максимальний внутрішній
локальний екран формації
– максимальний внутрішній
локальний екран формації  .
Формація
.
Формація 
 - замкнута (
- замкнута ( - замкнута) тоді й тільки тоді,
коли для будь - якого простого
- замкнута) тоді й тільки тоді,
коли для будь - якого простого  формація
формація 
 - замкнута (відповідно
- замкнута (відповідно  - замкнута).
- замкнута).
Доказ. Необхідність. Припустимо, що 
 - замкнуто (
- замкнуто ( - замкнута). Думаючи
- замкнута). Думаючи  й застосовуючи теорему , ми одержуємо, що
й застосовуючи теорему , ми одержуємо, що 
 - замкнуто (
- замкнуто ( - замкнута) для будь - якого простого
- замкнута) для будь - якого простого  .
.
Достатність. Нехай для будь - якого простого  формація
формація  є
є  - замкнутою (
- замкнутою ( - замкнутої). Нехай
- замкнутої). Нехай  – підгрупа (нормальна підгрупа) неодиничної
групи
– підгрупа (нормальна підгрупа) неодиничної
групи  . Покажемо, що
. Покажемо, що  . Тому що
. Тому що  , те
, те  володіє
володіє  - центральним головним рядом
- центральним головним рядом

Нехай  . Тому
що
. Тому
що

те , де
, де  . Нехай
. Нехай  . За умовою
. За умовою  й
й  . Звідси, через
. Звідси, через  , випливає, що
, випливає, що  . Тим самим установлено, що ряд
. Тим самим установлено, що ряд

є  - центральним
рядом групи
- центральним
рядом групи  . Теорема
доведена.
. Теорема
доведена.
Для будь - якого натурального числа 
 - замкнутий клас
- замкнутий клас  містить, по визначенню, кожну групу
містить, по визначенню, кожну групу  , у вигляді добутку
, у вигляді добутку  нормальних
нормальних  - підгруп. Послабляючи цю вимогу, ми
приходимо до наступного визначення.
- підгруп. Послабляючи цю вимогу, ми
приходимо до наступного визначення.
Визначення. Клас груп  назвемо слабко
назвемо слабко  - замкнутим,
- замкнутим,  , якщо
, якщо  містить усяку групу
містить усяку групу  , що має
, що має  нормальних
нормальних  - підгруп з попарно взаємно простими
індексами.
- підгруп з попарно взаємно простими
індексами.
Легко помітити, що якщо  й
й  – підгрупи групи
– підгрупи групи  причому
причому  й
й  взаємно прості, те
взаємно прості, те  .
.
Теорема Слепова 3 Нехай  – локальний екран формації
– локальний екран формації  й нехай для деякого натурального
числа
й нехай для деякого натурального
числа  виконується
наступна умова: для будь - якого простого
виконується
наступна умова: для будь - якого простого  формація
формація  або збігається з
або збігається з  , або входить в
, або входить в  і є слабко
і є слабко  - замкнутою. Тоді
- замкнутою. Тоді  слабко
слабко  - замкнута.
- замкнута.
Доказ. Припустимо, що теорема невірна. Тоді існують групи, що не
входять в  , але
, але  нормальних
нормальних  - підгруп з попарно взаємно простими
індексами. Виберемо серед всіх таких груп групу
- підгруп з попарно взаємно простими
індексами. Виберемо серед всіх таких груп групу  найменшого порядку. Таким чином,
найменшого порядку. Таким чином,  не належить
не належить  , але має нормальні
, але має нормальні  - підгрупи
- підгрупи  з попарно взаємно простими індексами. Ясно, що
всі підгрупи
з попарно взаємно простими індексами. Ясно, що
всі підгрупи  неодиничні.
неодиничні.
Нехай  –
мінімальна нормальна підгрупа групи
–
мінімальна нормальна підгрупа групи  . У
. У  підгрупи
підгрупи  мають попарно взаємно прості індекси й
належать
мають попарно взаємно прості індекси й
належать  . Тому що для
. Тому що для  теорема вірна, те
теорема вірна, те  . Ясно, що
. Ясно, що  – єдина мінімальна нормальна
підгрупа групи
– єдина мінімальна нормальна
підгрупа групи  ,
причому
,
причому  й
й  для кожного
для кожного  . Через теорему 4.3.
. Через теорему 4.3.  Тому що
Тому що  , те найдеться таке
, те найдеться таке  , що
, що  . Розглянемо
. Розглянемо  , де
, де  пробігає все
пробігає все  - головні фактори групи
- головні фактори групи  . Тому що
. Тому що  , те
, те ,
,  . Можливі два випадки.
. Можливі два випадки.
Випадок 1. Нехай  . Тоді
. Тоді  неабелева й
неабелева й  . Звідси й з одиничності
. Звідси й з одиничності  випливає, що
випливає, що  . Але тоді
. Але тоді  й, отже,
й, отже,  можна розглядати як деяку групу групи
можна розглядати як деяку групу групи  , що діє тотожно на всіх
, що діє тотожно на всіх  - головних факторах групи
- головних факторах групи  . По добре відомій теоремі
Ф. Холу
. По добре відомій теоремі
Ф. Холу  нильпотентна.
Тому що
нильпотентна.
Тому що  до того ж
нормальна в
до того ж
нормальна в  , те
, те  . Але тоді
. Але тоді  для будь - якого
для будь - якого  , а тому що формація
, а тому що формація  слабко
слабко  - замкнута за умовою, те
- замкнута за умовою, те  . Але тоді
. Але тоді  , тому що
, тому що  й за умовою
й за умовою  . Одержали протиріччя.
. Одержали протиріччя.
Випадок 2. Нехай  . Тоді
. Тоді  входить в
входить в  і є
і є  - групою. Тому що
- групою. Тому що  , те
, те  абелева. Нехай
абелева. Нехай  – максимальна підгрупа групи
– максимальна підгрупа групи  , не утримуюча
, не утримуюча  . Тоді
. Тоді  ,
,  ,
,  ,
,  . Звідси, через одиничність
. Звідси, через одиничність  , містимо, що
, містимо, що  , a виходить,
, a виходить,  . По лемі 3.10
. По лемі 3.10  є
є  - групою. Але тоді і
- групою. Але тоді і  є
є  - групою, причому
- групою, причому  . Ми одержуємо, таким чином, що
. Ми одержуємо, таким чином, що  для кожного
для кожного  . Але тоді
. Але тоді  , тому що
, тому що  слабко
слабко  - замкнута. Останнє означає, що
- замкнута. Останнє означає, що 
 - центральна в
- центральна в  , що суперечить рівності
, що суперечить рівності  . Знову одержали протиріччя.
. Знову одержали протиріччя.
Теорема доведена.
Наслідок 4 Нехай група  має дві нормальні
має дві нормальні  - понад розв'язні підгрупи, індекси яких
взаємно прості. Тоді
- понад розв'язні підгрупи, індекси яких
взаємно прості. Тоді 
 - понадрозв'язна.
- понадрозв'язна.
Для того щоб одержати цей наслідок, досить помітити, що побудований
екран задовольняє умові теореми при  .
.
Наслідок 5 Нехай група  має дві нормальні підгрупи, індекси яких
взаємно прості. Тоді
має дві нормальні підгрупи, індекси яких
взаємно прості. Тоді  понад
розв'язна .
понад
розв'язна .
Теорема Слепова 6 Нехай формація  має такий локальний екран
має такий локальний екран  , що для будь - якого
простого
, що для будь - якого
простого  формація
формація  або збігається з
або збігається з  , або входить в
, або входить в  і є
і є  - замкнутою. Тоді
- замкнутою. Тоді 
 - замкнута.
- замкнута.
Доказ. Повторюємо з очевидними змінами доказ теореми .
Теорема Слепова 7 Нехай  – максимальний внутрішній локальний екран
формації
– максимальний внутрішній локальний екран
формації  . Формація
. Формація 
 - замкнута (слабко
- замкнута (слабко  - замкнута,
- замкнута,  ) тоді й тільки тоді, коли для будь - якого
простого
) тоді й тільки тоді, коли для будь - якого
простого  формація
формація 
 - замкнута (відповідно слабко
- замкнута (відповідно слабко  - замкнута).
- замкнута).
Доказ. Достатність випливає з теорем і . Нехай 
 - замкнута (слабко
- замкнута (слабко  - замкнута,
- замкнута,  ). Нехай
). Нехай  , де
, де  – нормальні
– нормальні  - підгрупи (нормальні
- підгрупи (нормальні  - підгрупи з попарно взаємно простими
індексами). Тому що
- підгрупи з попарно взаємно простими
індексами). Тому що  ,
те
,
те  . Покажемо, що
. Покажемо, що  .
.
Нехай  , де
, де  ,
,  – елементарна абелева
– елементарна абелева  - група.
- група.  для кожного
для кожного  . Тому що
. Тому що 
 - замкнута (слабко
- замкнута (слабко  - замкнута), те звідси випливає, що
- замкнута), те звідси випливає, що  . Якщо
. Якщо  – перетинання в
– перетинання в  усіх
усіх  - головних факторів групи
- головних факторів групи  , то
, то

Тому що  , те
по лемі 3.10 підгрупа
, те
по лемі 3.10 підгрупа  є
є
 - групою. Але тоді
- групою. Але тоді  , тому що по теоремі 3.3
має місце рівність
, тому що по теоремі 3.3
має місце рівність  .
.
Теорема доведена.
Лема Чунихина 8 Нехай  ,
,  ,
,  . Тоді
. Тоді  . Зокрема, якщо
. Зокрема, якщо  й
й  , те
, те  непроста.
непроста.
Доказ. З рівності  треба, що
треба, що

Отже,  .
Звідси, через
.
Звідси, через  для
кожного
для
кожного  , одержуємо
, одержуємо  . Лема доведена.
. Лема доведена.
Теорема Виландт 9 Група  розв'язна, якщо вона має три розв'язні
підгрупи, індекси яких у
розв'язна, якщо вона має три розв'язні
підгрупи, індекси яких у  попарно
взаємно прості.
попарно
взаємно прості.
Доказ. Нехай група  має розв'язні підгрупи
має розв'язні підгрупи  ,
,  і
і  з попарно взаємно простими індексами. Тоді
з попарно взаємно простими індексами. Тоді  . Нехай
. Нехай  – мінімальна нормальна підгрупа з
– мінімальна нормальна підгрупа з  . Тому що
. Тому що  розв'язно, те
розв'язно, те ,
,  – простої число. Через умову теореми,
– простої число. Через умову теореми,  не ділить одночасно
не ділить одночасно  й
й  . Нехай, для визначеності,
. Нехай, для визначеності,  не ділить
не ділить  . Це значить, що силовська
. Це значить, що силовська  - підгрупа з
- підгрупа з  є силовською
є силовською  - підгрупою групи
- підгрупою групи  . Через теорему Силова
. Через теорему Силова  , де
, де  . Тому що
. Тому що  й
й  , те по лемі
, те по лемі  . Таким чином,
. Таким чином,  – неодинична розв'язна нормальна підгрупа
групи
– неодинична розв'язна нормальна підгрупа
групи  . У фактор - групі
. У фактор - групі
 індекси підгруп
індекси підгруп  ,
,  і
і  попарно взаємно прості. По індукції
попарно взаємно прості. По індукції  розв'язна, але тоді й
розв'язна, але тоді й  розв'язна. Теорема доведена.
розв'язна. Теорема доведена.
Випливаючи Крамеру, уведемо наступне визначення.
Визначення. Клас груп  називається
називається  - замкнутим (
- замкнутим ( – натуральне число), якщо
– натуральне число), якщо  містить усяку групу
містить усяку групу  , що має
, що має 
 - підгруп, індекси яких у
- підгруп, індекси яких у  при
при  попарно взаємно прості.
попарно взаємно прості.
По визначенню, порожня формація  - замкнута для кожного
- замкнута для кожного  . Єдиної
. Єдиної  - замкнутою непустою формацією, відмінної від
- замкнутою непустою формацією, відмінної від  , умовимося вважати
, умовимося вважати  .
.
Лема 10 Нехай  і
і  –
–  - замкнуті класи груп. Тоді
- замкнуті класи груп. Тоді  також
також  - замкнуть.
- замкнуть.
Доказ очевидно.
Наступна лема доведена Крамером.
Лема 11 Нехай формація  втримується в
втримується в  і
і  - замкнута,
- замкнута,  . Тоді формація
. Тоді формація  є
є  - замкнутою.
- замкнутою.
Доказ. Нехай група  має
має  - підгрупи
- підгрупи  ,
,  ,…,
,…, ,індекси яких у
,індекси яких у  попарно взаємно прості. Тому що
попарно взаємно прості. Тому що  , те по теоремі група
, те по теоремі група  розв'язна. При будь - якому
гомоморфізмі групи
розв'язна. При будь - якому
гомоморфізмі групи  образи
підгрупи
образи
підгрупи  належать
належать  і мають попарно взаємно
прості індекси. Тому можна вважати, що
і мають попарно взаємно
прості індекси. Тому можна вважати, що  - корадикал
- корадикал  групи
групи  є її єдиною мінімальною нормальною підгрупою.
Ясно, що
є її єдиною мінімальною нормальною підгрупою.
Ясно, що  є
є  - групою для якогось
- групою для якогось  . Підгрупа Фиттинга
. Підгрупа Фиттинга  групи
групи  також є
також є  - групою. Індекс будь - якої підгрупи, що не
містить
- групою. Індекс будь - якої підгрупи, що не
містить  , ділиться на
, ділиться на  . Тому
. Тому  втримується принаймні в
втримується принаймні в  підгрупах нашої системи
підгруп
підгрупах нашої системи
підгруп  . Будемо
вважати, що
. Будемо
вважати, що  ,
,  . Тому що
. Тому що  є
є  - групою, те
- групою, те  й
й  ,
,  . Звідси й з наслідку випливає, що
. Звідси й з наслідку випливає, що  ,
,  . Тому що
. Тому що  , те ми одержуємо, що
, те ми одержуємо, що  ,
,  . Скориставшись
. Скориставшись  - замкнутістю формації
- замкнутістю формації  , ми приходимо до того, що
, ми приходимо до того, що  .
.
Лема доведена.
Теорема Крамер 12 Нехай  – такий локальний
– такий локальний  - екран формації
- екран формації  , що для будь - якого простого
, що для будь - якого простого  формація
формація 
 - замкнута,
- замкнута,  . Тоді
. Тоді 
 - замкнута.
- замкнута.
Доказ. Тому що  –
–  - екран, то
- екран, то  для будь - якого простого
для будь - якого простого  , а виходить,
, а виходить,  . Нехай
. Нехай  . Через лему 4.5.
. Через лему 4.5.  Якщо
Якщо  , те
, те  й
й 
 - замкнута; якщо ж
- замкнута; якщо ж  , те по лемі формація
, те по лемі формація 
 - замкнута. У кожному разі
- замкнута. У кожному разі 
 - замкнута. По лемі
- замкнута. По лемі 
 - замкнута. Застосовуючи лему , ми бачимо, що й формація
- замкнута. Застосовуючи лему , ми бачимо, що й формація 
 - замкнута. Теорема
доведена.
- замкнута. Теорема
доведена.
Тому що формація  має одиничний екран, що задовольняє умові
теореми при
має одиничний екран, що задовольняє умові
теореми при  , те ми
одержуємо
, те ми
одержуємо
Наслідок Кегель 13 Група  нилъпотентна, якщо вона має три нильпотентні
підгрупи, індекси яких у
нилъпотентна, якщо вона має три нильпотентні
підгрупи, індекси яких у  попарно
взаємно прості.
попарно
взаємно прості.
Цей факт випливає також і з наступного результату Кегля.
Лема 14 Клас усіх  - замкнутих груп
- замкнутих груп  - замкнуть.
- замкнуть.
Доказ таке ж, як і в теореми .
Лема 15 Кожна формація нильпотентних груп є  - замкнутою.
- замкнутою.
Доказ. Нехай  –
деяка формація нильпотентних груп. Нехай група
–
деяка формація нильпотентних груп. Нехай група  має
має  - підгрупи
- підгрупи  ,
,  і
і  з попарно взаємно простими індексами. Тоді по
наслідку група
з попарно взаємно простими індексами. Тоді по
наслідку група  нильпотентна.
Якщо
нильпотентна.
Якщо  – найвищий
ступінь простого числа
– найвищий
ступінь простого числа  ,
що ділить
,
що ділить  , то
, то  ділить
ділить  для деякого
для деякого  , тому що
, тому що  не може ділити одночасно індекси всіх підгруп
не може ділити одночасно індекси всіх підгруп  ,
,  і
і  . Якщо
. Якщо  ділить
ділить , то силовська
, то силовська  - підгрупа
- підгрупа  із
із  входить в
входить в  і є силовскою
і є силовскою  - підгрупою групи
- підгрупою групи  . Тим самим показано, що всі силовські підгрупи
нильпотентної групи
. Тим самим показано, що всі силовські підгрупи
нильпотентної групи  є
є  - групами. Тому що
- групами. Тому що  – формація, те звідси
треба, що
– формація, те звідси
треба, що  .
.
Лема доведена.
Лема 16 Нехай  – якийсь
– якийсь  - замкнутий гомоморф
- замкнутий гомоморф  - замкнутих груп. Тоді клас
- замкнутих груп. Тоді клас 
 - замкнуть.
- замкнуть.
Доказ. Нехай група  має
має  - підгрупи
- підгрупи  ,
,  і
і  з попарно взаємно простими індексами. По лемі
з попарно взаємно простими індексами. По лемі  має нормальну силовску
має нормальну силовску  - підгрупу
- підгрупу  . Оскільки
. Оскільки  є силовскої
є силовскої  - підгрупою в
- підгрупою в  і
і  – гомоморф, те
– гомоморф, те  . У групі
. У групі  індекси підгруп
індекси підгруп  ,
, 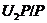 і
і  попарно взаємно прості. Тому через
попарно взаємно прості. Тому через  - замкнутість
- замкнутість  маємо
маємо  . Лема доведена.
. Лема доведена.
Лема 17 Для будь - якого простого  й будь - якої формації нильпотентних
груп
й будь - якої формації нильпотентних
груп  клас
клас  є
є  - замкнутою формацією.
- замкнутою формацією.
Доказ. По лемі клас 
 - замкнуть. По лемі клас
- замкнуть. По лемі клас 
 - замкнуть і по теоремі 1.1 є формацією.
- замкнуть і по теоремі 1.1 є формацією.
Теорема 18 Нехай  – локальна підформація формації
– локальна підформація формації  ,
,  – максимальний внутрішній локальний екран
формації
– максимальний внутрішній локальний екран
формації  . Якщо для
будь - якого простого
. Якщо для
будь - якого простого  формація
формація

 - замкнута,
- замкнута,  , то
, то 
 - замкнута.
- замкнута.
Доказ. Нехай  .
Через теорему 3.3 і леми 4.5,
.
Через теорему 3.3 і леми 4.5,  . Формація
. Формація 
 - замкнута. По лемі формація
- замкнута. По лемі формація 
 - замкнута. Теорема доведена.
- замкнута. Теорема доведена.
Теорема Крамер 19 Будь - яка локальна підформація
формації  є
є  - замкнутою.
- замкнутою.
Доказ. Нехай  –
локальна підформація формації
–
локальна підформація формації  .
.  має внутрішній локальний
має внутрішній локальний  - екран
- екран  . Нехай
. Нехай  – максимальний внутрішній локальний екран
формації
– максимальний внутрішній локальний екран
формації  . Тоді по
теоремі 3.3 для будь - якого простого
. Тоді по
теоремі 3.3 для будь - якого простого  має місце рівність
має місце рівність  . Тому що
. Тому що  , те по лемі формація
, те по лемі формація 
 - замкнута. Тоді по теоремі формація
- замкнута. Тоді по теоремі формація 
 - замкнута. Теорема доведена.
- замкнута. Теорема доведена.
Наслідок Д рк 20 Нехай група
рк 20 Нехай група  має чотири підгрупи, індекси яких у
має чотири підгрупи, індекси яких у  попарно взаємно прості.
попарно взаємно прості.
Висновок
У даній курсовій роботі ми дали визначення формації, добутку
формацій, а також операцій на класах груп. Познайомилися з поняттям екрана,
радикального й корадикального класів. У роботі розглянули ситуацію: кінцеві
розв'язні групи з нормальною максимальною підгрупою, що належить локальної
формації  формації
формації  всіх груп з нильпотентним
комутантом. Розглядали тільки кінцеві й розв'язні групи.
всіх груп з нильпотентним
комутантом. Розглядали тільки кінцеві й розв'язні групи.
Теорія кінцевих груп ніколи не випробовувала недоліку в загальних
методах, ідеях і невирішених проблемах, все - таки достаток отриманих
результатів з неминучістю привело до необхідності розробки нових загальних
методів і крапок, що систематизують, зору. Поштовх, зроблений роботою Гашюца,
викликав цілу лавину досліджень і привів до виникнення нового напрямку - теорії
формацій.
Література
2 Кертис Ч.,
Райнер И. Теорія подань кінцевих груп і асоціативних алгебр. – К., 2006
3
Чунихин С.А. О  - властивості
кінцевих груп. –К., 2001
- властивості
кінцевих груп. –К., 2001
4
Шеметков Л.А. Формація кінцевих груп. – К., 2002