Решение задач оптимизации в среде MatLab
МИНОБРНАУКИ
РОССИИ
Федеральное
государственное бюджетное образовательное учреждение высшего образования
“Тверской
государственный технический университет”
Лабораторная
работа №5
по
дисциплине: “Автоматизация технологических процессов и производств”
на
тему: “ Решение задач оптимизации в среде MatLab”
Выполнил: Мякатин И.Д.
Принял: Марголис Б.И.
Тверь
2016
Цель работы: Ознакомиться со способами решения
задач в среде MatLab.
Рассмотреть несколько типовых примеров задач оптимизации и реализовать
программу в среде MatLab
для их решения.
Optimization
ToolBox
Среда MatLab
содержит расширение “Optimization
ToolBox”, обеспечивающее
доступ к сервисным средствам обычной и крупномасштабной (большой размерности)
оптимизации.
Тулбокс Оптимизация содержит
подпрограммы для реализации наиболее широко используемых методов минимизации и
максимизации. Тулбокс включает в себя алгоритмы для решения многих типов задач
оптимизации, таких как:
· Современные
стандартные алгоритмы оптимизации.
· Нелинейная минимизация
без ограничений.
· Нелинейная
минимизация с ограничениями, включая задачи минимакса, достижения цели и
полубесконечной минимизации.
· Квадратичное и
линейное программирование.
· Нелинейный метод
наименьших квадратов и подбор кривых с границами.
· Решение системы
нелинейных уравнений.
· Линейный метод
наименьших квадратов с ограничениями.
· Специализированные
крупно-масштабные алгоритмы (большой размерности) для решения больших
разреженных задач.
· Подбор данных с
помощью подбора кривых, нелинейный метод наименьших квадратов, определение
нулей нелинейных уравнений и системы нелинейных уравнений.
· Гибкая среда,
которая обрабатывает ввод скаляра, вектора или матрицы.
Функции нелинейной оптимизации
С их помощью можно определить оптимум целевой
функции одной (fminbnd)
или нескольких (fminsearch)
переменных. Функции fminunc
и fmincon позволяют решать
оптимизационные задачи градиентными методами соответственно при отсутствии и
наличии ограничений. [2]
· fminbnd - поиск
функции одной переменной для фиксированного интервала.
· fmincon - поиск
минимума нелинейной задачи с ограничениями.
· fminsearch - поиск
минимума функции нескольких переменных без ограничений.
· fminunc - поиск
минимума функции нескольких переменных без ограничений.
· fseminf - поиск
минимума полубесконечной нелинейной функции нескольких переменных с
ограничениями. [4]
Реализуем программу в среде MatLab
для решения некоторых типовых задач оптимизации
. Поиск минимума функции одной переменной
вида 
. Поиск минимума функции нескольких
переменных вида 
. Поиск оптимальных настроек
ПИД-регулятора при наличии ограничений, путём минимизации целевой функции вида  ,
где
,
где 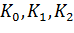 -
коэффициенты усиления дифференциальной, пропорциональной и интегральной
составляющих регулятора соответственно.
-
коэффициенты усиления дифференциальной, пропорциональной и интегральной
составляющих регулятора соответственно.
Листинг программы
нелинейный оптимизация целевой
регулятор
Файл-сценарийall
method=input(['Выберите метод
оптимизации(1-Метод золотого сечения,' ...
'параболическая интерполяция,2-Метод
Нелдера-Мида(Симплекс): '...
'3-Квазиньютоновский метод, 4-поиск оптимальных
настроек регулятора : ) ']);
optset=optimset('Display','iter','MaxFunEvals',500);method
case 1
nf=1;
[xmin,fval,exitflag,output]=fminbnd(@fun,-2,2,optset,nf)
case 2
nf=input('Введите номер функции: ');
if nf==1
x0=0;
else
x0=[0 0];
end;
[xmin,fval,exitflag,output]=fminsearch(@fun,x0,optset,nf)
case 3
if nf==1
x0=0;
else
x0=[0 0];
end;
[xmin,fval,exitflag,output]=fminunc(@fun,x0,optset,nf)
case 4W tz sigz mz
tz=10;sigz=20; mz=0.5;
W=tf([2],[1 2 2])
K=[1 1 1];
% K=[2.261 23.07 11.77]
A=[];b=[];Aeq=[];beq=[];nonlcon=[];
lb=[0 0 0];ub=[100 100 100];
[xmin,fval,exitflag,output]=fmincon(@fun2,K,A,b,Aeq,beq,lb,ub,@ogran,optset)
Wreg=tf([xmin(1) xmin(2) xmin(3)],[1
0])
Wzam=feedback(W*Wreg,1,-1);
[u,t]=step(Wzam);
tp=t(end);
disp(['Время переходного процесса:
',num2str(tp),' c'])
disp(['Перерегулирование: ',num2str(sig),' %'])
[numz,denz]=tfdata(Wzam,'v');
r=roots(denz);
q=1;
for c=1:length(r)
if( imag(r(c))~=0 )
m(q)=abs(real(r(c))/imag(r(c)));
q=q+1;
end;
end;=min(m);
disp(['Степень колебательности: ',num2str(m)])
step(Wzam)on;;
Файл-функция (функции для решения 1 и 2 задачи )
function y=fun(x,nf)nf
case 1
y=x^4+exp(-x);
case 2
y=4*x(1)+x(1)^2+8*x(2)+x(2)^2;
Файл-функция (Целевая функция для решения 3
задачи )
function y = fun2(K)tz sigz mz W
Wr=tf([K(1) ,K(2) ,K(3)],[1 0]);
Wz=feedback(W*Wr,1,-1);
[u,t]=step(Wz);
sig=((max(u)-u(end))/max(u))*100;
tp=t(end);
[~,denz]=tfdata(Wz,'v');
r=roots(denz);
q=1;
for c=1:length(r)
if( imag(r(c))~=0 )
m(q)=abs(real(r(c))/imag(r(c)));
q=q+1;
end;
end;=min(m);
wt=1/3;wsig=1/3;wm=1/3;
y=wt*abs(tp-tz)/tz+wsig*abs(sig-sigz)/sigz+wm*abs(m-mz)/mz;
end
Файл-функция (ограничения для решения 3 задачи)
function [c,ceq] = ogran(K)
c=-0.25+K(1)*K(3)/(K(2)*K(2));
ceq=[];
Полученные результаты
. Решение 1-й поставленной задачи:
Выберите метод оптимизации (1-Метод золотого
сечения, параболическая интерполяция, 2-Метод Нелдера-Мида(Симплекс):
3-Квазиньютоновский метод, 4-поиск оптимальных настроек регулятора: )1

Optimization terminated:
the current x satisfies the
termination criteria using OPTIONS.TolX of 1.000000e-004
xmin = 0.5283= 0.6675= 1
. Решение 2-й поставленной задачи
2.1. Выберите метод оптимизации(1-Метод золотого
сечения, параболическая интерполяция, 2-Метод Нелдера-Мида(Симплекс):
3-Квазиньютоновский метод, 4-поиск оптимальных настроек регулятора: )
Введите номер
функции:
2

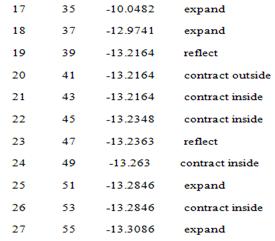

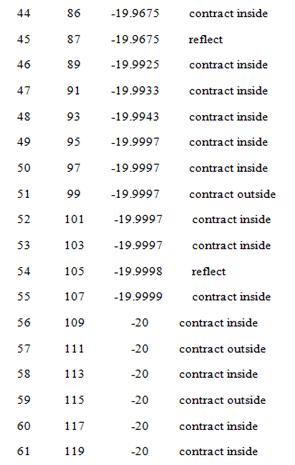

Optimization terminated:
the current x satisfies the
termination criteria using OPTIONS.TolX of 1.000000e-004
and F(X) satisfies the convergence
criteria using OPTIONS.TolFun of 1.000000e-004
xmin = -2.0000 -4.0000= -20.0000= 1
.2. Выберите метод оптимизации(1-Метод золотого
сечения, параболическая интерполяция, 2-Метод Нелдера-Мида(Симплекс):
3-Квазиньютоновский метод, 4-поиск оптимальных настроек регулятора: )3
Введите номер
функции:
2: Gradient must be provided forregion algorithm;
using line-search algorithm instead.
> In fminunc at 347
In laba5a at 29order

Local minimum found.completed
because the size of the gradient is less thandefault value of the function
tolerance.
<stopping criteria details>=
-2.0000 -4.0000= -20= 1
|
В
качестве начальных значений параметров регулятора [1 1 1]
|
Значения
параметров регулятора, полученные при помощи альтернативного метода РЧХ в
качестве начальных [2.261 23.07 11.77]
|
|
Выберите
метод оптимизации(1-Метод золотого сечения,параболическая
интерполяция,2-Метод Нелдера-Мида(Симплекс): 3-Квазиньютоновский метод,
4-поиск оптимальных настроек регулятора: )4 Transfer
function: 2 ------------- s^2 + 2 s + 2 K = 1 1 1 Local minimum possible.
Constraints satisfied. xmin = 0.2893 1.8760 2.6281 fval = 0.1462 exitflag = 5
Transfer function: 0.2893 s^2 + 1.876 s + 2.628
---------------------------- s Время переходного процесса:
10.2528 c Перерегулирование: 18.2325 % Степень колебательности: 0.33751 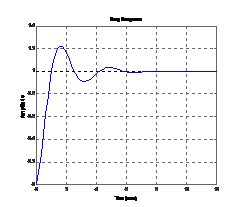
|
Выберите
метод оптимизации(1-Метод золотого сечения,параболическая
интерполяция,2-Метод Нелдера-Мида(Симплекс): 3-Квазиньютоновский метод,
4-поиск оптимальных настроек регулятора: )4 Transfer
function: 2 ------------- s^2 + 2 s + 2 K = 2.2610 23.0700 11.7700 Local
minimum possible. Constraints satisfied. xmin = 2.2856 23.0626 11.7730 fval =
0.0193 exitflag = 5 Transfer function: 2.286 s^2 + 23.06
s + 11.77 --------------------------- s Время переходного
процесса: 9.7925 c Перерегулирование: 19.4689 % Степень колебательности:
0.50525 
|
Рассмотрим одну из самых распространенных и
востребованных оптимизационных задач в логистике - транспортную задачу.
Необходимо найти оптимальный план
перевозок грузов от поставщиков к потребителям, если вектор мощностей
поставщиков равен 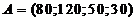 , вектор
мощностей потребителей
, вектор
мощностей потребителей 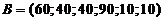 и задана
матрица транспортных издержек
и задана
матрица транспортных издержек

Суммарная мощность поставщиков равна
280, суммарная мощность потребителей равна 250, следовательно, задача является
открытой и необходимо свести ее к закрытой. Для этого нужно ввести фиктивного
потребителя, на которого будет приходиться 30 ед. продукции поставщиков.
Реализуем программу в среде MatLab для решения
поставленной задачи
Файл-сценарий:
clcallC X
B;=optimset('Display','iter','Algorithm','Active-set');
disp('Вектор мощностей
поставщиков')=[80,120,50,30]=[60,40,40,90,10,10];('Вектор мощностей
потребителей')
B(7)=sum(X)-sum(B)=[4 8 3 12 9 7;
2 1 24 7 8 5;
5 11 7 4 1 6;
6 7 4 3 8 8];(1,7)=zeros;('Матрица транспортных
издержек')
С=10*ones(size(C));=[];b=[];Aeq=[];beq=[];=zeros(size(C));ub=100*ones(size(C));
[xmin,fval]=fmincon(@fun,K,A,b,Aeq,beq,lb,ub,@ogr,optset);
disp('Матрица переменных')(['Наименьшее значение
целевой функции= ', num2str(fval)])
Файл-функция (Целевая функция)y = fun(M)
global C;=C.*M;
y=sum(V(:));
Файл-функция (ограничения)[c,ceq] = ogr(M)
global X
B=size(M);i=1:s(1)(i)=X(i)-sum(M(i,:));j=1:s(2)(i+j)=B(j)-sum(M(:,j));
ceq(i+j)=M(1,j,1)-B(j);
c=[];
Результаты работы программы
Вектор мощностей поставщиков= 80 120 50 30
Вектор мощностей потребителей= 60 40 40 90 10 10
30
Матрица транспортных издержек
C =
4 8 3 12 9 7 0
2 1 24 7 8 5 0
5 11 7 4 1 6 0
6 7 4 3 8 8 0
Max Line search Directional
First-order
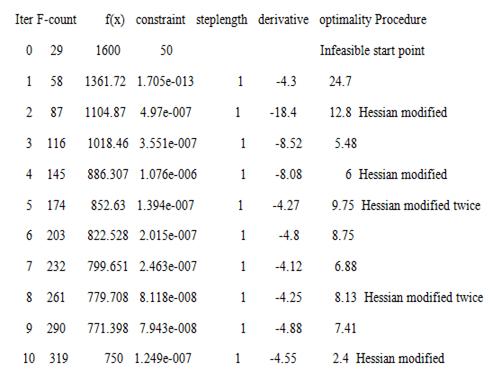
Local minimum found that satisfies
the constraints.completed because the objective function is non-decreasing in
feasible directions, to within the default value of the function tolerance, and
constraints were satisfied to within the default value of the constraint
tolerance.
<stopping criteria
details>inequalities (to within options.TolCon = 1e-006): lower upper
ineqlin ineqnonlin
4
5
7
8
10
11
12
13
17
18
20
23
24
26
27
28
Матрица переменных
xmin =

Наименьшее значение целевой функции = 750
Список литературы
1. Конспекты
лекций по курсу “АТПП”
. Марголис,
Б.И. Компьютерные методы анализа и синтеза систем автоматического регулирования
в среде Matlab /
Б.И.Марголис. - Учеб. Пособие для вузов. - Тверь: изд-во ТвГТУ, 2015.-92 с.
3. <http://matlab.exponenta.ru/optimiz/book_1/1.php>
. http://matlab.exponenta.ru/optimiz/book_4/