методы классификации матричных игр
Министерство
образования Московской области
Государственное
образовательное учреждение высшего образования Московской области
Государственный
гуманитарно-технологический университет
Факультет
математики и физики
Курсовая работа
по математике на тему:
«Методы
классификации матричных игр»
Выполнил:
студент 3 курса
очного отделения
факультета
математики и физики
Балакина Дарья
Дмитриевна
Научный
руководитель:
д. т. н.,
профессор Григорьев С.Г.
Орехово-Зуево
2015 г.
СОДЕРЖАНИЕ
Введение……………………………………………………………………3
1.
Теорияигр……………………………………………………………….5
2.
Антагонистические игры……………………………………………….7
3.
Матричные игры………………………………………………………..12
3.1.
Матричные
игры в чистых стратегиях………………………..…..13
3.2.
Матричные
игры в смешанных стратегиях……………………....16
Заключение………………………………………………………………..24
Список
используемой литературы……………………………………….25
ВВЕДЕНИЕ
Теория
игр – раздел математики, предметом которого является изучение математических моделей
принятия оптимальных решений в условиях конфликта.
Наиболее
полное изложение идей и методов теории игр впервые появилось в 1944 году в
научном труде «Теория игр и экономическое поведение» математика Джона фон
Неймана и экономиста Оскара Моргенштерна, которая распространила информацию
теорию игр на произвольное число участников и применила эту теорию к
экономическому поведению. Таким образом, теория игр – один из новейших разделов
в математике.
Механизмы
конкуренции, функционирования рынка, возникновения или краха монополий, способы
принятия ими решений в условиях конкурентной борьбы, то есть механизмы игры
монополий, действующие в экономической реальности, - все это является предметом
анализа теории игр. Главная задача теории игр - предсказать поведение
участников конфликта.
Таким
образом, конфликтные ситуации приводят к возникновению различных видов игр. Если
цели конфликтующих сторон противоположные, то такие игры получили название антагонистических
игр. При конечном выборе стратегий игры, антагонистические игры будут называться
матричными. Следовательно, матричные игры представляют собой конечные игры двух
сторон конфликта (далее игроков) с нулевой суммой. Матричные игры делятся на
два типа: матричные игры в чистых стратегиях и матричные игры в смешанных,
исходя из выбора стратегии игроками. Вданной курсовой работе мы рассмотрим
данную классификацию и изучим различие этих двух видов.
Поэтому
цельюкурсовой работы является изучение методов классификации матричных игр и выяснение
их различий, на основе выбора игровой стратегии.
Задача
– рассмотреть общие понятия теории игр, классификацию матричных игр, примеры
решения конкретных задач.
При
написании данной работы мы использовали в качестве основного источника
информации по данному вопросу учебникиЛунькова А.Д. «Теория игр»и Невежина В.П.
«Теория игр. Примеры и задачи».
Курсовая
работа состоит из введения, двух глав и заключения.В первой главе приведены
основные понятия и утверждения теории игр, теории матричных игр, с дальнейшим
переходом к классификации матричных игр.
Глава
вторая посвящена антагонистическим играм, частным случаем которых являются
матричные игры.
И,
наконец, третья глава полностью посвящена классификации матричных игр, а именно
матричным играм в чистой и смешанной стратегии. В ней будет приведена главная
теорема матричных игр с доказательством.
Каждая
глава курсовой работы содержит как теоритический материал, так и практический,
то есть будут рассмотрены примеры и приемы решения для конкретных матричных игр.
1.
Теория игр
Ситуации, в которых одна сторона
противостоит другой, отстаивая свои интересы, причем результат каждого
мероприятия (хода) одной стороны зависит от выбранного образа действия другой
стороны, называют конфликтной ситуацией. Необходимость обоснования оптимальных
решений в конфликтных ситуациях привела к возникновению теории игр.
Теория игр получила широкое
распространение и используется в различных областях экономики и производства,
бизнеса и финансов, сельского хозяйства, военного дела, биологии и политологии.
С одной стороны, теория игр – это математический метод изучения оптимальных
стратегий игр. [6].В данном случае теория представляет собой раздел прикладной
математики. Но с другой стороны – это раздел современной экономической теории,
что подтверждается большим количеством Нобелевских премий в области экономики,
присужденных самым выдающимся представителям данной науки.
Всюду, где только имеет место
взаимодействие самостоятельных субъектов, возникает игра. Игрой называют
упрощенную модель реальной конфликтной ситуации.Игра не может вестись без
определенных правил. Развитие происходит поэтапно, т.е. по ходам. Суть игры в
том, что каждый из ее участников принимает такие решения, которые могут
обеспечить ему наилучший результат (исход). Исход игры - это значение
некоторой функции, называемой функцией выигрыша (платежной функцией). Эта
функция задается либо таблицей, либо аналитическим выражением.
Стратегией игры называется совокупность
правил, которые определяют однозначный выбор при каждом личном ходе одного
игрока в зависимости от сложившейся в игре ситуации. [1]. Стратегии в конечных играх нередко называются чистыми
стратегиями.
Различные виды игр можно классифицировать по числу игроков, числу
стратегий, свойствам функции выигрыша, возможности предварительных переговоров
и взаимодействия между игроками в ходе игры. Далее рассмотрим эту
классификацию.
В зависимости от числа игроков различают игры с двумя, тремя и
более участниками.
Игрой
с нулевой суммой называется игра, в которой выигрышем одного игрока является
проигрыш другого, т.е. сумма выигрышей обеих сторон является нулевой. Их еще
называют антагонистическими играми. Именно так делятся игры по характеру
выигрышей. Также по характеру взаимодействия игры делятся на:
1. Бескоалиционные
- игроки не имеют права вступить в соглашения, образовать коалиции;
2. Коалиционные
- коалиции определены наперед.
Согласно другому принципу классификации – по количеству стратегий
– различают конечные и бесконечные игры. В конечных играх игроки располагают
конечным числом возможных стратегий. Соответственно, в бесконечных играх игроки
имеют бесконечное число возможных стратегий.
В зависимости от возможности предварительных переговоров между
игроками различают кооперативные и некооперативные игры. Игра называется
кооперативной, если до начала игры игроки образуют коалиции и принимают
взаимообязывающие соглашения о своих стратегиях. А игры, в которых игроки не
могут координировать свои стратегии, называются некооперативными. Необходимо
отметить, что все антагонистические игры могут служить примером некооперативных
игр.
И,
наконец, по виду функций выигрыша (или платежной функции)
игры делятся на: матричные, биматричные, непрерывные, выпуклые, сепарабельные,
типа дуэлей и другие.
Особого внимания заслуживают матричные игры. Поэтому третья глава
курсовой работы будет полностью посвящена матричным играм, а именно методу их
классифицирования, исходя из выбранной стратегии игроков.
2. Антагонистические
игры
Антагонистические
игры – парные игры, в которых выигрыш одного игрока равен проигрышу другого,
поэтому совместные действия игроков, их переговоры и соглашения лишены смысла.
Определяется
антагонистическая игра заданием множеств стратегий игроков и выигрышей первого
игрока в каждой ситуации, состоящей в выборе игроками каждой стратегии.
Наиболее
часто приводимым примером игр с ненулевой суммой является игра «Дилемма
заключенного». Суть игры состоит в том, что два преступника ожидают приговора
суда за содеянное. Адвокат конфиденциально предлагает каждому из преступников
облегчить его участь, если он сознается и даст показания против сообщника,
которому грозит угодить в тюрьму за совершенное преступление на 10 лет. Если
никто не сознается, то обоим угрожает заключение на определенный срок
(например, 1 год) по обвинению в незначительном преступлении. Если сознаются
оба то преступника, то, с учетом чистосердечного признания, им обоим грозит
попасть в тюрьму на 5 лет. Каждый заключенный имеет на выбор 2 стратегии: не
сознаться или сознаться, выдав при этом сообщника.
Обобщим
выше сказанное: 1 игрок – сознаться или не сознаться и 2 игрок – сознаться или
не сознаться. В итоге можно получить следующую матрицу «выигрышей» для обоих
игроков:
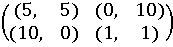 .
.
Основным
допущением при решении данных игр является то, что каждый игрок стремится
обеспечить себе максимально возможный выигрыш при любых действиях партнера.
В
игре могут участвовать как два игрока (её называют парной), так и множество. Но
наибольшее практическое значение имеют парные игры, в которых участников
обозначают за A и B. Простейшим видом стратегической игры – игра двух лиц с
нулевой суммой (т.е. сумма выигрышей сторон равна нулю).
Игра
состоит из двух ходов: игрок A выбирает одну из своих
возможных стратегий 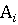 (i =
1, 2, …, m), а игрок B выбирает стратегию
(i =
1, 2, …, m), а игрок B выбирает стратегию 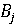 (j =
1, 2, .., n), причем каждый участник делает выбор в полной ситуации
незнании выбора другого игрока. В результате выигрыши
(j =
1, 2, .., n), причем каждый участник делает выбор в полной ситуации
незнании выбора другого игрока. В результате выигрыши 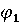 (
(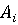 ,
, 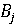 ) и
) и (
(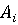 ,
, 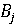 ) каждого из
игроков удовлетворяют соотношению
) каждого из
игроков удовлетворяют соотношению 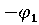 (
(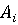 ,
,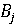 )+
)+ (
(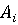 ,
, 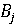 ) = 0
) = 0
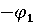 (
(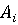 ,
,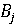 )+
)+ (
(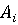 ,
, 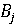 ) = 0,
) = 0,
откуда,
если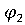 (
(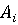 ,
,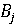 ) =
) =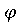 (
(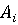 ,
, 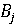 ), имеем
), имеем  .
.
Цель
игрока A – максимизировать
функцию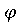 (
(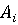 ,
, 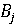 ) , а игрока В –
минимизировать эту же функцию. Каждый из игроков может выбирать одну из
переменных, от которых зависит значение функции. Если игрок А выбирает
некоторую из стратегий
) , а игрока В –
минимизировать эту же функцию. Каждый из игроков может выбирать одну из
переменных, от которых зависит значение функции. Если игрок А выбирает
некоторую из стратегий 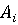 , то это может влиять
на значение функции
, то это может влиять
на значение функции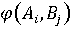 . Влияние
. Влияние 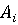 на величину
значения
на величину
значения 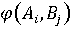 является
неопределенным, а определенность
является
неопределенным, а определенность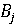 имеет место только
после выбора, например, игроком B переменной (при
этом
имеет место только
после выбора, например, игроком B переменной (при
этом 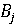 определяется
другим игроком).
определяется
другим игроком).
Пусть 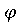 (
(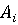 ,
, 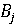 )
) , тогда составим
матрицу:
, тогда составим
матрицу:
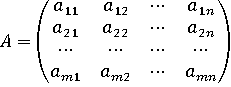
Строки
матрицы соответствуют стратегиям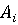 , столбцы – стратегиям
, столбцы – стратегиям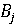 . Матрица
. Матрица 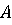 называется
матрицей игры, а элемент
называется
матрицей игры, а элемент  матрицы – выигрыш
игрока A, если он выбрал
стратегию
матрицы – выигрыш
игрока A, если он выбрал
стратегию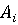 , а игрок B выбрал
стратегию
, а игрок B выбрал
стратегию 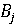 .
.
Пусть
игрок А выбрал некоторую стратегию 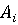 , тогда в худшем случае
он получит выигрыш, равный
, тогда в худшем случае
он получит выигрыш, равный  . Поэтому предвидя
такую возможность, игрок А должен выбрать ту стратегию,
которая позволит максимизировать его минимальный выигрыш
. Поэтому предвидя
такую возможность, игрок А должен выбрать ту стратегию,
которая позволит максимизировать его минимальный выигрыш  :
: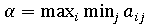 . Величина
. Величина  -
гарантированный выигрыш игрока А – называется нижней ценой
игры, а стратегия
-
гарантированный выигрыш игрока А – называется нижней ценой
игры, а стратегия 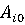 , обеспечивающая
получение
, обеспечивающая
получение  - максиминной.
- максиминной.
Игрок В ,
выбирая стратегию, исходит из следующего принципа: при выборе некоторой
стратегии 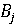 его проигрышнее
превысит максимального из значений элементов
его проигрышнее
превысит максимального из значений элементов 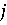 -го
столбца матрицы, т.е. меньше или равен
-го
столбца матрицы, т.е. меньше или равен  . Рассматривая
множество
. Рассматривая
множество  для различных
значений
для различных
значений 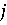 , игрок В выбирает
такое значение
, игрок В выбирает
такое значение 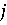 , при котором его
максимальный проигрыш
, при котором его
максимальный проигрыш 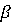 минимизируется:
минимизируется:
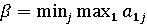 .
.
Величина 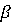 называется
верхней ценой игры, а соответствующая выигрышу
называется
верхней ценой игры, а соответствующая выигрышу 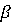 стратегия
стратегия  - минимаксной.
- минимаксной.
Фактический
выигрыш игрока 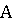 при
разумных действиях обоих участников ограничен нижней и верхней ценой игры. Если
эти выражения будут равны, т.е.
при
разумных действиях обоих участников ограничен нижней и верхней ценой игры. Если
эти выражения будут равны, т.е. 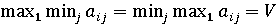 , то выигрыш
игрока
, то выигрыш
игрока 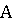 –
вполне определенное число, значит игра называется вполне определенной, а
выигрыш – значением игры и равен элементу матрицы
–
вполне определенное число, значит игра называется вполне определенной, а
выигрыш – значением игры и равен элементу матрицы  .
.
Вполне
определенные игры называют играми с седловой точкой. Элемент  в матрице такой игры
является одновременно минимальным в строке
в матрице такой игры
является одновременно минимальным в строке 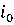 , максимальным в
столбце
, максимальным в
столбце  и называется
седловой точкой.
и называется
седловой точкой.
Точка
называется седловой из-за формы графика функции выигрыша в точке  , которая напоминает
седло, убывая при изменении одной из переменных и возрастая при изменении
другой переменной.
, которая напоминает
седло, убывая при изменении одной из переменных и возрастая при изменении
другой переменной.
Необходимо
отметить, что в случае, если цена антагонистической игры равна 0, игра
называется справедливой.
Задача:
определить верхнюю и нижнюю цены для игр, заданных платежными матрицами 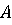 и
и
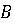 :
:
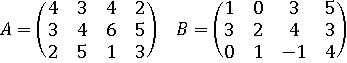
Решение:
минимальное значение  в строках
матрицы
в строках
матрицы 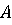 равны
соответственно 2,3,1. Максимальное значение из них равно 3.
Следовательно,
равны
соответственно 2,3,1. Максимальное значение из них равно 3.
Следовательно, 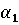 - нижняя цена
игры, которой соответствует матрица
- нижняя цена
игры, которой соответствует матрица 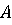 ,
равна 3.
,
равна 3.
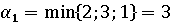
 Для
определения
Для
определения  (верхней цены игры)
найдем максимальные значения элементов в столбцах матрицы. По столбцам имеем:
4, 5, 6, 5. Следовательно,
(верхней цены игры)
найдем максимальные значения элементов в столбцах матрицы. По столбцам имеем:
4, 5, 6, 5. Следовательно, 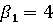 .
.
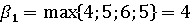
Для
матрицы 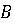 составляем
аналогично
составляем
аналогично 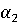 и
и 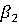 :
:

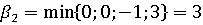
Таким
образом, 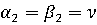 - цена
игры. Решение данной игры состоит в выборе игроком
- цена
игры. Решение данной игры состоит в выборе игроком 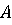 стратегии
стратегии  , при этом выигрыш
составит не меньше 4, а для игрока
, при этом выигрыш
составит не меньше 4, а для игрока 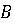 стратегия
стратегия 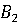 , позволяющая
ограничить проигрыш числом 3.
, позволяющая
ограничить проигрыш числом 3.
Игровые
системы, содержащие седловую точку, имеют заранее известное решение, т.к.
каждый из игроков применяет свою оптимальную стратегию. Решение игры, матрицы
которой не содержат седловой точки (т.е.  ),
довольно затруднительно. Каждый из игроков, применяя минимаксную стратегию,
хочет обеспечить себе выигрыш (не превышающий
),
довольно затруднительно. Каждый из игроков, применяя минимаксную стратегию,
хочет обеспечить себе выигрыш (не превышающий  )
и проигрыш (не меньше
)
и проигрыш (не меньше 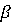 ). Для каждого из
игроков характерен вопрос о максимизации выигрыша и минимизации проигрыша.
Поэтому поиски данного решения заключаются в выборе оптимальной стратегии игры.
). Для каждого из
игроков характерен вопрос о максимизации выигрыша и минимизации проигрыша.
Поэтому поиски данного решения заключаются в выборе оптимальной стратегии игры.
Таким
образом, решением антагонистической игры является седловая точка 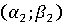 , а оптимальными
стратегиями первого и второго игроков являются первая и, соответственно, вторая
координата седловой точки. Поэтому решение антагонистической игры называют
также седловой точкой игры.
, а оптимальными
стратегиями первого и второго игроков являются первая и, соответственно, вторая
координата седловой точки. Поэтому решение антагонистической игры называют
также седловой точкой игры.
3. Матричные
игры
Антагонистическая
игры называется матричной, если в этой игре оба игрока имеют конечное число
стратегий X и Y,
то есть если оба множества X
и Y состоят из конечного числа
элементов. В матричной игре можно считать, что 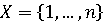 ,
, 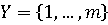 и положить
и положить  Таким образом,
матричная игра полностью определяется матрицей
Таким образом,
матричная игра полностью определяется матрицей 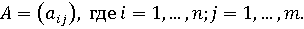
Следовательно, матричная игра – это
конечная игра двух игроков с нулевой суммой, в которой задается выигрыш игрока A в виде матрицы, в которой строка
матрицы соответствует номеру применяемой стратегии игрока B, столбец – номеру применяемой
стратегии игрока B; на пересечении
строки и столбца матрицы находится выигрыш игрока A, соответствующий применяемым стратегиям.
Теория матричных игр
позволяет нам рассматривать и с легкостью решать задачи принятия решений в
ситуациях с несколькими участниками, когда значение целевой функции для каждого
зависит также и от решений, принимаемых остальными участниками. Поэтому важная
роль в матричных играх отводится конфликтам и совместным действиям.
Область применения матричных игр не столь очевидна, но тоже
достаточно обширна. Например, совсем недавно были проведены исследования,
показавшие, что взаимоотношения различных видов животных на какой-либо
территории, их взлеты и падения, вымирание можно описать с помощью расширенной
до большего числа вариантов всем известной игры
"камень-ножницы-бумага". А данная игра, как известно, является ничем
иным, как матричной игрой.
Математическая
теория игр способна не только указать оптимальный путь к решению некоторых
проблем, но и прогнозировать их исход. Матричные игры серьёзно изучаются
специалистами, так как к ним могут быть сведены игры общего вида. Поэтому
теория матричных игр хорошо развита, существуют различные методы поиска решения
игр. Для матричных игр доказано, что любая из них имеет решение, и оно может
быть легко найдено путем сведения игры к задаче линейного программирования.
Но
в большинстве случаев решение матричных игр представляет собой трудный и
громоздкий процесс. Есть примеры, когда даже для матриц размера 3´3,
процесс поиска решения довольно трудоёмкий.
В теории матричных игр
предполагается, что функция выигрыша и множества стратегий, доступна и известна
каждому из игроков, т.е. каждый игрок знает свою функцию выигрыша и набор
имеющихся в его распоряжении стратегий, а также функций выигрыша и стратегий
все остальных игроков, и в соответствии с этой информацией организует свое
поведение.
3.1.
Матричные
игры в чистых стратегиях.
Пусть
игроки AиBрасполагают
конечным числом возможных действий — чистых стратегий. Обозначим их
соответственно 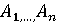 и
и 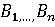 . Игрок
Aможет выбирать любую чистую
стратегию
. Игрок
Aможет выбирать любую чистую
стратегию  , в ответ на которую игрок
, в ответ на которую игрок 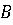 может
выбрать любую свою чистую стратегию
может
выбрать любую свою чистую стратегию  . Если игра состоит
только из личных ходов пары стратегий
. Если игра состоит
только из личных ходов пары стратегий однозначно определяет
результат
однозначно определяет
результат 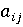 — выигрыш игрока A.
— выигрыш игрока A.
При
этом проигрыш игрока 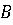 составляет—
составляет—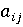 . Если
известны значения
. Если
известны значения 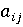 —выигрыша для каждой
пары
—выигрыша для каждой
пары  чистых стратегий, можно
составить матрицу выигрышей игрока
чистых стратегий, можно
составить матрицу выигрышей игрока 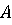 (проигрышей игрока B)
(таблица
1). Такая таблица называется платежной матрицей или просто матрицей игры.
(проигрышей игрока B)
(таблица
1). Такая таблица называется платежной матрицей или просто матрицей игры.
Таблица
1
В
таблице 1 приведены числа 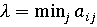 — минимальновозможный
выигрыш игрока
— минимальновозможный
выигрыш игрока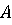 , применяющего
стратегию
, применяющего
стратегию  , и
, и 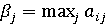 — максимально возможный
проигрыш игрока B, если он
пользуется стратегией
— максимально возможный
проигрыш игрока B, если он
пользуется стратегией .
.
Как
и в антагонистических играх, число называют нижней чистой ценой
игры(максимином), а соответствующую ему чистую стратегию -
называют нижней чистой ценой
игры(максимином), а соответствующую ему чистую стратегию -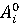 - максиминной.Число
λ показывает, какой минимальный гарантированный выигрыш может получить
игрок A, правильно
применяя свои чистые стратегии при любых действиях игрока B.
- максиминной.Число
λ показывает, какой минимальный гарантированный выигрыш может получить
игрок A, правильно
применяя свои чистые стратегии при любых действиях игрока B.
Число
 называют верхней
чистой ценной игры(минимаксом), а соответствующую чистую стратегию
называют верхней
чистой ценной игры(минимаксом), а соответствующую чистую стратегию 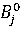 — минимаксной.Число β
показывает, какой минимальный гарантированный проигрыш может быть у игрока Bпри
правильном
выборе им своих чистых стратегий независимо от действий игрока A.
— минимаксной.Число β
показывает, какой минимальный гарантированный проигрыш может быть у игрока Bпри
правильном
выборе им своих чистых стратегий независимо от действий игрока A.
Следовательно,
игрок 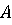 обеспечит себе выигрыш
не меньше λ, при правильном использовании своих чистых стратегий, а
игрок
обеспечит себе выигрыш
не меньше λ, при правильном использовании своих чистых стратегий, а
игрок 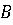 в результате правильного
применения своих чистых стратегий не позволит игроку Aвыиграть
больше, чем β. Из этого следует, что
в результате правильного
применения своих чистых стратегий не позволит игроку Aвыиграть
больше, чем β. Из этого следует, что  .Если
.Если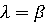 ,
то говорят, что игра имеет седловую точку в чистых стратегиях и чистую цену
игры
,
то говорят, что игра имеет седловую точку в чистых стратегиях и чистую цену
игры .
.
Пару
чистых стратегий  и
и  , соответствующих λ
и β, называют седловой точкойматричной игры,а элемент
, соответствующих λ
и β, называют седловой точкойматричной игры,а элемент  платежной матрицы,
стоящий на пересечении
платежной матрицы,
стоящий на пересечении 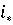 -й строки и
-й строки и  -гo
столбца, — седловым элементом платежной матрицы.Он одновременно является
минимальным в своей строке и максимальным в своем столбце, т. е.
-гo
столбца, — седловым элементом платежной матрицы.Он одновременно является
минимальным в своей строке и максимальным в своем столбце, т. е. 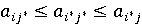 . Стратегии
. Стратегии  и
и  , образующие седловую
точку, являются оптимальными. Тройку
, образующие седловую
точку, являются оптимальными. Тройку  называют решением игры.
называют решением игры.
Пример
1. Пусть два игрока 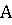 и
и 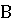 ,
не глядя друг на друга, кладут на стол по монете вверх гербом или вверх решкой,
по своему усмотрению. Если игроки выбрали одинаковые стороны (у обоих герб или
у обоих решка), то игрок
,
не глядя друг на друга, кладут на стол по монете вверх гербом или вверх решкой,
по своему усмотрению. Если игроки выбрали одинаковые стороны (у обоих герб или
у обоих решка), то игрок 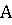 забирает обе монеты;
иначе их забирает игрок B.
Требуется проанализировать игру и составить ее матрицу.
забирает обе монеты;
иначе их забирает игрок B.
Требуется проанализировать игру и составить ее матрицу.
Решение.
Игра состоит только из двух ходов: ход игрока А и ход игрока В, оба хода
личные. Игра не принадлежит к играм с полной информацией, так как в момент хода
выполняющий его игрок не знает, что сделал другой. Так как у каждого из игроков
имеется только один личный ход, то стратегия игрока представляет собой выбор
при этом единственном личном ходе.
У
каждого игрока две стратегии:
1.
игрок
А:  выбрать герб,
выбрать герб, 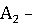 выбрать решку;
выбрать решку;
2.
игрок
В: 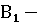 герб,
герб, 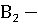 решка.
решка.
Таким
образом, данная игра есть игра 2×2. Пусть выигрыш монеты обозначается +1.
Матрица игры приведена в таблице 2. На примере этой игры можно уяснить
некоторые существенные идеи теории игр.
Таблица
2
Давайте
предположим, что эта игра выполняется только один раз. Тогда будет очевидно,
что других стратегий быть не может. Каждый из игроков с одинаковым основанием
может принять любое решение. Однако при повторении игры положение меняется.
Действительно,
положим, что игрок А выбрал себе какую-то стратегию 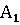 . Тогда уже по
результатам первых нескольких ходов противник догадывается о стратегии игрока А
и будет на нее отвечать наименее выгодным для него образом, то есть выбирать
решку. Но игроку А явно невыгодно всегда применять какую-то одну стратегию.
Чтобы не оказаться в проигрыше, он должен иногда выбирать герб, а иногда –
решку. Однако, если он будет чередовать гербы и решки, например, то противник
(игрок В) тоже может догадаться об этом и ответить на эту стратегию худшим для
игрока А образом. Очевидно, что игроку А нужно подобрать свою стратегию таким
образом, чтобы его противник не знал о ней, и, чтобы была такая организация
выбора при каждом ходе, что игрок А сам не знает значение своего хода. Например,
это можно обеспечить при помощи подбрасывания монеты.
. Тогда уже по
результатам первых нескольких ходов противник догадывается о стратегии игрока А
и будет на нее отвечать наименее выгодным для него образом, то есть выбирать
решку. Но игроку А явно невыгодно всегда применять какую-то одну стратегию.
Чтобы не оказаться в проигрыше, он должен иногда выбирать герб, а иногда –
решку. Однако, если он будет чередовать гербы и решки, например, то противник
(игрок В) тоже может догадаться об этом и ответить на эту стратегию худшим для
игрока А образом. Очевидно, что игроку А нужно подобрать свою стратегию таким
образом, чтобы его противник не знал о ней, и, чтобы была такая организация
выбора при каждом ходе, что игрок А сам не знает значение своего хода. Например,
это можно обеспечить при помощи подбрасывания монеты.
Исходя
из выше сказанного, путем интуитивных рассуждений можно прийти к выводу, что
речь идет о формировании важнейшего понятия в теории игр ˗ о понятии
«смешанной стратегии», то есть такой стратегии, когда «чистые» стратегии
чередуются случайно с определенными частотами.
Решение
в чистых стратегией является не надежным способом решения матричных игр из-за
наличия определенности ходов игроков. Поэтому, для гарантирования незнания
стратегииодного игрока используют решение матричных игр при помощи смешанных
стратегий. Об этом пойдет речь в следующем пункте курсовой работы.
3.2.
Матричные игры в смешанных стратегиях.
Среди
конечных игр, имеющих практическое значение, сравнительно редко встречаются
игры с седловой точкой. Более типичным является случай, когда нижняя и верхняя
цена игры различны. Анализируя матрицы таких игр, пришли к выводу, что если
каждому игроку предоставлен выбор одной и единственной стратегии, то в расчете
на разумно действующего противника этот выбор должен определяться принципом
минимакса. Придерживаясь своей максиминной стратегии, при любом поведении
противника заведомо гарантируется выигрыш, равный нижней цене игры  .
Такие комбинированные стратегии, состоящие в применении нескольких чистых
стратегий, чередующихся по случайному закону с определенным соотношением
частот, в теории игр называются смешанными стратегиями.
.
Такие комбинированные стратегии, состоящие в применении нескольких чистых
стратегий, чередующихся по случайному закону с определенным соотношением
частот, в теории игр называются смешанными стратегиями.
Действительно,
 есть максимальный
гарантированный выигрыш, который можно обеспечить, применяя только чистые
стратегии. Так как смешанные стратегии включают в себя в качестве частного
случая и все чистые, то
есть максимальный
гарантированный выигрыш, который можно обеспечить, применяя только чистые
стратегии. Так как смешанные стратегии включают в себя в качестве частного
случая и все чистые, то 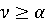 . Аналогично,
рассматривая возможности противника,
. Аналогично,
рассматривая возможности противника, 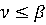 .
Откуда следует неравенство
.
Откуда следует неравенство 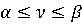 , где
, где 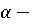 нижняя цена игры,
нижняя цена игры, 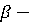 верхняя
цена игры,
верхняя
цена игры,  чистая цена игры.
чистая цена игры.
Смешанной
стратегией игрока 1 в матричной игре называется распределение вероятностей на
множестве его чистых стратегий, то есть любой вектор  , обладающий следующими
свойствами:
, обладающий следующими
свойствами:

С
другой стороны, смешанной стратегией игрока 2 в матричной игре называется
распределение вероятностей на множестве его чистых стратегий, то есть любой
вектор 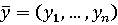 , обладающий
свойствами:
, обладающий
свойствами:

Число
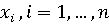 представляет собой вероятность
выбора i-й чистой стратегии игроком 1, а число
представляет собой вероятность
выбора i-й чистой стратегии игроком 1, а число 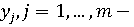 вероятность выбора j-й
чистой стратегии игроком 2, гдеi-й чистой стратегии игрока 1
соответствует смешанная стратегия
вероятность выбора j-й
чистой стратегии игроком 2, гдеi-й чистой стратегии игрока 1
соответствует смешанная стратегия 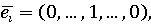 а j-й чистой
стратегии игрока 2 - смешанная стратегия
а j-й чистой
стратегии игрока 2 - смешанная стратегия 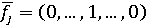 .
.
Из
этого можно сделать вывод, что множество смешанных стратегий бесконечно.
Применение смешанных стратегий превращает процесс игры в некоторое случайное
испытание, исходами которого являются ситуации игры, то есть пары 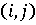 . Это случайное
испытание называется ситуацией в смешанных стратегиях и обозначается через
. Это случайное
испытание называется ситуацией в смешанных стратегиях и обозначается через 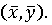 Отсутствие обмена
информацией между игроками в антагонистической игре делает случайные принятия
ими решения о своих стратегиях i и j независимыми. Поэтому каждая
ситуация
Отсутствие обмена
информацией между игроками в антагонистической игре делает случайные принятия
ими решения о своих стратегиях i и j независимыми. Поэтому каждая
ситуация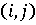 реализуется с
вероятностью
реализуется с
вероятностью  . Поскольку в этой
ситуации игрок 1 получает выигрыш
. Поскольку в этой
ситуации игрок 1 получает выигрыш 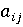 , математическое
ожидание его выигрыша равно
, математическое
ожидание его выигрыша равно
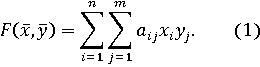
Таким
образом,матричной
игрой со смешанными стратегиями называется тройка Г=(Х, Y, F),
где Х - множество векторов, удовлетворяющих условиям:
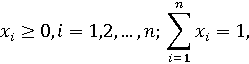
Y
-
множество векторов, удовлетворяющих условиям:

а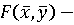 функция, заданная
формулой (1).
функция, заданная
формулой (1).
Имеют
место простые примеры смешанных стратегий.
Пример
2. Арбитр футбольного матча, чтобы определить первую атакующую команду, бросает
монету, т.е. вместо того, чтобы принять определенное решение, выбирает пару
чисел ( ), где первое число –
есть вероятность того, что атакующей будет первая команда, второе - вероятность
для второй команды.
), где первое число –
есть вероятность того, что атакующей будет первая команда, второе - вероятность
для второй команды.
Пример
3. Четыре студентки, проживающие в одной комнате, тянут четыре спички, одна из
которых короче остальных. Та, которой достанется короткая спичка, должна
вымыть пол. Поступая так, студентки добавляют к своим четырем стратегиям:
"моет пол Галя", "поет пол Вера", "моет пол
Наташа", "моет пол Лена" еще одну, а именно, вектор  . Дополнительная
стратегия
. Дополнительная
стратегия 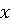 состоит в смешивании
четырех стратегий, каждой с вероятностью
состоит в смешивании
четырех стратегий, каждой с вероятностью  .
.
Уместно
доказать теорему, которая является основной теоремой для матричных игр, впервые
доказанная Джоном фон Нейманом. Она гласит: любая матричная игра имеет седловую
точку в смешанных стратегиях.
Доказательство.
Ограниченность Х и Y вытекает из условий
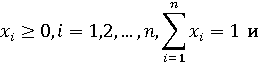
 Доказывается
замкнутость и выпуклость этих множеств. Доказательство проводится для Х,
для Y оно аналогично.
Доказывается
замкнутость и выпуклость этих множеств. Доказательство проводится для Х,
для Y оно аналогично.
Пусть
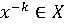 при всех
при всех 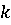 ,
,
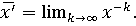 Доказывается, что и
Доказывается, что и 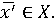 В самом деле,
В самом деле, 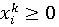 при всех k и
при всех k и 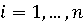 ,
следовательно,
,
следовательно, 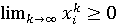 при всех
при всех 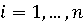 ,,
то есть
,,
то есть при всех
при всех 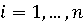 .
Далее, поскольку
.
Далее, поскольку
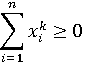
при
всех 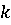 , то и
, то и

то
есть

Таким
образом, 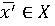 удовлетворяет условиям
удовлетворяет условиям 
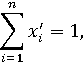
и
принадлежит Х. Итак, Х является замкнутым.
Пусть Так как
Так как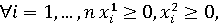 получаем:
получаем:  А условия
А условия

влекут
за собой соотношение:
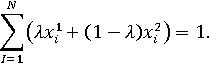
Следовательно,
 обладает свойствами
обладает свойствами

и
принадлежит Х. Таким образом, Х является выпуклым.
Непрерывность
функции , вогнутость по
, вогнутость по  и выпуклость по
и выпуклость по 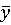 вытекает из ее
линейности.
вытекает из ее
линейности.
Таким
образом, матричная игра Г=(Х, Y, F) удовлетворяет всем условиям для
существования седловой точки. А значит, что матричная игра имеет седловую точку
в смешанных стратегиях, что и требовалось доказать.
Для
доказательства того, что применение смешанной стратегии дает одного игроку
реализовать преимущество, возникшее при данных правилах игры, над другим
игроком, будет рассмотрен пример. Этот пример доказывает также применение
матричных игр в военных действиях.
Пример
4. Сторона A посылает в район
расположения противника два бомбардировщика I
и II; I
летит спереди, II – сзади. Один
из бомбардировщиков, – заранее неизвестно какой, – должен нести бомбу, другой
выполняет функцию сопровождения. В районе противника бомбардировщики
подвергаются нападению истребителя стороны B.
Бомбардировщики вооружены пушками различной скорострельности. Если истребитель
атакует задний бомбардировщик II,
то по нему ведут огонь пушки только этого бомбардировщика; если же он атакует
передний бомбардировщик, то по нему ведут огонь пушки обоих бомбардировщиков.
Вероятность поражения истребителя в первом случает 0,3, во втором – 0,7.
Если
истребитель не сбит оборонительным огнем бомбардировщиков, то он поражает
выбранную им цель с вероятностью 0,6. Задача бомбардировщиков – донести бомбу
до цели; задача истребителя – воспрепятствовать этому, т.е. сбить
бомбардировщик-носитель. Требуется выбрать оптимальные стратегии сторон:
1.
для
стороны A: какой бомбардировщик
сделать носителем?
2.
для
стороны B: какой бомбардировщик
атаковать?
Решение.
Данная игра является случаем игры 2×2; выигрыш – вероятность не поражения
носителя.
Стратегии
стороны A:
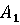 – носитель –
бомбардировщик I;
– носитель –
бомбардировщик I;
 – носитель –
бомбардировщик II.
– носитель –
бомбардировщик II.
Стратегии
стороны B:
 атакуется
бомбардировщик I;
атакуется
бомбардировщик I;
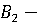 атакуется
бомбардировщик II.
атакуется
бомбардировщик II.
Для
составления матрицы игры, необходимо найти средний выигрыш при каждой
комбинации стратегии.
1.
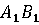 (носитель I,
атакуется I). Носитель не будет
поражен, если бомбардировщики собьют истребитель, или не собьют, но он не
поразит свою цель:
(носитель I,
атакуется I). Носитель не будет
поражен, если бомбардировщики собьют истребитель, или не собьют, но он не
поразит свою цель:
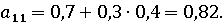
2.
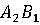 (носитель II,
атакуется I)
(носитель II,
атакуется I)
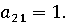
3.
 (носитель I,
атакуется II)
(носитель I,
атакуется II)
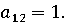
4.
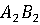 (носитель II,
атакуется II)
(носитель II,
атакуется II)

Матрица
игры имеет вид:
Нижняя
цена игры 0,82; верхняя цена равна 1. Матрица не имеет седловой точки, поэтому
решение находиться в смешанных стратегиях.
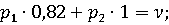
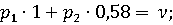

Отсюда
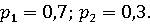
Оптимальная
стратегия игрока A имеет вид:
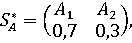
т.е.
в качестве носителя нужно чаще выбирать I,
чем II.
Цена
игры равна
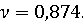
Зная
ν, можно определить 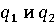 – частоты стратегий
– частоты стратегий  в оптимальной
стратегии противника
в оптимальной
стратегии противника 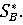 Тогда:
Тогда:
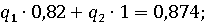

Откуда
 То есть оптимальная
стратегия игрока B имеет вид:
То есть оптимальная
стратегия игрока B имеет вид:
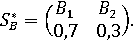
Таким
образом, рассмотренный пример игры 2×2 является упрощенным образчиком
игр, имеющих практическое значение. На данном примере можно убедиться в
различие матричных игр в смешанных стратегиях от матричных игр в чистых
стратегиях. Если игра не имеет седловой точки, то применение чистых стратегий
не дает оптимального решения, тогда приходиться чередовать чистые стратегии, а,
значит, применять смешанную стратегию.
ЗАКЛЮЧЕНИЕ
Матричные
игры – один из наиболее важных типов антагонистических игр. Матричная теория
изучена более подробно по сравнению с теорией антагонистических игр. Известны
различные алгоритмы поиска оптимальных стратегий игроков в матричной игре, они
в большинстве своём наглядны и просты в применении, выбор алгоритма зачастую
определяется размерностью матрицы.
Исследование
метода классификации матричных игр является очень важным вопросом, поскольку матричные
игры широко используются в системах принятия решений. Они могут служить математическими моделями многих простейших
конфликтных ситуаций из области экономики, математической статистики, военного
дела, биологии.
Прежде
чем решать игры вида 2×2, необходимо проверить, есть ли у данной игры
седловая точка. Если да, то игра имеет решение в чистых стратегиях. Если
седловой точки нет, то игру стоит решить с применением смешанных стратегий.
В
данной курсовой работе были представлены основные понятия теории игр, на
конкретных примерах из жизни было выявлено различие матричных игр в чистых и
смешанных стратегиях, представлена основная теорема матричных игр с
доказательством.
Математические модели простейших
конфликтных ситуаций.
Перечислить
примеры. Например матричные игры тоже. Далее по курсовой.
СПИСОК
ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1.
Вентцель
Е.С. Исследование операций. Задачи, принципы, методология. – М.: Высшая школа.
– 2007. – 208с.
2.
Деркач
Д.В. Матричные игры: задания и методические рекомендации по выполнению
самостоятельных расчетных работ: учебно-методическое пособие. - Армавир, 2010.
– 210 с.
3.
Луньков
А.Д. Теория игр. – Саратов: 2008. – 136 с.
4.
Лабскер
Л.Г., Ященко Н.А. Теория игр в экономике (практикум с решениями задач):
учебноепособие. – М.: КноРус, 2012. – 278 с.
5.
Моргенштерн
О., Нейман Дж. фон. Теория игр и экономическое поведение – М.: Книга по
Требованию, 2012. – 708 с.
6.
Невежин
В.П. Теория игр. Примеры и задачи: учебное пособие / В.П. Невежин. – М.: ФОРУМ:
ИНФРА-М, 2014. – 128 с. – (Высшее образование).
7.
Петросян
Л.А. Теория игр / Л.А. Петросян, Н.А. Зенкевич, Е.В. Шевкопляс. – 2-е издание,
перераб. и доп. – СПб.: БХВ-Петербург, 2012 – 432 с.: - (учебная литература для
вузов).
8.
Писарук
Н.Н. Введение в теорию игр — Минск: БГУ, 2015. – 256 с.
9.
Протасов
И.Д. Теория игр и исследование операций. Учебное пособие. – М.: Гелиос АРВ,
2006. – 368 с.
10.
Садовин
Н.С., Садовина Т.Н. Основы теории игр: учебное пособие. Мар. Гос. ун.т; –
Йошкар-Ола, 2011. – 119с.
11.
Самаров
К.Л. Элементы теории игр: учебно-методическое пособие. – М.: Резольвента, 2009.
– 21 с.
12.
Струченков
В.И. Методы оптимизации. Основы теории, задачи, обучающие компьютерные
программы: учебное пособие. – М.: Экзамен, 2005. – 256 с.