Исследование переходных характеристик типовых звеньев систем
Введение
Цель работы: экспериментальное исследование
взаимосвязей между параметрами типовых динамических звеньев и их
характеристиками. Приобретение навыков работы с типовыми звеньями систем.
Различные системы автоматического регулирования
при расчете обычно разбиваются на динамические звенья. Под динамическим звеном
понимают устройство любого физического вида и конструктивного оформления
(механические, электрические и т.д.), описываемое определенным дифференциальным
уравнением. В соответствии с этим классификация звеньев проводится именно по
виду дифференциального уравнения.
1. Исследование позиционных звеньев
Была получена переходная
характеристика 
пропорционально
звена (рисунок 1). Характеристика была исследована в программе Simulink.
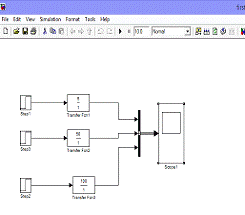
Рисунок 1 - Переходная
характеристика пропорционального звена
Было исследование влияние изменения
коэффициента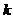 
(рисунок 2)
и влияние изменения постоянной времени 
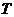(рисунок 3) на вид переходного
процесса апериодического звена первого порядка.
Рисунок 2 - Влияние изменения коэффициента
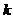на вид
переходного процесса апериодического звена первого порядка
динамический
звено демпфирование
Рисунок 3 - Влияние изменения
постоянной времени 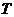на вид
переходного процесса апериодического звена первого порядка
Апериодическим называется такое
звено, у которого выходная величина после подачи на вход ступенчатого
воздействия изменяется монотонно, достигая некоторого установившегося значения.
. Исследование системы второго
порядка
На Simulink были
получены переходные характеристики системы второго порядка (рисунок 4), такие
как:
¾ Апериодическое звено второго
порядка;
¾ Консервативное звено.
Рисунок 4 - Переходные характеристики системы
второго порядка: апериодического звена второго порядка, колебательного звена,
консервативного звена
Была найдена зависимость Изменения
характеристик системы воторого порядка от постоянных времени 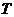(рисунок 5)
и коэффициента усиления 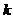(рисунок 6).
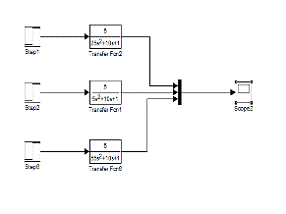
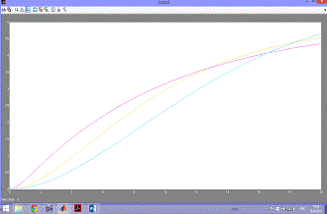
Рисунок 5 - Зависимость изменения
характеристик системы второго порядка от постоянных времени
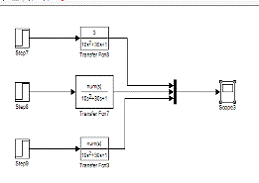
Рисунок 6 - Зависимость изменения
характеристик системы второго порядка от коэффициента усиления
Был построен график зависимости
числа колебаний переходного процесса от коэффициента демпфирования 
0, 0.1,
0.5, 1, 1.5, 2 при постоянных значениях постоянных времени 
и
коэффициента усиления 
(рисунок 7).
Были исследованы переходные характеристики
системы )(sG со звеном интегрирования (рисунок 8), дифференцирования (рисунок
9) и запаздывания (рисунок 10).
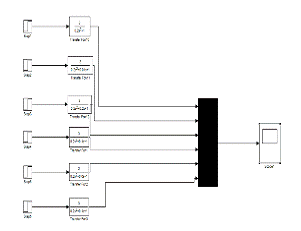
Рисунок 7 - График зависимости числа
колебаний переходного процесса от коэффициента демпфирования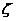 
, при
постоянных значениях постоянных времени 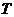и коэффициента усиления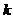
Рисунок 8 - Результат моделирования
системы со звеном интегрирования
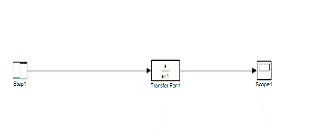
Рисунок 9 - Результат моделирования
системы со звеном дифференцирования
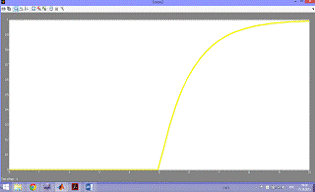
Рисунок 10 - Результат моделирования системы со
звеном запаздывания
Заключение
Лабораторной работе были изучены
типовые динамические звенья, приведены примеры динамических звеньев, их
передаточные функции и временные характеристики. Определены параметры звеньев
первого порядка. Изучено влияние изменения постоянной времени 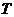и
коэффициента 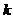на
переходные характеристики звеньев второго порядка. Изучено влияние коэффициента
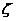демпфирования на характер
переходного процесса и влияние звена интегрирования, дифференцирования и
запаздывания на другие звенья.