Вычислительный процесс и вычислительные алгоритмы

вычислительный процесс и вычислительные алгоритмы

Содержание

Вычислительный алгоритм

Эффективность алгоритмов и оценка их вычислительной сложности

Модель вычислительного процесса

Классификация алгоритмов по вычислительной сложности

Стратегия дублирования (расщепления). Принцип «разделяй и властвуй».

Общие свойства базовых алгоритмов цифровой обработки сигналов

Примеры

Литература

Вычислительный алгоритм

Процесс построения вычислительного алгоритма цифровой обработки сигналов во многом определяется численным методом, под которым понимается такая интерпретация математической модели, которая доступна для реализации на заданных средствах обработки (ЭВМ, цифровые сигнальные процессоры, контроллеры). При переходе от математической модели к численному методу возникают погрешности, называемые погрешностью метода, связанные с точностью приближения. Выделяют погрешность дискретизации и погрешность округления.

Обычно построение численного метода разбивают на два этапа: формулировку дискретной задачи и разработка вычислительного алгоритма, позволяющего отыскать решение дискретной задачи. В этом случае говорят, что произошла дискретизация исходной математической задачи. Например, замена системы дифференциальных уравнений разностными алгебраическими уравнениями. Ясно, что решение дискретной задачи отличается от исходной задачи. Разность соответствующих решений и называется погрешностью дискретизации.

Входные данные при цифровой обработки часто задаются не точно, а с округлением. В результате решение будет отличаться от решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления. Величина этой погрешности определяется двумя факторами: точность. Представления вещественных (комплексных) чисел и чувствительностью данного алгоритма к погрешностям округления.

Требования к вычислительным методам. Можно выделить две группы требований к численным методам. Первая группа связана с адекватностью дискретной модели исходной математической задаче, вторая группа - с реализуемостью численного метода на средствах цифровой обработки. Основным препятствием для реализации корректно поставленного алгоритма является ограниченный объем вычислительной памяти, ограниченные ресурсы времени счета. Реальные вычислительные алгоритмы должны учитывать эти обстоятельства, т.е. они должны быть экономичными как по числу арифметических действий, так и по требуемому объему памяти.

Эффективность алгоритмов и оценка их вычислительной сложности

Вопросы сложности алгоритмов и устройств являются основополагающими в цифровой обработки сигналов. Понятие сложности имеет сложную историю развития. Понятие сложности алгоритма также допускает различные трактовки. Могут учитываться или не учитываться таки факторы, как размер машинного слова, емкость памяти, различие в длительности выполняемых команд и т.д.

Известен ряд моделей вычислительного процесса, позволяющих раскрыть сложность отдельных задач и сравнить различные алгоритмы.

Модель вычислительного процесса

алгоритм вычислительный цифровой сигнал

Неветвящаяся программа (НП). Представляет собой программу без циклов, в которой цикл заменяется копированием повторяющейся команды соответствующее число раз. Число шагов такой программы как функции времени от размера входа N называется вычислительной сложностью, а число переменных, участвующих в вычислениях - емкостной сложностью

Определение. Пусть заданы:

1)      набор входных переменных

2)      поле F (или кольцо K);

3)      множество базисных операций

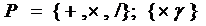
где 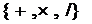 - бинарные арифметические операции,

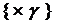 - унарная операция умножения на элемент поля (кольца).

Неветвящаяся программа представляет собой последовательность строк (команд), l-я из которых имеет вид

где

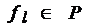
Определение

1)           для любой базисной операции из множества P фиксируется число l( f ), называемое сложностью этой операции;

2)      Сложностью НП называется сумма всех l( f ) по всем строкам этой программы;

)        Пусть l( f ) = 1, "f Î P . Тогда соответствующая сложность равна числу всех операций НП и называется тотальной ( Ct );

)        Пусть l( + ) = 1, а для всех остальных l( f ) = 0. Соответствующая сложность называется аддитивной ( Ca );

)        Пусть l( ´ ) = l( / ) = 1, а остальные операции не учитываются. Сложность такого рода называется мультипликативной ( Cm ).

Примеры

1)            тотальная сложность используется при анализе матричных процессов, в которых все операции оцениваются одинаково;

)              аддитивная сложность является хорошим критерием при обработке бинарных или троичных данных, элементы которых представляются в алфавитах {0,1}, {1,-1}, {1,0,-1}.

3)      Мультипликативная сложность используется , когда операция умножения существенно медленнее (дороже) операции сложения.

Определение

Качество (эффективность) алгоритма оценивается асимптотической сложностью, т.е. порядком роста сложности как функции от числа входов N при неограниченном росте N без учета мультипликативных констант.

Например, если N входных переменных обрабатываются за время cN 2 , где c - некоторая постоянная, то асимптотическая сложность этого алгоритма есть O(N 2), говорят «порядка N 2».

Классификация алгоритмов по вычислительной сложности

В зависимости от порядка сложности и вида результирующих данных алгоритмы обработки можно отнести к четырем уровням.

1)        к первому уровню относятся базовые арифметические операции. Считается, что их сложность O(1), хотя они отличаются по сложности битовых операций. Например, умножение двух m - разрядных чисел с фиксированной точкой требует O(m 2) битовых операций, а сложение - O(m);

2)      ко второму уровню относятся скалярные алгоритмы с вычислительной сложностью O(N). Этот уровень включает в себя вычисление скалярного произведения N - компонентных векторов, вычисление значения полинома по схеме Горнера, фильтрацию с БИХ (в частности численное интегрирование и дифференцирование);

)        К третьему уровню относятся векторные алгоритмы сложности O(N 2). Сюда включаются умножение матрицы на вектор для вычисления линейных преобразований (Фурье, Ганкеля-Теплица и др ), вычисление свертки векторов (полиномов) (их спектров и корреляций), фильтрация с КИХ и т.д. Некоторые из этих алгоритмов ( для случая специальных матриц) можно улучшить до оценки O(N log N ).Примером является быстрое преобразование Фурье (БПФ).

)        Алгоритмы сложности O(N 3) составляют четвертый уровень. Это - матричное произведение, вычисление собственных значений и векторов, прямые методы решения систем уравнений, сингулярное разложение и обращение матрицы, факторизация матрицы, метод наименьших квадратов, решение задач математического программирования, нахождение путей в графе, фильтрация по Калману и т.д.

Стратегия дублирования (расщепления). Принцип «разделяй и властвуй»

Выберем объем задачи N в качестве параметра и разобъем задачу на две подзадачи объема (N / 2) той же самой структуры, что и исходная задача. Если решение этих подзадач можно скомбинировать в решение исходной задачи, то получается эффективный алгоритм.

Стратегия дублирования может применяться при любом N, так как любое N можно увеличить до ближайшего двоично - рационального значения ( например, добавлением нулевых координат во входной вектор данных).

Общие свойства базовых алгоритмов цифровой обработки сигналов

Задача цифровой обработки сигналов заключается в определении некоторых параметров сигналов на основе анализа последовательности значений (отсчетов) x[nT], где n = 0,1,…, N - 1; T - интервал дискретизации сигнала, при n < 0, x = 0 . В большинстве радиотехнических применений исследуемый сигнал генерируется или отражается от какого-либо объекта (цели). Направление, с которого приходит этот сигнал, определяет местоположение объекта. Задержка между посылкой сигнала и приемом отраженного сигнала позволяет судить о расстоянии до объекта, а изменение частоты - о скорости его движения. Иногда, чтобы получить нужную информацию, необходимо сравнить параметры сигнала с заданными или вычисленными в процессе обработки величинами (порогами). Большинство параметров сигнала определяется с помощью выделения из него составляющих с заданными характеристиками. Этот процесс называется фильтрацией.

Существует три основных класса алгоритмов фильтрации :

1.     Свертка.

2.      Рекурсия.

.        Преобразование Фурье.

Эти алгоритмы называются базовыми алгоритмами обработки сигналов. Во всех базовых алгоритмах обработки сигналов основными арифметическими операциями являются умножение и сложение чисел. При этом в большинстве алгоритмов эти операции являются составляющими в скалярном умножении векторов вида

.

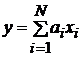Такую операцию иногда называют базовой микрооперацией.

Существует много разных способов реализации базовой микрооперации. Разные способы соответствуют разным схемам распределения вычислений во времени и в пространстве.

Базовые алгоритмы обработки сигналов относятся к типу алгоритмов с интенсивным вычислительным процессом. Это означает, что они характеризуются высоким отношением числа вычислительных операций к числу операций ввода - вывода.

Пример. Умножение матрицы на вектор. Пусть A - матрица m ´ n , а x - вектор длины n. Тогда

,

где aj - j - я строка матрица A, а 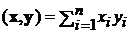- скалярное произведение векторов.

Таким образом, процесс умножения матрицы на вектор сводится к вычислению m скалярных произведений.

Пример. Сложение целых чисел. Пусть неотрицательные целые числа a и b заданы в системе счисления с основанием B:

= (an - 1 , an - 2, …, a0 )B = an - 1 B n - 1 + an - 2 B n - 2 +… + a1 B 1 + a0 ,= (bn - 1 , bn - 2, …, b0 )B = bn - 1 B n - 1 + bn - 2 B n - 2 +… + b1 B 1 + b0 ,

где 0 £ ai , bi < B. Для удобства считаем, что оба числа имеют равную длину, при необходимости старшие разряды меньшего числа заполняем нулями.

Алгоритм. Сложение целых чисел.

Вход. Целые числа a = (an - 1 , an - 2, …, a0 )B , b = (bn - 1 , bn - 2, …, b0 )B .

Выход. Сумма с = a + b = (cn , cn - 1, …, c0 )B .

2.      Для i = 0, 1, …, n - 1 выполнить следующие действия.

2.1.                      Вычислить t ¬ ai + bi + s.

2.2.   Положить,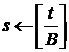

3.     Положить cn ¬ s.

4.      Результат: с = (cn , cn - 1, …, c0 )B.

Переменная s означает перенос в старший разряд. Сложность алгоритма равна O(n).

Пример. Умножение целых чисел.

Алгоритм. Умножение целых чисел «в столбик».

Вход. Целые числа a = (an - 1 , an - 2, …, a0 )B , b = (bn - 1 , bn - 2, …, b0 )B , 0<b£a.

Выход. Произведение c = a b = (c2n - 1 , c2n - 2, …, c0 )B.

1.     Для i = 0,1,…, n - 1 положить ci ¬ 0.

2.      Для i = 0,1,…, n - 1 выполнить следующие действия.

2.1.             Для j = 0,1,…, n - 1:

2.1.1.                Положить s ¬ 0.

2.1.2. Вычислить t ¬ ci+j + aibj + s, ci+j ¬ t(modB), /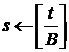

2.2.             Положить ci+n ¬ s.

3.     Результат: с = (cn , cn - 1, …, c0 )B.

Во внешнем цикле этого алгоритма вычисляются частичные произведения

 (bn - 1 , bn - 2, …, b0 )B,

а во внутреннем - произведения aibj.

Сложность алгоритма равна O(n2 ).

Пример. Вычисление наибольшего общего делителя. Для вычисления наибольшего общего делителя (НОД) применяется способ повторного деления с остатком, называемый алгоритмом Евклида

Алгоритм. Вычисление НОД по алгоритму Евклида.

Вход. Целые числа a, b; 0< b £ a.

Выход. Число d = НОД(a, b).

1.     Положить r0 ¬ a, ri¬ b, i¬ 1.

2.      Найти остаток ri+1 от деления ri-1 на ri.

.        Если ri+1 = 0б то положить d ¬ ri . В противном случае положить i¬i+1 и вернуться на шаг 2.

.        Результат: d.

Сложность алгоритма Евклида равна O(log2a).

Пример. Умножение в классах вычетов. Алгоритм, предложенный А. Шенхаге, использует китайскую теорему об остатках.

Теорема. Если целые числа m0, m1, …, mk-1 попарно взаимно просты, то каждому целому числу a, 0 £ a < M, где M = m0 m1 … mk-1 , единственным образом можно сопоставить набор элементов a0, a1, …, ak-1 классов вычетов по модулям mi , где ai º a (mod mi), 0 £ i < k .

Сумме, разности и произведению чисел по модулю M соответствуют суммы, разности и произведения по модулям mi.

Если a = (a0, a1, …, ak-1), b = (b0, b1, …, bk-1), то+ b ( mod M) = (c0, c1, …, ck-1);- b ( mod M) = (d0, d1, …, dk-1);b ( mod M) = (e0, e1, …, ek-1);

где

= ai + bi (mod mi);= ai - bi (mod mi);= ai bi (mod mi); = 0, 1, …, k - 1.

Наиболее трудоемкой операцией при вычислениях в классах вычетов является представление числа в классах вычетов и обратное восстановление по китайской теореме об остатках.

Асимпотическая сложность алгоритма умножения чисел в классах вычетов равна O(k logk). Практически данный метод умножения эффективнее, чем умножение «в столбик», лишь тогда, когда длина сомножителей превышает разрядность процессора в десятки раз.

Заметим, что наиболее быстрый алгоритм умножения использует быстрое преобразование Фурье.

Литература

1.              Лосев В.В. Микропроцессорные устройства обработки информации. Алгоритмы цифровой обработки: Учеб. пособие для вузов. - Мн.: Выш. шк., 1990.- 132 с.

2.      Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов.- М.: Мир, 1979.

.        Самсонов Б.Б., Плохов Е.М., Филоненко А.И. Компьютерная математика (основание информатики).- Ростов на Дону: «Феникс», 2002. - 512 с.